Encoding and Decoding Cortical Representations of Tactile Features in the Vibrissa System

Abstract

During behavior, rats and other rodents use their facial vibrissae to actively explore surfaces through whisking and head/body movement, resulting in complex sensory inputs that vary over a large range of angular velocities and temporal scales. How these complex sensory inputs manifest in the patterns of cortical firing events that ultimately form the perceptual experience is not well understood. Through single-unit cortical recordings of layer 4 neurons in S1 of the anesthetized rat, we systematically quantified the interactions between instantaneous velocity and timing of vibrissa motion, finding a strong interaction between angular velocity and timing of contacts on the tens of milliseconds time scale. From the quantification of these joint tuning properties, a detailed nonlinear encoding model was formulated that was highly predictive of firing probability and timing characteristics of the sparse cortical representation of complex patterned tactile inputs. Within a Bayesian framework, the encoding model was then used to decode tactile patterns under simple transformations of the stimulus along dimensions of velocity and timing, as a demonstration of the lower bound of the idealized perceptual capabilities of the animal.

Introduction

In the rodent vibrissa system, an array of facial vibrissae (whiskers) is endowed with acute tactile sensing mechanisms that serve as an important sensory modality in locomotion, balance, texture sensation, and wall following (Vincent, 1912). The mechanical signals transduced by mechanoreceptors embedded in the soft tissue surrounding the vibrissa follicles are strongly shaped by the geometry of vibrissa–surface contact, the mechanics of the vibrissa and the follicle complex, and the kinematics of body motion and whisking. Recent behavioral studies have demonstrated that in ethologically relevant conditions in which the animals were actively moving their vibrissae across textures, the vibrissae undergo patterns of discrete high-velocity transients (Ritt et al., 2008; Wolfe et al., 2008), where the velocity and timing of the transients depend on the textural properties and the precise nature of the behavior. Only recently are the effects of variations in vibrissa input on cortical representations being explored in the context of the textural environment (von Heimendahl et al., 2007; Jadhav et al., 2009).

Studies of cortical activity in response to electrically induced whisking across textured surfaces in anesthetized rats have revealed temporally precise, stimulus-locked spiking activity, described as a “kinetic signature” of neural activity defined by the temporal pattern of vibrissa deflections (Arabzadeh et al., 2005, 2006). In acute studies, the mean firing rate of neurons in the vibrissa region of the primary somatosensory cortex has been shown to depend strongly upon the velocity of isolated, punctate vibrissa deflections (Simons, 1978; Ito, 1985; Pinto et al., 2000). Impinging suppressive influences on thalamocortical neurons further complicate this selectivity by inducing a highly nonlinear dependence of single-cell responses on stimulus history for more complex stimuli, likely linked to the interplay between excitatory and inhibitory elements of the neural circuitry (Simons and Carvell, 1989; Kyriazi et al., 1994; Nicolelis and Fanselow, 2002; Webber and Stanley, 2004; Boloori and Stanley, 2006; Higley and Contreras, 2006, 2007; Heiss et al., 2008). The functional consequence of the interaction between velocity sensitivity and nonlinear dynamics of the excitatory/inhibitory interplay has not been investigated, yet is a key to understanding the dynamics of encoding in complex, natural environments.

Here, in the vibrissa system we explore the cortical representation along two primary dimensions: the moment-by-moment angular velocity and the timing of transient events within the stimulus pattern. Through single-unit extracellular cortical recordings in the anesthetized rat, the effects of angular velocity on cortical firing probability and timing were systematically quantified using simplified stimuli, and the tuning properties were used to formulate a nonlinear encoding model that was highly predictive of cortical firing activity in response to the more complex tactile patterns, capturing the spike count, latency, and precision of firing in localized firing events. The encoding model was then used for decoding in a Bayesian framework, showing through systematic transformation of the stimulus patterns along dimensions of velocity and timing that the encoding model captures a range of dynamic properties of the pathway.

Materials and Methods

Surgical preparation

For all acute experiments, all procedures were approved by the Animal Care and Use Committee at Harvard University, and are in agreement with guidelines established by the National Institutes of Health. See Webber and Stanley (2004) for a detailed description of experimental methods. Briefly, female albino rats (Sprague Dawley; 250–330 g) were sedated with 2% vaporized isoflurane, and anesthetized with sodium pentobarbital (50 mg/kg i.p., initial dose); supplemental doses of ∼12 mg/kg/h (Zhu and Connors, 1999) were given as needed to maintain a light level of anesthesia—confirmed by measurements of heart rate, respiration, and eyelid/pedal reflexes to averse stimuli (toe or tail pinch). Following initial anesthesia, the animal was mounted on a stereotaxic device (Kopf Instruments) in preparation for surgery and subsequent recordings. After the initial midline incision on the head, tissue and skin were resected and connective tissue was removed. A small craniotomy (∼2 mm in diameter) was made over the barrel field [stereotaxic coordinates: 1.0–4.0 mm caudal to the bregma, and 3.0–7.0 mm lateral to the midline (Paxinos and Watson, 1998)]. The dura layer was left intact for recordings with single tungsten microelectrodes. For recordings made by tetrodes (see below), the dura layer was carefully reflected. In all cases a dam was created with bone wax around the craniotomy and the cortex was covered with mineral oil solution to stabilize the recording and to provide additional protection for the cortical surface. Following the recording session, the animal was killed with an overdose of sodium pentobarbital solution (0.5 ml of Euthasol, Henry Schein).

Electrophysiology

Single-unit extracellular recordings were obtained using both single tungsten microelectrodes (impedance range: 3–7 MΩ; FHC), and tetrodes (impedance range: 1–2 MΩ; Acute Probe Model: a 2 × 2-tet, NeuroNexus Technologies). Data were collected using a 16-channel Plexon data-acquisition system (Plexon). Neuronal signals were filtered, amplified, and digitized at 40 kHz/channel. Both the tetrode and single-electrode recordings were analyzed using the OfflineSorter software suite (Plexon) to assign the recorded spike waveforms to single units on the basis of standard template matching techniques and physiologically plausible refractory periods (Lewicki, 1998).

All recorded cells were located at stereotaxic depths of 800–1200 μm, commensurate with cortical layers IV–V. For all recorded neurons, spontaneous activity was collected before the beginning of the stimulus trials, and again after all stimuli were presented. Cortical receptive fields were determined manually by identifying all vibrissae that elicited spiking responses for each recorded cell. The primary vibrissa (PV) was identified as the whisker generating maximal responses.

Only cells classifiable as regular-spike units (RSUs) were reported in this study (n = 44 cells). Based on latency analyses (PV: 9.5 ± 0.6 ms), all included cells were determined to reside in monosynaptic thalamocortical recipient zones. The additional criteria for their classification as SI RSUs were as follows: (1) stability of baseline responses to PV deflections over the duration of the experiment, used to ensure consistency over the long (∼3 h) recording interval; (2) width of action potentials (typically 1.5 ms) (McCormick et al., 1985), used to exclude putative inhibitory units (i.e., the fast spiking units, FSUs); (3) extracellular responses to at most 1–2 adjacent vibrissae (Simons and Carvell, 1989; Brumberg et al., 1996), to ensure that the neuron did not reside in the septal regions; and (4) shifts in response latency during periodic stimulation by up to a factor of 3, again implying that they likely do not reside in the septa (Ahissar et al., 2000, 2001). For the large set of neurons (n = 44), a full velocity tuning protocol was completed. For a smaller subset (n = 19), in addition to the velocity tuning with punctate stimuli, the influence of angular velocity on pairwise interactions of vibrissa deflections was measured. Finally, for a smaller subset of neurons (n = 15), we were able to measure both the velocity tuning and velocity-dependent pairwise interactions described above, as well as the response to patterns of vibrissa deflections and their corresponding transformations (recording duration ∼2.5 h, see below). All data were analyzed using Matlab (MathWorks) and C programming languages.

Vibrissa stimulation

A multilayered piezo-electric bending actuator (range of motion: 1 mm, bandwidth: 200 Hz; Polytec PI) generated the vibrissa deflections used to drive SI neurons. The actuator was placed 10 mm from the face, and the vibrissa was inserted into a 4 cm section of a 20 μl glass pipette that was fixed to the end of the actuator (∼0.57° per 100 μm deflection). Input to the actuators was generated through a custom-made GUI program written in Visual C++ 6.0.

In designing the command input to the actuators, we accounted for the free-vibration dynamics of the piezo-electric bender to minimize the bender's extraneous vibrations (i.e., “ringing”). The free-vibration dynamics of the piezo bender were estimated through white-noise analysis (see Marmarelis and Marmarelis, 1978), i.e., by presenting a white-noise input to the piezo, and recording the resulting vibrations with a photo-diode circuit [similar to those described by Andermann et al. (2004) and Arabzadeh et al. (2005)]. Briefly, as the tip of the actuator interrupts the path of the infrared beam generated by a slotted infrared switch (QVA11134, Fairchild Semiconductor), the output voltage of the optical switch varies in direct proportion to the tip displacement. This change in voltage was subsequently transformed to the corresponding change in actuator displacement using the inverse of the empirically determined relationship between small changes in beam occlusion (measured in terms of the displacement of the actuator tip), and the output voltage. The punctate pulse deflections consisted of exponential rising and falling phases, whose onset slopes (ω) corresponded to the desired velocity transient. These pulses were ∼10 ms in duration in all cases. Patterns consisted of punctate deflections in the rostral or caudal directions, with variable angular speed.

As shown in Figure 4 and used in Figures 5–7, stimulus deflection patterns were created from a range of angular velocities observed using high-speed videography of rats whose vibrissae were in contact with textured surfaces (36 grit sandpaper, see below).

Figure 4.

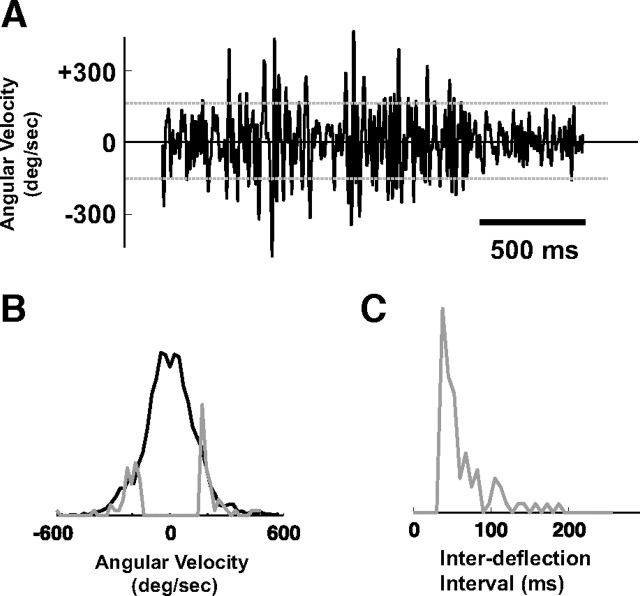
Design of stimulus deflection sequence from behavioral observations. A, Instantaneous velocity of a single vibrissa in contact with a coarse texture (36 grit sandpaper), as measured through high-speed videography (Jenks et al., 2010)—see Materials and Methods. The horizontal dashed gray lines represent a threshold imposed at ±160°/s, to restrict transient stimulus events to a velocity range within which the cortical neurons tend to be sensitive. B, The full distribution of instantaneous angular velocities (black). The gray curve represents the distribution excluding transient deflections below the threshold in A, and excluding those with interdeflection intervals less than 40 ms. Both distributions have unit area, but have been scaled for comparison of tails. C, Histogram of the observed interdeflection intervals, excluding those below 40 ms.

Figure 5.

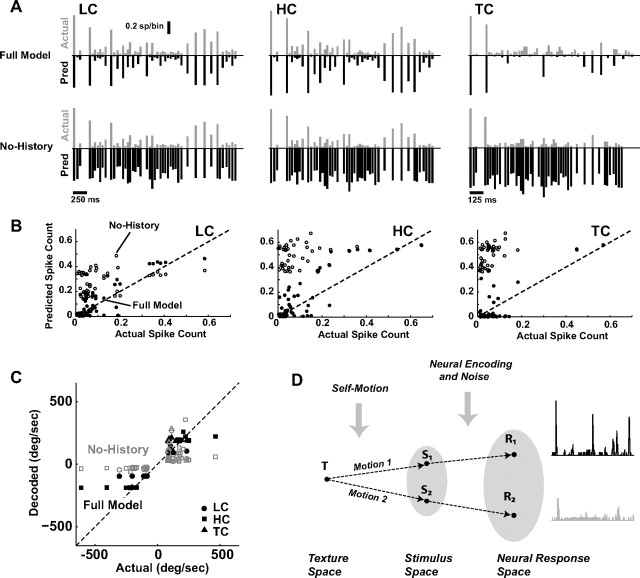
Model prediction of cortical activity. A, The top shows the sequence of vibrissa deflections, where the magnitude reflects the angular speed and the direction of the arrow reflects the direction in the rostral–caudal plane. Below is the measured PSTH in response to this stimulus sequence (black; averaged over n = 6 cells with similar time course of CTR; binned at 2 ms), along with the corresponding predicted (inverted scale) firing rates, for the Full Model (top), the model without taking into account velocity tuning (No-Velocity), and the model without taking into account history dependence (No-History). Localized Gaussian templates of the PSTH events were used for the plotting of the predicted response events, with the appropriate spike count, latency, and jitter as predicted by the encoding model. B, A comparison of the event-by-event spike count of the measured data (black) and the Full Model prediction (gray). The error bars for measured spike counts were not included for clarity, but show that all predictions are within the confidence band of the measurements. C, Model performance across the larger sample of cells (n = 15). The top plot shows the correlation coefficients between various model predictions and the measured responses (binned at 30 ms) for the Full Model, for the case in which velocity dependence is neglected (No-Velocity), and for the case in which history dependence is neglected (No-History). The bottom plot shows the magnitude of the MSE relative to the size of the neural response for the same model conditions as the top plots. All error bars represent the SEM (* indicates statistical significance at the level of p < 0.05).

Figure 6.

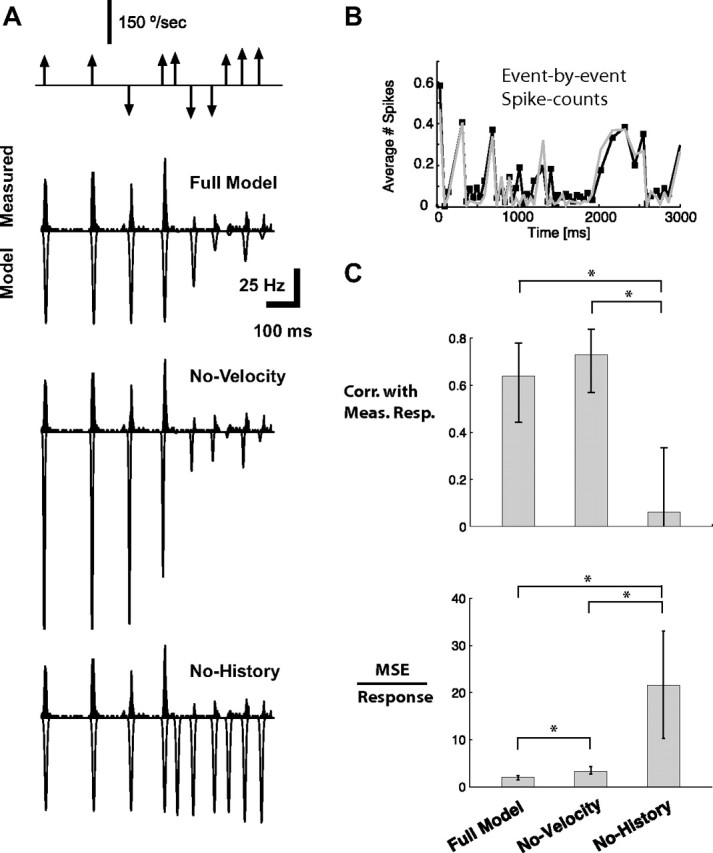
Bayesian decoding of tactile patterns. A, Average PSTH (gray, 2 ms bin size, n = 6 cortical neurons) and corresponding running estimate of local spike-count in a 30 ms bin (black). B, Response events were detected based on optimal Neyman–Pearson criterion (see Materials and Methods). Detected events are highlighted with gray bars. C, Shown is the corresponding sequence of deflections of varying angular velocity and timing. Stimulus events are parsed into those that correspond to detectable events in the cortical activity (gray) and those that result in an undetectable level of cortical activity (black), which are thus not predictable in the decoding process. D, Actual stimulus events that were detectable from the cortical response (gray), along with the corresponding decoded velocities (black) when only velocity tuning, and not history dependence, is taken into account (No-History). E, Actual stimulus events that were detectable from the cortical response (gray), along with the corresponding decoded velocities (black) for the Full Model. F, Actual versus predicted stimulus event velocities for the No-History (gray) and the Full Model (black). Dashed line is unity line.

Figure 7.

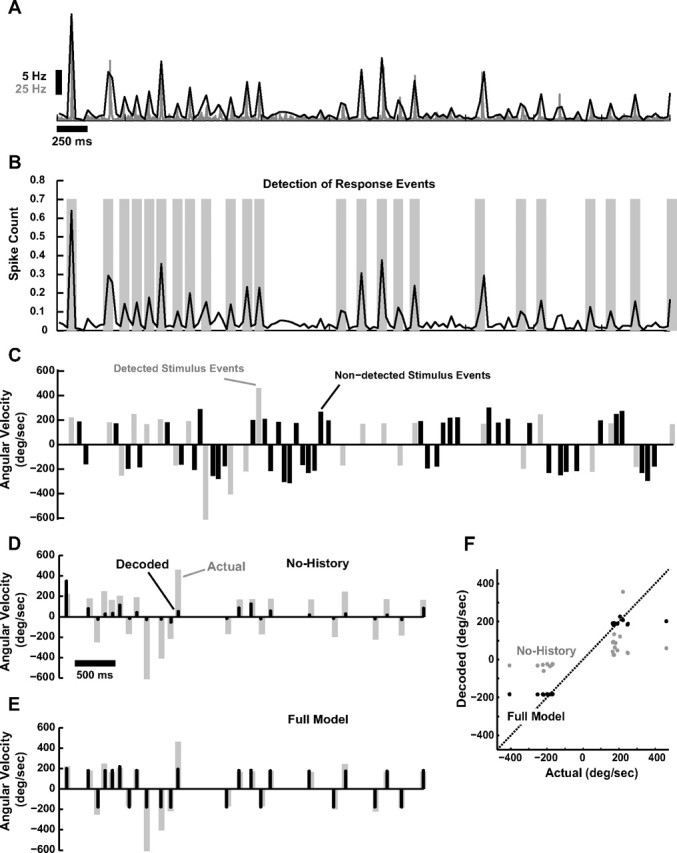
Cortical responses to simple transformations of tactile stimulus patterns. A, Deflection pattern inspired from naturalistic deflections (LC), along with the associated PSTH response of a single cortical cell over a 650 ms interval taken from the middle of a longer 6 s segment. All PSTHs in this figure share the same vertical scale. B, An HC version of the stimulus was created by scaling the LC sequence by a factor of 4. The HC response (gray) for the same cortical neuron is shown, along with the LC response for comparison (black, inverted scale). C, The TC stimulus was created by compressing the time axis of the LC sequence by a factor of 3, without altering the instantaneous velocities. The cortical response to the TC stimulus is shown (gray), along with the LC response (black, inverted scale) for comparison. Note the different timescale of the two traces.

High-speed videography of vibrissa motion

In an isolated set of noninvasive behavioral experiments in a previously published study (Jenks et al., 2010), adult female rats (Long–Evans; 250 g; Charles River Laboratories) were trained to run back and forth on a linear track. Briefly, we trimmed rows A, B, and E of the vibrissa array to facilitate imaging. Tactile stimuli were either oriented spatial grating, with periodic spacing of 4.19 mm, or standard sandpaper (36 grit) surfaces, that were placed on either side of the track. Video was acquired using a high-speed CMOS camera (Phantom v5, Vision Research), at 2000 frames per second and with a spatial resolution of between 700 × 400 and 950 × 512 pixels per frame, with a spatial resolution of between 5 and 8.35 pixels per mm. Tracking of head and vibrissa movements was implemented by modifying a software package provided by Knutsen, Derdikman, and Ahissar (Knutsen et al., 2005). The software uses code written in MatLab (v6.5, MathWorks) and the C programming language. Vibrissae were tracked in the head frame of reference using a three-point spline-fitting algorithm [see Knutsen et al. (2005) for details]. The angular deflection of a vibrissa close to its base was estimated by calculating the angle of a straight line segment between the extreme points of a short (3 mm long) spline fitted to a segment of the vibrissa close to its base (within 2 mm of the mystacial pad).

Response measures

Peristimulus time histograms (PSTHs) of single-cell responses to each stimulus type were generated using 60 repetitions of the stimulus and a time resolution of 2 ms. Spike count was computed as the average number of spikes within the 3–30 ms poststimulus interval, since RSUs have phasic responses to vibrissa deflections with latencies not exceeding 20–30 ms. In addition to spike count, the timing of single-cell responses was studied with two measures: (1) latency, defined as the average time delay between the stimulus and evoked spikes, and (2) jitter (Butts et al., 2007), quantifying the temporal precision of the transient responses to punctate deflections. Latency was computed as the center of mass of the single-cell PSTH response in the 3–30 ms poststimulus time window. Jitter was defined as the SD of the time to spike by the neuron over the 3–30 ms poststimulus time window.

The response to a stimulus pair illustrates the simplest type of response interaction. In this case, the response to the second deflection (termed the test) is attenuated as a function of the temporal separation between the test deflection and the preceding conditioning deflection. Earlier findings have described the suppressive effect of response integration in the SI cortex, where a single stimulus induces attenuation of the response to a second deflection over relatively long timescales (10–200 ms) (Simons, 1985; Simons and Carvell, 1989; Brumberg et al., 1996; Kleinfeld and Delaney, 1996; Mirabella et al., 2001). The observed cortical dynamics have been attributed to several mechanisms, including intracortical inhibition, depression of the thalamocortical synapse (Chung et al., 2002), and inhibitory feedback between the thalamic reticular nucleus (nRT) and the ventroposterior medial nucleus (VPM) (Desîlets-Roy et al., 2002). The conditioning–test ratio (CTR) curve (see Fig. 2C) was used to quantify the attenuation of the test spike count relative to its unattenuated (baseline) value. Previous studies (Simons and Carvell, 1989; Fanselow and Nicolelis, 1999; Webber and Stanley, 2004) have shown that the variation of the CTR curve with the interdeflection interval u is approximately sigmoidal. We therefore used the following parameterization to fit all measured CTR curves: f(u) = (1/2)A[1 + tanh((u − t₅₀)/τ)], where parameters {A, t₅₀, τ} were estimated through nonlinear least-squares fits.

Figure 2.

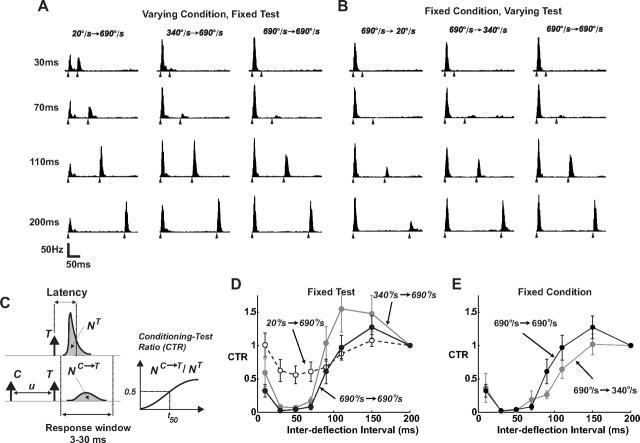
Responses of SI neurons systematically vary with stimulus history. A, Average PSTHs for paired-pulse deflection stimuli (n =19 neurons; bin size of 2 ms). The velocity of the second (test) stimulus was held constant, and the angular velocity of the first (conditioning) stimulus was varied, over a range of IDIs. The IDI for each case is noted on the left, and the filled triangles under each PSTH indicate the times of the paired deflections. B, Average PSTHs when the velocity of the first (conditioning) stimulus was held constant, and the angular velocity of the second (test) stimulus was varied. The same conventions are used as in A. C, The CTR was computed for a range of IDIs by computing the spike count response to the test (T) stimulus in presence of a preceding conditioning (C) deflection (N^C→T), and normalizing this quantity by the response measured when T is presented in isolation (N^T). Spike count is computed as the area under the measured PSTHs over the 3–30 ms poststimulus time window. D, Dependence of poststimulus suppression on the velocity of the conditioning stimulus, showing the average CTR curves obtained for a fixed test stimulus of 690°/s, and three different conditioning stimuli (20°/s: dashed, 340°/s: gray, and 690°/s: black). Error bars represent ±1 SEM, where averaging was over the sample of n = 19 cells, a subset of the total for the velocity tuning measurements in Figure 1. E, Dependence of poststimulus suppression on the velocity of the test stimulus, showing the average CTR curves obtained for a fixed conditioning stimulus of 690°/s, and test stimuli (340°/s: gray, and 690°/s: black). Note that the test stimulus of 20°/s produced a significant amount of variability in the response from neuron to neuron, precluding an accurate characterization of the CTR for this test velocity.

Velocity tuning curves

For each recorded cell, the dependence of spike count on instantaneous stimulus velocity was determined by measuring the mean number of spikes in the 3–30 ms window following vibrissa deflections of specified velocities. We averaged the resulting tuning curves for all recorded cells to obtain an averaged spike count tuning curve (see Fig. 1D). We developed an analytical form to describe how spike count varies with deflection velocity. Several functional forms of the relationship were explored, including exponential, but a power law was determined to best capture the behavior. The spike count is zero below the threshold of ±20°/s. At higher velocities, the spike count increases with increasing velocities but the rate of increase gradually decreases:

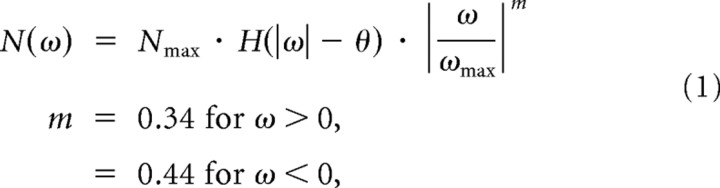where H(·) is the Heaviside step function, θ = 20°/s is the velocity threshold, ω_max = 850°/s, and N_max is the maximum spike count observed at the largest velocities. Note that the different values of m capture the observed asymmetry in the tuning curve. Analogous tuning curves for the dependence of latency μ (see Fig. 1E) and temporal jitter σ (see Fig. 1F) on the angular velocity of single vibrissa deflections were determined, and were fit analytically using nonlinear least-squares:

where A₁ = 17 ms, A₂ = 7.5 ms, λ₁ = 0.004 s/°, A₃ = 4 ms, A₄ = 2 ms, and λ₂ = 0.004 s/°.

Figure 1.

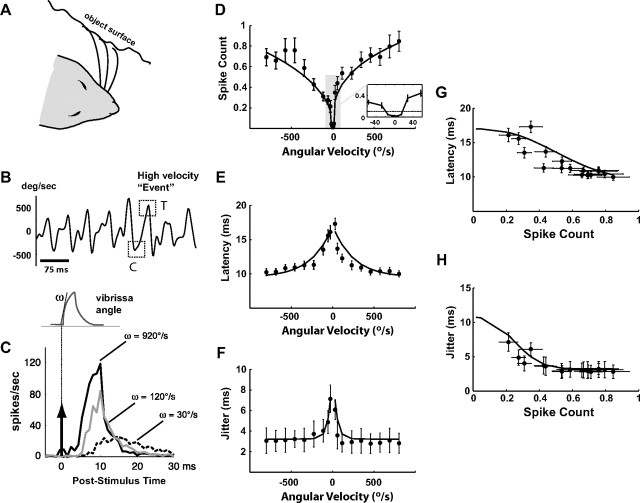
Responses of SI neurons systematically vary with vibrissa velocity. A, Illustration of vibrissa contact with surface during active exploration. B, Measured angular velocity during locomotion on linear track lined with coarse grating textures. Example high-velocity “events” are highlighted with dotted squares. C, The schematic shows the shape of the idealized deflection pulse presented, whereby the angular velocity is changed by varying the onset slope ω. All pulses were presented 60 times at a 1 Hz repetition rate. The traces on the right show the average firing rate responses to three angular velocities (dashed black: 30°/s, gray: 120°/s, solid black: 920°/s). The stimulus was presented at time 0. D–H, Relationships between various spiking response properties and the angular velocity of the punctate vibrissa deflection. All error bars in these plots represent ±1 SEM. All curves are parametric fits, as described in the Materials and Methods. D, For each stimulus velocity, the average number of spikes per presentation (spike count) was computed by summing the evoked PSTH over the 3–30 ms time window (n = 44 cells). E, Variation of mean response latency with velocity. F, Variation of response timing jitter with angular velocity. G, Latency as a function of spike count. H, Timing jitter as a function of spike count.

Encoding model of SI neurons

We developed a functional encoding model of SI neurons (see block diagram in Fig. 3), and fitted it to individual cells using experimental measurements. This dynamic model predicts single-neuron responses to sequences of deflections with varying instantaneous angular velocities. We should note that since the model is constructed from the separately measured tuning properties, velocity and history dependence are purposefully decoupled in this framework, but are likely intertwined in the context of continuous stimuli. The angular velocity of the vibrissae is obviously a continuously varying quantity, whose trajectory has a complex effect on the cortical response (see Discussion). We thus refer to the velocity dependence described here as instantaneous velocity dependence. The model here consists of three components, each of which is described in detail below: (1) velocity tuning, (2) suppression dynamics, capturing the effects of previous stimuli on the response to the current stimulus, and (3) integrate and fire, which captures the suprathreshold excitatory activity of the recorded cortical neuron.

Figure 3.

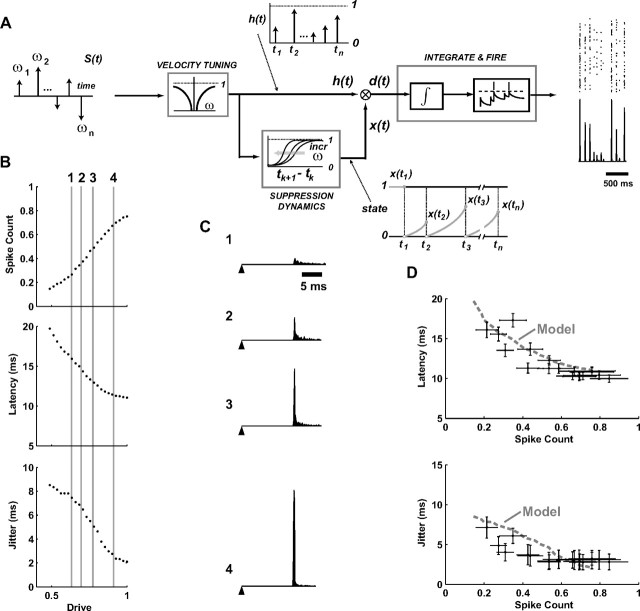
A dynamic encoding model for prediction of SI cortical responses to deflection patterns of varying velocity and timing. A, Transient deflections of the facial vibrissae are modeled as a series of impulses weighted by different angular velocity magnitudes and directions. The cortical activity is determined from an interaction between the velocity tuning properties and the history-dependent suppression dynamics, which serve as inputs to a standard integrate-and-fire model of neuronal firing. See the text for a more detailed description. B, The response properties of the integrate-and-fire mechanism for varying levels of input “drive.” Increasing magnitude of the input increases the spike count, decreases latency, and decreases timing jitter of the firing (for firing in a 30 ms bin, n = 500 trials). C, PSTHs are shown for four different levels of drive highlighted with the vertical lines in B, and numbered 1–4 for identification (n = 1000 trials). The filled triangle represents the time of a hypothetical punctate deflection of the vibrissa, followed by the PSTH at latencies from 16 to 12 ms, with increasing spike count and decreasing jitter (1 to 4). D, Spike count is shown versus latency (top) and timing jitter (bottom) for the model (dashed gray) curve, and the experimentally observed cortical responses from Figure 1, G and H.

Velocity tuning stage.

Based on the functional form of the instantaneous velocity tuning for the overall magnitude of the response (Eq. 1), we defined a scaling of the response due to changes in instantaneous angular velocity:

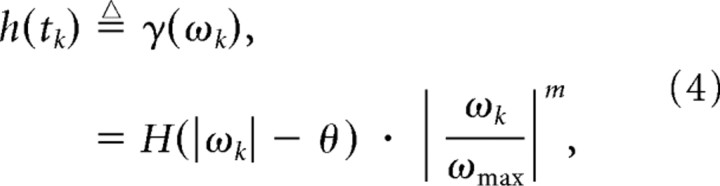where m = 0.4, now assuming symmetry with respect to positive and negative velocities, for simplicity. Note that h(t_k) varies between 0 and 1. We then characterized the velocity stimulus sequence as an impulse train: S(t) = Σ_iω_iδ(t − t_i), where {t_i} and {ω_i} are the occurrence times and the angular velocities of the sequence of deflections. Since S(t) is a sequence of delta functions weighted by the angular velocities, which range from −ω_max to ω_max, the resulting signal h(t) = γ(S(t)) is a sequence of delta functions with weightings scaled from 0 to 1, or h(t) = Σ_kγ(ω_k)δ(t − t_k). In the absence of history dependence, the response of the neuron is determined by these scaling terms (see the front end of the neural encoding model in Fig. 3).

Suppression dynamics stage.

An SI neuron's response to a given vibrissa deflection within a pattern is determined by a scaling relative to the response to a single vibrissa deflection, where the scaling captures the interactions between the suppressive effects of all preceding stimuli. This scaling is denoted by a state variable x(t) that ranges from 0 (in the case of complete suppression of the suprathreshold response) to 1 (in the absence of any suppression), and is Markov in the sense that regardless of past history, the present “state” is the only quantity necessary to predict how the neuron will respond to the next deflection. Note that in some cases the state can also exceed 1, representing a situation where the response is facilitated above the isolated vibrissa deflection response. As we previously showed, the profoundly nonlinear suppression following the response to a punctate stimulus does not depend upon the firing of the neuron in question, but instead reflects network dynamics and the evolution of the excitatory and inhibitory balance (Webber and Stanley, 2004)—see Discussion.

As an example, suppose the vibrissa is stimulated with a pair of velocity pulses, S(t) = Σ_i=1²ω_iδ(t − t_i). The state is assumed to be 1 before the first deflection, reflecting no suppression from prior stimuli (see the trajectory of the state before and following the first deflection, illustrated in the suppression stage of the block diagram in Fig. 3). Following the first deflection, the state immediately drops to zero, and gradually recovers over a timescale described by the paired-pulse measurements. The state at the time of the second deflection, given the history of stimulation up to that time, is f(t₂ − t₁; ω₁), where ω₁ denotes the dependence of the CTR curve on the angular velocity of the conditioning stimulus. In the model, the velocity dependence for the deflection at time t_k is captured by the scalar quantity h(t_k), which varies from 0 to 1. We therefore modify the notation for the CTR function to incorporate this dependence, f(t_k+1 − t_k; h(t_k)). A larger velocity ω_k, and therefore a larger h(t_k), results in a more profound suppression, and thus a lower value of f for the same time interval. This relationship is experimentally well described as follows:

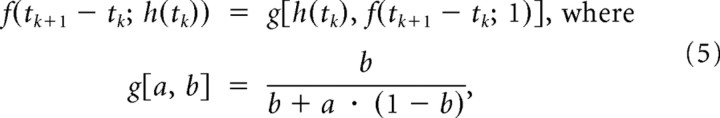and f(t_k+1 − t_k; 1) represents the CTR curve obtained when h(t_k) = 1 (i.e., ω_k ≥ ω_max, with ω_max being the velocity at which the velocity tuning curve saturates; see Fig. 1). Note that the expression g[a, b] for a = h(t_k) and b = f(t_k+1 − t_k; 1) can be intuitively interpreted. For a long time interval between deflections at t_k and t_k+1, the CTR curve f(t_k+1 − t_k; 1) goes to 1, as does b. In this case, g[a, b] goes to 1, yielding the maximal response, regardless of the strength of the scaled input h(t_k). For a short time interval between deflections at time t_k and t_k+1, the CTR curve f(t_k+1 − t_k; 1) goes to 0, as does b. In this case, g[a, b] goes to 0, yielding no response, regardless of the strength of the scaled input h(t_k). For intermediate values of the interdeflection interval t_k+1 − t_k, the velocity of the deflection at time t_k, captured by h(t_k), will influence the amount of suppression induced. For example, for an interdeflection interval such that the response is half of its maximum, and thus the CTR is 0.5, a strong preceding input of h(t_k) = 1 will result in g[a, b] = 0.5. However, a weaker preceding input h(t_k) = 0.5 will result in g[a, b] = 0.67, shifting the effective CTR to the left, or lessening the suppression on the response to the next deflection at t_k+1, consistent with the experimental observation.

Generalizing to a sequence of pulses with varying velocities, the evoked neural responses can be predicted using only the knowledge of pairwise interactions between stimuli—i.e., using only measurements of CTR curves. The following recursive relationship provides an accurate prediction of the state variable at the occurrence times of the stimulus {t_n}:

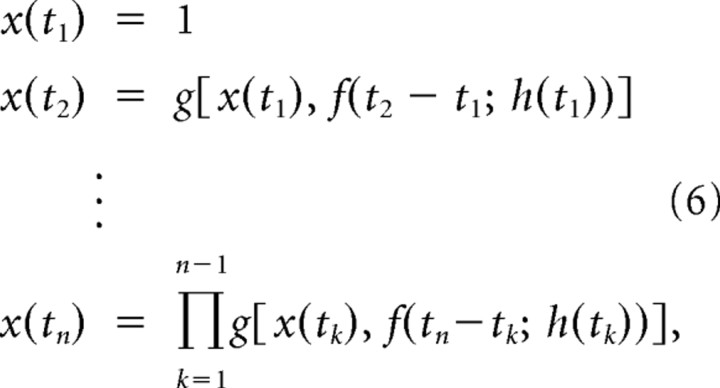which captures the nonlinear evolution of the suppression. Note that as we have previously described, the suppression does not simply “build-up,” but instead exhibits complex interactions (Webber and Stanley, 2004). Our previous studies have shown that in the context of sequences of transient, high-velocity vibrissa motion, the cortical response is strongly nonlinear, and is thus not well described with the cascade of a linear filter and a simple, rectifying static nonlinearity (Webber and Stanley, 2004; Boloori and Stanley, 2006)—see Results and Discussion. The suppression of a response to a deflection at t_k due to a prior deflection at t_k−1 results in a weaker suppression of the response to a deflection at t_k+1, which is captured by the above recursion.

Integrate-and-fire stage.

The firing response of the cortical neuron is then determined by the “drive” d(t) = x(t) · h(t), as shown in Figure 3A. We use a standard integrate-and-fire model of neuronal firing (Dayan and Abbott, 2001) to transform the sensory driven input to neuronal spikes:

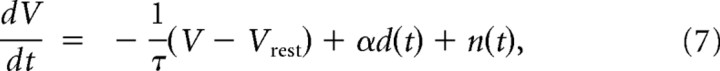where τ is the membrane time constant (set to 10 ms), d(t) is the sensory driven input scaled by a constant α, and n(t) is a noise term included to capture the timing variability in the model neuron response. When the potential reaches a threshold V_thresh, the model fires an action potential and resets (for implementation, V_rest was set to −70 mV, and V_thresh was set to −40 mV). The synaptic input to the integrator is the drive term αd(t), which is a pulse whose magnitude depends upon the state x(t), as described above. Depending on the past history of sensory input, a transient stimulus event produces a pulse input to the integrator, to which noise n(t) is added, resulting in a threshold crossing that is variable in its timing. The latency between the pulse input and the threshold crossing is determined by the magnitude of the drive input, resulting in varying the slope of the rising voltage. The noise was a Gaussian white noise process whose variance was set to yield the appropriate levels of timing jitter (the ratio of α to the SD of n(t) was 2.6, and the signal-to-noise ratio varied as a function of the magnitude of the drive d(t)). Importantly, stronger inputs produced shorter latencies, and decreased timing jitter, as seen in the experimental data, even though the variance of the noise was fixed, due to the changing relationship between the magnitude of the input and the fixed magnitude noise (Mainen and Sejnowski, 1995; Butts et al., 2007). As shown in Figure 3B–D, the integrate-and-fire mechanism produced spike counts, latencies, and jitters that were consistent with the experimental observations presented in Figure 1.

Decoding neural responses

The decoding of sensory inputs from the observed neural responses involves the detection of significant neural response events and Bayesian inference of the stimulus pattern from an assumed internal nonlinear model of neural encoding.

Detection of response events.

The first step in decoding is the classification of single-cell firing activity into significant response events or spurious noise. For the purpose of detecting the response events evoked by underlying deflections, neural firing rates were rebinned at 30 ms. From this point the measured neural firing rate (i.e., the PSTH) is referred to as the “firing rate,” whereas the 30 ms binned response is termed the “binned rate.” An ideal observer of spike counts seeks to detect the presence of stimulus deflections on the basis of observing the evoked binned rate. Two types of error are associated with this discrimination task: “misses” characterize occasions where the observer does not label a response event as significant, though an actual deflection had evoked its occurrence. A “false alarm,” on the other hand, denotes mistaken identification of spurious neural activity as that due to a stimulus.

Following classical detection theory (Green and Swets, 1966), optimal detection of a “signal” (i.e., presence of a stimulus deflection S within a time bin) that is corrupted by noise (i.e., due to spontaneous neural firing) uses two conditional probability distributions: (1) probability of the observed event size N, given the presence of a stimulus Pr[N|S], and (2) the probability of the observed event size N given the absence of a stimulus Pr[N|∼S]. For the observed spike count N′ in each time bin, we constructed the likelihood ratio L(N′) as follows:

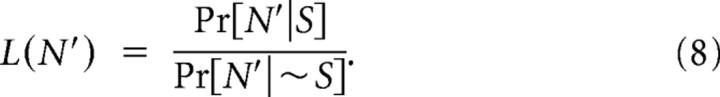The Neyman–Pearson criterion (Green and Swets, 1966) allows an observer to optimally detect the presence of stimuli subject to a maximum tolerated probability of false alarm. In practice, we performed the optimal detection through the likelihood-ratio test (Green and Swets, 1966): if L(N′) ≥ β, where β is a “threshold” value, then the observed response event of size N′ was attributed to a stimulus. For very small threshold values, almost all computed likelihood-ratio values were larger than the threshold, leading to identification of most response events as evoked by stimuli: both the false-alarm and correct-discrimination probabilities were therefore very high (close to 1). However, both the false-alarm and correct-discrimination probabilities decreased with increasing β. The optimal value of β depends on the specified probability of false alarm: β was increased from zero until the likelihood-ratio test provided the maximum tolerated rate of false-alarm observations of 0.10.

Decoding.

The outcome of the “detection” step was a sequence of observed spike counts {N_k}, and their occurrence times {t_k}. The decoding process consisted of the following steps that were performed in sequence for each observed spike count N_k, starting with the first observation: (1) For each observed significant spike count N_k, we estimated the drive d(t_k) at the time of observation as d̂(t_k) = N_k/N_max, for all t_k. (2) Next, x(t_k) and h(t_k) were estimated recursively. For k = 1, x̂(t₁) = 1, giving ĥ(t₁) = d̂(t₁). For k = 2, x̂(t₂) = f(t₂ − t₁; ĥ(t₁)), giving ĥ(t₂) = d̂(t₂)/x̂(t₂), and so on, for all t_k. Conceptually, this is based on an assumed internal model of the dynamics related to history dependence. (3) Finally, the absolute value of the angular velocity was estimated as |ω̂_k| = γ⁻¹(h(t_k)) for all t_k, using Equation 4. Note that the sign of the angular velocity, and therefore the direction of deflection, was ambiguous through the observation of a single neuron.

Results

During behavior, rats and other rodents use their facial vibrissae to actively explore surfaces through whisking and head/body movement, resulting in complex sensory inputs that vary over a large range of angular velocities and temporal scales. Through single-unit cortical recordings of monosynaptic thalamorecipient neurons in S1 of the anesthetized rat, we first systematically quantified the interactions between velocity and timing of vibrissa motion to form a predictive encoding model that captures the firing probability and the timing characteristics of the cortical representation.

Velocity tuning in SI cortex

During behavior in which the animal is actively exploring a surface (Fig. 1A), the vibrissae undergo patterns of discrete high-velocity transients (Ritt et al., 2008; Wolfe et al., 2008), where the velocity and timing of the transients depend on the textural properties, the intrinsic mechanics of the vibrissa complex, and the precise nature of the behavior. Figure 1B shows an example of the high-velocity transient events experienced by a single vibrissa in a behavioral setting, where the vibrissa motion was tracked using high-speed videography while the animal traversed a linear track lined with periodic textures (Jenks et al., 2010). In this ethologically relevant context, however, high-velocity transients (dotted boxes) are embedded within a highly complex sensory pattern, which precludes a simple analysis. To investigate these high-velocity transients in controlled conditions, we first recorded extracellularly from S1 neurons while stimulating the primary vibrissa with isolated, short-duration pulse deflections of varying onset slopes (see the schematic at the top of Fig. 1C). These simple stimuli allowed us to systematically parameterize the instantaneous velocity tuning effects on response timing and magnitude of topographically aligned neurons in cortical layer 4. Due to the short duration of the pulse (10 ms), the observed neural response was solely due to the onset slope, since the postexcitatory suppression induced by the rising phase completely suppressed the response to the falling phase (Webber and Stanley, 2004). Varying the onset slope allowed for the measurement of both the magnitude and temporal profile of single-cell response as a function of velocity. Each trace in Figure 1C shows the average firing rate response (peristimulus time histogram, or PSTH) to a different pulse velocity presented at time 0 (n = 44 cells; dashed black: 30°/s, gray: 120°/s, solid black: 920°/s). As stimulus velocity of the isolated punctate stimulus increased, cortical neurons responded with higher magnitude, lower latency, and increasing temporal precision (decreasing jitter).

The instantaneous velocity tuning curves in Figure 1D–F summarize the measurements and observations over a wide range of angular velocities. Figure 1D shows the average spike count per stimulus (computed by integrating the PSTH response over the 3–30 ms poststimulus time window) as a function of velocity, with nearly all neurons displaying saturation for velocities greater than 500°/s. The solid curve is a parametric power-law fit of the relationship between the angular velocity and the spike count, as described in the Materials and Methods. The average tuning curves for all recorded cells are approximately symmetric over rostral (positive) and caudal (negative) velocities. Additionally, almost all SI neurons studied possessed a velocity threshold below which they did not respond to pulse deflections—see inset highlighting the low-velocity regime of the tuning curve. Given the average measured spontaneous firing rate of ∼3 Hz, we estimate that the velocity threshold is approximately ±20°/s.

As expected from the variation of PSTH responses with instantaneous velocity from Figure 1C, the response latency smoothly decreased with increasing instantaneous stimulus speeds, as shown Figure 1E, again with the solid curves representing a parametric exponential fit of the relationship. Response latency had a lower bound of ∼10 ms at the highest measured velocities. The temporal precision of the response increased with instantaneous velocity, as evidenced by the decrease in temporal jitter in the bottom plot (see Materials and Methods). Importantly, the changes in spike count with angular velocity were accompanied by corresponding changes in latency and timing jitter, and the latency and jitter were well predicted by the spike count, as shown in Figure 1, G and H. In each, the timing (latency or jitter) is plotted as a function of the spike count, and the corresponding parametric fits in Figure 1, D and E, are combined to form explicit parametric relationships (solid curves).

History dependence of SI responses

In addition to the variations in the angular velocity of the vibrissa motion, the relative timing of the deflection transients is an important feature of the sensory input that is strongly influenced by behavior. The simplest way to systematically characterize the dependence of responses on the past history of stimulation—caused by poststimulus suppression—is through the conditioning–test paradigm (Kyriazi et al., 1994; Webber and Stanley, 2004; Boloori and Stanley, 2006). Note that we have previously shown that this form of history dependence is stimulus driven, rather than an intrinsic, biophysical property of the neurons triggered by action potentials (such as prolonged refractoriness or afterhyperpolarization) (Webber and Stanley, 2004). Drawing inspiration from patterns of high-velocity transients in behavioral contexts (Fig. 1B), a simple paired stimulus was used, consisting of a conditioning deflection (C) followed by a test deflection (T), as shown in Figure 2C (also conceptually highlighted by the high-velocity transients in Fig. 1B).

Although the conditioning–test paradigm has been well studied, the relationship between velocity tuning and interdeflection timing is not known. Figure 2, A and B, show the average PSTHs for a range of paired stimulus conditions. In Figure 2A, the PSTHs are shown for paired deflections in which the angular velocity of the second (test) deflection was fixed at 690°/s, but the angular velocity of the first (conditioning) deflection was varied, for a range of interdeflection intervals (IDIs). The responses qualitatively show that the response to the second deflection is increasingly suppressed for shorter IDIs, and that a higher velocity conditioning stimulus produces a more profound suppression of the response to the test stimulus for a given IDI. Figure 2B shows the same for a fixed conditioning stimulus at 690°/s, while varying the angular velocity of the test stimulus over a range of IDIs. Qualitatively, for a given IDI, we observe that increasing angular velocity of the test stimulus serves to allow the neuron to emerge from the suppression induced by the first deflection more quickly. It is important to note that the properties of the paired-deflection response shown in Figure 2 could arise from a very simple linear model/filter that involves an initial excitatory response, followed by a prolonged inhibitory tail. In this case, the response to a sequence of two deflections such as that in the figure would result in the response to the second deflection “riding” on the inhibitory tail, which when rectified, would result in an attenuated second response as a function of the interdeflection interval, as we observe. However, we have previously shown through a simple three deflection sequence that the mechanism is not additive, but instead divisive in nature, and strongly nonlinear (Webber and Stanley, 2004, 2006; Boloori and Stanley, 2006), also demonstrated in intracellular cortical recordings (Higley and Contreras, 2003), and thus more powerful models are required for complex stimulus patterns.

To better quantify these observations, the CTR was calculated for a given interdeflection interval as the ratio of the spike count in response to the test deflection preceded by the conditioning deflection to the spike count in response to the test deflection alone, where the spike count is taken in the 3–30 ms window following the deflection (Fig. 2C). The CTR describes, as a function of the interdeflection interval u, the degree to which the response to the test stimulus has been suppressed/excited by the conditioning stimulus, which is strongly nonlinear (Webber and Stanley, 2004; Boloori and Stanley, 2006). The timescale of poststimulus suppression depends significantly on the velocity of the conditioning stimulus. For a fixed test stimulus, progressively higher conditioning velocities evoked longer-lasting poststimulus suppression in a majority of cells, as shown by the slower recovery time of the corresponding CTR curves (Fig. 2D). For a specific interdeflection time-interval, therefore, the degree of suppression induced by a transient deflection is strongly dependent upon its angular velocity. Similarly, for a given velocity of conditioning stimulus, increasing the velocity of the test stimulus results in effectively shortening the time course of the suppression induced by the first deflection, as shown in Figure 2E. Again, changes in response magnitude were well correlated with other properties of the response suppression; a decrease in response magnitude was accompanied by a decrease in precision and an increased latency.

From the perspective of an observer of single-unit cortical activity, the above results point to ambiguities in the neural response when decoding the sensory input. On the one hand, the same isolated punctate stimulus deflection can result in dramatically different properties of the corresponding localized firing activity (spike count, precision), depending on past history, as illustrated by the CTR curves in Figure 2, D and E. On the other hand, observation of a small response event (i.e., low spike count) could arise from a low-velocity vibrissa deflection, as described in Figure 1, or from a high-velocity stimulus whose response has been suppressed by a preceding deflection, as described in Figure 2D, or a range of dynamic trajectories that ultimately lead to that specific level of suppression/excitation when paired with a transient deflection. Thus, a transient deflection at a specific velocity does not result in a unique neural response, but is instead strongly dependent upon the past history. From both perspectives, for proper decoding (and perceptual interpretation), an encoding model that takes into account these properties is necessary.

An encoding model of SI responses

To capture the encoding dynamics of the vibrissa pathway, we constructed a functional response model incorporating the dependence of SI response magnitude and timing on instantaneous deflection velocity and the nonlinear effects of stimulus history. Figure 3 schematizes the model, which transforms a sequence of vibrissa deflections into the firing activity of a single cell. The input to the vibrissa pathway can be envisioned as sequences of angular deflections, modeled here as punctate deflections with varying onset velocities (see Materials and Methods for a detailed description of the model). We should note that the biophysical processes that give rise to the observed cortical responses are complex, and that this model is not designed to capture this explicitly, but instead integrates the experimental observations described thus far within a functional framework that is analogous to functional models in other pathways (Paninski et al., 2004; Lesica et al., 2007; Mante et al., 2008; Pillow et al., 2008). Note, however, that at its core, the model presented here is highly nonlinear in form, differentiating it from sensory models based on linear filtering (see Discussion).

The velocity tuning stage of the model captures the scaling of the response as a function of the instantaneous angular velocity of the vibrissa deflection, quantified using a parametric fit to the experimentally measured tuning curve (see Materials and Methods). The history dependence of the pathway captures the nonlinear dynamics of the suppression that follows a vibrissa deflection, modeled through an evolution of a “state” variable x(t) based on temporal interactions of the experimentally measured CTR curves, which were fit parametrically. As described in the Materials and Methods, this is distinctly different from suppression of activity following spiking, due to refractory or other spike-history-dependent effects. This term instead reflects the relative level of the momentary balance between excitation and inhibition in the thalamocortical circuit, a highly nonlinear process. The resulting combination of velocity tuning and history dependence, which we denote the “drive” d(t), determines the firing activity through an integrate-and-fire stage of the model. In response to a transient deflection of the vibrissa, the input to the integrator is a pulse whose magnitude is determined by the drive d(t). The input, analogous to a synaptic current, is integrated, resulting in a depolarization that drives the mechanism to threshold, firing a spike. Noise is included in the input to the integrator, resulting in variability in timing of the integrate-and-fire model's spiking.

Figure 3B shows the firing event parameters (spike count, latency, and jitter) in response to repeated presentations of a single transient drive input to the integrate-and-fire mechanism for varying levels of drive. The response characteristics of the integrate-and-fire model are qualitatively similar to those observed in the velocity tuning of actual neurons (see, e.g., Fig. 1D–F). Increasing the magnitude of the input increases the spike count, decreases latency, and decreases timing jitter. Figure 3C shows the PSTH output of the integrate-and-fire mechanism for varying levels of drive, highlighted by the vertical lines in B. Note that latencies produced by the integrate-and-fire mechanism were superimposed on a latency of 10 ms to account for the synaptic delays from the periphery to cortical layer 4, since the integrate-and-fire model is conceptually meant to represent integration at the thalamocortical synapse. Finally, Figure 3D shows the relationships between the spike count and latency and spike count and timing jitter for the integrate-and-fire model (solid curves), along with the experimentally observed relationships from Figure 1, G and H (symbols with error bars), illustrating that predicting the overall drive in the circuit captures not only the magnitude of the response, as measured through spike count, but timing aspects of the response as well.

Model prediction of cortical response to stimulus patterns

To evaluate the predictive capability of the model, we designed simplified artificial stimulus sequences based on the range of behaviorally observed distributions of angular velocities. Figure 4A shows the instantaneous velocity of a single vibrissa in contact with a coarse texture (36 grit sandpaper), as measured through high speed videography (Jenks et al., 2010)—see Materials and Methods. The full distribution of instantaneous angular velocity is shown by the black curve in Figure 4B. The horizontal dashed gray lines in Figure 4A represent a threshold imposed at ±160°/s, to identify transient stimulus events of relatively high angular velocity. The interdeflection intervals were restricted to be >40 ms, resulting in the distribution of interdeflection events shown in Figure 4C. The final set of stimulus events had the angular velocity distribution shown by the gray curve in Figure 4B. Note that these stimulus sequences were designed to provide a simple, controlled input to explore the dynamics of the pathway, while using angular velocities and timings of transient vibrissa motions that are observed in more naturalistic settings.

The top panel of Figure 5A shows a short segment of a rostral–caudal vibrissa deflection sequence generated by random draws from the distributions in Figure 4, B and C. Each arrow indicates the time at which a punctate deflection was delivered, where the arrow height and direction indicate the velocity of the deflection (see Materials and Methods). The panels below the stimulus sequence show the experimentally measured PSTH response (PSTH averaged across a small subset of cells with similar dynamics, and therefore similar CTRs; n = 6) and the corresponding model prediction (inverted scale) for the Full Model, the model in the absence of the velocity dependence (No-Velocity, middle), and the model in the absence of the history dependence (No-History, bottom). The model was based on the average tuning curve and CTR measurements for the cells, and was used to predict cortical responses to stimulus sequences not used to fit the model. Localized Gaussian templates of the PSTH events were used for the plotting of the predicted response events, with the appropriate spike count, latency, and jitter as predicted by the encoding model. The Full Model prediction exhibits fairly good agreement with the experimentally measured data, predicting the presence of the firing events and the corresponding timing and magnitude, while also correctly predicting the absence of firing in response to some deflections (e.g., fifth stimulus event). In contrast, removing the velocity dependence results in a gross overestimation of the firing activity, and an underprediction of the latency and jitter (middle panel, No-Velocity). Most dramatically, however, when the strong nonlinearity of the paired-pulse suppression was excluded from the model, the model predicted significantly greater firing than measured experimentally, particularly predicting firing events in response to deflections during short IDIs that resulted in little or no actual firing (bottom panel, No-History).

For a quantitative assessment of the predictive capability of the model, event-by-event spike counts were evaluated for the measured responses and the model predictions, an example of which is shown for the Full Model in Figure 5B (measured spike count in black, model prediction in gray). The SEs in the measurements of spike counts are not shown for clarity, but at almost all points they overlap with the values predicted by the model.

To quantify the goodness-of-fit over the longer stimulus trial, the correlation coefficient and mean-squared error (MSE) were calculated between the predicted and actual spike count for a larger sample of cells (n = 15). Note that the MSE reflects absolute deviations from the experimental observations and thus penalizes for improper scaling, serving as a complement to the correlation coefficient. We performed two null tests to determine the relative importance of the different constituent elements that comprise the model. In the first test, we predicted the cortical response by retaining history dependence but ignoring velocity tuning (by setting the tuning curve to a flat curve equal to the maximum spike count, as previously shown in Fig. 5A, middle). As shown in Figure 5C, top panel, the resulting correlations between the predicted and the measured values (denoted as No-Velocity) were the same as those observed for the full model (bars indicate 99% confidence intervals). This was due to the fact that accounting for history dependence allowed the model to track the time course of suppression relatively well, even though the magnitudes of the predicted values were in error due to the neglect of velocity tuning. However, the resulting MSE for this test was significantly larger than that observed for the full model, showing that accounting for velocity tuning was important for the correct prediction of the magnitude of the responses (Fig. 5C, bottom, Full Model vs No-Velocity). In the second test, we predicted the cortical response by accounting only for velocity tuning, while ignoring history dependence, an example of which was previously shown in Figure 5A, bottom. The resulting correlation coefficient and MSE between these predictions and actual measurements are shown in Figure 5C (No-History). In comparison with the full model, ignoring history dependence drastically lowered the agreement of the predictions with the actual measurements in terms of both the linear correlation and the MSE. Similar results were obtained for other stimulus sequences generated (not shown). The above tests demonstrate the importance of both velocity tuning and history dependence to an accurate model. Comparison of the resulting correlation coefficients and prediction errors reveals that accounting for history dependence is necessary to appropriately predict the temporal pattern of the neural response, but that accounting for velocity tuning is critical in accurately predicting the magnitude of the firing events within the temporal pattern of the neural response. It should be noted that the predicted response from the full model achieved a correlation of 0.64 with the actual recorded response, which when compared to the correlations across subsets of the experimentally recorded responses (0.85) implies that the model captures ∼75% of the explainable variance (see Discussion).

The predictive capability of the model here is consistent with findings for single-unit model predictions at a number of sensory stages. Models of retinal ganglion cells predict 80–95% of the explainable variance (Pillow et al., 2008), under very well controlled, in vitro conditions. LGN models typically predict <56% (and as low as 24%) of the explainable variance (Mante et al., 2008). In primary visual cortex, the best models to date predict ∼40% of the explainable variance (personal communication, J. L. Gallant). The mismatch between the model prediction and the observed responses here could result from several factors. The encoding model imposed here is fairly parsimonious in nature, using only the power law fit to the velocity tuning (four parameters), the time course of the sigmoidal fit to the CTR (three parameters), and the integrate-and-fire model at the back end (three parameters, excluding V_rest and V_thresh). Further, this is fit to population-averaged data, thus the cell-to-cell variability in tuning properties could degrade the overall performance. Finally, the model does not take into account spike-history dependence, which may play a role in shaping the cortical response.

Bayesian decoding of tactile patterns

Given the fidelity of the above encoding model, we can then ask the question, how much does the observation of the cortical response reduce the uncertainty about the sensory stimulus? The cortical response, as we have described, is temporally localized and event-like, linked to discrete features of the vibrissa input. As described in the Materials and Methods, the first step in this process is thus to identify response events, as shown in Figure 6A.

Shown are the average cortical PSTH (gray) and corresponding spike-count measure in 30 ms windows (black) in response to a stimulus sequence of randomized punctate deflections of varying angular velocity and timing (shown in Fig. 6C). As described in the Materials and Methods, the Neyman–Pearson criterion was used to detect response events from the localized spike-count measured, indicated with the gray bands in Figure 6B. The stimulus sequence could then be parsed into stimulus events that correspond to detected response events and those that do not (gray and black, respectively, in Fig. 6C). The stimulus events that correspond to detected response events are thus those that are theoretically predictable from the observed cortical activity, while the remaining stimulus events cannot, and thus are not considered in the decoding of Figure 6, D and E. Using the Bayesian decoding framework described in the Materials and Methods, the observed sequence of response events, the population encoding model, and the prior distribution of the stimulus (Fig. 4B,C) were then used to infer the stimulus sequence that most likely induced the response. As previously noted, the angular velocities were both positive and negative (rostral and caudal), which creates an ambiguity in the decoding from a single neuron. For display purposes, here we assign the decoded stimulus velocity the correct sign (see Discussion), although the decoder yields a prediction that is sign-ambiguous. Figure 6, D and E, shows the actual stimulus events (gray), and the decoded stimulus events (black), for the Full Model (E) and the No-History (D) cases. The No-History case, as before, is where the decoding is based on velocity tuning only, neglecting the nonlinear suppressive dynamics. As shown in comparing the two cases, neglecting the history dependence of the suppression causes the decoder to consistently underestimate the angular velocity of the stimulus events. This is summarized in a scatter plot of the actual stimulus angular velocity versus the corresponding prediction from the Bayesian decoder, as shown in Figure 6F. Decoding in the No-History case (gray) results in points that are significantly below the unity line for positive angular velocities, and points that are significantly above the unity line for negative angular velocities. The predictions based on the Full Model (black), however, are found to lie consistently closer to the unity line.

Encoding and decoding under simple transformations

The tuning properties shown in Figures 1 and 2 reveal strong dependencies of the cortical response on deflection velocity and timing, and further testing of the model revealed that accounting for both is necessary for accurate prediction of the cortical response. We have recently quantified the degree of variability in vibrissa deflection patterns when the vibrissa array is engaged with various surfaces during free locomotion (Jenks et al., 2010). Head and body movements create a significant amount of variability in the vibrissa deflection patterns for the same surfaces, primarily manifested in the timing and amplitude/velocity of vibrissa contacts. Given the importance of both of these factors, and the associated variability that we observed behaviorally, we designed a new set of stimuli by scaling along the two axes of velocity and timing, to test the encoding and decoding under these transformations.

Figure 7A shows a short segment of a rostral–caudal vibrissa deflection sequence (top) and the corresponding PSTH of a typical cortical layer 4 single-unit response. As above, each arrow indicates the time at which a punctate deflection was delivered, where arrow length and direction indicate the velocity of the deflection (see Materials and Methods). Note that the 650 ms segment was taken from the middle of a longer 6 s segment. Figure 7B illustrates the same deflection pattern, preserving the temporal structure in A, but with all instantaneous velocities scaled up. Since this scaling was analogous to increasing the temporal “contrast,” we defined the deflection sequence in Figure 7A as the low-contrast (LC) sequence and that in B as the high-contrast (HC) sequence.

To independently explore the role of timing, we time compressed the original LC sequence, while retaining the same instantaneous velocities of each LC stimulus event. The resulting time-compressed (TC) sequence and the corresponding cortical response are shown in Figure 7C (TC, gray), along with the corresponding LC response for comparison (black, inverted scale). Note that the PSTH for the TC stimulus (gray) is shown at an expanded timescale to align both PSTHs to the same stimulus pattern.

The previously described encoding model was then used to predict the response stimulus patterns under this paradigm. Figure 8A shows the actual response (gray, positive axis) versus the model prediction (black, inverted axis) for the LC (left), HC (middle), and TC (right) cases (averaged actual response, n = 6 cortical neurons). The top row shows the performance of the Full Model, while the bottom row shows the same for the No-History case, where, as before, the predicted response is based solely on the velocity tuning properties.

Figure 8.

Encoding and decoding under stimulus transformations. A, The average actual (gray, positive axis) versus predicted (black, inverted axis) cortical response to the LC (left), HC (middle), and TC (right) stimuli, for the Full Model (top row) and the No-History case (bottom row). Note that the LC and HC have a different time scale as compared to the TC case. For this example, the velocity scaling from LC to HC was a factor of 2, while the temporal scaling from LC to TC was a compression by a factor of 2. The actual response was an average across a subgroup (n = 15 cortical neurons). B, The actual versus predicted event-by-event spike counts for the LC, HC, and TC stimuli. The model predictions were again conducted for the Full Model (filled symbol) and the model with the nonlinear, suppressive history term removed (No-History, open symbol). Correlation coefficient between actual and predicted response: Full Model, LC: 0.86, HC: 0.83, TC: 0.81; No-History, LC: 0.27, HC: 0.27, TC: 0.35. C, Actual versus decoded event-by-event angular velocity for the LC (circle), HC (square), and TC (triangle) stimuli. The Bayesian decoding was performed using the Full Model (filled symbols) and the model with the nonlinear, suppressive history term removed (No-History, open symbols). Correlation coefficient between actual and decoded angular velocity: Full Model, LC: 0.91, HC: 0.92, TC: 0.91; No-History, LC: 0.66, HC: 0.62, TC: 0.62. D, When the vibrissae engage a single surface/texture T, variations in the behavior/motion result in different sensory inputs to the pathway (S₁ and S₂ here), resulting in different patterns of cortical activity (R₁ and R₂). Conceptually, knowledge of the encoding properties of the pathway and knowledge of self-motion allow an observer of the cortical activity to infer invariant properties of the surface, despite variations in the neural response.

Removal of the nonlinear, suppressive history term resulted in a significant overestimation of the firing activity. The scatter plots in Figure 8B show the actual spike count versus the predicted spike count, for the Full Model (solid symbols) and the No-History case (open symbols), for LC, HC, and TC stimuli. The Full Model performed similarly well for the LC, HC, and TC cases, and the history term is critical for the model prediction (see figure caption for corresponding correlation coefficients). A single model thus captures the nature of the cortical response under different stimulus contexts.

Given knowledge of the encoding dynamics, we can then ask to what extent an ideal observer of the cortical activity can decode stimulus-related information from neural responses. As in Figure 6, the response events were first detected from the recorded responses, and then the encoding model was used in a Bayesian framework to infer the most likely stimulus sequence. Figure 8C shows the actual versus decoded event-by-event angular velocities. Note that again, the stimulus events shown are only those that correspond to a detectable response event, and the correct-sign of the angular velocity was assigned to the sign-ambiguous decoded angular velocity. Shown are the decoding results for LC, HC, and TC (circles, squares, triangles, respectively), for the Full Model (solid, black), and the No-History case (open, gray). Again the nonlinear, suppressive history term was critical in the decoding, with significant underestimates of the angular velocity when neglected. The decoding performed similarly well in each of the three stimulus classes (see figure caption for performance metrics). Theoretically, the three stimuli described here may give rise to different cortical activity, yet arise from transformations of the same surface/texture, as conceptually outlined in Figure 8D. The above results suggest that the same encoding model holds up under these hypothetical transformations, demonstrated through both predictive encoding and decoding in the stimulus space. However, to what extent the animal has access to internals models of self-motion, and how these might be combined with internal models of neural encoding, remains an open question.

Discussion

It is the underlying tenet of this work that features of the external environment are represented in the spiking activity of neurons in early sensory pathways over a relatively fine temporal scale (on the order of tens of milliseconds), rather than firing activity averaged over large temporal windows. Neural activity at fine timing precision has been demonstrated in a wide range of sensory areas, including the retina (Berry and Meister, 1998; Liu et al., 2001; Passaglia and Troy, 2004), visual thalamus (Reinagel and Reid, 2000; Butts et al., 2007; Desbordes et al., 2008), auditory periphery (Cariani and Delgutte, 1996), and visual (Bair and Koch, 1996; Buracas et al., 1998) and auditory (Wehr and Zador, 2003; DeWeese and Zador, 2006) cortices. Under acute conditions in the vibrissa pathway, in which precisely the same motion of the vibrissae can be repeated, cortical neurons exhibit temporally precise, stimulus-locked activity (Garabedian et al., 2003; Khatri et al., 2004; Boloori and Stanley, 2006) that suggests the possibility of such a neural code based on temporally precise neural activity reflective of textural properties, which has been described as a “kinetic signature” that is consistent with our findings here (Arabzadeh et al., 2005, 2006). However, recent chronic recordings from the awake animal engaged in a texture discrimination task have revealed patterns of cortical activity that are highly variable from trial to trial, which has led to the suggestion of a rate-based code in which the relevant information is encoded in the mean firing rate over hundreds of milliseconds (von Heimendahl et al., 2007). One central difference between these two experimental paradigms is that the acute studies permit the presentation of a precisely controlled tactile input that is repeatable across trials, whereas the behavioral studies are subject to trial-to-trial variations in sensory input even in the presence of the same tactile features of the external environment. It is important to note that although significant variability can exist from trial to trial for individual neurons, local populations on a single trial are all experiencing the same sensory input that has been shaped by the particular behavioral parameters during that trial; the degree of precision across populations remains an open question in this pathway. The lack of a temporally precise response across behavioral trials is not evidence against the importance of the precise features in the neural response, but instead makes more salient the need for internal models of self-motion for interpretation of the incoming, distributed sensory signal.

Velocity sensitivity and history dependence

The instantaneous velocity sensitivity of cortical neurons in the vibrissa system has been measured in a number of previous studies (Simons, 1978; Ito, 1985; Pinto et al., 2000; Shoykhet et al., 2000). The majority of work in this regard has focused on the spike count of the response to punctate or ramp-and-hold deflections, reporting a monotonic dependence of spike count on deflection velocity consistent with our present results. It has been shown that the timing of thalamic activity is important in the context of integration at the thalamocortical synapse (Usrey et al., 2000; Swadlow and Gusev, 2001), and asserted that the velocity dependence of the cortical spike count is established by thalamic timing (Pinto et al., 2000). Indeed, recent findings based on paired recordings of thalamic units and their cortical targets suggest that layer 4 cortical neurons in the vibrissa system are driven by weak input from a relatively large number of thalamic projections (Bruno and Sakmann, 2006). It is thus likely that the velocity sensitivity of the cortical spike count arises from the enhanced time-locking of thalamic neurons with increasingly strong stimuli. In addition, we showed that the velocity has a systematic effect on the latency and temporal precision of the cortical response, which together with the spike count shapes the cortical representation. Although cortical velocity sensitivity has been clearly established, the distribution of velocities experienced by the animal in more ethological settings has only recently been addressed in experimental and computational studies (Arabzadeh et al., 2005; Ritt et al., 2008; Wolfe et al., 2008). The simple patterns of velocity transients used here were designed to decouple the velocity and timing elements of the cortical representation of the vibrissa motion, rather than to explicitly represent naturalistic input to the pathway, which could potentially involve more continuous motion. However, there is recent evidence that vibrissae resonate transiently during discrete, high-velocity, and high-acceleration slip–stick events during whisking against surfaces of various types, and that the rate/pattern of these high-velocity vibrissa transients varies with the properties of the texture and self-motion (Ritt et al., 2008; Wolfe et al., 2008).

The history-dependent effects characterized by the conditioning–test ratio measurements we obtained through paired-pulse stimuli are similar to those previously reported (Simons, 1985; Simons and Carvell, 1989; Brumberg et al., 1996; Kleinfeld and Delaney, 1996; Mirabella et al., 2001; Webber and Stanley, 2004, 2006; Boloori and Stanley, 2006). Barbiturate anesthesia enhances and mimics the action of GABA at the GABA_A receptor complex, decreasing excitability at both cortical and subcortical stages, and thus likely affects the measurements presented here. There is a reported reduction in the amount of cortical adaptation with increased arousal, attributed to the overall depression of the thalamocortical synapse (Castro-Alamancos, 2004), although a more recent study showed that the thalamocortical synapse is not altered by the state of arousal, but instead the observed attenuation in response may result from a modulation in thalamic synchrony (Stoelzel et al., 2009). Paired-pulse electrical stimulation of the infraorbital nerve using a cuff electrode showed that the stimulus-induced suppression does persist in the aroused state, but over a shorter time course as compared to the awake but quiescent or anesthetized states (Fanselow and Nicolelis, 1999). The conceptual nature of the model proposed here thus is likely still relevant in behavioral contexts, although over shorter timescales (and thus higher frequencies), but this remains to be explicitly tested.

Encoding models of early sensory processing

General statistical techniques have long been used to model the functional properties of neurons in early sensory pathways (Jones and Palmer, 1987; Reid et al., 1997). Models of spiking activity of neurons in the retina, the lateral geniculate nucleus (LGN) of the thalamus, and cortical simple cells all rely on predominantly linear filtering of the sensory input in the prediction of the neuronal response passed through a static, rectifying nonlinearity (Chander and Chichilnisky, 2001; Mante et al., 2005; Lesica et al., 2007; Mante et al., 2008; Pillow et al., 2008). It has also previously been acknowledged that spike history plays a significant role in the patterns of neural activity observed experimentally (Brillinger, 1992; Berry and Meister, 1998), and recent modeling efforts have extended the quasi-linear framework to capture absolute and relative refractoriness in the neuronal response of retinal ganglion cell activity (Keat et al., 2001; Pillow et al., 2008). The nonlinear history dependence we describe here is a network phenomenon, which we have previously shown to occur independently of the spiking of the measured neuron and is thus predicted directly from the stimulus input rather than the past history of spiking (Webber and Stanley, 2004). Further, the model presented here was constructed from systematically measured tuning properties, and uses filter properties that are fundamentally nonlinear in nature that are based on the propagation of the suppressive effects that we have previously reported (Webber and Stanley, 2004, 2006; Boloori and Stanley, 2006).

It has recently been shown that, unlike neurons in the early visual pathway (including simple cells in V1), when driving the system with white noise vibrissa stimulation, spike-triggered averaging (STA) does not reveal a first-order relationship between the vibrissa motion and the cortical response (Maravall et al., 2007). However, consideration of the second-order structure of the spike-triggered distribution of the stimulus does reveal stimulus features to which the system is sensitive. Estimation of the input–output relationship relative to these stimulus features reveals a symmetry of the corresponding nonlinearities, capturing the responsiveness of a barrel cortex neuron to vibrissa motion in opposite directions. Similar work in the early visual pathway suggests that covariance methods provide complex feature selectivity (Fairhall et al., 2006), so it is possible that this approach would be predictive of the nonlinear interactions we demonstrate here on an event-by-event basis. It is also possible that STC-based models cannot accurately predict cortical responses to relatively strong stimuli. There is good reason to believe that the stimuli used in studies of other sensory pathways (e.g., spatiotemporal white noise in visual studies) are not strong enough to push the system into a strongly nonlinear regime, and that the punctate deflections of the vibrissae are strong in comparison. This would also explain why the linear models of the early visual pathway perform poorly in the context of natural visual scenes, where strong spatial correlations, and sudden transients, drive sparse, episodic firing at various stages of processing (Butts et al., 2007), suggesting the possible existence of similarly strong, suppressive mechanisms as those described here.

Cortical representations of the tactile scene

Representations of the tactile input in ethological conditions would be distributed across vibrissae and across the cortical population, ultimately placing limits on what we might expect to uncover through activity of a single neuron. For example, it is impossible for one to recover information on stimulus direction from observation of single-cell responses. However, we might envision downstream neurons receiving input from a population of neurons within a cortical column with a diversity of directional tuning properties, likely to collectively provide unambiguous information concerning stimulus direction. Such a population code would be more easily envisioned if the directional tuning map were arranged in a manner that would facilitate such a readout, as recently suggested in several studies (Bruno et al., 2003; Lee and Simons, 2004; Andermann and Moore, 2006). Second, consideration of responses from multiple barrels (perhaps as are available to supragranular and infragranular SI regions and higher cortical areas) would also yield information on stimulus direction: the order in which two adjacent vibrissae are deflected contains information about the direction of contact. Population coding in the vibrissa pathway has not been well studied until recently (Petersen and Diamond, 2000; Panzeri et al., 2003; Petersen et al., 2003), but likely plays an important role in the representation of more complex tactile sensations. The experiments and analyses here also provide an opportunity to speculate upon the possible perceptual implications of the described phenomena. In a passive setting, it would trivially be the case, for example, that a texture with a high spatial frequency presented at a low velocity would be indistinguishable from a texture with a low spatial frequency presented at a high velocity. Beyond this simple example, however, it is important to note that any past history of sensory input that places the system in the same “state” would have the same neural response to the same subsequent sensory input, despite vast differences in the stimulus history. It is possible that manipulating the stimulus history before a cued stimulus used in a discrimination task would potentially provide some clues about the time window over which the past stimulus history influences the percept (Gerdjikov et al., 2010), but this remains to be fully explored experimentally.