Abstract
The insulative properties of myelin sheaths in the central and peripheral nervous systems (CNS and PNS) are widely thought to derive from the high resistance and low capacitance of the constituent membranes. Although this view adequately accounts for myelin function in large diameter PNS fibers, it poorly reflects the behavior of small fibers that are prominent in many regions of the CNS. Herein, we develop a computational model to more accurately represent conduction in small fibers. By incorporating structural features that, hitherto, have not been simulated, we demonstrate that myelin tight junctions improve saltatory conduction by reducing current flow through the myelin, limiting axonal membrane depolarization and restraining the activation of ion channels beneath the myelin sheath. Accordingly, our simulations provide a novel view of myelin by which tight junctions minimize charging of the membrane capacitance and lower the membrane time constant to improve the speed and accuracy of transmission in small diameter fibers. This study establishes possible mechanisms whereby TJs affect conduction in the absence of overt perturbations to myelin architecture and may in part explain the tremor and gait abnormalities observed in Claudin 11-null mice.
Keywords: axoglial junctions, claudin, intercellular junctions, knockout, modeling, occluding, paranodal, permeability barrier, radial component, schizophrenia, multiple sclerosis, simulation, myelination, action potential
Introduction
In the CNS, myelin sheaths are elaborated by oligodendrocytes, which spirally-ensheath segments of axons with multilayered compact membranes. Molecular appreciation of the morphological complexities of myelin sheaths originally described by Cajal and del Rio Ortega (Cajal, 1899; del Rio-Hortega, 1928) have come to the fore over the last decade; however, the functional consequences of these complexities and the physiological changes that occur during demyelination and remyelination have been difficult to explore in detail using electrophysiology alone. Accordingly, computational modeling of myelinated axons (Brill et al., 1977; Halter and Clark, 1991; Shrager, 1993; McIntyre et al., 2002) has been used widely to fill this void and has highlighted the interplay between morphological features and the biophysical properties of myelin (reviewed in Waxman and Bangalore, 2004).
Early experimental measurements suggest that myelin insulates the internodal axonal membrane by forming a high resistance, low capacitance compartment around the axon (Tasaki, 1955). Intracellular recordings in large myelinated fibers have substantiated this view, but demonstrate that myelin is less resistive than originally thought. More recently, Blight (1985) evaluated myelin as a low resistance cable around the axon that decreases the internodal membrane capacitance and membrane time constant. This model recapitulates the behavior of axons typically found in the spinal cord and PNS; however, this model does not adequately account for conduction using dimensions of small optic nerve axons (Devaux and Gow, 2008). Thus, small caliber fibers, which are common in the CNS, may contain structural elements that are crucial for conduction and require incorporation into Blight’s model.
Our investigation into the neurological phenotype of Claudin 11-null mice reveals that autotypic tight junctions (TJs) in CNS myelin sheaths play a crucial role in saltatory conduction (Devaux and Gow, 2008). These junctions form a continuous diffusion barrier throughout the internode between successive layers of the myelin membrane sheet (Peters, 1961; Schnapp and Mugnaini, 1978) and are comprised only of claudin 11 (Gow et al., 1999; Morita et al., 1999). Importantly, the absence of these TJs has minimal impact on myelin architecture or axon structure, but conduction velocity (CV) is strongly reduced in small diameter fibers.
To define the mechanism that accounts for the conduction velocity abnormalities in Claudin 11-null optic nerves, we develop and characterize two novel computational models of small diameter fibers. The first model incorporates TJs in parallel with the compact myelin and is reminiscent of the double cable model (DCM). The second TJ model (TJM) considers TJs as a series resistance with the myelin. Both models also include axoglial junctions at paranodes that are consistent with ultrastructural studies of these junctions (reviewed by Rosenbluth, 1999) as well as our data showing that they are permeable to peptide toxins (Devaux and Gow, 2008). Herein, our simulations reveal that TJs decrease the capacitive charge of myelin in small fibers and recapitulate important aspects of the electrophysiology of optic nerves from Claudin 11-null mice (Devaux and Gow, 2008).
Methods
Simulation environment
The Cellbuilder module within the Neuron (version 5.9) simulation environment (http://www.neuron.yale.edu/neuron/) was used to generate models in the current study (Hines and Carnevale, 1997; 2001). Examples of 0.6 μm axons ehsheathed with 3 wraps of myelin membrane according to the DCM or the TJM are archived in ModelDB (Accession # 122442) for downloading from http://www.neuron.yale.edu/neuron/. Scalability within the simulation environment using the spreadsheet accompanying the archived models enables generation of a series of neurons with differing axonal diameters. In the current study, we characterize axons ranging between 0.3 – 4 μm. The Na+ and K+ channels comprising the active membrane properties are specified using the Channel Builder module. The specific parameters for axon dimensions and each ion channel are provided in Suppl. Tables 1 – 3.
Computational accuracy
For numerical accuracy and stability during computations, all compartments are further subdivided according to the d-lambda rule (Hines and Carnevale, 1997; 2001), with d-lambda = 0.01. Integrations of differential-algebraic equations are solved for variable time steps (absolute tolerance = 0.001) using the differential algebraic solver with preconditioned Krylov (DASPK).
Model compartmentalization
To accommodate the known complexity and domain organization of myelinated axons (Scherer and Arroyo, 2002), simulated neurons are compartmentalized at the level of the myelin sheath, with 1 nodal, 4 paranodal, 1 juxtaparanodal, 1 internodal, 1 juxtaparanodal and 4 paranodal compartments in a repeating pattern. The proximal and distal ends of the axons are closed with a cell soma (10 μm diameter) and a synapse (1 μm in length), respectively. In addition, the proximal-most myelin sheath is preceded by a 1 μm compartment of unmyelinated axon. The physical dimensions of each compartment are calculated using a series of equations detailed in the following sections.
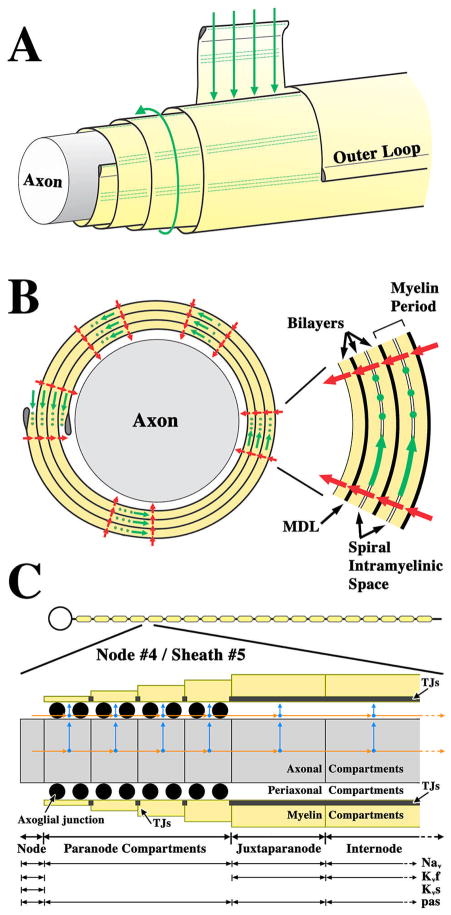
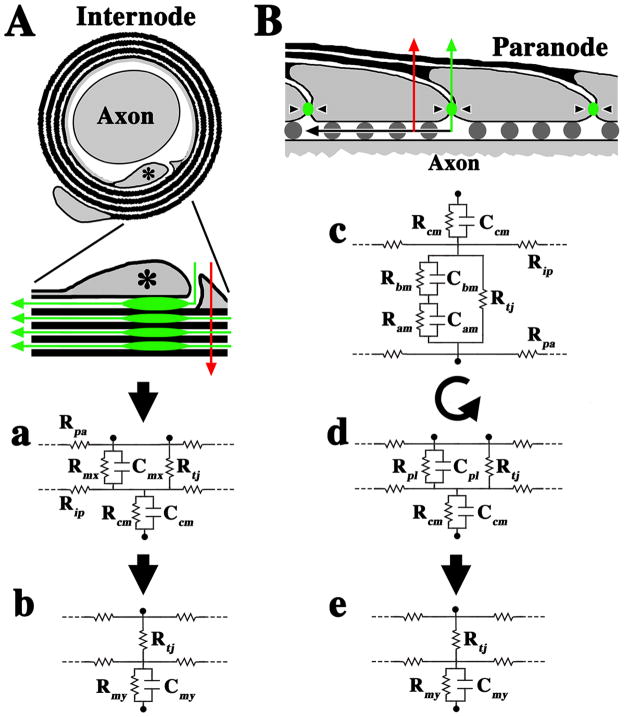
The schematic in Fig. 1A depicts several relevant structural and spatial complexities in a small axon ensheathed with four wraps of myelin membrane. The outer lamellae are shown cut away (left) to reveal underlying structures, particularly the TJs in the sheath, which are collectively known as the radial component of myelin (Peters, 1961). The radial component is visible with the electron microscope as local radial changes in membrane thickness across most myelin lamellae (green dots in Fig. 1B), and is particularly common in the vicinity of the outer and inner loop.
Fig. 1. Equivalent circuits for modeling myelin sheaths.
A. Schematic representation of an axon ensheathed with four wraps of myelin membrane. Outer layers are cut away (left) to reveal the underlying structures. Partial unraveling of the myelin shows it to be a flat membrane sheet spiraling around the axon. Current flow into the intramyelinic space between layers of the myelin membrane is normally blocked by TJs, which are parallel rows of intramembrane particles that seal the entire perimeter of the myelin sheath (green dots). This is analogous to the role that TJs play in sealing the paracellular space in polarized epithelia. The absence of TJs in Claudin 11-null mice would favor current flow through the intramyelinic space (green arrows). B. Cross section of a myelin sheath in A showing the spiral intramyelinic compartment and the path through the myelin sheath (green arrows) if TJs (green dots) were absent. Current can also flow through the myelin membrane (red arrows). The inset, right, shows in greater detail the lipid membrane spiral in the myelin and spiral intramyelinic compartment. C. Model of a myelinated neuron with 19 nodes of Ranvier and 20 myelin sheaths (top). The expanded view shows that 1 compartment is used for representing nodes, 4 for paranodes, 1 for juxtaparanodes and 1 for internodes. At paranodes, myelin thickness increases linearly away from the node and is constant across the juxtaparanode and internode. Arrows represent axial (orange) and radial (blue) current pathways. Axon diameter is constant along the fiber (Rosenbluth, 1995).
If the myelin sheath were unraveled from around the axon it would be a flat membrane sheet or envelope. The cytoplasmic surface of the membrane would be inside the envelope and the extracellular surface would be outside. Thus, in its native configuration the extracellular surfaces of adjacent spiral layers are juxtaposed and form the boundaries of a narrow spiral compartment called the intramyelinic space (inset in Fig. 1B), which extends the length of the myelin internode. In the absence of TJs, which normally define and seal this compartment, ions or other solutes may permeate the myelin sheath from the interstitium and periaxonal space (green arrows in Fig. 1A and B).
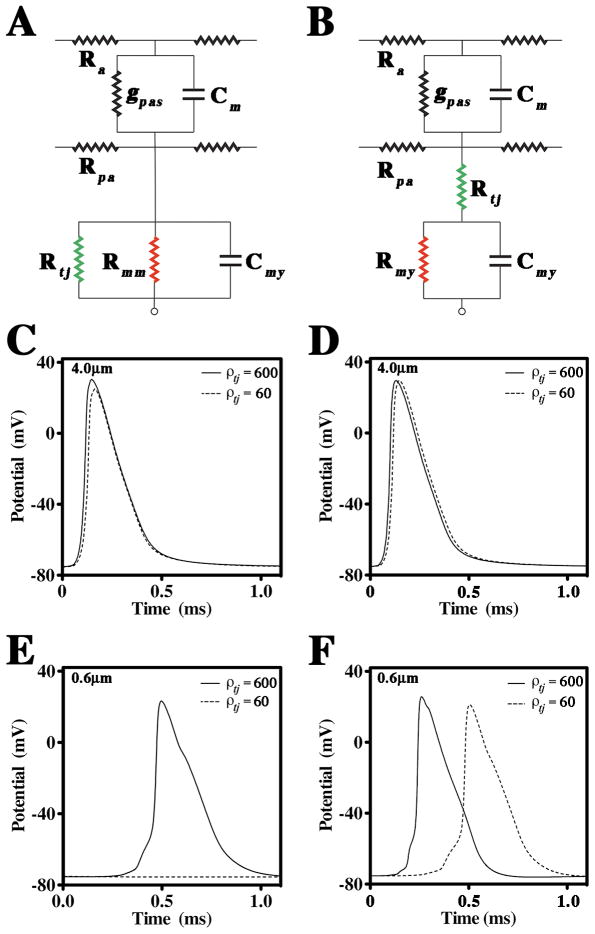
Such an organization suggests that TJs may form a series resistance with the myelin membrane (resistance and capacitance) to impede currents that would otherwise charge the myelin membrane. Thus, myelin may be represented as alternating TJs and myelin membranes in series. However, to enable computation, we have simplified this representation to a single TJ resistance in series with the myelin resistance and capacitance (Fig. 2A; TJM). Alternatively, myelin TJs could occlude current propagation along the radial (spiral)pathway across the myelin, which necessitates representation as a resistance in parallel with the myelin membrane layers. We simplified this representation to a single TJ resistance in parallel with the myelin resistance and capacitance (Fig. 2B; DCM).
Fig. 2. Geometry and equivalent circuits for the DCM and TJM.
A, B. Equivalent electrical circuits for the internode of a myelinated axon. In A, the double cable model (DCM) incorporates TJs as a low resistance path in parallel with the myelin membrane. In B, the TJM incorporates TJs in series with the myelin. The TJ capacitance is assumed to be negligible compared to the membrane capacitance (Clausen, 1989; Reuss, 2001) and is ignored. Ra and Rpa, axial resistances of the axoplasm and periaxonal space; gpas and Cm, conductance and capacitance of the axonal membrane; Rtj, TJ resistance; Rmy and Cmy, resistance and capacitance of myelin; Rmm, high resistance of a typical membrane bilayer. C, D. APs simulated in a 4 μm diameter axon (measured at the midpoint of node #4) using the DCM and TJM, respectively, in the presence (ρ tj = 600 Ohm.cm2) and absence of TJs (ρ tj = 60 Ohm.cm2). E, F. APs simulated in a 0.6 μm diameter axon using the DCM and TJM, respectively, in the presence (ρ tj = 600 Ohm.cm2) and absence of TJs (ρ tj = 60 Ohm.cm2).
Relationships for internodal axon diameter with paranodal length, myelin thickness and internodal length
Published data reveal linear relationships between axon diameter and several morphological parameters – paranode length, internode length, and myelin sheath thickness – enabling us to generate detailed neuron representations of different sizes. Thus, the length of each paranodal compartment is described by (Southwood et al., 2004):
| (1) |
where, Di = internodal axon diameter
The number of myelin wraps covering the axon at paranodes increases linearly with distance from the nodes and has constant thickness (internodal myelin thickness) in the juxtaparanode and internode compartments. The number of myelin wraps (n) at internodes is described by (Waxman and Bennett, 1972):
| (2) |
| (3) |
| (4) |
The length of the myelin sheath (8 paranodes + 2 juxtaparanodes + 1 internode) is described by (Ibrahim et al., 1995):
| (5) |
| (6) |
Internodal Delays
Conduction velocities were calculated for each myelinated fiber diameter (0.3 – 4 μm fiber diameter) according to the equation derived by Boyd and Kalu (1979) for small PNS axons. Internodal delay was then determined by:
| (7) |
where internodal length was calculated using equation (5) and CV = 4.6 × fiber diameter.
These data were fitted to a two-phase exponential decay curve (R2 = 0.9995) using Prism software (Graphpad Software Inc., San Diego, CA).
Relationships between resistivity and resistance, capacity and capacitance
In both computational models, we specify TJ resistivity (ρtj) as a transepithelial resistivity in Ohm.cm2. Similar to previous computational models of polarized epithelia, we assume that TJs have resistance but negligible capacitance compared with the membrane capacitance. For the TJM, the TJ resistance in each compartment is given by:
| (8) |
where, Stj is the planar surface area of non-compact myelin juxtaposed to the axolemma
Similarly, for the TJM, myelin resistance in each compartment is derived from the resistivity, ρmy (Ohm.cm2), by:
| (9) |
where, Smy is the surface area of compact myelin calculated using the radius midway between the inner and outer myelin surfaces
For the DCM, myelin resistance in each compartment is derived from the canonical myelin resistivity, ρmm (Ohm.cm2) and ρtj (Ohm.cm2), by:
| (10) |
The myelin capacitance in each compartment is derived from capacity, cmy, by:
| (11) |
The axon and the myelin sheath are separated by a narrow fluid-filled space referred to as the periaxonal space, the resistance of which is defined as:
| (12) |
where, ρpa = resistivity of the periaxonal space in Ohm.cm; L = compartment length; A = cross sectional area of the periaxonal space.
We have demonstrated that axoglial junctions at paranodes, also known as transverse bands, are porous to peptides in adult mouse optic nerve and rat spinal cord (Devaux and Gow, 2008) which contrasts with the prevailing view that these junctions seal the paranodal space between the axon and myelin sheath (reviewed in Hartline and Colman, 2007). Accordingly, we do not represent paranodal axoglial junctions as impermeable barriers in the current study but, rather, we estimate their resistance from morphologic data. Freeze fracture electron micrographs reveal that the paranodal periaxonal space is partially filled by the macromolecular complexes of axoglial junctions (Schnapp and Mugnaini, 1978), which occupy approximately 50 % of the volume. This might reasonably be expected to be double the resistance of Rpa. Thus, the axoglial junction resistance, Raj, in each paranodal compartment is defined by:
| (13) |
where, AGJ = the fractional occupancy of axoglial junctions (0.5)
To simplify the equivalent circuit, we assume that the capacitance of axoglial junctions is negligible.
Specification of active properties of the axonal membrane
To examine active properties, we have incorporated Nav, Kvf, and Kvs channels into appropriate compartments of the axolemma (Fig. 1C). These mechanisms are not all-inclusive of those known or thought to be present along myelinated axons; however, they reflect the sum of quantitatively-characterized mechanisms and are the dominant components modulating AP propagation. The Nav, Kvf, and Kvs currents are modeled using the Goldman-Hodgkin-Katz constant field equations:
| (14) |
| (15) |
| (16) |
where ghk() represents the Nernst equation for each monovalent cation (in parentheses)
| (17) |
where x = k(V − d)
| (18) |
The parameters A, k, and d are specified in Suppl. Table 2, and the maximum permeabilities of the channels in each axon compartment are indicated in Suppl. Table 3. Computational analyses are conducted (at 37°C) at the fourth node of Ranvier and fifth myelin sheath (Fig. 2A) after initiation of a propagating AP at the level of the cell body.
Simulation execution
Simulations are initiated and allowed to attain a resting state for 5 ms simulation time before current (2.5 – 7 nA) is injected into the mid-point of the soma as a square pulse of 100 μs duration. The propagation of the AP along the axon is measured up to 15 ms.
Measuring the membrane time and space constants
Tau and Lambda were measured in different myelin sheath compartments in the absence of active conductances (Nav, Kvf and Kvs), but in the presence of the passive leak conductance, to examine the passive cable proprieties of myelinated axons. For Tau, a square current pulse was injected directly into node #3 for 0.3 ms to depolarize the membrane > 100 mV and the voltage decay at the mid-points of node #4 and the proximal juxtaparanode and internode of myelin sheath #5 were plotted against time. Tau was computed as the time (ms) taken to fall to 37 % of the maximum voltage measured at the location of the measurement.
Lambda was determined by injecting a square pulse (2.5 nA) of 0.3 ms duration (the approximate rise time of an AP) into node #3 and plotting Vmax at the mid-points of 10 successive nodes, juxtaparanodes or internodes as a function of distance (mm). After fitting a single phase exponential decay curve to the data, Lambda was computed as the distance corresponding to 37 % of Vmax at the injection site. The fit of exponential decay curves to the data were evaluated using several statistical analyses, all of which were implemented using Prism software. First, Runs tests showed that all data sets did not differ statistically from a single phase exponential decay curve (P > 0.16). Second, Goodness of Fit tests showed that for all curves, R2 > 0.999. Third, Kolmogorov-Smirnov analyses indicated that residuals for all curves were normally distributed (P > 0.1).
Results
Novel computational models of TJs in CNS myelin sheaths
In the current study, we develop and characterize two novel computational models for small CNS myelinated fibers using appropriate physical dimensions from the literature and we incorporate TJ resistances into the myelin (Methods). An overview of the simulation (Fig. 1C) shows an axon with 20 myelin sheaths, a portion of which is expanded to show salient sub-compartments (Fig. 2A, B).
In our DCM computational model, we expand on a double cable configuration used previously for large diameter myelinated axons (Halter and Clark, 1991; McIntyre et al., 2002) by inserting TJs as a resistance in parallel with the myelin resistance and capacitance (Fig. 2A). In our TJM, we consider an alternative configuration that effectively places the TJ resistance in series between the axon and compact myelin membranes (Fig. 2B).
Tight junction resistance has not been measured directly in myelin sheaths of the CNS or PNS; however, TJ resistivity, ρtj, is known for other tissues and varies widely from 6 – 31,000 Ohm.cm2 (Claude and Goodenough, 1973; Reuss, 2001). The resistivity of Sertoli cell TJs, which are comprised solely of claudin 11 (Gow et al., 1999), has been reported and approximates 600 Ohm.cm2 (Janecki et al., 1991). In our preliminary analysis and for the present study, we tested a wide range of values for ρtj (Fig. 4 and Suppl. Fig. 1). These analyses suggest that the value for ρtj = 600 Ohm.cm2 is appropriate for simulations of myelin containing TJs and 60 Ohm.cm2 for myelin lacking TJs.
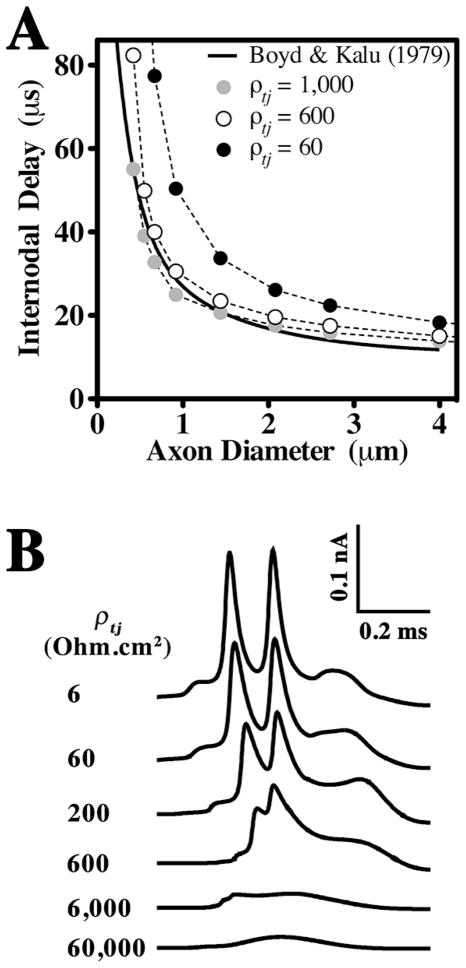
Fig. 4. Estimates of myelin TJ resistivity.
A. Internodal delays calculated from the equation of Boyd and Kalu (1979) (Methods) and using the TJM for several values of ρtj are plotted as functions of axon diameter. The TJM closely fits the published data (solid line) when ρtj is 600–1000 Ohm.cm2. B. Waveforms of internodal currents recorded at the mid-point of myelin sheath #5 for a 0.6 μm axon are shown for a series of ρtj values. Above a value for ρtj ~ 600 Ohm.cm2, internodal currents exhibit monotonic increases and decreases. Narrow split-peak waveforms are generated for smaller values of ρtj and are reminiscent of membrane currents recorded in vivo (Tasaki, 1955). Each peak in the waveforms reflects currents generated by APs at the proximal and distal nodes (respectively) of sheath #5.
Published measurements of total CNS myelin resistivity, ρmy, range from 100 – 1000 Ohm.cm2 (Tasaki, 1955; Barrett and Barrett, 1982; Blight, 1985; Halter and Clark, 1991; Stephanova and Bostock, 1996; Vabnick et al., 1999). Because myelin in the DCM is represented by the aggregate of the TJ and myelin membrane resistances in parallel, ρmy is dominated by ρtj and we use the canonical resistivity, ρmm = 20,000 Ohm.cm2, for a double membrane (Fig. 2A). Thus, we effectively equate the low resistance pathway through the myelin sheath originally postulated by Blight (1985) to TJs that seal the intramyelinic space. We make no such assumption in the TJM and we use ρmy = 300 Ohm.cm2 for the TJM, which still allows for the existence of a low resistance pathway of unknown origin.
The general shape and characteristics of APs generated by the DCM and TJM are similar in the presence of TJs (Fig. 2C and D; Suppl. Tables 4 and 5). For 4 μm diameter axons, the latency of APs is only marginally increased by the absence of TJs (dotted APs), which is consistent with a minimal effect of the ablation of Claudin 11 expression on conduction in spinal cord axons (Devaux and Gow, 2008). In contrast, the shape, duration, time to threshold (i.e. −55 mV), latency and amplitude (Vmax) of APs in 0.6 μm axons are significantly impacted by the absence of TJs in both models (Fig. 2E and F). In the DCM, small axons fail to conduct; however, they are functional for values of ρtj = 214 Ohm.cm2 and above (Fig. 2E) and exhibit shape changes similar to those for the TJM (Suppl. Tables 4 and 5). In the TJM, the latency is increased, Vmax is reduced and the APs are broadened. However, the width of the AP at half maximal voltage (Vmax/2) is independent of TJs, which indicates that AP broadening mainly stems from an increase in the time to threshold. Such effects are consistent with an increase in the membrane time constant, which also accounts for the longer latencies of APs when TJs are absent.
The TJ configuration of the TJM best accounts for the optic nerve data from Claudin 11-null mice
Although DCM and TJM simulations recapitulate the CV slowing observed in Claudin 11-null mice (Devaux and Gow, 2008), the TJM more effectively models this behavior and an analysis of CV as a function of axon diameter highlights further differences. As we demonstrated previously (Fig. 6A of Devaux and Gow, 2008), ratios of the CVs from wild type and Claudin 11-null optic nerves increase with axon diameter (filled diamonds, Fig. 3A) and the TJM reasonably simulates this behavior (open circles). The DCM also can approximate the experimental data (filled triangles), but only for axon diameters of 0.9 μm and above; smaller fibers simulated by the DCM fail to conduct when TJs are absent.
Fig. 3. CV as a function of axon diameter in the DCM and TJM.
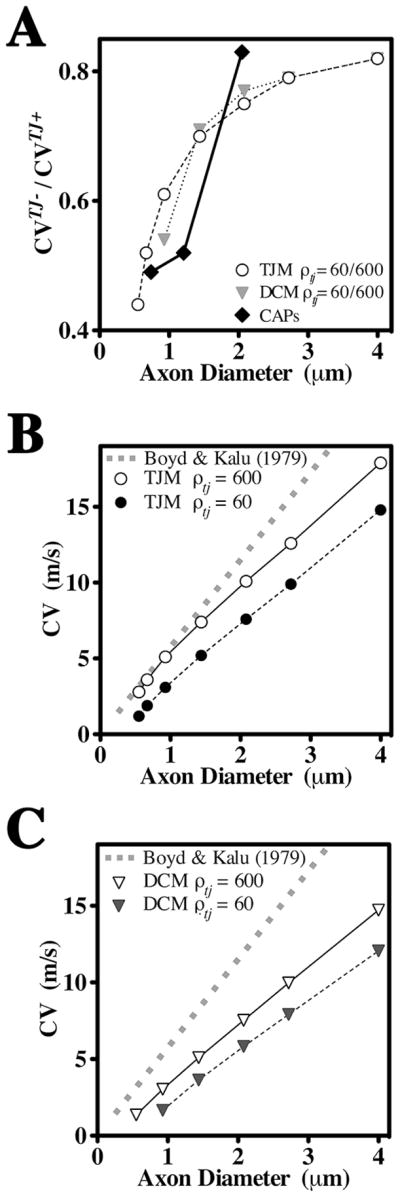
A. Ratios of CVs derived from optic nerves of wild type and Claudin 11-null mice (Devaux and Gow, 2008), and simulated by the DCM and TJM in the presence (ρtj = 600 Ohm.cm2) and absence (ρtj = 60 Ohm.cm2) of TJs, expressed as functions of axon diameter. B, C. Values of CVs calculated using the equation of Boyd and Kalu (1979) for small PNS axons are expressed as a function of axon diameter (gray dash) and compared with simulations from the TJM (B) and DCM (C) in the presence and absence of TJs.
A previous study demonstrated in small PNS axons that conduction velocities evolve linearly as a function of axon diameter (Di) with a factor of 4.6 m.s−1.μm−1(Boyd and Kalu, 1979). This relationship appears appropriate for central spinal axons (Blight, 1983; Blight and Someya, 1985) and is used herein to represent CVs of CNS axons (gray dash, Fig. 3B). The CVs derived from the TJM are in close agreement with the Boyd and Kalu (1979) data (open circles) but are significantly slower in the absence of TJs (filled circles). In contrast, CVs derived from the DCM are slower than the Boyd and Kalu data (1979) in the presence or absence of TJs and small fibers only conduct with TJs (Fig. 3C). Thus, the DCM does not adequately represent the electrophysiological properties of optic nerve axons in Claudin 11-null mice. Indeed, 50 % of the myelinated axons in optic nerve are smaller than 0.9 mm diameter and the experimental data from Claudin 11-null optic nerve indicates that these fibers conduct (Devaux and Gow, 2008).
Estimating the resistivity of CNS myelin TJs
In the absence of measurements for ρtj in myelin, the TJM provides two methods for estimating this parameter. First, previous studies show that the latency between APs at successive nodes, known as the internodal delay, is independent of axon diameter for large myelinated fibers (Rasminsky and Sears, 1972) but increases for axons below 4 μm. We calculated internodal delays using the Boyd and Kalu (1979) data for comparison with internodal delays obtained using the TJM (Fig. 4A). Testing several values for ρtj in the TJM yields internodal delays that adequately recapitulate the experimental data when ρtj = 600 – 1000 Ohm.cm2.
The second method to estimate ρtj involves consideration of the shape of internodal membrane currents recorded from single frog myelinated fibers, which exhibit a narrow split-peak waveform (Tasaki, 1955). Replicating the shape of these waveforms using the TJM requires values for ρtj of 200 – 600 Ohm.cm2 (Fig. 4B). The intersection of estimates from each method suggests a resistivity of approximately 600 Ohm.cm2 for claudin 11 TJs in CNS myelin, which agrees well with measurements in Sertoli cells (Janecki et al., 1991).
TJs isolate internodes from depolarization by APs
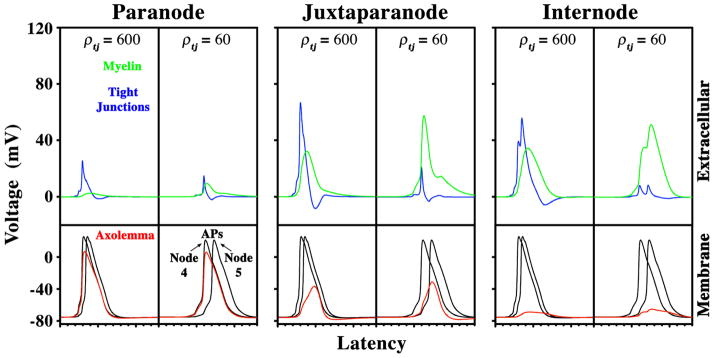
The presence of K+ channel-mediated hyperpolarizing afterpotentials in the optic nerves of Claudin 11-null mice (Devaux and Gow, 2008) suggests that APs depolarize internodal membranes and activate ion channels beneath the myelin. Voltages across the axolemma, TJs and myelin are shown in Fig. 5 for a 0.6 μm diameter axon. In the presence of TJs (ρtj = 600), most of the voltage drop at the paranode occurs across the axolemma and this does not change when TJs are absent. In the juxtaparanode, significant voltage drops occur across the axolemma, TJs and myelin sheath and the loss of TJs (ρtj = 60 Ohm.cm2) increases the voltage across the myelin. Importantly, the voltage across the juxtaparanodal axolemma increases by more than 5 mV, which significantly increases Na+ and K+ currents in this region (gray lines in Suppl. Fig. 1).
Fig. 5. Potentials across the myelin sheath in the presence or absence of TJs.
Using the TJM and ρtj = 600 Ohm.cm2, voltages across the axolemma, TJs and myelin sheath for a 0.6 μm axon have been determined at paranodes, juxtaparanodes and internodes. The loss of TJs has been simulated for ρtj = 60 Ohm.cm2. The voltages across the myelin increase substantially when the TJs are absent. The juxtaparanodal axonal membrane is significantly depolarized when TJs are present, but more so in the absence of TJs. Depolarization of the internodal axolemma is also increased in the absence of TJs.
Voltage drop in the internode occurs mainly across the TJs and myelin, but the axolemma is depolarized by 6 mV in the presence of TJs and by 9.5 mV when they are absent. Internodal Na+ channels participate in axolemmal depolarization in small axons, because lowering their permeability diminishes the depolarization amplitude. Thus, internodal depolarization stems from propagation of the nodal APs and activation of internodal Na+ channels. Large diameter fibers also develop large potentials across the myelin (Suppl. Fig. 2); however, the axonal membrane in the juxtaparanode and internode is minimally depolarized and ion channel activation is minimal.
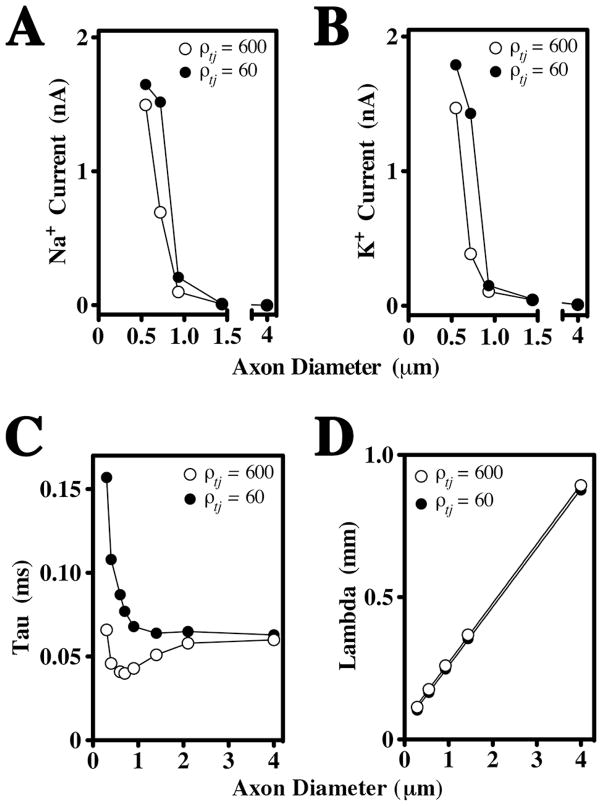
The dependence of juxtaparanodal axonal membrane potentials on TJs in small fibers is a key finding. As shown in Fig. 6A and B, juxtaparanodal Na+ and K+ currents are strongly influenced by the presence of TJs. In contrast, axons greater than 1 μm in diameter do not rely on TJs to suppress membrane currents, which likely stems from the thickness of the myelin sheath. However, myelin ensheathment of small axons comprises only a few wraps and is relatively leaky. As a result, the amplitude of juxtaparanodal membrane currents are dependent on ρtj and axon caliber. Thus, TJs dampen juxtaparanode (and internode) membrane depolarization and ion channel activation in small fibers, which are selectively vulnerable to the absence of TJs because of their rudimentary myelin ensheathment.
Fig. 6. TJs suppress juxtaparanodal currents in small fibers and increase the membrane time constant.
A, B. Juxtaparanodal Na+ (A) and K+ (B) currents are plotted as functions of axon diameter (0.6 – 4 μm) in the presence and absence of TJs in the TJM. Juxtaparanodal currents in the smallest fibers are activated by APs even in the presence of TJs, but increase further in the absence of TJs. These currents become negligible for axons greater in diameter than 0.9 μm in the presence or absence of TJs. C. The membrane time constant, Tau, is measured at nodes of Ranvier in the absence of active conductances and is plotted as a function of axon diameter (0.3 – 4 μm). The presence of TJs strongly reduces Tau in small axons but has little effect in axons larger then 2μm. D. The space constant, Lambda, measured at internodes (juxtaparanodes and nodes are not shown) is a linear function of axon diameter and is not significantly affected by the presence of TJs in either small or large fibers.
TJs modify the membrane time constant but not the length constant
The positive effect of TJs on CV indicates that they modify the passive cable properties of myelin. To understand the underlying mechanism, we removed the active ion conductances (Nav, Kvs and Kvf) from TJM axons and measured the membrane time constant, Tau, at three locations: internodes (Suppl. Fig. 3A), juxtaparanodes (Suppl. Fig. 3B) and nodes (Fig. 6C). At all three sites, Tau is invariant for axons greater than 2 μm diameter irrespective of the presence or absence of TJs. In axons smaller than 2 μm, TJs reduce Tau by as much as two-fold which indicates that they decrease the charging of myelin, thereby enhancing its insulation properties.
Tau increases sharply in axons below 1 μm, particularly in the internode, which reflects increased myelin capacitance and decreased myelin resistance in small fibers (shaded areas, Suppl. Fig. 4). Importantly, increases in Tau parallel the rise in Na+ and K+ currents, indicating that internodal depolarization stems from slow discharging of the myelin capacitance. Thus, in the absence of TJs the time constant of the axonal membrane is dictated by charging of the myelin capacitance. Because the myelin is thick for large fibers, its capacitance is very low and the presence of TJs does not appreciably influence the internodal time constant.
In small fibers, the increase of Tau at nodes in the absence of TJs (Fig. 6C) likely accounts for the increased AP thresholds observed in optic nerves from Claudin 11-null mice (Devaux and Gow, 2008). Accordingly, these findings demonstrate that TJs also play an important role in modulating the properties of axonal membrane domains outside of the myelin sheath to reduce the nodal time constant and minimize the time to AP thresholds in small fibers.
In contrast to Tau, Lambda is a linear function of axon diameter in the internode (Fig. 6D), juxtaparanode and node (not shown), and is minimally affected by the presence or absence of TJs, even in small fibers (Fig. 6D). Thus, the major impact of TJs on myelin function and saltatory conduction is through changes to the membrane time constant.
Paranodal myelin TJs do not play a major role in isolating the axolemma
Axoglial junctions in the CNS and PNS have received considerable attention following the molecular characterization of three major components of these macromolecular structures and because of strong phenotypes in knockout mice associated with the disruption of these junctions. Indeed, such studies have led to the view that the role of myelin in enabling saltatory conduction is critically dependent on the structural integrity of axoglial junctions for maintaining a boundary between nodal Na+ channels and juxtaparanodal K+ channels.
To determine if paranodal TJs also are important for saltatory conduction, we simulated the site-specific loss of TJs in paranodes, juxtaparanodes or internodes, and normalized the resulting CVs to myelin containing TJs. This ratio is shown as a function of axon diameter in Fig. 7. Reductions in CV are most pronounced in small axons, as expected; however, the absence of paranodal TJs minimally reduces CV compared with the loss of juxtaparanodal or internodal TJs. Thus, the function of TJs is clearly most important for minimizing the charging of the myelin sheath in regions that overlie ion channels in the axonal membrane, rather than minimizing current shunts between the node and the paranodal compartment.
Fig. 7. Relative contributions to CV of TJs in different regions of the myelin sheath.
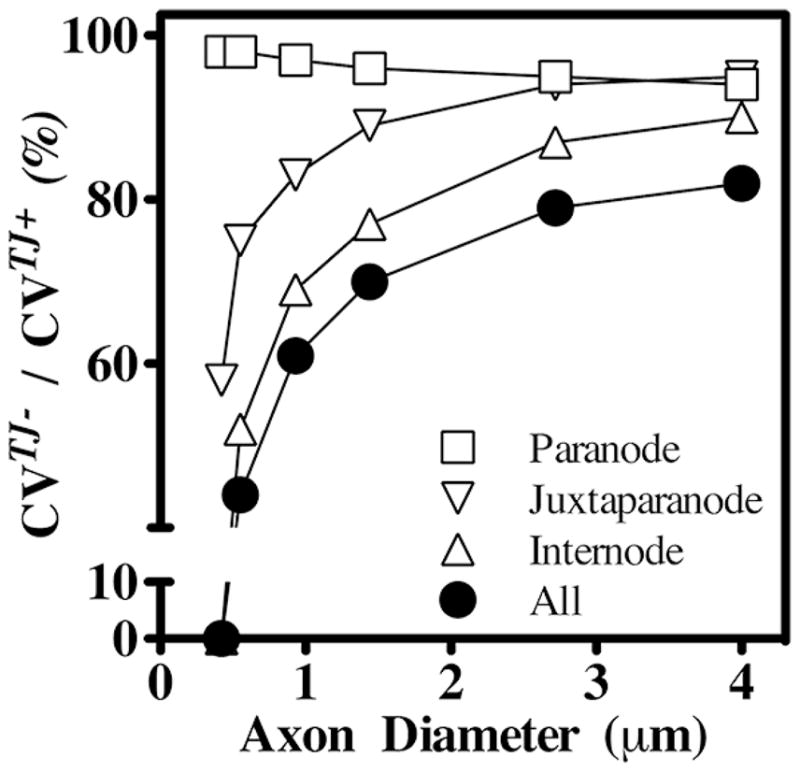
To determine the regional importance of myelin TJs in TJM simulations, ρtj have been decreased from 600 to 60 Ohm.cm2 in the paranodes, juxtaparanodes or internodes separately (open symbols) or collectively (closed symbols) and the effects on CVs have been computed as functions of axon diameter. The ratio of CVs in the presence (CVTJ+) or absence (CVTJ−) of TJs demonstrates that juxtaparanodal and internodal TJs are more important for conduction than paranodal TJs.
Discussion
The head-to-head comparisons of the TJM and the DCM performed in the current study and our preceding work (Devaux and Gow, 2008) indicates that the TJM more closely recapitulates several aspects of the electrophysiological properties of optic nerve fibers from Claudin 11-null mice than does the DCM. The TJM accounts for the slower CVs, higher AP thresholds and larger K+ currents observed in the absence of TJs as well as their dependences on axon diameter. Importantly, the TJM is much more robust than the DCM when simulating axons less than 0.9 μm in diameter. Axons in this category are abundant in optic nerve and most of them conduct in Claudin 11-null mice.
In Fig. 8, we highlight salient morphological features of a myelinated fiber that suggests an equivalent circuit with a series configuration for TJs in the myelin sheath. Our rationale stems from topographic similarities between polarized epithelia (Tsukita et al., 2001) and non-compact regions of myelin (paranodal loops and inner mesaxon). In both of these cases, the paracellular space is occluded by TJs and, accordingly, we represent the non-compact cytoplasmic loops of myelin as a polarized “microepithelial” compartment subjacent to layers of compact membrane. The equivalent circuit of polarized epithelia has been explored previously (Clausen, 1989; Reuss, 2001) and is adapted in the current study to describe non-compact and compact regions of myelin at the internode (Fig. 8Aa) and paranode (Fig. 8Bc). We hypothesize that current shunting across the TJs simplifies the circuit to that shown in Fig. 8Ab and 8Be.
Fig. 8. Morphological model and equivalent circuits to describe the TJM.
A. Cross-section of a myelinated internode showing compact membrane (black) overlying an inner mesaxon (asterisk). The expanded view shows a trans-myelin pathway (red) across the compact membrane layers (red arrow) and a spiral pathway across the TJs. The TJs are aligned in the myelin but do not form a transverse current pathway. Rather, the flow is spiral through the TJs, which are in series with each other in successive myelin wraps and form a spiral pathway through the intramyelinic space. a. An equivalent circuit for the non-compact inner loop “microepithelium” (upper portion) and the compact membrane stack (lower). Rpa, axial periaxonal resistance; Rip, axial lamellar resistance. Rmx, Cmx, resistance and capacitance of the mesaxonal membrane; Rcm and Ccm, the resistance and capacitance of the myelin; Rtj, TJ resistance. The TJ capacitance is assumed to be negligible compared to the membrane capacitance (Clausen, 1989; Reuss, 2001) and is ignored. b. Because the mesaxonal/paranodal membrane resistance is high (Chiu and Schwarz, 1987), transverse currents may be largely shunted through Rtj, and the circuit can be simplified by placing Rtj in series with the myelin resistance and capacitance, Rmy and Cmy. B. Longitudinal section of a paranode (gray) and overlying myelin lamellae (black). Red and green arrows represent trans-myelin and spiral TJ pathways, respectively. Black arrow represents axial pathways through the periaxonal space, which is partially filled with axoglial junctions (dark gray circles). c. The equivalent circuit of paranodal loops shows compact myelin membranes (upper portion) and the paranodal loop “microepithelium” (lower). Ram, Cam, resistance and capacitance of the apical membrane of the paranodal loops; Rbm, Cbm, the basal membrane. d. Partial simplification of the circuit, where Ram, Cam and Rbm, Cbm are combined to yield Rpl, Cpl and the circuit is rotated 180° for comparison with the circuit in Aa. e. Similar to Ab, the circuit in Bd is simplified.
The TJM fits the physiological data and resolves inconsistencies from previous models
In pioneering work, Blight (1985) conceived a novel computational model of large myelinated axons by representing the internode as a double cable (separating the myelin compartment from the axonal membrane) and the myelin as a low resistance pathway across the internode. The representation demonstrates that charging and discharging of the myelin capacitance accounts for the depolarizing afterpotentials which follow APs, and suggests the existence of a paranodal leakage pathway, such as the one observed in earlier electrophysiological studies (Barrett and Barrett, 1982).
Although Blight’s DCM accurately accounts for the propagation of APs in large PNS fibers with thick myelin sheaths, it poorly represents the properties of small fibers that are common in the CNS. Indeed, our attempts to model AP propagation in optic nerve fibers using the DCM in previous work (Devaux and Gow, 2008) and the current study are inconsistent with electrophysiological measurements from wild type and Claudin 11-null mice. In particular, this model cannot account for slowed CVs stemming from the loss of myelin TJs in axons smaller than 0.9 μm (representing > 50% of optic nerve axons). These inadequacies indicate that the DCM lacks important features of CNS myelin that play major roles in the mechanisms governing saltatory conduction.
In the current study, our characterization of the TJM reveals that TJs insulate internodal membranes and diminish the capacitive charging of myelin, particularly in small fibers. As such, the TJM both corroborates and provides a molecular basis for Blight’s hypothesis (1985) that myelin diminishes internodal capacitance and shortens the membrane time constant. Because of TJ localization to juxtaposed membrane surfaces around the perimeter of the myelin sheath, we conclude that these junctions seal the extracellular intramyelinic space within the internode and increase myelin resistance. Consequently, TJs increase CV, lower the threshold of AP generation at nodes and suppress ion channel activation at juxtaparanodes and internodes. Although K+ currents do not directly influence CV, they do regulate nodal excitability and firing frequency by reducing internodal depolarization that may otherwise re-excite Na+ channels and prolong the refractory period.
Our conception of electrically-tight TJs in myelin sheaths, which minimize depolarization of the internode, does not contradict the widely-held view that paranodal axoglial junctions are critical mediators of saltatory conduction. However, our results do indicate that these junctions are permeable to soluble peptide toxins (Devaux and Gow, 2008) and our simulations demonstrate that they need not be electrically-tight to enable saltatory conduction. To be sure, axoglial junctions are critical for adhering the edges of myelin lamellae to the paranode and for maintaining the subdomain organization of the paranodal region, particularly with respect to the targeting of ion channels. Nonetheless, both axoglial junctions and TJs contribute to the conduction properties of myelinated fibers, with TJs playing their most important role in small fibers with a few membrane wraps.
An unresolved issue in the current study is the inability of either the DCM or the TJM to simulate myelinated axons with CVs as slow as those we measure in Claudin 11-null optic nerve and controls at 35°C (Suppl. Fig. 5). We have considered several alternatives to account for these discrepancies. First, the magnitudes of the Nav channel permeability and the nodal and paranodal leak currents in the simulations may be inappropriate. Ion channel permeabilities are unknown for CNS axons and we use values obtained from PNS axons (Suppl. Tables 1 and 3). Simulations of 0.6 μm axons with higher nodal leak or lower Nav channel permeability exhibit significantly slower CVs in both models; however, internodal currents are grossly distorted (resulting in triple maxima waveforms) and resemble neither split-peak internodal currents in vivo (Tasaki, 1955) nor currents arising from the TJM in Fig. 4B. Second, we have assumed a high axial resistance for the intramyelinic space (Rip in Fig. 8) because of its narrow width (ca. 30 nm Agrawal et al., 2009) and considerable length along the internode and it is tempting to speculate that TJs may also contribute significantly to this resistance. However, simulations in which we lower the axial intramyelinic resistance when TJs are absent have no impact on conduction; thus, this parameter is unlikely to be a major source of CV discrepancies. Finally, to determine the length of myelin sheaths for different axons we use the internodal length versus fiber diameter equation derived by Ibrahim and colleagues (1995), which pertains to 1 – 12 μm CNS axons. Although this range of diameters largely overlaps the axons simulated in the current study, we cannot exclude the possibility that our estimates do not reflect the lengths of myelin sheaths in optic nerves in vivo.
Neurological phenotypes associated with disrupted myelin TJs
Previous molecular studies of white matter pathophysiology have focused on the roles of the paranode or axoglial junctions in causing abnormal localization of Na+ and K+ channels (Dupree et al., 1998; Bhat et al., 2001; Boyle et al., 2001; Sherman et al., 2005). Our data reveal a distinct mechanism whereby neurological abnormalities may stem from decreased juxtaparanodal and internodal TJ resistivity in the absence of abnormalities of the axoglial junction or other internodal abnormalities. Indeed, slowed CVs in the cerebellar, striatal, cerebral, or spinal white matter may easily account for the fine tremor, gate ataxia and hind limb weakness we observe in Claudin 11-null mice (Gow et al., 1999).
We also envision that neural network processing, which involves small myelinated axons connecting many regions of the brain through the corpus callosum, may be negatively impacted when myelin TJs are disrupted. If so, our data may account for some of the endophenotypes observed in patients with cognitive diseases. In this regard, reduced expression of CLAUDIN 11, and several other myelin-specific genes, has been reported in microarray analyses of autopsy samples from cingulate cortex and hippocampus of schizophrenia patients (Haroutunian et al., 2007). The neural pathways in these cortical regions are predominantly small myelinated fibers (Aboitiz et al., 1992), and significant temporal delays in transmission in the tens of milliseconds are likely in humans. Such delays would significantly perturb spike-timing dependent plasticity (Kampa et al., 2007), which suggests a plausible mechanism for the disconnectivity syndrome hypothesis (Stewart and Davis, 2004).
Together, this study accounts for, and provides mechanistic insights into, neurological abnormalities observed in Claudin 11-null mice and highlights the importance of claudin 11 TJs in small myelinated fibers for normal brain function (Devaux and Gow, 2008). Moreover, our data may provide unanticipated insight into schizophrenia endophenotypes and evoke novel therapeutic strategies focused on modulating ion channel activity, rather than neurotransmitters, to ameliorate disease symptoms.
Supplementary Material
Acknowledgments
We are grateful for guidance and support from Dr S. Scherer, Dept of Neurology University of Pennsylvania, PA; Drs M. Hines, Section of Neurobiology, and T. Carnevale, Dept of Psychology, Yale University, CT; Drs R. Andrade, Dept of Pharmacology, J. Li, Dept of Neurology, Ms Cherie Southwood, CMMG, Wayne State University, MI; Dr C. Abrams, SUNY Downstate Medical Center, NY. This work was supported by grants to A.G. from NINDS, NIH (NS43783), NIDCD, NIH (DC006262) the National Multiple Sclerosis Society (PP1372 and RG2891) and the William and Marie Carls Foundation, Detroit, Michigan, and to J.D. from the Association Française contre les Myopathiesand theNational Multiple Sclerosis Society (RG3839A1/T).
Footnotes
Statement of Interest
None.
References
- Aboitiz F, Scheibel AB, Fisher RS, Zaidel E. Fiber composition of the human corpus callosum. Brain Res. 1992;598:143–153. doi: 10.1016/0006-8993(92)90178-c. [DOI] [PubMed] [Google Scholar]
- Agrawal D, Hawk R, Avila RL, Inouye H, Kirschner DA. Internodal myelination during development quantitated using X-ray diffraction. J Struct Biol. 2009 doi: 10.1016/j.jsb.2009.06.019. [DOI] [PubMed] [Google Scholar]
- Barrett EF, Barrett JN. Intracellular recording from vertebrate myelinated axons: mechanism of the depolarizing afterpotential. J Physiol. 1982;323:117–144. doi: 10.1113/jphysiol.1982.sp014064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berthold C-H, Rydmark M. Morphology of normal peripheral axons. In: Waxman SG, Kocsis JD, Stys PK, editors. The Axon. Oxford University Press; 1995. pp. 13–48. [Google Scholar]
- Bhat MA, Rios JC, Lu Y, Garcia-Fresco GP, Ching W, Martin MS, Li J, Einheber S, Chesler M, Rosenbluth J, Salzer JL, Bellen HJ. Axon-glia interactions and the domain organization of myelinated axons requires neurexin iv/caspr/paranodin. Neuron. 2001;30:369–383. doi: 10.1016/s0896-6273(01)00294-x. [DOI] [PubMed] [Google Scholar]
- Blight AR. Axonal physiology of chronic spinal cord injury in the cat: intracellular recording in vitro. Neuroscience. 1983;10:1471–1486. doi: 10.1016/0306-4522(83)90128-8. [DOI] [PubMed] [Google Scholar]
- Blight AR. Computer simulation of action potentials and afterpotentials in mammalian myelinated axons: the case for a lower resistance myelin sheath. Neuroscience. 1985;15:13–31. doi: 10.1016/0306-4522(85)90119-8. [DOI] [PubMed] [Google Scholar]
- Blight AR, Someya S. Depolarizing afterpotentials in myelinated axons of mammalian spinal cord. Neuroscience. 1985;15:1–12. doi: 10.1016/0306-4522(85)90118-6. [DOI] [PubMed] [Google Scholar]
- Boyd IA, Kalu KU. Scaling factor relating conduction velocity and diameter for myelinated afferent nerve fibres in the cat hind limb. J Physiol. 1979;289:277–297. doi: 10.1113/jphysiol.1979.sp012737. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boyle ME, Berglund EO, Murai KK, Weber L, Peles E, Ranscht B. Contactin orchestrates assembly of the septate-like junctions at the paranode in myelinated peripheral nerve. Neuron. 2001;30:385–397. doi: 10.1016/s0896-6273(01)00296-3. [DOI] [PubMed] [Google Scholar]
- Brill MH, Waxman SG, Moore JW, Joyner RW. Conduction velocity and spike configuration in myelinated fibres: computed dependence on internode distance. J Neurol Neurosurg Psychiatry. 1977;40:769–774. doi: 10.1136/jnnp.40.8.769. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cajal SR. Texture of the Nervous System of Man and the Vertebrates. Springer; 1899. [Google Scholar]
- Chiu SY, Schwarz W. Sodium and potassium currents in acutely demyelinated internodes of rabbit sciatic nerves. J Physiol. 1987;391:631–649. doi: 10.1113/jphysiol.1987.sp016760. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Claude P, Goodenough DA. Fracture faces of zonulae occludentes from “tight” and “leaky” epithelia. J Cell Biol. 1973;58:390–400. doi: 10.1083/jcb.58.2.390. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clausen C. Impedance analysis in tight epithelia. Methods Enzymol. 1989;171:628–642. doi: 10.1016/s0076-6879(89)71035-1. [DOI] [PubMed] [Google Scholar]
- del Rio-Hortega P. Tercera aportacion al conocimiento morfologico e interpretacion funcional de la oligodendroglia. Mem Real Soc Espan Hist Nat. 1928;14:5–119. [Google Scholar]
- Devaux JJ, Gow A. Tight Junctions Potentiate The Insulative Properties Of Small CNS Myelinated Axons. J Cell Biol. 2008;183:909–921. doi: 10.1083/jcb.200808034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dupree JL, Coetzee T, Blight A, Suzuki K, Popko B. Myelin galactolipids are essential for proper node of Ranvier formation in the CNS. J Neurosci. 1998;18:1642–1649. doi: 10.1523/JNEUROSCI.18-05-01642.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frankenhaeuser B, Huxley AF. The Action Potential in the Myelinated Nerve Fiber of Xenopus Laevis as Computed on the Basis of Voltage Clamp Data. J Physiol. 1964;171:302–315. doi: 10.1113/jphysiol.1964.sp007378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gow A, Southwood CM, Li JS, Pariali M, Riordan GP, Brodie SE, Danias J, Bronstein JM, Kachar B, Lazzarini RA. CNS Myelin And Sertoli Cell Tight Junction Strands Are Absent In Osp/Claudin 11-Null Mice. Cell. 1999;99:649–659. doi: 10.1016/s0092-8674(00)81553-6. [DOI] [PubMed] [Google Scholar]
- Halter JA, Clark JW., Jr A distributed-parameter model of the myelinated nerve fiber. J Theor Biol. 1991;148:345–382. doi: 10.1016/s0022-5193(05)80242-5. [DOI] [PubMed] [Google Scholar]
- Haroutunian V, Katsel P, Dracheva S, Stewart DG, Davis KL. Variations in oligodendrocyte-related gene expression across multiple cortical regions: implications for the pathophysiology of schizophrenia. Int J Neuropsychopharmacol. 2007;10:565–573. doi: 10.1017/S1461145706007310. [DOI] [PubMed] [Google Scholar]
- Hartline DK, Colman DR. Rapid conduction and the evolution of giant axons and myelinated fibers. Curr Biol. 2007;17:R29–35. doi: 10.1016/j.cub.2006.11.042. [DOI] [PubMed] [Google Scholar]
- Hines ML, Carnevale NT. The NEURON simulation environment. Neural Comput. 1997;9:1179–1209. doi: 10.1162/neco.1997.9.6.1179. [DOI] [PubMed] [Google Scholar]
- Hines ML, Carnevale NT. NEURON: a tool for neuroscientists. Neuroscientist. 2001;7:123–135. doi: 10.1177/107385840100700207. [DOI] [PubMed] [Google Scholar]
- Ibrahim M, Butt AM, Berry M. Relationship between myelin sheath diameter and internodal length in axons of the anterior medullary velum of the adult rat. J Neurol Sci. 1995;133:119–127. doi: 10.1016/0022-510x(95)00174-z. [DOI] [PubMed] [Google Scholar]
- Ilyin VI, Katina IE, Lonskii AV, Makovsky VS, Polishchuk EV. The Cole-Moore effect in nodal membrane of the frog Rana ridibunda: evidence for fast and slow potassium channels. J Membr Biol. 1980;57:179–193. doi: 10.1007/BF01869586. [DOI] [PubMed] [Google Scholar]
- Janecki A, Jakubowiak A, Steinberger A. Regulation of transepithelial electrical resistance in two-compartment Sertoli cell cultures: in vitro model of the blood-testis barrier. Endocrinology. 1991;129:1489–1496. doi: 10.1210/endo-129-3-1489. [DOI] [PubMed] [Google Scholar]
- Kampa BM, Letzkus JJ, Stuart GJ. Dendritic mechanisms controlling spike-timing-dependent synaptic plasticity. Trends Neurosci. 2007;30:456–463. doi: 10.1016/j.tins.2007.06.010. [DOI] [PubMed] [Google Scholar]
- Kirschner DA, Ganser AL, Caspar DLD. Diffraction studies of molecular organization and membrane interactions in myelin. In: Morell P, editor. Myelin. Plenum; 1984. pp. 51–95. [Google Scholar]
- McIntyre CC, Richardson AG, Grill WM. Modeling the excitability of mammalian nerve fibers: influence of afterpotentials on the recovery cycle. J Neurophysiol. 2002;87:995–1006. doi: 10.1152/jn.00353.2001. [DOI] [PubMed] [Google Scholar]
- Morita K, Sasaki H, Fujimoto K, Furuse M, Tsukita S. Claudin- 11/OSP-based tight junctions of myelin sheaths in brain and Sertoli cells in testis. J Cell Biol. 1999;145:579–588. doi: 10.1083/jcb.145.3.579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peters A. A radial component of central myelin sheaths. J Biophys Biochem Cytol. 1961;11:733–735. doi: 10.1083/jcb.11.3.733. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peters A. The node of Ranvier in the central nervous system. Q J Exp Physiol Cogn Med Sci. 1966;51:229–236. doi: 10.1113/expphysiol.1966.sp001852. [DOI] [PubMed] [Google Scholar]
- Rasminsky M, Sears TA. Internodal conduction in undissected demyelinated nerve fibres. J Physiol. 1972;227:323–350. doi: 10.1113/jphysiol.1972.sp010035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reuss L. Tight junction permeability to ions and water. In: Anderson JM, Cereijido M, editors. Tight Junctions. CRC Press; 2001. pp. 61–88. [Google Scholar]
- Rosenbluth J. Glial membranes and axoglial junctions. In: Kettenmann H, Ransom BR, editors. Neuroglia. Oxford University Press; 1995. pp. 613–633. [Google Scholar]
- Rosenbluth J. A brief history of myelinated nerve fibers: one hundred and fifty years of controversy. J Neurocytol. 1999;28:251–262. doi: 10.1023/a:1007083409850. [DOI] [PubMed] [Google Scholar]
- Scherer SS, Arroyo EJ. Recent progress on the molecular organization of myelinated axons. J Peripher Nerv Syst. 2002;7:1–12. doi: 10.1046/j.1529-8027.2002.02001.x. [DOI] [PubMed] [Google Scholar]
- Schnapp B, Mugnaini E. Membrane architecture of myelinated fibers as seen by freeze-fracture. In: Waxman SG, editor. Physiology and Pathobiology of Axons. Raven; 1978. pp. 83–123. [Google Scholar]
- Schwarz JR, Eikhof G. Na currents and action potentials in rat myelinated nerve fibres at 20 and 37 degrees C. Pflugers Arch. 1987;409:569–577. doi: 10.1007/BF00584655. [DOI] [PubMed] [Google Scholar]
- Sherman DL, Tait S, Melrose S, Johnson R, Zonta B, Court FA, Macklin WB, Meek S, Smith AJ, Cottrell DF, Brophy PJ. Neurofascins are required to establish axonal domains for saltatory conduction. Neuron. 2005;48:737–742. doi: 10.1016/j.neuron.2005.10.019. [DOI] [PubMed] [Google Scholar]
- Shrager P. Axonal coding of action potentials in demyelinated nerve fibers. Brain Res. 1993;619:278–290. doi: 10.1016/0006-8993(93)91622-y. [DOI] [PubMed] [Google Scholar]
- Southwood C, He C, Garbern J, Kamholz J, Arroyo E, Gow A. CNS myelin paranodes require Nkx6-2 homeoprotein transcriptional activity for normal structure. J Neurosci. 2004;24:11215–11225. doi: 10.1523/JNEUROSCI.3479-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stephanova DI, Bostock H. A distributed-parameter model of the myelinated human motor nerve fibre: temporal and spatial distributions of electrotonic potentials and ionic currents. Biol Cybern. 1996;74:543–547. doi: 10.1007/BF00209425. [DOI] [PubMed] [Google Scholar]
- Stewart DG, Davis KL. Possible contributions of myelin and oligodendrocyte dysfunction to schizophrenia. Int Rev Neurobiol. 2004;59:381–424. doi: 10.1016/S0074-7742(04)59015-3. [DOI] [PubMed] [Google Scholar]
- Tasaki I. New measurements of the capacity and the resistance of the myelin sheath and the nodal membrane of the isolated frog nerve fiber. Am J Physiol. 1955;181:639–650. doi: 10.1152/ajplegacy.1955.181.3.639. [DOI] [PubMed] [Google Scholar]
- Tsukita S, Furuse M, Itoh M. Multifunctional strands in tight junctions. Nat Rev Mol Cell Biol. 2001;2:285–293. doi: 10.1038/35067088. [DOI] [PubMed] [Google Scholar]
- Vabnick I, Trimmer JS, Schwarz TL, Levinson SR, Risal D, Shrager P. Dynamic potassium channel distributions during axonal development prevent aberrant firing patterns. J Neurosci. 1999;19:747–758. doi: 10.1523/JNEUROSCI.19-02-00747.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Waxman SD, Bangalore L. Electrophysiological consequences of myelination. In: Lazzarini RA, editor. Myelin Biology and Disorders. Elsevier; 2004. pp. 117–141. [Google Scholar]
- Waxman SG, Bennett MV. Relative conduction velocities of small myelinated and non-myelinated fibres in the central nervous system. Nat New Biol. 1972;238:217–219. doi: 10.1038/newbio238217a0. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.