ABSTRACT
Purpose: To model change in knee range of motion (ROM) post total knee arthroplasty (TKA) and to show how this information can be incorporated into clinical decision making.
Method: We applied a variable-occasion repeated-measures study design. Patients' knee flexion and extension ROM were assessed pre- and post arthroplasty over the ensuing 60 weeks. We examined change in ROM post TKA using linear and nonlinear mixed-effects modelling, and examined whether age, body mass index, prearthroplasty ROM, and gender were determinants of recovery in post-arthroplasty ROM.
Results: Of 93 eligible patients, 74 provided pre- and post-arthroplasty data. A random intercept nonlinear model fit the flexion data best, and a random intercept linear model fit the extension data best. Pre-arthroplasty ROM was found to be a determinant of recovery in ROM post arthroplasty. This finding was common to both flexion and extension models.
Conclusions: Our study showed that the greatest improvement for knee ROM took place during the first 12 weeks post arthroplasty. Of the variables examined, only pre-arthroplasty ROM was a determinant of outcome (p<0.05). The study results provide clinicians with data to determine expected rates of improvement for patients as well as the projected maximum ROM, facilitating improved clinical decision making.
Key Words: arthroplasty, knee, osteoarthritis, prognosis, reliability
RÉSUMÉ
Objectif : Modéliser le changement dans l'amplitude de mouvement du genou à la suite d'une arthroplastie totale du genou et démontrer comment cette information peut être incorporée à la prise de décision clinique.
Méthode : Nous avons appliqué un modèle d'étude avec mesures répétées à des occasions variables. L'amplitude du mouvement du genou du patient au moment de la flexion et de l'extension a été évaluée avant et après l'arthroplastie, dans les 60 semaines qui ont suivi l'intervention. Nous avons examiné les changements à l'amplitude des mouvements après l'intervention à l'aide d'un modèle à effets mixtes linéaire et non linéaire, et tenté de voir si l'âge, l'indice de masse corporelle, l'amplitude de mouvement pré-arthroplastie et le sexe constituaient des déterminants dans la récupération de l'amplitude de mouvement post-arthroplastie.
Résultats : Des 93 patients admissibles, 74 ont fourni des données avant et après l'arthroplastie. Un modèle non linéaire d'interception aléatoire convenait mieux aux données sur la flexion, tandis qu'un modèle linéaire d'interception aléatoire convenait mieux aux données sur l'extension. On a constaté que l'amplitude de mouvement pré-arthroplastie était déterminante dans la récupération de l'amplitude de mouvement post-arthroplastie. Cette conclusion était la même pour la flexion que pour l'extension.
Conclusions : Notre étude a démontré que la plus grande amélioration à l'amplitude de mouvement du genou avait lieu dans les 12 semaines après l'arthroplastie. Parmi les autres variables examinées, seule l'amplitude de mouvement pré-arthroplastie constituait un résultat déterminant (p<0,05). Les résultats de l'étude offrent aux cliniciens des données qui permettent d'établir les taux d'amélioration possible chez les patients, de même que l'amplitude de mouvement maximale, et de faciliter ainsi la prise de meilleures décisions cliniques.
Mots clés : arthroplastie, arthrose, fiabilité, genou, pronostic
INTRODUCTION
Over the past decade the, number of knee-replacement procedures in Canada has more than doubled.1 Considering current volumes and projected increases in knee arthroplasty in the future, physical therapists need to be familiar with how to best manage this growing population, particularly in a period of significant resource pressures. Many patients achieve desired outcomes after knee arthroplasty; however, a percentage of patients will develop functional problems that can be disabling, requiring more intensive rehabilitation.2 Persistent stiffness (flexion loss or contractures) is one of the problems encountered. Although range of motion (ROM) may not be a strong predictor of function (quality of life, performance-based measures) at 6 months and beyond,3–5 it is important in the early post-arthroplasty stages and can be a significant predictor of patient dissatisfaction.6 Patients with persistent stiffness (flexion contracture and/or limited flexion) who do not show improvement with standard rehabilitation may become candidates for additional operations, such as manipulations under anaesthesia or arthroscopic debridement, the outcomes of which are variable and do not approach the results of primary knee arthroplasty.7,8 It is imperative that physical therapists identify and appropriately address ROM challenges early, before the 6- to 9-week period post arthroplasty when restrictions are often detected, so as to avoid additional operations.9 It is also important that physical therapists have an appreciation of ROM recovery beyond the first few months to affirm that progress is being maintained, to determine treatment intensity, and to help patients set realistic functional goals as they improve.
Although numerous studies have examined intra-operative and post-arthroplasty care,10–16 the typical study design compares pre-arthroplasty pain and function measurements to post-arthroplasty measurements obtained at fixed time-points (e.g., 3, 6, and 12 months). Although these fixed-point comparisons provide sufficient information to comment on the effectiveness of total knee arthroplasty (TKA) and supplementary interventions, they offer limited information about the rate and determinants of change. Physical therapists need this information to make meaningful decisions about the treatment they are providing to patients following TKA and to communicate treatment results appropriately to patients' surgeons. Studies investigating the use of outcome measures and evidence-based practice have shown that physical therapists often feel impeded by the lack of information available to interpret the outcome values obtained.17,18 In an effort to translate research findings into clinically meaningful information, previous investigations have modelled changes in pain and activity status (self-report and performance measures) in patients post arthroplasty.19,20 Building on this work, the current report describes the change and determinants of change in knee ROM during the first 60 weeks post TKA and to illustrate how this information can be applied to guide clinical decisions. We set the stage for our study by introducing a clinical vignette and posing several questions (Part 1), the answers to which are provided by the study and incorporated into Part 2 of the vignette presented in the Discussion section.
Clinical Vignette: Part 1
Mrs. Jones is a 65-year-old woman with a long-standing history of osteoarthritis (OA) of her left knee. Two weeks post TKA, she presents with left-knee ROM of 6° flexion to 91° flexion. Mrs. Jones's pre-TKA left-knee ROM was 8° flexion to 108° flexion. Questions arising from the assessment include the following: (1) How confident are you in the measured ROM values? (2) How much change is needed to be reasonably certain that Mrs. Jones's flexion and extension ranges have changed? (3) What factors should be considered when scheduling the interval between ROM assessments? (4) What is Mrs. Jones's left-knee ROM likely to be 8 weeks post surgery? (5) What is Mrs. Jones's maximum ROM likely to be?
Our primary aims were to model knee flexion and extension ROM in patients with OA of the knee undergoing TKA during the first 60 weeks post arthroplasty and to determine whether age, body mass index (BMI), gender, or pre-arthroplasty knee ROM were prognostic indicators of change in ROM during this period. A secondary goal was to estimate the test–retest reliability of knee flexion and extension measures over an approximate 3-month retest interval prior to TKA.
METHODS
This study represents a secondary analysis of data collected prospectively as part of a larger investigation to describe the time course of lower-extremity functional status recovery following total joint arthroplasty. It was conducted at the Holland Orthopaedic and Arthritic Centre of Sunnybrook Health Sciences Centre, a tertiary-care orthopaedic facility located in Toronto, Canada. The institution's research ethics review board approved the study, and all participants provided written informed consent.
Participants
Recruitment occurred either at the point of consultation with the orthopaedic surgeon or at the preadmission clinic visit prior to TKA. Patients were eligible for recruitment if they had a diagnosis of OA, were scheduled to undergo primary TKA, and were able to communicate in written and spoken English. Furthermore, to be eligible for the present investigation, patients had to provide a minimum of one pre-arthroplasty and one post-arthroplasty ROM measurement. Patients were excluded if they had neurological, respiratory, cardiac, or other conditions that would significantly compromise their lower-extremity functional status. Patients with OA secondary to inflammatory disease were also excluded from this study.
The test–retest reliability sample consisted of all patients who had pre-arthroplasty knee flexion and extension ROM measured on two occasions separated by approximately 3 months. These patients represented a sub-sample of patients contributing data to the post-arthroplasty analysis.
Design
Modelling Change
We applied a variable-occasion repeated-measures observational study design,21(p.86–98) which allowed patients to be assessed at different time points. Although our intent was to collect data up to 1 year (52 weeks) post arthroplasty, several patients, for reasons related to either their own schedule or their surgeon's, were assessed up to 60 weeks following TKA. Inclusion of these patients' observations adds to the stability of the modelled change near the 1-year mark. The variable-occasion design is valid provided that data are missing at random (i.e., that the value an individual would have obtained had a measure been performed was not a determinant of the missing value). This design has two advantages. First, sampling at different time points across patients allows for the modelling of a smoother curve than can be achieved when patients are assessed at common time points (i.e., when the common time points dictate the inflection points). Second, this design does not require the same number of assessments for all patients.
Test–Retest Reliability
A repeated-measures study design was also applied to assess test–retest reliability. Data collection for this aspect of the study took place prior to TKA; all patients who had their knee ROM assessed on two occasions separated by approximately 3 months contributed data. We chose a 3-month interval for two reasons: first, it is a common interval between physician assessments post arthroplasty; and, second, there is evidence supporting the stability of patients over a 3-month interval prior to arthroplasty.22
Measures
Active knee ROM with overpressure was assessed using a universal goniometer. With the patient positioned supine, the axis of the goniometer was aligned with the lateral epicondyle at the knee; the proximal arm was aligned with the greater trochanter; the distal arm was aligned with the lateral malleolus. To assess flexion, the patients actively flexed the knee and then the therapist applied overpressure. Extension was similarly assessed in supine with a roll positioned under the patient's ankle to enable the assistance of gravity. The zero starting method of expressing knee ROM was applied: flexion was documented in degrees of flexion; extension beyond zero was expressed as hyperextension; and “extension” measures where patients were unable to achieve zero degrees were recorded as degrees of flexion. For example, a patient whose terminal extension was 6° short of complete extension (i.e., 0°) and whose maximum active flexion with overpressure was 118° was reported to have a range from 6° flexion to 118° flexion.
Analysis
Modelling Change
To gain an impression of the pattern of change in flexion and extension over time, we began by plotting range versus weeks post arthroplasty. Based on our inspection of the plotted data, and to account for the longitudinal structure of the data, we applied mixed-effects linear and nonlinear modelling using S-Plus version 4 software (MathSoft, Seattle, WA).23 The mixed-effects framework includes fixed and random effects. The fixed-effects component allows for the estimation of the average pattern of change; the random-effects component accounts for orderly variations in the pattern of change among patients.24 Guided by the plotted data, we explored different linear and nonlinear models. Once the best-fitting model was established (i.e., the unconditional model), we examined the extent to which age, BMI, gender, and pre-arthroplasty range added to the predictive ability of the model. These were the only potentially predictive variables included in our database. In this type of modelling, in contrast to linear multiple regression analyses, one does not have the advantage of an automated model-construction procedure (e.g., there is no “forward stepwise,” “backward elimination,” or “hierarchical” option to select); the best-fitting model must be determined manually. Accordingly, we examined the effect of each potentially predictive variable individually and in combination with all other potentially predictive variables. Acknowledging that no single agreed-upon approach for maintaining variables in the model exists, we elected to maintain variables in the model that had regression (β) coefficients whose 95% confidence interval (CI) did not include zero, and additional variables that approached statistical significance (90% CI did not include zero) and demonstrated a large effect on the predicted range value.21
In a variable-occasion observational design, all participants may not provide the same number of assessments. To examine whether patients' pre-arthroplasty ROM influenced the number of post-arthroplasty assessments, we applied a one-way analysis of variance (ANOVA) using pre-arthroplasty ROM as the dependent variable and number of post-arthroplasty ROM assessments as the independent variable.
Test–Retest Reliability
We applied the Shapiro-Wilks test to assess the normality of the difference scores in ROM measurements between the two measurement occasions. We calculated relative and absolute reliability coefficients and their 95% confidence intervals.25 The Type 2,1 intraclass correlation coefficient (ICC)26 was applied to estimate relative reliability.
To estimate absolute reliability, we calculated the standard error of measurement (SEM), which quantifies error in the same units as the original measurement (in this case, degrees).25,27 Using the point estimate for the SEM, we calculated a 90% CI for a measured value of flexion or extension by multiplying the SEM by 1.65 (i.e., the z-value associated with a two-sided 90% CI). We also estimated the minimal detectable change at 90% CI (MDC90) as follows: SEM×1.65×√2.
RESULTS
Participant Characteristics
Of the 93 eligible patients, 74 (79.6%) were included as participants because they had pre-arthroplasty ROM measurements and at least one post-arthroplasty ROM measurement. Table 1 summarizes patient characteristics. There were no statistically significant differences in age (t91=0.13, p=0.89), BMI (t91=0.30, p=0.76), or gender (Fisher's exact p=0.80) composition between the 74 patients who contributed data to this study and the 19 patients who had missing ROM data.
Table 1.
Preoperative Characteristics for Participants (n=74) and Patients Excluded Because of Missing Range Values
| Characteristic | Female (n=39) Mean (SD) |
Male (n=35) Mean (SD) |
Combined (n=74) Mean (SD) |
Missing (n=19) Mean (SD) |
|---|---|---|---|---|
| Age (years) | 65.0 (8.1) | 67.6 (8.8) | 66.2 (8.5) | 65.9 (10.1) |
| Body mass index (kg/m2) | 32.2 (5.3) | 30.8 (4.9) | 31.6 (5.1) | 31.1 (5.3) |
| Pre-arthroplasty flexion range (degrees) | 107.7 (13.9) | 113.4 (12.2) | 110.4 (13.3) | missing |
| Pre-arthroplasty extension range (reported as degrees of flexion) |
4.8 (6.2) |
5.9 (5.5) |
5.3 (5.8) |
missing |
|
Reliability sub-sample (n=22) |
Female (n=12) Mean (SD) |
Male (n=10) Mean (SD) |
Combined (n=22) Mean (SD) |
|
| Age (years) | 62.0 (8.6) | 68.3 (9.9) | 64.8 (9.2) | |
| Body mass index (kg/m2) | 31.2 (6.2) | 31.9 (7.8) | 31.5 (6.9) | |
| Pre-arthroplasty flexion range (degrees) | 109.2 (10.3) | 115.9 (10.2) | 112.2 (10.3) | |
| Pre-arthroplasty extension range (reported as degrees of flexion) | 3.1 (3.5) | 7.1 (4.9) | 4.9 (4.3) |
The reliability sub-sample consisted of 22 patients. The gender-specific differences in age, BMI, flexion, and extension values did not differ significantly (p>0.05) from the entire sample's characteristics.
The number of post-arthroplasty ROM measurements per patient varied from one to five. The distribution of post-arthroplasty assessments was as follows: 1 patient provided 1 assessment; 20 patients provided 2 assessments; 30 patients provided 3 assessments; 14 patients provided 4 assessments; and 10 patients provided 5 assessments. For the ANOVA, we included the one patient who provided a single post-arthroplasty assessment with those who provided two assessments. Neither pre-arthroplasty flexion range (F(3,70)=0.31, p=0.82) nor extension range (F(3,70)=0.17, p=0.92) was associated with the number of post-arthroplasty assessments.
Modelling Change
Flexion
A nonlinear model provided the best fit for the flexion data. The unconditional model specified the limit, y-intercept, and change parameters as fixed effects, and the limit and y-intercept as random effects:
| flexion angle=limit+(y0−limit)×changeweeks |
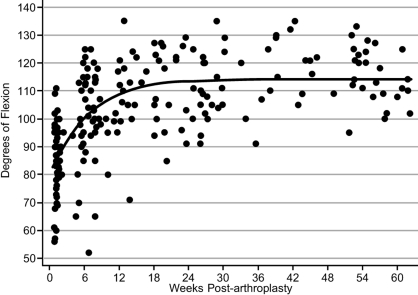
where limit is the parameter that represents the asymptote or maximum flexion angle, y0 is the parameter that represents the y-intercept value, change is the growth parameter (i.e., rate of improvement in ROM), and weeks is the number of weeks post arthroplasty. Table 2a reports the fixed-effect parameter estimates, 95% CIs, and random-effects parameter estimates. Also reported in Table 2a are the standard deviations of individual differences from the estimated average parameter values. For example, the standard deviation of individual differences from the average flexion limit value for the unconditional model was approximately 10°, which suggests that 68% (i.e., 1 SD) of participants displayed limit flexion ranges from 103° to 123°. Figure 1 depicts the flexion ROM recovery curve. We produced this curve by substituting the fixed-effects unconditional parameter values reported in Table 2a.
Table 2a.
Summary of Nonlinear Knee-Flexion ROM Analysis
| Effects | Unconditional Model β (95% CI) |
Conditional on Pre- arthroplasty Flexion β (95% CI) |
|---|---|---|
| Flexion Analysis | ||
| Fixed Effects | ||
| Parameters of Average Change | ||
| limit* | 113.33 (109.80, 116.19) | 94.49 (72.47, 116.50) |
| y-intercept | 79.38 (75.02, 83.73) | 79.65 (75.28, 84.02) |
| change (se) | 0.85 (0.81, 0.89) | 0.85 (0.81, 0.89) |
| pre-flexion** | N/A | 0.17 (0, 0.35) |
| Random Effects | ||
| Standard deviation of individual differences from average | ||
| limit | 10.15 | 9.60 |
| y-intercept | 9.55 | 9.63 |
| Within patient | 8.11 | 8.13 |
Standard error
Pre-arthroplasty flexion range
Figure 1.
Scatter plot of flexion data points with fixed-effect line of best fit
Our examination of potential predictive variables revealed that only pre-arthroplasty flexion range significantly influenced recovery. Specifically, the limit value was conditional on pre-arthroplasty ROM. The relationship is expressed in the following revised model:
| flexion angle=(limit+β×pre-flexion)+(y0−(limit+β×pre-flexion))×changeweeks |
where limit, y0, and change are as defined above and β is the coefficient for pre-flexion (0.17 for the conditional model in Table 2a). Substituting the conditional fixed-effects parameter values reported in Table 2a into this model reveals that patients with greater pre-arthroplasty flexion range achieved a greater limit, or maximum flexion range. For example, the projected 1-year knee-flexion ranges for three patients with pre-arthroplasty ranges of 105°, 115°, and 125° would be approximately 112°, 114°, and 116° respectively.
Extension
A linear model provided the best fit for the extension data. The unconditional model specified the y-intercept and slope parameters as fixed effects and the y-intercept as a random effect:
| extension angle=y0+(slope×lnweeks) |
where y0 is the parameter that represents the y-intercept value, slope is the growth parameter (i.e., rate of change in extension ROM), and lnweeks is the natural logarithm of the number of weeks post arthroplasty. Positive extension angles represent degrees of flexion. Inspection of the scatter plot suggested heterogeneity of the variance of extension values over time. Because of this finding, we modelled the extension data again using robust regression analysis for clustered data. The regression coefficients and 95% CIs for both analyses are reported in Table 2b, and their application is illustrated graphically in Figure 2. Although the regression coefficients for the two models differ slightly, and the standard errors for the robust analysis are marginally greater than those of the mixed-effects model, the predicted extension values are essentially the same. Both analyses found that only pre-arthroplasty extension range significantly influenced recovery. The relationship is expressed in the following revised model:
| extension angle=y0+(slope×lnweeks)+(β×pre-extension) |
where y0 and slope are as defined above and β is the coefficient for pre-extension (0.09 for the conditional model in Table 2b). The projected 1-year knee extension ranges for three patients with pre-arthroplasty ranges of 20°, 10°, and 0° degrees of flexion would therefore be approximately 2.2°, 1.3°, and 0.4° of flexion respectively.
Table 2b.
Summary of Linear Knee-Extension ROM Analysis
| Effects | Unconditional Model β (95% CI) |
Conditional on Pre-arthroplasty Extension β (95% CI) |
|---|---|---|
| Mixed-Effects Analysis | ||
| Fixed Effects | ||
| Parameters of Average Change | ||
| slope* | −0.77 (−1.08–−0.45) | −0.74 (−1.05–−0.43) |
| y-intercept | 3.82 (2.98–4.66) | 3.26 (2.28–4.24) |
| pre-extension** | N/A | 0.09 (0.01–0.17) |
| Random Effects | ||
| Standard deviation of individual differences from average | ||
| y-intercept | 1.49 | 1.43 |
| Within patient | 2.98 | 2.98 |
| Robust Analysis | ||
| Regression Coefficients | ||
| slope* | −0.74 (−1.09–−0.39) | −0.70 (−1.05–−0.35) |
| y-intercept | 3.83 (2.91–4.75) | 3.24 (2.14–4.34) |
| pre-extension** | N/A | 0.09 (0–0.19) |
Standard error
Pre-arthroplasty extension range
Figure 2.
Scatter plot of extension data points with robust model and mixed model fixed-effect lines of best fit
Test–Retest Reliability
Twenty-two of the 74 patients taking part in the modelling investigation had two pre-arthroplasty ROM measurements and contributed data to the test–retest reliability study. A summary of the reliability results appears in Table 3. The Shapiro-Wilks statistics were consistent with a normal distribution for the difference in range values between test and retest for flexion (0.97, df=22, p=0.70) and extension (0.94, df=22, p=0.24) values. The 95% CIs for flexion and extension measurements provide a probable set of values within which the population values are likely to lie. Applying the point estimate for the flexion SEM, the 90% CI for a measured value is ±6.8° (i.e., 4.1×1.65). Applying the point estimate of the extension SEM, the 90% CI for a measured value is ±4.4° (i.e., 2.7×1.65). The MDC90 for flexion was 9.6°, versus 6.3° for extension, meaning that 90% of stable patients will display random fluctuations equal to or less than these values.
Table 3.
Summary of Test–Retest Reliability Results
| Measure | Test Mean (SD) |
Retest Mean (SD) |
Difference (SDdiff) |
R (95% CI) |
SEM (95% CI) |
| Flexion | 111.8 (10.1) | 112.5 (9.8) | 0.7 (5.8) | 0.84 (0.64–0.93) | 4.1 (3.2–5.9) |
| Extension | 4.5 (4.0) | 4.7 (4.3) | 0.2 (3.8) | 0.60 (0.24–0.81) | 2.7 (2.1–3.8) |
SEM=standard error of measurement
DISCUSSION
The primary objective of this investigation was to model recovery post arthroplasty. A nonlinear model provided the best fit for the flexion data, and a linear model produced the best fit for the extension data. Common to both models was the finding that pre-arthroplasty ROM predicts post-arthroplasty ROM. As the recovery curves in Figures 1 and 2 show, the greatest improvement in knee ROM took place during the first 12 weeks, with modest improvement continuing to the 26-week mark. As will be illustrated below, the curves and table data provide a means for physical therapists to benchmark whether patients' ROM is changing as expected in the critical early period after TKA. If not, the treatment plan can be modified, with early communication to the surgeon as required. Our study also provided estimates of relative and absolute test–retest reliability.
Our regression analyses found that of the variables investigated, only pre-arthroplasty ROM predicted post-arthroplasty ROM. Although the regression coefficients associated with pre-arthroplasty flexion and extension ranges were statistically significant, their impact on the predicted terminal range was small. As an illustration, a 10° increase in pre-arthroplasty flexion predicted a 1.7° increase in terminal flexion; similarly, a 10° increase in pre-arthroplasty extension predicted a 1° increase in terminal extension range. Our finding that pre-arthroplasty range predicted post-arthroplasty range is consistent with the reports of others.9,28 However, given the different methodologies and reporting used, we cannot make a direct comparison between their findings and our results.
Mixed-effects modelling does not require that the number and timing of measurements be the same for all participants. To produce unbiased results, however, mixed-effects modelling does require that missing data be at random. A biased estimate of recovery will be obtained if the reason for the “missing” data points was related to the outcome that would have been observed. For example, a data point would be considered missing at random if a patient missed his assessment because he unexpectedly had to babysit his grandchild; by contrast, the data point would not be considered missing at random if the patient chose not to come to his appointment because his knee was particularly stiff that day. We have no way of knowing with absolute certainty why some patients appeared for more assessments than others. However, to the extent that pre-arthroplasty flexion is a determinant of post-arthroplasty range, our results found no difference in pre-arthroplasty flexion values between patients who provided different numbers of post-arthroplasty data points. We view this as supporting the premise that data were missing at random.
In addition, we sought support for our modelled recovery curve by comparing the modelled values shown in Figures 1 and 2 to fixed-point flexion values reported in the literature (summarized in Table 4).3,10–16 Our modelled values are consistent with fixed-point values reported in the literature. We believe this finding further supports the notion that our models provide unbiased estimates of recovery in knee ROM post arthroplasty.
Table 4.
Typical Fixed-Point Knee Flexion and Extension Ranges from Other Studies
| Study | Approximate Weeks Post Arthroplasty | ||||||
|---|---|---|---|---|---|---|---|
| Flexion | 1 | 4 | 6 | 8 | 12 | 26 | 52 |
| Mizner et al.3 | 94° | 109° | 114° | 116° | |||
| Kumar et al.11 | 84° | 104° | 113° | 115° | |||
| Kramer et al.12 | 100° | 105° | |||||
| Petterson et al.13 | 115° | 119° | |||||
| Lombardi et al.30 | 110° | ||||||
| Rajan et al.14 | 92° | 97° | 98° | ||||
| Genêt et al.15 | 107° | ||||||
| Chaudhary et al.16 | 100° | ||||||
| Ritter et al.28 | 111° | ||||||
| Extension | 1 | 4 | 6 | 8 | 12 | 26 | 52 |
| Mizner et al.3 | 5° | 3° | 2° | 1° | |||
| Kumar et al.11 | 9° | 6° | 3° | 2° | |||
| Petterson et al.13 | 2° | 1° | |||||
| Genêt et al.15 | 3° | ||||||
| Chaudhary et al.15 | 4° |
LIMITATIONS
A limitation of our study is that the sample size was one of convenience and not one based on a formal sample-size calculation. A consequence of this is the rather large confidence interval around the point estimates for the ICCs and SEMs. In an attempt to gauge the representativeness of our reliability estimates, we sought out other studies conducted on comparable patients. We found only one study that had estimated the reliability of knee ROM measurements for flexion and extension in patients with OA of the knee.29 From the work of Hayes et al.,29 we calculated relative and absolute reliabilities of 0.79 and 3.0° respectively for knee extension and of 0.96 and 4.7° respectively for knee flexion. For our study, the estimated relative and absolute reliabilities were 0.60 and 2.7° respectively for extension, and 0.84 and 4.1° respectively for flexion. Our findings are thus consistent with the results of Hayes et al.29 in two ways. First, our estimate of relative reliability was greater for knee flexion than for knee extension; and, second, our SEMs are almost identical to those reported by Hayes et al. In contrast, our estimates of relative reliability are less than those reported by Hayes et al. There are two likely explanations for this. First, Hayes et al.'s patients displayed greater variability than the patients in our study; for example, the standard deviation for flexion range was 18.7° in Hayes et al.'s study,29 compared to 10.1° for patients in our reliability sample. All else being equal, the larger the patient variance, the larger the relative reliability coefficient. Second, Hayes et al. reported a Type 3,1 ICC. This ICC omits the occasion-variance term from the denominator of the ICC calculation; thus, when this term is greater than zero, the Type 3,1 ICC will be larger than the Type 2,1 ICC. One strategy clinicians can use when outcome measures do not meet the desired reliability levels for individual patient use is to take repeated measurements and average them. A limitation both of our test–retest reliability study and of that of Hayes et al.29 is that in both investigations, reassessment intervals were of several months; as a result, one cannot rule out the possibility that true changes occurred over the reassessment intervals.
We now return to the clinical vignette presented earlier in the paper, in order to illustrate how the concepts and information from the modelling and reliability studies can be applied to assist goal setting and clinical decision making.
Clinical Vignette: Part 2
How confident are you in the measured ROM values?
This question focuses on the measurement error associated with flexion and extension measurements performed at a single time point. We apply the point estimates for the flexion and extension SEMs from the reliability study to answer this question for the 2-week post-TKA measured values of 6° flexion and 91° flexion. Referring to Table 3, we see that the SEM for extension was 2.7°. The 90% CI for a measured value of 6° is ±4.5° (i.e., 2.7×1.65). Applying a similar approach and a SEM of 4.1° for knee flexion, we find that the 90% CI for the measured flexion value of 91° is ±6.8° (i.e., 4.1×1.65).
How much change is needed to be reasonably certain that Mrs. Jones's flexion and extension ranges have changed?
The values for MDC90 are applied to answer this question. The MDC90 for extension is 6.3° (i.e., 2.7×1.65×√2), and MDC90 for flexion is 9.6° (i.e., 4.1×1.65×√2). Since 90% of truly stable patients will display random fluctuations equal to or less than the MDC90, changes greater than the MDC90 are considered likely to represent true change.
What factors should be considered when scheduling the interval between ROM assessments?
To answer this question, we must draw on two pieces of information: MDC90 and the recovery curve. Given an MDC90 of 10° based on a single flexion measurement, Mrs. Jones would need to achieve a flexion range of 101° for us to be reasonably certain that a true change in knee flexion has occurred. Based on the recovery curve shown in Figure 1, it appears that the typical patient will achieve this range at the 6-week mark. Accordingly, our goal for Mrs. Jones would be to increase her knee flexion range by 10° in 4 weeks (i.e., 6-week range of 101° minus 2-week range of 91°). Linking this goal to targeted interventions and functional activities may increase compliance with the treatment protocol and lead to more effective goal setting.
For extension, a change of 7° (i.e., >6.3°) is required. Given that Mrs. Jones's knee-extension range at 2 weeks post TKA is 6°, she would need to achieve 2° of hyperextension to be reasonably certain that her extension range has truly improved. Inspection of the recovery curve shown in Figure 2 suggests that the typical patient is unlikely to achieve a range of 2° hyperextension; in addition, this is not a desired outcome from a stability standpoint after knee arthroplasty. Recognizing this limitation, the physical therapist could invoke the measurement strategy of averaging extension measurements taken on two occasions separated by a day or two. This would be practical only if the patient were being seen regularly. Averaging measurements from two occasions reduces the measurement error by √2; thus, if two extension measurements were averaged, the MDC90 would be 5°. Once again, based on Figure 2, it appears that the typical patient achieves a range of 1° knee flexion by the 40-week mark.
What is Mrs. Jones's left-knee ROM likely to be 8 weeks post surgery?
The best answer to this question is obtained by applying Mrs. Jones's pre-arthroplasty extension and flexion values to the condition models, the coefficients of which are reported in Tables 2a and 2b. Taking this approach, we would expect Mrs. Jones's 8-week knee ROM to be from 3° flexion to 103° flexion. A reasonable approximation can also be obtained more easily by referring to the 8-week time point and drawing a line up to the recovery curve for the unconditional models (i.e., the models that do not take pre-arthroplasty ranges into consideration) shown in Figures 1 and 2 to determine the flexion or extension value.
What is Mrs. Jones's maximum ROM likely to be?
The answer to this question is also obtained by referring to the conditional model coefficients or to the recovery curves. Applying the conditional model coefficients yields an expected ROM of 1° flexion to 113° flexion for a person with pre-arthroplasty ranges similar to those of Mrs. Jones. These range estimates are almost identical to the ranges reported by the recovery curves for the unconditional models.
CONCLUSION
Our study showed that the greatest improvement in knee ROM took place during the first 12 weeks post arthroplasty. Modest improvement in ROM continued up to the 26-week mark, after which there was no appreciable change in ROM. Of the variables examined, only pre-arthroplasty ROM was a determinant of outcome. The results from our study can be applied to guide decisions related to both rate of improvement and projected maximum ROM. Equipping physical therapists to better predict their patients' pattern of recovery will facilitate goal setting, patient education, and treatment.
KEY MESSAGES
What Is Already Known on This Topic
To date, we are not aware of any investigations that have modelled change in knee range of motion (ROM) following total knee arthroplasty. However, point estimates of knee ROM have been reported sporadically at different time points by a number of investigators.
What This Study Adds
Our models of knee flexion and extension provide average terminal expected ranges of 114° and 1° respectively, with the greatest change occurring in the first 12 weeks post arthroplasty. As is evident on the graph for knee flexion, flexion values for a number of patients fell above or below this terminal flexion range. The 95% confidence interval for a reported value was estimated to be ±4.5° for extension and ±6.8° for flexion. For extension, a change of 6.3° or more is necessary to be reasonably certain that a patient has truly changed; for flexion, a change of 9.6° is required. This information can be applied to assist physical therapists in determining measurable treatment goals and in benchmarking patients' progress over time.
Stratford PW, Kennedy DM, Robarts S. Modelling knee range of motion post arthroplasty: clinical applications. Physiother Can. 2010;62:378–387
References
- 1.Canadian Institute for Health Information. Hip and knee replacements in Canada: Canadian Joint Replacement Registry (CJRR) 2008–2009 annual report. Ottawa: The Institute; 2009. [Google Scholar]
- 2.Bhave A, Mont M, Tennis S, Nickey M, Starr R, Etienne G. Functional problems and treatment solutions after total hip and knee joint arthroplasty. J Bone Joint Surg Am. 2005;87(Suppl 2):9–21. doi: 10.2106/JBJS.E.00628. doi: 10.2106/JBJS.E.00628. [DOI] [PubMed] [Google Scholar]
- 3.Mizner RL, Petterson SC, Snyder-Mackler L. Quadriceps strength and the time course of functional recovery after total knee arthroplasty. J Orthop Sport Phys Ther. 2005;35:424–36. doi: 10.2519/jospt.2005.35.7.424. doi: 10.2519/jospt.2005.2036. [DOI] [PubMed] [Google Scholar]
- 4.Miner AL, Lingard EA, Wright EA, Sledge CB, Katz JN. Knee range of motion after total knee arthroplasty: how important is this as an outcome measure? J Arthroplasty. 2003;18:286–94. doi: 10.1054/arth.2003.50046. doi: 10.1054/arth.2003.50046. [DOI] [PubMed] [Google Scholar]
- 5.Jones CA, Voaklander DC, Suarez-Alma ME. Determinants of function after total knee arthroplasty. Phys Ther. 2003;83:696–706. [PubMed] [Google Scholar]
- 6.Kim TK, Choi J, Shin KS, Chang CB, Seong SC. Patients' perspective on controversial issues in total knee arthroplasty. Knee Surg Sport Traumatol Arthrosc. 2008;16:297–304. doi: 10.1007/s00167-007-0468-8. doi: 10.1007/s00167-007-0468-8. [DOI] [PubMed] [Google Scholar]
- 7.Seyler TM, Marker DR, Bhave A, Plate JF, Marulanda GA, Bonutti PM, et al. Functional problems and arthrofibrosis following total knee arthroplasty. J Bone Joint Surg Am. 2007;89(Suppl 3):59–69. doi: 10.2106/JBJS.G.00457. doi: 10.2106/JBJS.G.00457. [DOI] [PubMed] [Google Scholar]
- 8.Kim J, Nelson CL, Lotke PA. Stiffness after total knee arthroplasty: prevalence of the complication and outcomes of revision. J Bone Joint Surg Am. 2004;86A:1479–84. [PubMed] [Google Scholar]
- 9.Gandhi R, de Beer J, Leone J, Petruccelli D, Winemaker M, Adili A. Predictive risk factors for stiff knees in total knee arthroplasty. J Arthroplasty. 2006;21:46–52. doi: 10.1016/j.arth.2005.06.004. doi: 10.1016/j.arth.2005.06.004. [DOI] [PubMed] [Google Scholar]
- 10.Lombardi AV, Jr, Berend KR, Walter CA, Aziz-Jacobo J, Cheney NA. Is recovery faster for mobile-bearing unicompartmental than total knee arthroplasty? Clin Orthop Relat Res. 2009;467:1450–7. doi: 10.1007/s11999-009-0731-z. doi: 10.1007/s11999-009-0731-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Kumar PJ, McPherson EJ, Dorr LD, Wan Z, Baldwin K. Rehabilitation after total knee arthroplasty: a comparison of 2 rehabilitation techniques. Clin Orthop Relat Res. 1996;331:93–101. doi: 10.1097/00003086-199610000-00013. [DOI] [PubMed] [Google Scholar]
- 12.Kramer JF, Speechley M, Bourne R, Rorabeck C, Vaz M. Comparison of clinic- and home-based rehabilitation programs after total knee arthroplasty. Clin Orthop Relat Res. 2003;410:225–34. doi: 10.1097/01.blo.0000063600.67412.11. doi: 10.1097/01.blo.0000063600.67412.11. [DOI] [PubMed] [Google Scholar]
- 13.Petterson SC, Mizner RL, Stevens JE, Raisis L, Bodenstab A, Newcomb W, et al. Improved function from progressive strengthening interventions after total knee arthroplasty: a randomized clinical trial with an imbedded prospective cohort. Arthritis Rheum. 2009;61:174–83. doi: 10.1002/art.24167. doi: 10.1002/art.24167. [DOI] [PubMed] [Google Scholar]
- 14.Rajan RA, Pack Y, Jackson H, Gillies C, Asirvatham R. No need for outpatient physiotherapy following total knee arthroplasty: a randomized trial of 120 patients. Acta Orthop Scand. 2004;75:71–3. doi: 10.1080/00016470410001708140. doi: 10.1080/00016470410001708140. [DOI] [PubMed] [Google Scholar]
- 15.Genet F, Schnitzler A, Lapeyre E, Roche N, Autret K, Fermanian C, et al. Change of impairment, disability and patient satisfaction after total knee arthroplasty in secondary care practice. Ann Readapt Med Phys. 2008;51:671–6. 6–82. doi: 10.1016/j.annrmp.2008.08.002. doi: 10.1016/j.annrmp.2008.08.002. [DOI] [PubMed] [Google Scholar]
- 16.Chaudhary R, Beaupre LA, Johnston DW. Knee range of motion during the first two years after use of posterior cruciate-stabilizing or posterior cruciate-retaining total knee prostheses: a randomized clinical trial. J Bone Joint Surg Am. 2008;90:2579–86. doi: 10.2106/JBJS.G.00995. doi: 10.2106/JBJS.G.00995. [DOI] [PubMed] [Google Scholar]
- 17.Kay TM, Myers AM, Huijbregts MPJ. How far have we come since 1992? a comparative survey of physiotherapists' use of outcome measures. Physiother Can. 2001;53:268–75. 81. [Google Scholar]
- 18.Salbach NM, Jaglal SB, Korner-Bitensky N, Rappolt S, Davis D. Practitioner and organizational barriers to evidence-based practice of physical therapists for people with stroke. Phys Ther. 2007;87:1284–303. discussion 304–6. doi: 10.2522/ptj.20070040. doi: 10.2522/ptj.20070040. [DOI] [PubMed] [Google Scholar]
- 19.Kennedy DM, Stratford PW, Hanna SE, Wessel J, Gollish JD. Modeling early recovery of physical function following hip and knee arthroplasty. BMC Musculoskelet Disord. 2006;7:100. doi: 10.1186/1471-2474-7-100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Kennedy DM, Stratford PW, Riddle DL, Hanna SE, Gollish JD. Assessing recovery and establishing prognosis following total knee arthroplasty. Phys Ther. 2008;88:22–32. doi: 10.2522/ptj.20070051. doi: 10.2522/ptj.20070051. [DOI] [PubMed] [Google Scholar]
- 21.Snijders T, Bosker R. Multilevel analysis: an introduction to basic and advanced multilevel modeling. London: Sage; 1999. [Google Scholar]
- 22.Kennedy DM, Stratford PW, Wessel J, Gollish JD, Penney D. Assessing stability and change of four performance measures: a longitudinal study evaluating outcome following total hip and knee arthroplasty. BMC Musculoskelet Disord. 2005;6:3. doi: 10.1186/1471-2474-6-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Pinheiro JC, Bates DM. Mixed effects models in S and S-Plus. New York: Springer; 2000. [Google Scholar]
- 24.Stratford PW, Hanna SE, Kennedy DM, Alcock GK. Hierarchial linear modelling: an effective analytic technique for examining change in clinical longitudinal data. Physiother Can. 2003;55:145–52. doi: 10.2310/6640.2003.2206. [Google Scholar]
- 25.Stratford PW, Goldsmith CH. Use of the standard error as a reliability index of interest: an applied example using elbow flexor strength data. Phys Ther. 1997;77:745–50. doi: 10.1093/ptj/77.7.745. [DOI] [PubMed] [Google Scholar]
- 26.Shrout PE, Fleiss JL. Intraclass correlation: uses in assessing rater reliability. Psychol Bull. 1979;86:420–8. doi: 10.1037//0033-2909.86.2.420. doi: 10.1037/0033-2909.86.2.420. [DOI] [PubMed] [Google Scholar]
- 27.Stratford PW. Getting more from the literature: estimating the standard error of measurement from reliability studies. Physiother Can. 2004;56:27–30. doi: 10.2310/6640.2004.15377. [Google Scholar]
- 28.Ritter MA, Harty LD, Davis KE, Meding JB, Berend ME. Predicting range of motion after total knee arthroplasty: clustering, log-linear regression, and regression tree analysis. J Bone Joint Surg Am. 2003;85A:1278–85. doi: 10.2106/00004623-200307000-00014. [DOI] [PubMed] [Google Scholar]
- 29.Hayes KW, Petersen C, Falconer J. An examination of Cyriax's passive motion tests with patients having osteoarthritis of the knee. Phys Ther. 1994;74:697–707. discussion 707–9. doi: 10.1093/ptj/74.8.697. [DOI] [PubMed] [Google Scholar]