Mathematical spatio-temporal model of drug delivery from low temperature sensitive liposomes during radiofrequency tumour ablation

Abstract

Purpose

Studies have demonstrated a synergistic effect between hyperthermia and chemotherapy, and clinical trials in image-guided drug delivery combine high-temperature thermal therapy (ablation) with chemotherapy agents released in the heating zone via low temperature sensitive liposomes (LTSL). The complex interplay between heat-based cancer treatments such as thermal ablation and chemotherapy may require computational models to identify the relationship between heat exposure and pharmacokinetics in order to optimise drug delivery.

Materials and methods

Spatio-temporal data on tissue temperature and perfusion from heat-transfer models of radiofrequency ablation were used as input data. A spatio-temporal multi-compartmental pharmacokinetic model was built to describe the release of doxorubicin (DOX) from LTSL into the tumour plasma space, and subsequent transport into the extracellular space, and the cells. Systemic plasma and tissue compartments were also included. We compared standard chemotherapy (free-DOX) to LTSL-DOX administered as bolus at a dose of 0.7 mg/kg body weight.

Results

Modelling LTSL-DOX treatment resulted in tumour tissue drug concentration of ~9.3 μg/g with highest values within 1 cm outside the ablation zone boundary. Free-DOX treatment produced comparably uniform tissue drug concentrations of ~3.0 μg/g. Administration of free-DOX resulted in a considerably higher peak level of drug concentration in the systemic plasma compartment (16.1 μg/g) compared to LTSL-DOX (4.4 μg/g). These results correlate well with a prior in vivo study.

Conclusions

Combination of LTSL-DOX with thermal ablation allows localised drug delivery with higher tumour tissue concentrations than conventional chemotherapy. Our model may facilitate drug delivery optimisation via investigation of the interplays among liposome properties, tumour perfusion, and heating regimen.

Introduction

Background

Radio frequency (RF) ablation is a minimally invasive treatment used for liver tumours, which are not amenable to surgery. Under image guidance a probe is inserted into the centre of the tumour and tissue is heated locally via radio frequency current. At prolonged temperatures above ~50°C tissue is destroyed by coagulation necrosis. One of the major limitations of RF ablation is that the margins of the thermal lesion are often treated inadequately, thus the ablated volume is insufficient. Several recent studies have demonstrated an advantage by combining a heat-based therapy, such as RF ablation, with free drug or a drug delivery system [1-4]. These approaches are designed to increase targeted cell death, and in the context of ablative therapies, destroy cells in the range of ~45–50°C (i.e. thermal margin) where cells often persist following ablation therapy [5, 6].

One of the most common drug delivery systems is a liposome [7]. Liposomes are vesicles of about 100nm diameter consisting of a lipid bilayer with an aqueous core that is often loaded with the standard chemotherapy drug doxorubicin (DOX). DOX-loaded liposomes have shown promising anti-tumour results in preclinical as well as clinical investigations leading to an FDA approved liposome for the treatment of ovarian cancer (e.g. Doxil) [8].

These promising liposomal formulations, called ‘stealth’ liposomes, employ polyethylene glycol on their surface to avoid detection by the reticuloendothelial system (RES) or immune system to improve their pharmacokinetic profile [9]. Temperature sensitive liposomes (TSL) that release their contents in response to heating above body temperature have been pursued in combination with focused hyperthermia for the activated release of drugs in a heated tumour [10]. Later generations of TSL have lysolipids incorporated into the liposomal membrane (see Figure 1), which allows for rapid release of their contents in response to mild hyperthermia (>39°C, see Figure 2), known as low temperature sensitive liposomes (LTSL) [7, 11, 12]. Similar to classic stealth liposomes, this strategy has the potential to increase the concentration of bioavailable drug in a tumour while limiting systemic exposure. However, the complex interplay between tissue heating and pharmacokinetics may require a computational model to identify the relationship between heat exposure and pharmacokinetics in order to optimise drug delivery. Such models could facilitate optimal drug plus device combination therapies, as well as guide future pre-clinical efforts by limiting the number of experimental arms or predicting and narrowing the range of variables to study.

Figure 1.

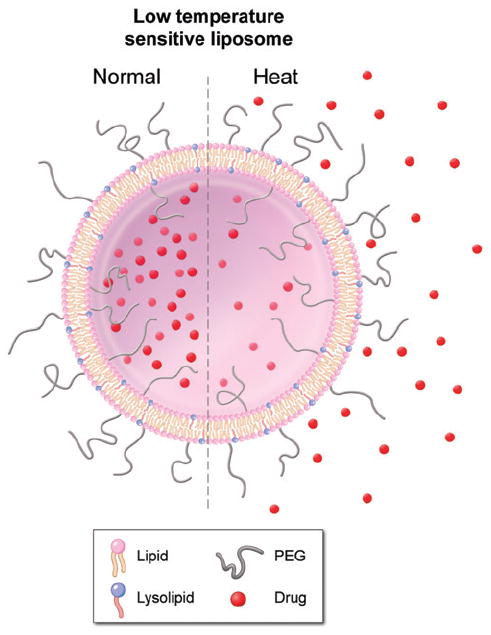
Low temperature sensitive liposome (LTSL):Lipid bilayer, which encapsulates (chemo-) therapeutic agents. They rapidly release their payload in response to heat.

Figure 2.

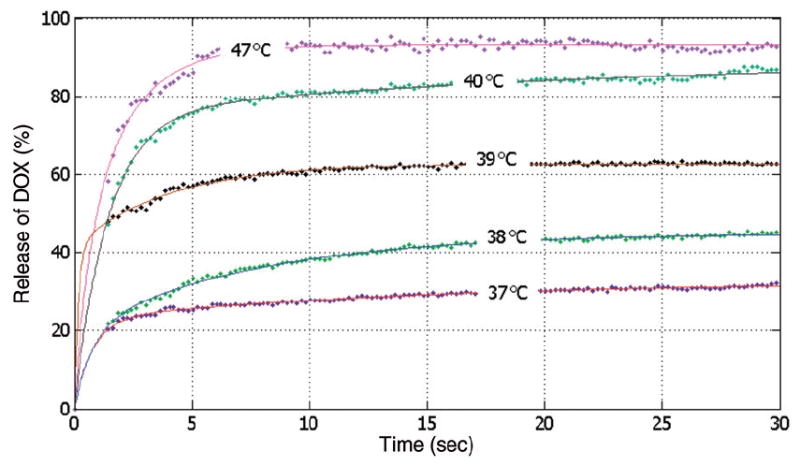
Release of DOX from LTSL for different temperatures [°C] versus time [s] (mean of n = 3). A bi-exponential fit (shown as solid lines) was made to the experimental data (shown as data points). Release fractions are fairly similar between ~40°C and 47°C for this particular LTSL, and results in this range are omitted for clarity.

Prior mathematical models have successfully simulated the pharmacokinetics of DOX as well as LTSL-DOX [13-17]. El-Kareh and Secomb [13] established a mathematical model where they compared bolus injection with continuous infusion of DOX for various durations and liposomal (both stealth liposomes and TSL) delivery of DOX to tumour cells. They calculated peak plasma concentrations and plasma area under the curve (AUC) to estimate toxicity. For the TSL delivery of DOX, they assumed a uniform temperature distribution and therefore a constant release of DOX from the TSL for the duration of hyperthermia. Jackson [14] developed a spatio-temporal model where the accumulation of intracellular DOX and the mechanism of action of DOX were investigated. Requisite threshold levels of intracellular sequestered DOX to trigger cell death signals were studied. In this approach a multi-compartment model was used to simulate the uptake of DOX and to describe its internalisation and intracellular sequestration. Qian et al. [16] investigated the transport of DOX from polymer millirods (for intratumoural drug delivery) in thermoablated rat livers, demonstrating the influence of tissue ablation (and devascularisation) on the transport of DOX.

The objective of this study was to develop a paired heat transfer and pharmacokinetic mathematical model to investigate the spatial and temporal variations in drug delivery for the combination of RF ablation and LTSL treatment. This model was developed to identify the predominant factors affecting drug delivery from LTSL and to guide future preclinical and clinical combinations.

Methods

Temperature induced release of Doxorubicin from LTSL in plasma

Measurements were performed in a commercially available LTSL formulation (Thermodox^®, Celsion, Columbia, MD). The fluorescence intensity of a solution of DOX-loaded liposomes is low due to DOX’s self-quenching. Upon DOX release from a liposome, the fluorescence intensity of a liposome solution is increased. DOX-release experiments were performed by adding a liposome suspension (10 μL, 2 mg/mL DOX) to 750 μL human plasma (plasma collected with apheresis, whole blood treated with 1:12 ACD – anticoagulant citrate dextrose solution A). Prior to adding liposomes, plasma was equilibrated to a predetermined temperature (25°, 37°–47°C) in 1 mL total volume cuvette (1 cm path length) for at least 5 min. The change in fluorescence intensity due to DOX release from the liposomes was monitored with a Cary Eclipse spectrofluorometer equipped with a Peltier temperature controller and Eclipse Kinetic Software (Varian, CA) for 60 s at various temperatures. 15 μL of 25% (wt/wt) Triton X-100 was added at the end of the 60 s to lyse the liposomes and induce maximum release of DOX from the liposome. Excitation and emission wave-lengths were set at 498 nm (5 nm slit width) and 593 nm (10 nm slit width), respectively. The amount of DOX released after time t was calculated according to Equation 1:

$$\%\mathrm{Release}\mathrm{of}\mathrm{DOX}=100\left[\frac{I_t-I_o}{I_{\max }-I_o}\right]$$ (1)

where I_t represents the intensity at time t. I_o is the fluorescence intensity at 25°C and I_max is the intensity after the addition of Triton. The experiment was repeated three separate times in different plasma samples and data are reported as the mean (n = 3).

Computational model

Heat-transfer model of RF ablation

Before simulation of drug delivery, a heat-transfer model was simulated to determine spatially and temporally varying temperature, and perfusion. Finite element models have been used frequently in the past to determine tissue heating during RF ablation [18-23]. Since temperature and perfusion are assumed independent of drug delivery, the heat-transfer model was treated independently and the temperature and perfusion data subsequently used in the drug delivery model as input data. Details on the heat transfer model have been published in a prior study [23]. A cooled needle electrode (Cool-tip, Covidien, Boulder, CO; 1.5 mm diameter) was simulated, where the distal 3 cm are electrically active and the remainder of the electrode is insulated; tissue heating from RF current occurs near the active part. The electric field problem must be solved to determine the local power density (=E·J) producing tissue heating, and in addition the heat-transfer problem has to be solved to determine the tissue temperature profile. We used Pennes’ bioheat equation for this purpose (Equation 2) [24], which considers the effects of thermal conduction, resistive heating due to RF energy deposition, and tissue cooling due to microvascular blood perfusion. In the absence of large blood vessels (i.e. macrovascular perfusion), the Pennes model has been shown to describe the effect of blood perfusion with acceptable accuracy [25]. Table I lists the various parameters in equation 2.

Table I.

Parameters of bioheat equation.

Variable	Description
ρ	Density (kg/m3)
c	Specific heat (J/(kg·K))
k	Thermal conductivity (W/(m·K))
J	Current density (A/m2)
E	Electric field intensity (V/m)
Tbl	Temperature of blood (°C)
ρbl	Blood density (kg/m3)
cbl	Specific heat of blood (J/(kg·K))
wbl	Blood perfusion (m3/(m3·s))

$$\rho c\frac{\partial T}{\partial t}=\nabla \cdot k\nabla T+\mathbf{J}\cdot \mathbf{E}-{\rho }_{\mathit{bl}}{c}_{\mathit{bl}}{w}_{\mathit{bl}}(T-T_{\mathit{bl}})$$ (2)

The initial temperature for all elements and the boundary temperature were set at 37°C. To simulate the internal cooling of the Cool-tip electrode, a boundary condition of 10°C (typically seen during clinical procedures) was applied to the entire electrode shaft. We simulated RF ablation for 12 min, which is the standard clinical treatment time for this electrode. We also simulated the post-ablation period where the cooling flow inside the needle is turned off to allow the ablation zone to fill in adjacent to the electrode.

Table II shows the material properties from the literature that were used in both models [26]. The temperature dependence of the electrical conductivity of liver tissue was implemented as a coefficient of 1.5%°C⁻¹ [27]. Temperature dependence of the thermal conductivity of liver tissue was implemented according to ex vivo measurements from a prior study [26]. The value of latent heat of vaporisation for water was used for liver tissue as in previous studies [28, 29].

Table II.

Model material properties, where ρ is mass density, c is specific heat, k is thermal conductivity, and σ is electrical conductivity. All values represent properties at 37°C.

Element	Material	ρ (kg/m3)	c (J/(kg·K))	k (W/(m·K))	σ (S/m)	Latent heat of vaporisation (J/kg)
Electrode	Stainless steel	21500	132	71	4 × 107	NA
Shaft	Polyurethane	70	1045	0.03	1 × 10−5	NA
Tissue	Liver	1060	3500	0.51	0.36	2.25 × 106

While in normal tissue typically a rise in perfusion at hyperthermic temperatures with subsequent decline during ablation is observed, in this study we simulated only a decline in perfusion which is typically seen in tumour tissue [30]. We included temperature dependence of perfusion such that perfusion decreased according to an Arrhenius model, similar to a prior study [23]. We defined a variable DS, representing degree of stasis, which is 1 initially and zero when perfusion completely stops:

$$\mathit{DS}=1-\exp -\left({\mathit{\int }}_0^{t}A{e}^{-\mathrm{\Delta }E/[\mathit{RT}(\tau )]}\mathrm{d}\tau \right)$$ (3)

T(τ) is the absolute temperature as a function of time, R is the universal gas constant (8.314 J mole⁻¹K⁻¹), A is the frequency factor (1.98 × 10¹⁰⁶ s⁻¹), and ΔE is the activation energy (6.67 × 10⁵ J mole⁻¹). The values for ΔE and A were taken from a previous experimental study in muscle tissue [31]. Depending on degree of stasis, perfusion was determined according to:

$$w_{\mathit{bl}}(t)=w_0(1-\mathit{DS})$$ (4)

As baseline perfusion we assumed w₀ = 1.08 mL/min/mL, which is the typical liver perfusion in humans [32]. Of note, tumour perfusion of primary liver tumours is in a similar range (~0.94 mL/min/mL), but tumour perfusion has in general considerably greater variability between tumours and patients compared to normal tissue perfusion [33].

Drug delivery model

The time and spatially dependent temperature and perfusion resulting from the computational heat-transfer model of RF ablation was used as input data to the drug delivery model. The finite element model (FEM) for drug delivery simulation was created with the FEM-Software Comsol (version 3.5a). This model was 2D axial symmetric with 9013 triangular elements and employed a multi-compartment model to describe the spatio-temporal release and transport of DOX in a human. The compartments represent the systemic plasma volume of the body, the normal body tissue volume (i.e. organs with a significant drug uptake), and the tumour volume (Figure 3). The tumour compartment is further divided into three sub-compartments: the plasma space, the extravascular extracellular space (EES), and the intracellular space (Figure 3, Figure 4). For the purpose of the model, the tumour sub-compartments were represented by spatially varying compartments; i.e. each location within the tumour was represented by its own sub-compartments, whereas the normal tissue was represented by a single compartment without considering spatial variation.

Figure 3.

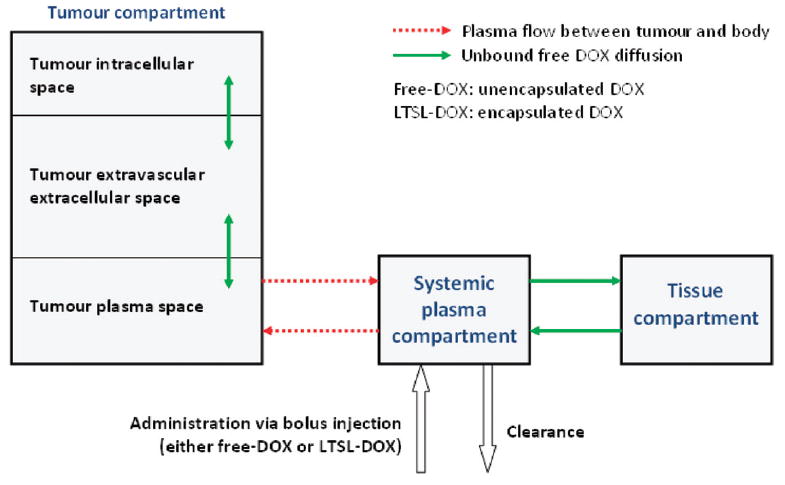
Multi-compartment model with systemic plasma-, tissue- and tumour compartments. The tumour compartment is spatially variable and divided further into intracellular space, EES and tumour plasma space (i.e. each location in the tumour can be visualised as being represented by its individual compartments). The systemic plasma and tissue concentrations ( $c_p^B,c_t^B$) vary only with time.

Figure 4.

DOX-loaded LTSL are administered intravenously (A). The LTSL release their content into the tumour plasma space as soon as the required temperature (~40°C) is reached (B). The released DOX can now cross the vessel wall (C) into the tumour tissue where the DOX can diffuse (D) and intracellular uptake (E) takes place. Some drug exits the tumour plasma space due to perfusion (F).

The systemic plasma compartment represents the total blood plasma volume with exception of the tumour. Administration of DOX (either free-DOX or LTSL-DOX at a dose of 0.7 mg per kg body weight) is modelled as a bolus injection into the systemic plasma compartment. The systemic plasma compartment exchanges DOX with the normal tissue compartment and with the tumour plasma space (Figure 3).

The concentration of the liposomal encapsulated DOX (c_{p_Lip}) in the systemic plasma compartment (and therefore also in the tumour plasma space) after a bolus injection can be described by the exponential fit to the systemic plasma concentration.

$$c_{p\_\mathit{Lip}}(t)=\frac{D}{V_p^B}{e}^{-k_{e\_\mathit{LTSL}}t}$$ (5)

where D is the total dose of encapsulated DOX injected, $V_p^B$ is the total plasma volume in the body and k_{e_LTSL} is the fitted transfer constant for clearance of LTSL from the systemic plasma (Table III). Extravasation of LTSL into the tissue is neglected given the low permeability of liposomes (3.4e-7 cm/s [42]) compared with free DOX (3.5e-5 cm/s [14]) and the short time scales examined, even though LTSL extravasation may be of significance for longer thermal treatments than a typical ablation procedure [43].

Table III.

Model parameters.

Symbol	Description	Value	Source
BW	Body weight	70 kg	assumed
D	Total dose of encapsulated DOX injected	49 mg	assumed
Hct	Haematocrit	0.45	[34]
Hcttumour	Haematocrit for tumour microvasculature	0.19	[35]
kp	Transfer constant from systemic plasma to tissue	1.6e-3 s−1	calculated with parameters from [36]
ke	Transfer constant for clearance	1.1e-3 s−1	calculated with parameters from [36]
kt	Transfer constant from tissue to systemic plasma	4.6809e-5 s−1	calculated with parameters from [36]
ke_LTSL	Rate constant of LTSL clearance	2.228e-4 s−1	fit to data from [37]
k1ci	Parameter for intracellular uptake	2.2572	[17]
k2ci	Parameter for intracellular uptake	0.0452 kg/m3	[17]
k3ci	Parameter for intracellular uptake	2.8056e-4 s−1	[17]
Kici	Parameter for intracellular uptake	5.2875e-4 kg/m3	[17]
PS	Permeability surface area product for DOX	7e-3 s−1	[14]
UDOX	Factor for binding of DOX to proteins	0.3	[38, 39]
$V_B^B$	Total blood volume in body	5.53 L	calculated with: blood = 7.9% of body weight [2]
$V_p^B$	Volume of systemic plasma	3.04 L	$V_B^B$ (1-Hct)
Vtissue	Volume for body tissue (organs, etc.)	64.47 L	calculated with: blood = 7.9% of body weight [2]
${\upsilon }_{\upsilon }^T$	Volume fraction of tumour vascular space	0.092	[40]
${\upsilon }_p^T$	Volume fraction of tumour plasma space	0.07452	${\upsilon }_{\upsilon }^T$ (1-Hcttumour)
${\upsilon }_e^T$	Volume fraction of tumour EES	0.454	[41]
${\upsilon }_i^T$	Volume fraction of tumour intracellular space	0.454	( $1­{\upsilon }_{\upsilon }^T­{\upsilon }_e^T$)
RR	Release rate of DOX from LTSL	Variable [s−1]	calculated
RR37	Release rate of DOX from LTSL at 37°C	Variable [s−1]	calculated
RR	Release fraction of DOX from LTSL	Variable	bi-exponential fit
$F_{p\upsilon }^T$	Plasma flow in tumour plasma space; note: Fpv=plasma flow/plasma volume	Variable [s−1]	calculated
T	Temperature	Variable [°C]	imported from a prior modeling study [23]
tres	Residence time	Variable [s]	$1/F_{p\upsilon }^T$
Diff	Diffusion coefficient for ablated tissue	1.1e-7 cm2/s	[16]
	Diffusion coefficient for non-ablated tissue	6.7e-7 cm2/s

The rate of release of DOX from the liposomes in the tumour plasma space depends on the local temperature (T). The release rate (R_R) of DOX from the LTSL was determined as follows: We used a bi-exponential fit of the experimental data of the time course of DOX release fraction (rf ) at temperatures between 37° and 47°C (Figure 2). The amount released depends on the residence time (t_res) of the LTSL in the heated region; t_res is in our model equal to $1/F_{p\upsilon }^T$, i.e. its change depends on local perfusion. The release rate R_R is then:

$$R_R(T,F_{p\upsilon }^T)=\frac{\mathit{rf}(T)}{t_{\mathit{res}}}=\mathit{rf}(T)\cdot F_{p\upsilon }^T$$ (6)

Note that $F_{p\upsilon }^T$ represents plasma flow per plasma volume, and not per tissue volume as is typically the case. As can be seen from Figure 2, there will be some amount of DOX released in the systemic plasma compartment throughout the simulation since the release fraction rf(T) at body temperature (37°C) is non-zero.

The transport of released DOX across the vessel wall depends on the difference of the concentration between the tumour plasma space and the EES ( $c_p^T$ and $c_e^T$, respectively), as well as on the permeability surface area product (PS).

$$\mathrm{transport}=\mathit{PS}\cdot U_{\mathit{DOX}}(c_p^T-c_e^T)$$ (7)

About 70% of the released DOX binds to proteins in both the blood plasma and in the EES [38, 39]. The extravasation of bound DOX is too slow relative to unbound DOX to be considered for transvascular transport; therefore we defined the variable ‘U_DOX’ for the plasma and for the EES as the fraction of unbound DOX available. The product of U_DOX and tumour plasma DOX concentration ( $c_p^T$) or extracellular DOX concentration ( $c_e^T$) represents the concentration of unbound DOX.

In addition to the transport of unbound DOX over the vessel wall into the tumour EES, some of the released DOX (bound and unbound) is removed from the tumour plasma space and transported into the systemic plasma compartment via perfusion. The rate of change of DOX concentration in the systemic plasma compartment due to transport of DOX from the tumour plasma space can be calculated by integrating over the model volume the product of the flow ( $F_{p\upsilon }^T$) and DOX concentration ( $c_p^T$) for each model element in the tumour plasma space times the volume fraction of the tumour plasma space ( ${\upsilon }_p^T$), divided by the total volume of the systemic plasma compartment ( $V_p^B$) (first term in Equation 8).

The overall rate of change of DOX concentration in the systemic plasma compartment is then calculated using Equation 8:

$$\frac{\mathrm{d}{c}_p^B}{\mathrm{d}t}=\frac{{\mathit{\int }}_V(F_{p\upsilon }^T{c}_p^T{\upsilon }_p^T)\mathrm{d}V}{V_p^B}+c_{p\_\mathit{Lip}}{R}_{R37}-k_e{c}_p^B-k_p{c}_p^B+k_t{c}_t^B-c_p^B\frac{\mathit{\int }{F}_{p\upsilon }^T\mathrm{d}V}{V_p^B}{\upsilon }_p^T$$ (8)

where the second term on the right side of Equation 8 is the release of DOX at 37°C, the third term is the clearance rate, the fourth and the fifth terms (respectively) are the rates of transport to and from the tissue compartment, and the final term describes the rate of transport back to the tumour plasma space. Since the transfer constants k_e, k_t, and k_p already account for plasma binding, those terms in Equation 8 are multiplied by the total DOX concentration in the appropriate compartment ( $c_p^B,c_t^B$) instead of the unbound drug concentration $\left(U_{\mathit{DOX}}\cdot c_p^B,U_{\mathit{DOX}}\cdot c_t^B\right)$.

The body tissue compartment represents the extravascular volume of organs with significant drug uptake, i.e. it doesn’t represent any specific tissue. The rate of change of concentration ( $c_t^B$) of the body tissue compartment is described by the exchange of DOX with the systemic plasma compartment:

$$\frac{\mathrm{d}{c}_t^B}{\mathrm{d}t}=k_p{c}_p^B-k_t{c}_t^B$$ (9)

The rate of change of concentration in the tumour plasma space is described by:

$$\frac{\mathrm{d}{c}_p^t}{\mathrm{d}t}=-\frac{1}{{\upsilon }_p^T}\mathit{PS}\cdot U_{\mathit{DOX}}(c_p^T-c_e^T)-F_{p\upsilon }^T{c}_p^T+F_{p\upsilon }^T{c}_p^B+c_{p\_\mathit{Lip}}{R}_R$$ (10)

where the first term describes the rate of transport of DOX into the tumour EES (see Equation 7), the second and the third terms describe the rate of transport of DOX into and out of the systemic plasma compartment, and the last term is the temperature dependent rate of release of DOX from the LTSL (as described above).

The rate of change of concentration of free-DOX in the tumour EES ( $c_e^T$) is described by:

$$\frac{\mathrm{d}{c}_e^T}{\mathrm{d}t}=\nabla \cdot (\mathit{Diff}\cdot \nabla c_e^T)+\frac{1}{{\upsilon }_e^T}\mathit{PS}\cdot U_{\mathit{DOX}}\left(c_p^T-c_e^T\right)-k_{3ci}\left(k_{1ci}{U}_{\mathit{DOX}}{c}_e^T+\frac{k_{2ci}{U}_{\mathit{DOX}}{c}_e^T}{K_{ici}+U_{\mathit{DOX}}{c}_e^T}-c_i^T\right)$$ (11)

In Equation 11, the first term describes the diffusion of drug within the EES, the second term describes the rate of transport of DOX from the tumour plasma space (see Equation 7). The last term describes the rate of uptake of DOX into the tumour intracellular space, described by Equation 12:

$$\frac{\mathrm{d}{c}_i^T}{\mathrm{d}t}=k_{3\mathit{ci}}\left(k_{1\mathit{ci}}{U}_{\mathit{DOX}}{c}_e^T+\frac{k_{2\mathit{ci}}{U}_{\mathit{DOX}}{c}_e^T}{K_{ici}+U_{\mathit{DOX}}{c}_e^T}-c_i^T\right)$$ (12)

We assume two different concurrent intracellular uptake mechanisms of DOX [17]: (1) passive diffusion across the cell membrane, and (2) an active transport mechanism, which is most likely endocytosis. Note that the intracellular uptake model likely varies for different cell types. In our model we used data for human lung cancer cells [44]. Some of the drug is sequestered inside the intracellular compartment, which allows the intracellular DOX concentration to be much higher than the extravascular extracellular tumour concentration at equilibrium.

In experimental studies typically tumour tissue concentrations rather than intra- or extravascular extracellular concentrations are obtained. Therefore we calculate the tumour tissue concentration (c_Tumourtissue) with the tumour extravascular extracellular and the tumour intracellular concentration ( $c_e^T,c_i^T$) according to their volume fractions of the tumour.

$$c_{\mathrm{Tumourtissue}}=c_i^T{\upsilon }_i^T+c_e^T{\upsilon }_e^T$$ (13)

Results

Figure 2 shows the release fraction data from LTSL at temperatures between 37° and 47°C including bi-exponential approximations which were used for the models. All following results are for a 12-min ablation procedure and Table IV shows a summary of the results.

Table IV.

Results: Conventional DOX treatment versus LTSL-DOX treatment.

	Free-DOX	LTSL-DOX	Ratio LTSL-DOX/free-DOX
Max. tumour tissue concentration of DOX (t = 30 min)	3.0 μg/g	9.3 μg/g	3.1
Mean tumour tissue concentration of DOX (t = 30 min)	2.9 μg/g	5.0 μg/g	1.7
Body tissue concentration of DOX (t = 30 min)	6.1 μg/g	3.4 μg/g	0.6
Tumour tissue concentration/body tissue concentration (t = 30 min)	0.47	1.4	3
Tumour mean transit time (tumour diameter: 3 cm)	3.7 s	3.7 s	NA
plasma AUC (t = 72 h)	4.0 (μg h)/g	2.5 (μg h)/g	0.6
Systemic peak plasma concentration of DOX	16.1 μg/g (at t = 0)	4.4 μg/g (at t = 24 s)	0.3

Figure 5 right shows the spatial distribution of temperature, which is higher next to the electrode and decreases with the distance, whereas the left half of the figure displays the tissue blood plasma perfusion, in which the dark blue zone represents an ablated region with no blood perfusion. Within the white lines of Figure 5 is the thermal margin (40–50°C) where cells survive the heat exposure and may be effectively treated with LTSL. Figure 6 shows the tumour tissue concentration of DOX comparing free-DOX to LTSL-DOX administration 30 min after the start of ablation using the temperature and perfusion simulation shown in Figure 4. Figure 5 clearly demonstrates a large spatial variation of DOX with the LTSL-DOX treatment compared with free-DOX. In contrast to the systemic plasma compartment, the maximum concentration of bioavailable DOX in the tumor plasma compartment was ~15 μg/g at ~12 minutes. Most importantly, this higher tumor plasma concentration resulted in greater accumulation of DOX in tumor tissue just outside of the coagulation zone (~9.3 μg/g) compared to normal tissue 3.4 μg/g at ~30 minutes after ablation was initiated. Figure 7 shows the tissue DOX concentration with distance from the RF electrode (dotted line in Figure 6), as well as perfusion confirming high concentration outside the ablation zone (i.e. zone devoid of perfusion). Figure 8 shows that LTSL-DOX results in considerably lower maximum concentration of bioavailable DOX in the systemic plasma compartment. With LTSL-DOX the maximum concentration of bioavailable DOX (i.e. after release from LTSL) in the systemic plasma compartment (peak plasma concentration) was 4.4 μg/g at ~24 s after start of ablation. This peak in the systemic plasma compartment is mostly due to leakage of DOX from the liposome rather than active heating. Figure 9 shows concentration time course at a location just outside the ablation zone (marked in Figure 6), as well as temperature and perfusion for comparison. Figure 10 shows concentration profile with distance from the RF electrode (dotted line in Figure 6) for plasma concentration, EES concentration, and intracellular concentration at the end of ablation (12 min), as well as at 30 min and 60 min after start of ablation. Local plasma and EES concentrations follow each other closely, and slow intracellular DOX uptake rate is evident.

Figure 5.

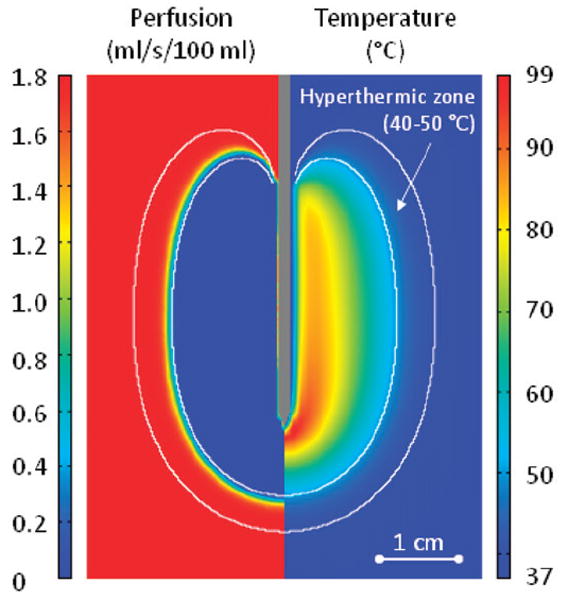
Section of tumour tissue with RF electrode inserted into the centre. The left side of the figure displays perfusion [mL/s/100 mL], the right side the temperature [°C] – both after a 12-min ablation. Perfusion and temperature are used as input data to determine drug release from LTSL. The white lines indicate the hyperthermic zone (40–50°C) where the combination of DOX+heat can kill cells not destroyed by heat alone.

Figure 6.

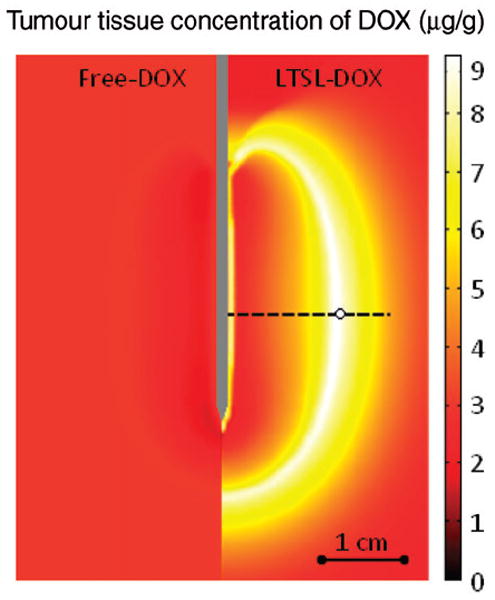
Comparison between free-DOX and LTSL-DOX treatment: LTSL-DOX results in considerably higher tumour tissue drug concentration (right side) compared to free-DOX (left side). Results are shown at 30 min after the start of a 12-min ablation procedure. Concentrations along the dashed line are shown in Figure 7. Time course of concentrations at circled location on dashed line are shown in Figure 9.

Figure 7.

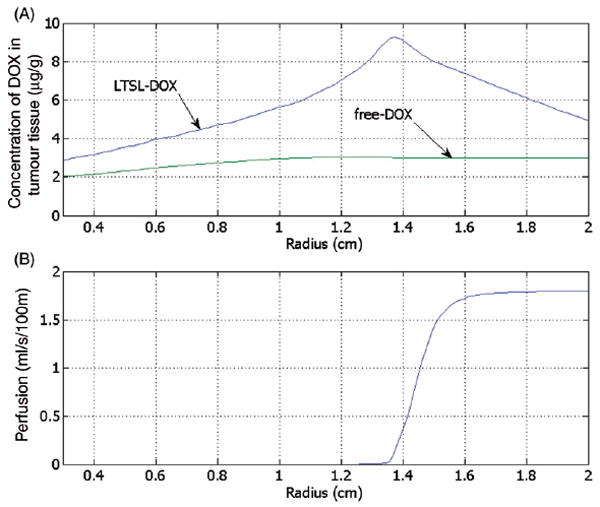
Concentration of DOX in the tumour tissue compartment for the administration of free-DOX and LTSL-DOX versus the radius (see Figure 6 for location), 30 min after start of ablation (A). DOX concentration for LTSL-DOX varies along the radius, whereas for free-DOX there is little variation. The maximum concentration of DOX in the LTSL-DOX case was reached just outside of the ablation zone in a region of considerably reduced perfusion (B).

Figure 8.

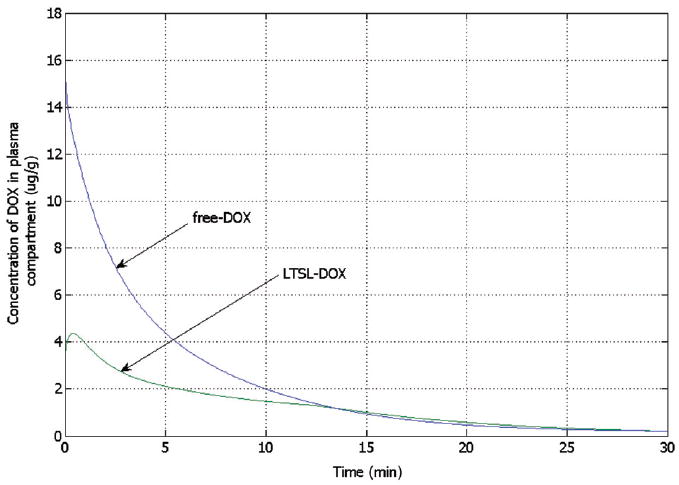
Concentration of bioavailable DOX from free-DOX and LTSL-DOX treatment in the systemic plasma compartment versus time, showing considerably higher peak concentration for free-DOX. For free-DOX, drug concentration is highest right after bolus injection followed by rapid decline, whereas for LTSL-DOX the concentration is zero initially and reaches a maximum after 24 s.

Figure 9.

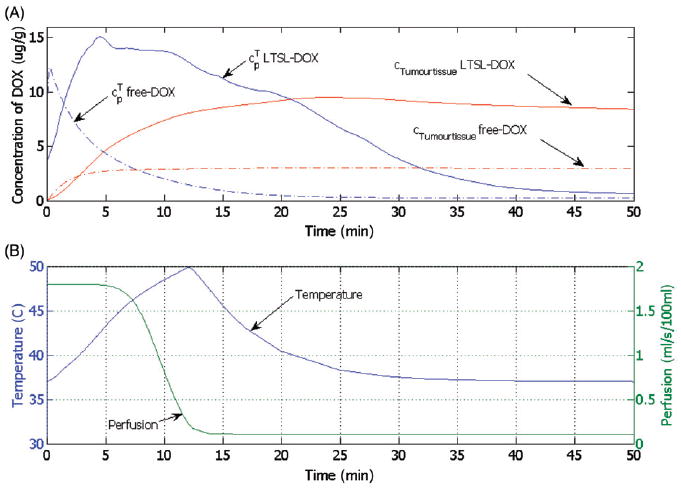
(A) Time course of DOX concentration for free-DOX and LTSL-DOX treatment at one location just outside the ablation zone (see Figure 6, circle on dotted line). Shown are concentrations for tumour plasma space ( $c_p^T$ free-DOX, $c_p^T$ LTSL-DOX) and tumour tissue compartment (c_Tumourtissuefree-DOX, c_TumourtissueLTSL-DOX). (B) Temperature and perfusion at the same location.

Figure 10.

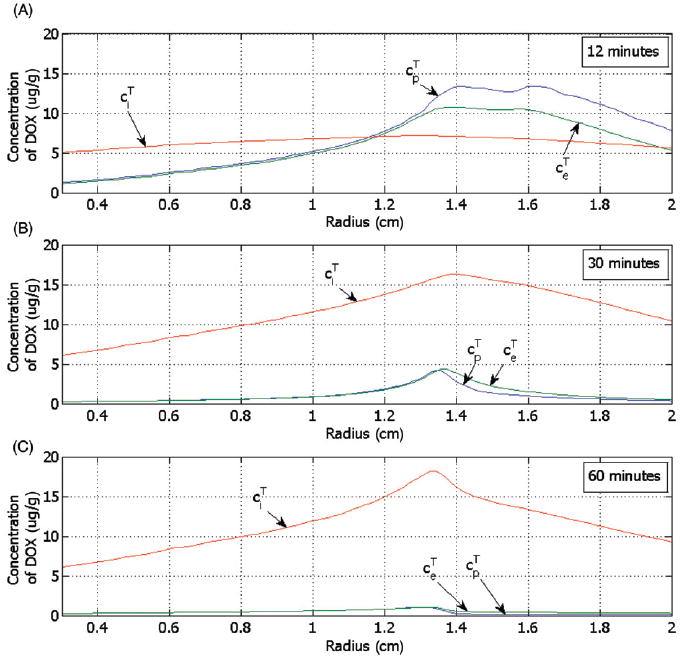
Concentration of DOX for the tumour plasma space ( $c_p^T$), the EES ( $c_e^T$) and the tumour intracellular space ( $c_i^T$) versus the radius (see Figure 6) for LTSL-DOX, shown at (A) 12 minutes, (B) 30 minutes and (C) 60 minutes after start of ablation.

Discussion

RF ablation is a common, minimally invasive treatment for primary and secondary liver tumours, which are not amenable to surgery. During the treatment, tissue is heated via radio frequency current and at a temperature of ≥50°C destroyed by coagulation necrosis. To avoid tumour recurrence, a margin of ~1 cm of normal tissue surrounding the tumour is typically ablated [45, 46]. Due to the vascular nature of liver tissue and physical limitations of the available electrodes, the accomplishable coagulation radius is limited and the required diameter of the ablation zone cannot always be reached [47-49]. Several recent studies have shown synergistic effects between RF ablation and adjuvant administration of DOX, where the volume of tissue necrosis was increased compared to either ablation or DOX alone [1, 5, 6]. More recently, the combination of thermal ablation with LTSL-DOX has received increased attention. LTSL circulate inside the vascular space with a half-life of typically 1.75 h [37]. LTSL release rapidly the encapsulated DOX upon heating to above ~39°C (Figure 2), thereby allowing for increased local drug concentration and reduced systemic toxicity. Since it takes 24–48 h for significant extravascular accumulation of LTSL due to hyperthermia-induced increased extravasation [50], this mechanism is not considered here. Recent in vivo studies have shown that this allows intravascular drug concentration to be kept locally at high levels, resulting in locally increased drug deposition into tissue.

In this study we combine a computational model of RF ablation as published in earlier studies [23] with a multi-compartmental drug delivery model (Figures 3 and 4). Time and spatially dependent tissue temperature and perfusion profiles (Figure 5) during RF ablation with a cooled needle electrode are used as input parameters to determine release rate of DOX from LTSL, and subsequent diffusion from tumour plasma space into EES. Tumour plasma space, EES and intracellular space inside the tumour are each represented by separate spatially dependent compartments (Figure 3). In addition, the remainder of the body tissue and systemic plasma volume is represented by separate compartments which are in connection with the tumour compartments (Figure 3). Either LTSL-DOX or free-DOX is administered into plasma via bolus injection at the beginning of RF ablation at a dose of 0.7 mg/kg. Figure 8 compares the systemic plasma concentration of unencapsulated bioavailable DOX for both cases. Free-DOX results in high initial plasma concentration with rapid decline due to clearance of the drug. Conversely, for LTSL-DOX a low, more or less constant concentration of unencapsulated DOX is observed in the systemic plasma throughout the treatment. The amount of DOX released into the tumour plasma space with LTSL-DOX treatment, and subsequently leaving the tumour does not significantly impact the concentration of DOX in the systemic plasma volume ( $c_p^B$) (Figure 8) due to the small volume of the heated region relative to total body volume. The DOX concentration in the systemic plasma compartment (dose limiting factor) is caused mainly by the release of DOX at body temperature (37°C, compare Figure 2). The dose-limiting toxicities (DLT) of DOX include neutropenia and cardiotoxicity [51]. With the LTSL-DOX treatment the DLT for neutropenia is at a similar dose level as for free-DOX administration, with no observed cardiotoxicity [37]. Systemic peak plasma concentration correlates with cardiotoxicity [52-55], while the plasma AUC is associated with neutropenia [53]. Therefore the much lower systemic peak plasma concentration of DOX seen during LTSL-DOX treatment may be responsible for the reduced cardiotoxicity.

The different pharmacokinetics of free-DOX and LTSL-DOX resulted in very different tissue concentration spatial profiles as shown 30 min after the start of ablation in Figure 6, the time at which maximum tissue concentration is achieved. While after administration of free-DOX the achieved tumour tissue concentration varies little throughout the tumour, there is large spatial variation after the administration of LTSL-DOX. Here, the highest concentration was reached just outside of the ablation zone because at this location the temperature is elevated for a long time period, and there is still some perfusion present (i.e. vessels are not yet coagulated) for most of the ablation period. Further distal from the ablation zone, perfusion is present but temperatures are not sufficiently elevated to cause rapid release from the LTSL, resulting in lower tissue concentrations in those regions.

In addition, reduced perfusion further facilitates increased extravasation as described below in more detail. Also note that the maximum DOX tissue concentration reached with the free-DOX treatment is considerably smaller than that reached with LTSL-DOX treatment. Figure 7 compares the radial drug concentration profile and perfusion profile (marked by a dotted line in Figure 6) 30 min after start of ablation. This time point was chosen to compare to a prior in vivo porcine animal study [56, 57] where tissue drug concentration was measured at several locations throughout the ablation zone in tissue that has been extracted from the animal 15 min after the end of ablation. The tissue concentration profile is comparable to our results with highest DOX tissue concentration just outside the ablation zone for LTSL-DOX, and similar DOX concentration throughout the tissue for the free-DOX case (note that LTSL-DOX was infused over 30 min, i.e. the experimental conditions are not identical).

Figure 9A shows the temporal dynamics of local plasma and tissue DOX concentrations in the tumour at the location where maximum tissue concentration is obtained after LTSL-DOX treatment (location marked by a circle on the dotted line in Figure 6). In the free-DOX case, the maximum plasma concentration is reached right after bolus injection followed by a rapid decline due to the short plasma half-life (see also Figure 8). Thus, the amount of drug that can accumulate in the tissue in the free-DOX case is restricted due to the short time where bioavailable DOX is present in the blood plasma at sufficient concentration (Figure 9A). The situation is rather different after the administration of LTSL-DOX, where the concentration of bioavailable DOX is zero right after injection of LTSL and starts to rise as DOX is released from the LTSL after sufficient temperatures are obtained (see Figure 9A). In the LTSL-DOX case the tumour plasma concentration is affected by both temperature and perfusion resulting in the plasma and EES concentrations in the tumour seen in Figure 9A. Figure 9B shows the relation between temperature and perfusion (location marked by a circle on the dotted line in Figure 6), where a decrease in perfusion due to vascular shutdown (after ~4 minutes in Figure 9B) is observed as temperature increases beyond ~42°C; at this particular location, however, perfusion does not completely cease due to insufficient time and/or temperature. Note also that the particular relationship between heating and perfusion may be different between tumours, and furthermore, perfusion change is considerably different for most normal tissues where an initial perfusion increase is seen followed by vascular shutdown at typically higher temperatures [30]. Release of DOX from the LTSL increases with temperature, although release fractions above ~40°C are fairly similar for this particular LTSL (Figure 2). With declining perfusion the LTSL residence time (i.e. the time the LTSL spent in the heated tumour microvasculature) increased resulting in more complete release from the LTSL, and higher resulting tissue extraction.

Compared to the free-DOX case, local DOX concentration stays at a high level for longer time periods, which allows for increased tissue accumulation of DOX (Figure 9A). Table IV summarises the differences in relevant parameters between LTSL-DOX and free-DOX treatments. Two major shortcomings of chemotherapeutic agents include short plasma half-life combined with a small therapeutic index (i.e. the range of drug concentrations between efficacy and toxicity) [7]. LTSL-DOX improves upon both of these limitations; first, plasma half-life is much higher compared to free-DOX. Secondly, the continuous release of DOX from LTSL locally keeps plasma concentration of bioavailable DOX high for as long as heating continues (note that the amount of DOX released from LTSL is small compared to total administered LTSL-DOX, i.e. depletion of LTSL-DOX due to release is not a relevant factor).

After DOX is released from LTSL it diffuses across the vascular wall until equilibrium is achieved between tumour plasma and EES. The time to equilibrium depends on the product of DOX vessel permeability and vessel surface area (PS). Once reaching the EES, intracellular uptake takes place. Here we assume two different concurrent intracellular uptake mechanisms of DOX [17]: (1) passive diffusion across the cell membrane, and (2) an active transport mechanism, which is most likely endocytosis. Note that the intracellular uptake model likely varies for different cell types. In our model we used data for human lung cancer cells [44]. Additional data from other tumour cell types would be desirable and would allow comparison of resulting intracellular concentrations. In particular, data on multi drug resistant (MDR) cancer cells would be of value, since MDR plays an important role in cancer recurrence after chemotherapy.

Figure 10 shows the DOX concentration in tumour plasma space ( $c_p^T$), EES ( $c_e^T$), and intracellular space ( $c_i^T$) for LTSL-DOX at different time points. EES tumour concentration of DOX ( $c_e^T$) follows the concentration of DOX in the tumour plasma space ( $c_p^T$), as the transvascular transport is based on diffusion. The intracellular concentration ( $c_i^T$) also increases over time with the extravascular extracellular tumour concentration ( $c_e^T$) but by contrast decreases very little as the extravascular extracellular concentration ( $c_e^T$) decreases. This is because some of the drug is sequestered inside the intracellular compartment, which allows the intracellular DOX concentration to be much higher than the extravascular extracellular tumour concentration at equilibrium. Note that the maximum intracellular concentration is the parameter that best correlates with cell survival [44].

To validate our model, we compared the results of our simulation to a prior in vivo study which was performed in swine [56, 57]. In that study conventional chemotherapy treatment (free-DOX) and the administration of LTSL-DOX with release rates similar to those shown in Figure 2 were compared. Drug was infused over 30 min and ablation started with a cooled needle electrode at constant temperature for 10 min (without needle cooling), and for another 15 min at maximum power with needle cooling. After ablation the animal was sacrificed, and tissue extracted. The tissue concentration of DOX reached with an LTSL-DOX treatment was considerably higher than with the administration of free-DOX. The highest DOX tissue concentration after LTSL-DOX administration of ~5 μg/g was obtained just outside of the ablation zone, with concentrations of ~2 μg/g measured inside the ablated tissue. At >3 cm distance from the ablation zone, DOX tissue concentrations were less than 1 μg/g. After free-DOX administration, tissue concentrations were less than 2 μg/g throughout the tissue with maximum measured again just outside the ablation zone. These results compare quantitatively well with our model, though we note that uptake in normal liver cells may be considerably different than in cancer cells. New liposomal formulations that include a contrast agent may provide an effective way for more detailed validation, allowing comparison of spatio-temporal release rates during heating [58].

Computer models play an important role in understanding and describing pharmacokinetic behaviour of drugs (e.g. absorption, distribution, elimination) and are used to predict parameters such as drug concentrations in different compartments, which are relevant for the toxicity and efficacy of a drug [59]. Computational models such as the one presented may facilitate the optimisation of tumour drug concentration via examination of parameters such as liposome properties, tumour perfusion, and heating regimen and method respectively (e.g. RF, focused ultrasound, etc.).