Measuring torsional eye movements by tracking stable iris features

Research highlights

▶ Maximally Stable Volumes are automatically detected features. ▶ Maximally Stable Volumes allow stable tracking through time. ▶ Robust to nonuniform illumination and large changes in eye position. ▶ Faster than cross-correlation.

Abstract

We propose a new method to measure torsional eye movements from videos taken of the eye. In this method, we track iris features that have been identified as Maximally Stable Volumes. These features, which are stable over time, are dark regions with bright borders that are steep in intensity. The advantage of Maximally Stable Volumes is that they are robust to nonuniform illumination and to large changes in eye and camera position. The method performs well even when the iris is partially occluded by reflections or eyelids, and is faster than cross-correlation. In addition, it is possible to use the method on videos of macaque eyes taken in the infrared, where the iris appears almost featureless.

1. Introduction

The accurate measurement of three-dimensional eye movements is desirable in many areas, such as in oculomotor and vestibular research, medical diagnostics, and photo-refractive surgery. The three main ways to measure three-dimensional eye movements are to use scleral search coils, electro-oculography, or video-oculography (Haslwanter and Clarke, 2010). Video-oculography is the only one of these options that is suited for clinical practice, since scleral search coils can be uncomfortable and electro-oculography has low spatial resolution.

Using video-oculography, horizontal and vertical eye movements tend to be easy to characterise, because they can be directly deduced from the position of the pupil. Torsional movements, which are rotational movements about the line of sight, are rather more difficult to measure; they cannot be directly deduced from the pupil, since the pupil is normally almost round and thus rotationally invariant. One effective way to measure torsion is to add artificial markers (physical markers, corneal tattoos, scleral markings, etc.) to the eye (Migliaccio et al., 2005; Clarke et al., 1999) and then track these markers. However, the invasive nature of this approach tends to rule it out for many applications. Non-invasive methods instead attempt to measure the rotation of the iris by tracking the movement of visible iris structures.

To measure a torsional movement of the iris, the image of the iris is typically transformed into polar co-ordinates about the centre of the pupil; in this co-ordinate system, a rotation of the iris is visible as a simple translation of the polar image along the angle axis. Then, this translation is measured in one of three ways: visually (Bos and de Graaf, 1994), by using cross-correlation or template matching (Clarke et al., 1991; Zhu et al., 2004), or by tracking the movement of iris features (Groen et al., 1996; Lee et al., 2007).

Methods based on visual inspection provide reliable estimates of the amount of torsion, but they are labour intensive and slow, especially when high accuracy is required. It can also be difficult to do visual matching when one of the pictures has an image of an eye in an eccentric gaze position.

If instead one uses a method based on cross-correlation or template matching, then the method will have difficulty coping with imperfect pupil tracking, eccentric gaze positions, changes in pupil size, and nonuniform lighting. There have been some attempts to deal with these difficulties (Haslwanter and Moore, 1995; Zhu et al., 2004), but even after the corrections have been applied, there is no guarantee that accurate tracking can be maintained. Indeed, each of the corrections can bias the results.

The remaining approach, tracking features in the iris image, can also be problematic. Features can be marked manually, but this process is time intensive, operator dependent, and can be difficult when the image contrast is low. Alternatively, one can use small local features like edges and corners. However, such features can disappear or shift when the lighting and shadowing on the iris changes, for example, during an eye movement or a change in ambient lighting. This means that it is necessary to compensate for the lighting in the image before calculating the amount of movement of each local feature.

In this paper, we attempt to overcome problems with the feature tracking method by applying a well established method from the field of image processing. We use image features called Maximally Stable Volumes (Donoser and Bischof, 2006), which have been shown to be stable under affine geometric transformation and changes in lighting (Matas et al., 2004; Mikolajczyk et al., 2005). These features allow us to generate estimates of torsional movement while the eye is making large movements under variable illumination.

To validate the correctness of our methodology, we check whether it works on a video of a human eye by comparing its torsional estimates with estimates obtained through visual matching. Then, we check to see whether the three-dimensional eye positions from a standard nine-point calibration obey Listing's law. We also test the methodology on videos of a corrugated annulus rotating ballistically under nonuniform lighting, both perpendicular and at 43° to the camera plane. Finally, we test the methodology on videos of macaque eyes taken in the infrared, where it has traditionally been considered difficult to find iris features.

We show that our methodology allows robust feature tracking under uneven lighting conditions and eccentric viewing position, even when the iris appears to have few visible features.

2. Materials and methods

The basic procedure to measure torsion is as follows: we make a video recording of the eye, import the video data, find the pupil edge and fit it with an ellipse, compensate for eccentric eye orientation (and thus also horizontal or vertical eye movements), perform a polar transform, detect iris features, and then determine the movement of these iris features over time. We describe the steps of this process in more detail below.

To develop the method, we recorded videos with the EyeSeeCam (Dera et al., 2006), a portable head-mounted video-oculography system. Our videos were recorded in the uncompressed Portable Graymap Format at 130 Hz in 8-bit greyscale. Each frame was 348 by 216 pixels in size, with a resolution of roughly 15 pixels/mm at the plane of the cornea (see Fig. 1 for an example image). However, we have tested the method with videos recorded with other systems, and the method described below also works on those videos after we account for the different image resolution, image quality, and sampling rate. Indeed, part of the validation described in this paper is performed with a Basler A602fc high speed camera, recording at 100 Hz.

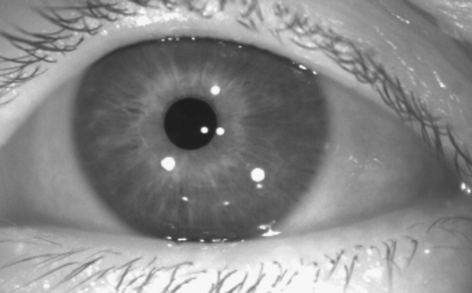
Fig. 1.

Raw infrared image captured by the EyeSeeCam video-oculography system. The bright white spots on the pupil and iris are reflections of infrared light emitting diodes.

In each frame, we automatically detect the pupil, which is characteristically a large, somewhat centrally located, dark area. Once the pupil has been successfully found in one frame, we carry this information across to the next frame to facilitate pupil detection there. The pupil edge is often obscured by reflections, the upper eyelid, or eyelashes, meaning that simple thresholding may provide us with false edge points. To determine the points on the pupil edge that are caused by artifacts, we detect regions of extreme curvature. These regions are then discarded, leaving only reliable pupil edge points. The method that we use is similar to that described by Zhu et al. (1999), but we automatically determine the curvature thresholds, which allows us to account for changing pupil size.

The next step is to correct for eccentric eye orientation, because the eye is not always looking directly at the camera. The standard way to do this is to perform a calibration, which makes it possible to infer the eye orientation from the position of the centre of the pupil. However, it is often difficult to perform a calibration for a subject with a vestibular disorder, and a calibration becomes invalid when the head moves relative to the camera. We instead decided to correct for the orientation of the eye by using the shape of the pupil. This is based on the observation that a circle will appear to be elliptical when it is viewed under central projection (Moore, 1989). A round pupil viewed from an angle will thus appear to be roughly elliptical—though not perfectly elliptical, since there is also shape deformation caused by refraction through the cornea. We start out by fitting an ellipse to the pupil edge points using the method published by Taubin (1991). We chose this method over the commonly used ellipse-specific fitting method described by Fitzgibbon et al. (1999) because the Taubin method produces the most reasonable ellipse fits when much of the pupil edge is absent (Fitzgibbon and Fisher, 1995). We compensate for eccentric eye orientation by applying an affine transformation that leaves the major axis of the ellipse unchanged and stretches the minor axis until it is as long as the major axis, transforming the ellipse into a circle. The intensities of the new pixel positions are calculated by linear interpolation.

To make the subsequent torsion tracking robust to small errors in the pupil tracking algorithm, we transform the eye image into polar co-ordinates about the detected pupil centre, using linear interpolation and an angular resolution of 3 pixels/degree. Fig 2a shows an example of a polar transformed image. Torsional movements then become translations of the iris along the angle axis. Errors in the ellipse fit to the pupil cause some features to appear to translate more than the amount of torsion, while others appear to translate less (Groen et al., 1996). Our method of torsion tracking is inherently robust to slight errors in the ellipse fitting, since we track multiple features to determine the size of torsional movements.

To detect iris features, we use the Maximally Stable Volumes detector (Donoser and Bischof, 2006). This detector has been used to identify three-dimensional features in a volumetric data set, for example, a collection of image slices through an object. It is an extension of the Maximally Stable Extremal Regions detector (Matas et al., 2004), which has been shown to be one of the best feature detectors, partly because it is robust to changes in camera position and lighting. A brief introduction to the concept of Maximally Stable Volumes is given in Appendix A.

In our application of the Maximally Stable Volumes detector, we choose the third dimension to be time, not space, which means that we can identify two-dimensional features that persist in time. The resulting features are maximally stable in space (2-D) and time (1-D), which means that they are 3-D intensity troughs with steep edges. Our implementation is based on the VLFeat library written by Vedaldi and Fulkerson (2008). However, the method of Maximally Stable Volumes is rather memory intensive, meaning that it can only be used for a small number of frames (in our case, 130 frames) at a time. Thus, we divide up the original movie into shorter overlapping movie segments for the purpose of finding features. We use an overlap of four frames, since the features become unreliable at the ends of each submovie. We set the parameters of the Maximally Stable Volumes detector such that we find almost all possible features. Of these features, we only use those that are near to the detected pupil centre (up to 6 mm away) and small (smaller than roughly 1% of the iris region). We remove features that are large in angular extent (the pupil and the edges of the eyelids), as well as features that are further from the pupil than the edges of the eyelids (eyelashes). We also remove features on the borders of the polar transformed images because these change size as they shift across the border, thus causing them to provide incorrect estimates of the torsional status of the eye. Fig. 2b shows the remaining features found in the image in Fig. 2a.

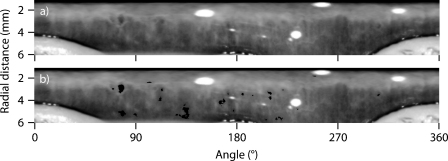
Fig. 2.

(a) Image derived by applying the polar transform to the raw image shown in Fig. 1. (b) The features that we use are shown superimposed on the polar transformed image in black. These features are found by using the Maximally Stable Volumes detector. We exclude features that are very dark, large, long in angular extent, or near the boundary.

We estimate the torsional position of the eye in each frame by tracking all of the features simultaneously. This allows us to compensate for the variable size of features over time, and the fact that not all features are present in all frames. The position of each feature over time provides an estimate of the torsional position of the iris, relative to the frame in which the feature first became visible. We reconcile differing estimates of the torsional position from the individual features by taking the median of the estimates. Table 1 shows an example of this torsional tracking method. In this example, we have a movie with five frames and four features, and three of the features are visible in only some of the frames. It is important to note that our method of torsional tracking is superior to simple incremental frame-by-frame tracking, since errors from spurious transient features tend not to persist over time.

Table 1.

A worked example to show our method to determine torsional position from many features. (a) Raw angular position of the centre of gravity of four features. Note that only the first feature is visible in all five frames. (b) Torsional position information from each feature, relative to the first frame in which the feature was visible. (c) Combined torsional position. We set the torsional position of frame F1 to zero, substitute this value into the positions for F2, then evaluate the median position. After the torsional position for F2 is determined, we substitute this value into the positions for F3, etc.

				Frame
				F1	F2	F3	F4	F5
(a)	Raw position	Feature	i	5	6	7	8	9
			ii	3	3	6	6	–
			iii	–	–	5	5	7
			iv	–	2	4	–	–
(b)	Position relative to initial frame	Feature	i	–	F1 + 1	F1 + 2	F1 + 3	F1 + 4
			ii	–	F1 + 0	F1 + 3	F1 + 3	–
			iii	–	–	–	F3 + 0	F3 + 2
			iv	–	–	F2 + 2	–	–
(c)	Final values, recursively filled	Feature	i	–	0 + 1	0 + 2	0 + 3	0 + 4
			ii	–	0 + 0	0 + 3	0 + 3	–
			iii	–	–	–	2.5 + 0	2.5 + 2
			iv	–	–	0.5 + 2	–	–
		Combined		0	0.5	2.5	3	4.25

3. Results

We tested our feature tracking method in a number of ways. Firstly, we applied the method to a video obtained from a subject actively rolling his head, and compared the torsion estimates to those obtained from cross-correlation and visual matching. We also used this video to investigate the sensitivity of our method to an incorrectly determined pupil centre. Next, we performed a standard nine-point calibration with the head both upright and tilted to the side by 45°, and checked to see whether the three-dimensional eye position estimates lie on Listing's planes. Then, we applied our method to two videos of an unevenly lit three-dimensional target rotating ballistically, and validated the position and velocity estimates. Finally, we demonstrated that stable features can be found even when the iris appears to be mostly featureless. We show the results of each of these validation steps below.

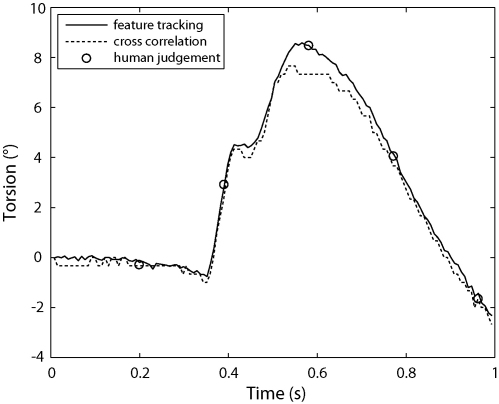
For the first set of validations, we use the EyeSeeCam system to record a video of a person rolling his head to induce torsional eye movements. We used our method of feature tracking to estimate the torsion of the left eye over time. To check this estimate, we took the polar transformed frames and generated estimates of torsion by cross-correlation. In addition, we also asked five human subjects to align five of the polar transformed frames to the initial frame along the angle axis, using a method similar to that used by Bos and de Graaf (1994). Fig. 3 shows the different estimates of torsion. Our method of feature tracking produces estimates that are consistent with those produced by human judgement. Note that cross-correlation underestimates the amount of torsion, which occurs because the polar transformed images contain light reflexes and eyelids that are not subject to the torsional movement.

Fig. 3.

Plot of torsion over time, estimated by using three different methods: our feature tracking method, cross-correlation, and human judgement (performed on only five frames). The human judgement values plotted here are the averages of the estimates made by five different people. The results for feature tracking are consistent with those of human judgement. Cross-correlation underestimates the amount of torsion because of the presence of reflections and eyelids in the image, which are not subject to torsional movement. Two 4° saccades between 0.35 and 0.55 s are clearly visible.

We performed all processing with a 32-bit version of MATLAB on an AMD Phenom(tm) 9600B Quad-Core Processor running at 2.3 GHz with 3.5 GB RAM. However, we did not actively use parallel processing to perform the polar transforms or feature finding. The processing time per frame is shown in Table 2.

Table 2.

Time required to perform each processing step. The cross-correlation was performed on the polar transformed images, independently of the feature finding and tracking steps. Here, the cross-correlation was restricted to a maximum angular shift of 10° (with 3 angular pixels per degree) and a maximum radial shift of 5 raw image pixels (with 2 radial pixels per raw image pixel).

Processing step	Time per frame (s)
Pupil fitting	0.03
Polar transform	0.08
Feature finding	0.36
Removing bad features	0.10
Feature tracking	0.02
Cross-correlation	0.94

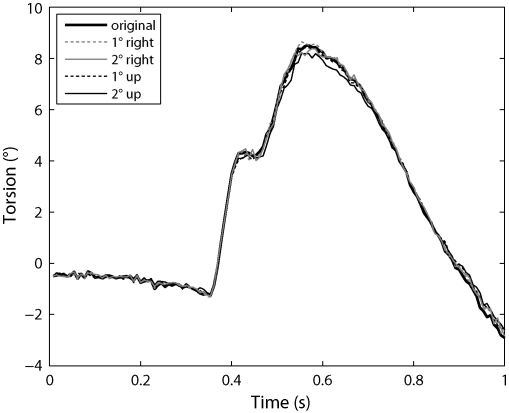
We used the same head-rolling video to check the sensitivity of our method to errors in the estimated pupil centre position. Here, we simply added artificial shifts (1° and 2° of gaze angle) to the pupil centre estimates before performing the polar transform on the images. In Fig. 4, the resulting torsion estimates are shown. The curves all show the same qualitative behaviour and the maximum torsional error is only 0.5°, even with 2° error in gaze direction. This shows that our method is robust to small errors in the pupil fits.

Fig. 4.

Effect of error in the pupil position on torsion estimates. Here, we added an error of 3 or 6 raw pixels to the pupil centre estimates, which correspond to an error of 1° and 2° of gaze angle, respectively. The resulting torsion estimates remain very close to the original torsion estimate.

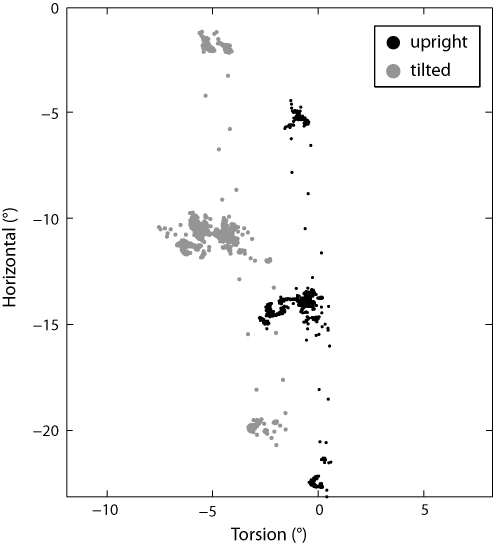
In the next step, we combined our torsional position estimates with the calibrated horizontal and vertical position data from the EyeSeeCam, and checked to see whether the combination obeys Listing's law—for an explanation of Listing's law, see Haslwanter (1995). One standard way to test Listing's law is to see whether the estimated eye positions lie on a plane. To generate the eye position data, we performed two standard nine-point calibrations, one with the head upright, and the other with the head tilted to the right by 45° in order to induce torsional counter-roll. We then used our method to calculate the torsion from the videos, and combined it with the horizontal and vertical eye position data that was output by the EyeSeeCam software. If the torsional axis angles are plotted against the horizontal axis angles, we see that the eye positions are roughly coplanar, both with head upright and with head tilted. In the head upright case, the standard deviation of the points from the best fit plane is 0.5°, and when the head is tilted, the standard deviation increases slightly to 0.7°. The expected torsional shift in eye position that was caused by the head tilt is clearly visible (Fig. 5).

Fig. 5.

Plot of horizontal eye position versus torsional eye position, either with head upright or with head tilted 45° to the right. The horizontal eye position was taken directly from the EyeSeeCam software, while the torsional eye position was calculated using the method described in the text. In both head positions, the eye positions lie roughly in a plane (“Listing's plane”). Note that the view here is not perfectly along the best fit plane. The torsional counter-roll of the eyes is clearly visible as a shift along the torsion axis.

Our next aim was to validate the position and velocity estimates from our method more directly. We chose not to use human data since human fixations are inherently inaccurate and unstable. Instead, we created an annulus of paper, crumpled it and unfolded it again to give it three-dimensional structure, mounted it on a stepper motor (Unitrain SO4204-7W), and illuminated it with a light source that was mounted to one side. We attached gyroscopes (Xsens MTx) to the back of the annulus to allow us to measure angular velocity data directly at 120 Hz. We mounted a high speed digital camera (Basler A602fc) directly facing the annulus and recorded videos at 100 Hz of the annulus rotating in a ballistic, open-loop fashion—this movement was meant to mimic a torsional saccadic movement. The resulting images are nonuniformly illuminated, and have features that are primarily the shadows cast by ridges. However, since the whole ring rotates, the shadows change their size and shape. This validation is motivated by the fact that video-oculography systems often record in the infrared, and features that are visible in the infrared are typically created by shadows cast by the ciliary muscle, not by pigmentation.

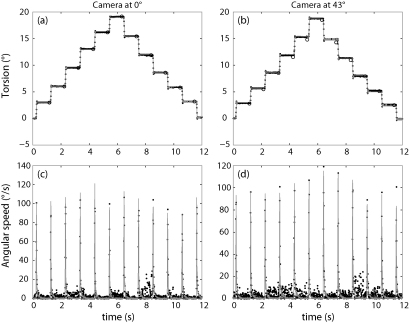
Fig. 6a shows the position estimates from our torsional tracking method. Since it was not possible to directly obtain position estimates from the stepper motor, we also generated human estimates of torsional position by superimposing a target frame and reference frame, and then rotating the target frame until the features aligned. These human estimates, as well as the torsional estimates from cross-correlation, are also shown in Fig. 6a. Our results from feature tracking clearly show the oscillations of the stepper motor at the completion of each movement. The method is accurate at estimating the magnitude of each jump, even though each full movement occurred within the span of only five frames, meaning that we only obtained valid torsion estimates from a few large features. Note that the unequal step sizes produced by the stepper motor are caused by the torque induced by the cable attached to the gyroscopes. The difference between the torsional position estimates from our torsional tracking method and the human estimates had a mean of 0.02° and a standard deviation of 0.04°; this is comparable in size to the uncertainty of our human estimates (±0.1°).

Fig. 6.

Plots of torsional position and speed over time for an annulus mounted on a stepper motor. (a) and (c) correspond to the video where the camera is directly in front of the annulus, while (b) and (d) correspond to the video where the camera has been placed such that it is imaging the annulus from 43° off-centre. In all plots, the points are the estimates from our method, and the circles are the estimates obtained by rotating and visually matching the images. For the position plots, the lines represent the estimates from cross-correlation, and in the angular speed plots, the lines represent the gyroscope data. The damped oscillations of the stepper motor just after each movement are also present in the torsion plots. The inherent granularity of the cross-correlation estimates resulting from the angular resolution of 3 pixels/degree is visible as an oscillation artefact with an amplitude of a third of a degree.

Fig. 6b shows the estimates of angular speed from our method, compared to the measurements from the gyroscopes. The estimates of peak angular speed, duration and timing of the ballistic movements agree well. The estimates from our method show some frame-to-frame jitter, which is caused by the uncertainty in obtaining an pupil ellipse fit from a pixelated image. For those data points where the gyroscope showed no movement (<2°/s), our method produced angular velocities with mean 0.0°/s and standard deviation 3.7°/s. For those data points where the gyroscope showed definite movement (>10°/s), the difference between our angular velocity estimates and the gyroscope data had mean −2.8°/s and standard deviation 5.9°/s.

We then took the camera and moved it to view the annulus with an eccentricity of 43°, so that the pupil appears to be elliptical. Again, we recorded videos of the rotating annulus and applied our torsional tracking method. Fig. 6c shows the position estimates as compared to those obtained from human judgement (performed as for Fig. 6a after stretching the frames such that the artificial iris was circular) and cross-correlation, and Fig. 6d shows the angular speed estimates as compared to those from the gyroscopes. The results appear to be almost as good as those obtained when the camera was positioned directly in front of the annulus. The difference between the torsional position estimates from our torsional tracking method and the human estimates had a mean of 0.25° and a standard deviation of 0.19°, which is slightly more than would be expected just from the uncertainty of our human estimates (±0.2°). For those data points where the gyroscope showed no movement (<2°/s), our method produced angular velocities with mean 0.0°/s and standard deviation 4.5°/s. For those data points where the gyroscope showed definite movement (>10°/s), the difference between our angular velocity estimates and the gyroscope data had mean 1.7°/s and standard deviation 8.1°/s.

The final step of our validation involved applying our torsional tracking method to a video of macaque iris, which was recorded in the infrared. Such videos are typically considered to be almost featureless, but nonetheless, our method was able to find features on the iris that are stable in time, meaning that we can track them. Fig. 7 shows the position of the features in one frame of the video. A number of the features found are caused by the eyelashes, since they appear to be a similar intensity to the iris. We could naturally remove these by explicitly finding the eyelids and excluding features near the eyelids, but in this case, they should not cause a problem, since there are so many other features present. For this video, the monkey was stationary, and since there was no torsional movement of the eyes, we have omitted the corresponding torsion plot.

Fig. 7.

(a) Image derived by applying the polar transform to a raw image taken from a video of a macaque eye. (b) The features that we find are shown superimposed on the polar transformed image in black. Here, three of the features are created by eyelashes because the macaque eyelashes are similar in intensity to the iris. However, these cause no problem for our tracking algorithm since there are so many other features present.

4. Discussion

We have suggested a new automated method of measuring torsional eye movements, based on tracking Maximally Stable Volumes. These stable persistent dark iris features allow us to produce estimates of torsional movement that are consistent with human estimates. Since we use the centre of gravity of multipixel features, we can track movements that are smaller than the pixel size in the polar transform. Because we track the movement of multiple features, the results are robust to slight errors in pupil finding. The method is robust to nonuniform illumination of the target, and performs well even when there are large changes in the position and torsional status of the eye. The same procedure can also be used with videos of macaque eyes taken in the infrared, where it has been typically difficult to find features.

One key features of the Maximally Stable Volumes feature tracker is that it automatically produces features that are connected not only in space, but also in time. This means that there is no need to additionally associate features between frames, but it requires that features overlap from one frame to the next. For eye tracking, this means that the videos must be taken with a high enough sampling rate to sample a number of intermediate points during a torsional saccade. From our results (see Fig. 3), it can be seen that a 4° torsional saccade (produced during a head roll) with a peak velocity of 100°/s can be tracked in a video recorded at 130 Hz. For lower sampling rates, larger features need to be used, which reduces the number of features and thus the accuracy of the tracking procedure.

One feature of our method is that we do not require horizontal and vertical eye position to be determined explicitly before creating the polar transform. If it is possible to perform a valid calibration, and this calibration stays valid for the whole recording, then the calibrated horizontal and vertical eye positions can naturally be used to compensate for eccentric eye position. For eyes with roughly circular pupils, our experience is that this compensation gives almost exactly the same results as our compensation based on pupil shape. If the pupil deviates significantly from being circular, it is conceivable that the compensation based on calibrated eye position may outperform our compensation. However, we chose our method of compensation because a calibration is likely to become invalid during large head movements, or when the cameras move with respect to the head. Also, if our correction is slightly incorrect, this is likely to have relatively little impact on the final torsional tracking results, as can be seen from the experiments where we artificially displaced the pupil centre. Of course, our method is likely to produce false torsional estimates when there are irregular changes in pupil shape during the recording. In this case, it may be possible to stabilise the pupil using a miotic agent like pilocarpine before performing the recording.

The affine transformation that we perform is equivalent to assuming a certain horizontal and vertical position of the eye. However, estimates of horizontal and vertical position based on pupil shape are imprecise, since pupil eccentricity changes only slowly as eye position changes. Thus, we do not recommend using the implicit horizontal and vertical positions directly. Instead, if it is possible to perform and maintain a valid calibration, we recommend combining our estimates of torsion with calibrated horizontal and vertical eye positions to reconstruct the full 3-D eye position.

A problem arises with our method if the pupil cannot be found, for example, during a blink, since we rely on at least some of the features to remain connected over time. After pupil tracking is re-established, one could estimate the torsion relative to a reference frame with cross-correlation, or alternatively, if only eye velocity is important, the torsion of the eye could be arbitrarily reset to zero. Another approach is to use a robust similarity measure like that proposed by Matas et al. (2004) to associate features from frames before and after the loss of pupil tracking.

The current running time of our method is dominated by the running time of the algorithm used to find Maximally Stable Volumes. The implementation that we use (Vedaldi and Fulkerson, 2008) is based on the original algorithm described by Matas et al. (2004). Recently, Murphy-Chutorian and Trivedi (2006) and Nistér and Stewénius (2008) have described different, independent ways to increase the speed of the algorithm. An implementation that incorporated their changes should be at least an order of magnitude faster than what we have described, which would make the feature finding run in near to real time. Other ways of speeding up our method are to crop the images appropriately, and to select only those frames that are of interest. Since the time taken to find features is proportional to the number of pixels to be processed, it is important that the image resolution and sampling rate are not excessively high.

It may also be possible to speed up our algorithm by finding features in the raw video, and then transforming the centres of gravity of these features into polar co-ordinates. The feature finding step should run more quickly because the raw frames typically have less pixels than the polar transformed frames, and the polar transform should become almost instantaneous, since we remove the need for interpolation.

We intend to validate our approach further in both experimental and clinical settings. Two experimental validations are already planned: simultaneous eye movement recordings from scleral search coils and video-oculography, and eye movement recordings while the subject is rotating under controlled conditions in a rotating chair. In our clinical validation, we intend to measure eye movements during clinical testing for benign paroxysmal position vertigo and see if the three-dimensional eye movement patterns match the diagnosis of the doctor.

Appendix A. Maximally Stable Volumes

Maximally Stable Volumes are three-dimensional extremal regions that satisfy a stability criterion. We will start out by explaining the concept of an extremal region, give the stability criterion, and then give the properties of Maximally Stable Volumes that make them so useful in torsion tracking. A more detailed explanation is given by Matas et al. (2004).

A region is a connected set of pixels. The boundary of a region is the set of pixels adjacent to, but not contained in, the region. A region is extremal if all of the intensities in the region are higher than the intensities in the boundary, or vice versa. Equivalently, an extremal region is a region that may be generated by thresholding image data. For torsion tracking, we currently only use dark extremal regions with bright borders.

For an extremal region to be stable, it needs to remain almost unchanged over a range of thresholds. The stability criterion is related to the rate of change of the size of the extremal region with respect to threshold intensity. Specifically, if E_T is an extremal region created by thresholding at intensity T, and N_T is the number of pixels in E_T, then the stability criterion S(T) is defined to be

$$S(T)=\frac{|N_{T+\Delta }-N_{T-\Delta }|}{N_T}\text{,}$$

for some chosen value of Δ. An extremal region $E_{T^{*}}$ is maximally stable if S(T) has a local minimum at T = T*. Maximally Stable Volumes are three-dimensional maximally stable extremal regions created from a stack of images.

Mikolajczyk et al. (2005) found that maximally stable extremal regions remain almost unaffected by changes in illumination, and that they can be found consistently even after changes in camera position as large as 60°. These properties are important in torsion tracking, since the scene illumination is unlikely to be uniform, and the eyes may rotate through large angles although the cameras remain roughly stationary.