UV Resonance Raman Investigation of Electronic Transitions in α-helical and Polyproline II-like Conformations

Abstract

UV resonance Raman (UVRR) excitation profiles and Raman depolarization ratios were measured for a 21-residue predominantly alanine peptide, AAAAA(AAARA)₃A (AP), excited between 194 and 218 nm. Excitation within the π→π* electronic transitions of the amide group results in UVRR spectra dominated by amide vibrations. The Raman cross sections and excitation profiles provide information about the nature of the electronic transitions of the α-helix and PPII-like peptide conformations. AP is known to be predominantly α-helical at low temperatures and takes on a polyproline II (PPII) helix-like conformation at high temperatures. The PPII-like and α-helix conformations show distinctly different Raman excitation profiles. The PPII-like conformation cross sections are approximately twice those of the α-helix. This is due to hypochromism that results from excitonic interactions between the NV₁ transition of one amide group with the higher energy electronic transitions of other amide groups, which decreases the α-helical NV₁ (π→π*) oscillator strengths. Excitation profiles of the α-helix and PPII-like conformations indicate that highest signal-to-noise Raman spectra of α-helix and PPII-like conformations are obtained at excitation wavelengths of 194 and 198 nm, respectively. We also see evidence of at least two electronic transitions underlying the Raman excitation profiles of both the α-helical and PPII-like conformations. In addition to the well known ∼190 nm π→π* transitions, the Raman excitation profiles and Raman depolarization ratio measurements show features between 205-207 nm, which in the α-helix likely results from the parallel excitonic component. The PPII-like helix appears to also undergo excitonic splitting of its π→ π* transition which leads to a 207 nm feature.

Introduction

UV resonance Raman (UVRR) spectroscopy is well established as a technique for probing secondary structure of peptides and proteins^1-29. Excitation between 180 to 215 nm, within the π→π* electronic transitions of the peptide backbone, results in the enhancement of amide vibrations^1-29. Amide π→π* electronic transitions show no emission and appear to be homogeneously broadened. Their broad absorption spectra provide little information about the underlying excited states. UVRR excitation profiles and Raman depolarization ratios are utilized here to examine the underlying amide electronic transitions^25,26,29. The present consensus is that predominantly three electronic transitions occur in simple amides in the 130 to 230 nm range. These electronic transitions are the weak n→π* transition (210 to 230 nm), the strong π→π* transition (170 to 195 nm), and a second, weaker π→π* transition (135 to 160 nm)^30-37. Along with the classically defined transitions, other transitions reported include charge transfer electronic transition states^36,37, as well as Rydberg transitions found in gas phase spectra^30-32,39,40

In α-helices a weak n→π* electronic transition occurs at ∼ 220 nm while a higher frequency π→π* electronic transition occurs at ∼ 190 nm. This π→π* transition is understood to undergo exciton splitting which gives rise to two dipole-allowed transitions: one perpendicular to the helical axis at 190 nm and the second parallel to the axis at 205 nm^41-46.

The melted state of α-helices has been demonstrated by our group, as well as others, to predominantly be a conformation closely related to the left-handed polyproline II (PPII) helix^12,47-50, and not a random coil, although there is some disagreement with this result^51,52. The high temperature AP spectra are identical to the spectra of the peptide XAO, which Shi et al., determined to be ∼90% PPII helix⁴⁸. We treat the non-α-helical conformation of AP as being a predominantly PPII helix, which means that the PPII structure is found primarily along the peptide chain, but also may include some β-turn like structures¹². The transitions in pure PPII helices involve an n→π* transition at ∼ 220 nm and a π→π* transition at ∼ 200 nm. Theory has not yet been able to accurately model the excited states found in a PPII helix such that it can predict circular dichroism (CD) and absorption spectra⁴⁶. It has been suggested that, for the PPII conformation, a mixing of the π→π* transition with higher energy transitions must be included in calculations to accurately reproduce the CD and absorption experimental data⁴⁶.

In this study, we characterize the UVRR excitation profiles and depolarization ratios of aqueous solutions of a 21-residue, mainly alanine peptide (AP) from 194 to 229 nm and at 5°C and 60°C. AP has been shown to be a mixture of α-helix and polyproline II (PPII) helix conformations at low temperatures (<25°C) and predominantly PPII helix-like at high temperatures (>25°C)^26,50,53. This high temperature PPII-like conformation is often referred to as the peptide unfolded state.

We observe the two exciton split classically defined components of the π→π* transition in the α-helix. In the PPII-like helix, however, we also observe two strong electronic transitions in the 190 to 230 nm range, which also likely derive from excitonic interactions.

Materials and Methods

Sample Preparation

The 21-residue poly-alanine peptide AAAAA(AAARA)₃A (AP) was prepared by AnaSpec (San Jose, CA) using solid-state peptide synthesis (HPLC pure). We used 2 mg/ml (1.13 mM) solutions for the UVRRS measurements, which contained sodium perchlorate (0.2 M) as an internal standard. For the circular dichroism (CD) spectra AP was used at 2.7 mM concentrations and for the absorption spectra, AP was used at 0.15 mM concentrations. The UVRR, CD, and absorption spectral measurements were taken at both 5° C ± 0.5° C (where AP is a mixture of α-helical and PPII conformations; Fig. 1) and at 60° C ± 0.5° C (the PPII-like conformation dominates).

Figure 1.

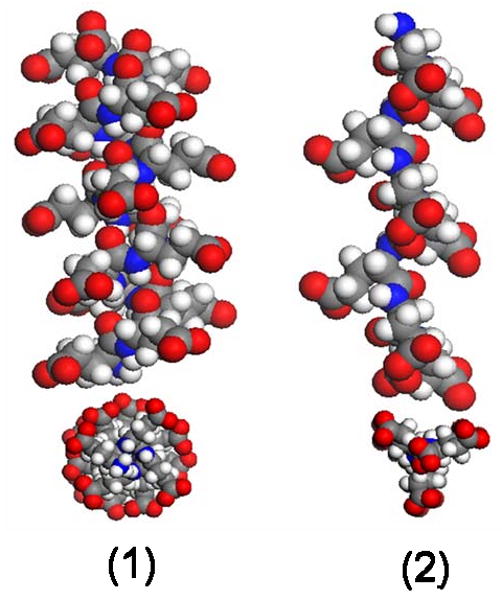
Examples of conformations adopted by AP (shown here for poly-glutamic acid). (1) α-helix: a right-handed helix with (Φ, Ψ) = (-58°, -47°), and an i − i+4 hydrogen bonding pattern; (2) poly-proline II-like (PPII): a left-handed helix with (Φ, Ψ) = (-75°, +145°) which hydrogen bonds to water and does not undergo intramolecular hydrogen bonding.

Raman Instrumentation

The UVRR spectroscopic instrumentation has previously been described in detail⁵¹. In brief, the laser sources were two Positive Light Co. Indigo-S Ti:Sapphire laser systems. The Indigo-S systems both utilize intra-cavity frequency doubled, Q-switch pulsed Nd:YLF Evolution 15 lasers (527 nm wavelength, 5 kHz repetition rate, 10 W average power) to pump Ti:Sapphire oscillators generating tunable radiation from 772 to 820 nm (laser #1) and 840 to 960 nm (laser #2). These tunable Ti:Sapphire lasers are frequency quadrupled and mixed utilizing two different harmonic crystal packages. The 210 nm laser (laser #2) utilizes two successive frequency doublers to convert the fundamental (840-960 nm) to the UV (210-240 nm). The 193 nm laser harmonics package (laser #1) mixes the third harmonic with the fundamental to produce tunable radiation between 193 and 210 nm. The average powers in the UV were between 2-5 mW (193-210 nm) and ∼10 mW (210-220 nm).

The laser beam was focused into a temperature-controlled, circulating flow stream which was purged with N₂ to eliminate Raman scattering from the O₂ band at 1555 cm^-1. The 20-mL sample of AP was irradiated for a maximum of 15 min. The scattered light was directed into the subtractive double monochromator⁵⁴ and the Raman scattered light was detected by a liquid nitrogen-cooled CCD (Princeton Instruments, Spec-10:400B). The Raman intensities were normalized to the 932 cm^-1 perchlorate (ClO₄^-) symmetric stretch vibration band. The spectra were analyzed and deconvoluted using Grams/32 AI software from Thermo Electron Corporation (Waltham, MA).

UV Raman depolarization ratios (ρ) were measured by using a 180° scattering geometry. The light scattered from the sample was directed through a UV linear dichroic polarizer (Oriel Instruments, Stratford, CT) and a crystalline quartz scrambler (Spex Industries, Edison, NJ) directly before the monochromator entrance slit. The depolarization ratios were collected at: 198, 202, 204, 206, 210 and 218 nm (Indigo S, Coherent, Santa Clara, CA), as well as 229 nm (intracavity frequency doubled-Ar⁺, Coherent). The incident beams were highly polarized. ρ was calculated as a ratio of the perpendicularly polarized light (I_┴) to the parallel polarized light (I_‖):

$$\rho =\frac{I_{\perp }}{I_{\parallel }}$$ (1)

The accuracy of the depolarization ratios was verified using the depolarization ratios of ClO₄^- and cyclohexane as standards⁵⁵.

Spectrometer Efficiency

The spectrometer we used is a modified Spex 1401 double monochromator that operates in the 193-270 nm range⁵⁴. Since the throughput efficiency of the spectrometer varies over this range, we corrected for the differences in throughput efficiency by recording the scattering of a standard intensity UV-deuterium lamp (Optronics Laboratories Inc., Orlando, FL) from the surface of packed BaSO₄ powder to determine the efficiency curve⁵⁴. The efficiency factors determined by Bykov et al., 2005 were used for the absolute Raman cross section calculations⁵⁴.

Absorption and CD Measurements

The UV absorbance spectra between 190 and 260 nm were measured by using a Cary 5000 Varian UV-Vis-NIR spectrophotometer. The CD spectra were measured using a Jasco J-710 spectropolarimeter. The spectra were measured in a temperature-controlled 0.2 mm path-length cell.

Results and Discussion

Absorption Spectrum

The absorption spectra and the structure of AP are shown in Fig. 2. As the wavelength decreases from 260 to 190 nm, the absorbance increases. The broad band at 190 nm derives from the amide π → π* transition(s). The conventional understanding of amide electronic transitions indicates that for pure α-helices, exciton splitting leads to two dipole-allowed transitions, one centered at 190 nm which is perpendicular to the helical axis⁴³, and a second transition dipole occurs parallel to the helical axis⁴⁴ and appears as a shoulder at 205 nm⁴². The band assignments are confirmed by CD data, with a strong positive band at 190 nm and weaker negative bands at 205 nm and 222 nm, which is assigned to the n→π* transition⁴⁶.

Figure 2.

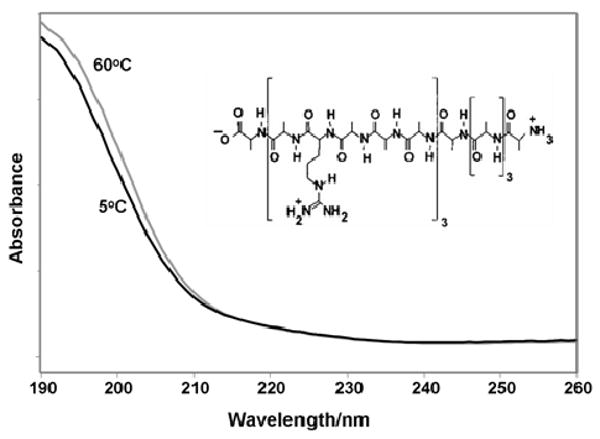
UV-vis absorption spectrum of AP at 5° C, where it is predominantly α-helical, and at 60° C, where it is in a mainly PPII-like conformation. Inset: Structure of AP.

For a “pure” PPII conformation, previously referred to as random coil, an absorption maximum is found at 192 nm, slightly red-shifted from the α-helix maximum⁴². This absorption maximum for the “pure” PPII conformation is significantly larger than that of the “pure” α-helix conformation. The increase in absorbance of the AP sample with increasing temperature results from the loss of α-helix hypochromism upon the conversion to the PPII-like conformation at 60° C. In the CD of peptides containing a large amount of PPII, a strong negative band is observed at ∼196 nm and a weak positive band at 215 nm (not observed for AP)⁴⁶.

UVRR Spectra

At 5° C, AP is approximately 55% α-helical and 45% PPII²⁶. AP melts to a predominantly PPII-like conformation by 60° C. Fig. 3 shows the UVRRS of AP at 60° C in the PPII-like conformation excited between 218 to 194 nm. The spectra shown are normalized with respect to the 932 cm^-1 ClO₄^- band, but are not corrected for self absorption or spectrometer efficiency. The enhanced amide vibrations for the PPII-like conformation include the Amide I (AmI) band at 1659 cm^-1, which originates primarily from C = O stretching (st). The Amide II (AmII) band, which results from coupling of C – N st and N –H in-plane bending (b), is located at 1548 cm^-1. The doublet from the C_α – H symmetric b vibration occurs at 1377 cm^-1 (C_α – H₁) and 1399 cm^-1 (C_α – H₂). The Amide III₃ (AmIII₃) and Amide III₂ (AmIII₂) bands at 1261 cm^-1 and 1303 cm^-1, respectively, derive from vibrations where C – N st couples with the N – H in-plane b. The relative intensities of the Raman bands in the UVRR spectra of AP increase as the laser excitation wavelength is decreased from 218 to 194 nm (Fig. 3). The spectrum at 198 nm shows the highest relative band intensities. A comparison of the AP PPII-like spectra across the entire excitation wavelength range demonstrates very similar enhancement patterns with essentially identical bands enhanced. The similarity of these spectra suggests that very similar or identical electronic transitions span this spectral region.

Figure 3.

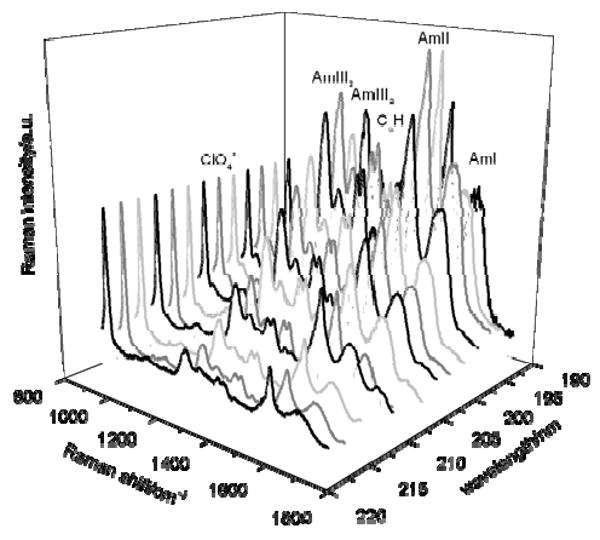
Observed UVRR spectra of AP in the PPII-like conformation at 60° C between 218 and 194 nm. The spectra were collected for 15 min at each wavelength. The spectral resolution is between 7 cm^-1 at 218 nm and 5.9 cm^-1 at 194 nm. All spectra were normalized to the ClO₄^- internal standard.

To determine the excitation profile of the α-helix spectra at 5° C, we numerically removed the contributions from the 45% concentration of the PPII conformation²⁶. We calculated the spectra of the PPII conformation at 5° C for excitation between 218 and 194 nm (Fig. 4) using Lednev et al.'s methodology, which modeled the temperature dependence of the frequencies, intensities, and bandwidths of PPII at 5° C from the high temperature PPII-like spectra²⁶. As discussed above, the relative intensities within spectra between different excitation wavelengths are very similar again suggesting similar electronic transitions span the 190 to 215 nm spectral region.

Figure 4.

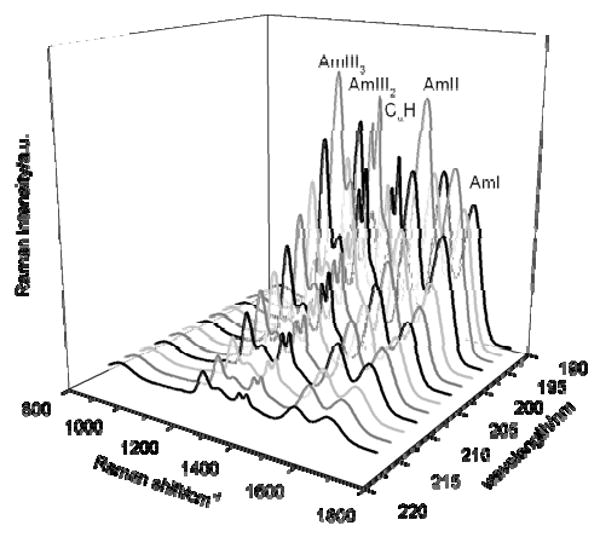
Calculated Raman spectra of AP in the PPII conformation at 5° C between 218 to 194 nm. See text for details.

These calculated PPII spectra were subtracted from the measured 5° C AP spectra to yield the pure 5° C AP α-helical Raman spectra. Fig. 5 compares the 204 nm excited AP mixed α-helix/PPII spectrum at 5° C to the calculated 5° C PPII-helix spectrum and to the resulting “pure” α-helix spectrum. Fig. 6 shows the calculated α-helical Raman spectra excited between 218 and 194 nm. The intensities of the Raman bands increase almost monotonically with decreasing excitation wavelengths from 218 to 194 nm. Comparing the PPII-like and α-helix spectra, we find that the PPII-like conformation Raman spectral intensities are greater than that of the α-helix. The AmIII₃ and AmIII₂ bands of the PPII-like conformation are broader and occur at lower frequency compared to those in the α-helix. In the α-helix there is a third AmIII band present at 1337 cm^-1 (AmIII₁). The AmII and AmI bands in the PPII-like conformation are also at lower frequency than in the α-helix.

Figure 5.

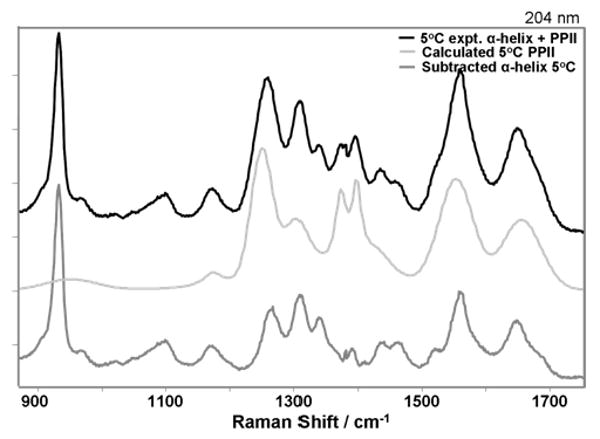
UVRR spectra of AP at 204 nm. Observed 5° C spectrum (black), calculated 5° C PPII spectrum (light gray), and subtracted 5° C α-helix spectrum (gray).

Figure 6.

Subtracted UVRR spectra of α-helix conformation of AP at 5° C between 218 and 194 nm. The spectral resolution is between 7 cm^-1 at 218 nm and 5.9 cm^-1 at 194 nm.

Absolute Raman Cross Sections

We calculated the Raman cross sections using ClO₄^- as an internal standard. We previously showed that the ClO₄^- Raman cross section dependence on excitation frequency is well modeled by²²:

$${\sigma }_R=K_2{\nu }_o{\left({\nu }_o-{\nu }_{mn}\right)}^3{\left[\frac{{\nu }_e^2+{\nu }_o^2}{{\nu }_e^2-{\nu }_o^2}\right]}^2$$ (2)

where K₂ is a constant, ν_o is the incident laser excitation frequency (cm^-1), ν_mn corresponds to the frequency of the Raman vibrational mode (cm^-1), and ν_e is the frequency of the transition to the resonant excited state (cm^-1). Dudik et al. found that the ClO₄^- symmetric stretching band shows an Albrecht A-term frequency dependence for excitation wavelengths from the visible to the UV to 220 nm²². We assume this cross section frequency dependence occurs down to 194 nm.

We normalized our AP UVRR spectra with respect to the ClO₄^- 932 cm^-1 band. The absolute Raman cross sections (with correction for self absorption) of AP in both the PPII-like and α-helix conformations were calculated as:

$${\sigma }_{AP}=\frac{I_{\mathit{\text{band}}}\cdot K({\lambda }_{\mathit{\text{ClO}}4})\cdot C_{\mathit{\text{ClO}}4}\cdot {\sigma }_{\mathit{\text{ClO}}4}}{I_{\mathit{\text{ClO}}4}\cdot K({\lambda }_{\mathit{\text{band}}})\cdot C_{AP}\cdot n_A}\cdot \left[\frac{{\varepsilon }_s+{\varepsilon }_o}{{\varepsilon }_r+{\varepsilon }_o}\right]$$ (3)

where I_band and I_ClO4 are the relative intensities of the amide bands and ClO₄^-, respectively; k(λ_band) and k(λ_ClO4) are the spectrometer efficiencies at the specific wavelengths of the bands; C_AP and C_ClO4 are the concentrations (M) of the AP and perchlorate; σ_ClO4 is the calculated ClO₄^- cross section at the specific wavelength; n_A is the number of amide bonds in the peptide; ε_o is the extinction coefficient for AP at the laser frequency; ε_s is the extinction coefficient for AP at each Raman band position; and ε_r is the extinction coefficient for ClO₄^- at each wavelength. The expression in the brackets corrects the Raman intensities for self absorption. We apply this small correction for self absorption to account for the differences in absorbance of AP at the various excitation and Raman scattered wavelengths^56,57.

Excitation Profiles

PPII-like Conformation

Fig. 7 shows the absolute Raman cross section excitation profiles for the AP amide bands in the PPII-like conformation. The Raman cross sections monotonically increase from 220 nm, reaching an excitation maximum at 198 nm. Interestingly, the AmIII₃, AmIII₂, and C_α-H vibration cross sections increase again at excitation wavelengths shorter than 194 nm.

Figure 7.

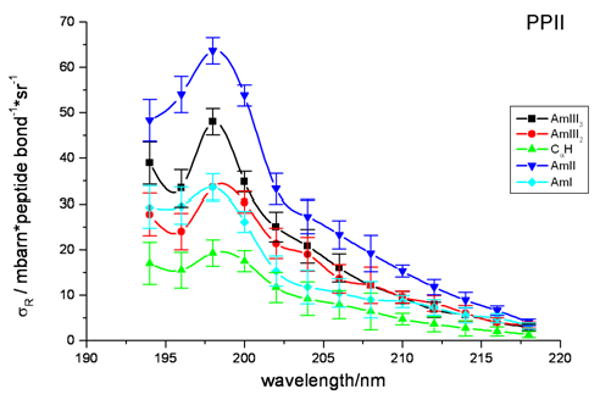
PPII-like conformation absolute Raman cross sections (mbarn*peptide bond^-1*sr^-1) excitation profiles between 194 to 218 nm.

The largest cross sections occur for the AmII vibration, which is comprised of C-N st coupled with N-H in-plane b. The AmII vibration was previously shown to be the most enhanced vibration in N-methylacetamide (NMA), because the large component of C-N st in the AmII vibration couples to the large ππ* excited state C-N bond length expansion¹⁸. It, thus, appears that the AP amide π→π* transitions for the PPII-like conformation (as well as for the α-helix as shown below) are similar to that in NMA.

The AmIII vibration is the next most intense vibration because it also contains a large amount of C-N bond stretching. In the PPII-like conformation of AP, two bands occur in the AmIII region. These AmIII₃ and AmIII₂ bands have Raman cross sections which are considerably less than that of the AmII vibration. This is consistent with previous data on the normal modes of a polyalanine peptide that indicate that the C-N motion contribution to the AmII vibration is two times greater than that of the AmIII vibrations⁵⁸.

In order to accurately examine the behavior of the AmI vibration in AP, we corrected for the contribution to the AmI band of the 1669 cm^-1 Arg band by removing the overlapping Arg contribution to this spectral region⁴. To estimate the contribution of this underlying Arg band to the integrated area of the AmI band, a spectrum of free Arg in solution was used to calculate the cross section of the 1669 cm^-1 Arg band. The Arg cross section was then subtracted from the AmI cross sections. The Arg band at 1669 cm^-1 accounts for ∼ 39% of the AmI band intensity. The small cross section for the AmI (C=O st) vibration compared to the AmII vibration is similar to that in NMA, presumably because the C=O bond in AP also exhibits only a minimal excited state expansion¹⁸. This weak AmI enhancement is also observed in the difference spectrum between Ala₅ (A₅) and Ala₃ (A₃), which displays the spectrum of the interior two peptide bonds in a PPII-like conformation.

In the PPII-like conformation there are two C_α-H bending bands at 1377 and 1399 cm^-1 which show almost identical excitation profiles. We calculated the average cross sections by integrating over both bands. In AP, the C_α-H bend couples with N-H bending motion to produce an excitation profile that is similar to that of the other amide bands. For the PPII-like conformation, the C_α-H bending bands show an excitation profile maximum at the same wavelength as all the other amide bands, λ_max = 198 nm.

α-helix Conformation

For the AP α–helical conformation, we see a broad excitation profile where the Raman cross sections increase continuously from 218 to 194 nm (Fig. 8). It is not clear whether the maximum occurs at 194 nm or at lower wavelength. As in the PPII-like excitation profile, the AmII band has the largest Raman cross section, indicating again, as in NMA, that the α-helix ππ* excited state displacement is mainly along the C-N bond, just as in for the PPII-like conformation. In the AmI region, the α-helix 1669 cm^-1 Arg band contribution was also subtracted to calculate the pure AmI cross sections. The AmIII₃, AmIII₂, AmII and AmI vibrations show very similar excitation profiles. The AmIII₁ vibration, however, shows a somewhat different profile than the AmIII₃ and AmIII₂ vibrations.

Figure 8.

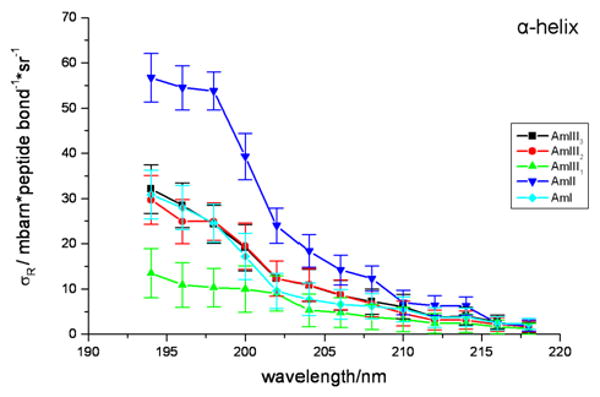
α-helix conformation absolute Raman cross sections (mbarn*peptide bond^-1*sr^-1) excitation profiles of AP between 194 to 218 nm.

The different excitation profile maxima for the PPII-like and α-helix conformations indicate different electronic transition frequencies for the underlying electronic transitions. Comparing the Raman cross section data for AP in both PPII-like (Table I) and α-helical (Table II) conformations, we find cross sections for PPII-like conformation are in general significantly larger than the α-helix, presumably due to hypochromism for the NV₁ (π → π*) absorption band of the α-helix^{59, 60}. For both conformations we find a shoulder in the excitation profile between 205-∼207 nm which is suggestive of an underlying electronic transition. The spacing between this shoulder and the ∼190-198 nm absorption maximum is too large to be consistent with a vibronic progression.

Table I. PPII-like conformation absolute Raman cross sections (mbarn*peptide bond^-1*sr^-1).

Wavelength (nm)	AmIII3 1247 cm-1	AmIII2 1311 cm-1	Cα- H (ave) 1377 & 1399 cm-1	AmII 1548 cm-1	AmI 1659 cm-1
194	38.9	27.7	17.0	48.3	29.3
196	33.4	24.0	15.5	54.0	29.6
198	48.0	33.6	19.3	63.6	33.6
200	34.8	20.4	17.5	53.8	26.1
202	25.0	21.4	11.7	33.3	15.3
204	20.8	19.0	9.2	27.2	11.8
206	16.0	13.6	7.9	23.3	10.5
208	12.2	12.2	6.4	19.2	9.0
210	9.5	9.6	4.7	15.3	8.6
212	6.8	8.2	3.6	11.8	7.3
214	5.6	6.0	2.7	8.9	5.6
216	4.0	4.0	2.0	6.6	4.9
218	2.9	3.4	1.3	4.0	3.2

Table II. α-helix conformation absolute Raman cross sections (mbarn*peptide bond^-1*sr^-1).

Wavelength (nm)	AmIII3 1261 cm-1	AmIII2 1303 cm-1	AmIII1 1337 cm-1	AmII 1538 cm-1	AmI 1657 cm-1
194	32.1	29.7	13.5	56.7	30.9
196	28.5	24.9	10.9	54.5	28.0
198	24.3	24.9	10.3	53.8	24.6
200	19.1	19.5	10.0	39.3	17.2
202	12.3	12.3	9.0	24.0	9.6
204	10.8	10.9	5.3	18.4	7.7
206	8.6	8.7	4.8	14.2	6.6
208	7.2	6.7	3.8	12.3	6.2
210	6.1	4.6	3.3	7.0	5.5
212	3.7	3.1	2.4	6.3	3.7
214	4.0	3.1	2.4	6.2	3.8
216	2.7	2.2	1.6	2.4	2.4
218	1.4	1.7	1.2	1.9	2.3

Comparison between UV Raman Excitation Profiles, Absorption and CD Spectra and Raman Depolarization Ratios

The excitation profiles of the α-helix and PPII-like conformations both reveal a shoulder centered at ∼207 nm, which suggests the presence of a second electronic transition. No similar feature is evident in the absorption spectrum, nor is there a clear 207 nm feature in the CD spectrum shown in Figure 9a (although there is a minimum in the CD spectrum at 204 nm) which compares the averaged AP Raman excitation profiles of the α-helix conformation with the measured absorption and CD spectrum at 5° C (where the α-helix predominates).

Figure 9.

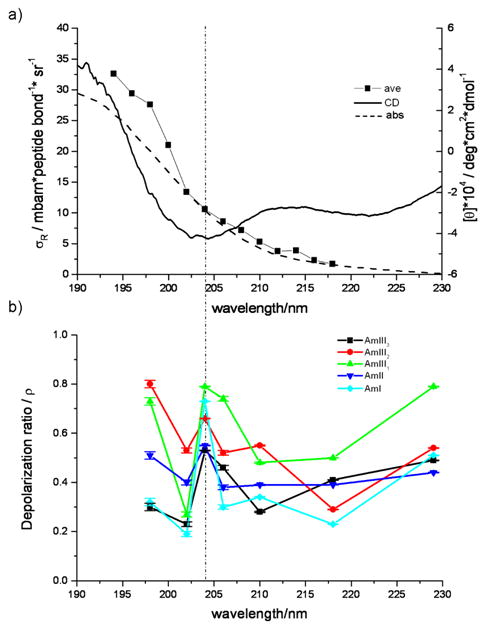
(a) The average amide band excitation profile for the α-helix conformation, excluding the AmI cross section; CD spectrum of AP at 5° C; absorption spectrum of AP at 5° C. (b) Raman depolarization ratios of AP at 5° C. The dashed line indicates the presence of the shoulder in the excitation profile.

α-helix Conformation

In the α-helix it is well established that the π→ π* transition undergoes excitonic splitting to result in two delocalized dipole-allowed transitions, one is perpendicular (190 nm) and the other parallel (205 nm) to the helical axis^{42-44, 46}. The parallel component of the π→ π* transition presents in the CD spectrum as a strong negative band at ∼205 nm⁴⁶. Thus, we straightforwardly assign the shoulder centered at ∼207 nm in the α-helix excitation profile as the parallel component of the α-helix π→ π* transition.

The Raman depolarization ratio measurements support this conclusion. A single, non-degenerate electronic transition will cause a single resonance Raman tensor element to dominate, giving a Raman depolarization ratio, ρ = 0.33 independent of excitation wavelength^24,27,61. For values of ρ ≠ 0.33 the resonance enhancement must arise from at least two diagonal elements of the Raman tensor. If ρ > 0.33, and if there are only two components of the Raman tensor, they must be of opposite sign. For ρ < 0.33, where only two elements contribute, the two diagonal elements must be of the same sign^24,27,61. Thus, ρ ≠ 0.33 requires that at least two electronic transitions contribute.

Two nondegerate electronic transitions with different transition moment orientations near one another which give rise to similar resonance Raman polarizability values (and which have the same sign, which is typical) in preresonance will give rise to ρ < 0.33 in preresonance at an excitation energy below the two transitions. The depolarization ratio will approach ρ = 0.33 as excitation occurs close to resonance with either of the transitions (assuming the homogeneous linewidths are less than the energy difference between transitions). However, for excitation at energies between the transitions, the two Raman polarizability values will be of opposite sign, leading to a peak in ρ which equals 0.75 for equal contributions Obviously, peaks in the value of ρ can be used to signal the existence of electronic transitions underlying broad absorption bands.

The situation for our case is likely to be more complex since more than two transitions exist. For example, there is a deep UV transition which is already known to be important for the Am I vibration enhancement²³. Further, for the ideal infinite α-helix the perpendicular exciton component is degenerate and should give rise to a resonance Raman ρ = 0.125.

For AP, the situation is even more complex, since the α-helix is of finite length and may include short α-helical segments. Further, we recently demonstrated that the AP α-helical state is actually composed of comparable amounts of α-helix, 3₁₀ helix and π-bulge conformations¹⁴. Thus, the α-helix Raman excitation profile, as well as the depolarization ratios will derive from the weighted summed contributions from each of the underlying components, which we expect to be similar.

From 230 to 210 nm the α-helix resonance Raman depolarization ratios are centered around ρ∼0.33, except for the AmIII₁ band. The AmI depolarization ratio measurement is complicated by overlap of the Arg band, and it is expected that ρ ≠0.33 because it is also expected to be strongly enhanced by a transition deep in the UV²³.

At 204 nm excitation, ρ shows a maximum for all of the amide vibrations (ρ >0.5, Fig. 9b, Table III) indicating the contribution of at least two components to the Raman tensor with opposite signs. This is followed by a sharp dip in the Raman depolarization ratios of all of the amide bands at 202 nm. This dispersion must be signaling the existence of an electronic transition centered ∼207 nm which coincides with the resonance Raman excitation profile shoulder (Figs 9a and 9b). Probably these features result from the parallel component of the α-helix-like π→ π* transition.

Table III.

Depolarization Ratios of AP at 5° C (α-helix).

	Wavelengths (nm)
band	198	202	204	206	210	218	229
AmIII3	0.30	0.23	0.53	0.46	0.28	0.41	0.49
AmIII2	0.80	0.53	0.66	0.52	0.55	0.29	0.54
AmIII1	0.73	0.27	0.79	0.74	0.48	0.5	0.79
AmII	0.51	0.40	0.55	0.38	0.39	0.39	0.44
AmI	0.32	0.19	0.73	0.30	0.34	0.23	0.51

PPII-like Conformation

The importance of excitonic interactions have not been clearly established for the PPII-like conformation. The lowest energy π→π* electronic transition is expected at ∼190 nm, while the weak n→ π* electronic transition occurs at 220 nm. The Raman excitation profiles and the Raman depolarization ratios of the PPII-like conformation are similar to those of the α-helix conformation with a shoulder at ∼205 nm and a depolarization ratio peak at 204 nm (Fig. 10, Table IV). The PPII-like Raman excitation profile maximum occurs at the same wavelength as the trough of the CD spectrum, affirming its assignment to the π → π* transition⁴⁶. The excitation profile shoulder (Fig. 10a) coincides approximately with the values of ρ ∼0.25 for all amide vibrations at ∼205 nm (Fig. 10b). This indicates the existence of an underlying electronic transition at ∼205 nm for the PPII-like conformation of AP.

Figure 10.

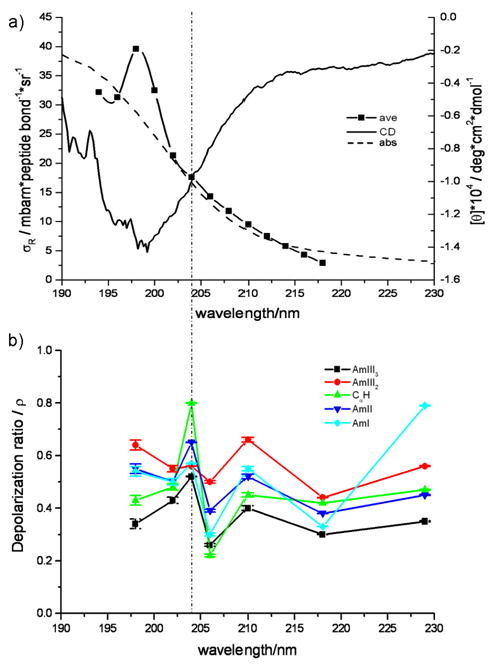
(a) The average amide band excitation profile for the PPII-like conformation, excluding the AmI vibration; CD spectrum of AP at 60° C; and absorption spectrum of AP at 60° C. (b) Raman depolarization ratios of AP at 60° C. The dashed line indicates the presence of the shoulder in the excitation profile.

Table IV.

Depolarization Ratios of AP at 60° C (PPII-like).

	Wavelengths (nm)
band	198	202	204	206	210	218	229
AmIII3	0.34	0.43	0.52	0.26	0.40	0.30	0.35
AmIII2	0.64	0.55	0.56	0.50	0.66	0.44	0.56
CαH	0.43	0.48	0.80	0.22	0.45	0.42	0.47
AmII	0.55	0.50	0.65	0.39	0.52	0.38	0.45
AmI	0.54	0.50	0.57	0.30	0.55	0.33	0.79

The similar enhancement patterns of the amide bands within the α-helical absorption spectrum indicates that the 207 nm transition is similar to the PPII ∼190 nm π→π* transition. Thus, these components are probably excitonically split transition pairs. This is the first clear indication of exciton splitting in PPII-like conformations.

AmIII₃ Deconvolution

Recent theoretical^62-64 and experimental^20,65 studies indicate that the α-helix solution conformation actually contains contributions from 3₁₀ helix⁶² and π-bulge^63,64 as underlying defect structures at temperatures below 30°C²⁰. We recently demonstrated that these different α-helix-like conformations show separate underlying Raman bands¹⁴.

We deconvoluted our measured α-helical Raman AmIII₃ region with Gaussians to resolve the 3₁₀ helix, π-bulge, and pure α helix contributions (Fig. 11) and calculated the individual Raman excitation profiles of these conformations (Fig. 12). The excitation profiles of these conformations significantly differ. For example, the pure α-helix excitation profile shows the 207 nm shoulder and shows a maximum at ∼197 nm. In contrast the 3₁₀ helix does not show the shoulder but only a peak at ∼196 nm, possibly demonstrating a lack of excitonic interactions. In contrast, the π-bulge shows a large, broad feature between 200 and 210 nm with an excitation profile maximum deeper in the UV below 194 nm. We conclude that these different conformations within the α-helix basin have very different excitonic interactions.

Figure 11.

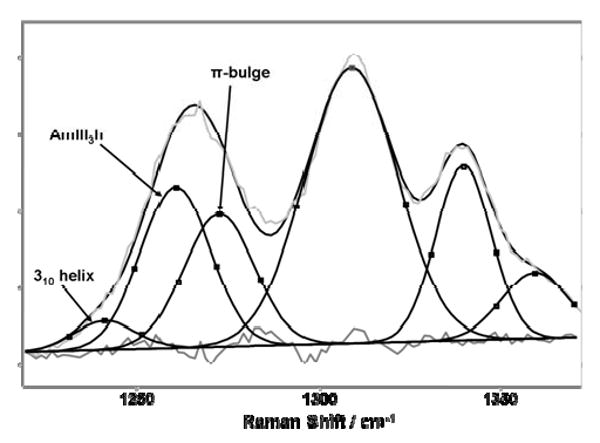
Spectral deconvolution of the AmIII₃ region of the α-helix-like conformations into Gaussian components. The measured and fitted Raman spectra are shown for the 3₁₀ helix (1241 cm^-1), the pure α-helix (1261 cm^-1), and the π-bulge (1273 cm^-1) and the residual.

Figure 12.

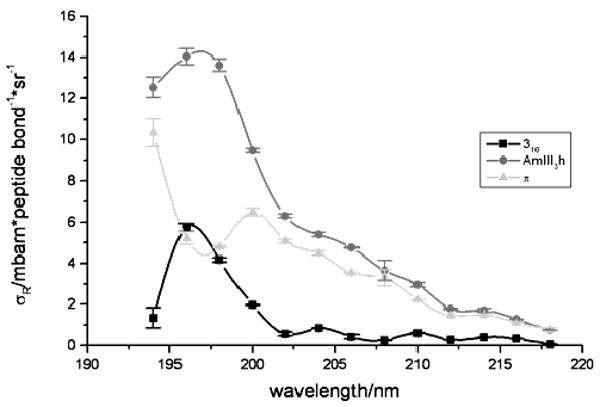
Raman excitation profiles of the AmIII₃ bands of the 3₁₀ helix (1241 cm^-1), the pure α-helix (1261 cm^-1), and the π-bulge (1273 cm^-1).

Conclusions

We measured the UVRR excitation profiles and Raman depolarization ratio dispersions for the α-helix and PPII-like conformations of a 21 amino acid mainly ala peptide, AP. Both excitation profiles show a shoulder at ∼205 nm. The PPII-like conformation shows a peak at ∼198 nm. The α-helix like state shows shorter wavelength peak at ∼194 nm. The Raman spectra and the depolarization ratios clearly signal that the 205-207 nm shoulders results from an underlying electronic transition similar to that of the shorter wavelength (∼195 nm) π → π* transitions. It is most likely that these transitions derive from the excitonically split amide π → π* electronic transitions. The α-helical 207 nm transition is clearly the parallel component of the excitonically split pair. The establishment of the existence of these underlying transitions will help advance the understanding of protein and peptide backbone electronic transitions. We also resolved the Raman excitation profiles of the pure α-helix, 3₁₀ helix and π-bulge conformations.

Our excitation profiles of the pure α-helix, the 3₁₀ helix, the π-bulge and the melted PPII-like conformations clearly indicate that different excitation wavelengths can be utilized to differentially enhance these different solution peptide conformations.