Properties of a general PK/PD model of antibody-ligand interactions for therapeutic antibodies that bind to soluble endogenous targets

Abstract

Antibodies that target endogenous soluble ligands are an important class of biotherapeutic agents. While much focus has been placed on characterization of antibody pharmacokinetics, less emphasis has been given to characterization of antibody effects on their soluble targets. We describe here the properties of a generalized mechanism-based PK/PD model used to characterize the in vivo interaction of an antibody and an endogenous soluble ligand. The assumptions and properties of the model are explored and situations are described when deviations from the basic assumptions may be necessary. This model is most useful for in vivo situations where both antibody and ligand levels are available following drug administration. For a given antibody exposure, the extent and duration of suppression of free ligand is impacted by the apparent affinity of the interaction, as well as by the rate of ligand turnover. The applicability of the general equilibrium model of in vivo antibody-ligand interaction is demonstrated with an anti-Aβ antibody.

Introduction

In recent years, antibodies and antibody-derived molecules have become an increasingly important class of therapeutic agents. A recent review article cited that more than 20 molecules from this class of compounds have been approved for use by the U.S. Food and Drug Administration (FDA), with more than 500 antibodies in various stages of development.¹ In parallel with this increased interest in antibodies as drugs, the use of model-based drug development has also dramatically increased. A number of examples of the use of pharmacokinetic (PK)/pharmacodynamic (PD) modeling to better understand antibody pharmacology and drug development have been published in recent years,^2–11 and the PK, PD and use of PK/PD modeling have been reviewed.^1,12,13 Despite the large number of antibodies in development and in clinical use, there are still relatively few examples of the use of PK/PD modeling to facilitate therapeutic antibody development in the primary literature.

Antibody agents that target soluble ligands are an important subclass of the antibody therapeutics. Approximately 25% of the FDA-approved antibody products fall into this subclass of molecules.¹ Much focus has been placed on characterization of the PK of these types of antibodies, but less emphasis has historically been placed on characterization of the antibody's effects on the soluble target. Given that the antibody is the binding molecule and the soluble target is actually the active agent, more emphasis on the characterization of the effects of the antibody on the target ligand is warranted. Further, understanding of the system gained by modeling the interaction between the antibody and target could help facilitate drug development, particularly in cases where establishing disease-specific biomarker relationships in early development are not feasible.

A number of recent articles have reviewed models of target-mediated drug disposition (TMDD) for biologics,^14–16 including antibodies, and more examples are beginning to appear in the published literature describing models for antibodies that bind to soluble ligands. While the latter have some similarities to the TMDD models, in many cases, the pharmacokinetics of the drug, e.g., the antibody, will not be affected by binding to the target, but rather the kinetics of the target will be affected by the drug. Balthasar and Fung provided perhaps the first in vivo PK/PD models for these types of antibodies when they described the effect of anti-drug antibodies on exogenously administered digoxin and methotrexate.^17,18 Various models have been proposed for antibodies and other biologics that target soluble endogenous ligands such as TNF,^4,8,9 IL13,¹¹ IgE,^5,7,9,10,19 DKK-1,²⁰ IL-1β²¹ and Factor IX.^2,3

The purpose of the present article is to describe and explore the properties of a generalized mechanism-based PK/PD model that can be used as a basis for the development of models that characterize the in vivo interaction of an antibody and an endogenous soluble ligand. We also offer perspectives on common issues to consider when examining antibody-ligand interactions and practical approaches to modeling these interactions based on these issues. This model is most useful for in vivo situations when both antibody levels and ligand levels are available following drug administration. The assumptions and properties of this general model are explored, and situations are described when deviation may be necessary from the basic assumptions of the model.

Results

Properties of the general equilibrium PK/PD model.

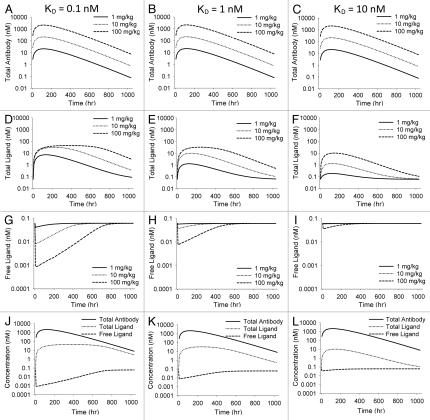
Simulations were generated to illustrate the antibody and ligand concentration-time profiles under a variety of scenarios. The results of these simulations are shown in Figures 2 and 3, with Figure 2 exploring the impact of altering K_D on total and free ligand concentration and Figure 3 highlighting the effect of altering ligand turnover on the ligand profiles. In general, administration of an anti-ligand antibody leads to increases in total ligand concentrations and decreases in free ligand concentrations. The extent and duration of these changes are governed by the dose of antibody administered, the affinity of the interaction and the kinetic parameters for both the antibody and ligand.

Figure 2.

Simulations illustrating effects of varying K_D in the general antibody-ligand PK/PD model. All parameters except K_D were held constant throughout simulations. K_D was 0.1, 1 and 10 nM for the three scenarios. Effect of varying K_D on total antibody concentration (A–C), total ligand (D–F) and free ligand (G–I) are shown. (J–L) show total antibody, total ligand and free ligand on the same plot for each scenario at a 100 mg/kg dose of antibody.

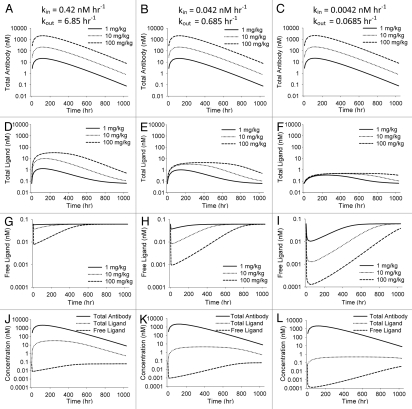
Figure 3.

Simulations illustrating effect of varying k_in and k_out in the general antibody-ligand PK/PD model. All parameters except k_in and k_out were held constant throughout simulations and the ratio of k_in to k_out was held constant at 0.061. k_in was 0.42, 0.042 and 0.0042 nM h⁻¹ for the three scenarios. Effect of varying k_in and k_out on total antibody concentration (A–C), total ligand concentration (D–F) and free ligand concentration (G–I) are shown. (J–L) show total antibody, total ligand and free ligand concentrations on the same plot for each scenario at a 100 mg/kg dose of antibody.

Figure 2 illustrates the impact of changing binding affinity on the projected free and total ligand profiles. For each simulation, the doses and PK parameters for the antibody remained constant, as did the input and elimination rate constants for the ligand. The affinity of the interaction varied over the range of 0.1–10 nM. Decreasing the affinity of the interaction leads to a smaller extent of maximal reduction in free ligand at any given dose, and a shorter duration of free ligand suppression at any given dose. Decreasing the affinity of the interaction also increases the antibody-excess (ratio between total antibody concentration and total ligand concentration).

Figure 3 illustrates the impact of changing ligand turnover, with antibody kinetics and affinity of the interaction remaining constant. For simplicity, the ratio of k_in/k_out for the ligand remained constant, i.e., constant baseline ligand concentration. For a given dose level, decreasing the turnover of the ligand leads to an increased extent and duration of free ligand suppression. It also decreases the maximum extent of total ligand accumulation. Antibody-excess during the terminal, parallel decline portion of the curves remains the same.

Application of general equilibrium model to in vivo data.

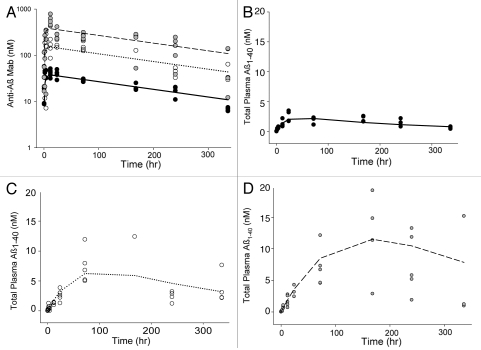
The applicability of the general equilibrium model of in vivo antibody-ligand interaction was demonstrated with an anti-Aβ antibody. The model predictions and observed data for both antibody and ligand (Aβ_1–40) are illustrated in Figure 4. After administration of anti-Aβ antibody to PDAPP mice, total Aβ_1–40 levels increased in a dramatic and dose dependent fashion and the data were well described by the general model described in Figure 1. Parameter values resultant from the fit of this data are shown in Table 1.

Figure 4.

Observed and model predicted antibody and ligand (Aβ_1–40) levels obtained using the general equilibrium model to fit m266 PK and ligand data in the PDAPP mouse. Symbols represent individual animal data and lines are population means for doses of 0.5 (●, —), 2 (○, ⋯) and 5 (●, ---) mg/kg of antibody. Antibody concentrations are shown in (A) with total ligand concentrations following 0.5, 2 and 5 mg/kg m266 shown in (B–D) respectively.

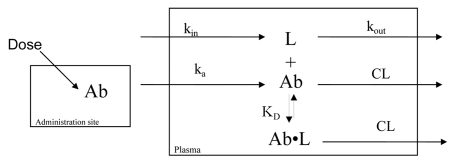
Figure 1.

Schematic diagram of the basic equilibrium model. Ab represents antibody concentration; k_a is a 1^st-order absorption rate constant for the antibody; V is the apparent volume of distribution for the antibody; CL is the apparent clearance for the antibody; L is free ligand concentration; k_in is a zero-order input rate constant for ligand (units of concentration/time); k_out is a 1^st-order rate constant for free ligand elimination; K_D is the equilibrium constant governing antibody-ligand binding; Ab•L is concentration of antibody-ligand complex.

Table 1.

Parameter estimates obtained by fitting the equilibrium model to anti-Aβ antibody and total Aβ_1–40 data

Parameter description	Population estimate (%SEE)
ka (hr−1)	0.53 (14.2)
CL/F (L hr−1 kg−1)	0.00065 (16.7)
V/F (L kg−1)	0.17 (6.59)
kin (nM hr−1)	0.17 (11.9)
kout (hr−1)	12.7 (7.87)
KD (nM)	0.17 (20.7)
Proportional residual error	53.9% (15.0)

SEE, Standard error of the estimate.

Comparison of equilibrium and non-equilibrium models.

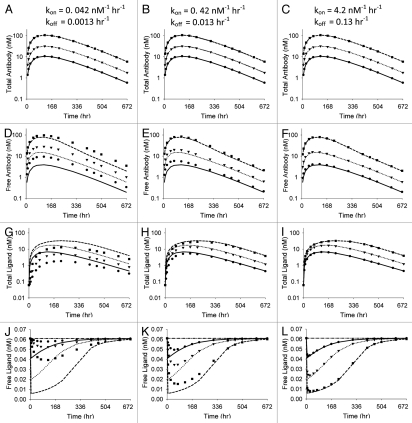
One of the primary assumptions of this basic model of antibody -ligand interactions is that the rates of antibody-ligand association and dissociation can be neglected and the binding can be assumed to be at equilibrium. A non-equilibrium model was established to probe the impact of this assumption. Simulations were generated over a range of micro-constant values for k_on and k_off, keeping the ratio, i.e., the affinity, of the interaction constant. Figure 5 shows the impact of increasing the k_on and k_off values on the profiles for total antibody, free antibody, total ligand and free ligand. Also shown on these figures are lines for the equilibrium K_D model. As expected, as k_on and k_off increase, the profiles converge to the profiles generated using the equilibrium model.

Figure 5.

Antibody and ligand levels obtained by simulation using the non-equilibrium model (symbols) for 3 k_on/k_off scenarios compared with simulations obtained using the equilibrium model (lines). All parameters except k_on and k_off were held constant throughout simulations and the ratio of k_off and k_on was held constant at 0.03 nM. Symbols and lines are population means for n = 4 for doses of 0.5 (●, —), 1.5 (▼, ···) and 5 (■, ---) mg/kg of antibody. Vehicle control is also shown for the free ligand plots (-●-). Total antibody concentrations (A–C), free antibody concentrations (D–F), total ligand concentrations (G–I) and free ligand concentrations (J–L) are shown.

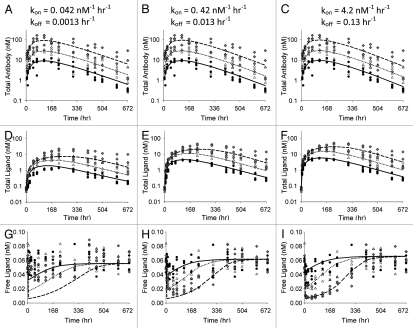
Although the non-equilibrium model is a closer representation to the actual system, we were also interested in exploring whether, and under what conditions, the simplified equilibrium model might be adequate to fit the data generated using the more realistic non-equilibrium model. In many cases in drug development, assays are not available for all four species of interest, i.e., total antibody, free antibody, total ligand and free ligand. In our experience to date, the two most commonly available measures for these systems are total antibody and total ligand. Additionally, as k_on and k_off increase, the expected profiles converge to the profiles generated using the equilibrium model. These two issues (limited data and convergence to the equilibrium profiles as k_on and k_off increase) led us to hypothesize that a general equilibrium model may be appropriate for many, if not most current drug development applications. Thus, Figure 6 demonstrates the best fits of the non-equilibrium model-generated data using the equilibrium model when only total antibody and total ligand data are available. Table 2 shows the parameter values from the fits. The three parts in Figure 6 represent the total antibody and total ligand fits for the three k_on/k_off scenarios. Also shown are the model-predicted free ligand profiles, together with simulated free ligand profiles for these sets of scenarios. In this exercise, it was assumed the free ligand concentrations were not available for the modeling. They are post-hoc observations to allow comparison of the equilibrium model predictions to the free ligand data generated by the ‘true’ non-equilibrium model. Again, as expected, the fits of total antibody and total ligand improve as k_on and k_off increase. However, even in the slow k_on and k_off case, the fits of the total antibody and ligand data are not unreasonable. Examination of the free ligand plots demonstrate that when k_on and k_off are slow, the extent of the free ligand suppression is over-predicted by the equilibrium model.

Figure 6.

Total antibody (A–C) and total ligand (D–F) concentrations for 3 k_on/k_off scenarios fitted to the equilibrium model. Symbols represent simulated data used for fitting and lines represent model predicted means for doses of 0.5 (●, —), 1.5 (△, ⋯) and 5 (◆, ---) mg/kg of antibody. Plots in (G–I) illustrate comparison between simulated data and model predicted mean free ligand concentrations.

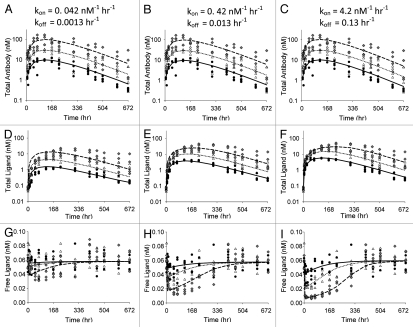
Figure 7 represents a scenario where total antibody, total ligand and free ligand concentrations are all available, with parameter values shown in Table 3. As with the data shown in Figure 6, the observed data were generated using the non-equilibrium model and the estimations were performed with the equilibrium model. Inclusion of the free ligand data into the modeling improves the model prediction in all k_on/k_off scenarios, relative to the situations where only total ligand data were available (Fig. 6).

Figure 7.

Total antibody (A–C), total ligand (D–F) and free ligand (G–I) concentrations for 3 k_on/k_off scenarios fitted simultaneously to the equilibrium model. Symbols represent simulated data used for fitting and lines represent model predicted means for doses of 0.5 (●, —), 1.5 (△, ⋯) and 5 (◆, ---) mg/kg of antibody.

Table 3.

Parameter estimates obtained by fitting the equilibrium model to total antibody, total ligand and free ligand data

Parameter description	Population estimate (%SEE)			Actual
	Scenario 1	Scenario 2	Scenario 3
ka (hr−1)	0.00872 (6.71)	0.00793 (3.35)	0.00898 (2.61)	0.00837
CL/F (L hr−1 kg−1)	0.00203 (8.52)	0.00206 (8.50)	0.00205 (8.05)	0.00193
V/F (L kg−1)	0.270 (6.63)	0.244 (4.04)	0.250 (4.36)	0.231
kin (nM hr−1)	0.686 (17.6)	0.506 (7.41)	0.400 (2.88)	0.417
kout (hr−1)	11.8 (18.0)	8.76 (9.01)	6.72 (4.81)	6.85
KD (nM)	0.309 (7.86)	0.0848 (6.86)	0.0395 (5.37)	0.03a
Variability
IIV in CL/F	34.1% (27.6)	30.9% (29.1)	27.9% (28.4)	28.3%
IIV in kout	0 (FIXED)	0 (FIXED)	0 (FIXED)	12.7%
Res_prop for PK	30.2% (13.0)	32.4% (12.1)	28.0% (11.6)	31.6%
Res_prop for PD	59.8% (10.0)	38.5% (7.30)	21.3% (6.97)	17.3%

SEE, Standard error of the estimate; IIV, Inter-individual variability; Res_prop, Proportional residual error.

^aSimulated dataset did not utilize K_D, but rather micro-constants that gave a K_D of 0.03 nM. k_on and k_off were 0.042 nM⁻¹.

Tables 4 and 5 show the parameter values obtained when using the non-equilibrium model to fit the data generated by simulating with the micro-constant values, using only total ligand data and both total and free ligand data, respectively. Because the ‘true’ model was used in these fits, the fits were very good; however, the difficulty that arises with using the non-equilibrium model pertains to the ability to estimate both k_on and k_off. Crude sensitivity experiments with the simulations, as well as practical experience with actual data (including the Aβ example in this paper), have shown that estimation of k_on and k_off with any degree of reliability can be very difficult, particularly as k_on and k_off become large and when the initial parameter estimates are not close to the ‘true’ values. In fact, even with this ideal experimental system, we were not able to obtain reliable parameter estimates for scenario 3 either with or without free ligand data available.

Table 4.

Parameter estimates obtained by fitting the non-equilibrium model to total antibody and total ligand data

Parameter description	Population estimate (%SEE)			Actual
	Scenario 1	Scenario 2	Scenario 3
ka (hr−1)	0.00854 (4.67)	0.00893 (9.33)	*	0.00837
CL/F (L hr−1 kg−1)	0.00214 (8.55)	0.00215 (8.42)	*	0.00193
V/F (L kg−1)	0.239 (6.36)	0.253 (11.3)	*	0.231
kin (nM hr−1)	0.518 (21.0)	0.438 (6.85)	*	0.417
kout (hr−1)	7.89 (21.9)	6.63 (9.47)	*	6.85
kon (nM−1 hr−1)	0.0401 (6.63)	0.419 (7.97)	*	0.042, 0.42, 4.2
koff (hr−1)	0.00174 (45.9)	0.0150 (20.1)	*	0.0013, 0.013, 0.13
Variability
IIV in CL/F	28.8% (28.4)	28.1% (27.8)	*	28.3%
IIV in kout	0 FIXED	0 (FIXED)	*	12.7%
Res_prop for PK	34.8% (14.8)	34.9% (14.9)	*	31.6%
Res_prop for PD	19.3% (10.0)	18.9% (9.97)	*	17.3%

SEE, Standard error of the estimate; IIV, Inter-individual variability; Res_prop, Proportional residual error.

Table 5.

Parameter estimates obtained by fitting the non-equilibrium model to total antibody, total ligand and free ligand data

Parameter description	Population estimate (%SEE)			Actual
	Scenario 1	Scenario 2	Scenario 3
ka (hr−1)	0.00847 (4.51)	0.00888 (5.87)	*	0.00837
CL/F (L hr−1 kg−1)	0.00214 (8.55)	0.00215 (8.19)	*	0.00193
V/F (L kg−1)	0.237 (6.96)	0.251 (8.01)	*	0.231
kin (nM hr−1)	0.437 (14.5)	0.419 (6.35)	*	0.417
kout (hr−1)	7.14 (15.1)	6.85 (7.23)	*	6.85
kon (nM−1 hr−1)	0.0450 (3.76)	0.470 (5.34)	*	0.042, 0.42, 4.2
koff (hr−1)	0.00182 (47.9)	0.0147 (14.4)	*	0.0013, 0.013, 0.13
Variability
IIV in CL/F	29.4% (27.9)	28.5% (27.6)	*	28.3%
IIV in kout	6.14% (40.1)	6.73% (47.7)	*	12.7%
Res_prop for PK	34.9% (14.5)	35.1% (14.9)	*	31.6%
Res_prop for PD	18.4% (8.62)	18.9% (7.48)	*	17.3%

SEE, Standard error of the estimate; IIV, Inter-individual variability; Res_prop, Proportional residual error. *Parameter estimates could not be obtained.

Discussion

This article explores the properties of a general PK/PD model to describe the in vivo interaction between a neutralizing antibody and its soluble ligand target. Similar models and examples of their use currently exist in published literature. This work reviews the most general form of this model, discusses some of the important assumptions made, and probes issues to consider when using these models. As the general equilibrium model discussed herein represents the most basic assumptions to characterize the antibody-ligand interaction in vivo, there will likely be many scenarios when more complex models may be necessary. These scenarios will be discussed further below; however, this general model is useful to derive and illustrate some basic properties of the antibody and ligand profiles observed following administration of a therapeutic antibody designed to target an endogenous, soluble ligand.

In many cases, administration of an anti-ligand antibody leads to substantial increases in total plasma levels of the target ligand. Figure 4 illustrates this increase for Aβ_1–40 following administration of an anti-Aβ antibody. The general model explored in this work assumes that the antibody-bound ligand takes on the elimination rate characteristics of the free antibody. Often, the free ligand has a substantially faster elimination rate constant compared to the antibody-bound ligand. As such, when ligand becomes bound to the antibody and takes on distribution and clearance properties of the antibody, there is a rapid and often remarkable increase in total ligand levels. This assumption of ligand-antibody complex adopting the elimination characteristics of the antibody may not hold in all cases, and indeed has been previously modeled by assigning parameters for the complex that are unique from those of the free antibody.^5,7,11 In such cases, differential elimination kinetics of the complex may be reflected in the antibody PK profiles, with faster antibody CL apparent as complex levels become a significant fraction of total antibody levels. However, in many cases, the antibody may prevent normal processes involved in clearance of smaller ligands,^1,12 e.g., diffusion to sites of catabolism, proteolysis, renal filtration, receptor-mediated clearance, and may not introduce additional clearance pathways, e.g., as in the case of the anti-Aβ antibody example in this article, thus giving the complex the clearance properties of the antibody. Unless data suggests otherwise, the simplest assumption that is reasonable is to allow the complex to be governed by the same parameters as the antibody.

In our experience, the most readily determined ligand measurement is total ligand; thus some general properties of the total ligand curves following antibody dosing are of note. These properties apply to the general case where the free ligand has a faster elimination rate constant than the antibody-ligand complex. Following dosing, the initial slope of the total ligand curve is indicative of the production or input rate of ligand into the system. The baseline levels of the ligand are determined by the ratio of k_in/k_out. The maximum possible increase in total ligand levels is determined by the ratio of the elimination rate constant for the free ligand to the elimination rate constant for the antibody-ligand complex. It is critical to obtain baseline measures of the ligand (more ideally, a full profile for negative control animals) to allow adequate inference of the basic PD parameters of the model.

For a given antibody exposure, the extent and duration of suppression of free ligand is impacted by the apparent affinity of the interaction (Fig. 2), as well as by the production and elimination rates of the free ligand (Fig. 3). Because there is no effect on the PK of total antibody due to the altered affinity, these simulations highlight one of the major pitfalls in attempting to use antibody PK in isolation to try to determine dosing frequency for a therapeutic antibody to a soluble endogenous ligand. If antibody PK were the primary determinant of dosing frequency, one might select the same dosing frequency for each of the K_D scenarios in Figure 2, but the effect on free ligand clearly wanes much more quickly when affinity is low, and more frequent dosing or higher dosing would be necessary to achieve the same effects of ligand suppression with the low affinity antibody relative to a high affinity antibody. Similarly, a common misconception when interpreting antibody PK is the assumption that if high concentrations of free antibody are present, that antibody is still available to further bind the target ligand and drive the effect. Again, this interpretation is overly simplistic and ligand binding and turnover must be considered to understand whether the presence of free antibody provides suppression of the target ligand. There will always be some level of free antibody present in the system and the affinity of the interaction will determine the level of antibody excess. These concepts are well illustrated in Figure 2J–L, demonstrating increasing antibody excess as affinity decreases. In each of these cases there is still free antibody present in the system, yet after a period of time, the free ligand levels return to baseline even in the presence of the free antibody. Thus, antibody PK alone is of limited utility in inferring effects on suppression of ligand.

In previously published reports of antibody-ligand PK/PD modeling, both equilibrium constants^5,7 and micro-constants^2,3,8,9,11 have been used to model the in vivo antibody-ligand interaction. Because antibody elimination is considered quite slow relative to antibody-ligand binding processes it has been assumed that equilibrium models may be adequate to capture the in vivo interaction.⁵ The equilibrium model has the obvious advantage of having fewer parameter values, and we have previously noticed difficulty estimating the micro-constants from the non-equilibrium model using only antibody levels and total ligand concentrations in certain situations (e.g., the Aβ data in this article). Therefore, we conducted simulations using the non-equilibrium model in an effort to explore the adequacy of the general equilibrium model to characterize data generated from the more realistic situation. As expected (Fig. 5), as k_on and k_off increase (the ratio constant), the non-equilibrium model converges to the same output as the equilibrium model; however, for scenario 1, where k_off for the antibody-ligand binding approaches the elimination rate of the antibody (CL/V), the effects on both total and free ligand are significantly greater for the equilibrium model.

Although simulations using the ‘true’ models for the equilibrium and non-equilibrium cases demonstrated significant differences as k_on and k_off decreased, we wanted to understand whether the equilibrium model could be used to fit the data generated by the non-equilibrium model. This may be possible because, when fitting the data, the model parameters could adjust to compensate for the model-misspecification. And in practice, if a good fit is obtained for the total ligand and total antibody data, and if free ligand data is not available, it will be impossible to determine whether the model is sufficiently parameterized. When population simulations were conducted, with inter-individual and residual error simulated, the general equilibrium model adequately described the total antibody and total ligand data (Fig. 6). The free ligand data was still slightly over-predicted, but not to the extent as predicted from the simulations alone (Fig. 5). When estimating the data, the k_in, k_out and K_D parameters compensated to allow a good estimate of the total ligand data and, in turn, gave better estimates for the free ligand data. This simulation highlights a couple of interesting observations. First, models are only representations of the system, thus are always misspecified. This makes it difficult to put absolute physiological meaning to the parameters for k_in, k_out and K_D, particularly in situations when limited data are available to characterize the entire system. Second, given only total antibody and total ligand data, in many cases it will be difficult to distinguish between the equilibrium model and the non-equilibrium model. Fortunately, the predictions of free ligand from the equilibrium model were quite reasonable, even in the worst case scenario (scenario 1). The equilibrium model performed even better to predict free ligand concentrations in the situation where total antibody, total ligand and free ligand were available (Fig. 7). For all practical purposes, it appears that an equilibrium model is likely sufficient for characterization of antibody-ligand binding and prediction of free ligand levels in many cases, as long as total (and/or free) ligand data are available and are well characterized by the model.

As k_on and k_off increase, it becomes increasingly difficult to capture the parameters of the non-equilibrium model through estimation (Tables 4 and 5). Additionally, as initial estimates for the parameters get further from the ‘true’ values, it also becomes difficult to specify these parameters. It is tempting to try to fix the binding parameters for the in vivo model to values obtained from in vitro binding experiments; however, because the in vivo situation is quite different from in vitro binding experiments that are used to determine affinity, this may not be a good practice. In our experience, in vitro and in vivo K_D values have at times differed significantly from one another (unpublished observations). We recommend starting with the general equilibrium model and fitting the apparent in vivo affinity constant to understand these interactions. If the equilibrium model appears insufficient, incorporation of k_on and k_off micro-constants could be considered, again using the in vivo data to obtain estimates of these values.

This article primarily focuses on theoretical aspects of modeling antibody-ligand interactions in vivo, but some practical aspects and complexities also must be addressed when considering use of modeling and simulation to facilitate antibody development. Perhaps most important are the difficulties and uncertainties associated with the most common bioanalytical assays used to measure antibodies and ligands. At present, most antibody assays are ELISA-based assays that attempt to measure either total or free antibody in plasma. While on the surface it may seem that an antigen-capture ELISA to measure free therapeutic antibody may be the most desirable antibody assay, there are complexities associated with this measurement. Because of the dilution involved, as well as the potential for exchange of antibody between that bound to ligand in the sample and ligand coated on the plate, in most cases it becomes unclear what exactly is being measured with respect to total or free antibody. Furthermore, because most therapeutic antibodies are now humanized or human, detecting total antibody in clinical studies is increasingly difficult. Ligand assays also suffer from several limitations and many questions arise. For total ligand assays, do the antibodies used in the assay have the same specificity as the therapeutic antibody? Is the standard representative of the endogenous ligand? Free ligand assays are currently difficult to make sufficiently sensitive for many ligands and are very difficult to validate. Because total ligand levels are often many orders of magnitude greater than free ligand levels, any degree of exchange or contamination from the total levels in the free assay will be very misleading. To model antibody-ligand data in vivo, at least one measure of antibody PK (total or free) and one measure of ligand levels (total or free) is necessary. Although ideally, all four measures would be desirable (total and free antibody and total and free ligand), this is often not practical or possible. Thus, we recommend using the measures that are determined most reliable, and using mechanism-based modeling to infer what cannot be measured.

In some cases, the simple general equilibrium model discussed herein will not be sufficient to characterize the PK/PD of antibody-ligand interactions in vivo and additional complexities must be considered. These complexities may include: whether the antibody-ligand complex takes on the distribution and elimination properties of the antibody or whether it needs unique properties; whether the antibody needs multiple compartments, e.g., following intravenous dosing; whether the antibody or antibody-ligand complex exhibit non-linear pharmacokinetics; and whether additional distribution compartments may be necessary for the ligand. Additionally, study design considerations such as sampling scheme may also influence model selection.

PK/PD modeling of antibody-ligand interactions in vivo is a new and exciting field related to therapeutic antibody development. To date, there are few published examples to probe the utility and complexities of modeling these interactions. Because understanding ligand modulation is much more important to pharmacology than antibody pharmacokinetics alone, more effort is warranted toward better understanding how to characterize and understand these interactions. The general equilibrium model discussed herein represents a starting place for both understanding conceptually the in vivo interaction, and for building PK/PD models with which to characterize in vivo data. The mechanism-based nature of the model provides a powerful tool to allow insight into potential effects on free ligand levels when only total ligand levels may be available. In concert with additional work on PK/PD modeling of these interactions, further effort is warranted to develop better analytical tools with which to measure free ligand levels in the presence of antibody in vivo. Not only would free ligand levels provide a more direct measure of the pharmacologic agent of interest, it would also allow for further probing and understanding of PK/PD models for these interactions and greater confidence in using these models in instances where free levels are not available.

Methods

General equilibrium PK/PD model of antibody ligand interactions.

A simplified general model of in vivo antibody-ligand interaction is shown in schematic form in Figure 1. This basic model represents a reasonable theoretical starting point for development of PK/PD models to characterize antibody effects on endogenous ligand concentrations. Additional complexities can be added to the model, as warranted by in vivo data. Since many therapeutic biologics in preclinical and clinical development are administered via the subcutaneous route,^5–7 and we cite here an example of an anti-Aβ antibody that was administered extravascularly to mice, we chose to establish this model for extravascular administration. The model can easily be adapted for intravenously administered biologics. Equations describing antibody and ligand concentration changes over time for the basic model are shown below.

Plasma antibody concentrations:

$$\frac{dA{b}_{total}}{dt}=\frac{k_a}{V}\times A_{adm}-\frac{CL}{V}\times A{b}_{total}$$ (1)

Plasma total ligand concentrations:

$$\frac{d{L}_{total}}{dt}=k_{in}-k_{out}\times L_{total}\times f_{f,L}-\frac{CL}{V}\times L_{total}\times f_{b,L}$$ (2)

Plasma free ligand concentrations:

$$L_f=L_{total}\times f_{f,L}$$ (3)

Free and bound ligand fractions as a function of total ligand and total antibody:

$$f_{b,L}=\frac{A{b}_{total}+L_{total}+K_D-\sqrt{{(A{b}_{total}+L_{total}+K_D)}^2}-4A{b}_{total}\times L_{total}}{2L_{total}}$$ (4)

$$f_{f,L}=1-f_{b,L}$$ (5)

In these equations, Ab_total represents total antibody concentration in plasma; k_a is a first-order absorption rate constant; A_adm is antibody mass at the extravascular administration site; V is the apparent volume of distribution for the antibody (V/F); CL is the apparent clearance for the antibody (CL/F); L_total is total ligand concentration in plasma; k_in is a zero-order input rate constant for ligand (units of concentration/time); k_out is a first-order rate constant for free ligand elimination; f_{f, L} is the fraction of ligand that is free in plasma; f_{b, L} is the fraction of ligand that is bound to antibody in plasma; K_D is the equilibrium constant governing antibody-ligand binding. This basic model assumes that the antibody-ligand binding is always in equilibrium. Standard mass balance and antibody-ligand binding equations were used for Ab and L to obtain the final relationship for f_{b, L} in equation 4.²² The model further assumes that the ligand will take on the clearance and distribution properties of the neutralizing antibody once the complex is formed.

These equations were used to probe the general characteristics of ligand concentration-time profiles following administration of an anti-ligand antibody. Simulations were performed to demonstrate the impact of changes in key PD parameters of the model: binding affinity and the ligand turnover parameters. For these simulations, antibody PK parameters were constant, with k_a = 0.00837 hr⁻¹, CL = 0.00193 Lhr⁻¹kg⁻¹ and V = 0.231 Lkg⁻¹. Antibody doses were 1, 10 and 100 mgkg⁻¹, corresponding to doses of 13.3, 133 and 1,333 nmolkg⁻¹ antibody binding sites. Antibody concentrations in the figures are in nM antibody binding sites, assuming 2 moles of binding sites for every mole of antibody. It was assumed that the binding at each site was independent, i.e., no cooperativity. For the simulations exploring effect of binding affinity, 3 K_D scenarios were represented: 0.1, 1 and 10 nM. Ligand turnover was fixed in those simulations at k_in = 0.42 nMhr⁻¹ and k_out = 6.85 hr⁻¹. For the simulations exploring varying ligand turnover, K_D was fixed at 1 nM and k_in/k_out values were 0.42 nMhr⁻¹ and 6.85 hr⁻¹ in scenario 1, 0.042 nMhr⁻¹ and 0.685 hr⁻¹ in scenario 2 and 0.0042 nM hr⁻¹ and 0.0685 nM hr⁻¹ in scenario 3. The parameter values selected for these (and subsequent) simulations do not correspond to a single antibody but were chosen to both cover a wide range of possible values, and to be representative of antibodies that might be considered for development. Additionally, all of the relevant parameter values may change depending on the species studied; the selected values were not for any particular species. Simulations were performed using either WinNonlin Enterprise version 5.0.1 or NONMEM VI. Plots were generated using SigmaPlot 10.0.

Application of general equilibrium PK/PD model to an anti-Aβ antibody.

To demonstrate the applicability of this general model to observed in vivo PK/PD data, the model was applied to data obtained from an anti-Aβ antibody. Briefly, anti-Aβ antibody m266 was administered via intraperitoneal injection to transgenic platelet-derived growth factor promoter expressing amyloid precursor protein (PDAPP) mice (0.5, 2 and 5 mg kg⁻¹ antibody). Plasma samples were collected for approximately 2 weeks following dosing (one sample per mouse) and were assayed for anti-Aβ antibody levels using an antigen capture ELISA and for total Aβ_1–40 levels using a sandwich ELISA developed for the purpose. Validation work was not performed to determine whether the ELISA for anti-Aβ antibody was a better representation of free or total antibody levels (see Discussion). However, since antibody levels are in significant excess to Aβ levels in this experiment, it is reasonable to assume that total and free antibody levels are sufficiently similar for the general model using total antibody concentration to be applicable to this system. Some animals had no antibody exposure and these animals were excluded from the PK/PD analysis. The plasma antibody and total Aβ_1–40 concentrations were characterized using model equations 1–5 shown above for the general model of antibody-ligand interactions. The modeling was implemented using NONMEM VI.

Probing the validity and applicability of the general equilibrium model.

A basic and major assumption of the general model discussed here is that of instantaneous equilibrium; however, the assumption of equilibrium binding may not hold under all situations. Therefore, to further probe the validity and applicability of the equilibrium model, the model was parameterized in terms of micro-constants (k_on/k_off) instead of K_D. Equations describing free, bound and total antibody and ligand concentration changes over time for the non-equilibrium model are shown below.

Plasma free antibody concentrations:

$$\begin{array}{l}\frac{dA{b}_{free}}{dt}=\frac{k_a}{V}\times A_{adm}-\frac{CL}{V}\times A{b}_{free}-k_{on}\\ \times A{b}_{free}\times L_f+k_{off}\times Ab·L\end{array}$$ (6)

Plasma free ligand concentrations:

$$\begin{array}{l}\frac{d{L}_{free}}{dt}=k_{in}-k_{out}\times L_{free}-k_{on}\times A{b}_{free}\\ \times L_{free}+k_{off}\times Ab·L\end{array}$$ (7)

Plasma antibody-ligand complex concentrations:

$$\begin{array}{l}\frac{dAb·L}{dt}=k_{on}\times A{b}_{free}\times L_{free}-k_{off}\\ \times Ab·L-\frac{CL}{V}\times Ab·L\end{array}$$ (8)

Plasma total antibody concentrations:

$$\frac{dA{b}_{total}}{dt}=\frac{dA{b}_{free}}{dt}+\frac{dAb•L}{dt}$$ (9)

Plasma total ligand concentrations:

$$\frac{dA{b}_{total}}{dt}=\frac{dA{b}_{free}}{dt}+\frac{dAb•L}{dt}$$ (10)

In addition to the terms described previously, in these equations, Ab_free represents free antibody concentration in plasma; L_free is free ligand concentration in plasma; Ab•L represents concentration of antibody-ligand complex in plasma; k_on is the association rate constant and k_off is the dissociation rate constant for antibody-ligand binding.

First, simulations were performed to compare free and total antibody and ligand concentration-time profiles obtained using the non-equilibrium model (equations 6–10) with those obtained using the equilibrium model (equations 1–5). For both simulations, antibody PK parameters and ligand turnover parameters were constant, with k_a = 0.00837 hr⁻¹, CL = 0.00193 Lhr⁻¹kg⁻¹, V = 0.231 Lkg⁻¹, k_in = 0.42 nMhr⁻¹ and k_out = 6.85 hr⁻¹. Antibody doses were 0.5, 1.5 and 5 mg kg⁻¹, corresponding to doses of 6.7, 20 and 67 nmol kg⁻¹ antibody binding sites. Antibody concentrations in the figures are in nM antibody binding sites. For the simulations using the non-equilibrium model, 3 k_on/k_off scenarios, all yielding the same K_D (0.03 nM), were explored: k_on/k_off values were 0.042 nM⁻¹hr⁻¹ and 0.0013 hr⁻¹ in scenario 1, 0.42 nM⁻¹hr⁻¹ and 0.013 hr⁻¹ in scenario 2 and 4.2 nM⁻¹hr⁻¹ and 0.13 hr⁻¹ in scenario 3. Simulations were performed using NONMEM VI. Plots were generated using SigmaPlot 10.0.

Our next aim was to assess whether the equilibrium model can adequately characterize total antibody and total ligand concentration-time profiles when these are the only data available. For this purpose, simulated datasets for the 3 k_on/k_off scenarios (n = 4 per dose level) were first generated by incorporating random effects (intersubject variability and residual error) in the non-equilibrium model. The equilibrium model was then fit to the total antibody and total ligand concentration-time data thus obtained and model-predicted free ligand concentration-time profiles were compared with ‘observed’ profiles obtained from the simulations. Further, we included the free ligand concentration-time data in the estimation process to explore whether inclusion of this data, when available, would improve the overall fit to the equilibrium model.

Finally, we wanted to explore what scenarios might allow reasonable estimates for k_on and k_off when fitting the non-equilibrium model to either total ligand data alone or both total and free ligand data. The estimation procedure was performed using the simulated data generated above for the 3 k_on/k_off scenarios.

Table 2.

Parameter estimates obtained by fitting the equilibrium model to total antibody and total ligand data

Parameter description	Population estimate (%SEE)			Actual
	Scenario 1	Scenario 2	Scenario 3
ka (hr−1)	0.0125 (10.0)	0.0110 (8.81)	0.0103 (7.52)	0.00837
CL/F (L hr−1 kg−1)	0.00216 (8.70)	0.00216 (8.43)	0.00215 (8.14)	0.00193
V/F (L kg−1)	0.364 (6.79)	0.321 (6.73)	0.294 (7.93)	0.231
kin (nM hr−1)	0.0810 (13.3)	0.239 (6.78)	0.368 (4.40)	0.417
kout (hr−1)	1.45 (11.9)	3.86 (6.89)	5.58 (6.68)	6.85
KD (nM)	0.179 (17.1)	0.0572 (14.0)	0.0373 (12.0)	0.03a
Variability
IIV in CL/F	31.9% (29.8)	27.8% (28.0)	26.7% (26.8)	28.3%
IIV in kout	0 (FIXED)	0 (FIXED)	0 (FIXED)	12.7%
Res_prop for PK	36.5% (16.2)	35.4% (15.1)	34.9% (15.1)	31.6%
Res_prop for PD	48.8% (6.89)	33.5% (7.61)	20.5% (8.55)	17.3%

SEE, Standard error of the estimate; IIV, Inter-individual variability; Res_prop, Proportional residual error.

^aSimulated dataset did not utilize K_D, but rather micro-constants that gave a K_D of 0.03 nM. k_on and k_off were 0.042 nM⁻¹ hr⁻¹ and 0.0013 hr⁻¹; 0.42 nM⁻¹ hr⁻¹ and 0.013 hr⁻¹; and 4.2 nM⁻¹ hr⁻¹ and 0.13 hr⁻¹ for scenarios 1, 2 and 3, respectively.

Conflict of Interest

J.D. and R.H. currently work for Eli Lilly and Company. There are no other conflicts of interest.