Metric learning for enzyme active-site search

Abstract

Motivation: Finding functionally analogous enzymes based on the local structures of active sites is an important problem. Conventional methods use templates of local structures to search for analogous sites, but their performance depends on the selection of atoms for inclusion in the templates.

Results: The automatic selection of atoms so that site matches can be discriminated from mismatches. The algorithm provides not only good predictions, but also some insights into which atoms are important for the prediction. Our experimental results suggest that the metric learning automatically provides more effective templates than those whose atoms are selected manually.

Availability: Online software is available at http://www.net-machine.net/∼kato/lpmetric1/

Contact: kato-tsuyoshi@k.u-tokyo.ac.jp

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

The influx of newly sequenced genomes has sparked the development of function-prediction methods that use global sequence/structure comparison for the annotation of genes and proteins (Loewenstein et al., 2009). For enzyme proteins, many such methods attempt to predict functions from protein sequences and structures based on the Enzyme Commission (EC) classification scheme (Loewenstein et al., 2009).

The EC classification scheme, which has been used worldwide for many years, is based mainly on the whole chemical structures of substrates and products, and on the cofactors involved (Webb, 1992). However, because the EC classification scheme neglects protein sequence and structure information, it is sometimes difficult to detect a correlation between an enzyme sequence/structure and functions based on it. For instance, some homologous enzymes that are a result of divergent evolution from the same ancestral enzyme might catalyze different reactions, whereas some non-homologous enzymes from different superfamilies might catalyze the same reaction because of the convergent evolution. The enzyme pair trypsin and subtilisin, which shares the Ser-His-Asp catalytic triad, is a typical example of ‘analogous enzymes’ produced by convergent evolution (Wright, 1972). Nagano (2005) analyzed the catalytic mechanisms of 270 enzymes (mainly hydrolases and transferases) from 131 superfamilies, which are manually compiled in the enzyme reaction database, EzCatDB. Analysis of the enzyme reactions has revealed several analogous reactions that are observed in non-homologous enzymes (Nagano et al., 2007). EzCatDB also provides a hierarchic classification of enzyme reactions, RLCP, which clusters the same reaction types together based on basic Reaction (R), Ligand group involved in catalysis (L), type of Catalytic mechanism (C), and residue/cofactors located on Proteins (P) (Nagano, 2005). Consequently, both the homologous reaction and the analogous reaction can be clustered together in the RLCP classification if they share the same catalytic mechanism and the same type of catalytic site (Nagano, 2005).

Results of a recent study also suggest that such cases of active sites shared by analogous enzymes are not rare (Gherardini et al., 2007). Consequently, for enzyme-function prediction, it is necessary to examine the specific local structures of the active sites that might reflect enzyme functions, rather than the global structures, such as the domain level or the chain level (Loewenstein et al., 2009). Regarding local structure comparison methods to detect similar active sites, several ‘template-based’ methods have been reported (Barker and Thornton, 2003; Chou and Cai, 2004; Fetrow and Skolnick, 1998; Ivanisenko et al., 2004; Kleywegt, 1999; Laskowski et al., 2005; Stark and Russell, 2003; Torrance et al., 2005; Wallace et al., 1997). Those template-based methods search for the occurrence of a predefined template structure that consists of active-site residue atoms, within target protein structures. However, some questions and problems remain in relation to the template-based methods: (i) the prediction accuracy might be dependent on the number and types of atoms in the templates. Because it is sometimes very difficult to determine which atoms in the catalytic site should be included in the templates, even experts on enzyme structure and function might have to create the best template through trial and error. (ii) Some atoms in the catalytic site might be more important for the catalytic reaction than other atoms are. According to a previous report, the sidechain of catalytic residues is used (92%) much more frequently than the mainchain (only 8%) (Bartlett et al., 2002). Moreover, charged and/or polar residues tend to be involved in catalysis (Bartlett et al., 2002). Are such catalytically necessary atoms also important for the templates? (iii) These template-based methods also yield a huge number of mismatches along with site matches. Is it possible to reduce the number of mismatches?

In this study, we developed a new metric learning algorithm to detect catalytic sites effectively in terms of search accuracy of RLCP classification (Nagano, 2005). One famous template-based method, TESS (Wallace et al., 1997) uses geometric hashing to search for local structures. JESS (Barker and Thornton, 2003) uses kd-tree data structures. Ultimately, both methods compute the unweighted RMSD for the search results. To improve the accuracy of the template search, we use the metric learning algorithm by determining the weights of the atoms in the templates. That method also enables us to compare the importance of the atoms within the template, particularly between the atoms in the manually created template and those in the automatically refined template, based on their determined weight values.

The Consurf algorithm (Ashkenazy et al., 2010), which has been developed to detect conserved positions in proteins, is distinct from template-based methods, but related to our study. The algorithm computes evolutionary conservation scores from multiple sequence analysis, in order to project the scores onto 3D structures. It depends on sequences around the active site, although analogous sites acquired by convergent evolution have no conserved regions around the sites. In contrast, our algorithm emphasizes only active sites so that analogous sites can also be detected.

This article is organized as follows. The next section presents a new algorithm of metric learning to search for functionally analogous enzymes. Numerical experiments in various conditions are conducted to confirm the effectiveness of our algorithm. Those conditions are described in Section 3. The results and discussion are presented in Section 4. The last section concludes this article with future work. Mathematical notations are given in Supplementary Material.

2 PRINCIPLES

2.1 Problem setting

Such template-based methods such as TESS (Wallace et al., 1997) are local structure searching (LSS) algorithms, which search for the occurrence of a predefined template structure that comprises active-site residue atoms, from unknown protein structures. In the first place, the template structure must be created by carefully selecting the atoms in the active site of the query enzyme protein, for the LSS algorithm. Here, the set of selected atoms is called a query template. The number of atoms is denoted by n. The LSS algorithm searches for proteins having a local structure with n atoms that is similar to the query template, from a database of protein tertiary structures, such as the Protein Data Bank (PDB). The output of the LSS algorithm could be a set of sites such as that presented in Table 1, where ℓ represents the number of hits. The conventional usage of the LSS algorithm is to compute the mean square deviation from the query template to each of the hits, and then to sort the hits based on the deviation values to discriminate site matches from mismatches, where site matches belong to the same functional class as the query template, and mismatches do not.

Table 1.

Variables of a dataset generated using the LSS algorithm

	Atom1	Atom2	…	Atomn	Class
Site 1	x1,1	x1,2	···	x1,n	y1
Site 2	x2,1	x2,2	···	x2,n	y2
⋮	⋮	⋮		⋮	⋮
Site ℓ	xℓ,1	xℓ,2	···	xℓ,n	yℓ

The ℓ sites are presumed to be hits by the LSS algorithm. Their functional classes are known. The vector x_i,j ∈ ℝ³ and the scalar y_i ∈ {±1}, respectively, represent the coordinate of the j-th atom and the binary class label of the i-th site.

In this article, we propose weighting each atom to achieve better prediction. Conventional approaches use the unweighted mean square deviation to measure how similar a hit is to the query. To give mathematical deviations, we designate the query template and a hit by X^query and X′, respectively. Query template X^query has n atoms and the three-dimensional coordinates are stored in the matrix as X^query = [x^query₁,…, x^query_n] ∈ ℝ^3×n where x^query_j ∈ {ℝ³ is the coordinate of the j-th atom in the query template. Similarly, hit X′ is the ordered set of three-dimensional coordinates. It is expressed as X′ = [x′₁,…, x′_n] ∈ ℝ^3×n where x′_j is the j-th atom in the hit. The unweighted mean square deviation is defined by the minimal value of the function

over rotation R ∈ 𝕆³ and translation v ∈ ℝ³. We denote the optimal values of the rotation matrix and the translation by 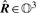and , respectively. The unweighted root mean square deviation (Unweighted RMSD) is also used frequently (Kato et al., 2004). The function E_unwei takes the average of distances without weighting atoms. Our proposal is the use of the weighted version of the distance. Letting w ∈ Δⁿ be the weight vector, we define the weighted mean square deviation as

In this study, rotation 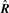and translation are precomputed so that they are optimized in the sense of the unweighted mean square distribution. One might consider, instead of using rotation 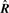and translation , optimizing the two variables so that the weighted mean square deviation is minimized. Although it is possible to optimize the rotation and the translation as well as the weights simultaneously, such an approach makes the learning algorithm fairly complicated.

Weighting is equivalent to adjusting the metric (Amari and Nagaoka, 2000) in the space of the coordinate set of n atoms. It will be revealed empirically in Section 4 that the metric should be determined automatically to achieve good prediction of the hits produced by the LSS algorithm. Hits with a distance less than the threshold are predicted as site matches. To determine the values of the weight parameters of the metric, w, hits whose functions are known are used for metric learning. Then, the data, an example of which is shown in Table 1, are obtainable. In the table, the number of known hits is ℓ. Vector x_i,j ∈ ℝ³ stores the three-dimensional coordinate of the j-th atom in the protein for the i-th site. Variable y_i ∈ {±1} is the class label of the protein for the i-th site where the value is +1 if the site is a site match; otherwise, it is −1.

Two symbols, ℐ₊ and ℐ₋, are used to denote the index set of site matches and mismatches, respectively: ℐ₊ ≡ {i ∈ ℕ_ℓ|y_i = +1} and ℐ₋ ≡ {i ∈ ℕ_ℓ|y_i = −1}. The i-th site is denoted by the matrix X⁽ⁱ⁾ ≡ [x_i1,…, x_in] ∈ ℝ^3×n, which corresponds to the i-th row in Table 1.

A new algorithm will be presented to perform automatic weighting, as described below.

2.2 Metric learning

Ideal weighting should produce weighted distances that separate site matches from mismatches completely by a threshold. In the ideal case, the distances of all site matches are less than threshold θ ∈ ℝ₊:

(1)

and the distances of all mismatches are greater than θ:

(2)

where .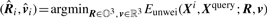

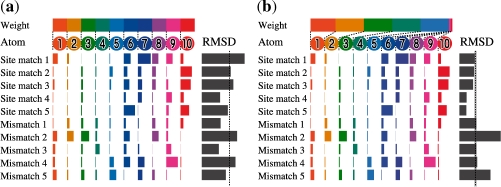
Figure 1 presents an illustrative example describing the difference between unweighted RMSD and weighted RMSD. The figure has five site matches and five mismatches. The situation in which unweighted RMSD cannot separate site matches from mismatches as in Figure 1a often happens, but the data are separable completely by adjusting the weights, as shown in Figure 1b.

Fig. 1.

Example of metric learning. Computing RMSD is a typical means to search for site matches from numerous hits aligned with a query template. It involves taking the unweighted average of distances of each atom. This toy example shows a case in which each of the five site matches and five mismatches is aligned with a query template having 10 atoms. In this case, no threshold separates site matches from mismatches perfectly as long as the average of distances is unweighted, as shown in (a). Three mismatches and two site matches can be predicted incorrectly if the threshold depicted in (a) is used. Our metric learning algorithm finds a weight for each atom to generate a distance that separates site matches from mismatches. For this example, weighted RMSD supports a complete separation of site matches from mismatches, as shown in (b).

In practice, however, a situation in which no weighting can separate site matches from mismatches completely can also happen. Supplementary Figure 5 shows the results of using template 1jfh. Supplementary Figure 5c depicts the distribution of unweighted RMSD for site matches and mismatches. Even if the weighted RMSD is used, this dataset cannot be separated by any weights. Therefore, the above conditions of weights, given in (1) and (2), are too strict for practical use. To relax the condition, each site is allowed to violate the inequalities to some degree. Non-negative variable ξ_i is introduced to describe the quantity of the violation and to modify the inequalities to

which can be summarized to

The total error is evaluated using the sum of the mean violation of positives, as and the mean violation of negatives, as . Our intention is to find the metric that can achieve the minimum total error. To avoid over-fitting, a constant upper bound C ∈ ℝ of the ℓ_∞-norm of the weight vector ‖w‖_∞ ≤ C is used. The value of C is set to 2/n in our experiments. The upper bound has the effect of regularization (Hastie et al., 2003). Then, the algorithm that is used to learn the metric is described as

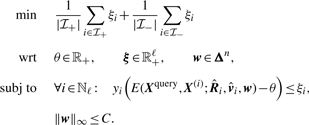(3)

Further analysis engenders the following theorem.

Theorem 1. —

The problem in (3) can be reduced to a linear program (Hinrichs et al., 2009).

The proof is given in the Supplementary Material. Linear programming has been studied well for many years as a class of convex programming (Boyd and Vandenberghe, 2004). There are several efficient solvers for linear programming problems (Dantzig, 2004).

Supplementary Figure 5d shows the resultant distribution of the weighted RMSD achieved by the metric learning algorithm using template 1jfh. Although no weighting can separate site matches from mismatches, the metric learning algorithm achieves almost complete separation of site matches from mismatches, with only a few exceptions.

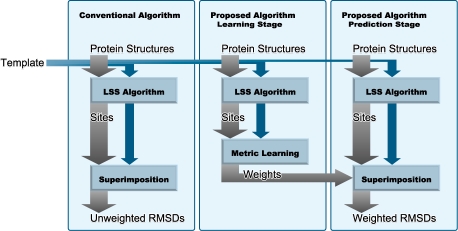
The procedures using the metric learning algorithm are summarized in Figure 2. Metric learning is performed in the learning stage. In the prediction stage, unknown local sites are superimposed onto templates with Euclidean metric and then weighted RMSDs are computed.

Fig. 2.

Flow of the respective algorithms. In the conventional algorithm, the sites found by LSS algorithms are predicted using unweighted RMSD. In our algorithm, the sites are predicted using weighted RMSD. The weights are obtained using metric learning from known active sites.

3 METHODS

To illustrate the usefulness of the metric learning algorithm, experiments that search for active-site structures were conducted over PDB datasets. To create query templates for the active-site structures, 48 protein structures were selected. The LSS algorithm that uses those templates was applied to the PDB dataset. In the next section, the experimental results are shown for the 45 templates presented in Supplementary Table 3. A query template comprises a set of atoms in a protein structure. To generate a query template, we roughly selected amino acid residues that play catalytic roles in enzyme proteins. In EzCatDB (Nagano, 2005), each amino acid in the active site is classified into one of four types: catalytic-site residue, co-factor binding site residue, modified residue and mainchain catalytic residue. For catalytic-site residues and modified residues, atoms from the sidechains of residues are automatically included in the query template, whereas all atoms are included in the query template for co-factor binding site residues. For mainchain catalytic residues, only the mainchain atoms are included in the query template. The qualities of the query template created in this manner would not depend on the abilities or knowledge of the persons who created the template. In this study, the query template created in this manner is defined as a ‘rough template’. The conventional approach requires that we choose carefully those atoms which are involved in enzyme reactions, based on literature information, to create an appropriate query template. A query template produced in this manner can be designated as the ‘precise template’. As described in this article, it will be shown whether the rough templates combined with metric learning can discriminate more effectively than the manually created precise templates. To this end, the precise templates for the 45 proteins were created by selecting atoms carefully from the corresponding atoms in the rough templates. Here, the atoms in the precise template are designated as ‘inner atoms’, whereas the remaining atoms in the rough template are designated as ‘outer atoms’.

In the first stage, an LSS algorithm reported by (Wallace et al., 1997) was adopted to identify candidates for active sites in the PDB datasets. To investigate the performance of algorithms, 5692 PDB structures registered in EzCatDB were implemented for the PDB datasets. Among all the hit local sites, local sites whose PDB ids belong to the corresponding reaction type, in the RLCP classification (Nagano, 2005), and which include residues registered as active sites in EzCatDB, were extracted as site matches. In contrast, local sites whose PDB ids do not belong to the corresponding reaction type in the RLCP classification, or which include residues that are not registered as active sites in EzCatDB, were considered as mismatches. In our experiments, these obtained sites were used as the dataset for the evaluation of the algorithms. The number of site matches and the number of mismatches are shown in Supplementary Table 3.

To evaluate the performance of the metric learning algorithm, half of the proteins in the datasets were used to learn the metric, and the remainder were used to evaluate the predictions based on the obtained metric. Evaluation criteria of two kinds were adopted: area under the curve (AUC) and sensitivity. AUC is the area under the receiver operating characteristic (ROC) curve, which plots the ratio of correctly predicted site matches against the ratio of wrongly predicted site matches over different possible thresholds. The sensitivity was computed with the threshold that is adjusted so that the specificity would be equal to 0.95. This procedure was repeated 100 times and the average of AUCs was considered to be the performance of each algorithm. Herein, note that ‘site matches’ and ‘mismatches’ in the LSS algorithm are treated as ‘positives’ and ‘negatives’ on computing these two criteria for performance evaluation, respectively.

Because rough templates have less dependence on the qualities of the query template as compared with precise templates, the use of rough templates would be favorable to achieve good prediction. Here, the following terminologies are defined to distinguish the methods using rough templates or precise templates in discussing the experimental results for comparison.

Condition 1 —

[Euclidean Metric with Rough Templates (EMR)]. In the Euclidean method with rough templates, the rough template is adopted to perform prediction based on the unweighted RMSD.

Consequently, EMR has a control condition that uses the rough template without metric learning.

Condition 2 —

[Metric Learning with Rough Templates (MLR)]. MLR is a method that adopts rough templates and performs prediction based on the weighted RMSD, where the weights are determined using the metric learning algorithm.

Here, inner atoms in the rough templates were selected as the catalytic atoms. They are expected to play an important role in catalysis. Therefore, the inner atoms are considered more important than the outer atoms, to obtain better predictions. A condition that uses additional constraints, which would make the weights for inner atoms no smaller than those for outer atoms, has been prepared as follows:

Condition 3 —

[MLR with constraints favorable to inner atoms (MLR-CI)]. In the MLR-CI, the constraints favorable to the inner atoms are set, so that the weighted RMSD from the rough templates is adopted to perform predictions. The metric learning algorithm to determine the weights can solve the optimization problem in (3) with additional constraints (∀j₁ ∈ 𝒥^inner, ∀j₂ ∈ ℕ_n∖𝒥^inner), w_j1 ≥ w_j2 where 𝒥^inner (⊆ℕ_n) is the index set of the inner atoms.

By expanding the idea of MLR-CI, further constraints were applied to obtain a better metric by introducing a priori knowledge. The importance of inner atoms for the catalytic reaction should not be equal; some atoms might be more important than the others. One might infer that a priori information will engender further improvement. To confirm that notion, several atoms (at least three) that are more important for catalytic reaction than the other atoms were selected carefully for each precise template. These atoms are designated as the ‘catalytically essential atoms’. Consequently, the constraints that the weights for catalytically essential atoms should not be smaller than those of the other inner atoms were also introduced.

Condition 4 —

[MLR with constraints favorable to catalytically essential atoms (MLR-CE)]. MLR-CE adopts the weighted mean square deviation from the rough templates. The metric learning algorithm solves the optimization problem in (3) with the following additional constraints: (∀j₁ ∈ 𝒥^inner, ∀j₂ ∈ ℕ_n∖𝒥^inner), w_j1 ≥ w_j2 and (∀j₁ ∈ 𝒥^ce, ∀j₂ ∈ ℕ_n∖𝒥^ce), w_j1 ≥ w_j2 where 𝒥^ce is the index set of the catalytically essential atoms.

The outer atoms might contain only irrelevant information for prediction. If the effects of irrelevant information are too large, then the metric learning algorithm would fail to get rid of the inappropriate effect. Better prediction is obtainable if all the outer atoms are removed. This would lead to use of the following method.

Condition 5 —

[Euclidean Metric with Precise Templates (EMP)]. EMP is a method that adopts the unweighted RMSD from the precise templates to perform predictions.

Metric obtained by learning might engender improvement. Moreover, its variants, which employ constraints favorable to the catalytically essential atoms, might be obtained. Consequently, the following two methods were introduced.

Condition 6 —

[Metric Learning with Precise Templates (MLP)]. MLP is a method that adopts the weighted mean square deviation from the precise templates to make predictions. The weights are determined using the metric learning algorithm given in (3).

Condition 7 —

[MLP with the constraints favorable to the catalytically essential atoms (MLP-CE)]. MLP-CE is a method that adopts the weighted mean square deviation from the precise templates. The method adds the following constraints to the optimization problem in (3): (∀j₁ ∈ 𝒥^ce, ∀j₂ ∈ ℕ_n∖𝒥^ce), w_j1 ≥ w_j2.

4 RESULTS

4.1 Effects of metric learning

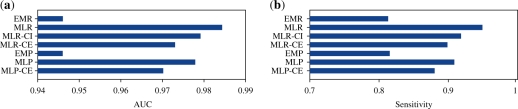
Figure 3a presents the average prediction performance. When rough templates are adopted, metric learning significantly improves the prediction performance; MLR achieved the AUC of 0.984 on average, whereas EMR obtained the AUC of 0.947 on average. These differences are statistically significant according to results of the one-sample t-test (Rosner, 2000) (P-value of 7.28 × 10⁻⁴).

Fig. 3.

Average AUCs and sensitivities. Forty-five templates are used for the experiments. The dataset was randomly split into a training set and a test set for each template 100 times, and the AUC and the sensitivity were computed for the 100 test sets. The bars show the average AUCs and the average sensitivities over the 100 trials and the 45 templates. EMR is the baseline method, whereas MLR is the main proposed method. The performances of the two methods are statistically significantly different in terms of P-value (by one-sample t-test) (Section 4). The other methods are prepared to investigate various conditions (Section 3).

In Supplementary Table 4, the AUC values are shown for all the templates in this study. Values in bold and red indicate the best AUC, although those underlined in blue indicate values for which statistically significant differences were not found relative to the best AUC. Here, the one-sample t-test was performed to detect statistically significant differences. The significance level was set to 1%. It was observed that plenty of empirical evidence supported the effectiveness of the metric learning algorithm. In 42 of the 45 templates, MLR (Condition 2) yielded the best performance or performance that did not differ from the best performance. The AUCs of MLR surpassed those of EMR in 30 templates, whereas the AUCs were equal for both MLR and EMR in 12 templates. Only in three templates—2ace, 2oke and 1dgy—was the AUC of EMR better than that of MLR in terms of statistical significance. However, the numbers of site matches in 2oke and 1dgy for performance evaluation were, respectively, five (= ⌊10/2⌋) and two (= ⌊5/2⌋). Those numbers are too small to obtain credible statistics for performance evaluation. Regarding the eight templates, 1bls, 1af0, 2oke, 2dhc, 1g42, 1isw, 1arg and 1cq7, the site matches were separated completely from the mismatches, even without metric learning. In six of the eight templates, MLR also separated site matches from mismatches completely. These data suggest that metric learning could rarely worsen the prediction performance of the good template datasets, which have already achieved favorable separation via the Euclidean metric. It is also noteworthy that MLR achieved complete prediction on four other templates (1eo4, 1f0o, 1ahg and 4tim), where EMR did not get complete prediction on the four templates.

Sensitivity values at the specificity threshold of 0.95 were also calculated. The AUC values for the ROC curves are often adopted for the prediction performance evaluation. By changing the threshold, various specificity values were obtained. The AUC values are the average sensitivity values relative to all the specificity values, and are often used for the evaluation of prediction performance (Kato et al., 2005). However, the evaluation with the AUC values has the following disadvantage. As shown in Supplementary Table 3, the LSS algorithm often yields many mismatches. In such cases, sensitivity at a low specificity tends to be pointless because it would be almost impossible to check hits in the lower order, when hits are checked in the order of highest to lowest. For this reason, the sensitivity at specificity 0.95 was adopted for the evaluation. The differences between EMR and MLR tended to be more remarkable for the sensitivity values at specificity 0.95 than for the AUC values. Average sensitivities are shown in Figure 3b. The average of the sensitivity was improved from 0.813 to 0.949. The change is statistically significant (P-value of 1.27 × 10⁻⁴). The individual sensitivities are shown in Supplementary Table 5. Except for three templates—2ace, 1ka1 and 2bvw—the sensitivity of EMR did not exceed that of MLR statistically significantly.

Supplementary Figure 5 shows detailed results of the template made from the active site of 1jfh (α-amylase). This template comprises 13 atoms from three amino acid residues. Supplementary Figure 5c shows the frequency distribution of unweighted RMSD for the training dataset with equal weights for the 13 template atoms. The normalized distributions of 24 site matches and 6486 mismatches in the training dataset are shown in the figure, so that the sums of the frequencies for the site matches and mismatches could be 1.0 and 1.0, respectively. Here, site matches and mismatches could not be separated in the distribution of the unweighted RMSD data. The metric learning algorithm that used the 24 site matches and 6486 mismatches produced the weights for the atoms (see Supplementary Fig. 5b and h). The weighted RMSD, calculated using the weight values, is shown in Supplementary Figure 5d, suggesting that the separation of site matches from mismatches could be improved. The distributions of the unweighted and weighted RMSD datasets for the evaluation, which were not used in the metric learning algorithm, are shown in Supplementary Figure 5e and f, respectively. Additionally, in the case of the evaluation data, site matches and mismatches were separated effectively. These data suggest that our metric learning algorithm can improve generalization capability without overfitting (Hastie et al., 2003).

Supplementary Figure 5g portrays a box plot of the distribution of distances between the query template and each hit for each atom. Two atoms, ‘OD1 ASP A 197’ and ‘CB GLU A 233’, were particularly inseparable. The weight values for these two atoms turned out to be zero. Moreover, the remaining oxygen atoms gave small weights, probably as a result of the inseparable distribution between the site matches and the mismatches. Therefore, the metric learning algorithm can automatically select important atoms from the template atoms.

4.2 Effects of outer atoms

We compared MLR-CI (Condition 3) with MLR (Condition 2), to investigate the effect of the constraint that the weights of the outer atoms be smaller than those of the inner atoms. However, we observed barely any improvement yielded by the additional constraints, as shown in Figure 3 obtained from Supplementary Tables 4 and 5. Of the templates shown in blue italic in Supplementary Tables 4 and 5, 32 have outer atoms, and therefore might give different predictions. The information in the tables suggests that the constraint does not improve the prediction performance. The AUCs of MLR-CI were significantly worse than those of MLR for 19 templates, and the sensitivities of MLR-CI were worse for nine templates. Actually, MLR-CI achieves better AUCs in only three templates, and better sensitivities in only four templates.

The rough template of 1map comprises 17 atoms from two residues. Thirteen atoms are inner atoms, whereas the other four atoms, N, CA, C and O of LYS 258, are the outer atoms, which are shown in gray in Supplementary Figure 6h. In the distribution of distances for each atom (Supplementary Fig. 6g), despite the outer atoms, the separations of site matches and mismatches are good. For the inner atoms, CB, CG and CD1 of TYR 225, and CB of LYS 258, the separations are unsatisfactory, resulting in small weights that are nearly zero.

In MLR-CE and MLP-CE experiments (conditions 4 and 7, respectively), the weights for the catalytically necessary atoms were set not to be smaller than those for any other atoms. This constraint could be a powerful prior knowledge for learning if it was true that the catalytically necessary atoms are useful for prediction. However, MLR-CE and MLP-CE did not show remarkable improvements. In fact, MLR-CE for 27 rough templates yielded significantly worse AUC than MLR did (Supplementary Table 4). Furthermore, the sensitivities of MLR-CE were worse for 14 rough templates (Supplementary Table 5). The MLR-CE improves AUCs for only six templates, and improves sensitivities for only five templates. Those results imply that, even if some atoms are catalytically necessary, they are not always important for prediction of active sites. Some concrete examples are presented below for illustration.

In the case of the template 1arg (aspartate aminotransferase) (Supplementary Fig. 4c), the weight value of the OH atom of TYR 225, which is catalytically important, was large—0.075—compared with those of the atoms CD1, CD2, CE1 and CE2, which were nearly zero. This result suggests that the axis atoms of the phenyl group, CB, CG, CA and OH, might be fixed, whereas the atoms, CD1, CD2, CE1 and CE2, could be rotated along the axis atoms, or at least positioned differently, depending on the active sites of true positives. In contrast to the template 1arg, for the template 3daa (d-alanine aminotransferase) (Supplementary Fig. 4d), the weight values for the atoms of TYR 31 do not vary.

As for the weight values of acidic residues, the templates 1psa (pepsin) and 1qk2 (lysozyme) showed entirely different tendencies (Supplementary Fig. 4a and b). The weights for the oxygen atoms of ASP 32 and ASP 215 were nearly zero in the template 1psa, although the template 1qk2 gave larger weight values to the oxygen atoms of ASP 221 and ASP 401. In both cases, the oxygen atoms of the acidic residues are catalytically important and involved in enzymatic reactions. However, in the case of 1psa, the catalytical importance does not always affect the weight values in the prediction. These data suggest the following:

• The inner atoms, which are directly involved in catalytic reactions, are not always conserved from a structural viewpoint, although the structures of the outer atoms are more conserved than those of the inner atoms.

• The distribution of distances for each atom in the mismatches is important to separate site matches from mismatches. The atoms that can separate site matches from mismatches are as important in the prediction as the structurally conserved atoms.

• Although each template has different properties, metric learning automatically finds the effective combination of atoms that improves the prediction performance.

Torrance et al. (2005) also investigated whether functional atoms, which carry out catalytic function, can discriminate site matches from mismatches more effectively than mainchain atoms can. According to their analyses, templates based on protein mainchain positions are more discriminating than those based on functional atoms from sidechains because sidechain atoms are more flexible than the mainchain of a protein, especially in the presence of ligand (Torrance et al., 2005). The inner atoms in our definition, which correspond to their functional atoms, can discriminate matches from mismatches less effectively than the outer atoms, which tend to be closer to the mainchain positions. Therefore, our results are apparently consistent with their results.

Furthermore, other results that might support the importance of outer atoms for prediction were obtained. In the MLP method, only atoms that are involved in catalytic reactions directly are included in the templates. Therefore, no outer atoms are incorporated into the computation for prediction. Although the MLP method is not disrupted by irrelevant information from outer atoms, MLP does not always achieve superior sensitivity to MLR. The AUCs and the sensitivities of MLP were significantly worse than those of MLR for 19 templates and 10 templates, respectively. The AUCs and the sensitivities of MLP were better for only three templates—2ace, 1rpa and 1vcz—which implies that it is not necessary to remove outer atoms in advance for most cases, and that it would be a better approach to use the metric learning algorithm to remove irrelevant atoms automatically.

4.3 Effects on residue selection

The results shown so far suggest that our algorithm selects predictive atoms in templates automatically. Even if users use rough templates, the residues that compose templates still must be selected manually. Our experiments adopt the TESS algorithm (Wallace et al., 1997) as an LSS algorithm. The algorithm searches for local structures that have the same residue types as those of the template. Therefore, because no residue in the local structures, which should be hit as the site matches, can be matched with the unrelated residue in the template, the LSS algorithm can miss the site matches if an unrelated residue is added to the template. In contrast, if a necessary residue is removed, the algorithm will pick up many mismatches. Supplementary Table 2 presents an example that shows how the selection of residues affects the prediction performance. The template 1acb contains four residues: HIS 57, ASP 102, GLY 193 and SER 195. A new template was created by removing the atoms in the residue GLY 193. Removal of the atom yields many mismatches: from 6300 to 19 066. Common hits to the previous four-residue template and the new three-residue template are used to investigate the effects of residue selection because it is necessary to analyze the same dataset for comparison of these performances. The MLR slightly reduced the sensitivity from 0.998 to 0.994. Actually, EMR is also degraded by removal of a residue, but the changes in sensitivity are much larger. Consequently, the performance depends on selection of residues, but the change in MLR is small compared with that in EMR. It should also be noted that selection of residues is much easier than selection of atoms.

4.4 Effects on re-superimposition

In determining the metric, the parameters of the rigid-body transformation are fixed. One could also superimpose the template again and predict the sites with the obtained weights. The ‘re-superimposition’ approach was tested to be compared with the original ‘single superimposition’ approach. The re-superimposition approach slightly reduced the average AUC from 0.984 to 0.977, and the average sensitivity from 0.949 to 0.934. The P-values of the differences are 0.004 and 0.021, respectively. The slight degradation of the performance may be because both the approaches optimize the metric for the first superimposition, not for the second superimposition, although the re-superimposition approach uses the metric for the second superimposition.

5 CONCLUSIONS

This article presents a new algorithm that learns the metric to assess data obtained by LSS algorithms and discriminate site matches from mismatches. We design the parameterization for the metric so that the parameters can be interpreted directly as weights of atoms. An advantage of our algorithm is that redundant atoms are removed clearly by making those weights zero. This characteristic is obtained using the definition of the domain of the weight parameter. The domain is the probability simplex, which plays the role of ℓ₁-regularization (Hastie et al., 2003). Some literatures (Yu et al., 2010) replace ℓ₁-regularization with another regularization. In our algorithm, the ℓ_∞-norm of the weight vector is forced to be bounded from above to improve the generalization performance. This is equivalent to combination of ℓ₁-regularization with ℓ_∞-regularization. As described in this article, we reported the results of family analyses that searches for active sites for one template. We are now developing an algorithm for library analyses that predicts the function of specified structures using a set of templates.