Accurate Determination of Interstrand Distances and Alignment in Amyloid Fibrils by Magic Angle Spinning NMR

Abstract

Amyloid fibrils are structurally ordered aggregates of proteins whose formation is associated with many neurodegenerative and other diseases. For that reason, their high resolution structures are of considerable interest and have been studied using a wide range of techniques, notably electron microscopy, x-ray diffraction, and magic angle spinning (MAS) NMR. Because of the excellent resolution in the spectra, MAS NMR is uniquely capable of delivering site-specific, atomic resolution information about all levels of amyloid structure: (1) the monomer, which packs into several (2) protofilaments that in turn associate to form a (3) fibril. Building upon our high resolution structure of the monomer of an amyloid-forming peptide from transthyretin (TTR_105-115), we introduce single 1-¹³C labeled amino acids at seven different sites in the peptide and measure intermolecular carbonyl-carbonyl distances with an accuracy of ~0.11 A. Our results conclusively establish a parallel, in register, topology for the packing of this peptide into a β-sheet and provide constraints essential for the determination of an atomic resolution structure of the fibril. Furthermore, the approach we employ, based on a combination of a double-quantum filtered variant of the DRAWS recoupling sequence and multispin numerical simulations in SPINEVOLUTION, is general and should be applicable to a wide range of systems.

INTRODUCTION

The structure of amyloid fibrils is of considerable interest because of the many debilitating diseases that are associated with amyloid formation¹. Accordingly, a wide range of techniques has been used to investigate these structures, including X-ray diffraction, electron microscopy, and magic angle spinning (MAS) NMR spectroscopy^2-8. Of these, only solid state NMR provides the site-specific information at atomic resolution that is necessary for the de novo determination of a high resolution structure. More specifically, the most valuable constraints provided by MAS NMR are measurements of ¹³C-¹⁵N^2,3 and ¹³C-¹³C distances⁴ and torsion angles^5-9. Even though the constraints provided by MAS NMR are generally more precise (± 0.1-0.5 Å) than those available in solution state NMR (± 1-2 Å), it remains important to have 5 or more constraints per residue if the resulting structure is to be of reasonable resolution. In the absence of this density of constraints, a smaller set of measurements can be combined with chemical knowledge and statistical databases¹⁰ that associate NMR chemical shifts with amino acid torsion angles to infer a model of the structure. However, such a model represents only an educated guess about the structure of the monomers that assemble to form an amyloid protofibril.

In several cases, MAS measurements have been used to refine well-constrained structures of the monomeric element of an amyloid fibril^11-13. However, the amyloid fibril is a mesoscopic structure assembled from monomers that associate into protofilaments that assemble further to form fibrils. The complete structure of the fibril can therefore be determined using MAS NMR through the following four stages: (1) determination of the structure of a monomer within the fibril; (2) orientation of the β-strands of the monomer within the β-sheets (parallel or antiparallel) and their register and separation with respect to one another; (3) determination of the registry of the β-sheets with respect to one another within a protofilament; and (4) the definition of the assembly of protofilaments into fibrils. The last step requires 3D translational information, and at present is best done in combination with data derived from an imaging technique such as electron microscopy data.

Indeed, we have followed this strategy for fibrils formed from a peptide fragment of transthyretin, a protein whose conversion into fibrils in vivo is associated with several highly debilitating diseases¹. The structure of the monomer corresponding to fibrils of TTR_105-115 (sequence YTIAALLSPYS) was solved at atomic resolution using ¹³C-¹⁵N and ¹³C-¹³C dipolar recoupling techniques by Jaroniec et al.¹¹ In early experiments, similar structural parameters were investigated at low resolution in other systems using ¹³C-¹³C rotational resonance^14,15, DRAWS dephasing¹⁶, and more recently RFDR¹⁷ experiments, and used to generate low resolution structural models. In this manuscript, we address the second hierarchy of structure for the TTR_105-115 peptide, and demonstrate that very precise measurements of interstrand distances can be obtained by a double-quantum filtered DRAWS^18,19 sequence^20,21. This is a well established MAS double quantum recoupling NMR experiment and has been used at low spinning frequencies for recoupling distant spins with large chemical shift tensors, where it can it yield accurate ¹³C-¹³C distances, as demonstrated in careful studies of spin pair systems²¹. Using numerical simulations in SPINEVOLUTION²² to model both dipolar couplings and incoherent relaxation, we demonstrate how DQF-DRAWS can provide distance measurements in dicarboxylic acid samples that are accurate to within ± 0.02 Å or better. Since a single labeled site in an amyloid fibril monomer forms an extended linear chain of spins when packed into a β-sheet fibril, we introduce periodic boundary conditions^23,24 into the simulations to approximate multispin interactions with as few as four spins. Most importantly, we have applied these methods to measure seven distances in fibrils formed from the TTR_105-115 peptide (precision of ± 0.11 A), conclusively demonstrating that the molecules assemble into in-register parallel β-sheets. The accurate knowledge of the interstrand arrangement that we obtain here is essential to determining the high resolution structure of the protofilament and subsequently of the entire fibril.

MATERIALS AND METHODS

Fibril Preparation

Seven samples of the peptide fragment TTR_105-115 (sequence: YTIAALLSPYS) were synthesized via solid-phase synthesis (CS Bio, Menlo Park, CA) with a single 1-¹³C labeled amino acid (Cambridge Isotope Laboratories, Andover, MA) at each of the positions from I107 to P113. The peptide samples were converted into fibrils by dissolution in 10% acetonitrile/water solutions (adjusted to pH 2 with HCl) at a concentration of 15 mg/ml, followed by incubation at 37°C for two days, and then 14 days at room temperature. The resulting fibrils were centrifuged to form a pellet (1 hr, 4°C, ~300k × g) and washed twice with 2 ml of a 10% acetonitrile/water solution at pH 2 with a 1 hr centrifugation step following each wash. Following the wash, the samples were then packed into a 4-mm NMR rotor (Revolution NMR, Fort Collins, CO). The rotor was sealed to avoid dehydration of the samples during extended measurements.

NMR Experiments

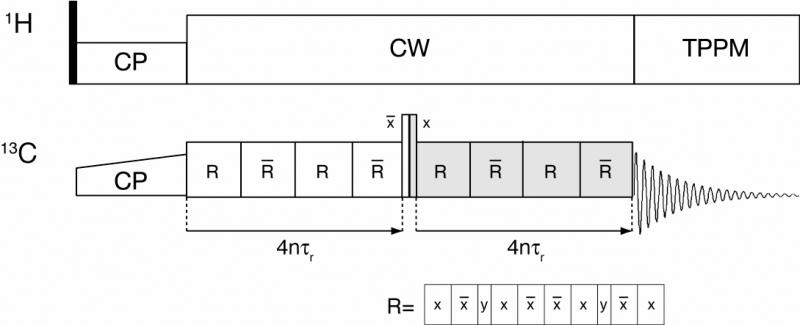
The NMR measurements were made using a Cambridge Instruments spectrometer (courtesy of D. J. Ruben, Francis Bitter Magnet Laboratory, Massachusetts Institute of Technology) operating at a ¹H frequency of 360 MHz, using a triple resonance (¹H, ¹³C, ¹⁵N) 4 mm MAS probe (Varian, Fort Collins, CO). The spinning frequency was regulated to 5882 ± 2Hz with a Bruker MAS spinning controller unit (Bruker-Biospin, Billerica, MA), and the samples were cooled to ~5°C with a nitrogen gas heat exchanger system²⁵. All simulations and data fitting were performed using the SPINEVOLUTION NMR software package²². DQF DRAWS was implemented as shown in Figure 1.

Figure 1.

Pulse sequence for DQF-DRAWS experiment. Following cross-polarization, the DQF-DRAWS sequence (basic element R) is applied for a variable dipolar build up time for two conjugate periods. TPPM is used during acquisition, but CW decoupling is applied during the mixing sequence to avoid interference effects with TPPM.⁷⁴

RESULTS AND DISCUSSION

In dipolar recoupling experiments whose goal is the measurement of internuclear distances, either the loss of transverse magnetization (dephasing) or the transfer of polarization from one spin to another is monitored as a function of the time during which the recoupling sequence is applied (mixing time)^4,26-28. The result is a dephasing or build-up curve whose form depends on the dipolar coupling of interest, but also to a lesser degree on the chemical shift anisotropy (CSA), any scalar (J) couplings, and also on incoherent relaxation processes²¹. When the confounding effects of relaxation are small, they can be modeled by a single, exponential damping parameter; failure to do so almost always reduces the accuracy of distance measurements. When relaxation is strong, on the other hand, it can significantly reduce the accuracy of distance measurements.

As an alternative to these recoupling methods, in which dipolar dynamics are recorded as a function of a variable mixing time, we have developed constant-time experiments^29,30 in which data points in the dipolar dimension are recorded as a function of an experimentally addressable resonance parameter that is varied through the range of values at which recoupling occurs. For example, this parameter is the spinning frequency in the case of rotational resonance^31-33 or an effective RF field in the case of rotational resonance tickling³⁴ (varied by changing the field amplitude or frequency offset). In these constant-time experiments, the contribution of relaxation at each point is relatively fixed, while the dipolar-driven dynamics change as a function of the resonance parameter. As a result, the dipolar coupling and the relaxation parameters can be accurately and independently extracted³⁵ during data fitting. In combination with multidimensional chemical shift correlation spectroscopy, this family of methods has been successfully applied to determine multiple distances in uniformly labeled peptides and proteins^36,37.

There is no robust tunable matching parameter for the case of ¹³CO-¹³CO recoupling experiments, however, as the carbonyl chemical shifts are nearly degenerate. Therefore, we used one of the several recoupling sequences developed for homonuclear distance measurements between spins of degenerate chemical shift, and we briefly summarize the reasons for our choice here. The first option is the RFDR zero-quantum (ZQ) recoupling sequence^38-41 used without decoupling⁴² at high MAS frequencies in a constant-time implementation (which produces a static dipolar Hamiltonian) by Tycko and co-workers⁴³ for homonuclear distance measurements in multispin systems. This approach has the advantage of being applicable at arbitrary MAS frequencies. However, sequences based on double quantum (DQ) spin pair filters have a number of important advantages that result in superior data quality and accuracy in distance measurements, as we demonstrate below. Among these are SPC5⁴⁴ and other γ-encoded DQ recoupling sequences which, while effective as mixing sequences in assignment experiments, suffer from reduced efficiency for the case of weak dipolar couplings in the presence of large chemical shift anisotropy^21,45. Sequences based on R22⁹₄ symmetry have been used by Levitt and co-workers^46,47 for homonuclear distance measurements in systems with large CSAs; however, this family of sequences is known to be sensitive to experimental artifacts such as spectrometer phase errors and switching transients. By contrast, the DRAWS sequence^18,21,48 has been frequently employed in similar applications shown to have a reduced sensitivity to variation in the CSA and to experimental artifacts. In spite of its high RF field requirement of 8.5 times the MAS frequency, DRAWS can be successfully used for homonuclear distance measurements in singly labeled samples at low magnetic fields. We note that we did not explore the use of CMRR^49,50 and related sequences in this study; we expect that they will have superior properties and continue to be applicable at high MAS frequencies even without ¹H decoupling.

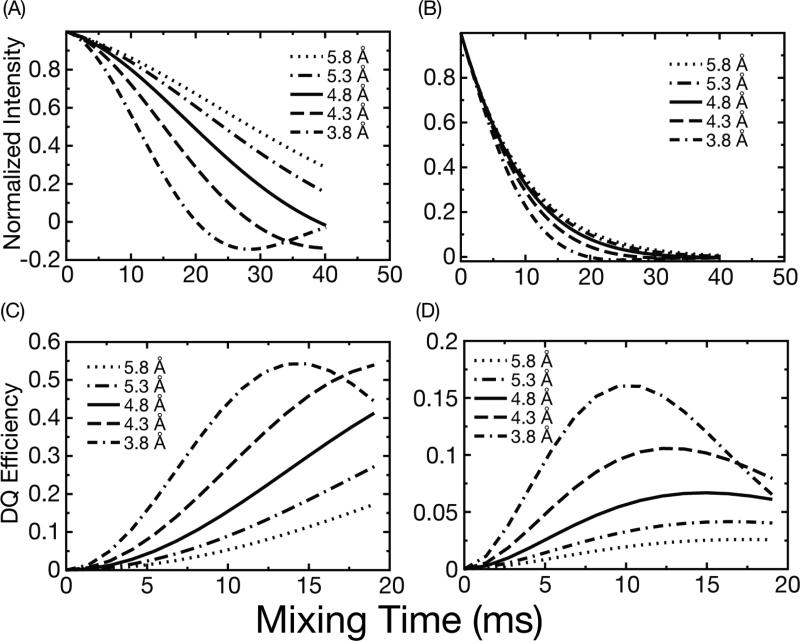
Even though we are using a recoupling sequence that is intrinsically robust in the presence of the CSA and experimental imperfections, we still cannot fit accurately the dipolar coupling from our data without introducing the aforementioned relaxation parameter. In fact, many previous studies have also used analytical simulations incorporating phenomenological transverse relaxation of the observed signal^20,21 for data fitting; the work of numerous investigators^51,52 including ourselves on this subject^30,53 demonstrate the importance of multi-quantum relaxation parameters in MAS NMR distance measurements. As we show in Figure 2, however, the reduced sensitivity of DQ DRAWS to these effects is still a profound advantage. In Figure 2, SPINEVOLUTION simulations²² of dephasing experiments show that it is possible to distinguish ¹³C-¹³C distances differing by ~0.5 Å (Fig. 2A) only in the absence of relaxation. When a realistic relaxation parameter is included in the calculations, the dephasing curves rapidly converge (Fig. 2B), and it is no longer possible to differentiate, for example, effects resulting from 3.8 Å to those from 5.8 Å in the presence of experimental noise. A similar dependence of the spin dynamics on relaxation has been reported for the case the RFDR experiment¹⁷. In contrast, simulations for the DQF-DRAWS experiments (Fig. 2C and D) show that it is still possible to discriminate visually between the various distances despite the reduction in the intensity of the buildup curves due to relaxation⁵⁴. Our simulations and results thus illustrate that double-quantum dipolar build-up curves provide a much more precise estimate of structurally relevant distances (between 3.8 Å and 5.8 Å) than other techniques commonly applied in amyloid fibril structure determination¹⁷.

Figure 2.

Simulations of DRAWS double quantum filtered dephasing and buildup curves using a 4-spin model representative of parallel β-sheets. Plots A and B show DRAWS dephasing curves with and without relaxation, respectively. Plots C and D show similar build up curves for DQF-DRAWS without and with relaxation, respectively. In B and D the relaxation parameters are similar to those found experimentally for TTR fibrils (T₂= 6-10 ms).

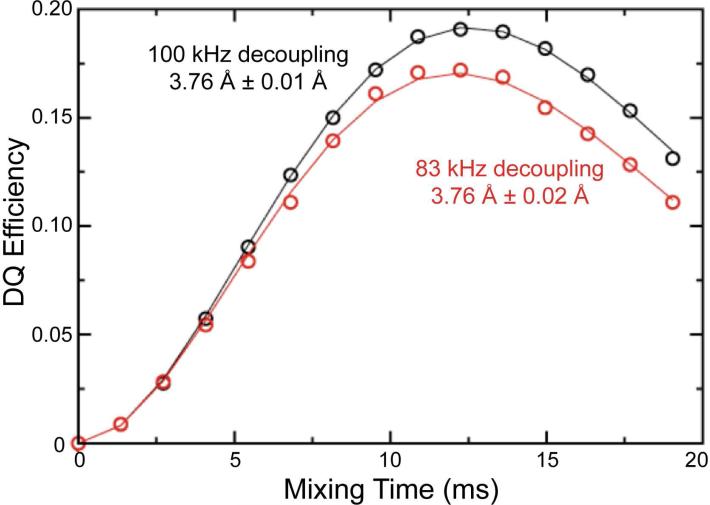
For initial experimental tests of our approach, we employed a sample of crystalline 1,4-¹³C-ammonium succinate diluted to 10% in naturally abundant ammonium succinate to remove any intermolecular dipolar couplings. In this sample, the DQF-DRAWS buildup curves shown in Fig. 3 were fitted to a two-spin model incorporating two fitting parameters: the 1,4-¹³C internuclear distance and a relaxation parameter, expressed numerically as an exponential damping in SPINEVOLUTION. The model also includes fixed CSA parameters, which were measured in a separate experiment^55,56, and contribute to the damping of the dipolar spin dynamics. The internuclear ¹³C-¹³C distance is found to be 3.76 Å which is identical to that reported by Karlsson, et al.²¹ Our results also demonstrate that insufficient ¹H decoupling power during the DRAWS recoupling period results only in a change in the relaxation parameter; the distance determined from the analysis remains unchanged. As such, the single parameter describing exponential relaxation models the effects of incoherent relaxation and experimental limitations such as insufficient decoupling. By fitting both it and the distance simultaneously, the precision of the distance measurement is improved dramatically relative to that reported previously in similar measurements. This improvement is particularly important because it suggests that the method should still be applicable to conductive biological samples, such as amyloid fibrils, where RF heating limits the decoupling power that can be applied.

Figure 3.

Double quantum buildup curves for 1,4-¹³C-succinate using 100 kHz (black circles) and 83 kHz (red circles) proton decoupling, and their corresponding best-fit simulations (black line and red line). The decrease in decoupling power results in a slight change in the best fit relaxation parameter, but the best fit distance parameter remains the same. These data and the data on the fibril samples were collected on a 360 MHz spectrometer using 4 mm rotors and ω_r/2π = 5.882 kHz.

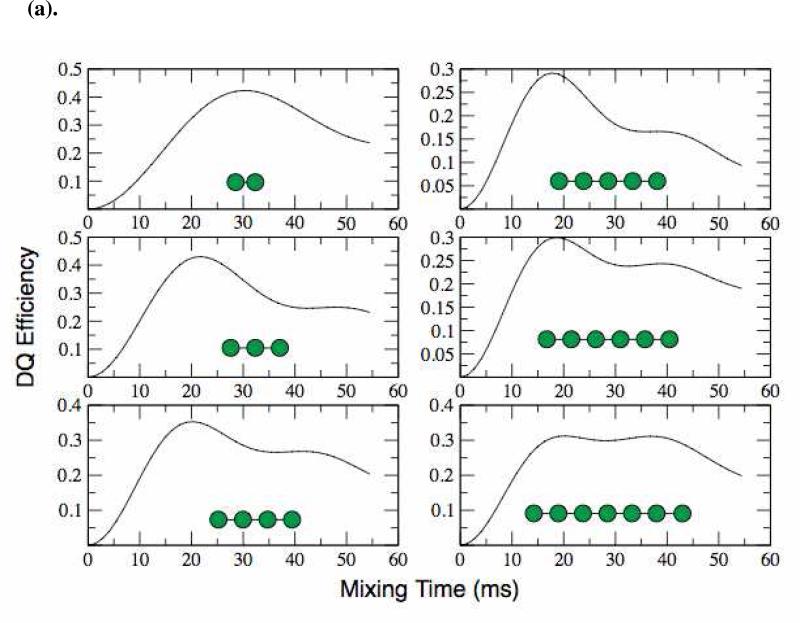
Having demonstrated the robustness of both our experimental approach and of the numerical simulation method in simple model compounds, we had to address several obstacles that prevented its immediate application to an amyloid fibril system. First, while a simple two-spin coupling model accurately represents a dilute, isolated, pair of spins in ammonium succinate, it does not represent or resemble the spin topology expected in an amyloid fibril. In particular, any ¹³CO site in an amyloid fibril with parallel, in-register β-sheets will form an extended spin chain in which, at the very least, any carbonyl site experiences two comparable dipolar couplings (illustrated in Figure 7) to its nearest neighbors. Furthermore, the effects of more distant dipolar couplings can contribute to the spin dynamics. This point is made clear by our numerical simulations of DQ-DRAWS buildup for a linear arrangement of spins (Figure 4(a)). Here, we build a spin chain whose dipolar couplings correspond to the average inter-carbonyl distance expected in an amyloid fibril (4.5 Å), and in which all spins have the same chemical shift value and are therefore detected as a sum polarization. We then monitor the DQ DRAWS buildup as a function of time, while adding more spins to the chain. The results in Figure 4(a) show that simulations of this topology fail to converge for 7 or fewer spins, even in the presence of realistic relaxation parameter. Thus, we conclude that the simulation method that worked well in our small molecule experiments will not be useful for experiments with amyloid fibrils.

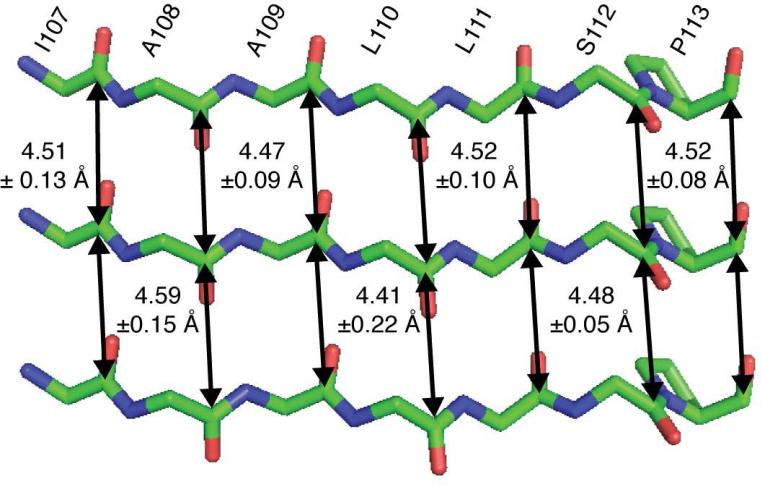
Figure 7.

Schematic arrangement of the peptide strands in amyloid fibrils of TTR_105-115 illustrating the seven ¹³C=O-¹³C=O distances measured with the DQF-DRAWS experiments together with estimates of their errors.

Figure 4.

(a). DQF-DRAWS simulations of linear chains of spins from 2 to 7 using SPINEVOLUTION. The simulations fail to converge for 7 or fewer spins. Simulations were preformed with internuclear distances similar to that in a parallel β-sheet (~4.7 Å). CSA parameters were explicitly included but T2 relaxation was not. (b) DQF-DRAWS simulations of chains of spins from 2 to 7 with periodic boundary conditions imposed. These simulations show a much better convergence than the linear chains and, for experimentally relevant times (< 20 ms), they converge with as few as 4 spins. Simulations were performed using SPINEVOLUTION with the same parameters as the previous figure.

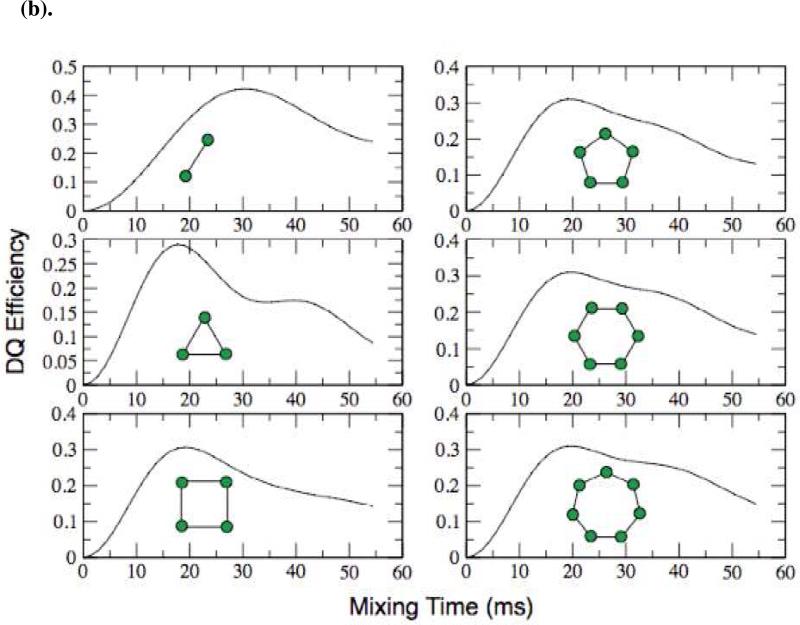
In developing an alternative simulation method, we realized that the chain of coupled spins in a real fibril is large compared to the distance between any single spin pair. This means that, to a good approximation, every spin pair is in an identical environment. In similar “nearest neighbor” problems that arise in analytical solutions of extended structures such as a crystallographic lattice or a continuous Ising spin chain, periodic boundary conditions are imposed to simulate a chain of infinite extent and to reduce the dependence of the result on the finite size of the simulation^23,24. We can simulate this situation by introducing a spin coupling matrix in SPINEVOLUTION in which only identical pair-wise, nearest-neighbor couplings are included, forming a kind of periodic boundary condition that eliminates the contribution of spins at the edge of a linear chain. Topologically, these resemble closed, loop-like structures as illustrated in Figure 4(b). Using this approach, simulations of the DQ buildup curves for experimentally relevant mixing periods (~20 ms) converge with as few as four spins (Figure 4(b)). We note that a multi-parameter fit in a system of 4 spins is only tractable due to the speed of SPINEVOLUTION simulations, making it a viable and convenient approach for data fitting. The use of SPINEVOLUTION for data analysis also permits us to extract robust statistics on the fitting errors, expressed here as the 95% confidence interval derived from the elements of the covariance matrix of the fit.

In spite of its advantages, one difficulty in our approach is that the CSA tensors cannot be oriented in a realistic way with respect to the dipolar couplings. Since DRAWS is known to be well-suited to the measurement of weak dipolar couplings in the presence of large chemical shift anisotropies²¹, we hoped that this would not compromise the accuracy of distance measurements. To verify this situation, we simulated the effect of various CSA orientations on the DRAWS buildup curves and found that the expected systematic error is indeed less than the random experimental error. Removing the CSA altogether does result in a larger, but still small, change in the buildup curves, so we include the CSA tensor and orient it so that it's largest principle axis is perpendicular to the plane of the spins⁵⁵ and thus perpendicular to the dipole coupling, as is found in the linear arrangement (Figure 5). We note in performing the experiments at a lower field (e.g. 360 MHz ¹H) will reduce the effects of the CSA, and could be a useful approach in cases where the CSA is large.

Figure 5.

A set of 10 DQF-DRAWS simulations with random orientations of all four CSA tensors. The differences in these curves are smaller than the experimental errors so for simplicity we used the orientation of CSA tensors in which the most shielded axis of each tensor is parallel to the z-axis, while the spins lie in the x-y plane.

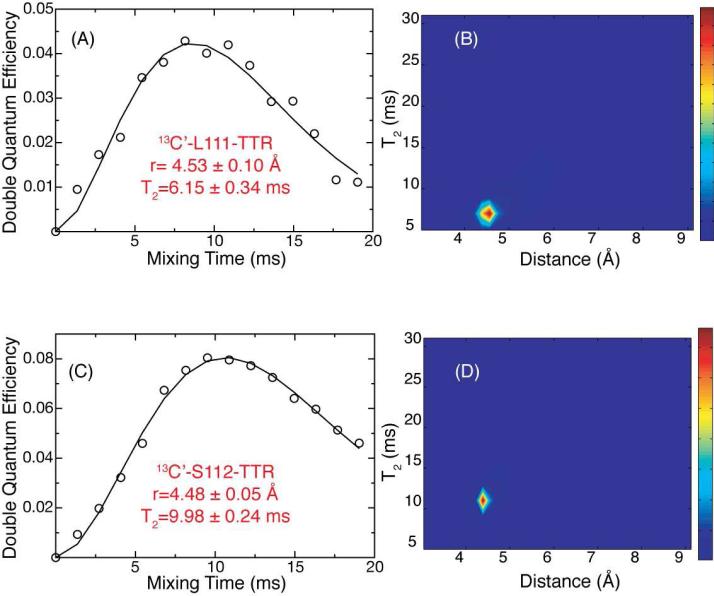
The DQF-DRAWS buildup curves, consisting of experimental data and simulations, for two of the seven samples are shown in Figure 6. The agreement between experimental data and simulations (A and C) is excellent, allowing estimation of the distances (B and D) to a far greater accuracy than has previously been possible by SSNMR. Further, all of the distances measured indicate clearly that the peptide molecules are arranged in parallel, in-register β-sheets with interstrand ¹³C-¹³C distances ranging from 4.41 Å to 4.59 Å with an average error of ±0.11 Å (Figure 7). The double quantum relaxation parameter is found to be in the range of 6-10 ms, which is consistent with the measurements of Liu, et al. (9.4 ms) in a similar system (amyloid nanotubes)⁵⁷. However, we note several important differences between our approach and that of Liu, et al. and others in the field. First, while the spin chain was approximated in the previous study by a linear array of three spins, we have found in our analysis that this method fails to converge even for seven spins and have instead used a periodic boundary condition to model the spin system more accurately. Second, while the relaxation behavior was measured previously in separate experiments, we avoid the need to construct and acquire appropriate control experiments by fitting the relaxation behavior directly and including the effects of the CSA in the numerical simulation. Finally, while previous approaches involve the presence of a single spin interaction with a precision of 0.3 Å, we are able to measure seven spins with an average precision of ±0.11 Å. The ability to obtain this number of distances with this degree of accuracy enables the objective determination of a high resolution structure to be achieved rather than inferring a model from a limited number of structural restraints.

Figure 6.

Double quantum buildup curves for TTR fibrils labeled with 1-¹³C-L111 (A) and 1-¹³C-S112 (C). Circles represent experimental data and lines the best-fit simulation. The corresponding probability surfaces for the two fits are shown in (B) and (D) for the L111 and S112 respectively. Both data sets fit to intermolecular distances consistent with parallel β-sheets with relatively small errors, which were extracted from the SPINEVOLUTION fitting routines.

We have also compared our results to those reported previously for Aβ peptides^16,17, which reveal that our distances are significantly shorter (~0.3-1.4 Å) than these cited values. Furthermore, the method may yield systematically smaller values of distances when compared to X-ray crystallographic measurements, as indicated by the succinate distance which is ~4% shorter than the distance obtained by X-ray diffraction measurements (3.76 Å vs. 3.91)²¹. If one assumes that internuclear distances in the fibrils systematically diverge from those measured by X-ray crystallography due to intrinsic differences in the methods, then the scaling by 4% results in our measurement of the average inter-fibril distance of 4.50 ± 0.11 scaling to 4.68 ± 0.11 agrees within the experimental error with those measured by powder diffraction (4.7 Å) ⁵⁸. Powder diffraction, however, lacks site-specific resolution and therefore cannot distinguish between the many possible topological arrangements of strands in the fibrils. Finally, it is also interesting to compare our data qualitatively to those reported by Balbach et al. using the constant-time RFDR sequence. On qualitative grounds, the agreement between data and experiment is significantly better for DQF-DRAWS, particularly at longer mixing times, and this is reflected in the accuracy of distances extracted by both methods. This may be due in part to the reduced sensitivity of DQF-DRAWS to relaxation as compared to RFDR, together with our fitting method that treats both the dipolar coupling and relaxation in a single global fit.

CONCLUSIONS

We have demonstrated in this work a robust method for the determination of homonuclear distance contraints in amyloid fibrils, and utilized this approach to establish the registry of the β-sheets consisting of monomers of TTR_105-115 that assemble into a protofilament. We also illustrate that numerical simulations using SPINEVOLUTION represents and invaluable means of extracting distance information from experiments that involve multispin dynamics. We anticipate that the quantitative restraints we measure in this work will be invaluable in determining a high-resolution structure of the entire amyloid fibril.

Beyond this specific application, the ability to make accurate measurement of distances in the range of ~3-6 Å is an important achievement, as distances of less than 3 Å are determined by covalent bonding geometry, but distances 3Å up to 6 Å represent near-neighbor non-covalent interactions that are crucial for observing conformational shifts of macromolecules. While other solid state NMR approaches involving the site-specific addition of ¹⁹F nuclei can be used to measure longer distances ^59-61, a distance of 6 Å may be the practical limit for ¹³C-¹³C distance measurements. We therefore anticipate that the approaches we describe here will be useful in many other contexts where homonuclear distance measurements must be performed in the presence of a large CSA; one specific example is the determination of the conformation of the retinal chromophore of bacteriorhodopsin and its homologs ^62-64. Several recent experimental developments, including dynamic nuclear polarization^65-71 and the use of resonant structures in MAS probes that screen the sample from the electric field to prevent heating (“E-Free”)^72,73, should enhance further the range of applicability of DQ experiments. Most importantly, we note that CMRR^49,50 and related sequences are likely to share in the advantages of our approach but will be applicable at higher MAS frequencies than DQF-DRAWS in experiments using uniformly isotopically labeled molecules, and without proton decoupling.