Biased diffusion in tubes formed by spherical compartments

Abstract

We study the effect of the driving force on Brownian motion of a point particle in a tube formed by identical spherical compartments, which create periodic entropy potential for the motion along the tube axis. The focus is on (i) the effective mobility and diffusion coefficient of the particle as functions of the driving force, (ii) localization of the particle in the central part of the tube induced by the driving force, and (iii) transit time of the particle between the openings connecting neighboring compartments. Some of the results at very small and large driving force are obtained analytically, while the majority of the results are obtained from Brownian dynamics simulations.

INTRODUCTION

In many cases, the motion of Brownian particles occurs in the presence of geometric constraints. When the constraints are periodic, say in the x-direction, they lead to a slowdown of the particle motion in this direction compared to that in space with no constraints. This happens because of the periodic entropy wells and barriers created by the constraints. This circle of questions has been actively studied in recent years^{1, 2, 3, 4, 5, 6, 7, 8, 9, 10} because geometric constraints are ubiquitous in nature and technology. The present paper is focused on the effects due to periodic constraints when motion of a point Brownian particle occurs in a tube formed by identical spherical compartments connected by openings through which the particle can go from one compartment to the other (Fig. 1).

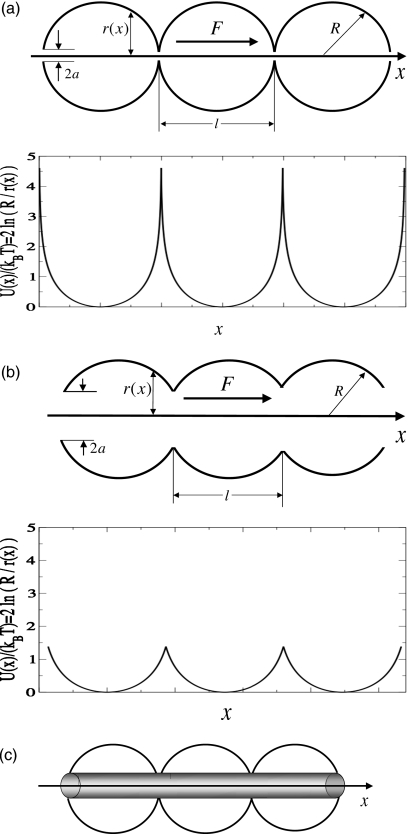
Figure 1.

Schematic representation of tubes formed by identical spherical compartments and corresponding dimensionless entropy potentials. The radii of the connecting openings are 0.1R in panel (a) and 0.5R in panel (b). Respectively, the dimensionless the entropy barriers are 4.6 and 1.4. In panel (c) we show the cylinder connecting the openings, in which the particle is localized when the driving force is large enough.

A specific feature of such a tube is that it provides an example of Brownian motion in periodic entropy potential when one can find the effective diffusion coefficient of the particle analytically. This can be done at both small^{5a, 5b} and moderate-to-large^5c openings. The patterns of the particle motion in the two cases are quite different. The distinction is due to the difference in the heights of the entropy barriers (Fig. 1). When the openings are small, and the entropy barriers are high, the time required for the particle to find an opening is much larger than the characteristic equilibration time in the compartment with “closed” openings. One can use this circumstance to map the particle motion onto a continuous-time nearest-neighbor random walk among the centers of connected compartments.^{5a, 5b} Then one can find the effective diffusion coefficient using well-known results of the random walk theory.

At moderate-to-large openings, one can find the effective diffusion coefficient using a different approach, which is based on the reduction to an effective one-dimensional description in terms of the generalized Fick–Jacobs equation.^{1, 2} In our case, this equation is the Smoluchowski equation with periodic entropy potential and position-dependent diffusion coefficient. Starting with this equation, one can find the effective diffusion coefficient^5c by means of the Lifson–Jackson formula.¹¹ A good agreement between the effective diffusion coefficients found in Brownian dynamics simulations and the two theoretical predictions has been demonstrated.^5c

Both approaches mentioned above fail in the presence of an external driving force. Therefore, in the present paper, we study how the driving force affects motion of Brownian particles in tubes formed by spherical compartments numerically using Brownian dynamics simulations. Specifically, we study the effective mobility and diffusion coefficient of the particle as functions on the driving force. In addition, we show that the particle distribution over the tube cross-section becomes highly nonuniform at large driving force, namely, the particle is mainly localized in the cylinder connecting the openings [Fig. 1c]. Variation of the distribution over the tube cross-section from uniform to strongly localized, induced by the driving force is discussed in detail.

Another quantity of our interest is the transit time of the particle between neighboring openings. The transit time is a random variable. We study the first four moments of its distribution as functions of the driving force. Using these moments we show that as the driving force tends to infinity, the probability density of the transit time tends to the delta-function centered at the mean transit time. Such a delta function distribution of the transit time is inherent in biased diffusion in a tube of constant diameter at sufficiently large driving force.

Numerical studies are carried out at three values of the opening radius a and, hence, the compartment length, l, $l=2\sqrt{R^2-a^2}$, which is identical to the tube period, where R is the compartment radius, namely, a∕R=0.5,0.3,0.1 and correspondingly l∕R≈1.72,1.91,1.99. Each tube can be characterized by the height of the entropy barrier measured in the thermal energy units, βΔU=ΔU∕(k_BT)=ln(A_max∕A_min), where k_B and T are the Boltzmann constant and the absolute temperature while A_max=πR² and A_min=πa² are the maximum and minimum values of the tube cross-section area. In our three cases the dimensionless heights of the entropy barriers, respectively, are βΔU=2 ln(R∕a)≈1.4,2.4,4.6. Thus, the entropy barrier is relatively high at a∕R=0.1 and low at a∕R=0.5 (Fig. 1). Conditional boundary separating small and moderate-to-large openings (high and moderate-to-low entropy barriers) corresponds to a∕R=0.2. It was shown^12a that the particle survival probability in a spherical cavity of radius R with a circular absorbing spot of radius a on the cavity wall decays as a single exponential when a∕R≤0.2, while at larger values of the spot radius the decay becomes multiexponential. [One can find rigorous analysis of the problem based on sophisticated asymptotic methods in Refs. ^{12b, 12c, 12d, 12e}.]

The present paper is a continuation of the study initiated in our recent Communication.^5h The Communication is focused on the comparison of the dependences of the effective mobility and diffusion coefficient on the driving force in tubes formed by identical compartments of different shapes, spherical and cylindrical. (A tube formed by cylindrical compartments is a cylindrical tube separated into compartments by infinitely thin periodic partitions containing circular openings in their centers, through which the particle can go from one compartment to the other.) For comparison, we chose the tubes with close parameters of the compartments, namely, the radii of the cylindrical and spherical compartments were identical, as well as the radii of the connecting openings, a∕R=0.3, and the difference in the compartment lengths was less than 5%, l∕R≈1.91 and 2 in the tubes formed by spherical and cylindrical compartments, respectively. One of the main results of the Communication is a demonstration of the fact that the dependences are qualitatively different although the parameters of the compartments are close.

The outline of the present paper is as follows. Dependences of the effective mobility and diffusion coefficient on the driving force obtained from Brownian dynamics simulations are discussed in Sec. 2. In this section, we also discuss the localization of the particle in the cylinder connecting the openings induced by the driving force. The transit time between neighboring openings is discussed in Sec. 3. Some concluding remarks are given in Sec. 4.

EFFECTIVE MOBILITY AND DIFFUSION COEFFICIENT

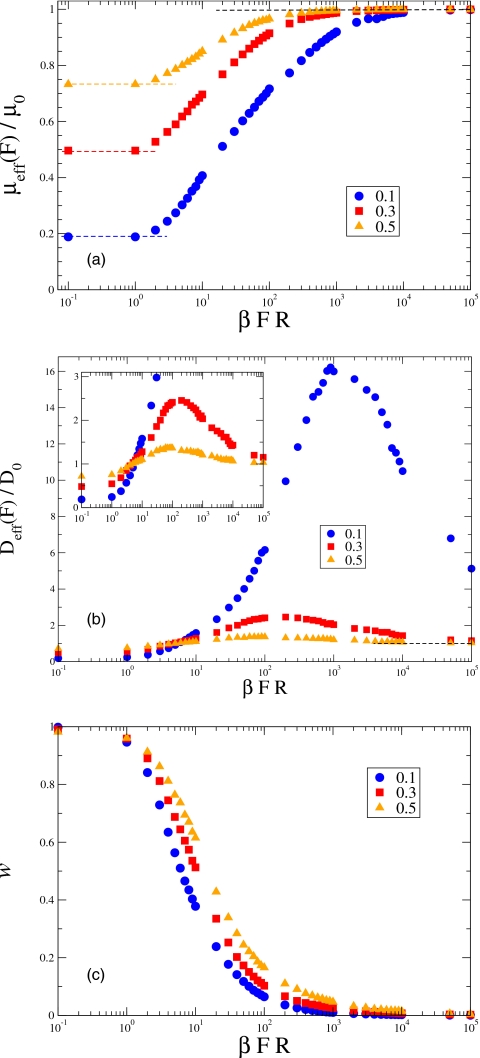
Dependences of the effective mobility and diffusion coefficient on the driving force F, μ_eff(F), and D_eff(F), respectively, were obtained from Brownian dynamics simulations carried out at the three values of the opening radius, a∕R=0.5,0.3,0.1. [The simulation details can be found in Ref. 5h.] Using the particle mobility μ₀ and diffusion coefficient D₀ in a tube of constant diameter as scaling factors, we presented the ratios μ_eff(F)∕μ₀ and D_eff(F)∕D₀ in Figs. 2a, 2b. The presence of periodic entropy barriers slows down the transitions between neighboring compartments. This is the reason why the effective mobility and diffusion coefficient are smaller than μ₀ and D₀ at small F. The higher is the entropy barrier, the stronger is the effect.

Figure 2.

Dependences of the effective mobility (a), diffusion coefficient (b), and function w(F) defined in Eq. 2.1 (c) on the driving force obtained from Brownian dynamics simulations. Different symbols show the results found at three different values of the opening radius.

The driving force suppresses the slowdown due to the entropy barriers. As F→∞, the effective mobility and diffusion coefficient tend to μ₀ and D₀, respectively. This happens because in this limiting case the particle spends all the time in the cylinder connecting the openings shown in Fig. 1c (see below for more details). Thus, the particle effectively moves in a tube of constant diameter where its mobility and diffusion coefficient are equal to μ₀ and D₀ independently of the driving force. As shown in Fig. 2a, effective mobilities monotonically increase from μ_eff(0) to μ₀ as F goes from zero to infinity. Dependences D_eff(F) shown in Fig. 2b are more complex. Functions D_eff(F) have maximums and approach their large-F limiting value D₀ from above. Again, the higher is the entropy barrier (the smaller is the opening), the stronger is the effect.

A similar behavior of the effective mobility and diffusion coefficient has been reported in the literature on Brownian motion in a one-dimensional regular (nonentropy) periodic potential¹³ as well as in periodic entropy potentials in quasi-two-dimensional systems (slits of periodically varying width).^{6, 8a} However, in a tube formed by cylindrical compartments, dependences of the effective mobility and diffusion coefficient on the driving force are qualitatively different. In such a tube μ_eff(∞)<μ_eff(0), and the effective mobility is a monotonically decreasing function of the driving force.^{5h, 9a} The effective diffusion coefficient in such a tube monotonically increases with the driving force and diverges as the driving force tends to infinity; its large-F asymptotic behavior is given by D_eff(F)∝F².^5h

A strong driving force induces localization of the particle in the cylinder connecting the openings [Fig. 1c]. To study this effect, we computed the mean times spent by the particle outside (out) and inside (in) the cylinder, ⟨τ_out(F)⟩ and ⟨τ_in(F)⟩. We use these times and the ratio of the fractions of the compartment volume outside and inside the cylinder, V_out∕V_in=2(R²−a²)∕(3a²) to introduce function w(F),

$$w\left(F\right)=\frac{⟨{\tau }_{\text{out}}\left(F\right)⟩V_{\text{in}}}{⟨{\tau }_{\text{in}}\left(F\right)⟩V_{\text{out}}},$$ (2.1)

which characterizes the degree of localization. At F=0 because of the ergodicity the ratio of the mean times is identical to the volume ratio,

$$\frac{⟨{\tau }_{\text{out}}\left(0\right)⟩}{⟨{\tau }_{\text{in}}\left(0\right)⟩}=\frac{V_{\text{out}}}{V_{\text{in}}}.$$ (2.2)

Therefore, w(0)=1. Dependences presented in Fig. 2c show that functions w(F) monotonically decrease from unity to zero when the driving force increases from zero to infinity. The fact that w(F) tends to zero as F→∞ implies localization of the particle in the cylinder connecting the openings [Fig. 1c]. The results presented in Fig. 2c show how the degree of localization depends on the driving force at different values of the opening radius. Similar localization induced by the driving force has been reported in quasi-two-dimensional systems with periodic entropy barriers (slits of periodically varying width).^{6b, 6e}

TRANSIT TIME

One can gain additional insight into the effect of the driving force on the particle motion in the tube by analyzing the transit time of the particle between neighboring openings. This is the goal of the present section.

Mean transit time at F=0

Several approximate formulas for the mean transit time between neighboring openings ⟨τ(0)⟩ can be obtained at F=0 using different approaches to the problem. When the openings are small (high entropy barriers) the mean transit time is given by the formula suggested by Berezhkovskii, Zitserman, and Shvartsman^{5a, 5b} (BZS), ⟨τ(0)⟩_BZS=V_comp∕(4D₀a), where V_comp is the volume of the compartment. Since $V_{\text{comp}}=\left(2\pi R^3∕3\right)\left(2+a^2∕R^2\right)\sqrt{1-a^2∕R^2}$, we obtain

$${⟨\tau \left(0\right)⟩}_{\text{BZS}}=\frac{\pi R^3}{6a{D}_0}\left(2+\frac{a^2}{R^2}\right)\sqrt{1-\frac{a^2}{R^2}}.$$ (3.1)

This formula is asymptotically exact as a→0. In this limiting case, the formula takes the form ⟨τ(0)⟩_BZS=πR³∕(3aD₀), which was used in Ref. 5a, 5b.

One can evaluate the mean transit time at moderate-to-large openings (low-to-moderate entropy barriers) using different versions of the Fick–Jacobs equation. Conventional Fick–Jacobs (FJ) equation¹⁴ leads to

$${⟨\tau \left(0\right)⟩}_{\text{FJ}}=\frac{R^2}{3D_0}\left(2+\frac{a^2}{R^2}\right)\sqrt{1-\frac{a^2}{R^2}}\text{ln}\frac{1+\sqrt{1-a^2∕R^2}}{1-\sqrt{1-a^2∕R^2}}.$$ (3.2)

Using the generalized Fick–Jacobs equation with the position-dependent diffusion coefficient suggested by Zwanzig¹ (Zw),

$$D_{\text{Zw}}\left(x\right)=\frac{D_0}{1+{\left[dr\left(x\right)∕dx\right]}^2∕2},$$ (3.3)

where r(x) is the tube radius as a function of the x-coordinate measured along the centerline of the tube, one can obtain

$${⟨\tau \left(0\right)⟩}_{\text{Zw}}=\frac{R^4}{6a^2{D}_0}\left(2+\frac{a^2}{R^2}\right)\sqrt{1-\frac{a^2}{R^2}}\left[\sqrt{1-\frac{a^2}{R^2}}+\frac{3a^2}{2R^2}\text{ln}\frac{1+\sqrt{1-a^2∕R^2}}{1-\sqrt{1-a^2∕R^2}}\right].$$ (3.4)

If the position-dependent diffusion coefficient in the generalized Fick–Jacobs equation is given by the formula suggested by Reguera and Rubi² (RR),

$$D_{\text{RR}}\left(x\right)=\frac{D_0}{\sqrt{1+{\left[dr\left(x\right)∕dx\right]}^2}},$$ (3.5)

one can obtain the following formula for the mean transit time:

$${⟨\tau \left(0\right)⟩}_{\text{RR}}=\frac{2R^3}{3a{D}_0}\left(2+\frac{a^2}{R^2}\right)\left(1-\frac{a^2}{R^2}\right),$$ (3.6)

In Table 1, we compare predictions for the mean transit time given by different formulas, Eqs. 3.1, 3.2, 3.4, 3.6 with the mean transit time ⟨τ(0)⟩ obtained from Brownian dynamics simulations. Comparison is made at the three values of the opening radius. One can see excellent agreement between ⟨τ(0)⟩ and ⟨τ(0)⟩_BZS at a∕R=0.1 and good agreement between ⟨τ(0)⟩ and both ⟨τ(0)⟩_BZS and ⟨τ(0)⟩_RR at a∕R=0.3 and 0.5.

Table 1.

The ratios of the mean transit times given in Eqs. 3.1, 3.2, 3.4, 3.6 to this time obtained from Brownian dynamics simulations. The ratios are computed at three different values of the opening radius.

a∕R	⟨τ⟩BZS∕⟨τ(0)⟩	⟨τ⟩RR∕⟨τ(0)⟩	⟨τ⟩Zw∕⟨τ(0)⟩	⟨τ⟩FJ∕⟨τ(0)⟩
0.1	0.99	1.26	3.43	0.37
0.3	0.92	1.12	1.43	0.66
0.5	0.97	1.07	1.15	0.81

Effect of the driving force

In the presence of the driving force, the mean transit time, ⟨τ(F)⟩ decreases compared to its value at F=0, ⟨τ(0)⟩. As F→∞, the mean transit time tends zero. The asymptotic behavior of ⟨τ(F)⟩ at large values of the driving force is given by the ratio l∕v_eff(F). In this limiting case, v_eff(F) is equal to μ₀F, and we have

$$⟨\tau \left(R\right)⟩\to \frac{l}{{\mu }_{0}F}=\frac{2\sqrt{R^2-a^2}}{{\mu }_{0}F},F\to \infty .$$ (3.7)

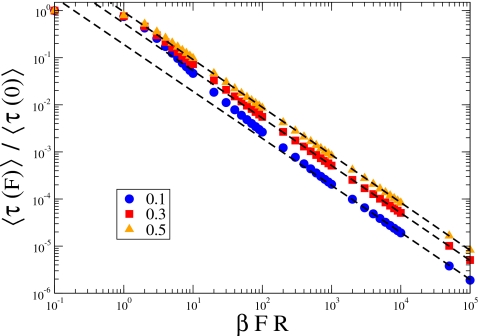
This dependence is inherent in biased diffusion of a particle in a tube of constant diameter at sufficiently large driving force. The decrease of the mean transit time in the presence of the driving force is illustrated in Fig. 3 in which we presented the ratios ⟨τ(F)⟩∕⟨τ(0)⟩ obtained from simulations at the three values of the opening radius. Dashed lines represent the large-F asymptotic behavior of the ratios,

$$\frac{⟨\tau \left(F\right)⟩}{⟨\tau \left(0\right)⟩}=\frac{2\sqrt{R^2-a^2}}{{\mu }_{0}F⟨\tau \left(0\right)⟩},F\to \infty .$$ (3.8)

The results presented in Fig. 3 show that the smaller is the radius of the openings, the larger values of the driving force are required for transition of the ratio to its asymptotic form, Eq. 3.8.

Figure 3.

The mean transit time between neighboring openings as a function of the driving force. Different symbols show the result obtained from Brownian dynamics simulations at three different values of the opening radius. Dashed lines show the asymptotic behavior at large driving force, Eq. 3.8.

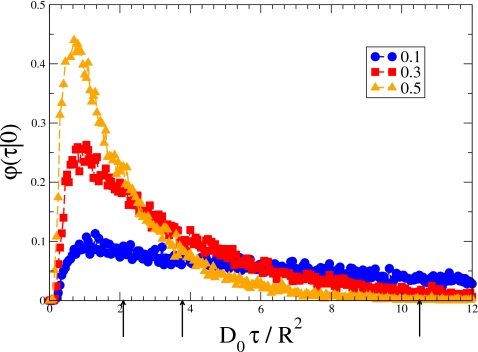
The probability density of the transit time, φ(τ|F), is a bell-shaped function. In Fig. 4, we show φ(τ|0) obtained from Brownian dynamics simulations at the three values of the opening radius. The distribution bell shape gets narrower as the driving force increases. As F→∞, the probability density tends to the delta function centered at ⟨t(F)⟩ given in Eq. 3.7,

$$\phi \left(\tau |F\right)\to \delta \left(\tau -\frac{2\sqrt{R^2-a^2}}{{\mu }_{0}F}\right),F\to \infty .$$ (3.9)

As a consequence, the nth moment of the transit time ⟨τⁿ(F)⟩ tends to ⟨τ(F)⟩ⁿ. The moment ratios presented in Tables 2, 3, 4 illustrate the narrowing of the distribution of the transit time in tubes formed by spherical compartments with different connecting openings. These results show that the smaller is the opening radius, the slower the probability density approaches its asymptotic form, Eq. 3.9.

Figure 4.

The probability density of the transit time between neighboring openings in the absence of the driving force at the three values of the opening radius: circles, squares, and triangles correspond to the opening radii equal to 0.1R, 0.3R, and 0.5R, respectively. The arrows indicate corresponding values of D₀⟨τ(0)⟩∕R².

Table 2.

The ratios of the transit time moments as functions of the driving force. The moments are obtained from Brownian dynamics simulations run in the tube formed by spherical compartments with the opening radius equal to 0.1R.

βFR	⟨τ(F)2⟩∕⟨τ(F)⟩2	⟨τ(F)3⟩∕⟨τ(F)⟩3	⟨τ(F)4⟩∕⟨τ(F)⟩4
0	1.91	5.50	20.91
1	1.88	5.23	19.08
10	1.39	2.68	6.83
102	1.09	1.33	1.81
103	1.01	1.05	1.12
104	1.00	1.00	1.00
105	1.00	1.00	1.00

Table 3.

The ratios of the transit time moments as functions of the driving force. The moments are obtained from Brownian dynamics simulations run in the tube formed by spherical compartments with the opening radius equal to 0.3R.

βFR	⟨τ(F)2⟩∕⟨τ(F)⟩2	⟨τ(F)3⟩∕⟨τ(F)⟩3	⟨τ(F)4⟩∕⟨τ(F)⟩4
0	1.79	4.81	17.16
1	1.75	4.57	15.84
10	1.18	1.68	2.82
102	1.02	1.08	1.19
103	1.00	1.00	1.01
104	1.00	1.00	1.00
105	1.00	1.00	1.00

Table 4.

The ratios of the transit time moments as functions of the driving force. The moments are obtained from Brownian dynamics simulations run in the tube formed by spherical compartments with the opening radius equal to 0.5R.

βFR	⟨τ(F)2⟩∕⟨τ(F)⟩2	⟨τ(F)3⟩∕⟨τ(F)⟩3	⟨τ(F)4⟩∕⟨τ(F)⟩4
0	1.73	4.47	15.45
1	1.67	4.09	13.21
10	1.14	1.51	2.29
102	1.01	1.05	1.10
103	1.00	1.00	1.00
104	1.00	1.00	1.00
105	1.00	1.00	1.00

The convergence of the moment ratio to unity at large values of the driving force, Tables 2, 3, 4, is in sharp contrast with the divergence of the similar ratios of the transit time moments in tubes formed by cylindrical compartments.^5h In such tubes when F is large enough, the probability density of the transit time has a slowly decaying tale. The tale is due to the intermittency in the particle transitions between neighboring openings. Because of this tale, the moment ratio diverges as F→∞. The large-F asymptotic behavior of the moment ratio is given by ⟨τⁿ(F)⟩∕⟨τ(F)⟩ⁿ∝Fⁿ⁻¹.^5h Thus, the difference between the tubes formed by spherical and cylindrical compartments manifests itself not only in qualitatively different behavior of the effective mobilities and diffusion coefficients considered as functions of the driving force. The difference also manifests itself in how the driving force affects the particle transit time between the neighboring openings.

CONCLUDING REMARKS

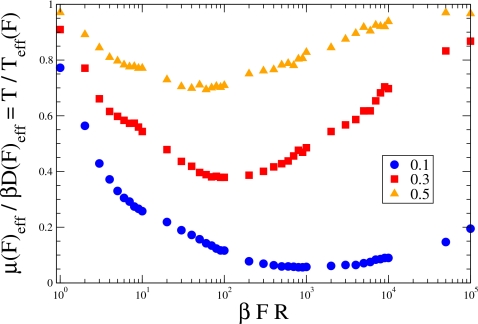
Having in hand a formula for the mean transit time in the absence of the driving force, ⟨τ(0)⟩, Eq. 3.1 or Eq. 3.6, one can find the effective diffusion coefficient at F=0 using the relation D_eff(0)=l²∕(2⟨τ(0)⟩). Then one can find the small-F limiting value of the effective mobility using the Einstein relation, μ_eff(0)=βD_eff(0). The large-F limiting values of the effective mobility and diffusion coefficient, μ₀ and D₀ also satisfy the Einstein relation, μ₀=βD₀. However, in between the two limits, the Einstein relation is not fulfilled, and the ratio μ_eff(F)∕(βD_eff(F)) may be much smaller than unity. This is illustrated in Fig. 5 where we have used μ_eff(F) and D_eff(F) obtained from our Brownian dynamics simulations.

Figure 5.

The ratio μ_eff(F)∕(βD_eff(F))=T∕T_eff(F) as a function of the driving force. Different symbols represent the result obtained from Brownian dynamics simulations at three different values of the opening radius.

Introducing the notation k_BT_eff(F) for the ratio of the effective diffusion coefficient to the effective mobility, D_eff(F)∕μ_eff(F)=k_BT_eff(F), where T_eff(F) can be interpreted as an effective temperature that depends on the driving force, we can write the ratio μ_eff(F)∕(βD_eff(F)) as μ_eff(F)∕(βD_eff(F))=T∕T_eff(F). The results presented in Fig. 5 show that the effective temperature is a nonmonotonic function of the driving force that approaches real temperature T as F→0 and ∞. In between, the effective temperature may be much higher than the real temperature. The smaller is the opening radius, the larger is the maximum value of T_eff(F), and the stronger driving force is required to reach the maximum. Similar nonmonotonic dependence of the effective temperature has been reported in quasi-two-dimensional systems with periodic entropy barriers (slits of periodically varying width).^6e

In summary, in the present paper we report on a detailed numerical study of the driving force effect on the effective mobility and diffusion coefficient of a point Brownian particle in a tube formed by identical spherical compartments. We also study localization of the particle in the central part of the tube induced by the driving force, as well as how the driving force affects the transit time between neighboring openings. We found that the driving force effect on transport in tubes formed by spherical compartments in many respects is similar to that on transport in one-dimensional regular (nonentropy) potentials¹³ and in quasi-two-dimensional systems with periodic entropy potentials.^{6, 8} However, the effect differs qualitatively from that in tubes formed by identical cylindrical compartments.^{5h, 9a}