Brain Networks Maintain a Scale-Free Organization across Consciousness, Anesthesia, and Recovery: Evidence for Adaptive Reconfiguration

Abstract

Background

Loss of consciousness is an essential feature of general anesthesia. Although alterations of neural networks during anesthesia have been identified in the spatial domain, there has been relatively little study of temporal organization.

Methods

Ten normal male volunteers were anesthetized with an induction dose of propofol on two separate occasions. The duration of network connections in the brain was analyzed by multichannel electroencephalography and the minimum spanning tree method. Entropy of the connections was calculated based on Shannon entropy. The global temporal configuration of networks was investigated by constructing the cumulative distribution function of connection times in different frequency bands and different states of consciousness.

Results

General anesthesia was associated with a significant reduction in the number of network connections, as well as significant alterations of their duration. These changes were most prominent in the delta bandwidth and were also associated with a significant reduction in entropy of the connection matrix. Despite these and other changes, a global “scale-free” organization was consistently preserved across multiple subjects, multiple anesthetic exposures, multiple states of consciousness and multiple frequencies of the electroencephalogram.

Conclusions

Our data suggest a fundamental principle of temporal organization of network connectivity that is maintained during both consciousness and anesthesia, despite local changes. These findings are consistent with a process of adaptive reconfiguration during general anesthesia.

Introduction

In the early 18^th century, mathematician Leonhard Euler solved the problem of the seven bridges of Königsberg, the Prussian city that spanned both sides of the Pregel river. The land mass of Königsberg, as well as several large islands, were connected by seven bridges—the puzzle consisted in finding a way to walk through the city while crossing each bridge only once. Euler mathematically demonstrated that no such path existed and by doing so put forth the first theorem in what is now known as graph theory. A “graph” could be used to solve this problem, since each land mass could be represented as a “node” (or “vertex”) and each bridge connecting two nodes could be represented as an “edge” (or “arc”) (Table 1).

Table 1. Graph Theory Glossary.

A definition of terms relating to graph theory that are used throughout the text.

Term	Definition
Node (or vertex)	A point on a graph.
Edge (or arc)	A connection between nodes.
Degree	The number of connections that link to the rest of network.
Power law behavior	The mathematical expression of a probability distribution that is invariant in the range of small or large values, which indicates that it lacks scale.
Scale-free network	A network with a power law degree distribution, in which very large scale degrees still exist with certain nodes being densely connected and serving as “hubs” like the airport system.
Exponential (Gaussian) behavior	When a distribution is determined by its mean and variance, leading to the bell-shaped curve in which the probability of an event at small or large scales exponentially decays.
Random network	A network in which the probability of nodes being connected is equal, resulting in a Gaussian and symmetrically centered degree distribution.
Adaptive reconfiguration	The process by which the brain maintains an overall optimal state of the network (such as scale-free organization), despite local changes.
Minimal Spanning Tree	A graph that connects all N nodes, without forming loops and with the shortest edge weights over N-1 connections. The reconstructed network shares topological properties with the original network.

Similarly, graph theory is now used to represent connectivity in the brain, where neural regions are the “nodes” and the relationship between them the “edges.”^1,2 The graphs used to represent functional networks in the brain have a particular organization that is thought to be “scale free.” Scale-free organization can be identified mathematically when a system follows a “power law” versus an exponential or Gaussian behavior (Table 1). Unlike a random network, scale-free networks following a power law have a number of important hubs that are more densely connected (such as an airport system). This scale-free property has been widely observed in both the structure and function of the human brain and is thought to enable rapid synchronization, rapid information transfer, minimal wiring costs, and a balance between local segregation and global integration.^1–8

General anesthesia induces a profound alteration of consciousness and is associated with changes in local and global networks in the brain.^9,10 Altered functional connectivity during anesthesia has been demonstrated within neural networks involving the thalamocortical and corticocortical systems^11,12 and may be dose-dependent.¹³ A recent functional magnetic resonance imaging study reported that brain activities related to primary sensory areas and the default mode network were not significantly different after exposure to low concentrations of sevoflurane anesthesia, while higher order cognitive regions were significantly altered.¹⁴ It was suggested that functional brain organization is preserved under low levels of anesthesia, which is consistent with previous studies demonstrating a preserved default mode network even under deep anesthesia in monkeys.¹⁵

In order to investigate the activity of neural networks during general anesthesia, we developed a novel technique derived from graph theory that uses objective criteria to reconstruct electroencephalographic channel connections based on the minimum spanning tree (MST) method. Since general anesthesia is associated with altered functional connectivity and loss of consciousness, we hypothesized that the optimal scale-free organization of human brain networks would be disrupted after induction with propofol. Contrary to our hypothesis, we found that—despite significant local network changes—a global scale-free organization was preserved across consciousness, anesthesia, and recovery. These findings are consistent with “adaptive reconfiguration,” a previously identified process¹ in which the brain maintains a globally optimal state (such as scale-free organization) despite local changes. The implications of these findings for the mechanisms of anesthetic-induced unconsciousness are discussed.

Materials and Methods

Methodological Overview

After Institutional Review Board approval (Asan Medical Center, Seoul, Korea) and informed consent, ten normal human participants were studied on two separate occasions with 21-channel electroencephalography. Three states were investigated: 1) baseline consciousness, 2) general anesthesia, defined as loss of response to a command after induction with 2mg/kg of the intravenous agent propofol, and 3) recovery from general anesthesia, defined by a return of responsiveness. These electroencephalographic data were originally gathered for a study of the frontoparietal system,¹⁰ but underwent a completely different analysis for the current study.

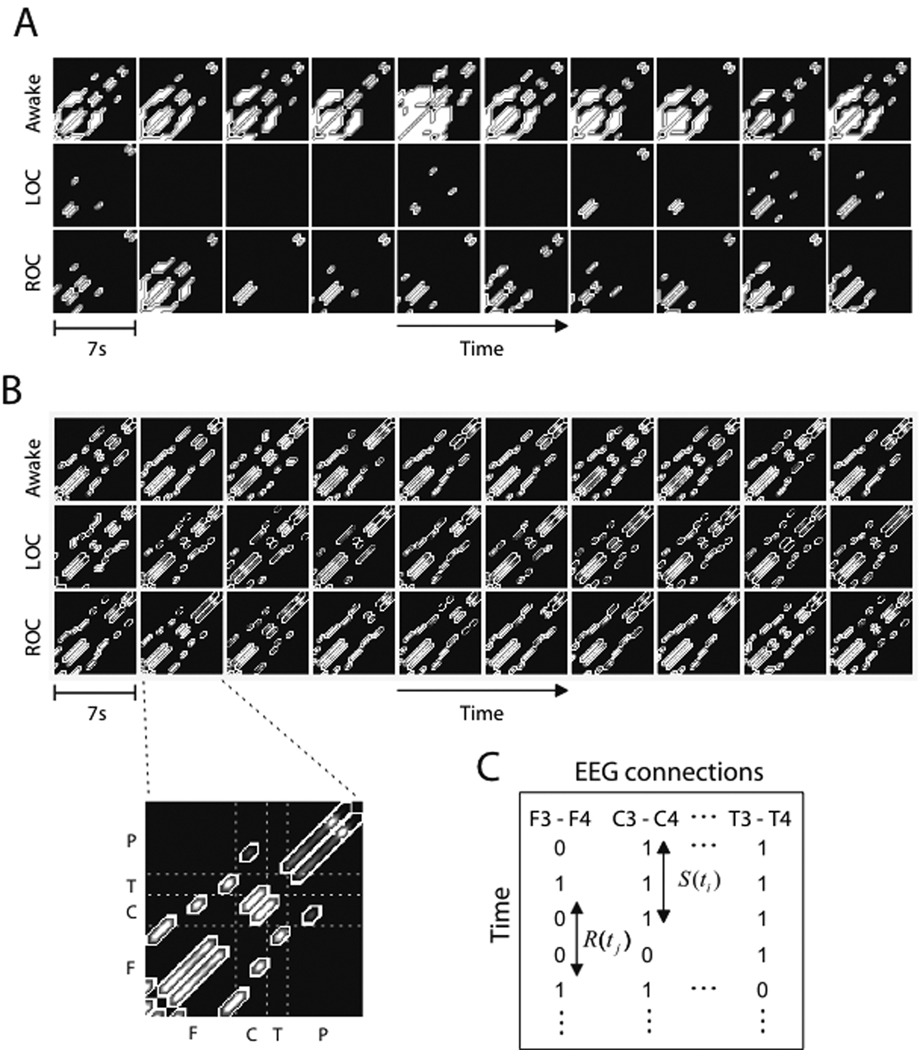
Since previous work has focused on spatial network attributes, the focus of this investigation was temporal organization. In order to study the temporal evolution of network connectivity among electroencephalographic channels, the MST method and the moving window method were used.^16,17 The MST is the skeleton of a complex network that reflects the primary edge connections of the original network.^18–20 We constructed a sequence of MSTs from the moving electroencephalographic windows, then examined the temporal evolution of edge connections during different states of consciousness (See Methods: MST). The conventional method of defining a connection, which requires a subjective threshold for connection strength, is not appropriate for general anesthesia because of the significant change of average electroencephalographic coherence. If a threshold is set in the baseline state, the construction of an edge connection will not be optimal in the unconscious state, showing only a few small islands or nothing at all on a connection matrix. This is demonstrated in Figure 1A. The white patterns in Figure 1A denote the connected channels, for which the Pearson correlation coefficients are above the threshold; the black patterns represent the unconnected channels below the threshold.

Figure 1. Analysis of networks using a conventional versus the minimum spanning tree method.

(A) This demonstrates the conventional method of using a threshold for connections, resulting in some connection matrices with only small islands (denoted with white) or no connections at all because of significantly different mean correlation coefficients across states. As an example, the first ten connection matrices of the alpha band electroencephalograph for three states are presented (each box represents a 7 second non-overlapping window). The connection matrices are constructed with a zero-lag Pearson correlation coefficient and a threshold. (B) In this example, functional connections were constructed by the minimum spanning tree method in a 7 second non-overlapping window. The connections on the minimum spanning tree are denoted with gray colored patterns on the 21 by 21 connection matrix with elements $0\le d_{\mathit{\text{ij}}}\le \sqrt{2}$ (F: Fp1, Fp2, F3, F4, F5, F6, F7, F8, Fz, C: C3, C4, Cz, T: T7, T8, P: P3, P4, P5, P6, P7, P8, Pz). (C) Each type of electroencephalographic channel connection and its connectivity (denoted as 1 for connected and 0 for disconnected) is represented over time on a newly defined connection matrix. The matrix represents the connectivity among electroencephalographic channels over the entire recording period. Each row on the matrix corresponds to the electroencephalographic channel connection for each minimum spanning tree. S(t) denotes the time a connection lasts, and R(t) denotes the time required to re-establish a connection once it has been terminated. LOC=loss of consciousness; ROC=return of consciousness; EEG = electroencephalography

In order to investigate connection time, we segmented the raw 21-channel electroencephalography into 7s windows moving at 40ms and then applied the MST method to assess network relationships using Pearson correlation. The output for each window is a set of primary network connections on the MST that can be shown to be connected or disconnected over time. Figure 1B demonstrates an example of MST sequences, which are constructed with alpha band electroencephalographic data for three states. The gray patterns denote the connected channels that have distance values, while the black patterns denote unconnected channels. By assigning a “1” to maintained connections and “0” to terminated connections, a connection matrix can be generated with sequential MSTs. Figure 1C is a schematic depicting the generation of such a connection matrix, with two temporal variables of interest: 1) the duration of an edge connection, S(t), (i.e., the Survival time of a connection) and 2) the reconnection time, R(t), (i.e., the time required to re-establish a connection once it has been terminated). Since we ultimately found a reciprocal relationship between connection and reconnection times, only connection time data are presented here. We constructed a connection matrix and calculated “connection entropy,” which is based on the concept of Shannon Entropy and quantifies the complexity of the temporal configuration of network connections. This enables the direct comparison of temporal configurations of brain functions for different conscious states.

In order to investigate the overall temporal organization of network connections, the cumulative density function of connection times was examined for different states and all frequency bands. The maximum likelihood method and Kolmogorov-Smirnov (KS) statistics were used to fit the cumulative density function of connection times. To find the best fit for the connection time data we used the KS statistics and the root-mean-square error (RMSE) method for the alternative models (power law, stretched exponential, log-normal and exponential distribution models). Power law models reflect a scale-free organization.

Drug Administration and Electroencephalography

Each volunteer fasted for 8 hours before study drug administration. We excluded volunteers who had known allergy to propofol (AstraZeneca, London, United Kingdom), medical problems, abnormal laboratory findings with clinical significance, or a body weight that was not within 30% of ideal. The average age was 23 ± 2 yr (range, 20 – 28 yr).

An 18-gauge angio-catheter was placed in a vein of the antecubital area. Subjects received an initial intravenous bolus of 2.0 mg/kg of propofol over 20 seconds. Time to loss of consciousness was determined every 5 seconds by the loss of response to verbal command. If respiratory depression occurred, lungs were manually ventilated with 100% oxygen via facemask, to maintain an end-tidal carbon dioxide concentration of 35–45 mmHg. Manual ventilation was discontinued when the spontaneous respiratory rate exceeded 12 breaths/min and end-tidal carbon dioxide was less than 45 mmHg. Time to return of consciousness after the intravenous bolus of 2.0 mg/kg of propofol was determined by the recovery of response to verbal command. Upon completion of the measurement of electroencephalographic activity, subjects were transferred to the postanesthesia care unit, breathing room air. They were monitored with electrocardiography, pulse oximetry and non-invasive blood pressure measurement for 1 hour in recovery. If vital signs were stable and full recovery from sedation was confirmed, the subject was discharged. Each subject carried out the same experimental protocol separated by a 7-day washout period.

The electroencephalographs of 21 channels (Fp1, Fp2, F3, F4, F5, F6, F7, F8, Fz, C3, C4, Cz, T7, T8, P3, P4, P5, P6, P7, P8, Pz referenced by A2, 10–20 system) were recorded on the bed with closed eyes, with a sampling frequency of 256 Hz and 16-bits analog-to-digital precision by WEEG-32^®(LXE3232-RF, Laxtha Inc., Daejeon, Korea). Baseline electroencephalography was recorded for 5 min before an intravenous bolus of propofol. Electroencephalography was recorded continuously during and after the intravenous bolus of propofol, and up to 10 min after return of consciousness. The same procedure was repeated for the same 10 normal male subjects one week later.

Minimum Spanning Tree (MST)

MST is one way to define global network relationships among channels for electroencephalographic data. The MST is defined as the connected, loopless subgraph consisting of (N-1) links reaching all N nodes while minimizing the sum of the relative edge weights. For satisfying the minimum weight condition in the linkage of N channels, each electroencephalographic channel is linked to the most closely correlated channel without making a loop in the reconstructed network. In this study, therefore, the edge connection and disconnection for a pair of channels was defined as whether the “closest relationship” on the MST was maintained or not; we limited network reconstruction to the 20 most closely correlated channels, reflecting the principal network structure. The MST structure also shares similar topological properties with the original network, such as betweenness centralities, clustering coefficient and degree distribution.^18–20

First, we defined a distance matrix based on the Pearson correlation coefficients, −1 ≤ C_ij ≤ 1, among 21 electroencephalographic channels (i, j = 1, …, N. N=21). Zero-lag correlations were studied because they enabled a non-parametric analytic technique. Next, the N×N matrix of correlation coefficients was transformed into an N×N distance matrix with elements $d_{\mathit{\text{ij}}}=\sqrt{2(1-|C_{\mathit{\text{ij}}}|)}$, such that $0\le d_{\mathit{\text{ij}}}\le \sqrt{2}$, which were introduced by Mantegna.²¹ By this definition, the elements d_ij satisfy the axioms for the metric distances, as well as those for ultrametric distances (a stronger triangular inequality), producing a tree-like hierarchical connection structure among all nodes. For the metric distance, the difference of negative or positive correlation coefficient was ignored. The MST is constructed by connecting all the N channels with N-1 connections such that the sum of all connections, ∑_(i,j) d_ij, is a minimum. If we assume that no electroencephalographic channels are the same, it enables us to define the unique network connections for a given multichannel electroencephalographic dataset by the minimum condition. This method is advantageous because it avoids subjective parameter decisions in the conventional way, reflects the original network with small number of connections (N-1) instead of (N×N), and maintains topological attributes. Therefore, we were able to construct the sequence of edge connections corresponding to all electroencephalographic windows, irrespective of significant change of average electroencephalographic coherence during general anesthesia.

Connection Entropy

To quantify the complexity of a connection matrix, we used a measure based on the definition of Shannon entropy. This process quantifies the temporal complexity of network connectivity for multi-channel electroencephalographs and enabled us to quantitatively compare the temporal configurations of brain functions for different conscious states.

For a connection matrix, each type of electroencephalographic connection derived from the MST (each column on the connection matrix) is considered as an event among all possible events (N), consisting of edge connections occurring for a given electroencephalogram. The frequency of an event is counted by the number “1” in the corresponding column of the connection matrix. The probability of an event (for instance, an edge connection between channel i and j) is defined as p_ij = n_ij / M, where n_ij is the frequency of an event (i,j) and M is the total number of samples (that is, the total number of segmented windows, M=7,325 for a 5 minute epoch with a 7 second window size moving every 40 ms). The connection entropy is defined by the Shannon entropy, $H=-{\displaystyle \sum _{\mathit{\text{ij}}=1}^N{p}_{\mathit{\text{ij}}}{\text{log}}_2{p}_{\mathit{\text{ij}}}}$.

If the chance of an edge connection is equiprobable over all pairs of electroencephalographic channels, the connection entropy has a higher value. On the other hand, if the connections are dominated by a few pairs of electroencephalographic channels, the connection entropy has a smaller value. This procedure was applied to the electroencephalographic data after Fourier-based band-pass filtering of the following frequency bands in the three different states of consciousness: delta (0.5–4Hz), theta (4–8Hz), alpha (8–13Hz), beta (13–35Hz) and original (0.5–55Hz). High frequency (gamma) activity (>35Hz) was not analyzed separately in order to avoid electromyographic artifact.

Power Law Test

A statistical test of power-law distribution was performed, which would reflect scale-free organization. First, we used the maximum likelihood method to fit the cumulative density function of connection times. Second, we used the KS statistic to estimate where the scaling region begins (> X_min). This method gives the empirically best scaling region by optimizing the KS goodness of fit statistic. Third, we tested the goodness of fit by the KS statistic, in which the null hypothesis is that the empirical data follow the hypothesized power law distribution. The KS statistic calculates the maximum discrepancy between the empirical distribution and the theoretical one; here if statistical significance p>0.01, the null hypothesis of a power law model cannot be rejected with the significance level of 99%. Finally, we compared the alternative models (power law, stretched exponential, log-normal and exponential distribution models) for the best fit to the connection times data, with the following procedure: 1) for fitting a given data with the power-law model, we performed the first and the second processes above to get the empirically best scaling region in the data, 2) RMSE was calculated over the optimal scaling region, 3) we applied the stretched exponential, log-normal and exponential models, respectively, for fitting the same data, and 4) we compared the RMSE of the all fitting models within the optimal scaling region (> X_min). We used the Matlab and R codes released for the first to the third process above; for the RMSE calculation of all fitting models the Matlab statistics toolbox (The MathWorks, Inc., Natick, MA) was used.

Random Connections

To compare the network connectivity of electroencephalographs with a random process, we generated a random electroencephalographic dataset. The values of each channel were randomly shuffled by a Fourier based-phase randomized method,²² eliminating the original correlation between electroencephalographic channels and within each electroencephalographic channel. Next, a connection matrix of randomized electroencephalograms was constructed in the same way as described above for the actual electroencephalographic data. The connection duration was calculated for the connection matrices generated from randomized electroencephalographs. The distributions of connection times for the randomized data were compared with those of original electroencephalograms in different states.

Statistical Analysis

In addition to the statistical tests used to analyze distribution patterns, the connection times and the connection entropy were compared across three states of consciousness (baseline, unconscious, recovery) with 20 electroencephalographic datasets (10 subjects undergoing two trials each). The significance was assessed by a repeated measures one-way analysis of variance with post-hoc analysis using Scheffé’s multi-comparison; p<0.05 was considered significant. The post-hoc Scheffé’s test is considered more conservative then the post-hoc Tukey test. A formal statistical consultation was obtained at the University of Michigan and the Matlab statistical toolbox was used. Data are expressed as mean ± standard deviation.

Results

Local Network Connections and Connection Times

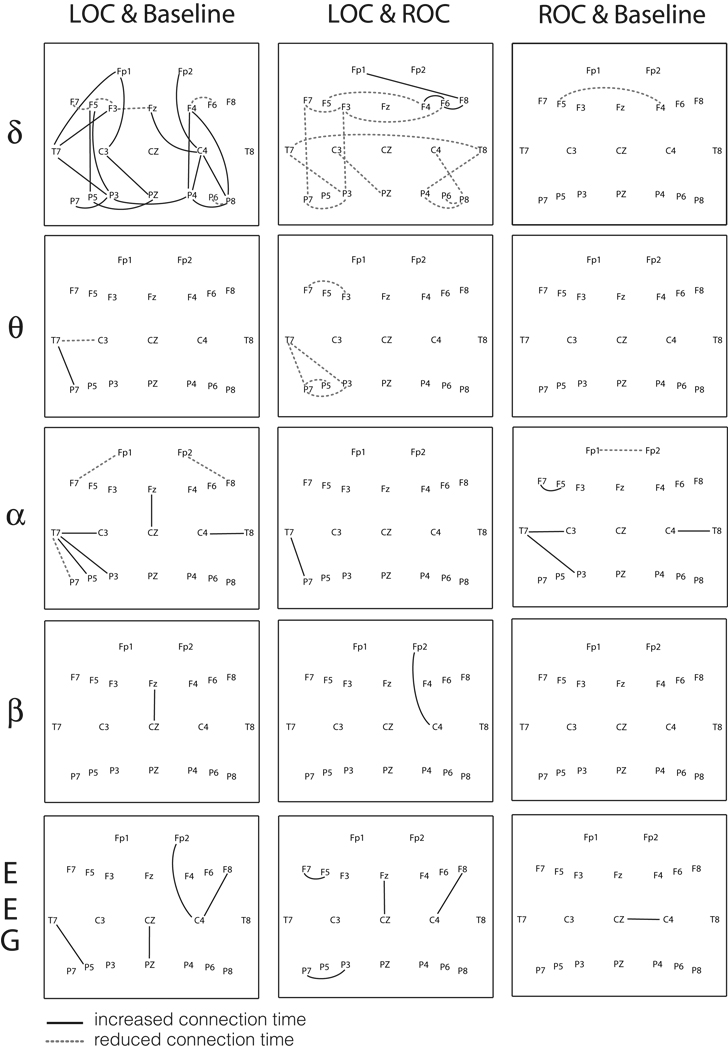
Using the moving window method and the MST method, we constructed connection matrices for temporal analysis of edge connections during different states of consciousness. After induction of general anesthesia, the duration of local edge connections was significantly changed in the transition of states across different frequency bands (p<0.05, Scheffé’s post-hoc test). For each pair of electroencephalographic channels, the 20 connection times defined by the MST were compared across three states. If the connection time was significantly different than the mean value, the edge between channels was denoted with dotted and solid lines on a 2-dimensional scalp map (Figure 2). Dotted lines denoting significantly reduced connection times and solid lines denoting significantly increased connection times are presented in Figure 2 across different frequency bands (p<0.05, Scheffé’s post-hoc test). Although there were numerous changes, the delta band demonstrated the most significant alterations of local connections after loss and return of consciousness.

Figure 2. Significant changes of the connection time at local functional connections.

The solid lines and dotted lines indicate significant differences of connection time comparing the three states for each pair of electroencephalographic channels (p<0.05, Scheffé’s post-hoc test). LOC=loss of consciousness; ROC=return of consciousness; EEG=electroencephalograph. The solid line in each figure means that LOC > Baseline for the comparison of LOC & Baseline, ROC > LOC for the comparison of LOC & ROC, and ROC > Baseline for the comparison of ROC & Baseline. The dotted line indicates the reverse. The channel names are positioned by the international 10–20 system of electrode placement.

Entropy of the Connection Matrix

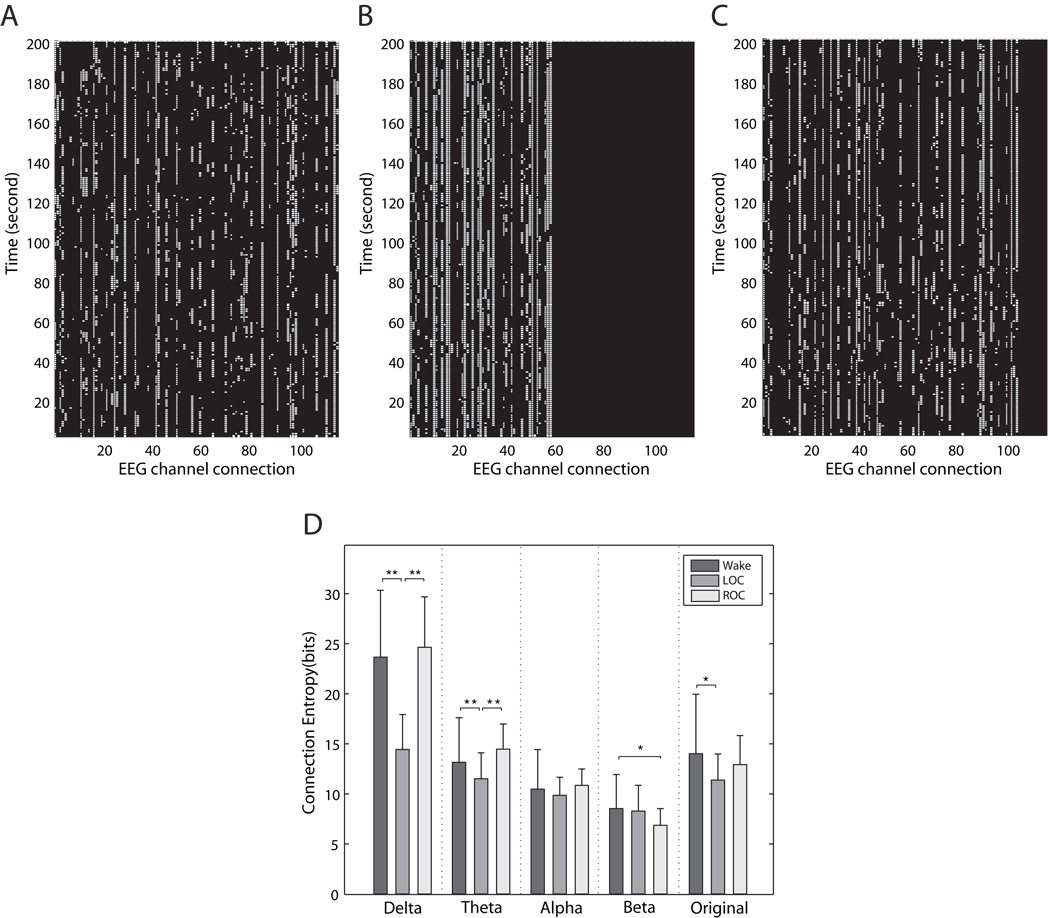
Changes in duration of local connections in the different bandwidths during anesthesia were paralleled by changes in the overall entropy of the connection matrices. Figure 3 demonstrates connection matrices for the delta band of the electroencephalogram during consciousness (3A), anesthesia (3B), and recovery (3C). We focused on the delta band because of the numerous local changes demonstrated in Figure 2. The connection entropy of the delta and theta bands was significantly decreased after induction of general anesthesia and returned again after recovery of consciousness (p<0.05, Scheffé’s post-hoc test; p=7.9e-10 for delta band, p=0.0004 for theta band) (Figure 3D). The connection entropy of the original electroencephalogram (0.5–55Hz) was also significantly reduced after loss of consciousness (p<0.05, Scheffé’s post-hoc test). The connection entropies of all frequency bands were completely discriminated from that of randomized electroencephalographs (Mean±SD = 65.27±0.2 bits), with significantly lower entropies than that of randomized electroencephalographic data.

Figure 3. The generation of connection matrices and alterations of connection entropy.

Examples of connection matrices, constructed with the electroencephalographs of the delta band, are presented for (A) the baseline conscious state, (B) unconscious state and (C) recovery state. For a 5 minute long electroencephalograph, we can derive 7,325 minimum spanning trees from 7,325 segmented moving windows. Theoretically, we could get 210 possible edges, but because of limitations relating to the timeframe as well as the neural architecture itself, some edges are not formed. In Figure 3A–C, approximately 150 edges appeared for baseline conscious state, approximately 60 edges for loss of consciousness and approximately 100 edges for return of consciousness. The number of total edges is different depending on the subject and state. These matrices were generated using the method described in Figure 1C. For each “1” representing a connection, a white dot is placed. Each row represents a minimum spanning tree identifying the channels connected—thus, of all of the connections observed, only the top 20 derived from the method are shown on each row. The decrease in heterogeneity of connected channels and increase in the duration of the retained channels can be seen after loss of consciousness. The exact types of connection edges (i.e., electroencephalography channel connections) are not matched on the x-axes. (D) The mean connection entropies of the five frequency bands in the three states are presented (the error bar denotes standard deviation; ** = p<0.01, * = p<0.05, Scheffé’s post-hoc test). LOC=loss of consciousness; ROC=return of consciousness; EEG=electroencephalograph

Scale-Free, Power-Law Distribution

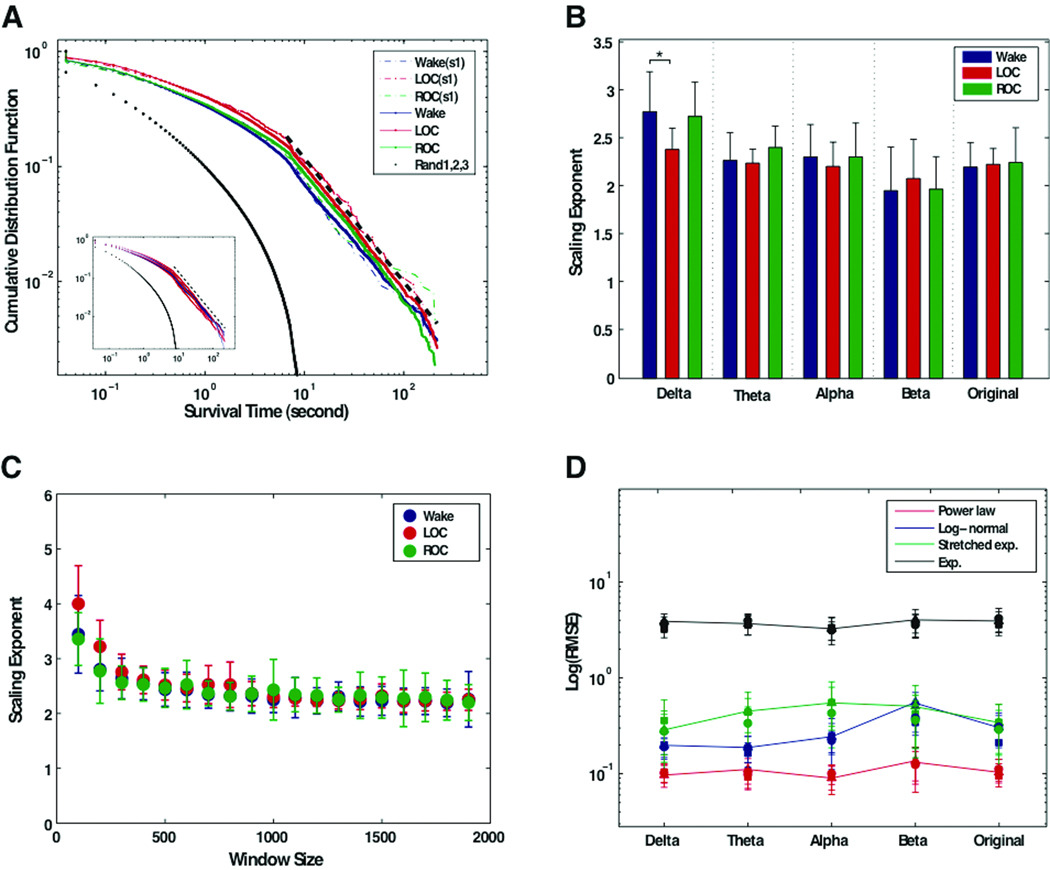
Despite statistically significant differences in the connection times and connection entropies associated with consciousness, anesthesia, and recovery, the distribution of connection times primarily followed a power-law distribution in all three states, which is indicative of preserved scale-free organization (Figure 4A). The exponents of the distribution, as well as their relationship to window size, are demonstrated in Figure 4B and 4C. In practice, few empirical phenomena obey power laws for all values. Instead, the power law applies only for values greater than some minimum value (X_min).²³ In our data, the power distribution appeared on the tail of the distribution of connection times (>10 second), while exogenous and endogenous random effects of empirical data were reflected on smaller duration range (<10s) despite clear discrimination from the randomized electroencephalographic data (Figure 4A).

Figure 4. Scale-free distribution of survival times across multiple states of consciousness.

(A) The cumulative distribution function for the pooled survival times of all subjects (and each subject) in the three states. The cumulative distribution function of the pooled survival time of the original electroencephalograph shows straight lines on the log-log scale graph, as well as for an individual subject (s1). The cumulative distribution function of the connection times of randomized electroencephalographic data shows exponential (i.e., Gaussian) distributions, which is clearly distinguishable from that of the connection time data of the original electroencephalogram. (blue dot = baseline conscious state; red dot = unconscious state; green dot = recovery state; black dots = three randomized electroencephalograms; black dashed line = best scale region determined by Kolmogorov-Smirnov statistic). In the inset, the red and blue colored lines denote the three states for the first and second (1 week later) datasets, respectively, demonstrating the reproducibility of the finding. (B) The mean scaling exponents fitted from cumulative distribution function for all data sets in the window size 1,800 (~7 second). The error bar denotes standard deviation. The scaling exponents across the three states are indistinguishable across all frequency bands, except for baseline delta. (C) The mean scaling exponents of the original electroencephalograph for three states over the different window sizes. This demonstrates that the scaling exponents converge around the window size 500 (~2 seconds). (D) The root-mean square error (RMSE) of the alternative fitting models for the survival time data in the frequency bands in the three states are presented in double logarithm scales. The RMSE of the power law is consistently lower than those of the other models in all cases (circle = baseline; square = LOC, loss of consciousness; triangle = ROC, return of consciousness).

The slope of the linear portion of the distribution is indistinguishable across all subjects, all states, and all electroencephalographic bands except the baseline delta. More than 80% of connection duration data of all subjects in all frequencies and states passed the KS test, which has the null hypothesis for a power-law model. The goodness of fit for the power law model by the KS statistic showed that 82.4% of the connection duration data of 20 electroencephalographic data sets for all frequency bands and all states have p>0.05 in the case of window size 1,800 (76.6% for baseline conscious state, 87.0% for unconscious state and 80.5% for recovery state, respectively). In terms of test-test reproducibility, the two data sets at one week time intervals demonstrated the same power law distributions for all frequency bands (see inset of Figure 4A). Comparing the KS statistics across the two anesthetic exposures, 82.1% and 82.7% of the first and second data sets, respectively, passed the null hypothesis with p>0.05. For the dependency of p-values on window size, the hypothesis of the power law model cannot be rejected for most of the connection duration data beyond a certain window size (>1000 (~ 4 seconds)).

The comparison with alternative models (power law, stretched exponential, log-normal and exponential distributions) demonstrates that the power law is the best fitting model for the connection time data for all frequency bands in all states (Figure 4D). The limited length of the electroencephalographic data and relatively small number of electroencephalographic channels may reduce the possibility of rare events of connection times, which is one of the distinctive characteristics of a power law distribution compared to stretched exponential and log-normal distributions. Nonetheless, the comparison of the RMSE consistently indicates the power law as the best fitting model for the probability distribution of connection durations over all frequency bands (Figure 4D).

Discussion

With the use of a method based on graph theory, we have identified changes in the temporal organization of brain networks across consciousness, anesthesia, and recovery. More importantly, however, there is the strong indication of a preserved scale-free or power-law organization that persists across multiple subjects, multiple anesthetic exposures, multiple states of consciousness and multiple electroencephalographic bandwidths. Thus, despite the fact that consciousness is suppressed during general anesthesia or altered during recovery—both reflected by significant changes in the connection times and entropy—a fundamental principle of temporal organization appears to be maintained. Maintaining a global scale-free organization in the face of local alterations is suggestive of a process referred to as “adaptive reconfiguration.”¹

Temporal Organization of Networks

In terms of local organization, we observed that the connection entropy of the lower frequency bands (delta, theta) were significantly reduced after loss of consciousness and returned after return of consciousness. These results suggest that the network connectivity of the lower frequency bands becomes less random during anesthesia, which is consistent with past findings.²⁴ In terms of global organization, numerous studies have reported scale-free and self-similar properties for other temporal variables in the brain, including the amplitude fluctuation of electroencephalographic oscillations,³ the global synchronization of electroencephalographic signals,²⁵ and the power spectral density.⁷ Using two methods of neuroimaging, a recent study in normal volunteers demonstrated that phase-locked intervals for two signals were in a power-law distribution.²⁶ These studies strongly suggest that the power law is a plausible model for the temporal configuration of networks in the brain. Our data support this by showing persistent scale-free organization of connection durations across multiple subjects, multiple anesthetic exposures, multiple states and multiple electroencephalographic bandwidths.

The inability to assert with complete certainty that the distribution pattern observed is based on a power law is mirrored in similar controversies regarding distribution patterns of connectivity in the spatial domain.^4,5,27,28 What is critical to note is that—independently of the precise identity of distribution of these temporal parameters—Figure 4C demonstrates clearly that the scaling exponents are preserved across states as the window size increases. The consistent organization in the temporal domain during consciousness, general anesthesia, and recovery is an unexpected finding, especially given the numerous local perturbations, as well as the dramatic change of the behavioral state.

Implications for Anesthetic Mechanisms

Recent data in both animal models²⁹ and humans^9,10,30 have validated frameworks describing the deintegration^31,32 or unbinding^33–35 of cortical processing as a mechanism of anesthetic-induced consciousness. The current data suggest, however, that although higher-order cortical integration may be disrupted during general anesthesia, certain dynamic principles of the underlying network are maintained. Thus, the state of general anesthesia does not appear to be a complete network failure in which a breakdown of scale-free organization occurs. Indeed, our findings are consistent with data in humans demonstrating that neural networks are characterized by scale-free organization in the spatial domain,^1,2,4–6 but that the brain undergoes an “adaptive reconfiguration” preserving global topological parameters despite a change in state associated with the performance of a task.^1,36 Because the scale-free properties of the connection times were maintained in our study, a similar process may occur under general anesthesia. Our data therefore point to a mechanism that maintains the optimal brain state by the reconfiguration of neural networks, despite significant alteration of local network connections due to the effects of anesthesia.

In order to clarify the precise relationship of anesthetic mechanisms and network organization, further work is required. First, it is important to note that the MST method reflects the principal network structure, not the entire network. Network properties may vary with different definitions of connectivity and different modeling techniques. For example, including non-phase lagged connections that reflect long-range communication in the brain could yield different results. Second, a more precise understanding of differential network effects is required. For example, it is clear that certain network structures, such as the default mode network, are preserved even under anesthesia.¹⁵ It is possible that other networks mediating conscious processing are nonetheless selectively disrupted and may lose scale-free organization. Third, it is important to note that we excluded higher frequency gamma activity because of the potential confound of electromyographic activity, although findings in the gamma band were consistent with those of other frequencies (data not shown). It has previously been demonstrated by John et al³⁷ that loss of gamma band coherence was associated with the loss of consciousness induced by multiple agents. We have also shown a selective breakdown of gamma activity after anesthetic-induced unconsciousness.⁹ Future studies should include the analysis of higher frequency activity that controls for electromyography artifact. Finally, the combined analysis of neurophysiological data with anatomical data, such as electroencephalography during functional magnetic resonance imaging,³⁸ may yield further insights into the temporal and spatial network changes during general anesthesia.

Limitations

Our study has numerous limitations. First, a relatively small number of young, healthy males were studied—further work on females, older subjects, and those with co-morbidities will be necessary to establish this finding. Second, a bolus dose rather than a steady-state concentration of propofol was studied, but this models the routine clinical event of anesthetic induction. The preservation of scale-free organization after an induction dose of propofol is perhaps more compelling and unexpected than after a small change in steady-state concentration, as a bolus dose is likely far more disruptive to neural processing. Third, we studied only one intravenous agent—future studies should include other intravenous agents, as well as inhalational anesthetics. Finally, disadvantages of both the MST method and electroencephalography in general are suboptimal spatial resolution and potentially confounding effects from unexpected artifacts and common source input.

Conclusion

The induction of general anesthesia with propofol is associated with numerous local changes in the temporal organization of network connections, most notably in the delta bandwidth. Despite these and other changes in connection entropy, a global scale-free organization is preserved across multiple subjects, multiple anesthetic exposures, multiple states of consciousness, and multiple bandwidths of the electroencephalograph. This study highlights the utility of graph theory in the study of anesthetic mechanisms and introduces the possibility of adaptive reconfiguration as a neural property of general anesthesia.