A Robust Methodology for In Vivo T₁ Mapping

Introduction

The T₁ parameter is an intrinsic MR property of tissue, and mapping T₁ in vivo is useful in several ways. First, knowledge of T₁ helps in optimizing the MR protocol, e.g., by setting the Ernst angle appropriately. In addition, it provides a tool to evaluate contrast uptake, blood perfusion and volume, as well as disease progression during a longitudinal study. Furthermore, it is often desirable to compare T₁ measurements across subjects and across scanners. While there are many techniques for T₁ mapping (1), there is also a wide range of reported T₁ values in tissue (2), an inconsistency that raises the issue of reproducibility and standardization.

The gold standard for T₁ mapping was developed from NMR experiments performed in the late 1940s (3, 4). The method is known as inversion recovery T₁ mapping (IR), and it consists of inverting the longitudinal magnetization M_z and sampling the MR signal as it recovers with an exponential recovery time T₁. Different models have been used for T₁ mapping (1). With all models, the fit is traditionally performed using a Levenberg-Marquardt (LM) algorithm (5). Many methods have been proposed to speed up the scanning and fitting procedures, at the expense of accuracy and precision.

In this paper, we first justify the need for a four-parameter model when accurate T₁ mapping is desired. We show that this model is equivalent in terms of accuracy and precision of the T₁ estimation to a more general five-parameter model. We propose to solve a nonlinear least squares (NLS) problem to fit complex data to the five-parameter model. The problem is reduced to a search over one dimension, which substantially decreases the computational complexity. When only magnitude data are available, the algorithm is adapted to concurrently restore polarity. We perform Monte-Carlo simulations to compare the proposed algorithms to the conventional LM algorithm and to evaluate the influence of signal-to-noise ratio (SNR) on fitting performance. We then define a robust methodology for in vivo T₁ mapping. The method is validated with phantom scans and applied to brain and skin imaging.

1 Theory

1.1 Models

Let us recall the signal equations for the gradient-echo inversion recovery (GRE-IR) and spin-echo inversion recovery (SE-IR) sequences. We first consider the GRE-IR sequence {θ₁ — TI — θ₂ — (TR – TI)}, where θ₁ and θ₂ are the RF pulses, typically prescribed as 180° and 90°, respectively; TI is the inversion time; and TR the repetition time. If we assume instantaneous pulses, perfect spoiling of M_xy after θ₁, and no off-resonance effects, then (6):

$$M_z=M_0\frac{1-\text{cos}({\theta }_1)e^{-\frac{TR}{T_1}}-[1-\text{cos}({\theta }_1)]e^{-\frac{TI}{T_1}}}{1-\text{cos}({\theta }_1)\text{cos}({\theta }_2)e^{-\frac{TR}{T_1}}}.$$ (1)

Similarly, for a SE-IR sequence {θ₁ — TI — θ₂ — TE/2 — θ₃ — (TR – TI – TE/2)}, where θ₃ is prescribed as 180°, and TE is the echo time, if the same assumptions are made, then (7):

$$M_z=M_0\frac{1-\text{cos}({\theta }_1)\text{cos}({\theta }_3)e^{-\frac{TR}{T_1}}-\text{cos}({\theta }_1)[1-\text{cos}({\theta }_3)]e^{-\frac{TR-\frac{TE}{2}}{T_1}}-[1-\text{cos}({\theta }_1)]e^{-\frac{TI}{T_1}}}{1-\text{cos}({\theta }_1)\text{cos}({\theta }_2)\text{cos}({\theta }_3)e^{-\frac{TR}{T_1}}}.$$ (2)

Therefore, for both sequences, sampling the magnetization M_z at different inversion times TI_n leads to the following data equation for the received signal:

$$S(T{I}_n)=K{M}_z=e^{i\varphi }\left(r_a+r_b{e}^{-\frac{T{I}_n}{T_1}}\right),$$ (3)

where

$$r_a=\{\begin{array}{ll}|K|M_0\frac{1-\text{cos}({\theta }_1)e^{-\frac{TR}{T_1}}}{1-\text{cos}({\theta }_1)\text{cos}({\theta }_2)e^{-\frac{TR}{T_1}}}\hfill & \text{for GRE-IR},\hfill \\ |K|M_0\frac{1-\text{cos}({\theta }_1)\text{cos}({\theta }_3)e^{-\frac{TR}{T_1}}-\text{cos}({\theta }_1)[1-\text{cos}({\theta }_3)]e^{-\frac{TR-\frac{TE}{2}}{T_1}}}{1-\text{cos}({\theta }_1)\text{cos}({\theta }_2)\text{cos}({\theta }_3)e^{-\frac{TR}{T_1}}}\hfill & \text{for SE-IR},\hfill \end{array}$$ (4)

$$r_b=\{\begin{array}{ll}-|K|M_0\frac{1-\text{cos}({\theta }_1)}{1-\text{cos}({\theta }_1)\text{cos}({\theta }_2)e^{-\frac{TR}{T_1}}}\hfill & \text{for GRE-IR},\hfill \\ -|K|M_0\frac{1-\text{cos}({\theta }_1)}{1-\text{cos}({\theta }_1)\text{cos}({\theta }_2)\text{cos}({\theta }_3)e^{-\frac{TR}{T_1}}}\hfill & \text{for SE-IR},\hfill \end{array}$$ (5)

and ϕ ∈ [−π, π) is the phase of K, which has contributions from T₂ (SE–IR) or $T_2^{*}$ (GRE-IR) and coil sensitivity. The model in Eq. 3 therefore has four real-valued unknown parameters: ϕ, r_a, r_b, and T₁.

We will also consider the following overparametrization of the model in Eq. 3, which will turn out to be useful mathematically:

$$S(T{I}_n)=a+b{e}^{-\frac{T{I}_n}{T_1}},$$ (6)

where a and b are complex-valued parameters. This model has five unknown real-valued parameters: Re{a}, Im{a}, Re{b}, Im{b}, and T₁, where Re{x} and Im{x} denote the real part and imaginary part of x, respectively. Equation 6 with a = e^iϕr_a and b = e^iϕr_b—i.e., if a and b are assumed to have the same phase ϕ—reduces to Eq. 3.

Sampling the magnetization at three time points provides six equations, which are sufficient for T₁ estimation. More time points are often used to improve the quality of fit over the range of expected T₁ values.

Equations 1 and 2 can be simplified to a different four-parameter model if TR ≫ T₁

$$S(T{I}_n)=c\left(1-[1-\text{cos}({\theta }_1)]e^{-\frac{T{I}_n}{T_1}}\right)$$ (7)

or to a three-parameter model if TR ≫ T₁ and θ₁ = 180°

$$S(T{I}_n)=c\left(1-2e^{-\frac{T{I}_n}{T_1}}\right),$$ (8)

where c is complex-valued.

A drawback with using Eq. 7 instead of Eq. 3 or Eq. 6 is that it assumes TR ≫ T₁ and perfect knowledge of TI_n. TI_n is usually defined as the time between the middle of the inversion pulse θ₁ and the middle of the imaging pulse θ₂. However, inversion is not complete until the end of the inversion pulse. This systematic error is not a problem in Eq. 3 or Eq. 6, as it is absorbed in the parameter r_b or b. Another drawback of Eq. 7 is that the limited range of the cosine function introduces a bias in the estimation of θ₁, which is an issue for θ₁ close to 180° in the presence of noise or imperfections (2).

The three-parameter model in Eq. 8 is attractive since the LM fitting procedure is much faster when the number of parameters is reduced. Furthermore, the variance of the estimate of T₁ is usually expected to decrease (8–10). However, beyond the requirement that TR ≫ T₁, the three-parameter model assumes a perfect inversion pulse (180°), an assumption that is rarely valid. Even if an adiabatic RF pulse is used, the effective flip angle will depend on both T₁ and T₂ (11). In addition, transition bands of the inversion profile are often partially included in the imaging slice to enable multi-slice imaging, and the effective flip angle should be taken as the integral of the inversion profile over the slice thickness. Using the three-parameter model, imperfections in the inversion profile can result in significant T₁ variations (7,12). Adiabatic RF pulses should still be preferred; even if they do not provide a perfect 180°, they get as close as possible to it and, therefore, maximize the available dynamic range and hence the SNR.

With these considerations in mind, we focus on the four- and five-parameter models in Eqs. 3 and 6. Interestingly enough, the Cramér-Rao Lower Bounds (CRLB)¹ of the T₁ estimate obtained using the four-parameter model in Eq. 3 and using the five-parameter model in Eq. 6 are identical (cf. Appendix A). Consequently, the variances of the T₁ estimate from these two models are expected to be very similar.

1.2 Fitting Procedures

Specific fitting procedures were derived for handling complex data and magnitude data. For complex data, the use of the five-parameter model in Eq. 6 allows the derivation of a fast fitting procedure. Monte-Carlo simulations then show that the proposed algorithm reaches the CRLBs, therefore the phase constraint on a and b improves neither the accuracy nor the precision in T₁ estimation. For magnitude data, the phase constraint is needed to restore polarity.

1.2.1 Complex Data

If complex data are available, Eq. 6 can be used directly. The unknown parameters a ∈ ℂ, b ∈ ℂ, and T₁ ∈ ℝ can be estimated as the minimizers of the fitting criterion

$$J_1={\displaystyle \sum _{n=1}^N{\left|S(T{I}_n)-\left(a+b{e}^{-\frac{T{I}_n}{T_1}}\right)\right|}^2,}$$ (9)

where N is the number of sampling points. Equation 9 is traditionally solved using the LM algorithm, which requires a five-dimensional search with proper initialization. The fit is therefore computationally demanding. In this work, we instead propose a reduced-dimension NLS (RD-NLS) approach to solve Eq. 9 (13), which allows for a separation of the unknown variables in J₁. The estimates, denoted by ^, are then obtained as (cf. Appendix B for details)

$${\widehat{T}}_1=\text{arg}\underset{T_1}{\text{max}}\frac{|\mathrm{\Gamma }(T_1){|}^2}{\mathrm{\Psi }(T_1)},$$ (10)

$$\widehat{b}=\frac{\mathrm{\Gamma }({\widehat{T}}_1)}{\mathrm{\Psi }({\widehat{T}}_1)},$$ (11)

$$\widehat{a}=\frac{1}{N}\left({\displaystyle \sum _{n=1}^{N}S(T{I}_n)-\widehat{b}{\displaystyle \sum _{n=1}^N{e}^{-\frac{T{I}_n}{{\widehat{T}}_1}}}}\right),$$ (12)

where

$$\mathrm{\Gamma }(T_1)={\displaystyle \sum _{n=1}^N{e}^{-\frac{T{I}_n}{T_1}}}S(T{I}_n)-\frac{1}{N}\left({\displaystyle \sum _{n=1}^N{e}^{-\frac{T{I}_n}{T_1}}}\right)\left({\displaystyle \sum _{n=1}^{N}S(T{I}_n)}\right),$$ (13)

$$\mathrm{\Psi }(T_1)={\displaystyle \sum _{n=1}^N{e}^{-\frac{2T{I}_n}{T_1}}}-\frac{1}{N}{\left({\displaystyle \sum _{n=1}^N{e}^{-\frac{T{I}_n}{T_1}}}\right)}^2.$$ (14)

T₁ is therefore obtained through a one-dimensional (1D) search, and the remaining parameters are given in closed form.

We could use a similar approach for the model in Eq. 3, but the necessary calculations and the resulting algorithm are more involved than those corresponding to the model in Eq. 6. Owing to this reason and to the fact that there is no statistical performance gain associated with using the model in Eq. 3 compared to using the model in Eq. 6 (cf. Appendix A, where the CRLBs for the different models are derived and compared), we did not pursue the idea of getting an RD-NLS algorithm for the model in Eq. 3.

1.2.2 Magnitude Data

If only magnitude data are available, Eq. 3 becomes

$$y(TI)\triangleq |S(TI)|=\left|r_a+r_b{e}^{-\frac{TI}{T_1}}\right|,$$ (15)

leaving us with three unknowns: r_a ∈ ℝ, r_b ∈ ℝ, and T₁ ∈ ℝ. Using the model in Eq. 15 to estimate the unknowns would not be a simple task since the minimization criterion would not be differentiable everywhere. A remedy for this would be to use the square of the data, yielding the following NLS minimization criterion:

$$J_2={\displaystyle \sum _{n=1}^N{\left[y^2(T{I}_n)-{\left(r_a+r_b{e}^{-\frac{T{I}_n}{T_1}}\right)}^2\right]}^2}.$$ (16)

Regrettably, there is no straightforward derivation of an RD-NLS-type algorithm for Eq. 16. However, as we assume $r_a+r_b{e}^{-\frac{TI}{T_1}}$ to be a monotonically increasing function in TI (Eqs. 4 and 5), we instead propose a technique that combines polarity restoration, a method commonly used to preserve noise statistics (14–17), and the RD-NLS approach in Sec. 1.2.1. The estimation method, called RD-NLS-PR (RD-NLS with polarity restoration), is outlined as follows.

Let the sign-shifting function γ be defined as

$${\gamma }_{\tau }(TI)=\{\begin{array}{ll}1\hfill & \text{if}TI\ge \tau ,\hfill \\ -1\hfill & \text{if}TI<\tau ,\hfill \end{array}$$ (17)

where τ is defined such that

$$r_a+r_b{e}^{-\frac{\tau }{T_1}}=0;$$ (18)

i.e., τ is the zero crossing point. Estimates of r_a, r_b, T₁, and τ can then be found as the minimizers of the following fitting criterion:

$$J_{\tau }={\displaystyle \sum _{n=1}^N{\left[{\gamma }_{\tau }(T{I}_n)y(T{I}_n)-\left(r_a+r_b{e}^{-\frac{T{I}_n}{T_1}}\right)\right]}^2,}$$ (19)

where the dependence of τ on r_a, r_b, and T₁ should in principle be observed (note from Eq. 18 that τ = T₁ ln(−r_b/r_a)). However, this minimization problem is rather complicated. To simplify it, reminiscent of (18), we take the TI corresponding to the minimum signal intensity as an approximation of τ. Signal polarity is reversed up to this sampling point, denoted TI_min. It then remains to be determined whether the polarity of y(TI_min) should be reversed. This is done by comparing the minimum values of the criterion in Eq. 19 for τ = TI_min and τ = TI_min+1, where the latter refers to the next sampling point after TI_min (assuming that TI₁ < TI₂ < ⋯ < TI_N). We then obtain the following estimates (cf. Appendix B for details):

$$\widehat{\tau }=\text{arg}\underset{\tau \in \{T{I}_{min},T{I}_{min+1}\}}{\text{min}}{J}_{\tau },$$ (20)

$${\widehat{T}}_1=\text{arg}\underset{T_1}{\text{max}}\frac{{[{\mathrm{\Gamma }}_{mag}(T_1|\widehat{\tau })]}^2}{\mathrm{\Psi }(T_1)},$$ (21)

$${\widehat{r}}_b=\frac{{\mathrm{\Gamma }}_{mag}({\widehat{T}}_1|\widehat{\tau })}{\mathrm{\Psi }({\widehat{T}}_1)},$$ (22)

$${\widehat{r}}_a=\frac{1}{N}\left({\displaystyle \sum _{n=1}^N{\gamma }_{\widehat{\tau }}(T{I}_n)y(T{I}_n)-{\widehat{r}}_b{\displaystyle \sum _{n=1}^N{e}^{-\frac{T{I}_n}{{\widehat{T}}_1}}}}\right),$$ (23)

where

$${\mathrm{\Gamma }}_{mag}(T_1|\widehat{\tau })={\displaystyle \sum _{n=1}^N{e}^{-\frac{T{I}_n}{T_1}}{\gamma }_{\widehat{\tau }}(T{I}_n)y(T{I}_n)-\frac{1}{N}\left({\displaystyle \sum _{n=1}^N{e}^{-\frac{T{I}_n}{T_1}}}\right)\left({\displaystyle \sum _{n=1}^N{\gamma }_{\widehat{\tau }}(T{I}_n)y(T{I}_n)}\right)},$$ (24)

and Ψ is defined in Eq. 14. The RD-NLS-PR method thus requires minimizing Eq. 19 two times; i.e., it requires two 1D searches over T₁. Solving Eq. 19 using the LM algorithm requires instead two 3D searches, a computationally more demanding task (16, 18).

1.2.3 Grid Search

Using the RD-NLS or RD-NLS-PR approaches proposed here, an estimate of T₁ can be found through a 1D search. Estimates of the other unknowns are then obtained in closed form (Eqs. 11 and 12 or Eqs. 22 and 23). This should be compared with the traditional LM algorithm fit, where the search has to be performed over five dimensions (Eq. 6), over four dimensions (Eq. 3), or over three dimensions (Eq. 3 with magnitude data). There are many algorithms for solving the 1D search problem in Eq. 10; e.g., Newton’s method and steepest descent (19). However, as we know the range of possible T₁ estimates, a global grid search can be used. Doing so, there is no need for initialization, and the global optimum is always found. Furthermore, a resolution for T₁ of 1 ms is sufficient (16). We typically searched over T₁ = {1, …, 5000} ms. This range can be reduced if a priori information is available.

2 Methods

The novel fitting algorithms were compared to conventional LM algorithms in terms of accuracy, precision, and speed. The respective influence of SNR and T₁ was also investigated. A robust scanning procedure was then defined. Phantom scans were used to validate the proposed T₁ mapping methodology, and in vivo scans were performed.

2.1 Simulations

2.1.1 Validation of the NLS Algorithms

To compare the conventional LM algorithm and the proposed RD-NLS algorithms, simulations were performed using Matlab 7.5 (The Mathworks, Natick, MA, USA). The data were generated according to Eq. 1, to which circularly Gaussian-distributed, zero-mean, white complex noise with variance ${\sigma }_n^2$ was added. The parameters were set to σ_n = 0.03, θ₁ = 172°, θ₂ = 90°, TI = [50 400 1100 2500] ms (20, 21), TR = 2550 ms, T₁ = 263 ms, and M₀ = 1. T₁ was then estimated from 20,000 Monte-Carlo simulations, using the RD-NLS and LM algorithms. For the complex data, the LM algorithm was used with both the four-parameter model in Eq. 3 and the five-parameter model in Eq. 6. To initialize the LM algorithms, T₁ was set to 500 ms and the remaining parameters as follows. When fitting the parameters to complex data, with the five-parameter model in Eq. 6, we had a⁽⁰⁾ = S(TI_N) and b⁽⁰⁾ = −2a⁽⁰⁾; i.e., to initialize a and b, we assumed full recovery of the magnetization at the longest sampling point TI. With the four-parameter model in Eq. 3, we did the change of variables c ≜ e^iϕr_a and k ≜ −r_b/r_a, and we used the LM algorithm to fit the data to the following model:

$$S(TI)=c\left(1-k{e}^{-\frac{TI}{T_1}}\right).$$ (25)

The LM fit with Eq. 25 was then initialized by setting c⁽⁰⁾ = S(TI_N) and k⁽⁰⁾ = 2. When fitting the parameters to magnitude data, we let $r_a^{(0)}=y(T{I}_N)$, and $r_b^{(0)}=-2r_a^{(0)}$. The LM fit was performed using both Eq. 16 directly and the polarity restoration method.

2.1.2 Influence of SNR

We simulated data with different σ_n and computed the root mean squared error (RMSE) of the T₁ estimates. 10,000 Monte-Carlo simulations were performed with the same parameters as in Sec. 2.1.1.

2.1.3 Influence of T₁

We performed Monte-Carlo simulations to see how the precision of the T₁ estimation varies with T₁. The same parameters as in Sec. 2.1.1 were used. True T₁ values from 250 ms to 1500 ms spaced by 10 ms were considered, and 10,000 different noise realizations were simulated for each true T₁ value.

2.2 Imaging Protocol

Two sequences were used: a product 2D SE-IR sequence and a 2D GRE-IR sequence that we implemented. Both sequences feature the same 8.64 ms Silver-Hoult adiabatic inversion pulse (22). GRE-IR offers a shorter TE than SE-IR, which can be beneficial for imaging short-T₂ species. With GRE-IR, a fractional echo was used to minimize TE, and magnitude-only images were reconstructed using a homodyne method (23).

With all T₁ mapping methods, several considerations should be kept in mind. Partial volume effects are a concern for in vivo experiments (24). Magnetization transfer (MT) affects the longitudinal relaxation, especially in multi-slice T₁ measurements. In our experiments, we ignored MT effects because of the spacing of the slices and the long TR (25). Finally, T₁ increases with temperature by 2–3% per degree Celsius (26, 27). This is usually not a concern for in vivo imaging of healthy volunteers when the core temperature is stable (37°C). However, for phantom and ex vivo imaging, controlling temperature is essential.

2.2.1 Phantom Scans

First, experiments were performed with a 1.5 T GE scanner (GE Healthcare, Milwaukee, WI, USA) on a loading phantom. The GRE-IR sequence and the SE-IR sequence were used successively. The ambient temperature was measured at the beginning and at the end of each scan. A birdcage head coil and the following parameters were used (8): TR = 2550 ms, TE = 14/7 ms (SE/GRE), TI = [50, 400, 1100, 2500] ms, bandwidth (BW) = ±32 kHz, Field-of-View (FOV) = 15 × 15 cm², slice thickness = 2 mm, and matrix size = 128 × 128.

2.2.2 Brain Imaging

Our methodology was then applied to brain T₁ mapping of a healthy volunteer at 1.5 T. We complied with the regulations of our institution’s human ethics committee. We acquired three slices using the SE-IR sequence, a birdcage head coil, and the following parameters: TR = 2550 ms, TE = 10 ms, TI = [50, 400, 1100, 2500] ms, BW = ±32 kHz, FOV = 24 × 18 cm², slice thickness = 5 mm, and matrix size = 128 × 96. Each of the four scans took 4 min 35 sec.

2.2.3 Skin Imaging

Our interest in T₁ mapping was originally triggered by our work in high-resolution skin imaging. High-field (e.g., 7 T) systems are attractive for skin imaging primarily because of the signal gain they provide. In addition, imaging the skin requires small (typically 1-inch-diameter) surface coils to achieve adequate SNR at the desired resolution. For such small coils, body noise dominance is easier to achieve at higher-field strengths (28), which further increases the SNR. Last, wavelength effects—often a concern at high fields—are likely to be negligible because of the small FOV.

One potential concern with higher-field strengths is the increase in T₁ (29), which reduces the SNR efficiency and might offset the SNR benefits of increasing the field strength (30,31). To check if this is indeed the case, we decided to perform skin T₁ mapping at 1.5 T, 3 T, and 7 T.

Skin is composed of three main layers. The outermost layer, the epidermis, is typically 0.1 mm thick. Beneath the epidermis lie the dermis (≈ 1 mm thick) and the hypodermis (≈ 10 mm thick). The epidermis is mainly composed of keratinocytes and the hypodermis of lipids. The dermis is a heterogeneous structure, in which several different types of macromolecules are present. The dermis therefore has short-T₂ components (32, 33). Skin temperature depends on the ambient temperature and on perfusion (34).

GE 1.5 T, 3 T, and 7 T scanners with maximum gradient amplitude 40 mT/m and maximum slew rate 150 mT/m/ms were used. Receive-only coils of 1-inch diameter were built and tuned for 1.5 T and 3 T imaging respectively. At 7 T, because there is no body coil, a 1-inch-diameter transmit/receive coil was first built. As muscle T₁ could not be assessed when imaging with the transmit/receive coil (because of its limited sensitivity), a 1-inch-diameter receive-only coil was eventually built and tuned for 7 T, and a Nova quadrature head coil was then adapted to be used as the transmitter (Nova Medical, Wilmington, MA, USA). Both the GRE-IR and the SE-IR sequences were employed, as GRE-IR was expected to give better results in the dermis, where short-T₂ components are present. We acquired two slices using the following parameters: TR = 2550 ms, TE = 14/7 ms (SE/GRE), TI = [50, 400, 1100, 2500] ms, BW = ±32 kHz, FOV = 6 × 6 cm², slice thickness = 2 mm and matrix size = 512 × 128. Each scan took 5 min 57 sec. To resolve the different skin layers, the readout direction was usually chosen perpendicular to the skin surface.

The calf of two healthy volunteers was imaged. For each experiment, the subjects were supine with the coil beneath them. Motion can significantly degrade high-resolution skin images (35). To ensure stability, we used padding when imaging with the Nova coil and an Aircast plastic walker boot (DJO, Vista, CA, USA) glued to a heavy plank when imaging with the body coil. The ambient temperature was measured at the beginning and at the end of each scan.

2.3 Image Processing

Image processing was carried out using Matlab. For the scans, DICOM images with a reconstructed matrix size of 256 × 256 (phantom and brain) or 512 × 512 (skin) were processed. An intensity mask was applied to the images prior to the fit, so that only pixels with sufficient SNR were considered. In vivo, we used region growing to select specific Regions-of-Interest (ROIs) (36). In these ROIs, histograms were computed with a bin size matching the grid size (1 ms). Bins were centered on the grid points and labeled on their center. For the in vivo scans, histograms were smoothed with a 10 ms median filter (37). For the simulation and phantom scans, because the ROIs are homogeneous, T₁ values were fitted to Gaussian distributions. For the in vivo scans, the T₁ value of each tissue was determined as the mode of the histogram and the root mean square deviation about the mode was computed.

The code is available for general use at http://www-mrsrl.stanford.edu/~jbarral/t1map.html.

3 Results

3.1 Simulations

3.1.1 Validation of the NLS Algorithms

Simulations were performed on an IBM X3455 dual Opteron 2220SE with a 2.8 GHz processor and 8 GB RAM. Table 1 presents the results. As can be seen, the RD-NLS and the LM algorithms with phase constraint show very similar performance, both in terms of accuracy; i.e., correct mean, and precision; i.e., variance. For the magnitude data fit, without phase restoration the LM algorithm shows a slightly larger variance. In addition, the RD-NLS algorithms are much faster than the LM algorithms. For the simulated data, the RD-NLS algorithm was 74 times faster than the five-parameter LM algorithm computed with the model in Eq. 6 and 42 times faster than the four-parameter LM algorithm fitted to Eq. 3. For the magnitude data, the RD-NLS-PR was 28 times faster than its corresponding LM algorithm and 14 times faster than the LM algorithm used on Eq. 16.

Table 1.

Monte-Carlo Simulations (20,000 pixels): (top) complex and (bottom) magnitude data fits with the RD-NLS and LM algorithms (mean μ, standard deviation σ, and processing time are given). T₁ = 263 ms was used to generate the data.

Algorithm (model)	µ [ms]	σ [ms]	Time [min:sec]
LM (five-parameter)	263	12	13:39
LM (four-parameter)	263	12	7:39
RD-NLS (five-parameter)	263	12	0:11

Algorithm (model)	µ [ms]	σ [ms]	Time [min:sec]
LM (three-parameter)	263	13	3:52
LM-PR (three-parameter)	263	12	7:32
RD-NLS-PR (three-parameter)	263	12	0:16

For the complex data fit we can compute the CRLB, which gives a minimum standard deviation of 11.9. We therefore conclude that the fitting methods are efficient, as the variance has reached the CRLB, and further improvements in terms of variance cannot be gained for this setup.

3.1.2 Influence of SNR

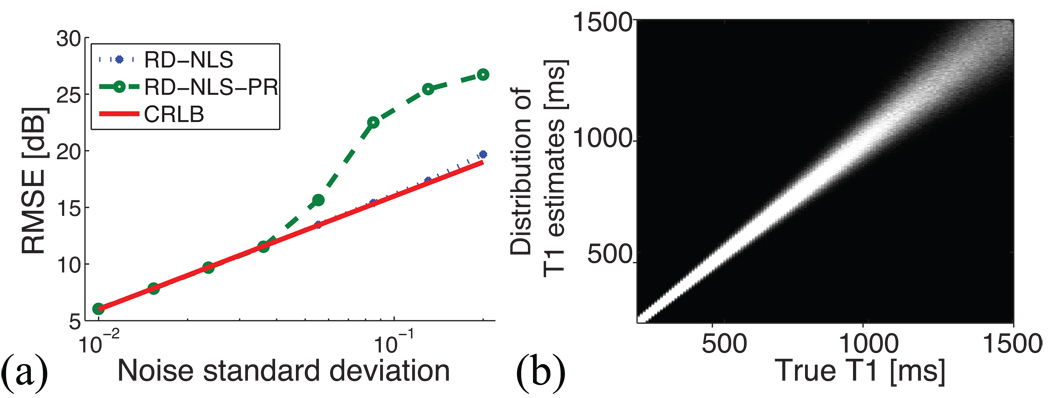
Figure 1a displays the RMSE of the T₁ estimates using the complex data (RD-NLS) and the polarity-restored magnitude data (RD-NLS-PR), together with the CRLB, for different values of the noise standard deviation σ_n. We see that for σ_n = 0.03, which is the noise standard deviation that we used to validate the algorithms, the same results are obtained with both the complex data and the magnitude data. Furthermore, the CRLB is reached. However, for lower SNR, the performance of the estimators degrades, and for σ_n ≈ 0.05, RD-NLS-PR is no longer efficient whereas RD-NLS still is. Using the complex data, the RD-NLS algorithm starts deviating from the CRLB only at σ_n ≈ 0.2. We therefore conclude that for the SNR of the phantom experiments, both methods will perform similarly. For lower SNR, though, using the complex data is beneficial.

Figure 1.

Influence of SNR and T₁. (a) RMSE of the T₁ estimates using the complex data (RD-NLS) and the polarity-restored magnitude data (RD-NLS-PR), together with the CRLB, for different σ_n. (b) T₁ estimates as a function of true T₁ values. Each column gives a histogram of the T₁ estimate distribution for a given true T₁. The precision worsens as the true T₁ increases.

3.1.3 Influence of T₁

Figure 1b displays the histograms of T₁ estimates vs. true T₁ values. We see that the larger the true T₁, the larger the standard deviation of the estimate. The smooth increase in standard deviation with T₁ suggests that the exact distribution of sampling points TIs with respect to the true T₁ has little impact on the fitting performance as long as it covers the expected range of T₁ values.

3.2 Phantom Scans

The temperature was 20.7°C at the beginning of the scanning session and 20.2°C at the end of it.

3.2.1 Validation of the NLS Algorithms

The complex data obtained with the SE-IR sequence were fitted using the different algorithms to confirm the Monte-Carlo simulations. Results are presented in Table 2. As was seen with the simulations, all algorithms give similar accuracy and precision, except the LM algorithm without phase restoration for the magnitude data fit, which here shows a slightly lower mean. Moreover, the RD-NLS algorithms show a large benefit in terms of speed over the LM algorithms. RD-NLS is 52 times faster than the five-parameter LM algorithm and 36 times faster than the four-parameter LM algorithm. Regarding the magnitude data, RD-NLS-PR is 30 times faster than the polarity-restored LM algorithm and 34 times faster than the LM algorithm computed using Eq. 16.

Table 2.

Phantom SE-IR Scan (20,719 pixels): (top) complex and (bottom) magnitude data fits with the RD-NLS and LM algorithms (mean μ, standard deviation σ, and processing time are given).

Algorithm (model)	µ [ms]	σ [ms]	Time [min:sec]
LM (five-parameter)	263	12	9:40
LM (four-parameter)	263	12	6:37
RD-NLS (five-parameter)	263	12	0:11

Algorithm (model)	µ [ms]	σ [ms]	Time [min:sec]
LM (three-parameter)	262	12	9:28
LM-PR (three-parameter)	263	12	8:18
RD-NLS-PR (three-parameter)	263	12	0:17

3.2.2 Validation of the Pulse Sequences

To compare the two pulse sequences, the complex data obtained with the SE-IR sequence were fitted using the RD-NLS algorithm and the magnitude data obtained with the GRE-IR sequence were fitted using the RD-NLS-PR algorithm. The same ROI comprising 20,464 pixels was used. For the SE-IR data, a mean T₁ estimate of 263 ms and a standard deviation of 12 ms were found. For the GRE-IR data, a mean T₁ estimate of 263 ms and a standard deviation of 10 ms were found.

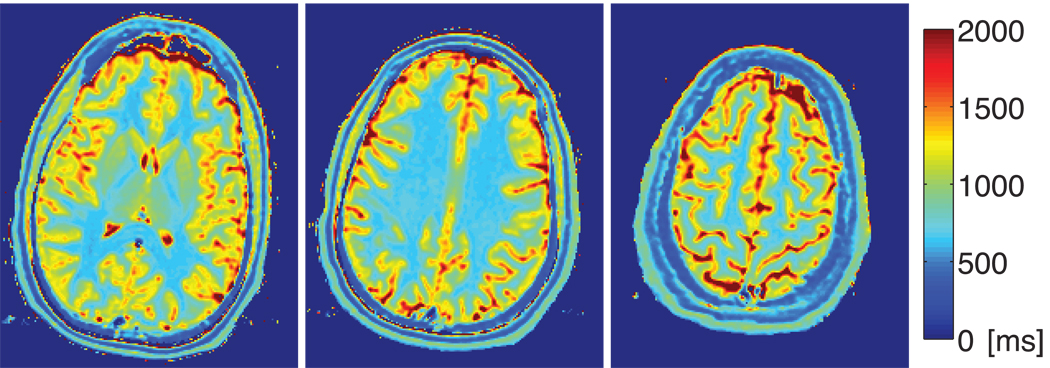
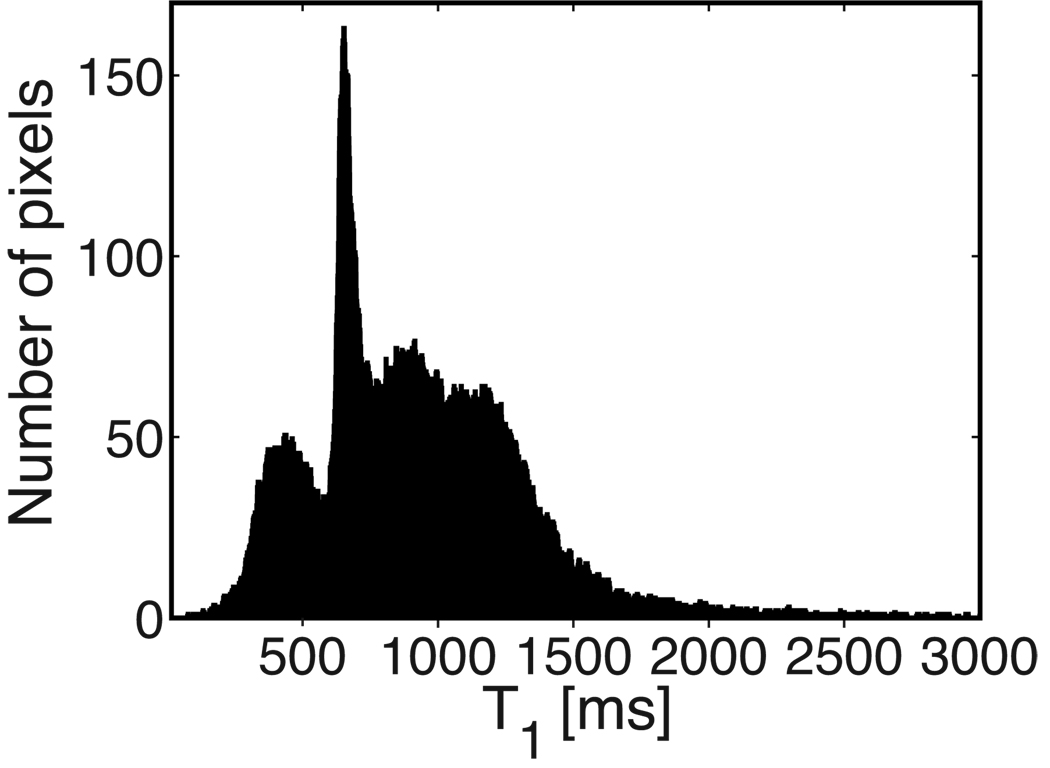
3.3 Brain Scan

Figure 2 shows the T₁ map of the three brain slices imaged, and Fig. 3 displays the corresponding histogram. Gray matter and white matter were segmented, and their T₁ histograms were computed. T₁ was estimated as 1173 ± 207 ms (29,360 pixels) in gray matter and 653 ± 55 ms (12,135 pixels) in white matter. The sharp cutoff in the histograms is due to the region-growing method that was used for segmentation, with a fixed threshold. More elaborate methods could be used if necessary (38).

Figure 2.

Brain T₁ maps at 1.5 T. Three slices were imaged and the RD-NLS algorithm was used on the complex data.

Figure 3.

Brain T₁ histogram. The three imaged slices were aggregated. Peaks corresponding to white matter (653 ms) and gray matter (1173 ms) are visible. The leftmost peak corresponds to skull and is segmented out when ROIs are specified.

3.4 Skin Scans

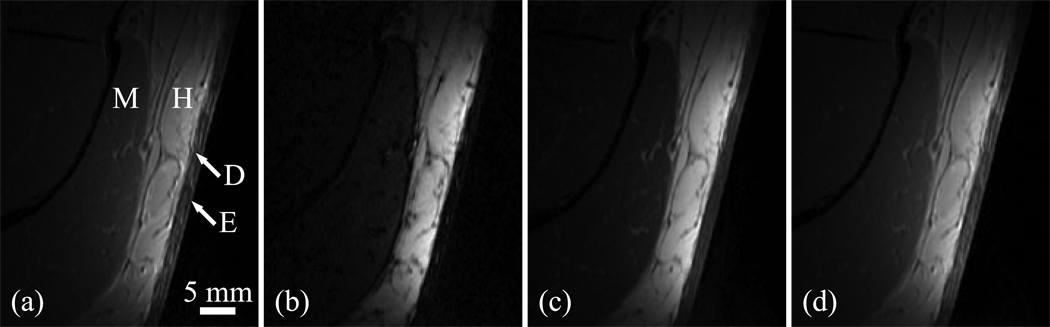
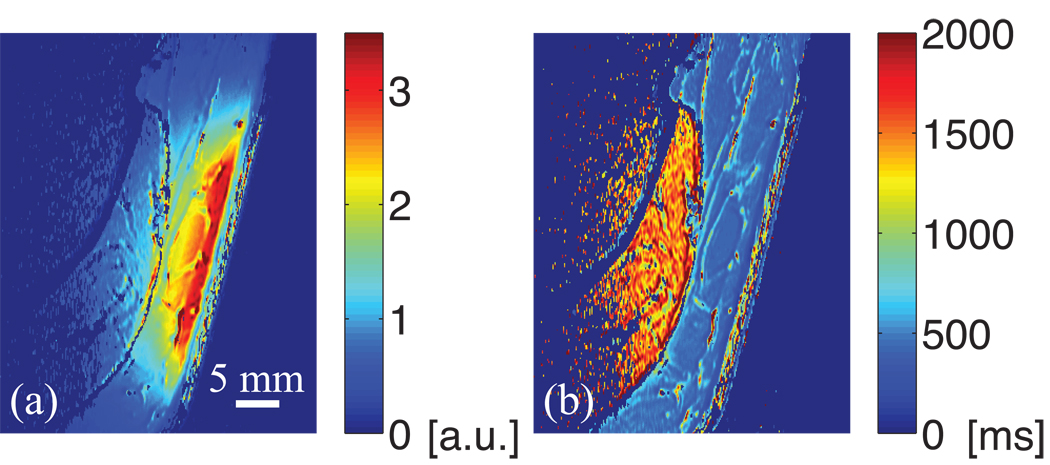
Figure 4 shows four images obtained at 3 T using a receive-only coil with the SE-IR sequence (only one of the two acquired slices is shown). Figure 5 presents the corresponding map of the a parameter (magnitude) and the T₁ map obtained with the RD-NLS algorithm fitting the complex data. The a map has contributions from T₂, the proton density, and coil sensitivity. Figure 6 displays the ROIs generated by the region growing procedure (same slice as Fig. 4), and Fig. 7 shows the corresponding histograms (the two slices were aggregated). For each histogram, the mode and root mean square deviation about the mode (σ) are reported.

Figure 4.

Skin images obtained at 3 T with the SE-IR sequence. Inversion times are (a) 50 ms, (b) 400 ms, (c) 1100 ms, and (d) 2500 ms. The following structures can be recognized: E: epidermis; D: dermis; H: hypodermis; M: muscle.

Figure 5.

(a) Map of the a parameter (magnitude) and (b) T₁ map obtained at 3 T with the SE-IR sequence. The a map has contributions from T₂, proton density, and coil sensitivity. The dermis has a low proton density and a short T₂ (32). The coil sensitivity drops as the distance from the skin surface increases. The T₁ map shows the dermis heterogeneity.

Figure 6.

ROI in (a) dermis, (b) hypodermis, and (c) muscle. Hypodermis and muscle are segmented using a region growing algorithm. The threshold used is the same for hypodermis and muscle, and the ROIs are independent of the seed position. The dermis is obtained by subtraction, and therefore includes the epidermis.

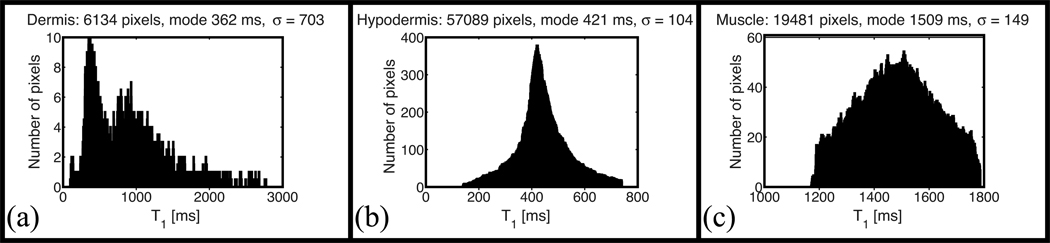
Figure 7.

Histograms obtained in (a) dermis, (b) hypodermis, and (c) muscle at 3 T with the SE-IR sequence. σ is the root mean square deviation about the mode.

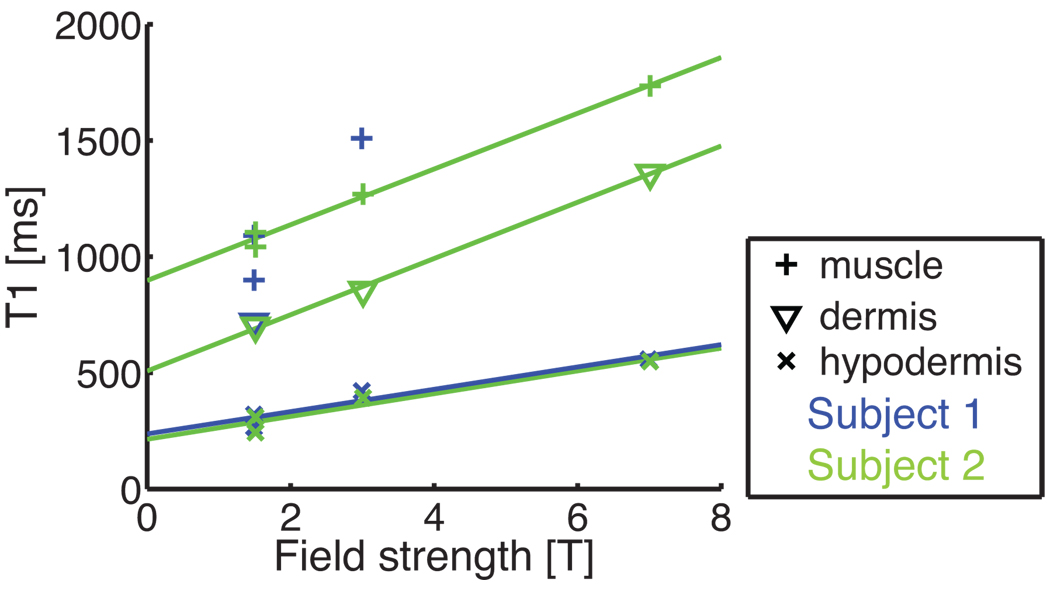
Table 3 and Fig. 8 summarize the values found. Temperature was steady within 1°C for each experiment, but it varied from 21°C to 23°C between scan sessions. Between 1.5 T and 7 T, dermis T₁ increased by 97%, hypodermis T₁ by 94%, and muscle T₁ by 61%.

Table 3.

Skin scans: T₁ values (in ms) found in dermis, hypodermis, and muscle at 1.5 T, 3 T, and 7 T (mode ± root mean square deviation about the mode (number of pixels)). NA means that the corresponding value was Not Available. Muscle values could not be assessed when a transmit/receive (Tx-Rc) coil was used, because of the limited sensitivity. Dermis T₁ was hard to determine because of tissue heterogeneity, and values were not reported when the distribution had more than one peak, due to partial volume effects (e.g., Fig. 7a).

Subject	Sequence	Field	Coil	T1 dermis	T1 hypodermis	T1 muscle
1	SE-IR	1.5	Rc	NA	320 ± 89 (67,120)	899 ± 183 (50,584)
1	GRE-IR	1.5	Rc	718 ± 347 (6,865)	266 ± 72 (51,091)	1091 ± 158 (19,168)
2	SE-IR	1.5	Rc	701 ± 304 (2,466)	309 ± 102 (32,872)	1042 ± 163 (87,528)
2	GRE-IR	1.5	Rc	NA	243 ± 82 (19,286)	1105 ± 154 (56,977)
1	SE-IR	3	Rc	NA	421 ± 104 (57,089)	1509 ± 150 (20,521)
2	SE-IR	3	Rc	855 ± 546 (12,281)	392 ± 132 (24,688)	1269 ±141 (93,202)
1	SE-IR	7	Tx- Rc	NA	558 ±115 (27,539)	NA
2	SE-IR1	7	Rc	1359 ± 487 (4,272)	549±138 (11,546)	1735±178 (27,741)

¹The readout direction was chosen parallel to the skin surface for this experiment.

Figure 8.

Dispersion plot obtained from Table 3. For the hypodermis, T₁ depends linearly on the field strength. A linear trend is also observed in dermis and muscle, but variability is more pronounced.

4 Discussion

4.1 Fitting Procedure

The proposed RD-NLS fitting algorithms are not only as accurate and precise as LM fitting techniques, but also much faster. Moreover, if additional information about the range of possible T₁ values is available, the search range for the RD-NLS algorithms can be restricted, thereby further decreasing the computing time. Additionally, our approach avoids the delicate task of choosing initial parameters, as it allows for a global search where only the range of possible T₁ values needs to be set. The proposed methods can also be generalized to any T₁ mapping model and to other relaxometry techniques.

In (39), a T₁ estimation method based on VARPRO (40) was proposed. This approach is similar to ours but results in a 2D search and is therefore not as fast. Furthermore, VARPRO was derived for real data, and the approach in (39) is therefore not directly applicable to complex data.

In vivo, T₁ values in different ROIs do not always follow Gaussian distributions. This is partially due to tissue heterogeneity (e.g., for fat) and to coil sensitivity (e.g., for skin imaging).

Note that manually selecting ROIs results in undesirable user-dependent variability. This problem is avoided when region growing is used to define ROIs. Such an approach was found to be simple and robust. The same threshold was used for all maps, and the values obtained were independent of the seed position.

4.2 Phantom Scans

Looking at the respective variance of the complex data fit and the magnitude data fit, good agreement is found between the phantom scans (Table 2) and the simulations (Table 1).

Owing to its shorter TE, the GRE-IR sequence provides data with an improved SNR and therefore a better precision than the SE-IR sequence.

4.3 Brain Scan

The gray matter value found (1173 ms) is in agreement with the value found by Stanisz et al. ex vivo (1124 ms). The white matter value found (653 ms), however, is significantly lower than his (884 ms) (41). Our value is in good agreement with values reported by Kingsley et al. in vivo (636 in frontal white matter and 648 in occipital white matter) (7). As already mentioned, values reported in the literature span a wide range (2). As a relatively low resolution was used and partial volume effects are not accounted for by our simple segmentation method, a large variance is observed in the T₁ estimates.

4.4 Skin Scans

As the hypodermis has the highest SNR (Fig. 5a) and the shortest T₁ value, it also presents the lowest variance (Fig. 1). The dermis is a heterogeneous layer, and a broad range of T₁ values is found in the histogram of the dermis at all field strengths.

When comparing across experiments at a given field strength, we find reasonable agreement between the two sequences used, GRE-IR and SE-IR. The observed differences can be explained by physiological variations between the two scan sessions (temperature, perfusion), $T_2^{*}$ signal loss with GRE-IR, or sensitivity to different T₂ components because a shorter TE is used with GRE-IR (33). In addition, since a fractional echo is used with GRE-IR, only magnitude data are available, which might degrade the fitting performance if SNR is low.

In the early days of skin imaging, Richard et al. reported T₁ values of 870 ms in the dermis and 393 ms in the hypodermis (32), when scanning the calf at 1.5 T. We found significantly lower values. Our values are in good agreement with those reported by Stanisz et al. (41) for muscle and those reported by Gold et al. (42) for hypodermis (subcutaneous fat) and muscle. The large variance found in muscle can be attributed to tissue heterogeneity, partial volume effects, or the natural variability between different muscle tissues.

We conclude that the T₁ increase slightly attenuates the SNR benefits of increasing the field strength but is far from offsetting them.

4.5 Limitations

The main limitation of our approach is the scanning procedure: 24 min were typically required to collect the skin data. Since our novel fitting procedures can be used with any T₁ mapping method, we believe that the long protocol should be used as a gold standard to validate faster scanning procedures on phantoms, before using the faster techniques in vivo. Note that when imaging phantoms, monitoring temperature is critical.

For skin, the protocol was chosen to be applicable at the three field strengths considered. However, if a single field strength is used, the protocol could be adapted. In particular, the limits of the protocol used in this work are reached at 7 T: chemical shift displaces fat by 8 pixels, aliasing is a concern, and scanner drift might become an issue.

Conclusion

We have introduced a robust methodology for T₁ mapping consisting of a gold standard scanning procedure and a novel fitting procedure.

The data, either magnitude data or complex data, were fitted to a five-parameter model. We proposed a reduced-dimension nonlinear least squares fitting algorithm, which was shown to be accurate, precise, and fast. Our algorithm can be adapted to fit data to any T₁ mapping model.

APPENDIX A– Derivation of the CRLBs for the different models

Let φ denote a vector containing the unknown parameters and assume that the additive noise is a circularly Gaussian-distributed, zero-mean, white complex process with variance ${\sigma }_n^2$. The Fisher information matrix (FIM) can then be expressed, using the Slepian-Bang formula (13), as

$$\text{FIM}=\frac{2}{{\sigma }_n^2}{\displaystyle \sum _{n=1}^N\text{Re}\left\{\left(\frac{\partial S(T{I}_n)}{\partial \phi }\right){\left(\frac{\partial S(T{I}_n)}{\partial \phi }\right)}^{*}\right\},}$$ (A-1)

where x* and Re{x} denote the conjugate of x and the real part of x, respectively. The CRLB is then given by the diagonal elements of the inverse of the FIM.

The Four-Parameter Models

The Model in Eq. 3

From Eq. 3, φ = [ϕ r_a r_b T₁]^T, so the FIM is a 4 × 4 matrix containing the partial derivatives

$$\begin{array}{ll}\frac{\partial S(TI)}{\partial \varphi }=i{e}^{i\varphi }\left(r_a+r_b{e}^{-\frac{TI}{T_1}}\right),\hfill & \frac{\partial S(TI)}{\partial r_b}=e^{i\varphi }{e}^{-\frac{TI}{T_1}},\hfill \\ \frac{\partial S(TI)}{\partial r_a}=e^{i\varphi },\hfill & \frac{\partial S(TI)}{\partial T_1}=e^{i\varphi }{r}_b{T}_1^{-2}TI{e}^{-\frac{TI}{T_1}}.\hfill \end{array}$$

We perform the inversion of the FIM using Matlab’s Symbolic Math Toolbox and we obtain the following analytical expression for the CRLB of T₁:

$$\begin{array}{ll}\text{CRLB}(T_1)\hfill & ={[{\text{FIM}}^{-1}]}_{44}\hfill \\ \hfill & =\frac{{\sigma }_n^2(S_1^2-N{S}_2)}{2r_b^2{T}_1^{-4}(S_1^2{S}_{22}-2S_1{S}_{12}{S}_{11}-N{S}_2{S}_{22}+N{S}_{12}^2+S_2{S}_{11}^2)},\hfill \end{array}$$ (A-2)

where

$$\begin{array}{ll}{S}_1={\displaystyle {\sum }_{n=1}^N{e}^{-\frac{T{I}_n}{T_1}},}\hfill & S_2={\displaystyle {\sum }_{n=1}^N{e}^{-\frac{2T{I}_n}{T_1}},}\hfill \\ S_{11}={\displaystyle {\sum }_{n=1}^{N}T{I}_n{e}^{-\frac{T{I}_n}{T_1}},}\hfill & S_{12}={\displaystyle {\sum }_{n=1}^{N}T{I}_n{e}^{-\frac{2T{I}_n}{T_1}},}\hfill \\ S_{22}={\displaystyle {\sum }_{n=1}^{N}T{I}_n^2{e}^{-\frac{2T{I}_n}{T_1}}.}\hfill & \hfill \end{array}$$ (A-3)

The Model in Eq. 7

From Eq. 7, φ = [c_R c_I θ₁ T₁]^T, where c_R = Re{c} and c_I = Im{c}: this is just a change of coordinates from the model in Eq. 3. The CRLB of T₁ derived from Eq. 7 is thus identical to that in Eq. A-2.

The Five-Parameter Model

Equation 6 gives φ = [a_R a_I b_R b_I T₁]^T, where a_R = Re{a}, a_I = Im{a}, b_R = Re{b}, and b_I = Im{b}. The FIM for the five-parameter model is therefore a 5 × 5 matrix containing the partial derivatives

$$\begin{array}{ll}\frac{\partial S(TI)}{\partial a_R}=1,\hfill & \frac{\partial S(TI)}{\partial b_R}=e^{-\frac{TI}{T_1}},\hfill \\ \frac{\partial S(TI)}{\partial a_I}=i,\hfill & \frac{\partial S(TI)}{\partial b_I}=i{e}^{-\frac{TI}{T_1}},\hfill \\ \frac{\partial S(TI)}{\partial T_1}=b{T}_1^{-2}TI{e}^{-\frac{TI}{T_1}}.\hfill & \hfill \end{array}$$ (A-4)

We use the Symbolic Math Toolbox in Matlab to compute the inverse of the FIM and we obtain

$$\begin{array}{ll}\text{CRLB}(T_1)\hfill & ={[{\text{FIM}}^{-1}]}_{55}\hfill \\ \hfill & =\frac{{\sigma }_n^2(S_1^2-N{S}_2)}{2|b{|}^2{T}_1^{-4}(S_1^2{S}_{22}-2S_1{S}_{12}{S}_{11}-N{S}_2{S}_{22}+N{S}_{12}^2+S_2{S}_{11}^2)},\hfill \end{array}$$ (A-5)

where S₁, S₂, S₁₁, S₁₂, and S₂₂ are defined in Eq. A-3. We note that this CRLB is identical to that of the four-parameter models (Eq. A-2).

APPENDIX B – Derivation of the RD-NLS Algorithms

Complex Data

Expanding Eq. 9 yields

$$J_1={\displaystyle \sum _{n=1}^N|S(T{I}_n){|}^2-2}{\displaystyle \sum _{n=1}^N\text{Re}\left\{S^{*}(T{I}_n)\left(a+b{e}^{-\frac{T{I}_n}{T_1}}\right)\right\}+{\displaystyle \sum _{n=1}^N{\left|a+b{e}^{-\frac{T{I}_n}{T_1}}\right|}^2}.}$$ (B-1)

By further expanding and by completing the square we get the following expression for J₁:

$$J_1=f_1(S(TI))+N{\left|a-\frac{1}{N}\left({\displaystyle \sum _{n=1}^{N}S(T{I}_n)-b{\displaystyle \sum _{n=1}^N{e}^{-\frac{T{I}_n}{T_1}}}}\right)\right|}^2+{\left|b-\frac{\mathrm{\Gamma }(T_1)}{\mathrm{\Psi }(T_1)}\right|}^2\left[{\displaystyle \sum _{n=1}^N{e}^{-\frac{2T{I}_n}{T_1}}-\frac{1}{N}{\left({\displaystyle \sum _{n=1}^N{e}^{-\frac{T{I}_n}{T_1}}}\right)}^2}\right]-\frac{|\mathrm{\Gamma }(T_1){|}^2}{\mathrm{\Psi }(T_1)},$$ (B-2)

where f₁(S(TI)) denotes a function that depends only on the data, and Γ(T₁) and Ψ(T₁) are defined in Eqs. 13 and 14, respectively. The minimizer of J₁ with respect to a and b is thus given by

$$\widehat{a}=\frac{1}{N}\left({\displaystyle \sum _{n=1}^{N}S(T{I}_n)-b{\displaystyle \sum _{n=1}^N{e}^{\frac{T{I}_n}{T_1}}}}\right),$$ (B-3)

$$\widehat{b}=\frac{\mathrm{\Gamma }(T_1)}{\mathrm{\Psi }(T_1)}.$$ (B-4)

Inserting Eqs. B-3 and B-4 in B-2 then yields the following optimal estimate of T₁:

$${\widehat{T}}_1=\text{arg}\underset{T_1}{\text{max}}\frac{|\mathrm{\Gamma }(T_1){|}^2}{\mathrm{\Psi }(T_1)}.$$ (B-5)

Magnitude Data

We expand Eq. 19 similarly to the case of complex data, which gives

$$J_{\tau }={\displaystyle \sum _{n=1}^N{[{\gamma }_{\tau }(T{I}_n)y(T{I}_n)]}^2-2}{\displaystyle \sum _{n=1}^N{\gamma }_{\tau }(T{I}_n)y(T{I}_n)\left(r_a+r_b{e}^{-\frac{T{I}_n}{T_1}}\right)}+{\displaystyle \sum _{n=1}^N{\left(r_a+r_b{e}^{-\frac{T{I}_n}{T_1}}\right)}^2.}$$ (B-6)

Again, this can be further expanded and we obtain the following minimization criterion:

$$J_{\tau }=f_2({\gamma }_{\tau }(TI)y(TI))+N{\left[r_a-\frac{1}{N}\left({\displaystyle \sum _{n=1}^N{\gamma }_{\tau }(T{I}_n)y(T{I}_n)-r_b{\displaystyle \sum _{n=1}^N{e}^{-\frac{T{I}_n}{T_1}}}}\right)\right]}^2+{\left[r_b-\frac{\mathrm{\Gamma }(T_1|\tau )}{\mathrm{\Psi }(T_1)}\right]}^2\left[{\displaystyle \sum _{n=1}^N{e}^{-\frac{2T{I}_n}{T_1}}-\frac{1}{N}{\left({\displaystyle \sum _{n=1}^N{e}^{-\frac{T{I}_n}{T_1}}}\right)}^2}\right]-\frac{{[\mathrm{\Gamma }(T_1|\tau )]}^2}{\mathrm{\Psi }(T_1)},$$ (B-7)

where f₂(γ_τ(TI)y(TI)) is a function that depends only on the data, and Γ(T₁|τ) and Ψ(T₁) are defined in Eqs. 24 and 14, respectively. For a given τ, the minimizer of J_τ with respect to r_a and r_b is thus given by

$${\widehat{r}}_a=\frac{1}{N}\left({\displaystyle \sum _{n=1}^N{\gamma }_{\tau }(T{I}_n)y(T{I}_n)-r_b{\displaystyle \sum _{n=1}^N{e}^{\frac{T{I}_n}{T_1}}}}\right),$$ (B-8)

$${\widehat{r}}_b=\frac{\mathrm{\Gamma }(T_1|\tau )}{\mathrm{\Psi }(T_1)},$$ (B-9)

which, re-inserted in Eq. B-7, gives the following optimal estimate of T₁:

$${\widehat{T}}_1=\text{arg}\underset{T_1}{\text{max}}\frac{{[{\mathrm{\Gamma }}_{mag}(T_1|\tau )]}^2}{\mathrm{\Psi }(T_1)}.$$ (B-10)

This is done for τ = TI_min and τ = TI_min+1, and an approximation of τ is found as

$$\widehat{\tau }=\text{arg}\underset{\tau \in \{T{I}_{min},T{I}_{min+1}\}}{\text{min}}{J}_{\tau },$$ (B-11)

which, reinserted in Eq. B-10, provides an estimate of T₁.