Summary
High-resolution (200 × 200 × 1,500 (μm3) imaging was performed to derive quantitative cerebral blood flow (CBF) and apparent diffusion coefficient (ADC) maps in stroke rats (permanent occlusion) every 30 minutes up to 3 hours after occlusion onset, followed by histology at 24 hours. An improved automated iterative-self-organizing-data-analysis-algorithm (ISODATA) was developed to dynamically track ischemic tissue fate on a pixel-by-pixel basis during the acute phase. ISODATA-resolved clusters were overlaid on the CBF-ADC scatterplots and image spaces. Tissue volume ADC, and CBF of each ISODATA cluster were derived. In contrast to the single-cluster normal left hemisphere (ADC = 0.74 ± 0.02 × 10−3 mm2/s, CBF = 1.36 ± 0.22 mL g−1min−1, mean ± SD, n = 8), the right ischemic hemisphere exhibited three ISODATA clusters, namely: “normal” (normal ADC and CBF), “ischemic core” (low CBF and ADC), and at-risk “perfusion-diffusion mismatch” (low CBF but normal ADC). At 180 minutes, the mismatch disappeared in five rats (Group I, 180-minute “core” lesion volume = 255 ± 62 mm3 and 24-hour infarct volume = 253 ± 55 mm3, P > 0.05), while a substantial mismatch persisted in three rats (Group II, 180-minute CBF-abnormal volume = 198 ± 7 mm3 and 24-hour infarct volume 148 ± 18 mm3, P < 0.05). The CBF (0.3 ± 0.09 mL g−1min−1) of the “persistent mismatch” (Group II, 0.3 ± 0.09 mL g−1 min−1) was above the CBF viability threshold (0.2 to 0.3 mL g−1min−1) throughout and its ADC (0.70 ± 0.03 × 10−3 mm2/s) did not decrease as ischemia progressed. In contrast, the CBF (0.08 ± 0.03 mL g−1min−1) of the analogous brain region in Group I was below the CBF viability threshold, and its ADC gradually decreased from 0.63 ± 0.05 to 0.43 ± 0.03 × 10−3 mm2/s (ADC viability threshold = 0.53 ± 0.02 × 10−3 mm2/s). The modified ISODATA analysis of the ADC and CBF tissue characteristics during the acute phase could provide a useful and unbiased means to characterize and predict tissue fates in ischemic brain injury and to monitor therapeutic intervention.
Keywords: Viability thresholds, Penumbra, Perfusion-diffusion mismatch, Diffusion-weighted imaging, Perfusion-weighted imaging, Multispectral analysis
Magnetic resonance imaging (MRI) offers multiple contrasts for staging ischemic brain injury in a single setting. T1- and T2-weighted MRI yields excellent delineation of subacute and chronic stroke, whereas diffusion- and perfusion-weighted imaging techniques have the ability for early detection of acute ischemic brain injury before changes in T1 and T2 relaxation times are detectable (Helpern et al., 1993; Knight et al. 1994). Hyperintense regions on diffusion-weighted imaging correspond to tissues with reduced apparent diffusion coefficients (ADC) of water (Mosely et al., 1991). It has been postulated that the combined use of perfusion and diffusion imaging is capable of mapping both reversible and irreversible injury. During the early onset of ischemic brain injury, a central core with severely compromised cerebral blood flow (CBF) and severe ADC reduction is generally surrounded by a rim of moderately ischemic tissue with diminished CBF and impaired electrical activity but preserved cellular metabolism (where ADC remains near normal to normal), commonly referred to as the “ischemic penumbra” (Astrup et al., 1981). The penumbra is the region at risk of eventual infarction and is of most interest for potential therapy. The “perfusion-diffusion mismatch” seen initially after stroke onset has been suggested to approximate the “ischemic penumbra.” Thus, automated analysis of the “perfusion-diffusion” mismatch could offer a means to identify “tissue signature” and a “clock window” for therapeutic intervention (Albers, 1999).
Most analyses of stroke MRI data had been carried out using volumetric approach and involved the use of region-of-interest (ROI) analysis. These ROIs contain tissues with different ADC and CBF characteristics, thereby inadvertently mixing the characteristics that one is trying to resolve. The complex temporal and spatial evolution of focal cerebral ischemia had prompted the use of various combinations of MR parameters and more sophisticated analysis methods (Welch et al., 1995; Jiang et al., 1997; Carano et al., 1998, 2000; Jacobs et al., 2000, 2001a, 2001b; Wu et al., 2001; Mitsias et al., 2002) for performing unsupervised multiparametric segmentation on a pixel-by-pixel basis to stage stroke outcome. Multispectral analyses based on K-mean and Fuzzy c-mean clustering techniques have been used to investigate the ischemic penumbra using CBF index maps, T2 and ADC maps in a rat stroke model (Carano et al., 1998, 2000). This approach, however, requires the number of tissue clusters to be assigned a priori. In practice, the number of tissue clusters is generally unknown during the evolution of cerebral ischemia. Jacobs et al. (2001a) and Mitsias et al. (2002) eloquently incorporated the iterative self-organizing data analysis algorithm (ISODATA) (Ball and Hall, 1965) for analyzing T1-, T2- and diffusion-weighted images in human stroke. This approach had also been applied to analyze T1-, T2-, and diffusion-weighted images in an animal stroke model (4 hours to 1 week) (Jacobs et al., 2001b). Unlike many other existing techniques, ISODATA analysis requires minimal user intervention, and the number of clusters is statistically determined. Studies thus far used ISODATA analysis of T1-, T2- and diffusion-weighted data during the subacute phase to correlate lesion volumes with histology and found that a multiparametric ISODATA analysis outperformed analysis using any single parameter alone. None of these studies, however, used ISODATA to dynamically track tissue fate on a pixel-by-pixel basis as ischemia evolves during the acute phase, i.e., where the perfusion-diffusion mismatch is dynamically evolving.
In this study, the automated ISODATA technique was extended to include spatial contiguity and a Mahalanobis (instead of Euclidean) distance measure. More importantly, the modified ISODATA technique was applied to analyze stroke data with the aim of dynamically tracking tissue fates on a pixel-by-pixel basis during the acute ischemic phase, with particular focus on the “perfusion-diffusion” mismatch dynamics. This was made possible by the use of multislice, high-resolution, quantitative perfusion and diffusion imaging. Imaging was performed every 30 minutes up to 3 hours after occlusion followed by histology at 24 hours. The main goals were (1) to statistically resolve different pixel clusters on the ADC-CBF scatterplots and overlay on the image spaces; (2) to characterize the temporal and spatial dynamics of each cluster on a pixel-by-pixel basis, and (3) to track the tissue volumes, CBF, and ADC values of the “perfusion-diffusion” mismatch and other pixel clusters as ischemia evolved during the acute phase.
Methods
Animal preparations
Stroke surgery and the anesthetic protocol were identical to those of Shen et al. (2003; 2004). Eight male Sprague-Dawley rats (300 to 350 g, Taconic Farms, NY, U.S.A.) were initially anesthetized with choral hydrate (400 mg/kg, i.p., Sigma, St. Louis, MO, U.S.A.). The left femoral artery was catheterized. Permanent focal brain ischemia of the right hemisphere was induced using the intraluminal middle cerebral artery occlusion method. Rectal temperature was maintained at 37.4 ± 0.8°C (mean ± SD, n = 8) throughout. Heart rate and mean arterial blood pressure via the arterial line were recorded continuously onto a PC via the Biopac system (Santa Barbara, CA, U.S.A.). Respiration rate was derived from the slow modulations on top of the cardiac waveforms. Anesthesia was switched to 1% isoflurane once the animal was in the magnet and during imaging. MRI data were acquired at 30, 60, 90, 120, and 180 minutes.
Histology
TTC (2,3,5-triphenyltetrazolium chloride) staining was performed at 24 hours after ischemia. Eight 1.5-mm slices corresponding to the MR slices were carefully sectioned coronally and incubated in 2% TTC solution at 37°C for 30 minutes and fixed in 10% buffered formalin solution. TTC infarct volumes with edema correction were derived as described elsewhere (Tatlisumak et al., 1998).
MR experiments
Magnetic resonance imaging was performed on a Bruker 4.7-T/40-cm (Billerica, MA, U.S.A.) and a 20-G/cm gradient insert (ID = 12 cm, 120-microsecond rise time). The animal was placed in a stereotaxic headset and onto an animal holder, which consisted of a surface coil (2.3-cm ID) for brain imaging and a neck coil for CBF labeling. Coil-to-coil interaction was actively decoupled.
ADCav was obtained by averaging three ADC maps acquired separately with diffusion-sensitive gradients applied along the x, y, or z direction (Stejskal and Tanner, 1965). ADCav was used because it yielded a single representative ADC value, which minimized structural anisotropy (Lythgoe et al., 1997). Four-segment, spin-echo, echo-planar images were acquired with spectral width = 200 kHz, TR = 2 seconds per segment (90° flip angle), TE = 37.5 milliseconds, b = 10 and 1,270 seconds/mm2, Δ = 17.53 milliseconds, δ = 5.6 milliseconds, field of view = 2.56 cm × 2.56 cm, eight 1.5-mm slices, and 16 averages (total time = 8.5 minutes).
Quantitative CBF was measured using the continuous arterial spin-labeling technique (Silva et al., 1999; Duong et al., 2000) with four-segment, gradient-echo echo-planar images, spectral width = 200 kHz, field of view = 2.56 cm × 2.56 cm, eight 1.5-mm slices, TE = 15 milliseconds, and TR = 2 seconds (90° flip angle). Paired images were acquired alternately: one with arterial spin-labeling and the other without spin-labeling (control) preparation. Seventy-five pairs of images were acquired for signal averaging (total time = 20 minutes). Although differences in dephasing effects between spin-echo and gradient-echo echo-planar images in the diffusion and perfusion measurements, respectively, could cause pixel misalignment at the skull–brain interface, it was minimized by using a short gradient echo time, relatively high spatial resolution (reduced intravoxel dephasing), similar echo-planar readout time, and careful shimming. Furthermore, a conservative ROI avoiding the brain-skull interface was used for data analysis.
In practice, ADC and CBF measurements were interleaved using the following scheme: 6.7-minute CBF (25 pairs), 2-minute ADC (bx = 10 seconds/mm2), 2-minute ADC (bx = 1,270 seconds/mm2), 6.7-minute CBF, 2-minute ADC (by = 1,270 seconds/mm2), 2-minute ADC (bz = 1,270 seconds/mm2), and 6.7-minute CBF.
Data analysis
Magnetic resonance data analysis used code written in Mat-lab (MathWorks, Natick, MA, U.S.A.) and the STIMULATE (Strupp, 1996) software. All data in text were reported as mean ± SD and all error bars on graphs as standard errors of the means (SEM). Correlation analysis between ISODATA-lesion volumes and TTC-infarct volumes was analyzed. Statistical comparisons used two-tailed paired t-test.
Calculation of apparent diffusion coefficient and cerebral blood flow maps
Apparent diffusion coefficient maps with intensity in units of square millimeters per second were calculated pixel-by-pixel by using (Stejskal and Tanner, 1965) ADC = −ln (S1 / So)/(b1 − bo) where bi = γ2 Gi2 δ2 (Δ − δ/3) with i = 0 or 1, ln is the natural logarithm, So and S1 are the signal intensities obtained with bo and b1, respectively. The b-value is proportional to the gradient strength (G), magnetogyric ratio (γ), duration of each gradient pulse (δ), and the time (Δ) between applications of the two gradient pulses.
Cerebral blood flow images (SCBF) with intensity in units of milliliters per gram per minute were calculated (Silva et al., 1999; Duong et al., 2000) pixel-by-pixel using, SCBF = λ/T1·(Sc − SL)/(SL + (2α − 1) Sc), where SC and SL are signal intensities of the control and labeled images, respectively. λ, the water brain–blood partition coefficient, was taken to be 0.9 (Herscovitch and Raichle, 1985). T1, the water spin-lattice relaxation time of tissue, was measured to be 1.5 seconds at 4.7 T. α, the arterial spin-labeling efficiency (Williams et al., 1992), was measured to be 0.75. Although consistent with many established invasive techniques, the accuracy of this CBF technique could be subjected to errors arising from magnetization-transfer (Silva et al., 1999; Duong et al., 2000), transit-time (Calamante et al., 1996; Zhou et al., 2001), and water-exchange (Silva et al., 1997a, 1997b; Zhou et al., 2001; Parkes and Tofts, 2002) effects. Magnetization-transfer effect was not an issue with the actively decoupled two-coil system (Silva et al., 1999; Duong et al., 2000). Transit-time and water-exchange effects had been demonstrated to be small (Silva et al., 1997a, 1997b; Zhou et al., 2001; Parkes and Tofts, 2002) and were unlikely to alter the conclusions of this study.
Improved ISODATA cluster analysis
The ISODATA technique is an unsupervised segmentation method based on K-means clustering algorithm with the addition of iterative splitting and merging steps that allow statistical adjustment of the number of clusters and the cluster centers. Two major improvements based on Jacobs et al.'s algorithm (2001a) were incorporated, namely: the use of Mahalanobis distance measure and spatial contiguity.
In the original ISODATA method used to analyze stroke data (Ball and Hall, 1965; Soltanian-Zadeh et al., 1997; Jacobs et al., 2001a), Euclidean distance was used, which did not take into account the variances of the feature parameter. Mahalanobis metric (Duda and Hart, 1973) removes several of the limitations of the Euclidean metric, namely (1) it automatically accounts for the scaling of the coordinate axes, (2) it corrects for correlation between the different features, and (3) it provides curved, in addition to linear, decision boundaries. The Mahalanobis distance r can be written as,
| [1] |
where r is the Mahalanobis distance from the feature vector x to the mean vector mx, and Cx is the covariance matrix for x. The surfaces on which r is constant are ellipsoids that are centered about the mean mx. In the special case where the features are uncorrelated and the variances in all directions are the same, these surfaces are spheres, and the Mahalanobis distance measure reduces to the Euclidean distance measure.
Details of the ISODATA technique per se had been described elsewhere (Ball and Hall, 1965; Jacobs et al., 2001a). Major ISODATA steps were as follows (Jacobs et al., 2001a): Step 1: Clustering parameters were initialized, which included minimum cluster size (θN), initial guess of the number of clusters (K), splitting parameter (θS), maximum number of iterations (I), maximum number of pairs of clusters that could be lumped in one iteration (L), and convergence error (Er). Herein, θN, K, θS, I, L, and Er were typically set to be 100, 3, 0.5, 1, 80, 1, and 1 × 10−5, respectively. Step 2: Pixel vectors were distributed among the cluster centers based on the smallest Mahalanobis distance. Step 3: Cluster centers with fewer pixel vectors than the minimum cluster size were discarded and the pixel vectors in the discarded clusters were redistributed among the remaining cluster centers. Step 4: Intra- and inter-Mahalanobis distances were calculated between pixel vectors and cluster centers. Step 5: Splitting and merging of clusters were performed based on the number of clusters, size of clusters, intra- and inter-Mahalanobis distances, etc. Step 6: Steps 2 to 5 were repeated until the algorithm converged or reached the maximum number of iterations was reached. Step 7: If the algorithm converged, spatial contiguity correction (see below) was performed to remove “misclassified” pixels. If the algorithm did not converge, it returned to step 1 to adjust initial cluster parameters. Cluster classification per se used the K-mean algorithm (Tou and Gonzales, 1974).
Spatial contiguity incorporates spatial information when assigning clusters. Because of “noise” in the ADC and CBF measurements, a small fraction of (often single) pixels could be mistakenly assigned to a different membership. Consequently, a few scattered pixels of one class could be embedded in another class. For “misclassified” pixel identification, the (dis)contiguity at a single pixel (j) was defined as the fraction of its spatial neighbors that are not in the same cluster:
| [2a] |
where k(j) is the cluster to which j belongs, and k(i) is the cluster to which j's neighbors i belongs. Eight neighbors were used in this study. For cluster reassignment, another contiguity index of pixel j, Djl, was defined as
| [2b] |
where L = 1 to n_cluster and L ≠ k(j) (n_cluster is the total number of clusters). Pixels were reassigned if they had six or more of eight possible neighbors belonging to another class (Dj ≥ 6/8) and the class to which these pixels were to be reassigned had to have five or more of eight possible neighbors (Djl ≥ 5/8). Both conditions needed to be satisfied; otherwise, the pixel would not be reassigned. The goal was to remove 1 or 2 “noisy” pixels only, while avoiding erroneously reassigning pixels, especially at 30 minutes after occlusion where small “islands” of normal tissues could be embedded in large abnormal lesions.
Tissue volumes, ADC, and CBF values of ISODATA clusters
For ISODATA analysis and correlation with TTC, only five anterior slices were used to avoid susceptibility distortion around the ear canals. To increase computational efficiency, conservative ROIs of the whole brain were carefully drawn to avoid the edge of the brain–skull interface based on CBF maps with reference to ADC maps. Pixels with CBF larger than 4 mL g−1 min−1 or ADC larger than 1.2 × 10−3 mm2/s (as displayed on scatterplots) were excluded; the excluded pixels were mostly: 1) cerebrospinal-fluid pixels due to their large ADC and 2) “noise” pixels arising from dividing a small number in the CBF calculation or arising from large blood vessels. Although tighter limits could be used, doing so could risk unjustly eliminating pixels. Nonetheless, the excluded number of pixels was very small (< 5%). ISODATA analysis was performed on the “brain” pixels of each animal individually and at each time point. Multiple ISODATA clusters were resolved and CBF–ADC pixel-by-pixel scatterplots of different ISODATA clusters were generated, color-coded pixel-by-pixel, and mapped onto the image spaces. Tissue volume, ADC, and CBF of each cluster were evaluated at each time point.
Evolution of “mismatch” pixels
The evolution of the “mismatch” pixels was investigated with the 30-minute time point as a reference. The temporal evolution of the “mismatch” pixels, defined at 30 minutes after occlusion, was evaluated as they migrated to different clusters. Tissue volumes ADC, and CBF values of the pixels that subsequently migrated into the normal zone, core zone, or remained in the mismatch zone, were determined at each time point.
Cerebral-blood-flow and apparent diffusion coefficient evolution of the “persistent mismatch”
The “perfusion-diffusion” mismatch in a few animals did not disappear completely at 180 minutes (persistent mismatch, Group II). ROI analysis of the CBF and ADC evolution of the persistent mismatch were performed and compared to the homologous region in the normal left (contralateral) hemisphere. Similar ROI analysis of the analogous brain regions was also performed on another group of animals (Group I) where the mismatch disappeared completely at 180 minutes. ADC and CBF of these brain regions were plotted as a function of time.
Results
Fig. 1 shows representative CBF-ADC scatterplots and the ISODATA cluster analysis using normalized Euclidean and Mahalanobis distance measures (both without spatial contiguity) and Mahalanobis distance measures with spatial contiguity. Normalized Euclidean distance measure was used for fair comparison with the Mahalanobis distance measure because the latter is normalized by default. In the normalized Euclidean distance measure, unexpected linear cluster boundaries and/or more clusters segregated along the CBF axis were observed because the CBF distribution had a larger variance than the ADC distribution. Mahalanobis distance measure took into account the differences in variances among the feature parameters. Additionally, a few single or a small numbers of pixels of one cluster membership occasionally were found to embed in another because of “measurement noise.” With the spatial contiguity criterion, these scattered pixels were reclassified using spatial information. All subsequent analyses below used a Mahalanobis distance measure with the spatial contiguity criterion.
FIG. 1.
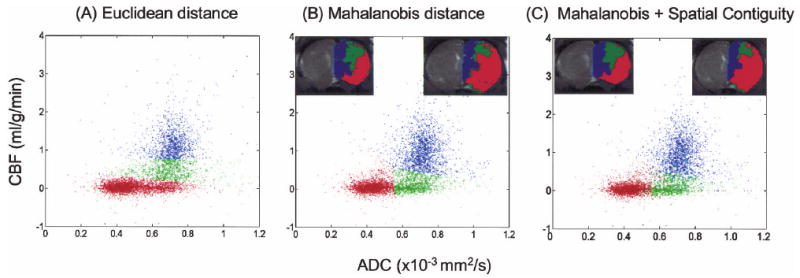
Representative ISODATA analysis of the pixel-by-pixel scatterplots of cerebral blood flow (CBF) and apparent diffusion coefficient (ADC) using (A) normalized Euclidean distance measure without spatial contiguity criterion and (B) Mahalanobis distance measure without spatial contiguity criterion, and (C) Mahalanobis distance measure with spatial contiguity. The ISODATA results were color-coded and mapped on the image spaces as shown in the insets.
Visual inspection of all the ADC and CBF maps in all animals indicated that there was a substantial “perfusion-diffusion” mismatch at 30 minutes after occlusion, consistent with a previous report (Shen et al., 2003). Essentially all the “perfusion-diffusion” mismatch disappeared in some animals (Group I, n = 5), whereas a substantial mismatch persisted in others (Group II, n = 3) at 180 minutes after occlusion. For clarity of presentation, Group I and Group II data are shown side by side where appropriate for comparisons.
Fig. 2A shows representative ADC and CBF maps at 30 and 180 minutes after occlusion. The ADC and CBF lesion volumes can be clearly visualized. There was a substantial “perfusion-diffusion” mismatch at 30 minutes after occlusion. In Group I, essentially all of the mismatch pixels disappeared at 180 minutes, and in Group II some of the mismatch persisted at 180 minutes. Fig. 2B shows the ISODATA cluster analysis of the CBF-ADC scatterplots. In contrast to the normal left hemisphere, which exhibited a single cluster, the ischemic right hemisphere showed 3 clusters at 30 minutes, namely, the normal (blue), core (red), and mismatch (green) cluster. At 180 minutes, the scatterplots showed that the mismatch had largely disappeared in Group I but some mismatch persisted in Group II. Regions of the persistent mismatch were generally located in the sensory and motor cortices, in the vicinity of the anterior communicating artery territory. Different pixel clusters resolved on the scatter-plots were mapped onto the image spaces (Fig. 2C). Mismatch was located peripherally to the ischemic core. The ischemic “core” volumes grew and the “mismatch” volumes decreased as ischemia progressed. The ISODATA-derived lesion volumes showed excellent slice-by-slice correspondence with the TTC infarct volumes for Group I, less so for Group II, presumably because some of the persistent mismatch showed delayed infarction. Both the “core” volumes at 3 hours and infarct volumes at 24 hours were smaller in Group II compared to Group I.
FIG. 2.
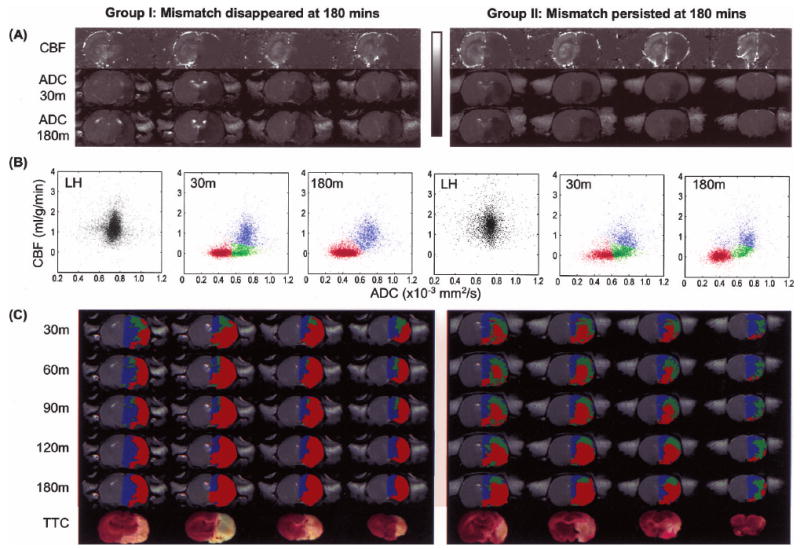
Representative data from a stroke rat with “perfusion-diffusion” mismatch disappeared at 180 minutes after ischemia (Group I, left) and another rat with some “perfusion-diffusion” mismatch remained at 180 minutes (Group II, right). (A) Cerebral blood flow (CBF) maps, and apparent diffusion coefficient (ADC) maps at 30 minutes and 180 minutes. The grayscale bar: ADC ranges from 0 to 0.001 mm2/s, CBF ranges from −1 to 2 mL g−1 min−1. (B) CBF-ADC scatterplots of the normal left hemisphere at 30 minutes, ISODATA cluster analysis results of the right hemisphere at 30 and 180 minutes. (C) Pixel clusters from the CBF-ADC scatterplots were overlaid on the image space at 30, 60, 90, 120, and 180 minutes. In the right hemisphere, blue, green, and red are assigned as “normal,” “perfusion-diffusion” mismatch, and “ischemic core” clusters, respectively. TTC slides at 24 hours are also shown.
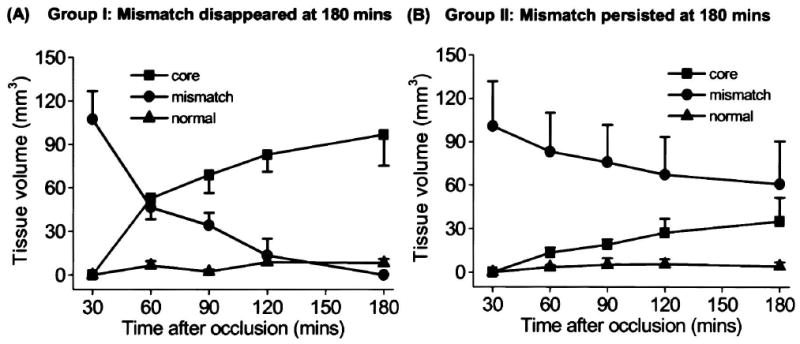
Group-average tissue-volume evolutions for the ISODATA-resolved clusters are shown in Fig. 3. The “abnormal” cluster is the sum of the core and the mismatch cluster. In Group I, the core volumes at 3 hours (255 ± 62 mm3) were very similar to the TTC infarct volumes at 24 hours (253 ± 55 mm3) (P > 0.05). In Group II, the mismatch volumes decreased by a smaller magnitude relative to that of Group I. The TTC infarct volumes at 24 hours (148 ± 18 mm3) was similar to the “core” lesion volumes at 3 hours (140 ± 8 mm) (P > 0.05) but smaller than the abnormal volumes at 3 hours (198 ± 7 mm3) (P < 0.05).
FIG. 3.
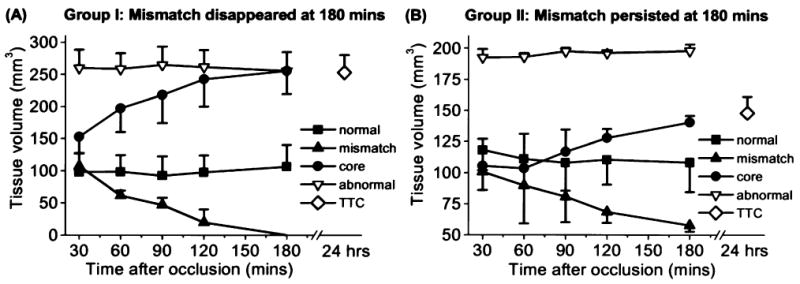
Temporal evolution of the group-average tissue volumes of the normal, mismatch, core, and “abnormal” (core + mismatch) clusters for (A) a group of animals with “perfusion-diffusion” mismatch disappeared at 180 minutes after ischemia (Group I, mean ± SEM, n = 5), and (B) another group of animals with some “perfusion-diffusion” mismatch persisted at 180 minutes (Group II, n = 3). TTC infarct volumes were obtained at 24 hours after ischemia.
A correlation analysis was performed between ISODATA-derived lesion volumes and TTC infarct volumes for each animal at each time point after occlusion (Fig. 4). Groups I and II were plotted and analyzed together. The correlation coefficients with respect to the unity line for 30, 60, 90, 120, and 180 minutes after ischemia were 0.62, 0.74, 0.83, 0.94, 0.99, respectively, indicating ISODATA-derived lesion volumes at 180 minutes showed the best correlation with TTC infarct volumes.
FIG. 4.
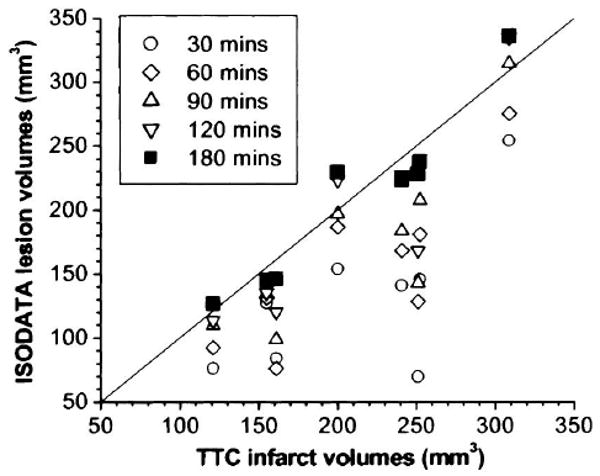
Correlation plot of ISODATA-derived lesion volumes and TTC infarct volumes at each time point after ischemia. Group I and II were plotted and analyzed together where the data points with three smallest TTC infarct volumes belonged to Group II. The correlation values with respective to the unity line for 30, 60, 90, 120, and 180 minutes after ischemia were 0.62, 0.74, 0.83, 0.94, and 0.99, respectively.
Tissue fates of the perfusion–diffusion mismatch
The fate of the “perfusion–diffusion” mismatch pixels was dynamically tracked in terms of their tissue volumes, ADC, and CBF values as these pixels migrated to different clusters (Fig. 5). The “normal” left hemisphere ADC and CBF were 0.74 ± 0.02 × 10−3 mm2/s and 1.36 ± 0.22 mL g−1 min−1, respectively, consistent with those reported previously in normal (Sicard et al, 2003; Liu et al., in press) and stroke (Shen et al., 2003; 2004) animals under similar experimental conditions. In Group I, the mismatch volume gradually decreased as ischemia progressed with essentially all pixels migrating exclusively to the “core” zone at 180 minutes. The ADC of the pixels that subsequently migrated to the “core” zone were 0.68 ± 0.02 × 10−3 and 0.46 ± 0.04 × 10−3 mm2/s at 30 and 180 minutes, respectively; the corresponding CBF values were 0.24 ± 0.20 and 0.05 ± 0.03 mL g−1 min−1.
FIG. 5.
The temporal evolution of the group-average “perfusion-diffusion mismatch” tissue volumes before and after migration to different zones as ischemia progressed. (A) A group of animals with the mismatch disappeared at 180 minutes (Group I, mean ± SEM, n = 5). (B) Another group of animals with some mismatch persisted at 180 minutes (Group II, n = 3).
In Group II, the mismatch volume also gradually decreased as ischemia progressed, but a substantial number of mismatch pixels remained at 180 minutes. The ADC of the pixels that subsequently migrated to the “core” zone was 0.66 ± 0.02 × 10−3 and 0.45 ± 0.05 × 10−3 mm2/s at 30 and 180 minutes, respectively; the mean CBF was 0.13 ± 0.10 and 0.08 ± 0.13 mL g−1 min−1 at 30 and 180 minutes, respectively. The mean ADC of the pixels remaining in the mismatch zone was 0.70 ± 0.02 × 10−3 and 0.67 ± 0.04 × 10−3 mm2/s at 30 and 180 minutes, respectively; their mean CBF was 0.22 ± 0.05 and 0.20 ± 0.09 mL g−1 min−1 at 30 and 180 minutes, respectively.
Characterization of “persistent mismatch”
Cerebral blood flow and ADC of the “persistent mismatch” at 180 minutes were characterized in detail. Fig. 6A shows the CBF results. The mean CBF of the “persistent mismatch” (ischemic right hemisphere) in Group II (0.3 ± 0.09 mL/g/min) was statistically higher (30 minutes: P < 0.05; other time points: P < 0.01) than the CBF from the analogous region in Group I where the mismatch disappeared at 180 minutes (0.08 ± 0.03 mL g−1 min−1). For reference, CBF in the homologous regions in the normal left hemisphere showed no statistical differences (P > 0.05) at all time points between Group I (1.42 ± 0.53 mL g−1 min−1) and Group II (1.36 ± 0.11 mL g−1 min−1).
FIG. 6.
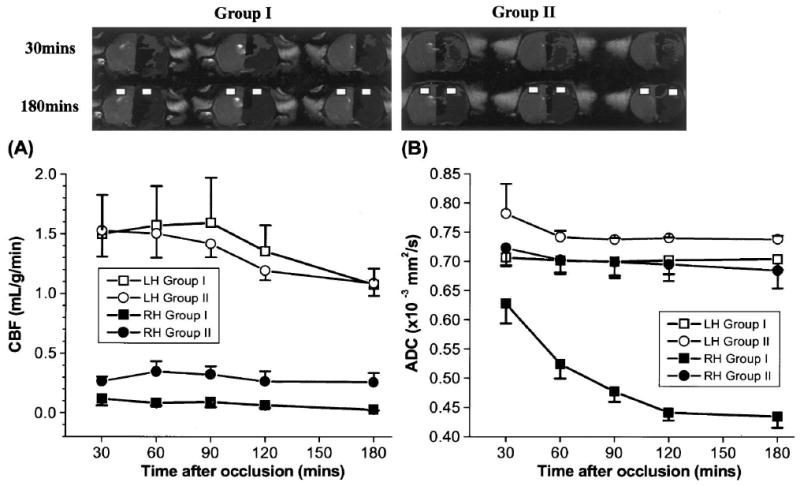
Temporal evolution of (A) cerebral blood flow (CBF) and (B) apparent diffusion coefficient (ADC) of the brain regions with and without “persistent mismatch” at 180 minutes (Group I, n = 5; Group II, n = 3). Regions of persistent mismatch generally located at the sensory and motor cortices. Representative regions of interest used in the analyses are shown. Error bars are SEMs.
Fig. 6B shows the ADC results. In Group II, the ADCs of the “persistent mismatch” (right hemisphere) did not decrease as ischemia progressed and were not statistically different from the ADCs in the homologous regions of the left hemisphere (P > 0.05). In marked contrast, the mean ADC of the analogous brain regions in the ischemic right hemisphere of Group I gradually decreased as ischemia progressed from 0.63 ± 0.05 mm2/s (30 minutes) to 0.43 ± 0.03 mm2/s (180 minutes). These results were consistent with the endpoint histology.
Discussion
The major findings of this study can be summarized as follows: (1) an improved algorithm based on the automated ISODATA technique was developed and applied to characterize the spatiotemporal dynamic evolution of ischemic brain injury based on high-resolution, quantitative perfusion and diffusion measurements. (2) In contrast to the normal left hemisphere, multiple clusters were resolved in the ischemic right hemisphere, corresponding to the “normal”, “at risk” (“perfusion-diffusion” mismatch), and “ischemic core” tissues. (3) Tissue volumes, ADC, and CBF of each ISODATA cluster were quantified. Pixels of different ISODATA clusters were color-coded and mapped onto the image and ADC-CBF spaces. (4) In some animals, essentially all the “perfusion-diffusion” mismatch pixels disappeared, while in other animals some mismatch pixels persisted at 180 minutes after occlusion. (5) CBF of the “persistent mismatch” at 180 minutes was statistically higher than the CBF from the analogous region where the mismatch disappeared at 180 minutes. The ADC of the “persistent mismatch” did not decrease as ischemia progressed. In marked contrast, the ADC of analogous brain regions where the mismatch disappeared at 180 minutes decreased precipitously as ischemia progressed.
Multiparametric analysis had been correlated with histology or stroke outcomes (Welch et al., 1995; Jiang et al., 1997; Carano et al., 1998; Carano et al., 2000; Jacobs et al., 2000, 2001a, 2001b; Wu et al., 2001; Mitsias et al., 2002). However, none of these studies used ISODATA analysis to dynamically track tissue fates on a pixel-by-pixel basis as ischemia progresses during the acute phase where the perfusion-diffusion mismatch is dynamically evolving and can potentially be salvaged. “Perfusion-diffusion mismatch” had been widely observed in acute human stroke (Albers, 1999; Schlaug et al., 1999; Rohl et al., 2001); similar observation on animal stroke models, however, had been limited (Lythgoe et al., 1999; Carano et al., 2000). Recently, Shen et al. (2003; 2004) characterized the spatiotemporal dynamic evolution of the “perfusion-diffusion mismatch” in rats by using quantitative perfusion and diffusion imaging during the acute phase (albeit lower spatial resolution compared to the current study) where proton density, T1, and T2 relaxation times were generally unaffected. “Viability thresholds” were derived via correlation of CBF- and ADC-defined lesion volumes at 3 hours with histo-logical (TTC) staining at 24 hours, consistent with viability thresholds derived using other correlation techniques (Busza et al., 1992; Hoehn-Berlage et al., 1995; Kohno et al., 1995; Shen et al., 2003). These “viability thresholds” were used to characterize different tissue clusters, particularly the “perfusion-diffusion” mismatch, in permanent (Shen et al., 2003) and transient (Shen et al., 2004, in press) ischemic brain injury. Classification of pixel clusters using fixed viability thresholds has some advantages and disadvantages. The advantages are as follows: it is simple to use, it can be correlated to a specific ischemic event, and it yields reasonably accurate information regarding tissue properties. The disadvantages are as follows: the number of clusters is fixed, the results are subjected to errors from cross-modality comparison, and there are potentially different thresholds depending on which “gold standard” is used for correlation.
The improved automated ISODATA technique is ideal for analyzing stroke data during the acute phase. The “perfusion-diffusion” mismatch is of particular interest because its cluster membership, tissue volume, ADC, and CBF dynamically evolve as ischemia progresses. Resolving tissue fates using ISODATA analysis of ADC and CBF data during the dynamic acute phase posed a more challenging problem, relative to previous ISODATA analysis using T1-weighted, T2-weighted, and diffusion-weighted imaging data where the clusters in the feature spaces are relatively more separated in the subacute or chronic phase. In our case, pixel clusters on the CBF-ADC scatterplots showed substantial overlap during the acute phase. Critical to the ISODATA analysis of the CBF and ADC during the acute phase are the implementation of the Mahalanobis distance measure, spatial contiguity, and high-resolution quantitative imaging. The high-resolution ADC and CBF data yielded a finer discrimination at the border zones of different tissue fates via reduction of partial-volume effects (albeit with a lower signal-to-noise ratio) as well as quadrupling the pixel density relative to low resolution imaging (64 × 64 matrix) and, thus, improved the statistics of the cluster analysis. To partially compensate for the reduced signal-to-noise ratio at high spatial resolution, surface coil and imaging parameters were carefully optimized and the total acquisition time was lengthened (from 10 to 30 minutes) relative to previous studies performed at lower spatial resolution (Shen et al., 2003; 2004). The lengthened total acquisition time could result in temporal averaging in the ischemic evolution, especially during the early time points (i.e., 30 and 60 minutes); such temporal averaging had less effect on the later time points. Although the relatively wider CBF distribution in the left hemisphere relative to ADC arose primarily from intrinsic tissue CBF heterogeneity, improved accuracy of the CBF measurement is expected to improve ISODATA results.
The presence or absence of “persistent mismatch” at 3 hours could arise from different degree of occlusion (i.e., position and size of occluders) and the extent of collateral perfusion, as well as interanimal variation of the vascular structures. CBF (0.3 mL g−1 min−1 at all time points) of the pixels that showed persistent mismatch at 180 minutes (Group II) was above or similar to the viability CBF threshold of 0.2 to 0.3 mL g−1 min−1 (Busza et al., 1992; Hoehn-Berlage et al., 1995; Kohno et al., 1995; Shen et al., 2003). Our measured CBF was likely to be the lower limit because of increased transit time in the ischemic right hemisphere; thus, the actual CBF of the persistent mismatch was likely higher than 0.3 mL g−1 min−1 and thus above the CBF viability threshold. In marked contrast, CBF (0.1 mL g−1 min−1, at all time points) in analogous brain regions of Group I where the perfusion–diffusion mismatch at 180 minutes disappeared was below the viability CBF threshold.
CBF viability thresholds were derived using various correlation techniques. For example, Crockard et al. (1987) used a hydrogen-clearance-electrode technique and reported a CBF threshold of 0.2 mL g−1 min−1 that best correlated with the loss of high-energy phosphates. Naritomi et al. (1988) used 14C-iodoantipyrine autoradiography and reported a CBF threshold of 0.12 to 0.20 mL g−1 min−1 that best correlated with the loss of sodium-ATPase pump failure. Hoehn-Berlage et al. (1995) used 14C-iodoantipyrine autoradiography and derived a CBF threshold of 0.2 mL g−1 min−1 based on correlation with loss of energy metabolism (ATP depletion stained by postmortem bioluminescent technique). Shen et al. (2003) used TTC histology correlation and derive a CBF threshold of 0.3 mL g−1 min−1. Kohno et al. (1995) used 14C-iodoantipyrine autoradiography and reported a CBF threshold of 0.31 mL g−1 min−1, which correlated with the onset of reduced glucose metabolism and lactate acidosis but before energetic failure. Belayev et al. (1997) and Zhao et al. (1997) used 14C-iodoantipyrine autoradiography and derived an average penumbral CBF threshold of 0.3 mL g−1 min−1. Although these critical thresholds were derived using different CBF measurement techniques, different stroke models and correlation with different ischemic events, they showed consistent values ranging from 0.2 to 0.3 mL g−1 min−1.
The CBF profiles indeed had critical effects on the ADC values. In Group II where there was a persistent mismatch, the ADC in regions with persistent mismatch (right hemisphere) was not statistically different from that of the homologous regions in the normal left hemisphere and did not decrease as ischemia progressed. In Group I where the persistent mismatch disappeared at 180 minutes, the ADC in that region dropped below the critical ADC threshold [0.53 ± 0.02 × 10−3 mm2/s (Shen et al., 2003)] at 120 minutes after occlusion. These results clearly indicated that quantitative CBF and ADC could be used to track and predict tissue fates in ischemic brain injury during the acute phase.
Finally, additional clusters could exist in principle. From the biological standpoint, for example, an oligemic cluster could be present, and the persistent mismatch and the mismatch that disappeared at 180 minutes should belong to different clusters. However, tissue CBF is highly heterogeneous and shows substantial overlap among different types and different tissue status. Consequently, ISODATA analysis failed to distinguish various biologically relevant clusters. Improved signal-to-noise ratios in CBF and ADC measurements as well as inclusion of other measured parameters, such as functional MRI data (Duong and Fisher, 2004) could potentially make resolving other biologically relevant clusters possible. Clinical applications of automated cluster analysis to resolve and track ischemic tissue fates are feasible in principle. Potential problems could arise because quantitative CBF is not yet widely available (qualitative CBF measurements generally necessitates a contralateral hemisphere comparison) and currently available CBF techniques in human applications have relatively poorer combined signal-to-noise ratio and spatial resolution. Furthermore, CBF and ADC are likely to be more heterogeneous in the human brain compared to the rat brain. Rat brain constitutes mostly of gray matter; white matter (mainly the corpus callosum) constitutes a small volume fraction of cerebrum and could be judicially ignored or readily segmented out. In humans, white matter is intricately mixed with gray matter and needs to be classified, which is expected to add complexity to the ISODATA analysis. Nonetheless, clinical applications of the automated ISODATA technique have the potential to become routine (Mitsias et al., 2002).
Conclusions
An improved ISODATA algorithm was developed to dynamically track ischemic tissue fates on a pixel-by-pixel basis during the acute phase using high-resolution, quantitative perfusion and diffusion imaging. Tissue volumes, ADC, and CBF distributions of each cluster were evaluated, and different ISODATA clusters were overlaid on the CBF-ADC scatterplots and the image spaces. CBF of the “persistent mismatch” was above the CBF viability threshold, and its ADC did not decrease as ischemia progressed. In marked contrast, CBF of analogous brain regions where the mismatch disappeared at 180 minutes was below the CBF viability threshold and its ADC decreased precipitously as ischemia progressed. This analysis approach is expected to be useful in predicting tissue fates and monitoring the spatiotemporal dynamics in cluster membership as a function of therapeutic intervention.
Acknowledgments
Supported in part by a Scientist Development Grant from the American Heart Association and a grant from the National Institute of Health (NINDS, R01-NS045879)TQD.
References
- Albers GW. Expanding the window for thrombolytic therapy in acute stroke: The potential role of acute MRI for patient selection. Stroke. 1999;30:2230–2237. doi: 10.1161/01.str.30.10.2230. [DOI] [PubMed] [Google Scholar]
- Astrup J, Symon L, Siesjo BK. Thresholds in cerebral ischemia: the ischemic penumbra. Stroke. 1981;12:723–725. doi: 10.1161/01.str.12.6.723. [DOI] [PubMed] [Google Scholar]
- Ball GH, Hall DJ. ISODATA: A novel method of data analysis and pattern classification. Menlo Park, CA: Stanford Research Institute; 1965. [Google Scholar]
- Belayev L, Zhao W, Busto R, Ginsberg MD. Transient middle cerebral artery occlusion by intraluminal suture: I. Three-dimensional autoradiographic image-analysis of local cerebral glucose metabolism-blood flow interrelationships during ischemia and early recirculation. J Cereb Blood Flow Metab. 1997;17:1266–1280. doi: 10.1097/00004647-199712000-00002. [DOI] [PubMed] [Google Scholar]
- Busza AL, Allen KL, King MD, van Bruggen N, Williams SR, Gadian DG. Diffusion-weighted imaging studies of cerebral ischemia in gerbils: Potential relevance to energy failure. Stroke. 1992;23:1602–1612. doi: 10.1161/01.str.23.11.1602. [DOI] [PubMed] [Google Scholar]
- Calamante F, Williams SR, van Bruggen N, Kwong KK, Turner R. A model for quantification of perfusion in pulsed labeling techniques. NMR Biomed. 1996;9:79–83. doi: 10.1002/(SICI)1099-1492(199604)9:2<79::AID-NBM399>3.0.CO;2-4. [DOI] [PubMed] [Google Scholar]
- Carano RA, Takano K, Helmer KG, Tatlisumak T, Irie K, Petruccelli JD, Fisher M, Sotak CH. Determination of focal ischemic lesion volume in the rat brain using multispectral analysis. J Magn Reson Imaging. 1998:1266–1278. doi: 10.1002/jmri.1880080614. [DOI] [PubMed] [Google Scholar]
- Carano RA, Li F, Irie K, Helmer KG, Silva MD, Fisher M, Sotak CH. Multispectral analysis of the temporal evolution of cerebral ischemia in the rat brain. J Magn Reson Imag. 2000;12:842–858. doi: 10.1002/1522-2586(200012)12:6<842::aid-jmri7>3.0.co;2-5. [DOI] [PubMed] [Google Scholar]
- Crockard HA, Gadian DG, Frackowiak RS, Proctor E, Allen K, Williams SR, Russell RW. Acute cerebral ischaemia: concurrent changes in cerebral blood flow, energy metabolites, pH, and lactate measured with hydrogen clearance and 31P and 1H nuclear magnetic resonance spectroscopy. II. Changes during ischaemia. J Cereb Blood Flow Metab. 1987;7:394–402. doi: 10.1038/jcbfm.1987.82. [DOI] [PubMed] [Google Scholar]
- Duda RO, Hart PE. Pattern classification and scene analysis. New York, NY: John Wiley & Sons; 1973. [Google Scholar]
- Duong TQ, Fisher M. Application of perfusion/diffusion MRI in experimental and clinical aspects of stroke. Curr Atherosclerosis Rep. 2004;6:267–273. doi: 10.1007/s11883-004-0057-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duong TQ, Silva AC, Lee SP, Kim SG. Functional MRI of calcium-dependent synaptic activity: cross correlation with CBF and BOLD measurements. Magn Reson Med. 2000;43:383–392. doi: 10.1002/(sici)1522-2594(200003)43:3<383::aid-mrm10>3.0.co;2-q. [DOI] [PubMed] [Google Scholar]
- Helpern JA, Dereski MO, Knight RA, Ordidge RJ, Chopp M, Qing ZX. Histopathological correlations of nuclear magnetic resonance imaging parameters in experimental cerebral ischemia. Magn Reson Imaging. 1993;11:241–246. doi: 10.1016/0730-725x(93)90028-c. [DOI] [PubMed] [Google Scholar]
- Herscovitch P, Raichle ME. What is the correct value for the brain-blood partition coefficient for water? J Cereb Blood Flow Metab. 1985;5:65–69. doi: 10.1038/jcbfm.1985.9. [DOI] [PubMed] [Google Scholar]
- Hoehn-Berlage M, Norris DG, Kohno K, Mies G, Leibfritz D, Hoss-mann KA. Evolution of regional changes in apparent diffusion coefficient during focal ischemia of rat brain: The relationship of quantitative diffusion NMR imaging to reduction in cerebral blood flow and metabolic disturbances. J Cereb Blood Flow Metab. 1995;15:1002–1011. doi: 10.1038/jcbfm.1995.126. [DOI] [PubMed] [Google Scholar]
- Jacobs MA, Knight RA, Soltanian-Zadeh H, Zheng ZG, Goussev AV, Peck DJ, Windham JP, Chopp M. Unsupervised segmentation of multiparameter MRI in experimental cerebral ischemia with comparison to T2, diffusion, and ADC MRI parameters and his-topathological validation. J Magn Reson Imag. 2000;11:425–437. doi: 10.1002/(sici)1522-2586(200004)11:4<425::aid-jmri11>3.0.co;2-0. [DOI] [PubMed] [Google Scholar]
- Jacobs MA, Mitsias P, Soltaniaan-Zadeh H, Santhakumar S, Ghanei A, Hammound R, Peck DJ, Chopp M, Patel S. Multiparamet-ric MRI tissue characterization in clinical stroke with correlation to clinical outcome: Part 2. Stroke. 2001a;32:950–957. doi: 10.1161/01.str.32.4.950. [DOI] [PubMed] [Google Scholar]
- Jacobs MA, Zhang ZG, Knight RA, Soltanian-Zadeh H, Goussev AV, Peck DJ, Chopp M. A model for multiparametric MRI tissue characterization in experimental cerebral ischemia with his-tological validation in rat: Part 1. Stroke. 2001b;32:943–949. doi: 10.1161/01.str.32.4.943. [DOI] [PubMed] [Google Scholar]
- Jiang Q, Chopp M, Zhang ZG, Knight RA, Jacobs MA, Windham JP, Peck DJ, Ewing JR, Welch KMA. The temporal evolution of MRI tissue signatures after transient middle cerebral artery occlusion in rat. J Neurol Sci. 1997;145:15–23. doi: 10.1016/s0022-510x(96)00286-9. [DOI] [PubMed] [Google Scholar]
- Knight RA, Dereski MO, Helpern JA, Ordidge RJ, Chopp M. MRI assessment of evolving focal cerebral ischemia; comparison with histopathology in rats. Stroke. 1994;25:1252–1262. doi: 10.1161/01.str.25.6.1252. [DOI] [PubMed] [Google Scholar]
- Kohno K, Hoehn-Berlage M, Mies G, Back T, Hossmann KA. Relationship between diffusion-weighted MR images, cerebral blood flow, and energy state in experimental brain infarction. Magn Reson Imag. 1995;13:73–80. doi: 10.1016/0730-725x(94)00080-m. [DOI] [PubMed] [Google Scholar]
- Liu ZM, Schmidt K, Sicard KM, Duong TQ. Imaging oxygen consumption in forepaw stimulation under isoflurane anesthesia. Magn Reson Med. 2004 doi: 10.1002/mrm.20148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lythgoe MF, Busza AL, Calamante F, Sotak CH, King MD, Bingham AC, Williams SR, Gadian DG. Effects of diffusion anisotropy on lesion delineation in a rat model of cerebral ischemia. Magn Reson Med. 1997;38:662–668. doi: 10.1002/mrm.1910380421. [DOI] [PubMed] [Google Scholar]
- Lythgoe MF, Williams SR, Busza AL, Wiebe L, McEwan AJ, Gadian DG, Gordon I. The relationship between magnetic resonance diffusion imaging and autoradiographic markers of cerebral blood flow and hypoxia in an animal stroke model. Magn Reson Imag. 1999;41:706–714. doi: 10.1002/(sici)1522-2594(199904)41:4<706::aid-mrm8>3.0.co;2-8. [DOI] [PubMed] [Google Scholar]
- Mitsias PD, Jacobs MA, Hammound R, Pasnoor M, Santhakumar S, Papamitsakis NIH, Soltanian-Zadeh H, Lu M, Chopp M, Patel SC. Multiparametric MRI ISODATA ischemic lesion analysis correlation with the clinical neurological deficit and single-parameter MRI techniques. Stroke. 2002:2839–2844. doi: 10.1161/01.str.0000043072.76353.7c. [DOI] [PubMed] [Google Scholar]
- Moseley ME, Cohen Y, Mintorovitch J, Chileuitt L, Shimizu H, Kucha-rczyk J, Wendland MF, Weinstein PR. Early detection of regional cerebral ischemia in cats: comparison of diffusion- and T2-weighted MRI and spectroscopy. Magn Reson Med. 1990;14(2):330–346. doi: 10.1002/mrm.1910140218. [DOI] [PubMed] [Google Scholar]
- Naritomi H, Sasaki M, Kanashiro M. Flow thresholds for cerebral energy disturbance and Na+ pump failure as studied by in vivo 31P and 23Na nuclear magnetic resonance spectroscopy. J Cereb Blood Flow Metab. 1988;8:16–23. doi: 10.1038/jcbfm.1988.3. [DOI] [PubMed] [Google Scholar]
- Parkes LM, Tofts PS. Improved accuracy of human cerebral blood perfusion measurements using arterial spin labeling: Accounting for capillary water permeability. Magn Reson Med. 2002;48:27–41. doi: 10.1002/mrm.10180. [DOI] [PubMed] [Google Scholar]
- Rohl L, Ostergaard L, Simonsen CZ, Vestergaard-Poulsen P, Andersen G, Sakoh M, Le Bihan D, Gyldensted C. Viability thresholds of ischemic penumbra of hyperacute stroke defined by perfusion-weighted MRI and apparent diffusion coefficient. Stroke. 2001;32:1140–1146. doi: 10.1161/01.str.32.5.1140. [DOI] [PubMed] [Google Scholar]
- Schlaug G, Benfield A, Baird AE, Siewert B, Lovblad KO, Parker RA, Edelman RR, Warach S. The ischemic penumbra: operationally defined by diffusion and perfusion MRI. Neurology. 1999;53:1528–1537. doi: 10.1212/wnl.53.7.1528. [DOI] [PubMed] [Google Scholar]
- Shen Q, Meng X, Fisher M, Sotak CH, Duong TQ. Pixel-by-pixel spatiotemporal progression of focal ischemia derived using quantitative perfusion and diffusion imaging. J Cereb Blood Flow Metab. 2003;23:1479–1488. doi: 10.1097/01.WCB.0000100064.36077.03. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen Q, Fisher M, Sotak CH, Duong TQ. Effect of reperfusion on ADC and CBF pixel-by-pixel dynamics in stroke: Characterizing tissue fates using quantitative diffusion and perfusion imaging. J Cereb Blood Flow Metab. 2004;24:280–290. doi: 10.1097/01.WCB.0000110048.43905.E5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sicard K, Shen Q, Brevard ME, Sullivan R, Ferris CF, King JA, Duong TQ. Regional cerebral blood flow and BOLD responses in conscious and anesthetized rats under basal and hypercapnic conditions: implications for functional MRI studies. J Cereb Blood Flow Metab. 2003;23(4):472–481. doi: 10.1097/01.WCB.0000054755.93668.20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Silva A, Williams D, Koretsky A. Evidence for the exchange of arterial spin-labeled water with tissue water in rat brain from diffusion-sensitized measurements of perfusion. Magn Reson Med. 1997a;38:232–237. doi: 10.1002/mrm.1910380211. [DOI] [PubMed] [Google Scholar]
- Silva AC, Zhang W, Williams DS, Koretsky AP. Estimation of water extraction fractions in rat brain using magnetic resonance measurement of perfusion with arterial spin labeling. Magn Reson Med. 1997b;37:58–68. doi: 10.1002/mrm.1910370110. [DOI] [PubMed] [Google Scholar]
- Silva AC, Lee SP, Yang C, Iadecola C, Kim SG. Simultaneous BOLD and perfusion functional MRI during forepaw stimulation in rats. J Cereb Blood Flow Metab. 1999;19:871–879. doi: 10.1097/00004647-199908000-00006. [DOI] [PubMed] [Google Scholar]
- Soltanian-Zadeh H, Windham J, Robbins L. Semi-supervised segmentation of MRI stroke studies. Proc SPIE. 1997;3034:437–448. [Google Scholar]
- Stejskal EO, Tanner JE. Spin diffusion measurements: Spin echoes in the presence of a time-dependent field gradient. J Chem Physics. 1965;42:288–292. [Google Scholar]
- Strupp JP. Stimulate: A GUI based fMRI analysis software package. NeuroImage. 1996;3:S607. [Google Scholar]
- Tatlisumak T, Carano RA, Takano K, Opgenorth T, Sotak CH, Fisher M. A novel endothelin antagonist, A-127722, attenuates ischemic lesion size in rats with temporal middle cerebral artery occlusion: a diffusion and perfusion MRI study. Stroke. 1998;29:850–858. doi: 10.1161/01.str.29.4.850. [DOI] [PubMed] [Google Scholar]
- Tou T, Gonzales RC. Pattern recognition principles. Reading, MA: Addision-Wesley; 1974. [Google Scholar]
- Welch KM, Windham J, Knight RA, Negesh V, Hugg NV, Jacobs MA, Peck D, Booker P, Dereski MO, Levine SR. A model to predict the histopathology of human stroke using diffusion and T2-weighted magnetic resonance imaging. Stroke. 1995;26:1983–1989. doi: 10.1161/01.str.26.11.1983. [DOI] [PubMed] [Google Scholar]
- Williams DS, Detre JA, Leigh JS, Koretsky AP. Magnetic resonance imaging of perfusion using spin inversion of arterial water. Proc Natl Acad Sci U S A. 1992;89:212–216. doi: 10.1073/pnas.89.1.212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu O, Koroshetz WJ, Ostergard L, Buonanno FS, Copen W, Gonzales R, Rordorf G, Rosen BR, Schwamm LH, Weisskoff RM, Sorensen AG. Predicting tissue outcome in acute human cerebral ischemia using combined diffusion- and perfusion-weighted MR imaging. Stroke. 2001;32:933–942. doi: 10.1161/01.str.32.4.933. [DOI] [PubMed] [Google Scholar]
- Zhao W, Belayev L, Ginsberg MD. Transient middle cerebral artery occlusion by intraluminal suture: II. Neurological deficits, and pixel-based correlation of histopathology with local blood flow and glucose utilization. J Cereb Blood Flow Metab. 1997;17:1281–1290. doi: 10.1097/00004647-199712000-00003. [DOI] [PubMed] [Google Scholar]
- Zhou J, Wilson DA, Ulatowski JA, Traystman RJ, van Zijl PC. Two-compartment exchange model for perfusion quantification using arterial spin tagging. J Cereb Blood Flow Metab. 2001;21:440–455. doi: 10.1097/00004647-200104000-00013. [DOI] [PubMed] [Google Scholar]


