Models to Approximate the Motions of Protein Loops

Abstract

We approximate the loop motions of various proteins by using a coarse-grained model and the theory of rubberlike elasticity of polymer chains. The loops are considered as chains where only the first and the last residues thereof are tethered by their connections to the main structure; while within the loop, the loop residues are connected only to their sequence neighbors. We applied these approximate models to five proteins. Our approximation shows that the loop motions can usually be computed locally which shows these motions are robust and not random. But most interestingly, the new method presented here can be used to compute the likely motions of loops that are missing in the structures.

INTRODUCTION

Coarse-grained Elastic Network Models (ENM) have been extremely successful in predicting the large-scale motions of proteins, RNA and other biological structures, even for the largest complexes such as the ribosome. The predicted fluctuations of the positions of amino acids in the coarse-grained representations usually give excellent agreement with the experimental B-factors reported by crystallographers,^1–3 the ensembles reports by NMR scientists,⁴ and the variability in structures manifested in the known multiple structures of the same protein ^4,5. The only information required in the ENMs is the structure of the protein, to furnish the coarse-grained coordinates of essential atoms, usually those of the of C^α atoms (but they could be other points representing the amino acids, such as centers of mass of side chains) for residue-level coarse graining. It has been shown that fluctuations of residues in proteins depend mostly on the protein’s shape.⁶ Because of this the ENMs give excellent results even for relatively low-resolution structural data, such as electron micrographs.

The problem of modeling the conformations of external protein loops is a really important problem. These are generally the most mobile parts of the protein localized on their surface and are the functional sites for many protein activities, particularly for encounter complexes and binding. Because of their relatively high mobilities they are often unresolved in the crystal structures, particularly for larger loops. Because of this, frequently the PDB coordinates for residues in loops are either missing, or have alternative positions. When obtaining an experimental structure, often the loops are the most uncertain parts of the structure.

Functions of biomolecules depend on their structures and are often exerted through functional motions. This makes understanding loop motions in proteins a particularly critical problem. Often interactions with other proteins or ligands, can lead to apparent rearrangements of loops to accommodate functional ligands. For drug binding, the reconfiguration of target protein loops is relevant. Thus the frequent involvement of external loops in function makes the prediction of their conformations essential for many structural applications in molecular biology, medicine, pharmacy and drug design. The motions of loops computed by using ENMs have been intriguing, since often these move together with motions of the large-scale domains, either as rigid parts of domains or as separate parts moving in an anticorrelated way, but controlled by the domain motions. We have observed that the functionally meaningful loops most often appear to move under the control of the entire structure and its domain motions. Protein loops have been the focus of many previous studies. Modeling of loops has a significant role in making comparisons between protein structures,⁷ since these may be found in one structure and missing in the other. The field of structural genomics often requires building loop structures ⁸. Methods for the automated classification of the structures of protein loops have been developed ⁹. In principle, the study of loops can aid the understanding of protein evolution ¹⁰. Panchenko and Madej ¹⁰ noted that protein loops are far from being random coils, regardless of their size. Changes in the conformations of protein loops have also been a subject of some specific study.¹¹ The importance of protein loops for protein function has been widely acknowledged.¹² Conformations of loops play a large role in protein docking as has been pointed out in References 13–16. The motion of protein loops, especially where they are flexible is an important factor for understanding the various roles that proteins play. The website https://simtk.org/home/looptk provides a toolkit to model the kinematics of protein loops. In Reference ¹⁷ a novel approach for loop prediction was presented and analyzed. Kolodny et al.¹⁸ describe an algorithm for generating conformations of candidate loops for a gap of a given size. A similar work also appeared in Reference.¹⁹ Protein loops are also essential for protein folding.²⁰ Conformational evaluation of loops and their major role in protein design was discussed in Reference ²¹. The importance of loop prediction was emphasized also in Reference.²² In this paper we devise a method for specifying how a protein loop can adopt different configurations. Our simple approximate model accounts only for the sequential connections within the loop and the loop’s connections at the two ends, and this is a surprisingly successful model for generating loop forms. The issues of other interactions of the loop with the body of the protein are not explicitly taken into account in this work.

To overcome the difficulties with loop predictions, here we have applied the analytical theory of fluctuations in Gaussian Phantom Networks originally developed in the rubber-like elasticity theory of polymers by James and Guth,^23–26 and others.^27–33 The theory assumes that polymer chains are phantom-like, i.e. they can pass freely through one another, so that excluded volume effects are to be completely neglected. . It is also assumed that the distributions of the end-to-end vectors for polymer chains are Gaussian. This means that mechanically the network behaves as a collection of nodes (junctions) connected by simple Hookean springs and both chains and junctions fluctuate harmonically around their mean positions. Kloczkowski et al.²⁸ obtained analytical solutions for this model by assuming that all junctions in the network have the same connectivity φ (i.e. each junction is connected to φ other chains) and that a polymer network has the topology of an infinite tree. The theory provides analytical expressions for fluctuations of chains and junctions in such networks and for correlations of instantaneous fluctuations of two different points within the network.

The theory of phantom elastomeric networks was successfully adapted to treat protein motions originally as the Gaussian Network Model (GNM) by Bahar and Erman¹ and others.^3,6,34–38 Their coarse-grained model was based on an earlier work of Tirion ³⁹ who proposed that both non-bonded and covalently bonded atomic contacts in proteins could be modeled using a universal single spring constant in a harmonic analysis of protein dynamics. She assumed that two atoms are connected by a spring if they are separated by a distance smaller than a specified cutoff value. This defines a connectivity matrix for a system of nodes connected by springs. The coarse-grained GNM model enables computation of fluctuations of residues around their mean positions in protein structures directly from this connectivity matrix. Fluctuations of residues are simply expressed by the diagonal elements of the inverse of the connectivity matrix. Theoretical predictions are usually in quite good agreement with crystallographic temperature factors (B-factors) that measure the extent of disorder in crystallographically-determined positions of atoms resulting from thermal motions. Several variations of the elastic network approach to treat protein dynamics have been proposed recently,^{4,35,36,40,41} that additionally improve agreement of theoretical results with B-factors.

In the present paper we will apply analytical results from the theory of polymer networks obtained originally for tree-like networks to the external loops in proteins, and then we compare these results with results from GNM computations (based on the known packing details within a protein structure). It is worthwhile mentioning that both the original theory of phantom polymer networks and the elastic network models of proteins are based on the assumption that excluded volume effects are completely negligible. The theory of phantom Gaussian networks, although developed for polymer networks with the topology of an ideal infinite tree, works well for real polymer networks that contain many loops. This means that the detailed topology of the network is really not so essential for studies of individual chains.

The theory of phantom Gaussian networks provides analytical expressions for fluctuations of chains and junctions in the polymer network having connectivity φ (where φ is the number of polymer chains connected at each junction), which is constant. However, since each end of the chain in an exterior loop of a protein can be connected to a different number of springs, the original theory²⁸ had to be modified to reflect having junctions at the two opposite ends of the loop with different functionalities φ₁ andφ₂. We analytically compute the mean-square fluctuations and correlations of the instantaneous fluctuations for junctions and points along the polymer chains in such a tree-like network,⁴² and here apply these analytical results to treat protein loops. The comparison of analytical predictions with the results of GNM computations for proteins with known crystallographic coordinates of loops overall show an excellent agreement. Our results demonstrate that it is possible to model theoretically the motions of protein loops using the Gaussian model from the polymer network, without knowing the structural details of the loop itself.

The structure of the present paper is as follows. First we describe briefly the Gaussian theory of random polymer networks, and show how fluctuations of chains and junctions (cross-links) and covariances among them can be computed analytically for a network with an ideal tree-like topology. In the next section we discuss the Gaussian Network Model (GNM) of proteins, and its relationship to the earlier discussed theory of random polymer networks. Later we compare the results from the GNM for several proteins with large external loops having known structures with the analytical results based on the theory of random polymer networks and the experimental B factors. Other possible applications of our method for computing the structures of loops could be made to treat loops in nucleic acids, and other loops in large biological structures, such as the ribosome, for the prediction of protein function, and for drug design.

METHODS

Theory of Random Polymer Networks

The first theory of rubber elasticity was proposed by Kuhn in late thirties.⁴³ The theory was further developed by Treloar.^30,31 It was based on the assumptions that the rubber network consists on ν freely-jointed Gaussian chains, which are cross-linked. It was also assumed that positions of the junctions (points of the chemical cross-links) deform affinely upon mechanical deformation of the rubber. The theory of phantom networks was developed in the 1940s by James and Guth.^23–26,44 They also considered the network to be composed of cross-linked Gaussian chains. Additionally they assumed that there are two types of network junctions. Junctions which are at the surface of the rubber are fixed and deform affinely with the macroscopic strain, while the junctions inside the network are free to fluctuate around their mean positions. They assumed that the behavior of the network is determined only by the connectivities of network chains and neglected the effect of the excluded volume of the chains. The chains in their model are phantom-like; i.e. they may pass freely through one another.

Chain dimensions and fluctuations in random elastomeric networks were studied by Flory,²⁷ and by Kloczkowski, Mark and Erman ²⁸ who examined in detail the behavior of phantom Gaussian networks in the undeformed state. It can be shown that the mean-square fluctuations in position of a junction i <(ΔR_i)²> are related to the element ${\mathrm{\Gamma }}_{\text{ii}}^{-1}$ of the inverse of the connectivity matrix Γ, and more generally the covariances in positions of points i and j <(ΔR_i· ΔR_j)> are related to ${\mathrm{\Gamma }}_{\text{ij}}^{-1}$ as

$$<(\mathrm{\Delta }{\mathbf{R}}_i·\mathrm{\Delta }{\mathbf{R}}_j)>=\frac{3{<r^2>}_0}{2}{\mathrm{\Gamma }}_{ij}^{-1}$$ (1)

The elements of the inverse matrix have been calculated analytically for the network with the topology of an infinite tree, composed of chains of equal length (unimodal network), with equal mean square end-to-end distances <r²>₀ in the undeformed state. It is assumed that the network has functionality φ, i.e. that each free junction connects exactly φ chains. Examples of unifuctional networks, recurrence relations between fluctuations of junctions in the neighboring tiers of the tree, recurrence relations between fluctuations of two junctions m and n separated by d other junctions along the path joining m and n, recurrence relations between fluctuations of points along the chains in the network and covariances of fluctuations among such points, recurrence relations between the elements of the inverse connectivity matrix Gamma;⁻¹ are given by Kloczkowski et al. in Reference (28) and presented briefly in Appendix A in the Supplementary Materials.

Because most models of real polymer networks use phantom network as a reference state for the construction of the real network models, these results are significant for rubber elasticity. The Gaussian network model has been also extended to proteins, as will be described later.

Theory of Random Polymer Networks with alternating functionality

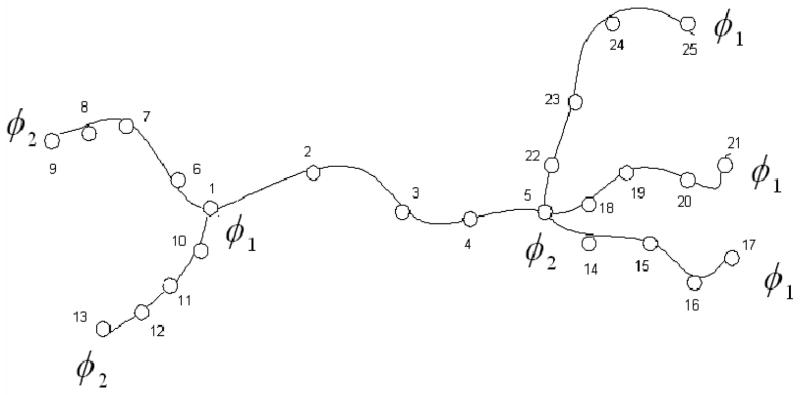
The theory was developed in Skliros et al.^42,45 and is presented briefly in Appendix B in the Supplementary Materials. To study fluctuations of points along the chain we follow the method proposed in reference ⁴⁶, and assume that all chains consist of n equal length segments and of n − 1 junctions of functionality 2, which connect these segments. Fig. 1 illustrates this approach, and the method of numbering all junctions for a tree-like network with alternating multifunctional functionalities composed of two tiers.

Figure 1.

Tree-like network with alternating functionalities separating each chain into four segments of equal length by three additional 2-functional junctions.

Although we have obtained the most general solution of the problem when two points i and j can be separated by several multifunctional junctions,⁴² we show here only the results when these two points belong to the same chain, i.e. there are no multifunctional junctions between them. Additionally since the network is assumed to be infinite we will concentrate on the case for the central first tier shown in the center of Fig. 1.

The positions of 2-functional junctions i and j can be expressed as the fraction of the chain between φ₁ – functional and φ₂ – functional junctions, counted from the closest φ₁ – functional junction on the left of points i or j in Fig. 1; $\zeta =\frac{i-1}{n};\theta =\frac{j-1}{n}$.

The final result is:

$$\left[\begin{array}{cc}<{(\mathrm{\Delta }{R}_i)}^2>& <\mathrm{\Delta }{\mathbf{R}}_i·\mathrm{\Delta }{\mathbf{R}}_j>\\ <\mathrm{\Delta }{\mathbf{R}}_i·\mathrm{\Delta }{\mathbf{R}}_j>& <{(\mathrm{\Delta }{R}_j)}^2>\end{array}\right]=\frac{3n}{2{\gamma }_0}\times \left[\begin{array}{cc}\frac{{\phi }_2({\phi }_1-1)}{{\phi }_1({\phi }_1{\phi }_2-{\phi }_1-{\phi }_2)}+\frac{\zeta (1-\zeta )({\phi }_1{\phi }_2-{\phi }_1-{\phi }_2)+\zeta ({\phi }_1-{\phi }_2)}{{\phi }_1{\phi }_2}& \frac{{\phi }_2({\phi }_1-1)}{{\phi }_1({\phi }_1{\phi }_2-{\phi }_1-{\phi }_2)}+\frac{({\phi }_1{\phi }_2-{\phi }_1-{\phi }_2)}{{\phi }_1{\phi }_2}[min(\zeta ,\theta )-\zeta \theta ]+\frac{min(\zeta ,\theta )}{{\phi }_2}-\frac{max(\zeta ,\theta )}{{\phi }_1}\\ \frac{{\phi }_2({\phi }_1-1)}{{\phi }_1({\phi }_1{\phi }_2-{\phi }_1-{\phi }_2)}+\frac{({\phi }_1{\phi }_2-{\phi }_1-{\phi }_2)}{{\phi }_1{\phi }_2}[min(\zeta ,\theta )-\zeta \theta ]+\frac{min(\zeta ,\theta )}{{\phi }_2}-\frac{max(\zeta ,\theta )}{{\phi }_1}& \frac{{\phi }_2({\phi }_1-1)}{{\phi }_1({\phi }_1{\phi }_2-{\phi }_1-{\phi }_2)}+\frac{\theta (1-\theta )({\phi }_1{\phi }_2-{\phi }_1-{\phi }_2)+\theta ({\phi }_1-{\phi }_2)}{{\phi }_1{\phi }_2}\end{array}\right]$$ (2)

Gaussian Network Model of Proteins

The Gaussian Network Model (GNM) was originally developed for the theory of rubber-like elasticity of random polymer networks^27,28 to calculate fluctuations of junctions and chains inside the network. That physical situation is quite different from that prevailing in a protein; because the polymer chains have random forms and the protein may be a more fixed form. The model has been adapted to coarse-grained proteins in 1997 by Bahar and Erman ^1,47 based on the earlier result of Tirion ³⁹ with a single harmonic force parameter, which successfully described the large scale motions in proteins.

The GNM is based on coarse-grained modeling of protein structure, with a single site per residue representing proteins. Positions of these sites are usually identified with the coordinates of C^α atoms in proteins, and it is assumed that both bonded and non-bonded contacts in protein structure are connected by uniform massless harmonic springs. Significantly the atomic version gives only slightly better results than the coarse-grained model,³ indicating that the motions are mostly representative of the overall structure, and not so much of it details.

To define which sites are in contact, a uniform cutoff distance R_c is used.^1,38,40,47 Residues separated by this distance or closer than R_c (including neighbors along the sequence) are assumed to be in contact, and are connected with identical springs. This leads to the elastic network representation of a protein, in the folded state that bears a resemblance to a random polymer network. While this model of a protein is closely similar to that of a rubbery network, the main difference is that in the rubber the coordinations are defined by covalent links whereas in the GNMs and ENMs the connections are primarily non-bonded contacts arising from close packing within the structure. While the GNM formally neglects the excluded volume, regions with a higher density of atoms are represented by higher density of springs, while less dense regions are represented by few springs.

The distance vector between the ith and jth sites is R_ij., with ΔR_ij being the instantaneous displacement of R_ij from the mean value ${\mathit{R}}_{ij}^0$, and (ΔR_ij)² is given by the scalar product (ΔR_ij^T · ΔR_ij). The reference structure is usually the crystal structure taken from the Protein Data Bank (PDB), but could be a modeled structure or even the shape of a structure from an electron micrograph, which was filled with lattice points.⁴⁸ It can be shown ^27,28 that

$$<\mathrm{\Delta }{\mathit{R}}_i·\mathrm{\Delta }{\mathit{R}}_j>=\frac{3k_{B}T}{2\gamma }{({\mathit{\Gamma }}^{-1})}_{ij}$$ (3)

where (Γ⁻¹)_ij is the ij-th element of the inverse of the connectivity matrix Γ.

It should be note that the connectivity matrix Γ has been defined so that all elements in every row (or column) sum to zero. Because of this detΓ = 0, the matrix is singular, and only the pseudoinverse of Γ can be computed by the use of the singular value decomposition method. The pseudoinverse of Γ may be written as Γ⁻¹ = U(Λ⁻¹)U^T where U is the matrix composed of eigenvectors u_i (1 ≤ i ≤ N) of Γ, and Λ is the matrix having eigenvalues of Γ on the diagonal, and zeros off-diagonal. Additionally, it can be proven that all eigenvalues λ_i of Γ are non-negative.

Mean-square fluctuations of each C^α computed from Eq. 3 can be compared with the Debye-Waller factors for the C^α atoms. These temperature factors are frequently measured by X-ray crystallography for all heavy atoms in the protein structure and are deposited in the Protein Data Bank as temperature B-factors. The computed B-factors for the i-th residue are given by:

$$B_i=8{\pi }^2<{(\mathrm{\Delta }{R}_i)}^2>/3$$ (4)

The B-factors computed by the GNM usually are in excellent agreement with experimental data,² although even better agreement is found when compared with the averages of internal distances from NMR ensembles.^4,49

The matrix Γ⁻¹ can be written as the sum of contributions from individual modes⁵⁰

$${\mathit{\Gamma }}^{-1}=\sum _k{\lambda }_k^{-1}{\mathit{u}}_k{\mathit{u}}_k^T$$ (5)

where the zero eigenvalues (physically corresponding to motions of the center of mass of the system) are excluded from the sum. The i-th component of the eigenvector u_k (corresponding to the k-th normal mode) specifies the magnitude of fluctuational motions of the i-th residue in the protein exerted by the k-th mode. If the eigenvalues are ordered according in an ascending order starting from zero, then the most meaningful contributions in Eq. 5 are given by the smallest non-zero eigenvalues λ_k, which correspond to the large-scale slow modes. The slowest modes play a dominant role in the fluctuational dynamics of structures, because their contributions to the mean-square fluctuations scale with ${\lambda }_k^{-1}$. It has been shown that the most essential motions of proteins^51–53 or large biological structures such as the ribosome,^54–57 which are associated with their biological function, are clearly identifiable within a few of the slowest modes of the GNM or ENM. The large-scale changes of protein conformations between ‘open’ and ‘closed’ forms, or domain swapping in proteins can be also explained well by these ENMs ^58,59. The Gaussian Network Model is the simplest version of several different ENMs. It has been extended to treat anisotropic fluctuations with vector directions for the motions,⁴⁰ and hierarchical³⁵ or mixed³⁶ levels of coarse graining.

RESULTS AND DISCUSSION

Prediction of motions of loops in proteins

We have studied in detail the motions of external loops in five different proteins: tubulin (PDB code 1tub, tubulin α/β dimer), reverse transcriptase (1n5y), triose phosphate isomerase (1tph, human triose phosphate isomerase), protease (1j71, extracellular aspartic proteinase from Candida tropicalis yeast) and myoglobin (2v1k, ferrous deoxymyoglobin at pH 6.8). Tubulin, reverse transcriptase and triose phosphate isomerase are composed of two monomers and have 867, 910, and 496 residues, respectively. Protease and myoglobin each contain single chains with 338, and 163 residues, respectively. We first locate loops of these proteins that are on the surface and compute the mean-square fluctuations of all the residues in these loops, and their cross-correlations (covariances) between fluctuations of two different residues by using both the GNM (Eq. 4) and the analytical formula (Eq. 2) derived for a polymer network with alternating functionality. More specifically we consider the loops as chains where the first and the last residue are junctions with functionalities equal to the actual connectivities for these residues with the remainder of the protein as given for a cut off distance (7 Å); the other residues of the loop are considered as junctions having functionality two. Now since the functionality of the two terminal loop residues may be different, in order to find the auto and cross covariances of the loop residues we use Equation 2. For the case of the GNM model, we find the connectivity matrix (for the whole protein including PDB data for residues forming loops) and then we find the pseudoinverse thereof by using Singular Value Decomposition. The fluctuations and the covariances of the residues of each loop resiude are found based on Equation 4.

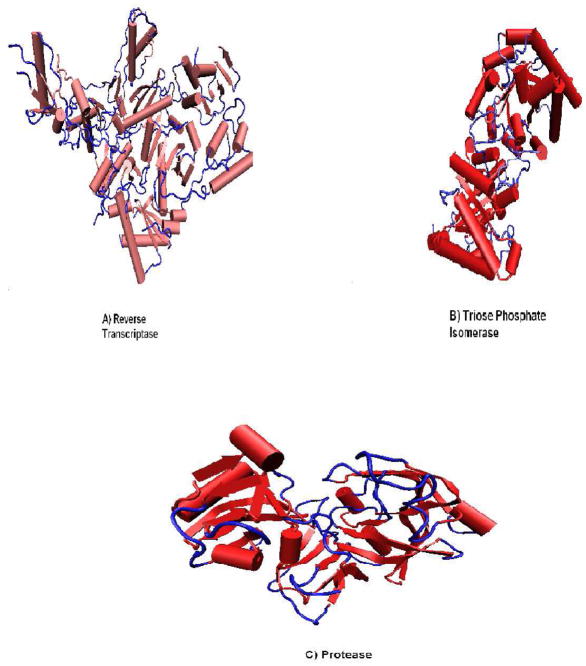
We identify protein loops by first excluding helices and beta-strands in the protein structure, leaving only coils. The criterion for a loop is the requirement that four or more consecutive coil residues are located on the protein surface. We illustrate these loops in protein structures for three of the studied proteins by coloring them blue in Fig. 2.

Figure 2.

(A) Loops (colored in blue) of reverse transcriptase (A), triose phosphate isomerase (B) and protease (C).

We calculated covariances of instantaneous fluctuations of residues in loops both from Equation 2 (polymer theory of rubberlike elasticity) and from Equation 4 (GNM computations based on the complete protein structure). The results obtained are shown in Figs. 3–7. Curves with squares show covariances calculated from Equation 2 using only information on the connectivity of the terminal residues of protein loops (functionality of their junctions) and the length of a loop, while curves with dots display covariances calculated from Equation 4 for GNM applied to the whole protein. The pattern for the residue-residue indexing is as follows: initially the index shows the covariance of the first residue in the loop with itself and with all others, then of the second residue with itself and with all others (except the first one), etc. For a loop composed of n residues the residue-residues index changes from 1 to n (n + 1)/2.

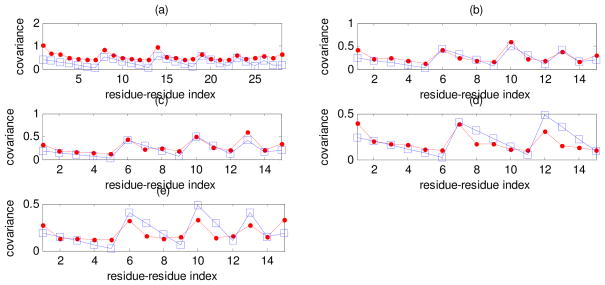
Figure 3.

Covariances of instantaneous fluctuations calculated by using theory of rubberlike elasticity (Equation 2) (squares) and GNM (Equation 4) (dots) for the following individual loops: (a) Reverse transcriptase loop number 4, (b) Tubulin loop number 4, (c) Triose phosphate isomerase loop number 3, (d) Protease loop number 7 and (e) Myoglobin loop number 4. The abscissa shows the index for pairs of residues.

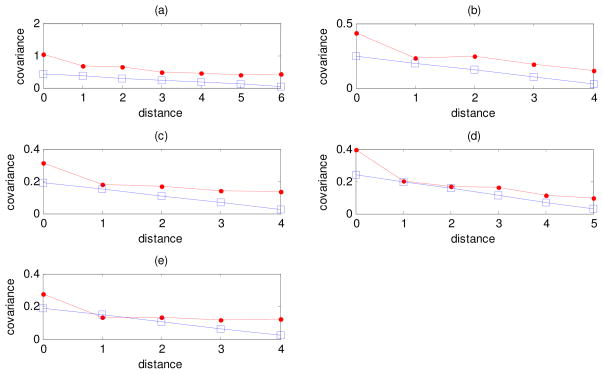
Figure 7.

Covariances of instantaneous fluctuations of the first residue of the loop with other residues in the same loop as a function of the sequence distance between them for: (a) reverse transcriptase loop no. 4, (b) tubulin loop no. 4, (c) triose phosphate isomerase loop no. 3, (d) protease loop no. 7 and (e) myoglobin loop no. 4. Results computed from polymer theory of rubberlike elasticity (squares), and from GNM (dots) are compared.

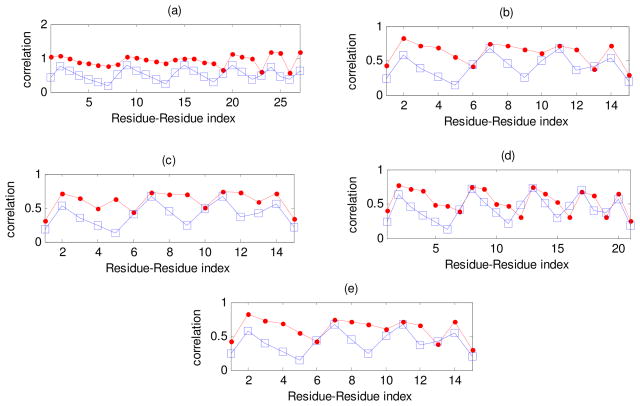
Figure 3 shows the values of covariances calculated from polymer rubberlike elasticity theory (squares) and from GNM (dots) for the following loops (for indexing of all loops see Appendix C in Supplementary Materials): (a) reverse transcriptase loop number 4 (n = 7), (b) tubulin loop number 4 (n = 5), (c) triose phosphate isomerase loop number 3 (n = 5), (d) protease loop number 7 (n = 6) and (e) myoglobin loop number 4 (n = 5). We see that for these cases the local approximation based on Eq. 2 provides an excellent result that very well approximates the whole structure result based on the GNM.

In addition to covariances of the instantaneous fluctuations it is interesting to analyze correlations among them defined by

$$\mathit{Corr}=\frac{<(\mathrm{\Delta }{\mathbf{R}}_i·\mathrm{\Delta }{\mathbf{R}}_j)>}{\sqrt{<{(\mathrm{\Delta }{\mathbf{R}}_i)}^2><{(\mathrm{\Delta }{\mathbf{R}}_j)}^2)>}}$$ (6)

Figure 4 shows the correlations obtained by the GNM and the polymer elastic theory for the loops analyzed earlier in Fig. 3.

Figure 4.

Correlations of instantaneous fluctuations computed by using the theory of rubberlike elasticity (Equation 2) (squares) and the GNM (Equation 4) (dots) for the following individual loops: (a) Reverse transcriptase loop number 4, (b) Tubulin loop number 4, (c) Triose phosphate isomerase loop number 3, (d) Protease loop number 7 and (e) Myoglobin loop number 4. The abscissa shows the index for pairs of residues.

Figure 5 shows the values of covariances computed for four loops of reverse transcriptase with asymmetry in the connectivities φ₁, φ₂ of the terminal junctions for loops: (a) loop number 4 (n = 7, φ₁ = 4, φ₂ = 11), (b) number 5 (n = 5, φ₁ = 8, φ₂ = 3), (c) number 11 (n = 6, φ₁ = 5, φ₂ = 10), and (d) number 14 (n = 4, φ₁ = 5, φ₂ = 13). We see that the local approximations based on the polymer network model are more successful for longer loops than for short ones.

Figure 5.

Covariances of the instantaneous fluctuations calculated by using the theory of rubber elasticity (Equation 2) (squares) and GNM (Equation 4) (dots) for loops number 4, 5, 11, and 14 of reverse transcriptase. The abscissa shows the index for pairs of residues, with indexing described in the text.

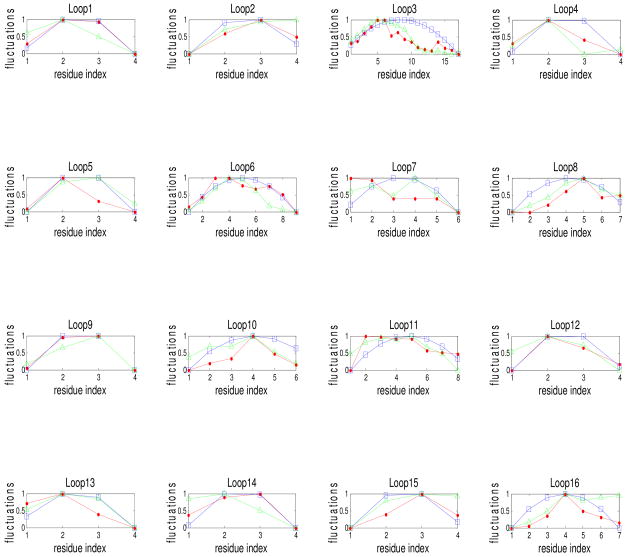
It is also relevant to examine the relationships between the fluctuations of the loop residues computed from polymer rubberlike elasticity model, and from GNM with experimental B-factors. Figure 6 shows plots of the mean square fluctuations of loop residues obtained from these three different sources for all 16 loops of the protease. For purposes of comparison all three quantities are normalized. (For example ${B_i}^{\mathit{norm}}=\frac{B_i-B_{min}}{B_{max}-B_{min}}$ where i is the residue index for the particular loop. The same normalization is carried for the fluctuations computed from GNM and from polymer phantom network model). We see that for some of these cases the local approximation based on our model approximates the GNM results very well. The main reason for the good or bad approximation by the local method to the GNM results are the connectivities of the residues of the loops.

Figure 6.

Fluctuations of the residues for all loops of protease. Fluctuations computed from polymer theory of rubberlike elasticity (squares), and from GNM (dots) are compared with B-factors (triangles). All fluctuations have been normalized. The abscissa is the residue index in the loop.

Another crucial issue is whether the covariances of instantaneous fluctuations decay similarly with respect to the sequence distance between the residues. To address this problem we have plotted in Fig. 7 the covariances of the first residue in each loop with respect to the other residues of the same loop as a function of the sequence distance between these two residues.

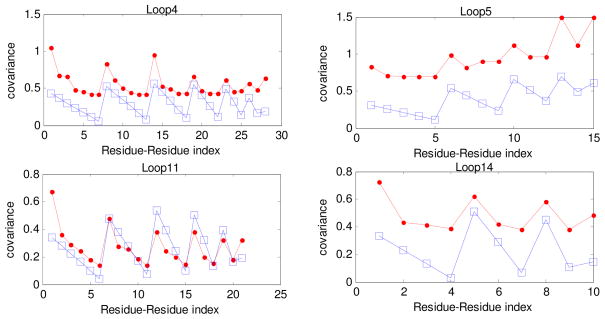
Figures 3–7 indicate that the covariances of instantaneous fluctuations obtained both by considering the loops as individual entities (theoretical model) and as a whole structure (GNM) are closely similar. We computed the correlations of these covariances for all loops for all the proteins studied here. Our computations indicate that the average correlation of covariances (averaged over all loops in a given protein) is the largest (0.70) for triose phosphate isomerase, 0.66 for reverse transcriptase, and the smallest (0.38) for myoglobin, which has only four very short loops. All profiles shown in these figures show a close resemblance between the behavior of our new loop modeling and the whole protein modeling with the Gaussian Network model. This is at first surprising, since previous results with the Gaussian Network Model indicated that the whole structure was needed in order to compute the motions of any part. What we are seeing here is that the individual loops and their simplified representations are generally sufficient to compute the relative mobilities for the individual parts of the loop. Information contained in Figs. 3–7 for additional loops of the proteins are provided in Appendix D in the Supplementary Materials. Appendix E gives the correlations of the covariances for every loop of each protein we have studied as a function of the sum of the functionalities of the two terminal junctions in each loop. We have not noticed any apparent relationship between these two quantities. Appendix F shows results of computations of covariances of instantaneous fluctuations of residues belonging to helices for the proteins of study, similarly as was done earlier for loops. Our computations show that polymer network approximation does not work as well for helices as for the loops. Appendix G shows the computed correlation coefficients between the predicted amplitudes of fluctuations of loop residues (using both the present analytical model and GNM theory) and the experimental B-factors.

Discussion

We have presented a comparison of the loop motions using both the GNM and a new approach based on theory of rubberlike elasticity of polymer networks. For the latter, the loop is modeled by assuming that the two ends have functionalities φ₁ and φ₂ connecting them with the remainder of the protein structure, whereas the intermediate residues of the loop uniformly have the functionality of two, connecting them only to their sequence neighbors. We then calculated the mean square fluctuations (variances) and covariances for the loop residues by using formulas derived analytically by us for a tree-like polymer network with alternating functionalities. We then applied this new approach to all external loops in five different proteins (reverse transcriptase, triose phosphate isomerase, tubulin, protease and myoglobin) and compared analytical results for the mean square fluctuations and the covariances with GNM computations based on the coordinates for all residues of the loops. For each loop we have plotted the covariances between instantaneous fluctuations of pairs of residues of the loop, and the mean square fluctuations of individual loop residues. We have also compared the covariance of instantaneous fluctuations between two residues of the loop as a function of the distance between them. The comparisons between these two models show that the local approximation of the loops that describes the motion of the loop residues based on polymer tree-like network topology independently from the rest of the protein structure closely approximates the results obtained from GNM where the whole protein structure is taken into account.

Loop mobilities have long been considered to be important for function. Loops on the surfaces of proteins are often the most uncertain parts of structures. It is quite likely that many loops are artificially immobilized and compressed against the body of the protein in the crystal environment. What has been done in the present work is to develop and compare two simple models for loop mobilities. These two quite different approaches yield similar results. Our finding - that computed loop motions are similar whether treated as independent or in the context of the whole protein structure – implies that the loop motions are occurring along relatively well defined pathways, which likely could be mapped out in future computations. This approach may be used not only for loops of proteins, but also for the large loops frequently occurring in nucleic acid stem-loop structures, as well as the much larger loops originating in double stranded DNA, when multiple subunit proteins bind at widely separated positions. This critical problem for transcription regulation requires coarse-graining of the structure since the loops can be thousands of base pairs in length. The more difficult problem may be how to introduce additional interactions within these DNA loops when supercoiling is introduced.

Utility of this approach for describing the motions of loops with unknown structures

Often in protein structures loops are missing in the crystal structure. The approach described in this paper could be used to predict probably structures for these missing loops since the only requirement is knowing the connectivity numbers for the two ends and the number of residues in the loop.

In the present work we have considered only the relative magnitudes of these motions, which compare favorably. In the future it will be essential to develop a vector version of the present loop modeling to define actual pathways, to compare with the ANM and the anisotropic temperature factors. These pathways will be presented in future work, where we also investigate the effects of interactions between loop residues and the body of the protein. The results from the present work indicate that our new approach based on polymer elasticity theory provides a close approximation to the GNM model that includes the effects of the whole structure.

The polymer rubberlike elasticity model only predicts a relatively simple pattern of fluctuations of residues across a loop with a convex shape, and with the residues close the center of the loops having a higher amplitude. However, according to this model the central residue of the loop does not always have the maximum amplitude of fluctuations. We have also an effect from the functionality of junctions on both ends of the loop. The maximum is shifted towards the junction which having lower functionality. This effect is also observed for experimental B-factors for loop residues, although sometimes there are exceptions to this rule, due to significant interactions of loop residues with the remainder of the protein. Our predictions are limited somewhat by the simplicity of the theoretical model, and by the assumption that the motions of loops are unobstructed by the remaining part of the protein, but nevertheless they do enable predicting the basic features of these motions.