Nonparametric tests for right-censored data with biased sampling

Summary

Testing the equality of two survival distributions can be difficult in a prevalent cohort study when non random sampling of subjects is involved. Due to the biased sampling scheme, independent censoring assumption is often violated. Although the issues about biased inference caused by length-biased sampling have been widely recognized in statistical, epidemiological and economical literature, there is no satisfactory solution for efficient two-sample testing. We propose an asymptotic most efficient nonparametric test by properly adjusting for length-biased sampling. The test statistic is derived from a full likelihood function, and can be generalized from the two-sample test to a k-sample test. The asymptotic properties of the test statistic under the null hypothesis are derived using its asymptotic independent and identically distributed representation. We conduct extensive Monte Carlo simulations to evaluate the performance of the proposed test statistics and compare them with the conditional test and the standard logrank test for different biased sampling schemes and right-censoring mechanisms. For length-biased data, empirical studies demonstrated that the proposed test is substantially more powerful than the existing methods. For general left-truncated data, the proposed test is robust, still maintains accurate control of type I error rate, and is also more powerful than the existing methods, if the truncation patterns and right-censoring patterns are the same between the groups. We illustrate the methods using two real data examples.

1. Introduction

Prospective prevalent cohort studies are performed to evaluate the natural history of a disease (e.g., time to death or onset of AIDS) among recruited individuals who have been diagnosed with the disease of interest (e.g., cancer or infected with HIV). An important special sampling scheme assumes that the probability of individuals selected from the target population is proportional to the time from diagnosis to the failure event (Zelen and Feinleib, 1969; Vardi, 1989; Zelen, 2004). We give two examples of such data. In a study of shrubs (Muttlak and McDonald, 1990), the data on the shrubs’ widths were collected using the line-intercept sampling method, in which the probability of the inclusion of a shrub in the sample was proportional to the width of the shrub. In an epidemiologic study to explore survival among patients with dementia, subjects age 65 and older were recruited and then screened for dementia (Wolfson et al., 2001). For those subjects confirmed to have dementia, the dates of death or censoring were prospectively collected. In both examples, selection bias occurred because the observed widths of shrubs or time intervals from onset of dementia to death tended to be larger or longer for subjects in the observed cohorts compared to subjects in the target population. In fact, the statistical issues related to selection bias beyond length-biased data have also attracted considerable attention in recent literature (Jensen et al., 2000; Begg, 2002; Cole et al., 2004; Scheike and Keiding, 2006; McCullagh, 2008).

The issues of length bias and biased sampling in various applications have been well recognized in the epidemiology and statistics literature for decades. Wicksell (1925) first noted biased sampling in the “corpuscle problem”. Since then, a series of papers in this area have been motivated by industrial applications (Blumenthal, 1967; Cox, 1969; Kvam, 2008); survey sampling studies for wildlife population (Cook and Martin, 1974; Patil and Rao, 1978); human genetics research in linkage mapping (Terwilliger et al., 1997); economics studies on unemployment durations (De Uña-Álvarez et al., 2003); cancer screening trials (Zelen and Feinleib, 1969) and prevalent cohort epidemiology studies for natural histories of HIV infections and other chronic diseases (Lancaster, 1979; Brookmeyer and Gail, 1994; Greenberg et al., 2005; Song et al., 2006). A longstanding problem in analyzing such data is the need to correct for bias in estimation and inference. Studies in the literature have focused on one-sample estimates for the length-biased failure time distribution either conditional on the observed truncation times (Turnbull, 1976; Lagakos et al., 1988; Wang, 1991), or with an unconditional approach (Vardi, 1982, 1989; Asgharian et al., 2002; Asgharian and Wolfson, 2005). There is little work considering efficient nonparametric two-sample and k-sample tests to compare underlying survival distributions when observed right-censored data are subject to biased sampling.

For traditional survival analyses, there is substantial literature on testing the equality of survival distributions for right-censored survival data. The logrank test has been among the most commonly used tests (Mantel, 1966; Peto and Peto, 1972), and has proven to be asymptotically most efficient under the proportional hazards alternatives (Aalen, 1978; Gill, 1980; Fleming et al., 1987). Under biased sampling, these tests may not be applicable because the significance level can be severely inflated due to the dependent censoring mechanism with the observed failure time data.

For general left-truncated data, Lagakos et al. (1988) proposed a nonparametric truncation logrank type test by modifying the definition of the risk set; Bilker and Wang (1996) considered a semiparametric truncation test without right censoring; Shen (2007) extended the weighted Kaplan-Meier statistics using the maximized likelihood estimator of survival functions from the likelihood conditional on the observed truncation times; and Finkelstein et al. (1993) studied the score test of the conditional likelihood based on proportional hazards models. However, few have explicitly considered length-biased data. Length-biased data are a special case of left truncated data in which the truncation times are uniformly distributed on a defined interval. The aforementioned tests for left-truncated data are conditional on the observed truncation times, and thus would be less efficient/powerful than tests based on the full likelihood for length-biased data. Wang (1996) considered the estimation of hazard under the Cox regression model for length biased data. Unfortunately her method cannot be applied to data with right censoring.

In this paper, we propose an asymptotically most efficient test under the proportional hazards alternative for right-censored length-biased data, which is analogous to the logrank test for traditional right-censored data. We can also extend the proposed test to general left-truncated survival data when the stationarity assumption is violated. The stationarity assumption implies that the initiation times follow a stationary Poisson process (Wang, 1991). We introduce the notations, and derive the test statistics and the asymptotic properties of the test statistics in Section 2. We investigate the validity of logrank test for length-biased and left-truncated data in Section 3. We summarize the simulation results in Section 4, and two applications of the proposed test in Section 5. We conclude with a discussion in Section 6, and provide details of the proofs in the Appendix.

2. Test Procedures

Consider a prevalent cohort study in which subjects are diagnosed with a disease and are at risk for a failure event. Let X̃_ij be the unbiased time measured from initiation to failure, A_ij denote the time of recruitment measured from initiation, V_ij denote the time from recruitment to failure, and C_ij be the censoring time measured from recruitment for the jth individual in the ith group, j = 1, · · ·, n_i, and i = 1, 2. The censoring indicator is denoted by δ_ij = I(V_ij ≤ C_ij). A major sampling constraint is that the value of X̃_ij is observed only when the X̃_ij > A_ij. We denote the length-biased time and the observed length-biased time under right censoring as ${\stackrel{\sim }{X}}_{ij}^L$ and $X_{ij}=min\{{\stackrel{\sim }{X}}_{ij}^L,A_{ij}+C_{ij}\}$, respectively. Within the ith group, we assume that X̃_ij are independently and identically distributed with unbiased survival function S_i(.) and density function f_i(.). The censoring time C_ij is assumed to be independent of (A_ij, V_ij) within the ith group, with survival and cumulative distribution functions defined by S_Ci(.) and F_Ci(.). Note that the censoring time measured from the initiation A_ij + C_ij is mechanistically dependent on failure time A_ij + V_ij even if C_ij is independent of (A_ij, V_ij).

For the observed length-biased data without censoring, the density function of ${\stackrel{\sim }{X}}_{ij}^L$ is

$$g_i(x)=\frac{x{f}_i(x)}{{\mu }_i},{\mu }_i={\int }_0^{\infty }{S}_i(t)dt,x>0,i=1,2.$$

We define the corresponding survival distributions of the uncensored length biased data as G₁ and G₂. Our goal is to test the equality of two unbiased survival distributions under the proportional hazards alternatives, $S_2(t)=S_1^{\beta }(t)$. The null and alternative hypothesis of interest are

$$H_0:\beta =1;H_1:\beta \ne 1.$$

2.1. Two-Sample Test Without Censoring

Motivated by the shrub study, we start with the data without right censoring. Given the observed biased failure times, the joint density of (A_ij, V_ij) is

$$f_{A_i,V_i}(a,v)=\frac{f_i(a+v)I(a>0,v>0)}{{\mu }_i}=\frac{f_i(x)I(a>0,v>0)}{{\mu }_i}.$$

Without right censoring, the log-likelihood based on the joint density function of (A_ij, V_ij) is

$$\ell (\beta )=\sum _{j=1}^{n_1}[log{\lambda }_1(x_{1j})+log{S}_1(x_{1j})-log{\mu }_1]+\sum _{j=1}^{n_2}[log\beta +log{\lambda }_1(x_{2j})+\beta log{S}_1(x_{2j})-log{\mu }_2],$$ (1)

where λ_i(.) is the hazard function of S_i(.). Taking the first derivative of the log-likelihood with respect to β, we have

$$\frac{\partial \ell }{\partial \beta }=\sum _{j=1}^{n_2}\left[{\beta }^{-1}+log{S}_1(x_{2j})-\frac{\int S_1^{\beta }(t)log{S}_1(t)dt}{\int S_1^{\beta }(t)dt}\right].$$

Thus, the score function under the null hypothesis (i.e., S₁ = S₂ = S and μ₁ = μ₂ = μ) is

$$T_0=\sum _{j=1}^{n_2}\left[1+logS(x_{2j})-\frac{\int S(t)logS(t)dt}{\int S(t)dt}\right].$$

It is then easy to prove the expectation of T₀ to be zero using integration by parts under H₀, because

$$E[logS(X_2)]=-{\mu }^{-1}\int \mathit{t}log\mathit{S}(t)dS(t)={\mu }^{-1}\int S(t)logS(t)dt-1.$$

Unlike score test statistics without unknown quantities, the aforementioned T₀ requires estimating the unknown survival function. Let the pooled observed times and the corresponding sample indexes be defined by {x_k, k = 1, · · ·, n = n₁+n₂} = {x₁₁, · · ·, x_1n1, x₂₁, · · ·, x_2n2} and {z_k, k = 1, · · ·, n} = {0_1×n1, 1_1×n2}, respectively. Under the null hypothesis, S(t) and μ could be estimated empirically by the pooled data,

$$\widehat{S}(t)=\sum _{k=1}^n{x}_k^{-1}I(x_k\ge t){\left\{\sum _{k=1}^n{x}_k^{-1}\right\}}^{-1},\text{and}\widehat{\mu }=n{\left\{\sum _{k=1}^n{x}_k^{-1}\right\}}^{-1}.$$

After plugging in the above consistent estimators to T₀, the asymptotically equivalent score statistic is

$$T_0^{\ast }=\sum _{j=1}^{n_2}\left[1+log\widehat{S}(x_{2j})-\frac{\int \widehat{S}(t)log\widehat{S}(t)dt}{\int \widehat{S}(t)dt}\right].$$

Replacing −log(Ŝ(t)) with Λ̂(t), which is the nonparametric estimator of the cumulative hazards function, and using integration by parts, $T_0^{\ast }$ can be expressed as

$$\begin{array}{l}{T}_0^{\ast }=\sum _{i=1}^n{z}_i\left[1-\widehat{\mathrm{\Lambda }}(x_i)-\frac{-{\sum }_{k=1}^n\widehat{\mathrm{\Lambda }}(x_k){\left\{{\sum }_{k=1}^n{x}_k^{-1}\right\}}^{-1}+n{\left\{{\sum }_{k=1}^n{x}_k^{-1}\right\}}^{-1}}{n{\left\{{\sum }_{k=1}^n{x}_k^{-1}\right\}}^{-1}}\right]\\ =\frac{n_1{n}_2}{n}\left\{\frac{{\sum }_{j=1}^{n_1}\widehat{\mathrm{\Lambda }}(x_{1j})}{n_1}-\frac{{\sum }_{j=1}^{n_2}\widehat{\mathrm{\Lambda }}(x_{2j})}{n_2}\right\}.\end{array}$$

Without censoring, G₁ and G₂ can be consistently estimated by their empirical counterparts, ${\widehat{G}}_1(t)=n_1^{-1}{\sum }_{j=1}^{n_1}I\{x_{1j}\ge t\}$ and ${\widehat{G}}_2(t)=n_2^{-1}{\sum }_{j=1}^{n_2}I\{x_{2j}\ge t\}$. Then $T_0^{\ast }$ is equivalent to

$$T_0^{\ast }=\frac{n_1{n}_2}{n}\left\{\int {\widehat{G}}_1(t)d\widehat{\mathrm{\Lambda }}(t)-\int {\widehat{G}}_2(t)d\widehat{\mathrm{\Lambda }}(t)\right\}.$$ (2)

Let ρ = lim n₁/n, 0 < ρ < 1. Under the null hypothesis (G = G₁ = G₂),

$$T_0^{\ast }/\sqrt{n}=\rho (1-\rho )\sqrt{n}\int \left[\left\{{\widehat{G}}_1(t)-G(t)\right\}-\left\{{\widehat{G}}_2(t)-G(t)\right\}\right]d\mathrm{\Lambda }(t)+o_p(1)$$

converges in distribution to a zero-mean normal distribution with variance

$${\sigma }_0^2=\rho (1-\rho )E{\left[\int I(X\ge t)d\mathrm{\Lambda }(t)\right]}^2.$$

The variance can be estimated by inserting the consistent estimator of Λ(t), denoted by ${\widehat{\sigma }}_0^2$. The null hypothesis will be rejected at significance level α if $\mid T_0^{\ast }/\sqrt{n{\widehat{\sigma }}_0^2}\mid \ge Z_{\alpha /2}$, where Z_α/2 is the upper α/2 percentile of a standard normal distribution.

2.2. Two-Sample Test in the Presence of Censoring

In the presence of right censoring, the joint density distributions of the observed failure time and censoring indicator are

$$\begin{array}{l}{f}_{X_i,{\delta }_i}(t,1)={\int }_0^t{f}_{A_i,V_i}(t-v,v)S_{C_i}(v)dv=\frac{f_i(t)}{{\mu }_i}{\int }_0^t{S}_{C_i}(v)dv,\\ f_{X_i,{\delta }_i}(t,0)={\int }_0^t{\int }_c^{\infty }{f}_{A_i,V_i}(t-c,v){\mathit{dvdF}}_{C_i}(c)=\frac{S_i(t)}{{\mu }_i}{F}_{C_i}(t),\end{array}$$

relying on the property derived in Asgharian and Wolfson (2005) for length-biased data. Given group indicator i, the full likelihood function for the observed biased samples (X_ij, δ_ij) is

$$L(\beta )=\prod _{i=1}^2\prod _{j=1}^{n_i}{\left[\frac{f_i(x_{ij})}{{\mu }_i}{\int }_0^{x_{ij}}{S}_{C_i}(v)dv\right]}^{{\delta }_{ij}}{\left[\frac{S_i(x_{ij})}{{\mu }_i}{F}_{C_i}(x_{ij})\right]}^{1-{\delta }_{ij}},$$

and the log-likelihood function is proportional to

$$\ell (\beta )\propto \sum _{j=1}^{n_1}[{\delta }_{1j}log{\lambda }_1(x_{1j})+log{S}_1(x_{1j})-log{\mu }_1]+\sum _{j=1}^{n_2}[{\delta }_{2j}\{log\beta +log{\lambda }_1(x_{2j})\}+\beta log{S}_1(x_{2j})-log{\mu }_2];$$ (3)

this leads to the score function under H₀ (i.e., β = 1):

$$T_1=\sum _{j=1}^{n_2}\left[{\delta }_{2j}+logS(x_{2j})-\frac{\int S(t)logS(t)dt}{\int S(t)dt}\right].$$ (4)

Under the null hypothesis, we have the following equation using integration by parts:

$$\begin{array}{l}E[{\delta }_2+logS(X_2)]=\frac{1}{\mu }\int \{1+logS(t)\}f(t){\int }_0^t{S}_{C_2}(c)\mathit{dvdt}+\frac{1}{\mu }\int logS(t)S(t)F_{C_2}(t)dt\\ ={\mu }^{-1}\int S(t)logS(t)dt.\end{array}$$ (5)

Given (5), the score function has mean zero under H₀. In general, S(.) is unknown but can be consistently estimated using Vardi’s estimator via Ĝ(.) (Vardi, 1989), from the pooled observed right-censored length-biased data

$$\widehat{S}(t)=\frac{{\int }_t^{\infty }\frac{1}{x}d\widehat{G}(x)}{{\int }_0^{\infty }\frac{1}{x}d\widehat{G}(x)},\text{for}\text{t}\ge 0.$$

The sample score statistic, which has a zero mean asymptotically, follows

$$T_1^{\ast }=\sum _{j=1}^{n_2}\left[{\delta }_{2j}+log\widehat{S}(x_{2j})-\frac{\int \widehat{S}(t)log\widehat{S}(t)dt}{\int \widehat{S}(t)dt}\right].$$

Similar to the asymptotic variance of $T_0^{\ast }$ in Section 2.1, the asymptotic variance of the test statistic $T_1^{\ast }$ is not the negative second derivative of ℓ(β) with respect to β, because there is additional variation induced by the estimation of the unknown survival function. To study the limiting distribution of test statistic $T_1^{\ast }$, we need the following regularity conditions:

1. The survival function S(.) is a continuous function, and τ = inf{t: S(t) = 0} < ∞.

2. $\left\{\frac{2\tau }{{\int }_0^{\tau }{S}_C(u)du}-1\right\}\{1-S_C(\tau )\}<1$, where S_C(t) = ρS_C1(t) + (1 − ρ)S_C2(t).

Assumption (b) is to ensure that the uniform consistency of Vardi’s estimator holds for all 0 < t < τ (Asgharian and Wolfson, 2005). In an earlier paper, Asgharian et al. (2002) used a sufficient but more intuitive alternative for assumption (b), which is S_C(t) > 0.59. This sufficient condition implies that heavy right censoring may cause instability at the tail for the estimated survival distribution Ĝ(t).

Let G^*(t) = P (A + V ≤ t|δ = 1) and F^*(t) = P (A + V ≤ t|δ = 0) with corresponding conditional density functions g^*(t) and f^*(t), $f_r(t)={\int }_t^{\infty }{z}^{-1}dG(z)$ and p₁ = P(δ = 1). For the difference between $T_1^{\ast }$ and T₁, we derive an asymptotic representation as a sum of independent and identically distributed (i.i.d.) random variables,

$$T_1^{\ast }-T_1=\sum _{k=1}^n\left[I_k-(1-\rho )\left\{\frac{\int {\mathcal{G}}_k(t)\{logS(t)+1\}dt}{\int S(t)dt}-\frac{\int S(t)logS(t)dt\int {\mathcal{G}}_k(t)dt}{{(\int S(t)dt)}^2}\right\}\right]+o_p(\sqrt{n}),$$

where

$$\begin{array}{l}{I}_k=\underset{n\to \infty }{lim}\frac{{\sum }_{j=1}^{n_2}\frac{1}{S(x_{2j})}{\mathcal{G}}_k(x_{2j})}{n}\\ {\mathcal{G}}_k(y)=\frac{{\int }_0^{\infty }\frac{1}{x}dG(x){\int }_y^{\infty }\frac{1}{x}d{\mathcal{F}}^{-1}(V_k(x))-{\int }_y^{\infty }\frac{1}{x}dG(x){\int }_0^{\infty }\frac{1}{x}d{\mathcal{F}}^{-1}(V_k(x))}{{\int }_y^{\infty }\frac{1}{x}dG(x){\int }_0^{\infty }\frac{1}{x}dG(x)},\\ V_k(t)=\{I(x_k\ge t,{\delta }_k=1)-p_1{G}^{\ast }(t)\}+f_r(t){\int }_{0<z\le t}\{I(x_k\ge z,{\delta }_k=0)-(1-p_1)F^{\ast }(z)\}d\frac{1}{f_r(z)}+p_1{\left(\frac{p_1}{1-p_1}\right)}^{1/2}\{G^{\ast }(t)-G(t)\}\frac{\{(I({\delta }_k=1)-p_1)\}}{\sqrt{p_1(1-p_1)}},\end{array}$$

and 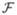is an invertible linear operator,

$$\mathcal{F}(u)(t)=p_1{\int }_{0<x\le t}\frac{g^{\ast }(x)}{g(x)}du(x)+(1-p_1){\int }_{0<y\le t}y\left({\int }_{y\le z}\frac{u(z)}{z^2}dz\right)d\left\{\left(\frac{f_r(t)}{f_r(y)}-1\right)\frac{f^{\ast }(y)}{f_r(y)}\right\}.$$

This representation, when taken together with the fact that T₁ is an i.i.d. sum implies that the test statistic converges in distribution to a zero-mean normal distribution. See the Appendix for the details of the proof.

Theorem 1

Under the null hypothesis and regularity conditions (a) and (b), $n^{-1/2}{T}_1^{\ast }$ converges in distribution to a zero-mean normal distribution with variance

$${\sigma }_1^2=E{\left[I_k-(1-\rho )\left\{\frac{\int {\mathcal{G}}_k(t)\{logS(t)+1\}dt}{\int S(t)dt}-\frac{\int S(t)logS(t)dt\int {\mathcal{G}}_k(t)dt}{{(\int S(t)dt)}^2}\right\}+Z_k\left\{{\delta }_k+logS(X_k)-\frac{\int S(t)logS(t)dt}{\int S(t)dt}\right\}\right]}^2.$$

Though it is of theoretic interest to get the explicit form of the asymptotic variance of the test statistic, it is difficult to propose a consistent variance estimator when there is right censoring. Alternatively, resampling procedures can be used to obtain the critical regions for the score test. When the censoring distributions of two groups are equal, the standard permutation procedure yields a valid P-value for the test (Jennrich, 1983; Hesterberg et al., 2005). Specifically, the permutation test resamples pairs (x_ij, δ_ij) from the pooled data without replacement, assigning the first n₁ pairs to group 1 and the remaining n₂ pairs to group 2. The permutation distribution is generated by resamples, and the null hypotheses is rejected at significance level α, if the observed test statistic lies outside of the critical region formed by the α/2 and 1 − α/2 percentiles of the permutation distribution of the test statistic $T_1^{\ast }$. Actually the permutation procedure for our test is not computationally intensive due to the fact that we do not need to estimate the survival function S(.) for each resampling. When the censoring distributions are different, the observed times may not be exchangeable even under the null hypothesis, suggesting that the standard permutation procedure may not be a valid way to obtain the distribution of the test statistic. Hence, we apply the following conditional bootstrap procedure to test the hypothesis (Reid, 1981):

1. Obtain the nonparametric maximum likelihood estimator (NPMLE) of the length-biased survival distribution Ĝ using the pooled data, and estimate the NPMLEs of the residual censoring time distributions for the two groups, Ŝ_C1 and Ŝ_C2.

2. Draw length-biased times, censoring times and truncation times from the estimated NPMLEs: ${\stackrel{\sim }{X}}_{ij}^L\sim \widehat{G}$, C_ij ~ Ŝ_Ci, $A_{ij}\mid X_{ij}^L\sim \mathit{Uniform}(0,{\stackrel{\sim }{X}}_{ij}^L)$, i = 1, 2; j = 1, · · ·, n_i.

3. Calculate the test statistic $T_1^{\ast }$ using the data generated in step 2.

   Repeat step 2 and step 3 to get the bootstrap distribution of the test statistic. The test rejects the null hypothesis if the test statistic based on the original data falls outside of the critical region of the bootstrap null distribution.

2.3. k-Sample Test Procedure

In the second of our motivating examples, it is of interest to compare the underlying survival distributions among 3 different dementia diagnosis groups simultaneously. We generalize the proposed two-sample test statistic to a k-sample test statistic with k > 2. Specifically, the model assumption is $S_1(t)=S_2^{1/{\beta }_2}(t)=\cdots =S_K^{1/{\beta }_K}(t)$, and we wish to test for

$$H_{0K}:{\beta }_2=\cdots ={\beta }_K=1.$$

The log-likelihood can be expressed as

$${\ell }_K(\beta )\propto \sum _{j=1}^{n_1}[{\delta }_{1j}log{\lambda }_1(x_{1j})+log{S}_1(x_{1j})-log{\mu }_1]+\sum _{i=2}^K\sum _{j=1}^{n_i}[{\delta }_{ij}\{log{\beta }_i+log{\lambda }_1(x_{ij})\}+{\beta }_{i}log{S}_1(x_{ij}\}-log{\mu }_i],$$

where μ_j = ∫S_j (t)dt. Taking the first derivative of the log-likelihood with respect to β = (β₂, · · ·, β_K)^T, we have

$${\eta }_K=\frac{\partial \ell }{\partial \beta }{\mid }_{{\beta }_2=\cdots ={\beta }_K=1}=\left(\begin{array}{c}{\sum }_{j=1}^{n_2}\left[{\delta }_{2j}+log{S}_1(x_{2j})-\frac{\int S_1(t)log{S}_1(t)dt}{\int S_1(t)dt}\right]\\ \cdots \\ {\sum }_{j=1}^{n_K}\left[{\delta }_{Kj}+log{S}_1(x_{Kj})-\frac{\int S_1(t)log{S}_1(t)dt}{\int S_1(t)dt}\right]\end{array}\right).$$

By replacing S₁(t) in η_K with its NPMLE Ŝ(t) using the pooled data, denoted by η̂_K, a test statistic can be constructed as

$$T_K^{\ast }={\{{\widehat{\eta }}_K-E({\widehat{\eta }}_K)\}}^T\{{\widehat{\eta }}_K-E({\widehat{\eta }}_K)\}.$$

As shown in Janssen and Pauls (2003), the bootstrap resampling method can be used to determine the critical region of a test statistic, if the weak convergence holds for the test statistic. We can show that n^−1/2η̂_K converges to a zero-mean multivariate normal distribution using arguments similar to those in the proof of Theorem 1. Because the components in the vector of η̂_K are correlated to each other, the test statistic $n^{-1}{T}_K^{\ast }$ converges weakly to a weighted ${\chi }_1^2$ distribution (Theorem 4.4.4 of Graybill (1976), page 136), which is sufficient to guarantee that the bootstrap resampling procedure described in Section 2.2 is valid.

2.4. General Left Truncated Data

It is clear that the aforementioned score test statistics are derived based on the stationarity assumption for length-biased data. Interestingly, the proposed score test statistics are valid as well as efficient for general left-truncated data which may not satisfy the stationarity assumption, as long as the two groups have the same pattern of left truncation. Suppose that truncation time A has a known cumulative density distribution, H(a). One can observe X if and only if X̃ > A, which is equivalent to H(X̃) > H(A), since H is a monotone increasing function. Note also that H(A) has a uniform distribution, which leads to the length-biased data structure for the transformed data (H(X), H(A), δ). Under the proportional hazards alternative for X̃, $S_2(t)=S_1^{\beta }(t)$, H(X̃) also has a proportional hazards alternative because

$$Pr(H({\stackrel{\sim }{X}}_2)\ge t)=Pr({\stackrel{\sim }{X}}_2\ge H^{-1}(t))={\left\{Pr({\stackrel{\sim }{X}}_1\ge H^{-1}(t))\right\}}^{\beta }={\left\{Pr(H({\stackrel{\sim }{X}}_1)\ge t)\right\}}^{\beta }.$$

Therefore, if one considers the transformed data (H(X), H(A), δ), which is length-biased data, the corresponding score test statistic $T_1^{\ast }$ remains to be asymptotically most efficient under the proportional hazards alternatives.

3. Logrank and Truncation Logrank Tests under Biased Sampling

For traditional right-censored data, the popularity of the logrank test can be attributed to its asymptotic efficiency under the proportional hazards alternatives. The logrank statistic is the score test statistic of the partial likelihood under the proportional hazards model. We will investigate the validity of the logrank test for length-biased data and general left-truncated data under different censoring schemes. Recall that the logrank test can be expressed as

$$T_{LR}=\sum _{k=1}^h\left(O_{2k}-O_k\frac{N_{2k}}{N_k}\right),$$ (6)

where t₁ < · · · < t_h are the distinct failure times of pooled samples. For each t_k, let N_ik be the number of subjects “at risk” in the ith group and N_k = N_1k + N_2k. The observed numbers of events at t_k are defined as O_1k, O_2k, and Q_k for each group and combined group, respectively.

For length-biased data, the probabilities of observing a failure event at time t_k for a subject given that the subject is “at risk” at that time are

$$\begin{array}{l}{f}_{X_1,{\delta }_1}(t_k,1\mid X_1\ge t_k)=\frac{f_1(t_k){\int }_0^{t_k}{S}_{C_1}(u)du}{{\int }_{t_k}^{\infty }{f}_1(s){\int }_0^s{S}_{C_1}(u)\mathit{duds}}\\ f_{X_2,{\delta }_2}(t_k,1\mid X_2\ge t_k)=\frac{f_2(t_k){\int }_0^{t_k}{S}_{C_2}(u)du}{{\int }_{t_k}^{\infty }{f}_2(s){\int }_0^s{S}_{C_2}(u)\mathit{duds}}.\end{array}$$

Under the null hypothesis f₁(.) = f₂(.) = f(.), the expectation of the logrank test statistic can be expressed as

$$E\left\{E\left(O_{2k}-O_k\frac{N_{2k}}{N_k}\mid N_k,N_{1k},N_{2k}\right)\mid H_0\right\}=E\left\{N_{2k}\left(\frac{f(t_k)W_2(t_k)}{{\int }_{t_k}^{\infty }f(s)W_{2}s(ds)}-\frac{N_{1k}\frac{f(t_k)W_1(t_k)}{{\int }_{t_k}^{\infty }f(s)W_1(s)ds}+N_{2k}\frac{f(t_k)W_2(t_k)}{{\int }_{t_k}^{\infty }f(s)W_2(s)ds}}{N_{1k}+N_{2k}}\right)\right\},$$ (7)

where $W_1(s)={\int }_0^s{S}_{C_1}(u)du$ and $W_2(s)={\int }_0^s{S}_{C_2}(u)du$. When the two groups have equal censoring distribution (including no censoring as a special case), S_C1(t) = S_C2(t), the expectation of (7) is zero under H₀. Therefore, the logrank test is a valid statistic to test the equality of survival distributions for length-biased data under equal censoring. When the censoring distributions are different, the logrank test statistic does not have a zero expectation under the null hypothesis from (7) due to the informative censoring induced by the sampling scheme. Subsequently, the standard logrank test may not preserve the nominal significance level under the null hypothesis when the censoring distributions in the two groups are different. Using the arguments similar to those in Section 2.4 and the fact that the logrank test is rank-based statistic, the logrank test is also valid for general left-truncated data as long as the censoring distributions in the two arms are the same.

For traditional right-censored survival data, the logrank statistic is asymptotically most efficient test under the proportional hazards alternatives. It is not surprising that the proposed score test reduces to the logrank test when there is no left truncation. Recall that the proposed score statistic is

$$\begin{array}{l}{T}_1^{\ast }=\sum _{j=1}^{n_2}\left\{{\delta }_{2j}+log\widehat{S}(x_{2j})\right\}\\ =\sum _{j=1}^h{O}_{2j}-\sum _{j=1}^n\sum _{t_k\le x_{2j}}\frac{O_k}{N_k}\\ =\sum _{j=1}^h\left(O_{2j}-O_j\frac{N_{2j}}{N_j}\right).\end{array}$$ (8)

When there is no left truncation, the unknown survival distribution in equation (8) is reduced to the Nelson-Aalen estimator, thereby $T_1^{\ast }$ can be expressed as a summation of the differences between the observed number of events and the expected number of events.

By modifying the risk set at time t as R^* = {k: X_k ≥ t ≥ A_k}, Lagakos and De Gruttola (1988) proposed the logrank type of test statistic for general left-truncated data as follows, which we refer to as truncation logrank test:

$$T_{LT}=\sum _{k=1}^h\left(O_{2k}-O_k\frac{N_{2k}^{\ast }}{N_{1k}^{\ast }+N_{2k}^{\ast }}\right),$$

where $N_{1k}^{\ast }$ and $N_{2k}^{\ast }$ denote the numbers of subjects “at risk” based on the revised risk set R^* for groups 1 and 2, respectively. Note that the observed truncated survival times and censoring times are independent conditional on the observed truncation times. Thus, under H₀ the expectation of T_LT is zero. Since the truncation logrank test is conditional on the observed truncation times, it would be less efficient than the unconditional score test for length-biased data. Efficiency and robustness comparisons between them will be further investigated in the following simulation studies.

4. Simulation

We used Monte Carlo simulations to evaluate and compare the performance (size and power) of the proposed test, the standard logrank test, and the truncation logrank test under different biased sampling schemes and censoring distributions. We used small (50) to moderate sample size(150) per group and a significance level of 0.05. The size and power were calculated from 5000 replications of the tests, and the resampling procedure used 500 resamples. We considered scenarios with unequal sample sizes in the groups as well as scenarios with equal sample sizes.

We generated independent pairs of (A_ij, X̃_ij), i = 1, 2, j = 1, · · ·, n_i, with the failure time generated from the Weibull distribution $\left(S_j(t)=exp\left\{-{\left(\frac{t}{{\beta }_j}\right)}^{{\alpha }_j}\right\}\right)$ for several choices of scale parameter β₂ and a fixed scale parameter β₁ = 1 in group 1 and fixed shape parameters α_j = 2; A_ij was generated from a uniform distribution to ensure the stationarity assumption or from an exponential distribution for general left-truncated data. Under each setting, we kept the pairs with A_ij < X̃_ij in the cohort. The censoring variables measured from the examination time, C_ij, were independently generated from uniform distributions. The conditional bootstrap procedure is more computationally intensive than the standard permutation procedure. An interesting question is whether the permutation procedure is robust with respect to the assumption of equal censoring distributions. We thereby assess the robustness of the standard permutation procedure.

Tables 1–3 respectively list the percentages of rejecting the null hypothesis at significance level 0.05 based on the simulations with small, moderate, and unbalanced sample sizes. We found that the type I error rates for the proposed test in all scenarios were reasonably close to the nominal value 0.05, and that the power increased with the increase in sample size and decreased with the increase in degree of censoring. With the equal total sample sizes, the proposed test was more powerful under the balanced design (n₁ = n₂, see Table 2) than under the unbalanced design (n₁ ≠ n₂, see Table 3).

Table 1.

Simulation results. Proportions of rejection of three test statistics for length-biased data based on sample size 50 per group with 5000 simulations

X1 ~ Weibull(2,1), $X_2\sim \text{Weibull}(2,1/\sqrt{\beta })$
β	Cen1%	Cen2%	Prop. of rejection	Prop. of rejection	Prop. of rejection
			Proposed test	Truncation logrank	Standard Logrank
			$T_1^{\ast }$	TLT	TLR
No censoring
1	0%	0%	0.051	0.050	0.052
1.2	0%	0%	0.203	0.131	0.202
1.4	0%	0%	0.530	0.368	0.534
0.8	0%	0%	0.266	0.193	0.273
0.6	0%	0%	0.847	0.678	0.849
Same censoring distributions SC1 = SC2
1	20%	20%	0.053	0.052	0.049
1.2	20%	18%	0.180	0.137	0.183
1.4	20%	17%	0.464	0.310	0.456
0.8	20%	23%	0.229	0.148	0.221
0.6	20%	26%	0.817	0.586	0.812
1	40%	40%	0.051	0.050	0.048
1.2	40%	36%	0.162	0.098	0.160
1.4	40%	34%	0.406	0.244	0.393
0.8	40%	43%	0.216	0.132	0.194
0.6	40%	48%	0.729	0.406	0.708
Different censoring distributions SC1 ≠ SC2
1	20%	6%	0.049 (0.052)	0.051	0.059
1.2	20%	5%	0.190 (0.222)	0.128	0.227
1.4	20%	5%	0.501 (0.510)	0.329	0.553
0.8	20%	6%	0.224 (0.240)	0.164	0.175
0.6	20%	7%	0.816 (0.811)	0.631	0.774
1	40%	10%	0.048 (0.054)	0.049	0.074
1.2	40%	9%	0.218 (0.212)	0.115	0.300
1.4	40%	9%	0.524 (0.539)	0.285	0.636
0.8	40%	12%	0.191 (0.223)	0.146	0.128
0.6	40%	14%	0.699 (0.721)	0.528	0.555

Table 3.

Simulation results. Proportions of rejection of three test statistics for length-biased data based on n₁ = 50 and n₂ = 150 and with 5000 simulations

X1 ~ Weibull(2,1), $X_2\sim \text{Weibull}(2,1/\sqrt{\beta })$
β	Cen1%	Cen2%	Proposed test	Prop. of rejection	Prop. of rejection
			Prop. of rejection	Truncation logrank	Standard Logrank
			$T_1^{\ast }$	TLT	TLR
No censoring
1	0%	0%	0.049	0.051	0.048
1.2	0%	0%	0.317	0.205	0.274
1.4	0%	0%	0.749	0.528	0.709
0.8	0%	0%	0.345	0.262	0.391
0.6	0%	0%	0.963	0.870	0.975
Same censoring distributions SC1 = SC2
1	20%	20%	0.052	0.051	0.051
1.2	20%	18%	0.254	0.150	0.205
1.4	20%	17%	0.659	0.423	0.608
0.8	20%	23%	0.288	0.220	0.327
0.6	20%	26%	0.936	0.778	0.947
1	40%	40%	0.051	0.052	0.051
1.2	40%	36%	0.263	0.124	0.215
1.4	40%	34%	0.591	0.330	0.518
0.8	40%	43%	0.307	0.200	0.333
0.6	40%	48%	0.889	0.681	0.887
Different censoring distributions SC1 ≠ SC2
1	20%	6%	0.049 (0.053)	0.051	0.056
1.2	20%	5%	0.282 (0.296)	0.164	0.297
1.4	20%	5%	0.674 (0.694)	0.450	0.700
0.8	20%	6%	0.269 (0.283)	0.230	0.258
0.6	20%	7%	0.910 (0.930)	0.779	0.909
1	40%	10%	0.047 (0.052)	0.049	0.084
1.2	40%	9%	0.259 (0.275)	0.143	0.389
1.4	40%	9%	0.642 (0.663)	0.381	0.761
0.8	40%	12%	0.210 (0.250)	0.202	0.151
0.6	40%	13%	0.843 (0.854)	0.696	0.768

Table 2.

Simulation results. Proportions of rejection of three test statistics for length-biased data based on sample size 100 per group with 5000 simulations

X1 ~ Weibull(2,1), $X_2\sim \text{Weibull}(2,1/\sqrt{\beta })$
β	Cen1%	Cen2%	Prop. of rejection	Prop. of rejection	Prop. of rejection
			Proposed test	Truncation logrank	Standard Logrank
			$T_1^{\ast }$	TLT	TLR
No censoring
1	0%	0%	0.049	0.048	0.049
1.2	0%	0%	0.323	0.204	0.308
1.4	0%	0%	0.802	0.628	0.807
0.8	0%	0%	0.465	0.331	0.471
0.6	0%	0%	0.989	0.943	0.987
Same censoring distributions SC1 = SC2
1	20%	20%	0.053	0.052	0.053
1.2	20%	18%	0.323	0.212	0.323
1.4	20%	17%	0.748	0.551	0.742
0.8	20%	23%	0.433	0.294	0.430
0.6	20%	26%	0.990	0.876	0.989
1	40%	40%	0.048	0.048	0.046
1.2	40%	36%	0.252	0.169	0.235
1.4	40%	34%	0.709	0.468	0.707
0.8	40%	43%	0.372	0.216	0.363
0.6	40%	48%	0.952	0.748	0.942
Different censoring distributions SC1 ≠ SC2
1	20%	6%	0.051 (0.050)	0.048	0.062
1.2	20%	5%	0.341 (0.358)	0.207	0.411
1.4	20%	5%	0.806 (0.804)	0.596	0.856
0.8	20%	6%	0.455 (0.477)	0.298	0.359
0.6	20%	7%	0.985 (0.984)	0.899	0.970
1	40%	10%	0.052 (0.053)	0.051	0.103
1.2	40%	9%	0.314 (0.318)	0.168	0.518
1.4	40%	9%	0.793 (0.802)	0.525	0.896
0.8	40%	12%	0.336 (0.335)	0.238	0.174
0.6	40%	13%	0.963 (0.956)	0.816	0.859

When the right censoring patterns were the same between two groups, the sizes of the three tests considered here were all in a reasonable range as expected. For the power comparison, the proposed score test exhibited superior power than the truncation logrank test. For example, in Table 1 the proposed test achieves 25 to 89% greater power than the truncation logrank test for the investigated scenarios based on a sample size of 50 per group. Somewhat surprisingly, the proposed test and the standard logrank test produced comparable powers, suggesting that the standard logrank test may not lose too much efficiency compared to the asymptotically most efficient score test under length-biased sampling.

As the two censoring distributions became dissimilar, we used two resampling procedures (standard permutation and conditional bootstrap) for the proposed score test. The rejection percentages obtained by the conditional bootstrap procedure are displayed in parentheses in Tables 1–3. Although the assumption of equal censoring was violated, the two procedures produced similar results in all of the simulation settings, indicating that the standard permutation procedure is quite robust to the assumption of equal censoring distributions. Again, the proposed score test outperformed the truncation logrank test, although both of them preserved the nominal error rate under the null hypothesis. Unlike $T_1^{\ast }$ and T_LT, the standard logrank test cannot preserve the specified significance level as shown in equation (7) for unequal censoring. For instance, the size of the standard logrank test is 0.103, much larger than the nominal value 0.05, in the last scenario in Table 2.

As demonstrated in Section 2.4, when the truncation distribution is known and the same for the two groups, the proposed test statistic is valid for general left-truncated data under a data transformation. However, because the truncation distribution is often unknown in practice, we investigated the performance of the proposed test under the non-uniform distributions of the truncation variable and assessed the robustness of the test without transforming the data. We compared the type I error rate and power for the proposed test with the standard and truncation logrank tests when the truncation was not uniform (generated from an exponential distribution) and followed the same or different truncation pattern for the two groups (Table 4). The simulation results show that the proposed test had correct sizes around the nominal value 0.05 under the same truncation pattern even though the truncation distribution was not uniform and the data were not transformed. When the truncation patterns were different in the two groups, the proposed test tended to have slightly inflated sizes ranging from 0.054 to 0.056. Similar to our finding for length-biased data, the standard logrank test produced results comparable to those of the proposed test for general left-truncated data under equal censoring distributions, though the standard logrank test cannot maintain the correct type I error rate when the censoring distributions in the two groups are different (not presented due to limited space). The validity of the truncation logrank test, which was originally proposed for general left-truncated data, is not in doubt. However, the truncation logrank test showed a loss of power due to the conditional approach when compared to the proposed test and naive logrank test under equal censoring. It is interesting to note that the proposed test statistic is in fact quite robust to the general truncation distribution without performing data transformation under the same truncation pattern, given the results listed in Table 4, although the validity of the test is not analytically verified under this more general setting. In the absence of right censoring, the validity of the proposed test for general truncation distribution without data transformation has been proven in equation (2) at the end of Section 2.1, which has also been confirmed by the empirical studies.

Table 4.

Simulation results. Proportions of rejection of three test statistics for left-truncated data without satisfying stationarity assumption based on sample size 100 per group with 5000 simulations

X1 ~ Weibull(2,1), $X_2\sim \text{Weibull}(2,1/\sqrt{\beta })$
β	Cen1%	Cen2%	Prop. of rejection	Prop. of rejection	Prop. of rejection
			Proposed test	Truncation logrank	Standard Logrank
			$T_1^{\ast }$	TLT	TLR
A1 ~ Exponential(1/10), A2 ~ Exponential(1/10)
No censoring
1	0%	0%	0.048	0.048	0.049
1.2	0%	0%	0.356	0.233	0.353
1.4	0%	0%	0.820	0.648	0.829
0.8	0%	0%	0.461	0.318	0.452
0.6	0%	0%	0.990	0.941	0.989
Same censoring distributions SC1 = SC2
1	20%	20%	0.050	0.049	0.052
1.2	20%	19%	0.295	0.194	0.291
1.4	20%	17%	0.735	0.521	0.732
0.8	20%	23%	0.419	0.263	0.410
0.6	20%	26%	0.982	0.865	0.983
1	40%	40%	0.051	0.052	0.053
1.2	40%	37%	0.252	0.146	0.237
1.4	40%	34%	0.698	0.454	0.685
0.8	40%	44%	0.366	0.223	0.366
0.6	40%	49%	0.946	0.721	0.937
A1 ~ Uniform(0, 20), A2 ~ Exponential(1/10)
No censoring
1	0%	0%	0.054	0.048	0.056
1.2	0%	0%	0.267	0.242	0.265
1.4	0%	0%	0.763	0.649	0.775
0.8	0%	0%	0.572	0.316	0.567
0.6	0%	0%	0.999	0.928	0.998
Same censoring distributions SC1 = SC2
1	20%	20%	0.055	0.052	0.058
1.2	20%	19%	0.244	0.199	0.242
1.4	20%	17%	0.702	0.568	0.700
0.8	20%	23%	0.504	0.278	0.495
0.6	20%	26%	0.984	0.862	0.979
1	40%	40%	0.056	0.053	0.055
1.2	40%	37%	0.212	0.176	0.220
1.4	40%	34%	0.631	0.460	0.624
0.8	40%	44%	0.422	0.199	0.400
0.6	40%	49%	0.969	0.739	0.959

5. Data Application

We apply the proposed test in two applications for illustration. The shrub data includes 46 complete widths of shrub from three trasects (18 from transect I, 22 from transect II, and 6 from transect III). The data were given in Muttlak and McDonald (1990) and further analysed by Wang (1996) for testing the equality of shrub’s widths from three transects. The truncation logrank test for left-truncated data could not be used in this example because there were no records for truncated widths. We performed both pairwise comparisons among the three groups and an overall k-sample test using the proposed score test and standard logrank test. Table 5 gives corresponding P-values for the tests. The analysis results from the proposed two-sample test and logrank test both indicated statistically significant differences in width between the transect I and transect II groups and transect I and transect III groups. Similar to the result of Wang (1996), there was no significant difference in width between transect II and transect III. For the three-sample comparison, the proposed and logrank three-sample tests both showed a significant difference among shrub widths from the three transects.

Table 5.

Examples: P-values from three test statistics for the shrub study and dementia trial

	Proposed test	Truncation logrank	Standard logrank
	$T_1^{\ast }$	TLT	TLR
Transect I vs II	0.01	NA	0.01
Transect I vs III	0.00	NA	0.02
Transect II vs III	0.71	NA	0.82
Three-sample test	0.04	NA	0.01
Vascular vs probable Alzheimer’s	0.35	0.42	0.46
Vascular vs possible Alzeimer’s	0.02	0.33	0.02
Probable vs possible Alzeimer’s	0.04	0.71	0.04
Three-sample test	0.05	0.54	0.05

The purpose of the second example is to compare the survival times following the onset of dementia for three diagnostic categories of dementia using data from the Canadian Study of Health and Aging (CSHA) (Wolfson et al., 2001). In the first phase of the CSHA, over 10,000 Canadians age 65 and older were screened for dementia in 1991. At that time, 1132 subjects with dementia were identified and classified into one of three diagnostic categories: (1) probable Alzheimer’s disease, (2) possible Alzheimer’s disease, and (3) vascular dementia. Information about the date of onset of dementia was collected from the medical history of these subjects. In the second phase of CSHA, the date of death or censoring between 1991 and 1996 was prospectively recorded for the subjects who had been diagnosed with dementia in the first phase of CSHA. The available data include 818 subjects with dementia: 393 with probable Alzheimer’s disease, 252 with possible Alzheimer’s disease, and 173 with vascular dementia. For each subject in the cohort, the date of disease onset, the entry date to the study, and the death indicator are also provided. Subjects with rapidly progressive dementia often died quickly, thereby they were more likely to be left truncated. Thus, the observed survival duration from the onset of dementia would tend to be longer in the prevalent cohort.

Using an analytic test to examine the stationarity assumption proposed by Addona and Wolfson (2006), we obtained the two-sided p-values of 0.72 for the vascular dementia group, 0.79 for the probable Alzheimer group, and 0.14 for the possible Alzheimer group. Asgharian et al. (2006) used the same data and estimated the nonparametric survival curves of the forward and backward recurrent times, which are almost indistinguishable and suggest no obvious violation of the stationarity assumption. The three estimated Kaplan-Meier curves for the censoring variable (not presented due to limited space) indicate that the three curves are almost indistinguishable, which suggests no obvious violation of the assumption about the equal censoring distributions (the corresponding logrank test P-value=0.27). Therefore, we also used the standard logrank test for comparison.

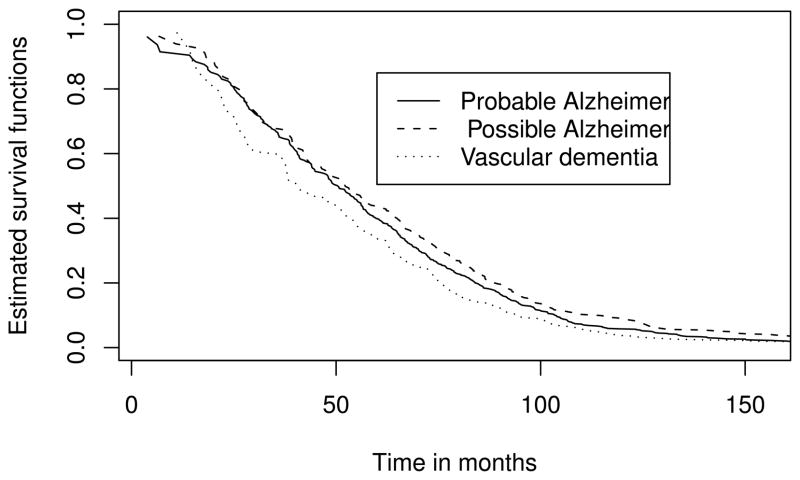
We performed both pairwise comparisons and overall comparisons among the three groups using three different tests. The P-values from the proposed two-sample test and standard logrank test both indicated that the long-term survival distributions are significantly different between groups with vascular dementia and with possible Alzheimer’s dementia, and between groups with probable Alzheimer’s dementia and with possible Alzheimer’s dementia (see Figure 1). The P-values of the overall comparison by the proposed three-sample test and logrank test again suggested an overall marginally significant difference in long-term survival distributions among the three subtypes of dementia. In contrast, the less efficient truncation logrank test could not detect the differences in survival distributions among the vascular dementia group and the other two groups, and produced P-values much bigger than 0.05.

Fig. 1.

Estimated survival functions after adjustment for length bias

6. Conclusion Remarks

We have focused on the development of a nonparametric score test statistic for length-biased data under proportional hazards alternatives, which is analogous to the logrank test for traditional survival data. Because of the invariant property of the proportional hazards alternatives, the proposed score test has proven to be applicable to and remains the asymptotically most efficient test under the proportional hazards alternatives for general left-truncated data with a transformation when the pattern of left truncation is the same for all the groups. Under equal censoring distribution, we find P-values and critical regions by permutation procedure. Even though the procedure involves permutation, the computation is fast and efficient because it is unnecessary to estimate the survival function in each permutation. Unlike the truncation logrank test, the proposed score test statistic with the corresponding permutation distribution does not need information on truncation times under equal censoring distribution. The information on truncation times is required for the conditional bootstrap procedure under unequal censoring distributions.

Although in this work we focused our attention on the proportional hazards alternatives, the score test can also be derived for other types of semi-parametric alternatives, such as the proportional odds ratio model, by straightforward extension. An interesting finding for us is that the standard logrank test ignoring biased sampling can be a valid test statistic if the censoring distributions between the groups are equal. Moreover, the loss of efficiency for the logrank test compared to the most efficient score test seems to be limited. In contrast, the conditional approach, which was originally proposed for general left-truncated data, is much less efficient than the proposed score test in all investigated settings. The inefficiency of conditional approaches has been noted earlier in Wang (1991). A critical condition for the use of the nonparametric logrank test under biased sampling is the requirement for equal censoring distributions between the groups. Any violation of this condition would lead to an inflated type I error rate for the logrank test because the biased sampling scheme induces dependent censoring, which is not the case for the standard logrank test proposed for traditional noninformative right censoring data. There is an essential difference between estimating a covariate coefficient, β, and testing whether β = 0 under the Cox model for length-biased data. While the traditional logrank test is valid to test β = 0, when the censoring distributions are equal for length-biased data, the covariate coefficient estimator from the conventional partial likelihood under the Cox model can be biased regardless of whether the censoring distributions are equal or not.

As one referee pointed out, there can be a loss of efficiency for the proposed test when the likelihood of covariates subject to left truncation is not used, when the marginal distribution of covariates is known (Bergeron et al., 2008). However, if the marginal distribution of covariates in the target population is unknown, which is common in most practical applications, there is no loss of information and the test based on the likelihood conditional on covariates can achieve the same efficiency as the full likelihood (Mandel and Ritov, 2009).

A. Appendix

A.1. Weak convergence of $T_1^{\ast }$

Following from the asymptotic properties of Vardi’s estimator (Asgharian and Wolfson, 2005), we can express Ĝ(t) − G(t) as a sum of i.i.d. random variables plus a reminder:

$$\widehat{G}(t)-G(t)={\mathcal{F}}^{-1}\left(\frac{{\sum }_{k=1}^n{V}_k(t)}{n}\right)+o_p(\frac{1}{\sqrt{n}}),$$ (9)

where is an invertible linear operator,

$$\begin{array}{l}\mathcal{F}(u)(t)=p_1{\int }_{0<x\le t}\frac{g^{\ast }(x)}{g(x)}du(x)+(1-p_1){\int }_{0<y\le t}y\left({\int }_{y\le z}\frac{u(z)}{z^2}dz\right)d\left\{\left(\frac{f_r(t)}{f_r(y)}-1\right)\frac{f^{\ast }(y)}{f_r(y)}\right\},\\ V_k(t)=\{I(x_k>t,{\delta }_k=1)-p_1{G}^{\ast }(t)\}+f_r(t){\int }_{0<z\le t}\{I(x_k\ge z,{\delta }_k=0)-(1-p_1)F^{\ast }(z)\}d\frac{1}{f_r(z)}+p_1{\left(\frac{p_1}{1-p_1}\right)}^{1/2}\{G^{\ast }(t)-G(t)\}\frac{\{(I({\delta }_k=1)-p_1\}}{\sqrt{p_1(1-p_1)}}.\end{array}$$

With equation (9), we derive the asymptotic representation of the NPMLE of unbiased distribution:

$$\begin{array}{l}\sqrt{n}\{\widehat{S}(y)-S(y)\}=\sqrt{n}\left\{\frac{{\int }_y^{\infty }\frac{1}{x}d\widehat{G}(x)}{{\int }_0^{\infty }\frac{1}{x}d\widehat{G}(x)}-\frac{{\int }_y^{\infty }\frac{1}{x}dG(x)}{{\int }_0^{\infty }\frac{1}{x}dG(x)}\right\}\\ =\sqrt{n}\frac{{\int }_0^{\infty }\frac{1}{x}dG(x)\left\{{\int }_y^{\infty }\frac{1}{x}d\widehat{G}(x)-{\int }_y^{\infty }\frac{1}{x}dG(x)\right\}-{\int }_y^{\infty }\frac{1}{x}dG(x)\left\{{\int }_0^{\infty }\frac{1}{x}d\widehat{G}(x)-{\int }_0^{\infty }\frac{1}{x}dG(x)\right\}}{{\int }_y^{\infty }\frac{1}{x}dG(x){\int }_0^{\infty }\frac{1}{x}dG(x)}+o_p(1)\\ =1/\sqrt{n}\sum _k^n\frac{{\int }_0^{\infty }\frac{1}{x}dG(x){\int }_y^{\infty }\frac{1}{x}d{\mathcal{F}}^{-1}(V_k(x))-{\int }_y^{\infty }\frac{1}{x}dG(x){\int }_0^{\infty }\frac{1}{x}d{\mathcal{F}}^{-1}(V_k(x))}{{\int }_y^{\infty }\frac{1}{x}dG(x){\int }_0^{\infty }\frac{1}{x}dG(x)}+o_p(1).\end{array}$$ (10)

For simplicity of notation, let

$$\begin{array}{c}{\mathcal{G}}_k(y)=\frac{{\int }_0^{\infty }\frac{1}{x}dG(x){\int }_y^{\infty }\frac{1}{x}d{\mathcal{F}}^{-1}(V_k(x))-{\int }_y^{\infty }\frac{1}{x}dG(x){\int }_0^{\infty }\frac{1}{x}d{\mathcal{F}}^{-1}(V_k(x))}{{\int }_y^{\infty }\frac{1}{x}dG(x){\int }_0^{\infty }\frac{1}{x}dG(x)},\\ I_k=\underset{n\to \infty }{lim}\frac{{\sum }_{j=1}^{n_2}\frac{1}{S(x_{2j})}{\mathcal{G}}_k(x_{2j})}{n}.\end{array}$$

By inserting equation (10), (y) and I_k, we have

$$\begin{array}{l}\frac{1}{\sqrt{n}}\sum _{j=1}^{n_2}\frac{1}{S(x_{2j})}\left\{\widehat{S}(x_{j2})-S(x_{2j})\right\}=\frac{1}{\sqrt{n}}\sum _{j=1}^{n_2}\frac{1}{S(x_{2j})}\sum _{k=1}^n{\mathcal{G}}_k(x_{2j})/n+o_p(1)\\ =\frac{1}{\sqrt{n}}\sum _{k=1}^n\frac{{\sum }_{j=1}^{n_2}\frac{1}{S(x_{2j})}{\mathcal{G}}_k(x_{2j})}{n}+o_p(1)\\ =\frac{1}{\sqrt{n}}\sum _{k=1}^n{I}_k+o_p(1).\end{array}$$ (11)

On the other hand, note that

$$\begin{array}{l}\sqrt{n}\frac{\int \widehat{S}(t)log\widehat{S}(t)dt}{\int \widehat{S}(t)dt}-\frac{\int S(t)logS(t)dt}{\int S(t)dt}=\sqrt{n}\frac{\int S(t)dt\left\{\int \widehat{S}(t)log\widehat{S}(t)dt-\int S(t)logS(t)dt\right\}}{{(\int S(t)dt)}^2}-\sqrt{n}\frac{\int S(t)logS(t)dt\left\{\int \widehat{S}(t)dt-\int S(t)dt\right\}}{{(\int S(t)dt)}^2}+o_p(1)\\ =\sqrt{n}\frac{\int S(t)dt\left[\int \{\widehat{S}(t)-S(t)\}logS(t)dt+\int \{\widehat{S}(t)-S(t)\}dt\right]}{{(\int S(t)dt)}^2}-\sqrt{n}\frac{\int S(t)logS(t)dt\int \{\widehat{S}(t)-S(t)\}dt}{{(\int S(t)dt)}^2}+o_p(1)\\ =\frac{1}{\sqrt{n}}\sum _{k=1}^n\left[\frac{\int {\mathcal{G}}_k(t))\{logS(t)+1\}dt}{\int S(t)dt}-\frac{\int S(t)logS(t)dt\int {\mathcal{G}}_k(t)dt}{{(\int S(t)dt)}^2}\right]+o_p(1).\end{array}$$ (12)

Therefore, after applying (11) and (12), one can write

$$\begin{array}{l}{T}_1^{\ast }-T_1=\sum _{j=1}^{n_2}\left\{log\widehat{S}(x_{2j})-logS(x_{2j})-\frac{\int \widehat{S}(t)log\widehat{S}(t)dt}{\int \widehat{S}(t)dt}+\frac{\int S(t)logS(t)dt}{\int S(t)dt}\right\}\\ =\sum _{j=1}^{n_2}\left\{\frac{1}{S(x_{2j})}\left(\widehat{S}(x_{2j})-S(x_{2j})\right)-\frac{\int \widehat{S}(t)log\widehat{S}(t)dt}{\int \widehat{S}(t)dt}+\frac{\int S(t)logS(t)dt}{\int S(t)dt}\right\}+o_p(\sqrt{n})\\ =\sum _{k=1}^n\left[I_k-(1-\rho )\left\{\frac{\int {\mathcal{G}}_k(t)\{logS(t)+1\}dt}{\int S(t)dt}-\frac{\int S(t)logS(t)dt\int {\mathcal{G}}_k(t)dt}{{(\int S(t)dt)}^2}\right\}\right]+o_p(\sqrt{n}).\end{array}$$

Then the independent and identically distributed (i.i.d.) representation of the test statistic is

$$T_1^{\ast }=\sum _{k=1}^n\left[I_k-(1-\rho )\left\{\frac{\int {\mathcal{G}}_k(t)\{logS(t)+1\}dt}{\int S(t)dt}-\frac{\int S(t)logS(t)dt\int {\mathcal{G}}_k(t)dt}{{(\int S(t)dt)}^2}\right\}\right]+\sum _{k=1}^n{z}_k\left\{{\delta }_k+logS(x_k)-\frac{\int S(t)logS(t)dt}{\int S(t)dt}\right\}+o_p(\sqrt{n}),$$ (13)

where z_k = 1 if the observation k is in the second sample, z_k = 0 otherwise. The central limit theorem, taken together with the i.i.d. representation (13) implies that $T_1^{\ast }/\sqrt{n}$ converges in distribution to a zero-mean normal distribution.