Abstract
Whole bone morphology, cortical geometry, and tissue material properties modulate skeletal stresses and strains that in turn influence skeletal physiology and remodeling. Understanding how bone stiffness, the relationship between applied load and tissue strain, is regulated by developmental changes in bone structure and tissue material properties is important in implementing biophysical strategies for promoting healthy bone growth and preventing bone loss. The goal of this study was to relate developmental patterns of in vivo whole bone stiffness to whole bone morphology, cross-sectional geometry, and tissue properties using a mouse axial loading model. We measured in vivo tibial stiffness in three age groups (6wks, 10wks, 16wks old) of female C57Bl/6 mice during cyclic tibial compression. Tibial stiffness was then related to cortical geometry, longitudinal bone curvature, and tissue mineral density using microcomputed tomography (microCT). Tibial stiffness and the stresses induced by axial compression were generally maintained from 6 to 16wks of age. Growth-related increases in cortical cross-sectional geometry and longitudinal bone curvature had counteracting effects on induced bone stresses and, therefore, maintained tibial stiffness similarly with growth. Tissue mineral density increased slightly from 6 to 16wks of age, and although the effects of this increase on tibial stiffness were not directly measured, its role in the modulation of whole bone stiffness was likely minor over the age range examined. Thus, whole bone morphology, as characterized by longitudinal curvature, along with cortical geometry, plays an important role in modulating bone stiffness during development and should be considered when evaluating and designing in vivo loading studies and biophysical skeletal therapies.
Keywords: mouse, tibia, applied load, stiffness, bone curvature
Introduction
Bone stiffness, the relationship between applied load and induced tissue strain, is modulated by bone morphology and tissue material properties. Because tissue-level strain is a critical regulator of bone growth and remodeling (Carter, 1982; Frost, 1983; Lanyon, 1987), understanding how stiffness is regulated by bone morphology and material properties during development is important for designing biophysical stimuli to promote healthy bone growth and prevent bone loss.
Long bone stiffness increases during development at the whole bone and tissue levels in traditional material tests (Brear et al., 1990; Carrier, 1983; Carrier and Leon, 1990; Currey and Butler, 1975; Currey and Pond, 1989; Ferguson et al., 2003; Torzilli et al., 1981; Zioupos and Currey, 1998). Age-related changes in rodent long bone stiffness measured in situ or calculated using engineering beam theory are dependent on the applied loading mode. Rat tibial stiffness measured in four point bending was similar in 9 and 19 month (mo) old rats (Turner et al., 1994; Turner et al., 1995). Similar results were reported for mouse tibiae loaded in cantilever bending at 10 weeks (wks) and 21mos of age (Gross et al., 2002; Srinivasan et al., 2003). In contrast, rat ulnar stiffness measured during axial loading doubled from 5wks to 8mos of age (Hsieh et al., 2001; Warden et al., 2007). However, the primary focus of these previous studies was the adaptive response of the skeleton to load and did not consider how tissue and structural properties modulated in vivo whole bone stiffness during development.
Whole bone morphology is an important determinant of skeletal mechanics during locomotion and in applied loading models. Developmental changes in bone morphology, including longitudinal curvature, alter the moments acting on the skeleton and consequently, the induced stresses and strains (Carrier, 1983; Carrier and Leon, 1990; Main and Biewener, 2004; Main and Biewener, 2007). In vivo axial loading models of long bones use the natural curvature to produce a physiological combination of axial and bending loads. Thus, bone curvature was likely important in the age-related increases in bone stiffness in previous axial loading models (Hsieh et al., 2001; Warden et al., 2007). However, measures of curvature were not reported in these studies, so the effects of developmental changes in whole bone morphology on bone stiffness can not be assessed. To determine how in vivo bone stiffness is modulated during development, age-related changes in whole bone structure, cross-sectional geometry, and tissue material properties must be considered together.
The goal of this study was to relate in vivo bone stiffness to whole bone morphology, cross-sectional geometry, and tissue composition during development. We measured in vivo tibial stiffness in three age groups of female mice using an established axial tibial loading protocol (Fritton et al., 2005; Fritton et al., 2008) and related tibial stiffness to measures of whole bone and cortical geometry and tissue mineral density from microcomputed tomography. We hypothesized that tibial stiffness would increase with age due to increased cross-sectional bone geometry and tissue material properties. The increased stiffness would, however, be mitigated by larger bending moments and stresses in the tibiae of older mice caused by increased tibial curvature with age, similar to the increased bone curvature reported during growth in other vertebrates (Biewener and Bertram, 1994; Main and Biewener, 2004; Main and Biewener, 2007).
Materials and Methods
Tibial stiffness measurements
Tibial stiffness was measured in three groups of female C57Bl/6 mice at 6, 10, and 16wks of age (N=4, 4, and 5, respectively, Jackson Laboratory). The mice weighed 16.4 ± 0.9g, 18.8 ± 1.2g, and 20.2 ± 0.6g at these ages, respectively. The 6wk old mice were rapidly growing post-pubescent mice (Richman et al., 2001; Sheng et al., 1999; Somerville et al., 2004) whose tibiae were just large enough to provide a flat surface to accommodate the strain gauges to measure bone stiffness. At 16wks of age, female C57Bl/6 mice are sexually mature, active growth has decreased, and peak bone mass is achieved (Beamer et al., 1996; Sheng et al., 1999; Somerville et al., 2004). The 10wk group was an intermediate age, similar to mice used in our previous loading experiments (Fritton et al., 2005; Fritton et al., 2008). All mice were housed 4–5 per cage and maintained on a 12:12 light-dark cycle with ad libitum access to commercial rodent diet and water.
A single element strain gauge was attached to the surface of the medial mid-diaphysis of the left tibia in each mouse. The medial mid-diaphysis is easily accessible, has a flat surface for gauge attachment, and did not require significant disruption of muscle attachments. Additionally, the tensile loading environment induced by axial compression on the medial surface of the tibia has been well described both experimentally and computationally (Fritton et al., 2005; Stadelmann et al., 2009; Sugiyama et al., 2008). Each animal was anesthetized (2% isoflurane, 1.0L/min O2) and an incision made over the medial surface of the tibia. Overlying skin and soft tissues were retracted, the tibia lightly scraped with a periosteal elevator, and cleaned and degreased using methyl ethyl ketone (Sigma Chemical). A single element strain gauge (EA-06-015LA-120, prepared dimensions: 0.6mm × 2.3mm, Micromeasurements) was aligned to the long axis of the bone and bonded just proximal to the medial midshaft and just distal to the anterior tibial crest (Figure 1) using self-catalyzing cyanoacrylate adhesive (Duro, Henkel Loctite Corp.). Strain gauges were trimmed and prepared following previous methods (Biewener, 1992). Following gauge application, the incision remained open with the gauge wires freely exiting. The strain gauge was connected to quarter-bridge completion and analog input modules (NI9944 and NI9237, National Instruments), and calibrated and zeroed using software supplied by the manufacturer.
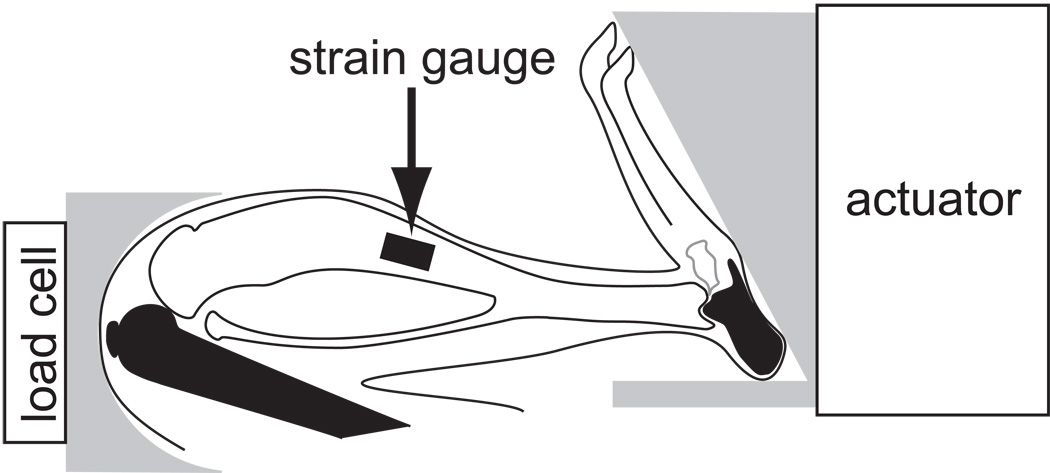
Figure 1.
Schematic of the device used to load the mouse hindlimb. Compressive loads were applied at the footplate by an electromagnetic actuator and transmitted loads were measured with a load cell at the knee cup. Load was primarily transmitted to the tibia (in white) through the calcaneus distally and the femur proximally (in black). A single element strain gauge bonded at the mid-diaphysis on the medial surface of the tibia measured the strains induced in the tibia as a function of applied load to determine bone stiffness.
While anesthetized, dynamic compressive loads were applied to the tibia with a custom-built loading device (Figure 1, Fritton et al., 2005) and controlled using a feedback loop to maintain consistent load magnitudes (Labview, v.8.5, National Instruments). Applied loads were measured with a load cell (ELFS-T3E-20L, Measurement Specialties, Inc.) in series with the tibia and actuator. Triangle waveform loads were applied at 4Hz and characterized by 0.15sec of symmetric active loading/unloading with a 0.10sec rest insertion between load cycles (Figure 2A). A pre-load of −1.5N was maintained during the ‘rest’ phase. Four load levels were applied to each tibia (−3.8N, −6.3N, −8.6N, −11.3N) and the load and strain data recorded simultaneously at 2.5kHz. The duration of each load trial was dependent upon the time to reach repeatable peak strains (typically < 30sec). Following data collection, the lead wires to the gauge were cut and the gauge left intact on the bone. Mice were euthanized by carbon dioxide inhalation, and the tibiae dissected free of soft tissue and stored in 70% ethanol at room temperature. All experimental procedures were approved by Cornell University’s IACUC.
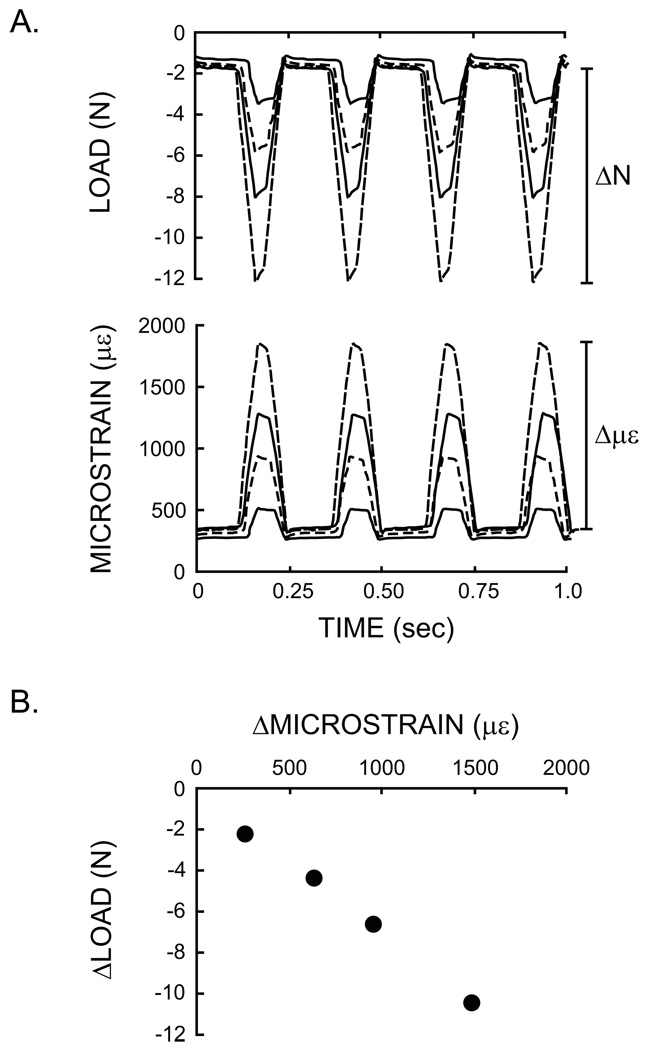
Figure 2.
Measurement of tibial stiffness. (A) Sample data from four successively greater peak loads applied cyclically to the tibia and the corresponding tibial deformation recorded by the strain gauge. (B) Stiffness was determined as the change in load (ΔN) over the change in strain (Δμε) during each load cycle. This relationship was linear with increasing load. Each point plotted is a mean of four load cycles. Mean stiffness for each tibia was taken as the average of the four stiffness values plotted in (B).
In vivo tibial stiffness was determined for each age group. Stiffness for each load level was calculated as the change in load (ΔN) over the change in strain (Δμε) during the loading portion of the waveform and averaged across four consecutive load cycles (Figure 2B). Stiffness at each of the four load levels was averaged to obtain a mean tibial stiffness per mouse. Stiffness and bone geometry were compared for the left and right tibiae in the 10wk old mice and did not differ (paired t-test, p > 0.05). Thus, these measures were only made in the left tibiae for the 6 and 16wk old mice.
Morphometric and stress analyses
Morphometric analyses were conducted by microCT. The solder leads were removed from the strain gauges and the tibiae scanned in phosphate-buffered saline (μCT 35, Scanco Medical; 55kVp, 145µA, 600ms integration time, no frame averaging). A 0.5mm aluminum filter reduced the effects of beam hardening. Diaphyseal scans at 15µm isotropic voxel resolution included the strain gauge and midshaft. Whole bone scans were made at a voxel resolution of 20µm. A preset hydroxyapatite (HA) calibration was used to convert the linear attenuation for each voxel to g HA/cm3. No artifact was visible in the scans due to the strain gauges attached to the bones. All scans were aligned prior to analysis using anatomical landmarks common to all mice.
Once aligned, a volume of interest was centered at the midpoint of the gauge in the cortical segment, extending a total of 2.5% of the bone’s length. Age-specific thresholds were set at one third of the bone peak for the microCT attenuation histogram. The age-specific thresholds for the 6, 10, and 16wk old groups were 0.27, 0.30, and 0.31 g HA/cm3. Cortical outcome variables included cortical area (Ct.Ar, mm2), the principal moments of inertia (IMAX, IMIN, mm4), and tissue mineral density (TMD, g HA/cm3).
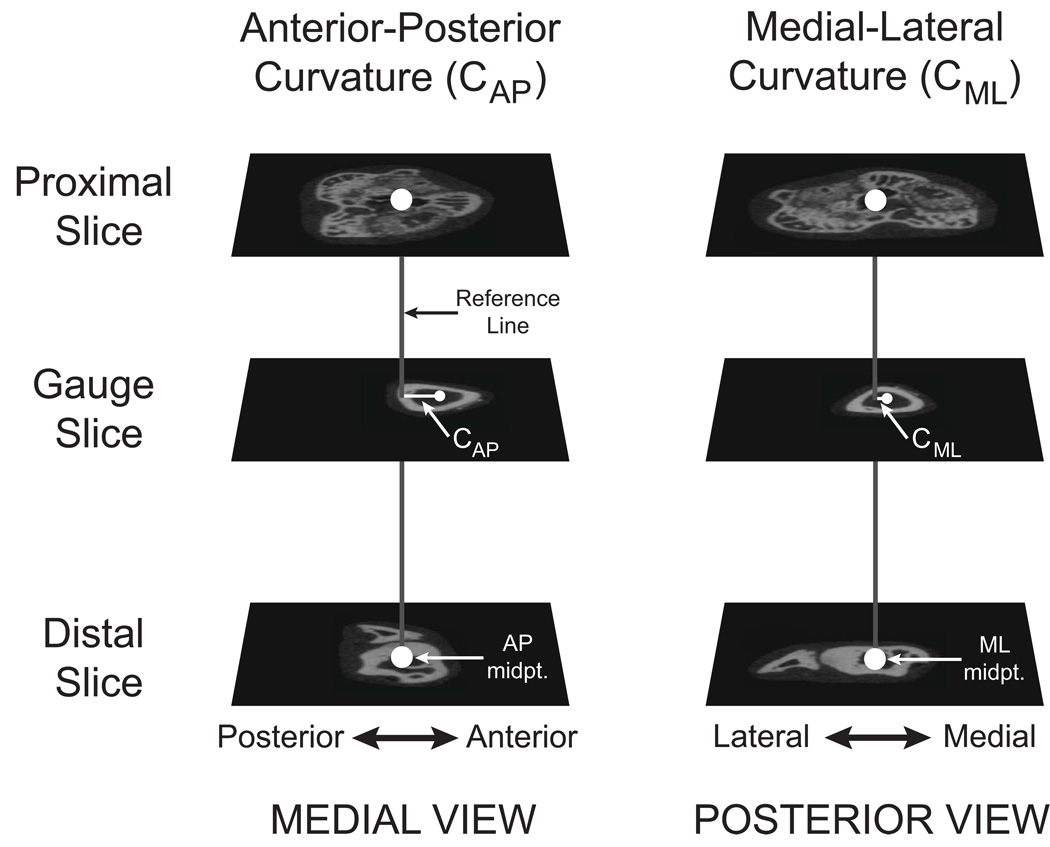
The anterior-posterior and medial-lateral radii of curvature (CAP and CML, mm) were measured on whole bone scans by adapting previous methods for making these measurements on radiographs or whole bone specimens (Biewener, 1983a; Main and Biewener, 2007). Midpoints for the AP and ML bone diameters for each tibia at its widest proximal and distal epiphyseal dimensions were determined from transverse microCT slices (Figure 3). Proximal-distal AP and ML reference lines were created using these two midpoints. CAP and CML were measured as the perpendicular distances between the AP and ML reference lines and the AP and ML midpoints of the bone at mid-gauge level. The proximal-distal reference lines represent the orientation of the compressive force vector. Consequently, CAP and CML are the moment arms about which this compressive fore vector acts to produce bending moments about the bone’s long axis. Positive values for CAP and CML represent anterior and medial convexities, respectively. Bone length and AP and ML bone diameters at the level of the strain gauge were also measured from the whole bone scans.
Figure 3.
Measurement of tibial longitudinal bone curvature. The anterior-posterior and medial-lateral longitudinal bone curvatures (CAP and CML) were measured using transverse slices from the whole bone microCT scans. A reference line (gray) was created between the AP and ML midpoints in the proximal and distal slices (large white circles). The AP and ML midpoints at the mid-gauge slice (small white circles) were determined and the perpendicular distances between these and the reference lines measured in the AP and ML directions (CAP and CML). This figure shows the anterior and smaller medial convexities commonly measured for the mouse tibiae in this study.
To understand how morphological changes with age affected tibial stiffness, axial and bending stresses induced by a 9N compressive axial load were calculated at the level of the strain gauge. A single load was used for all age groups to directly compare the effects of differences in bone morphology on load-induced stresses and bone stiffness. The 9N load level was consistent with other tibial loading experiments in our lab (Main et al., 2009; Main et al., 2010). The axial stress (σax) induced by the compressive load was calculated as:
| (1) |
where P = −9N and Ct.Ar is the bone cross-sectional area at the level of gauge attachment. AP and ML bending stresses (σb,AP, σb,ML) were calculated as:
| (2) |
where x is the AP or ML plane and Cx and rx are the radius of curvature and radius of the tibia at the mid-gauge level. IAP and IML are the moments of inertia about the ML and AP planes and differed from IMAX and IMIN by 2%, respectively. Due to the typically convex anterior and medial curvatures of the tibiae at the gauge site (Figure 3), σb was positive (tensile) on the anterior and medial bone surfaces.
Statistical analyses
Differences in tibial stiffness, morphology, and stress were determined by ANOVA with age as the independent variable. The Tukey-Kramer post hoc test was used to examine specific differences with age (SPSS, v.15.0). When the ANOVA requirement for equal variance between groups was not satisfied, non-parametric Kruskall-Wallis tests were used with a post hoc Mann-Whitney U test (Dytham, 2003). All data are presented as mean ± 1 SD. Statistical significance is indicated at p < 0.05.
Results
Morphometric measures and tissue mineral density generally increased with age (Table 1, Figure 4). Ct.Ar and IMIN increased from 6 to 10wks of age but were similar at 10 and 16wks of age. IMAX also increased from 6 to 16wks of age, but did not differ significantly from these two groups in 10wk old mice. CAP increased with age, where the tibiae of 16wk old mice had a significantly greater anterior convex curvature than in 6wk old mice. CML was less than CAP at all ages and showed a trend (ANOVA, p=0.063) for increasing convex medial curvature with age. TMD was significantly less in 6wk old mice than in 10 and 16wk old mice, but did not differ between the 10 and 16wk old groups.
Table 1.
Morphological parameters and bone density for mouse tibiae (mean ± SD)
| 6wk | 10wk | 16wk | Statistical Test | |
|---|---|---|---|---|
| Bone length (mm) | 15.78 ± 0.13a | 16.99 ± 0.15b | 17.50 ± 0.12c | A |
| AP diameter (mm) | 1.13 ± 0.08 | 1.22 ± 0.10 | 1.21 ± 0.01 | KW |
| ML diameter (mm) | 1.06 ± 0.04a | 1.15 ± 0.06b | 1.13 ± 0.03a,b | A |
| Ct.Ar (mm2) | 0.50 ± 0.03a | 0.62 ± 0.04b | 0.65 ± 0.02b | A |
| IMAX (mm4) | 0.062 ± 0.010a | 0.086 ± 0.017a,b | 0.084 ± 0.004b | KW |
| IMIN (mm4) | 0.046 ± 0.007a | 0.064 ± 0.011b | 0.067 ± 0.005b | A |
| CAP (mm) | 0.63 ± 0.09a | 0.77 ± 0.09a,b | 0.84 ± 0.05b | KW |
| CML(mm) | 0.11 ± 0.10 | 0.22 ± 0.08 | 0.25 ± 0.05 | A |
| TMD (g HA/cm3) | 0.81 ± 0.04a | 0.91 ± 0.01b | 0.93 ± 0.03b | A |
AP: anterior-posterior, ML: medial-lateral, Ct.Ar: cortical area, IMAX, IMIN maximum and minimum principal moments of inertia, CAP, CML AP and ML radius of curvature, TMD: tissue mineral density, HA: hydroxyapatite. Different superscript letters indicate significant differences between age groups at p < 0.05. ANOVA (A) with Tukey-Kramer post hoc test and non-parametric Kruskall Wallis (KW) and post hoc Mann-Whitney U tests were used to distinguish age-related differences in the measured parameters.
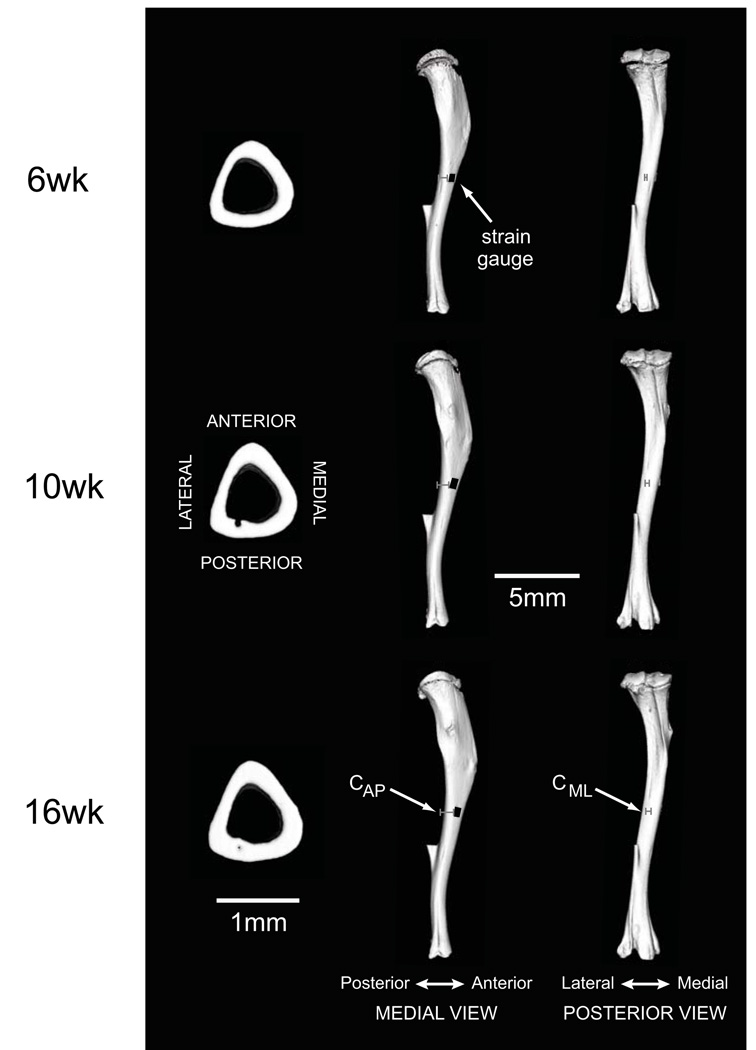
Figure 4.
Tibial morphology during growth and development. Three-dimensional cross-sectional and whole bone reconstructions from microCT scans illustrate developmental changes in diaphyseal and whole bone morphology. Medial and posterior views of the tibiae illustrate representative measures for CAP and CML, respectively, in the three age groups (gray bars). Representative strain gauge positions on the anterior-medial aspects of the tibial diaphyses are indicated in black in the medial view. The fibulae were also scanned, but were excluded from analysis during processing of the microCT scans.
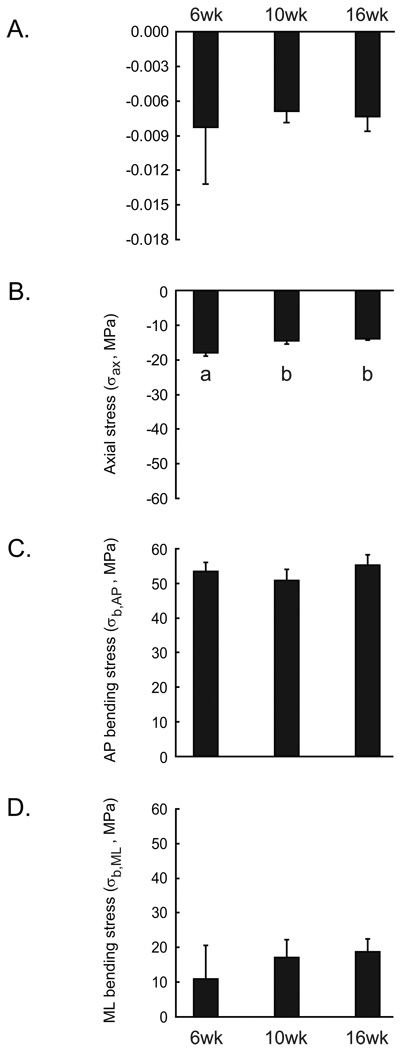
Tibial stiffness and the bending stresses induced by a 9N compressive load did not vary with age while axial stresses decreased from 6wks to 10 and 16wks of age (Figure 5). In vivo stiffness and AP bending stresses (σb,AP) were remarkably similar at all ages. ML bending stresses (σb,ML) were more variable at each time point examined and did not change significantly with age. Reflecting the increase in cortical area with age, axial stress (σax) decreased from 6 to 10wks of age but did not change from 10 to 16wks of age.
Figure 5.
Tibial stiffness (N/με) measured at the medial mid-diaphysis and (B) axial stress (σax), (C) anterior-posterior bending stress (σb,AP), and (D) medial-lateral bending stress (σb,ML) induced at the mid-diaphysis by a 9N compressive load for 6wk, 10wk, and 16wk old mice. Values are mean ± 1 SD. Different letters indicate p < 0.05 by ANOVA and Tukey-Kramer post hoc test.
Discussion
In vivo tibial stiffness in female mice remained similar during development due to the counteracting effects of increased cortical geometry and bone curvature with age on load-induced tibial stresses. The age-related increase in cortical area caused a small decrease in axial stresses in older mice. Greater AP bone curvature in older mice increased the bending moments induced by the axial load, counteracting increased bone geometry, such that AP bending stresses remained remarkably similar with age. The two-fold increase in ML bone curvature from 6 to 16wks of age did not increase bone stresses significantly due to attenuation by increased bone mass with age and relatively high inter-individual variation in bone curvature.
The effect of increased tissue mineral density (TMD) from 6 to 16wks of age on tissue material properties and bone stiffness was not directly measured in this study. Because stiffness remained similar across the age groups examined, the effects of growth-related changes in TMD and morphology on tibial stiffness could not be determined statistically by linear correlation. However, maintenance of the calculated stresses, which are independent of tissue material properties, and tibial stiffness suggest a minor role for the increase in TMD with age in modulating bone stiffness. Additionally, continuum-level and solid phase measures of elastic modulus indicate that modulus does not change significantly following sexual maturation in female rodents (Busa et al., 2005; Keller et al. 1986; Miller et al., 2007; Somerville et al., 2004), which occurs at 4–5wks of age in female mice (Richman et al., 2001; Sheng et al., 1999). Specifically, elastic moduli in female C57Bl/6 tibiae did not change over the age range examined here (Somerville et al., 2004) and bone tissue stiffness in 40 day old BALB/cByJ mice was not significantly different from mature bone despite lower TMD and mineralization levels (Miller et al., 2007). If the longitudinal elastic moduli for the C57Bl/6 tibiae examined in this study followed similar trends as those reported in the literature, in vivo tibial stiffness was maintained primarily by the counteracting effects of changes in cross-sectional geometry and longitudinal curvature, with less modulation due to changes in tissue material properties.
Stiffness at the medial midshaft surface was measured over a broad range of loads to induce functional strain levels in the tibia. The minimum load (−3.8N) was the lowest applied load for which repeatable strains could be measured in the tibia during axial compression. The maximum load (−11.3N) corresponded to midshaft tibial deformations of about +2000με, which are similar to peak in vivo bone strains measured in rodent ulnae (Mosley et al., 1997; Lee et al., 2002) and the limb bones of numerous vertebrate groups (Rubin and Lanyon, 1982; Biewener, 1993). As the strain environment induced in the tibia by axial compression is non-uniform (Stadelmann et al., 2009; de Souza et al., 2005), the measures of bone stiffness made here are specific to the tibia’s medial midshaft. Although absolute stiffness measurements will vary at different sites, the developmental modulation of bone stiffness at the tibia’s medial mid-diaphysis is assumed to be representative of other diaphyseal sites. Verification of this hypothesis could be performed using finite element analyses of representative tibiae during axial compression for the three age groups examined.
Bone curvature is a critical determinant of bone stress and, ultimately, stiffness during skeletal loading. Axial components of the muscle and ground reaction forces act about the longitudinal bone curvature to induce multi-directional bending moments in the limb bones. The bending stresses caused by these moments are often the dominant component of skeletal loading in a wide range of mammals (Biewener, 1983b; Biewener et al., 1983; Biewener, 1991). In vivo axial loading protocols, like that used for the mouse tibia in this study, take advantage of bone curvature to produce a physiological combination of axial and multi-directional bending stresses in the bone. In contrast, three or four point bending assessments of whole bone stiffness that induce bending about a single plane (Akhter et al., 1992; Turner et al., 1991) account for the contributions by cross-sectional geometry and tissue properties (van der Meulen et al., 2001), but can not capture the effects of whole bone morphology on structural mechanical behaviour. Whole bone morphology, in conjunction with cortical geometry and tissue material properties, significantly affects functional bone stiffness and the loading environment engendered in the tissue (Lanyon, 1987) and should be considered more widely for assessing the outcome of in vivo loading studies.
Although the group sizes in this study were small, significant differences were measured and our experimental design is consistent with the in vivo strain and applied loading literature. Our group sizes were similar to many previous in vivo bone strain studies (Biewener and Dial, 1995; Biewener and Taylor, 1986; Biewener et al., 1986; Blob and Biewener, 1999; Butcher et al., 2008; Goodship et al., 1979; Lanyon et al., 1982; Loitz and Zernicke, 1992; Rabkin et al., 2001) and greater than the numbers typically used to calibrate rodent in vivo loading protocols (de Souza et al., 2005; Fritton et al., 2005; Gross et al., 2002; Hsieh et al., 2001; Lee et al., 2002; Robling and Turner, 2002; Warden et al., 2007). Based on post hoc power analyses of our data, the AP and ML bending stresses calculated here would require >25 mice per age group to demonstrate significant age-related differences with 90% confidence, given the level of variation measured here (Zar, 1999). Similarly, about 180 mice per group would be necessary to show significant age-related differences in tibial stiffness. These numbers are well beyond those used in any study characterizing rodent skeletal structure or mechanics, providing additional confidence in the stiffness patterns reported here during skeletal growth in the mouse tibia.
In summary, in vivo tibial stiffness measured under applied compressive load was maintained similarly in growing and adult female mice as a result of developmental increases in cortical geometry and bone curvature. The importance of developmental changes in whole bone morphology, particularly bone curvature, in maintaining mouse tibial stiffness under in vivo axial loading, despite increased cross-sectional geometry with age, reflects its critical role in skeletal mechanics and physiology during in vivo loading. Thus, the role of whole bone morphology in modulating bone stiffness is an important consideration, in addition to traditional assessments of cross-sectional geometry and material properties, when planning or evaluating developmental loading studies or biophysical skeletal therapies.
Acknowledgements
The authors thank Thomas Schmicker, Daniel Walsh, and Frank Ko for their assistance during experimental procedures. Rasesh Kapadia, Dr. Andres Laib, and Lyudamila Lukashova provided assistance with microCT scanning and analysis. Dr. James Booth and Shamil Sadigov of the Cornell University Statistical Consulting Unit provided statistical advice. This work was supported by NIH grants R01-AG028664, P30-AR46121, S10-RR024547, and F32-AR054676 (RPM) and a NSF Graduate Research Fellowship (MEL). The content in this paper is the responsibility of the authors and does not necessarily represent the official views of the individual granting agencies within the National Institutes of Health.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Conflict of Interest Statement: The authors have no conflicts of interest.
References
- Akhter MP, Raab DM, Turner CH, Kimmel DB, Recker RR. Characterization of in vivo strain in the rat tibia during external application of a four-point bending load. Journal of Biomechanics. 1992;25:1241–1246. doi: 10.1016/0021-9290(92)90082-c. [DOI] [PubMed] [Google Scholar]
- Beamer WG, Donahue LR, Rosen CJ, Baylink DJ. Genetic variability in adult bone density among inbred strains of mice. Bone. 1996;18:397–403. doi: 10.1016/8756-3282(96)00047-6. [DOI] [PubMed] [Google Scholar]
- Biewener AA. Allometry of quadrupedal locomotion: the scaling of duty factor, bone curvature and limb orientation to body size. Journal of Experimental Biology. 1983a;105:147–171. doi: 10.1242/jeb.105.1.147. [DOI] [PubMed] [Google Scholar]
- Biewener AA. Locomotory stresses in the limb bones of two small mammals: the ground squirrel and chipmunk. Journal of Experimental Biology. 1983b;103:131–154. doi: 10.1242/jeb.103.1.131. [DOI] [PubMed] [Google Scholar]
- Biewener AA. Musculoskeletal design in relation to body size. Journal of Biomechanics. 1991;24:19–29. doi: 10.1016/0021-9290(91)90374-v. [DOI] [PubMed] [Google Scholar]
- Biewener AA. In vivo measurement of bone strain and tendon force. In: Biewener AA, editor. Biomechanics- Structures and Systems, The Practical Approach Series. New York: Oxford University Press; 1992. pp. 123–147. [Google Scholar]
- Biewener AA. Safety factors in bone strength. Calcified Tissue International. 1993;53:S68–S74. doi: 10.1007/BF01673406. [DOI] [PubMed] [Google Scholar]
- Biewener AA, Bertram JEA. Structural response of growing bone to exercise and disuse. Journal of Applied Physiology. 1994;76:946–955. doi: 10.1152/jappl.1994.76.2.946. [DOI] [PubMed] [Google Scholar]
- Biewener AA, Dial KP. In vivo strain in the humerus of pigeons (Columba livia) during flight. Journal of Morphology. 1995;225:61–75. [Google Scholar]
- Biewener AA, Swartz SM, Bertram JEA. Bone modeling during growth: Dynamic strain equilibrium in the chick tibiotarsus. Calcified Tissue International. 1986;39:390–395. doi: 10.1007/BF02555177. [DOI] [PubMed] [Google Scholar]
- Biewener AA, Taylor CR. Bone strain: A determinant of gait and speed? Journal of Experimental Biology. 1986;123:383–400. doi: 10.1242/jeb.123.1.383. [DOI] [PubMed] [Google Scholar]
- Biewener AA, Thomason J, Lanyon LE. Mechanics of locomotion in the forelimb of the horse (Equus): in vivo stress developed in the radius and metacarpus. Journal of Zoology, London. 1983;201:67–82. [Google Scholar]
- Blob RW, Biewener AA. In vivo locomotor strain in the hindlimb bones of Alligator mississippiensis and Iguana iguana: Implications for the evolution of limb bone safety factor and non-sprawling limb posture. Journal of Experimental Biology. 1999;202:1023–1046. doi: 10.1242/jeb.202.9.1023. [DOI] [PubMed] [Google Scholar]
- Brear K, Currey JD, Pond CM. Ontogenetic changes in the mechanical properties of the femur of the polar bear Ursus maritimus. Journal of Zoology, London. 1990;222:49–58. [Google Scholar]
- Busa B, Miller LM, Rubin CT, Qin Y-X, Judex S. Rapid establishment of chemical and mechanical properties during lamellar bone formation. Calcified Tissue International. 2005;77:386–394. doi: 10.1007/s00223-005-0148-y. [DOI] [PubMed] [Google Scholar]
- Butcher MT, Espinoza NR, Cirilo SR, Blob RW. In vivo strains in the femur of river cooter turtles (Pseudemys concinna) during terrestrial locomotion: tests of force-platform models of loading mechanics. Journal of Experimental Biology. 2008;211:2397–2407. doi: 10.1242/jeb.018986. [DOI] [PubMed] [Google Scholar]
- Carrier D. Postnatal ontogeny of the musculo-skeletal system in the Black-tailed jack rabbit (Lepus californicus) Journal of Zoology, London. 1983;201:27–55. [Google Scholar]
- Carrier D, Leon L. Skeletal growth in the California gull (Larus californicus) Journal of Zoology, London. 1990;222:375–389. [Google Scholar]
- Carter DR. The relationship between in vivo strains and cortical bone remodeling. CRC Critical Reviews in Biomedical Engineering. 1982;8:1–27. [PubMed] [Google Scholar]
- Currey J, Butler G. The mechanical properties on bone tissue in children. Journal of Bone and Joint Surgery. 1975;57-A:810–814. [PubMed] [Google Scholar]
- Currey JD, Pond CM. Mechanical properties of very young bone in the axis deer (Axis axis) and humans. Journal of Zoology, London. 1989;218:59–67. [Google Scholar]
- de Souza RL, Matsuura M, Eckstein F, Rawlinson SCF, Lanyon LE, Pitsillides AA. Non-invasive axial loading of mouse tibiae increases cortical bone formation and modifies trabecular organization: a new model to study cortical and cancellous compartments in a single loaded element. Bone. 2005;37:810–818. doi: 10.1016/j.bone.2005.07.022. [DOI] [PubMed] [Google Scholar]
- Dytham C. Choosing and using statistics: a biologist's guide. Oxford: Blackwell Publishing; 2003. [Google Scholar]
- Ferguson VL, Ayers RA, Bateman TA, Simske SJ. Bone development and age-related bone loss in male C57Bl/6J mice. Bone. 2003;33:387–398. doi: 10.1016/s8756-3282(03)00199-6. [DOI] [PubMed] [Google Scholar]
- Fritton JC, Myers ER, Wright TM, van der Meulen MCH. Loading induces site-specific increases in mineral content asessed by microcomputed tomography of the mouse tibia. Bone. 2005;36:1030–1038. doi: 10.1016/j.bone.2005.02.013. [DOI] [PubMed] [Google Scholar]
- Fritton JC, Myers ER, Wright TM, van der Meulen MCH. Bone mass is preserved and cancellous architecture altered due to cyclic loading of the mouse tibia after orchidectomy. Journal of Bone and Mineral Research. 2008;23:663–671. doi: 10.1359/JBMR.080104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frost HM. A determinant of bone architecture: the minimum effective strain. Clinical Orthopaedics and Related Research. 1983;175:286–292. [PubMed] [Google Scholar]
- Goodship AE, Lanyon LE, McFie H. Functional adaptation of bone to increased stress - an experimental study. Journal of Bone and Joint Surgery. 1979;61-A:539–546. [PubMed] [Google Scholar]
- Gross TS, Srinivasan S, Liu CC, Clemens TL, Bain SD. Noninvasive loading of the murine tibia: an in vivo model for the study of mechanotransduction. Journal of Bone and Mineral Research. 2002;17:493–501. doi: 10.1359/jbmr.2002.17.3.493. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hsieh Y-F, Robling AG, Ambrosius WT, Burr DB, Turner CH. Mechanical loading of diaphyseal bone in vivo: the strain threshold for an osteogenic response varies with location. Journal of Bone and Mineral Research. 2001;16:2291–2297. doi: 10.1359/jbmr.2001.16.12.2291. [DOI] [PubMed] [Google Scholar]
- Keller TS, Spengler DM, Carter DR. Geometric, elastic, and structural properties of maturing rat femora. Journal of Orthopaedic Research. 1986;4:57–67. doi: 10.1002/jor.1100040107. [DOI] [PubMed] [Google Scholar]
- Lanyon LE. Functional strain in bone tissue as an objective, and controlling stimulus for adaptive bone remodelling. Journal of Biomechanics. 1987;20:1083–1093. doi: 10.1016/0021-9290(87)90026-1. [DOI] [PubMed] [Google Scholar]
- Lanyon LE, Goodship AE, Pye CJ, MacFie JH. Mechanically adaptive bone remodeling. Journal of Biomechanics. 1982;15:141–154. doi: 10.1016/0021-9290(82)90246-9. [DOI] [PubMed] [Google Scholar]
- Lee KCL, Maxwell A, Lanyon LE. Validation of a technique for studying functional adaptation of the mouse ulna in response to mechanical loading. Bone. 2002;31:1–9. doi: 10.1016/s8756-3282(02)00842-6. [DOI] [PubMed] [Google Scholar]
- Loitz BJ, Zernicke RF. Strenuous exercise-induced remodelling of mature bone: relationships between in vivo strains and bone mechanics. Journal of Experimental Biology. 1992;170:1–18. doi: 10.1242/jeb.170.1.1. [DOI] [PubMed] [Google Scholar]
- Main RP, Biewener AA. Ontogenetic patterns of limb loading, in vivo bone strains and growth in the goat radius. Journal of Experimental Biology. 2004;207:2577–2588. doi: 10.1242/jeb.01065. [DOI] [PubMed] [Google Scholar]
- Main RP, Biewener AA. Skeletal strain patterns and growth in the emu hind limb during ontogeny. Journal of Experimental Biology. 2007;210:2676–2690. doi: 10.1242/jeb.004580. [DOI] [PubMed] [Google Scholar]
- Main R, Lynch M, Ko F, van der Meulen M. Estrogen receptor-alpha is critical to cancellous and cortical adaptation to load in the mouse tibia. Transactions of the 56th annual meeting of the Orthopaedic Research Society; New Orleans, LA, USA. 2010. [Google Scholar]
- Main R, Lynch M, Schmicker T, Walsh D, van der Meulen M. Applied loads increase bone geometry but not tibial stiffness in growing female mice. Proceedings of the 31st annual meeting of the American Society for Bone and Mineral Research; Denver, CO, USA. 2009. [Google Scholar]
- Miller LM, Little W, Schirmer A, Sheik F, Busa B, Judex S. Accretion of bone quantity and quality in the developing mouse skeleton. Journal of Bone and Mineral Research. 2007;22:1037–1045. doi: 10.1359/jbmr.070402. [DOI] [PubMed] [Google Scholar]
- Mosley JR, March BM, Lynch J, Lanyon LE. Strain magnitude related changes in whole bone architecture in growing rats. Bone. 1997;20:191–198. doi: 10.1016/s8756-3282(96)00385-7. [DOI] [PubMed] [Google Scholar]
- Rabkin BA, Szivek JA, Schonfeld JE, Halloran BP. Long-term measurement of bone strain in vivo: the rat tibia. Journal of Biomedical Materials Research. 2001;58:277–281. doi: 10.1002/1097-4636(2001)58:3<277::aid-jbm1017>3.0.co;2-t. [DOI] [PubMed] [Google Scholar]
- Richman C, Kutilek S, Miyakoshi N, Srivastava AK, Beamer WG, Donahue LR, Rosen CJ, Wergedal JE, Baylink DJ, Mohan S. Postnatal and pubertal skeletal changes contribute predominantly to the differences in peak bone density between C3H/HeJ and C57Bl/6J mice. Journal of Bone and Mineral Research. 2001;16:386–397. doi: 10.1359/jbmr.2001.16.2.386. [DOI] [PubMed] [Google Scholar]
- Robling AG, Turner CH. Mechanotransduction in bone: genetic effects on mechanosensitivity in mice. Bone. 2002;31:562–569. doi: 10.1016/s8756-3282(02)00871-2. [DOI] [PubMed] [Google Scholar]
- Rubin CT, Lanyon LE. Limb mechanics as a function of speed and gait: a study of functional strains in the radius and tibia of horse and dog. Journal of Experimental Biology. 1982;101:187–211. doi: 10.1242/jeb.101.1.187. [DOI] [PubMed] [Google Scholar]
- Sheng MH-C, Baylink DJ, Beamer WG, Donahue LR, Rosen CJ, Lau K-HW, Wergedal JE. Histomorphometric studies show that bone formation and bone mineral apposition rates are greater in C3H/HeJ (high-density) than C57Bl/6J (low-density) mice during growth. Bone. 1999;25:421–429. doi: 10.1016/s8756-3282(99)00184-2. [DOI] [PubMed] [Google Scholar]
- Somerville JM, Aspden RM, Armour KE, Armour KJ, Reid DM. Growth of C57Bl/6 mice and the material and mechanical properties of cortical bone from the tibia. Calcified Tissue International. 2004;74:469–475. doi: 10.1007/s00223-003-0101-x. [DOI] [PubMed] [Google Scholar]
- Srinivasan S, Agans SC, King KA, Moy NY, Poliachik SL, Gross TS. Enabling bone formation in the aged skeleton via rest-inserted mechanical loading. Bone. 2003;33:946–955. doi: 10.1016/j.bone.2003.07.009. [DOI] [PubMed] [Google Scholar]
- Stadelmann VA, Hocke J, Verhelle J, Forster V, Merlini F, Terrier A, Pioletti DP. 3D strain map of axially loaded mouse tibia: a numerical analysis validated by experimental measurements. Computer Methods in Biomechanics and Biomedical Engineering. 2009;12:95–100. doi: 10.1080/10255840903077287. [DOI] [PubMed] [Google Scholar]
- Sugiyama T, Saxon LK, Zaman G, Moustafa A, Sunters A, Price JS, Lanyon LE. Mechanical loading enhances the anabolic effects of intermittent parathyroid hormone (1–34) on trabecular and cortical bone in mice. Bone. 2008;43:238–248. doi: 10.1016/j.bone.2008.04.012. [DOI] [PubMed] [Google Scholar]
- Torzilli P, Takebe K, Burstein A, Heiple K. Structural properties of immature canine bone. Transactions of the ASME. 1981;103:232–238. doi: 10.1115/1.3138286. [DOI] [PubMed] [Google Scholar]
- Turner CH, Akhter MP, Raab DM, Kimmel DB, Recker RR. A noninvasive, in vivo model for studying strain adaptive bone modeling. Bone. 1991;12:73–79. doi: 10.1016/8756-3282(91)90003-2. [DOI] [PubMed] [Google Scholar]
- Turner CH, Forwood MR, Rho J-Y, Yoshikawa T. Mechanical loading thresholds for lamellar and woven bone formation. Journal of Bone and Mineral Research. 1994;9:87–97. doi: 10.1002/jbmr.5650090113. [DOI] [PubMed] [Google Scholar]
- Turner CH, Takano Y, Owan I. Aging changes mechanical loading thresholds for bone formation in rats. Journal of Bone and Mineral Research. 1995;10:1544–1549. doi: 10.1002/jbmr.5650101016. [DOI] [PubMed] [Google Scholar]
- van der Meulen MCH, Jepsen KJ, Mikic B. Understanding bone strength: size isn't everything. Bone. 2001;29:101–104. doi: 10.1016/s8756-3282(01)00491-4. [DOI] [PubMed] [Google Scholar]
- Warden SJ, Fuchs RK, Castillo AB, Nelson IR, Turner CH. Exercise when young provides lifelong benefits to bone structure and strength. Journal of Bone and Mineral Research. 2007;22:251–259. doi: 10.1359/jbmr.061107. [DOI] [PubMed] [Google Scholar]
- Zar JH. Biostatistical Analysis. Upper Saddle River, New Jersey: Prentice Hall; 1999. [Google Scholar]
- Zioupos P, Currey JD. Changes in stiffness, strength, and toughness of human cortical bone with age. Bone. 1998;22:57–66. doi: 10.1016/s8756-3282(97)00228-7. [DOI] [PubMed] [Google Scholar]