Individual (N-of-1) trials can be combined to give population comparative treatment effect estimates: Methodologic considerations

Abstract/Summary

Objective

To compare different statistical models for combining N-of-1 trials to estimate a population treatment effect.

Study Design and Setting

Data from a published series of N-of-1 trials comparing amitriptyline therapy and combination treatment (amitriptyline + fluoxetine ) were analyzed to compare summary and individual participant data meta-analysis, repeated measures models, Bayesian hierarchical models, single-period, single-pair and averaged outcome crossover models.

Results

The best fitting model included a random intercept (response on amitriptyline) and fixed treatment effect (added fluoxetine). Results supported a common, uncorrelated within-patient covariance structure that is equal between-treatments and across patients. Assuming unequal within-patient variances, a random effects model was favored. Bayesian hierarchical models improved precision and were highly sensitive to within-patient variance priors.

Conclusion

Optimal models for combining N-of-1 trials need to consider goals, data sources, and relative within and between patient variances. Without sufficient patients, between-patient variation will be hard to explain with covariates. N-of-1 data with few observations per patients may not support models with heterogeneous within-patient variation. With common variances, models appear robust. Bayesian models may improve parameter estimation but are sensitive to prior assumptions about variance components. With limited resources, improving within-patient precision must be balanced by increased participants to explain population variation.

INTRODUCTION

N-of-1 trials are often multi-crossover, randomized, blinded single-patient trials in which an individual generally tries two interventions (two treatments or a treatment and a placebo), each multiple times, to determine which is more effective [1]. By providing more rigorous comparative effectiveness assessments for an individual, these trials may offer an approach for providing evidence-based, personalized medicine. Classically, these single patient (N=1) trials were designed to aid personal clinical decision-making and to focus solely on the individual’s response to treatments. Thus the frequency of N-of-1 trial use in current practice is not known since individual care-focused trials comparing approved treatments and undertaken solely for personal treatment management are not typically published. Most published reports of N-of-1 trials summarize and compare results across trials from a prospectively-designed series. We have proposed combining series of similarly designed N-of-1 trials using a Bayesian hierarchical model for comparative effectiveness research [2]. In addition to incorporating external information, this methodology gives both a comparative treatment effect estimate for the population as well as potentially improved effectiveness estimates for individuals by borrowing strength from the trials of others to learn about between and within-patient variation. The N-of-1 trial’s presumption of individual uniqueness and its goal of personal prediction would seem to contrast with the usual clinical trial objective of identifying a common treatment effect to then apply to each individual in the population. Because combining a series of N-of-1 trials can provide an estimate of overall effect, it is important to understand when one might use this approach and how this approach and its resulting estimate might agree or differ from more standard clinical trial designs.

N-of-1 trials have been used to compare interventions for a range of chronic conditions (e.g., arthritis[3], fibromyalgia [4;5],Chronic airflow limitation [6]gastric reflux [7],etc [8;9]). Criteria for using this trial design have been described and are similar to those required for standard crossover trials.[10;11] The condition must be chronic and stable. The interventions must be symptomatic (not permanently changing the condition status) and the interventions need to have appropriate on/off kinetics to limit possible carryover and period effects. Because there are repeated exposures to the same interventions, N-of-1 trials may be most appropriate for comparing later phase (e.g., phase IV) therapeutics and for head to head comparisons of approved medications.

To undertake combined N-of-1 trials research, one might use results (if made available) from already completed trials independently done for personal treatment management. One instead might undertake a prospective series with the clear population research objective. Or one might use a combination of trial sources. If one is using already completed trials, what is the best way to combine their data? If one is prospectively collecting data, do additional measures per patient increase the precision of the population estimate? Do repeated measurements on individuals allow for models that are better than those based on one or two measurements per patient? Although improved estimation of each patient’s individual response is a prime advantage of N-of-1 trials and having these embedded within population trials might provide implementation benefits [12], we focus in this paper on the analytic considerations and models for estimating the population effect.

Each N-of-1 trial provides information not only about within-patient treatment comparisons, but also about the variation of responses within each patient to each treatment. Therefore, we wanted to assess whether and how this within-patient variation might best be incorporated into a population estimate that presumably depends more on between-patient than within-patient variation. To combine N-of-1 trials, one might first follow the summary meta-analysis paradigm and combine results within each (patient’s) trial to estimate individual patient effects and then average across (patients’) trials to obtain an overall effect [13;14]. This type of analysis can use available data either by patient-period or aggregated to the patient level (for example, if one has a 2 period trial one would use the simple within-subject difference between the 2 treatments’ outcomes) Alternatively, with patient-period data, as with individual-patient data meta analysis, one could use mixed-models to combine within and across patient periods simultaneously [15-18]. For prospectively designed trials with treatment order randomized across trials, use of only a subset of the periods would mirror more standard population designs. For example, analyzing randomized first-period treatment outcomes corresponds to a randomized parallel group trial; using outcomes from the pair-randomized treatments in the first two periods corresponds to an AB/BA crossover design. But not all trial series are prospectively designed and randomized together for combined N-of-1 analysis. Comparing the subset analyses to models that use all periods can help evaluate the information added by the multiple crossovers (obtained at higher cost to participants and to the healthcare/research system).

To inform our comparisons of the various models for optimally combining N-of-1 trials, we use data from our study of N-of-1 trials comparing amitriptyline and the combination of amitriptyline plus fluoxetine for treating fibromyalgia syndrome [5] By re-analyzing the data from this series of similarly designed N-of-1 trials we compare and contrast meta-analysis, repeated measures models, Bayesian hierarchical models, single-period and single-pair crossover models for combining N-of-1 trials to obtain a population estimate of comparative treatment-effectiveness. We consider key sources of variation (within patient, between patient and random) as well as the assumptions of these different models, and use our data to aid in choosing between the various analytic options.

METHODS

1. Data collection and selection

The data come from a series of 58 N-of-1 trials that compared two therapies for fibromyalgia syndrome (FMS) and were carried out at seven community-based rheumatology practices and at one FMS referral center [5]. Each N-of-1 trial had six treatment periods divided into 3 sets of paired treatments – one period on combination therapy (amitriptyline [AMT] + Fluoxetine fl) and one on the “control” medication (AMT). For treatment allocation, the first treatment pair was block randomized (for every 20 trial kits, 10 started with AMT and 10 with AMT+FL). The other 2 pairs were random in their start medications. The Fibromyalgia Impact Questionnaire (FIQ) score [19] was the outcome measured once at baseline (absent FMS medications) and once at the end of each of the six 6-week treatment periods. The FIQ is a patient assessed quality of life assessment tool scored continuously between 0 (best score) and 100 (worst score). Analyses reported here used data from the forty-six patients who completed at least two treatment periods (one on each treatment), of whom 34 completed all 6 treatment periods[5].

2. Analytic Approaches for Combining N-of-1 Trials

We investigated three analytic methods for combining all data available from the N-of-1 trials: (i) summary data meta-analysis, (ii) linear mixed models using maximum likelihood (individual participant data [IPD] meta-analysis), and (iii) Bayesian hierarchical models with and without informative prior information. We compared these answers with analyses applied to portions of the data that mirrored more standard clinical trial designs: (i) a t-test applied to only the first period measurement from each trial (analogous to a randomized parallel group trial) and (ii) a paired t-test of data from only the first two periods (one on each treatment) of each N-of-1 trial (analogous to a typical AB/BA single crossover design). We also used a paired t-test to estimate the mean difference of each patient’s averaged outcome on each treatment across the N-of-1 trials. To simplify model comparisons, we focus here on analyses using data from the 34 individuals who completed their N-of-1 trials (all 6 treatment periods) and thus have balanced trial designs. Later, we discuss some results obtained using data from all the individuals (N=46) with at least two completed periods (one on each treatment) in beginning to explore analyses of unbalanced N-of-1 trial designs.

2.1. Summary Data Meta-Analyses: Considering each N-of-1 study as a separate trial

A typical estimate of the pooled treatment effect combines summary data from each trial to form a weighted average $\widehat{\mu }={\sum }_{\mathrm{i}=1}^{\mathrm{N}}{\mathrm{w}}_{\mathrm{i}}{\mathrm{y}}_{\mathrm{i}}∕{\sum }_{\mathrm{i}=1}^{\mathrm{N}}{\mathrm{w}}_{\mathrm{i}}$ of the individual study estimates, y_i with weights, w_i. In a fixed effects model one assumes that each study has the same true mean effect, μ, while in a random effects model, each study can have a different effect, μ_i, but these effects are assumed to follow a common distribution, often assumed normal N(μ, τ²). In a fixed effects model, the studies’ weights w_i = 1/σ_i² are often supplied by the inverse of their variances,σ_i² ; in a random effects model, the weights $w_i=1∕({\tau }_{\beta }^2+{\sigma }_i^2)$ also include a between-study variance component τ². Because this between-study variance component is the same for all the studies being aggregated, the resulting weights are more equal than in the fixed-effects model and are less sensitive to large differences among their within-study variances.

Using this summary data meta-analysis approach, a set of N-of-1 trials could be combined using the studies’ observed mean effects y and variances σ_i². But unlike a typical summary data meta-analyses in which large population trials supply good estimates of within-trial variances, N-of-1 studies typically have only a handful of observations and so their within-trial variances are not well-estimated.

Many years ago, Cochran [20] suggested that when combining results of small population studies it may be better to assume a common within-study variance formed by pooling across trials. Within-study inverse variance weights are then proportional to the studies’ sample sizes. When the trials’ designs are balanced and have the same number of unit measurements their weights are equal. We fit fixed and random effects combined N-of-1 summary meta-analysis models with both separate and common variances to the combined N-of-1 data. Within-study variance was estimated using a standard sample variance formula. The between-study variance component was estimated using the method of DerSimonian and Laird [13] and models were fit using S-Plus 6.2.

2.2 Linear Mixed Models: Combining Individual-Patient Data [ IPD] Across Trials

Increasingly, meta-analyses use mixed models to combine individual participants’ data (IPD) across trials [14-17] while accounting for correlations in the data that derive from the clustering of participants within the trials. When these clusters (studies) are treated as a random sample from a population of potential clusters, the model contains additional variance components to represent the between-study variation. In typical IPD meta-analyses, the participants are the units providing the correlated measurements within the study clusters. In contrast, in series of N-of-1 trials, the correlated data are the multiple comparative measurements taken on individuals and the model then has within-patient variance components, as in longitudinal studies [21]. If these patients are then nested within a clinical practice or a specific trial series, the correlated data structure may be extended further to reflect this.

To use a linear mixed model to aggregate trials’ data requires clearly defined assumptions about the model’s multiple components and their relationships. In combining our N-of-1 trials these include: (i) determining the model parameters, (ii) characterizing parameters’ effects on the outcome (fixed versus random effect assumptions) and (iii) defining assumptions regarding the several variance components.

Model Parameters

We let Y_ij be the observed FIQ score for the i^th patient in the j^th period (j = 1, 2, …, J) and let Y_i = (Y_i1, Y_i2, …, Y_iJ) denote the collection of FIQ scores for the i^th patient. We assume Y_i follows a multivariate normal distribution with mean μ_i, and a JxJ covariance matrix Σ_i, expressed Y_i ~ N (μ_i, Σ_i). In the balanced repeated crossover design in our study, half of the measurements were taken under AMT+FL (treatment) and half under AMT (control). The mean treatment effect vector μ_i then consists of separate values for the two treatments. Using an indicator variable X_ij = 1 for treatment with AMT+FL and X_ij = 0 for AMT, we write each individual period mean as: μ_ij = α_i + β_iX_ij where α_i is the control mean (mean FIQ score on AMT alone) and β_i is the difference between the two treatments’ means. In addition to the treatment effect, other covariates (such as trial period, practice setting, and participant characteristics) might be included in the model. To incorporate these variables, we can generalize the mean to μ_i = X_iθ_i (a function of a set of regression covariates X_i with a vector of regression parameters, θ_i). In the single treatment model, θ_i = (α_i,β_i).

Mean Parameter Specifications (Fixed versus random effects)

In this model, when θ_i is the same for each patient (θ_i = θ), θ is a fixed effect. Alternatively, if the regression varies across patients, θ_i would be a random effect as for example, if each patient’s response were to depend on many patient-specific characteristics that affect the outcome in both treatment groups. Expressed in a general form: θ_i = θ + δ_i where θ are the fixed effects and δ_i ~ N(0, D) are random effects with covariance matrix D. The normal distribution for δ_i specifies the form of this random variation across individuals. Effects with only a fixed component have the corresponding elements in D set to zero.

Multi-level model structures

Another way of representing this linear mixed model is to use a hierarchical or multilevel form:

$$\begin{array}{cc}\hfill & {\mathit{Y}}_{\mathit{i}}={\mathit{X}}_i{\theta }_i+{\epsilon }_i\text{with}{\epsilon }_i\sim N(0,{\Sigma }_{\mathit{i}});\hfill \\ \hfill & {\theta }_i\sim \mathrm{N}(\theta ,\mathit{D}).\hfill \end{array}$$

As an example, if the outcome depends only on treatment, we can write this model as:

$$\begin{array}{cc}\hfill Y_{ij}& ={\alpha }_i+{\beta }_i{X}_{ij}+e_{ij}\text{with}{e}_{ij}\sim N(0,{\sigma }_i^2)\hfill \\ \hfill {\alpha }_i& \sim \mathrm{N}(\alpha ,{\tau }_{\alpha }^2)\hfill \\ \hfill {\beta }_i& \sim \mathrm{N}(\beta ,{\tau }_{\beta }^2)\hfill \end{array}$$

In specifying how each of the different subjects’ models relates to each other, this structure reduces the number of parameters that need to be fit for estimation while still allowing the mean (and possibly variance) to vary across individuals. Estimating the random intercepts α_i and the random slopes β_i, requires only 2 mean parameters (α and β) and 3 variance parameters (σ_i², ${\tau }_{\alpha }^2$ and ${\tau }_{\beta }^2$). An additional correlation between α_i and β_i may also be added. The random effects summary meta-analysis model is a form of this model with a single summary statistic (e.g., the difference between the mean of the treatment and the mean of the control groups) as a univariate outcome. The treatment effect β_i has mean β (the overall treatment effect) and between-patient variance ${\tau }_{\beta }^2$ and a within-patient varianceσ_i², that varies across patients. The fixed effects model follows by setting${\tau }_{\beta }^2=0$.

Variance structures

Covariance matrices may be structured within patients and may vary across patients. When few observations are available from each patient, the same within-patient covariance matrix, Σ, for all patients is often assumed, i.e., Y_i ~ N (μ_i, Σ). We investigated several forms for Σ including: (i) unstructured (general Σ); (ii) first-order autoregressive in which each measurement has the same variance and measurements that are k visits apart have correlation ρ^k; (iii)uncorrelated errors with common variance σ² at each period; and (iv) uncorrelated errors with separate variances for measurements on each treatment. The unstructured form, while the most general, requires fitting J (in our completed trial J=6) variance and J(J+1)/2 (i.e., 21) covariance terms and so may be over-parameterized. The first-order autoregressive form reflects the longitudinal nature of the short time series of measurements taken on each individual and uses two parameters, σ² and ρ. The common variance form (across patients) with uncorrelated and identically distributed errors is the simplest possible structure, requiring only one parameter, σ². A variant of this common form allowing separate variances by treatment group can account for the possibility that response variability differs by treatment.

While most mixed models assume a common within-patient covariance matrix across patients, if sufficient within-patient data are available, it may be possible to remove this restriction. The simplest model assumes an uncorrelated common variance structure for each patient with different variances across patients, i.e., Σ_i = σ_i²I. The number of variances to be estimated may be reduced by grouping them according to some characteristic of the patients. For example, if we thought that FIQ scores for patients treated in the community might vary differently from those of patients treated at the referral center, we could set Σ_i = Σ_A for community-based patients and Σ_i = Σ_B for patients treated at the referral center. A simple form reflecting no within-person correlation and a common variance across measurements within a group of patients has ${\Sigma }_{\mathrm{A}})={\sigma }_{\mathrm{A}}^2\mathbf{I}$ and ${\Sigma }_{\mathrm{B}})={\sigma }_{\mathrm{B}}^2\mathbf{I}$.

In model development, the order of testing assumptions can impact model structure. For our models, we first considered whether factors besides the patient and the treatment significantly impacted treatment effect. These variables (in our example, time and site) were selected since they were integral to our prospective study design [5]. We fit the linear mixed models using the lme function in S-Plus 6.1. Models comparisons used the Bayesian information criterion (BIC; [22]) that penalizes the likelihood for the addition of parameters. BIC has been shown to maximize the posterior probability that one model out of a considered set is correct under the assumption that no models are preferable a priori. Models with lower BIC are preferred because they provide the best fit with the fewest number of parameters.

2.3 Bayesian Hierarchical Models

Bayesian methods enable the incorporation of prior information regarding the treatment effect and inference about the resulting posterior probability estimates. The Bayesian version of the mixed model employs the same hierarchical structure while adding prior distributions on the model parameters. For a model with treatment as the sole covariate, this involves the addition of prior distributions for α, β, σ_i², ${\tau }_{\alpha }^2$ and ${\tau }_{\beta }^2$. We derived [5] the prior distributions from a published crossover trial [23] that used the same medications and dosages. That trial’s results suggested a mean of 8 points and a standard deviation of 3.9 for β, the mean difference between FIQ scores on AMT+FL and AMT, and a mean of 50 points with a standard deviation of 4.6 for α, the mean response on AMT (“control” treatment).

We had limited information about the variance parameters ${\tau }_{\alpha }^2$, ${\tau }_{\beta }^2$ (between-patients) and σ_i² (within-patient). Inverse gamma (IG) distributions are convenient computational choices for distributions of variances and we chose a fairly non-informative IG(1,8) prior distribution for all of these variance parameters. In addition to assuming random treatment effects, we also tested models assuming constant treatment effects across patients (β_i = β) by setting τ_β² = 0 and a common within-patient variance model (σ_i² = σ²) with an IG(1,8) prior on σ².

To extend the Bayesian models for comparison with the non-Bayesian mixed model analyses and to assess the impact of the prior distributions, we also examined these models using non-informative prior distributions for all parameters. We chose normal distributions centered at 0 with very large variances of 10⁶ for the means, α and β, and chose uniform distributions over the range 0 to 10⁴ for square roots of the variance parameters [24]. Bayesian models were fit using Markov chain Monte Carlo with the WinBUGS 1.4.3 software (available from: http://www.mrc-bsu.cam.ac.uk/bugs/winbugs/contents.shtml)

2.4 Standard Trial Design Analyses

We compared these more complex models to standard population research design analyses. We mimicked a parallel arm RCT by comparing outcomes from only the first treatment period from each N-of-1 trial (AMT or AMT+FL) using a t-test. We analyzed outcomes from the first pair of periods (one period on each treatment) from each N-of-1 trial using a paired t-test as in an AB/BA crossover trial design[25]. We then also used a paired t-test to compare the difference in each individual’s averaged outcome (i.e. mean outcome from all completed periods, on each treatment) across all the N-of-1 trials, here termed the averaged crossover design.

3.0 Additional Considerations: More Measures vs. More Patients

Finally, we compared the impacts of adding treatment periods and patients into a series of N-of-1 trials. Using a simple random effects model [14], we calculated the approximate precision (inverse of the variance) of the mean effect with M patients and N paired treatment periods per patient relative to a classic 2 period (AB/BA) crossover design (M = 46 and N = 1) under several combinations of between-patient and within-patient variance. Precision was calculated as the sum of the weights on individual patients where the weight on an individual was the sum of the within-patient and the between-patient variances (σ² and τ², respectively). Patients are assumed independent so the precision is calculated as M(τ² + σ²/N).

RESULTS

We used the data from 46 N-of-1 trials with at least 2 completed treatment periods (one on each therapy) from our combined N-of-1 implementation study[5]. Among the 34 completed trials (all 6 periods), the reported mean differences in FIQ scores comparing treatment groups ranged from 31.3 points in favor of AMT+FL (i.e., a 31.3 point decline in FIQ score with this treatment) to 13.6 points in favor of control (i.e., a 13.6 point increase in FIQ score with treatment compared to AMT only). Standard errors for these differences ranged from 1.3 to 21.7 and the size and direction of these mean differences did not correlate directly with the extent of within-patient variation across individuals. Lack of evidence of carryover or time trend supported the assumption of measure independence from time and treatment order [5].

Linear mixed models provide great flexibility for meta-analysis and we investigated a variety of regression covariates and covariance structures as part of our model building. No added covariates, including practice setting and trial period, contributed significantly to the model with treatment effects (data not shown). So, henceforth, we focus on the treatment effects of AMT and AMT+FL.

Table 1 presents the results of various mixed models using random and fixed effects for the regression intercept and treatment effect as well as unstructured, autoregressive, common and separate covariance models. We have ordered these from best to worst model according to the Bayesian Information Criterion (BIC) where the best model has lowest BIC. These results suggest that:

1. Random intercepts (scores on AMT alone) fit better than fixed intercepts (model 1 vs. model 5, model 6 vs. model 12),

2. Fixed treatment effects fit as well or better than random treatment effects (models 1 vs. 4; models 6 vs.8, models 9 vs.10) under a variety of covariance structures.

3. Among the fixed treatment effects models, the common variance structure (model 1) fit best (model 1 vs. 2, 3, 6, 9, 12). The addition of an autoregressive term for correlation among time periods (model 2) and an additional variance component for separate variances by treatment group (model 3) do not improve model fit enough to overcome the added parameter. Use of an unstructured covariance matrix (model 6) adds many parameters to the model and has a much worse fit than the simpler covariance structures,

4. The fixed treatment itself is highly significant (model 6 vs. model 7).

Table 1.

Results of a representative selection of the assessed mixed models using the treatment parameters and varied assumptions as noted. Models are listed according to the Bayesian Information Criterion (BIC; [22]), with the best model having the lowest numeric value.

Model	Intercept	Treatment	Patients’ Variances	Within-Patient Variance Variance(s)/Covariance structure	Treatment Effect	Standard Error	Number of parameters	Bayesian Information Criterion
1	Random	Fixed	Equal	Single/Uncorrelated	−6.83	2.00	4	1722
2	Random	Fixed	Equal	Single/Autoregressive	−6.76	2.02	5	1727
3	Random	Fixed	Equal	Separate by Treatment/ Uncorrelated	−6.83	2.00	5	1727
4	Random	Random	Equal	Single/ Uncorrelated	−6.83	2.00	6	1736
5	Fixed	Fixed	Equal	Single / Uncorrelated	−6.83	2.41	3	1755
6	Random	Fixed	Equal	Unstructured	−7.61	1.95	19	1789
7	Random	----------	Equal	Unstructured	-----	-----	18	1797
8	Random	Random	Equal	Unstructured	−7.60	1.95	21	1800
9	Random	Fixed	Unequal	Single /Uncorrelated	−5.43	1.48	37	1848
10	Random	Random	Unequal	Single /Uncorrelated	−5.18	1.70	39	1856
11	Fixed	Random	Unequal	Single /Uncorrelated	−4.03	1.87	37	1863
12	Fixed	Fixed	Equal	Unstructured	−4.3	5.1	39	1882

Table 2 compares treatment effect estimates from summary and individual-participant data (IPD) meta-analyses and Bayesian hierarchical models, each with assumptions of fixed and random treatment effects and with common and separate variances for each individual. We used two data sets: balanced trial results from the 34 individuals who completed all six periods (section A) and unbalanced trial results from the 46 individuals who finished at least the first 2 periods (section B).

Table 2.

Mean Treatment Effect estimates¹ obtained using various analytic models with data from the 34 completed (6 periods) trials and data from the 46 trials with at least one period completed on each treatment.

					Mean Difference ± Standard Error 2
					A 6-period completers (N=34) Equal Number of Periods		B >2 period completers (N=46) Unequal Number of Periods
Between Patient Variance	Model	Treatment Effect Prior	Variance Priors		Fixed Effects	Random Effects	Fixed Effects	Random Effects
Common			Between Patients	Within Patients
	Parallel Design 3	-------------	-------------		−8.1 ± 5.6		−5.3 ± 4.6
	AB/BA Crossover 4	-------------	-------------		−8.0 ± 3.7		−6.7 ±3.3
	Averaged Crossover 5	-------------	--------------		−6.8 ± 1.8		−5.2 ± 2.2
	Summary Meta-Analysis	-------------	--------------		−6.8± 2.0	−6.8 ± 2.2	--------------13	--------------13
	Individual Patient Data: Likelihood	-------------	--------------		−6.8± 2.0	−6.8± 2.0	−6.1± 1.8	−6.1± 1.8
	Individual Patient Data: Bayesian	Non- informative 6	Uniform8		−6.8± 2.0	−6.8± 2.0	−6.1± 1.8	−6.1± 2.0
			Weak9		−6.8± 2.0	−6.8 ± 2.1	−6.1±1.9	−6.2±1.9
			Strong5		−6.8± 2.0	−6.8 ± 2.1	−6.1± 1.8	−6.1± 1.9
		Informative 7	Uniform8		−7.1 ± 1.8	−7.1 ± 1.8	−6.5± 1.7	−6.6± 1.8
			Weak9		−7.1± 1.8	−7.1 ± 1.8	−6.5±1.6	−6.6 ±1.7
			Strong10		−7.1 ± 1.8	−7.1 ± 1.8	−6.5± 1.6	−6.6 ±1.7
			Strong10	Uniform8	−7.1 ± 1.7	−7.0 ± 1.8	−6.5± 1.6	−6.6 ±1.7
			Uniform8	Strong10	−7.1 ± 1.8	−7.1 ± 2.0	−6.5± 1.7	−6.5 ±1.7
Separate
	Summary Meta-Analysis	-------------	-------------		−0.2± 1.0 11,12	−5.6 ± 1.9 12	--------------13	--------------13
	Individual Patient Data: Likelihood	-------------	-------------		−5.4± 1.5	−5.2± 1.7	−5.7± 0.06 14	−5.4± 0.33 14
	Individual Patient Data: Bayesian	Non- informative6,12	Uniform8		−5.2± 2.2	−5.1± 2.2	−4.0±1.9	−4.0±1.9
			Weak9		−5.5± 1.6	−5.5 ± 1.7	−3.6± 1.3	−3.9± 1.4
			Strong10		−6.8± 2.0	−6.8 ± 2.1	−6.0± 1.9	−6.1± 1.9
			Strong10	Uniform8	−5.2± 2.1	−4.9 ± 2.4	−4.0± 1.9	−3.7± 1.9
			Uniform8	Strong10	−6.8± 2.0	−6.7 ± 2.2	−6.0± 1.9	−6.1± 1.9
		Informative 7	Uniform8		−5.9± 1.8	−5.9 ± 1.9	−4.9±1.6	−4.8±1.7
			Weak9		−5.9± 1.4	−5.9 ± 1.6	−4.2± 1.3	−4.4 ± 1.3
			Strong10		−7.0± 1.8	−7.0± 1.8	−6.5± 1.6	−6.5± 1.7
			Strong10	Uniform8	−5.9± 1.8	−5.6 ± 1.9	−4.9± 1.6	−4.6 ± 1.7
			Uniform8	Strong10	−7.1± 1.8	−7.0± 1.9	−6.5± 1.7	−6.5± 1.7

¹Mean Difference = Difference in FIQ scores on the combination (AMT+FL) treatment minus the control (AMT) treatment. A lower FIQ score reflects better condition status and a negative mean difference reflects greater improvement on the combination treatment.

²Confidence intervals = mean estimates ± (SE *1.96)

³t-test using results of first periods only

⁴Paired t-test of outcomes on AMT+FL minus AMT from first pair of periods.

⁵Paired t-test of each trial’s averaged outcome on AMT+FL minus averaged outcome on AMT from all completed periods from each trial.

⁶α ~ N(0,0.000001); β ~ N(0,0.000001);

⁷α ~ N(50,21.05); β ~ N(−8,15.05);

⁸τ_α ~ U (0,100); τ_β ~ U (0,100); σ~ U (0,100);

⁹${\tau }_{\alpha }^2\sim \mathrm{IG}(1,8)$, ${\tau }_{\beta }^2\sim \mathrm{IG}(1,8)$ and σ² ~ IG(1,8);

¹⁰Using posterior distribution of variance parameters as a new prior ${\tau }_{\alpha }^2\sim \mathrm{IG}(9.99,970.50)$, ${\tau }_{\beta }^2\sim \mathrm{IG}(2.742,29.19)$ and ${\sigma }_i^2\sim \mathrm{IG}(83.03,17003.35)$

¹¹Omitting outlier, estimate is −6.86±1.64 (p = 0.0001); omitting the outlier from the Bayesian analyses of the balanced trials yields outcomes similar to the equal variances models.

¹²If assuming unequal variances, test of the heterogeneity of the means supports using a random effects model (p=0.03).

¹³Not enough data to calculate individual patient variances;

¹⁴Using trials with 3 or more periods (N=41): −3.7±1.1 and −4.6±1.4, respectively

Results from the 34 balanced (completed) trials using a common within-patient variance are similar, showing roughly a 7 point advantage (decrease in FIQ score) with treatment, under both fixed and random effects assumptions using summary or individual patient data. Estimates under a separate variances assumption are smaller. Of note, the summary data meta-analysis estimate under the fixed effects treatment assumption with separate variances is very small and is the only one of all the complex model estimates not to differ significantly from zero. This anomalous result occurs because of a single patient who had an extremely precise estimate of no treatment benefit. The small variance received a large weight in the fixed effect analysis. Omission of this outlier returned the estimate −6.86, in line with the other models. Very precise treatment effect estimates might result from a trial in which outcomes differ by treatment but where the measurements are highly consistent within each treatment. However, since measurement variation stems from both individual baseline measurements and the treatment effect, measures might likely be more consistent when there is no treatment effect. Using a separate variances fixed effects model might then bias the resulting mean estimates towards the null. Thus, a major advantage of the random effects model is its robustness to such outliers.

As expected, the results using the Bayesian hierarchical model with uniform (non-informative) priors for the treatment effect behaved much like the non-Bayesian models. Because the prior treatment mean (8.0) was larger than the treatment mean observed in our study, the posterior means incorporating the informative priors are larger. The posterior standard errors are smaller, reflecting the additional information introduced by the priors.

Assuming a common within-patient variance, results are not sensitive to the choice of variance priors. With unequal between-patient variances, however, results are very sensitive to the prior distributions placed on the within-patient variance (but not the between-patient variances). This is not surprising since each trial has limited within-patient information (6 measures), but when pooled there are enough trials to provide information on a common within-patient variance and on the between-patient variances. A similar impact is seen using a stronger (more informative) prior. Not surprisingly, removing the “outlier” (i.e., reducing heterogeneity) from the random effects models yields results closer to those of the fixed effects models.

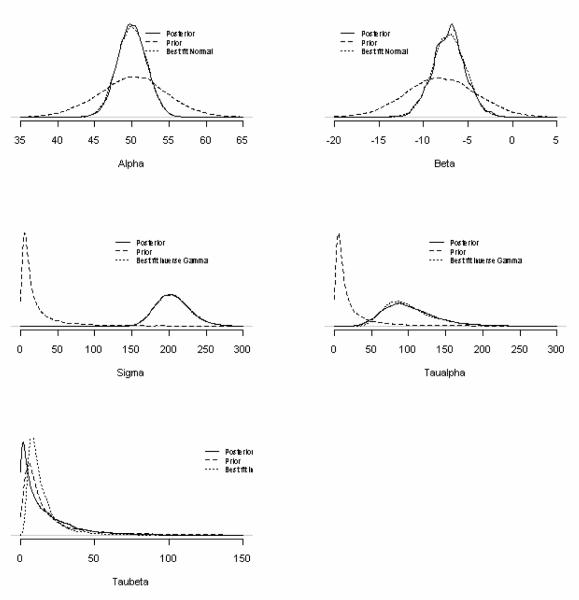
Figure 1 illustrates the various prior and posterior distributions (for the parameters in a model with a common within-patient variance, random intercepts, but fixed treatment effect parameters. The empirical posterior distributions, for the intercept (α) and slope (β), are well approximated by normal distributions matched to the parameters’ respective posterior means and standard deviations (estimated from the Markov Chain Monte Carlo model). These posteriors are more precise than their respective prior distributions, but their rough agreement reflects the information on the means available from the prior published study. The empirical posterior distributions of the between-patient variances (τ_α and τ_β) and the within patient variance (σ²) are well-estimated by inverse gamma distributions but with larger scale (corresponding roughly to the degrees of freedom) and shape (a sum of squares about the mean) parameters than the initially chosen prior distributions. These reflect the additional information available from the data, not available from the previous trial.

Figure 1.

Density plots of the prior and posterior distributions for the population level parameters used for analyses in Table 2. Graphs represent estimates for the mean parameters (α and β) and 3 variance parameters, within (σ_i²) and between (${\tau }_{\alpha }^2$ and ${\tau }_{\beta }^2$) patients. Each plot shows the weakly informative priors given in footnotes 2 and 4 of Table 2, the empirical posterior from the MCMC analysis and the approximated normal (for means) or inverse gamma (for variances) distributions found by matching means and variances.

The right-hand side of Table 2 (Section B) presents results using the various models with data from the 46 participants who completed at least 2 treatment periods (12 non-completers finished fewer than 6 periods). The estimates and standard errors using these unbalanced trial designs indicate that the additional information improved precision, and also reduced the average treatment effect. The latter suggests that non-completers were more likely to have small or no treatment effects, and was the most common reason given for dropping out [5]. The extreme increased precision seen with likelihood analysis of IPD likely reflects incorrect estimation of precision when no repeated measures are available. If only trials with more than two periods are used, variance estimates are increased (see table footnote).

In Table 2 we also present results of analyses that mirror more standard parallel and crossover trial designs. Using only results from the first trial period, analyses mirror a parallel group design. The first pair of periods and the averaged treatment outcomes from the N-of-1 trials were analyzed as a standard and averaged AB/BA crossover trial designs, respectively. Compared to other models, the average treatment effects estimated using the single period parallel design were somewhat higher (−8.1± 5.6) using data from the 34 completed N-of-1 trials and somewhat lower (−5.3 ± 4.6) using data from the 46 trials with at least 2 periods completed. Standard errors were higher for both and neither one was statistically significant (0.16 and 0.26 using 34 and 46 trials, respectively). The estimates using the two-period crossover design were −8.0± 3.7 and −6.7 ± 3.3, using the 34 and 46 trials respectively and both were statistically significant (p= 0.04 and p=0.05, respectively). As expected, using the second period measurements substantially improved the estimates’ precision and as shown in table 2, adding repeated measures further improved precision.

In the case of the averaged crossover analysis, the estimated effect using data from the 34 balanced trials was similar to the results from the other non-Bayesian common-variance models, although the standard error was slightly different. In the averaged crossover analysis, the effect estimate and precision were derived by equally weighting the treatment differences from each trial, ignoring the number of periods each had completed. In effect, this means that the between-study variance is accounted for, but not the within-study variances. In contrast, the fixed effects common variance estimate uses the within-study variances, but not the between-study variance. In both analyses, then, total variance is underestimated because one of the two variance components is ignored.

A question raised then relates to the trade-off between studying many patients for a few time periods or few patients for many time periods. Table 3 shows the relative efficiency achieved by varying the number of pairs of treatment periods and the number of patients enrolled for three combinations of within-patient and between-patient variances in a random effects model. Table 3A uses the estimates from our data (200 and 100, respectively) whereas Tables 3B and 3C show results when the within-patient or between-patient variance is reduced. We included some extreme hypothetical designs (e.g., an impractical trial with 100 treatment pairs) to illustrate that the participant/period trade off relates not only to analytic efficiency but perhaps even more to feasibility and practical considerations including recruitment and retention. As described in our implementation study [5], this ultimately shapes the available data. As expected, precision increases with longer follow-up (more repeated measures) and with higher enrollment. But the number of patients and the number of periods are not of equal importance. For example, with our study’s variances (between-patient variance of 100 and within-patient variance of 200), taking 10 pairs of measurements on 25 patients (500 measurements) is only about twice as efficient as taking 1 pair of measurements on 46 patients (92 measurements). In this case (Table 3A), doubling the number of patients doubles efficiency, but doubling the number of pairs increases efficiency by a fraction that decreases as the number of pairs increases. After the first few repeats, therefore, additional measurements add little to precision.

Table 3.

Approximate precision of the mean effect for a random effects design with M patients and N paired treatment periods per patient relative to one with M = 46 and N = 1, using several within- and between-patient variances: (A) 100,200; (B) 10,200; (C) 100;20; respectively. Reference is 46 patients and 1 pair of treatment periods.

A) Between-Patient Variance = 100; Within-Patient Variance = 200
Pairs of Treatments	Number of Participants Enrolled
	10	20	25	30	46	60	100
1 pair	0.22	0.43	0.54	0.65	1.00	1.30	2.17
2 pairs	0.36	0.72	0.91	1.09	1.67	2.17	3.62
3 pairs	0.47	0.93	1.16	1.40	2.14	2.80	4.66
4 pairs	0.54	1.09	1.36	1.63	2.50	3.26	5.43
5 pairs	0.60	1.21	1.51	1.81	2.78	3.62	6.04
7 pairs	0.69	1.38	1.73	2.08	3.18	4.15	6.92
10 pairs	0.78	1.55	1.94	2.33	3.57	4.66	7.76
100 pairs	1.05	2.09	2.61	3.14	4.81	6.27	10.45

B) Between-Patient Variance = 10; Within-Patient Variance = 200
Pairs of Treatments	Number of Participants Enrolled
	10	20	25	30	46	60	100
1 pair	0.22	0.43	0.54	0.65	1.00	1.30	2.17
2 pairs	0.42	0.85	1.06	1.27	1.95	2.55	4.24
3 pairs	0.62	1.24	1.55	1.87	2.86	3.73	6.22
4 pairs	0.81	1.62	2.03	2.43	3.73	4.86	8.10
5 pairs	0.99	1.98	2.48	2.97	4.56	5.94	9.90
7 pairs	1.33	2.65	3.32	3.98	6.11	7.96	13.27
10 pairs	1.78	3.57	4.46	5.35	8.20	10.70	17.83
100 pairs	6.37	12.73	15.92	19.10	29.29	38.20	63.66

C) Between-Patient Variance =100; Within-Patient Variance = 20
Pairs of Treatments	Number of Participants Enrolled
	10	20	25	30	46	60	100
1 pair	0.22	0.43	0.54	0.65	1.00	1.30	2.17
2 pairs	0.25	0.51	0.63	0.76	1.17	1.52	2.54
3 pairs	0.27	0.54	0.67	0.81	1.24	1.61	2.69
4 pairs	0.28	0.55	0.69	0.83	1.27	1.66	2.77
5 pairs	0.28	0.56	0.70	0.85	1.30	1.69	2.82
7 pairs	0.29	0.58	0.72	0.86	1.32	1.73	2.88
10 pairs	0.29	0.59	0.73	0.88	1.35	1.76	2.93
100 pairs	0.30	0.61	0.76	0.91	1.39	1.82	3.03

This relative efficiency changes, however, with different amounts of between- and within-patient variability. Table 3B demonstrates that additional measurements on individual patients remain valuable when the between-patient variability is small relative to the within-patient variability. Thus, 10 pairs of measurements on 70 patients are nearly as valuable as 1 pair on 60 patients. Conversely, when the within-patient variance is small relative to the between-patient (Table 3C), additional measurements on patients add little because the action is occurring between, rather than within, patients.

DISCUSSION

In this paper, we have explored analytic approaches for combining N-of-1 trials’ data to estimate a treatment effect for the population. N-of-1 trials not only provide information about comparative response, but also about the variability of an individual’s responses to each treatment. A usual premise in undertaking N-of-1 trials is that individuals differ in their responses to treatments and that repeated measurements help to more accurately determine the comparative effectiveness of the interventions for an individual. In typical population studies, on the other hand, we assume participants are similar and pool their results to estimate an average effect that can be applied to future patients in the population. Thus, in combining N-of-1 trials, we struggle to balance individuals’ differences with presumed similarities in deciding how best to incorporate the within-patient information into a representative estimate of the treatment effect for the population.

We considered and tested models with varied frameworks and assumptions. Paralleling the meta-analysis of multi-person trials, each of the N-of-1 studies could be viewed as a separate trial and their summary data combined [13]. Alternatively, the N-of-1 trials might be viewed as IPD and their results handled as independent or correlated repeated measures [16;17]. Both approaches support incorporating prior information through Bayesian hierarchical models. Also, lack of any detected trends within-patients over time supports the N-of-1 trial assumption of independent measurements.

We found that under a variety of within-patient covariance structures, the data supported a fixed treatment effect rather than a random treatment effect. This implies that the effect of added fluoxetine is the same for all patients, as is generally assumed in a clinical trial. In this respect, the meta-analysis of our N-of-1 trials differs from many meta-analyses of clinical trials that require random effects to model differences in treatments across studies. This is perhaps not surprising as the N-of-1 trials we used had a common protocol. This assumption may not hold when combining N-of-1 trials that have different protocols or if the therapies are unrelated (e.g., not a common treatment [AMT] with or without an addition fl). Patient outcomes did differ however, as evidenced by the need for random intercepts that reflects the different FIQ levels on AMT across patients. The lack of any additional explanatory power by patient-level covariates to explain the between-patient variation reinforces the need for larger numbers of patients to explore heterogeneity of patient response. Further study (e.g. simulations) is needed to assess the impact of repeated measures in facilitating discovery of treatment interactions with risk factors.

The best fitting model used a common within-patient variance with zero correlation between measurements. As with the fixed treatment effect, a common variance is a standard assumption for estimating an overall population effect in many parallel and crossover trial designs. But since an N-of-1 design with multiple crossovers intends to measure the effect of treatment on an individual, we might anticipate that N-of-1 data would support estimation using individual-specific variances. Our analysis, however, did not find any heteroscedasticity of variances, most likely because six crossovers were too few to estimate these variances well enough. In other words, the data provided insufficient evidence to reject the simpler common variance assumption. An N-of-1 trial can be designed with more than six crossovers, but in practice participants may not tolerate additional treatment switches especially if there are clinically appreciable differences in the treatments’ effectiveness. As such, for our series and in many others, more complex covariance structures may not be supported. The lack of correlation between period responses in the individuals’ trials also suggests that the time intervals between measurements provided sufficient washout periods to eliminate any correlations.

As expected, use of prior information modified our knowledge about the value and precision of estimates of model parameters. Because the average treatment effect size in our study was smaller than that in the previous crossover trial (mean difference =−8.0; [23]), the posterior effects were reduced relative to the prior ones but increased relative to those from our current study’s data. These posterior estimates were also much more precise than estimates based only on our trials’ data. As more N-of-1 trials accrue, this precision only increases. The use of information from other N-of-1 trials and other clinical trials will then strengthen the conclusions drawn about the average treatment effect. Practically, a sequential approach, similar to cumulative meta-analysis [26], that builds these prior distributions from a combination of clinical experience and pilot studies of within-patient variation would seem recommended.

The multilevel structure accounts for both within and between-patient variation and thereby gives more accurate predictions than either analyzing each individual trial separately or pooling all the results together with a common slope and intercept [27]. But it is important to keep in mind that results are sensitive to assumptions about the prior distribution of the variances. Future experience with N-of-1 studies may allow construction of more informative variance priors. These may help make posteriors more robust to outliers as well. Posterior variances from previous studies may be useful, in this regard. Results with our data-derived priors demonstrated the particular sensitivity of the random effects models to within-patient variance information. The posteriors from our current study might be used with the next series of N-of-1 trials for fibromyalgia therapies using the FIQ.

In general, additional data increased efficiency. The N-of-1 multi-crossover design increased precision compared with a single period design or a two period AB//BA design. Using the averaged crossover analysis the results reflect the advantage of the repeated measures when the trials have balanced designs. Less clear is the benefit of this averaging approach for combining trials with varied repeated measures. Inclusion of partially completed trials (the 12 additional trials with at least two completed treatment periods) generally increased precision, but did not take into account any potential bias introduced by the missing periods and was susceptible to the effect of outliers. While incorporating partially completed trials is important, analysis must carefully consider potential biases from incomplete data and the increased analytic complexities.

In combining N-of-1 trials, we also need to keep in mind the broader research considerations and our reasons for combining these trials. One can use the combined N-of-1 approach to aggregate data from already completed trials each of which presumably was undertaken solely for an individual’s treatment management. This enables estimation of a population effect and better estimation of individual’s effects by borrowing strength from other patients. In this case, the N-of-1 trial design’s increased cost (time and materials) may be justified by the individual benefits that originally supported the use of these trials for personal treatment management (e.g., greater evaluation validity, outcome precision and patient involvement in self-care). If we are considering designing a prospective study, however, we want to consider what, if any, are the benefits of using a series of N-of-1 trials for obtaining an overall population estimate rather than using a more standard trial design.

Although more treatment periods and informative prior distributions increase model estimate precision, they cannot substitute for larger numbers of patients if we seek increased knowledge about between-patient heterogeneity. That said, particularly when dealing with fast-acting treatments with short-lasting effects, allocating resources to more visits per patient rather than to recruiting more patients may enable N-of-1 designs to be more efficient than single period designs. As Table 3 indicates, additional periods are most useful when within-patient variances are large relative to between-patient variances.

Non-statistical considerations may also motivate the use of the combined N-of-1 design. These include improving evaluation of “real world” effectiveness, promoting head-to-head comparative effectiveness studies of already approved or alternative therapies that might not otherwise be studied, increasing trial participant diversity through practice-based research, and providing personalized comparative effectiveness assessments to participants. Considerations that extend beyond data analysis may impact cost-benefit evaluations of this research approach. For example, preliminary reports suggest that making individualized outcome data available by using N-of-1 trials in population studies may enhance participation in clinical trials [5;12]. Individual and practical implementation benefits coupled with the potential to extend clinical research into routine clinical care, might favor this approach over a standard multi-period crossover design in which participants’ results are not individually assessed and used.

A combined N-of-1 approach to estimating population effects comes with a large caveat regarding generalizability of the resulting population estimate. As with other population research, outcome generalizability depends on how representative trial patients are of the overall population. In our implementation study [5], although we sought broad inclusion, those ultimately enrolled represented only a narrow subset of treatment-naïve patients with fibromyalgia syndrome. As in all clinical trials, patient selection impacts outcome and this impact may be greater in the combined N-of-1 design if resource allocation to repeated measurements limits the range of patients studied.

We conclude by noting that the combined N-of-1 trials design permits a sequential approach to estimating average treatment effectiveness using patients recruited to a study primarily focused on individual effectiveness. The multiple measurements collected on each patient enable estimation of patient-specific effects and their precision and also enable the researcher to balance individual and populations effectiveness objectives. With consideration of the resulting model complexities, the use of these designs may enhance research capacity.

What is new?

Key findings

In combining N-of-1 trials to estimate a population treatment effect:

• With few observations per patient and little information about within-patient variation, combined N-of-1 trials data may not support models that include complex variance structures.

• Prior information with Bayesian models can be useful for increasing the precision of estimates but are very sensitive to prior assumptions about variance components.

• Models with fixed treatment effects and common variances are robust and lead to conclusions that are similar to, though more precise than, single period or single-crossover study designs.

What this adds to what was known

• N of 1 studies can be combined to estimate population effects and depending on the analytic models used might offer different estimates and insights compared with more standard clinical trials.

What is the implication? What should change now?

• Combining N-of-1 trials provides an approach for estimating population treatment effects although with limited resources, improved within-patient precision from repeated measures must be balanced by increased participants to explain population variation, to give representative population effect estimates and to address patient care and research goals.