Abstract
Malignant tumours are characterised by higher rates of acid production and a lower extracellular pH than normal tissues. Previous mathematical modelling has indicated that the tumour-derived production of acid leads to a gradient of low pH in the interior of the tumour extending to a normal pH in the peritumoural tissue. This paper uses mathematical modelling to examine the potential of leaky vessels as an additional source of stromal acidification in tumours. We explore whether and to what extent increasing vascular permeability in vessels can lead to a breakdown of the acid gradient from the core of the tumour to the normal tissue, and a progressive acidification of the peritumoural stroma. We compare our mathematical simulations to experimental results found in vivo with a tumour implanted in the mammary fat pad of a mouse in a window chamber construct. We find that leaky vasculature can cause a net acidification of the normal tissue away from the tumour boundary, though not a progressive acidification over time as seen in the experiments. Only through progressively increasing the leakiness can the model qualitatively reproduce the experimental results. Furthermore, the extent of the acidification predicted by the mathematical model is less than seen in the window chamber, indicating not only that vessel leakiness might be acting as a source of acid, but also that it is not the only factor contributing to this phenomenon. Nevertheless, tumour destruction of vasculature could result in enhanced stromal acidification and invasion, hence current therapies aimed at buffering tumour pH should also examine the possibility of preventing vessel disruption.
Keywords: Cancer, pH, Acidity, Veins, Microenvironment
3 Introduction
It is well established that malignant tumours exhibit increased glycolysis to produce lactic acid even in the presence of oxygen, a phenomenon called the Warburg effect and discovered by Otto Warburg in the 1930s (Warburg, 1956, Gatenby and Gillies, 2004, Gillies et al., 2008). The upregulated glucose consumption is used regularly in the diagnosis of malignancies through FDG-PET imaging, which images the high uptake of a glucose analogue (Kroemer, 2006). A consequence of the enhanced levels of aerobic glycolysis is the production of high amounts of acid. As a result, malignant tumours have a lower extracellular pH than normal tissues, at around 6.6–7.0, reduced from the normal pH of 7.2–7.4 (Helmlinger et al., 1997, Schornack and Gillies, 2003, Tannock and Rotin, 1989).
Despite the discovery of the Warburg effect nearly a century ago, the reason malignant tumours consistently utilise aerobic glycolysis has remained speculative. In a series of publications, Gatenby and co-workers have hypothesised that tumour acidification confers an advantage to the tumour cells, by producing a harsh environment which facilitates tumour proliferation and invasion by promoting normal cell death (Gatenby and Gawlinski, 1996, 2003, Gatenby and Gillies, 2004, Gatenby et al., 2006, Gatenby and Gillies, 2007, Smallbone et al., 2007, Gillies et al., 2008).
Previous mathematical modelling has shown that the production of acid by the tumour leads to a gradient of acidity, characterised by low pH in the tumour interior, which extends into the normal tissue (Gatenby and Gawlinski, 1996). This qualitative prediction has been confirmed in vivo through the use of pH imaging of tumour bearing mice using a window chamber construct (Gatenby et al., 2006).
Window chamber experiments are excellent tools for examining small spatial changes in tumour pH in vivo. These window chambers allow the non-invasive observation of fine-scale pH gradients between the tumour and surrounding tissue over time. In the Gatenby et al. (2006) experiments, a dorsal skinfold window chamber was surgically implanted in a mouse, and a slurry of tumour cells placed in the centre of the chamber. Tumour growth and extracellular pH were subsequently monitored.
As the tumour grew in the window chamber construct the normal peritumoural tissue in the chamber acidified, while the intratumoural tissue became less acidic, reducing the pH gradient from the interior to the exterior of the tumour (Gatenby et al., 2006). It is unclear if this normal tissue acidification is an artifact of the window chamber itself, or a naturally occurring phenomenon of tumour growth. Experimental evidence of this disruption is shown in Figure 1, with the normal tissue acidifying and tumour tissue becoming less acidic as time progresses from day 2 to day 6. Additionally, a local maximum in pH appears to develop near the tumour boundary (0.1–0.2 mm into the peritumoural stroma) by day 6.
Figure 1.
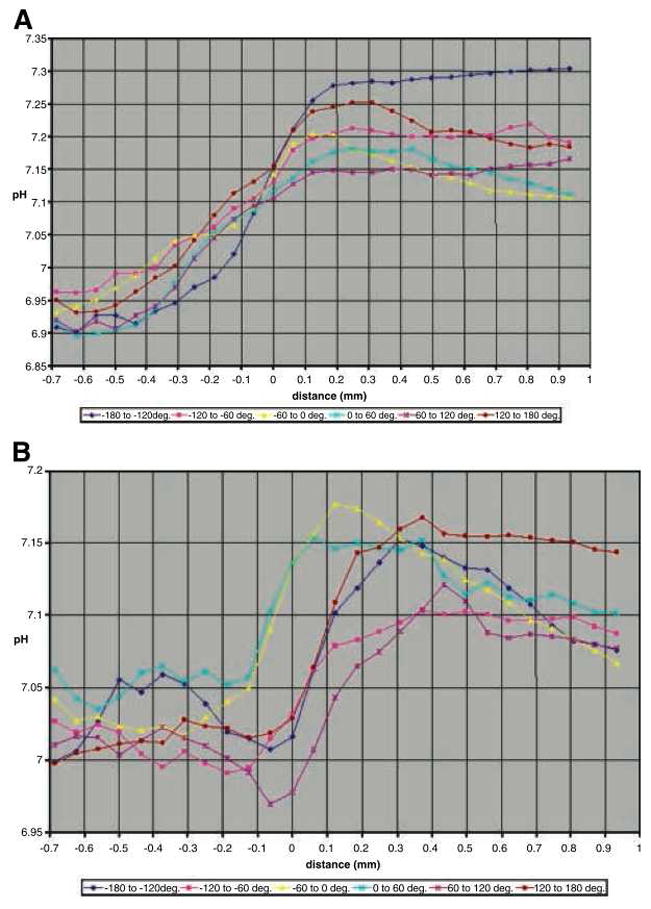
In colour online. Experimentally derived pH gradients at the tumour-host interface in a window chamber of a mouse. The tumour front is located at 0 on the horizontal axis (which accounts for tumour cell movement), and hence the implanted tumour has an initial radius of 0.7mm, which does not increase over the short timescale of the experiment. Note the slightly different horizontal axis scale between the two figures. A) Radial pH values (shown in varying colours) from the centre of the tumour into the surrounding tissue at 2 days post injection. Here, the tumour pH varies from a low of 6.9 in the core to around 7.0–7.15 at the tumour boundary, and then rises to between 7.1 and 7.3 in the peritumoural tissue. B) Radial pH values at 6 days post injection. Compared to day 2, the tumour pH has risen slightly to between 7 and 7.05 in the tumour core, is relatively steady (6.97–7.12) at the tumour boundary, and greatly acidified in the peritumoural tissue, ranging from 7.07 to 7.17. Overall, the intratumoural pH has become slightly less acidic, and the peritumoural pH more acidic over time. Additionally, there appears to be a local maximum in the pH just past the tumour boundary into the peritumoural stroma (0.1–0.3 mm in the figure). Reprinted with permission from Cancer Research (Figure 3 in Gatenby et al. (2006)).
One hypothesis for the acidification of the normal tissue in the chamber is that the vasculature transporting the excess acid out of the tumour is leaky. If so, the vessels might act as a source of acid in the surrounding normal tissue, thereby destroying the pH gradient between the tumour and normal tissue. Additionally, the alkalinisation in the interior of the tumour could be explained by cellular death due to the high numbers of implanted cells which initially exceed the carrying capacity.
In order to examine this leaky vessel hypothesis, we have extended the Gatenby-Gawlinski acid-invasion model (1996) to explicitly incorporate the vascular evacuation of excess acid from the tumour. Their ‘acid-mediated invasion model’ proposes that tumour-derived acid facilitates invasion by promoting normal cell death. By using a mathematical model incorporating the production of acid, destruction of normal cells, and subsequent movement of tumour cells, they were able to examine intratumoural-peritumoural pH gradients and the subsequent effect on invasion.
Vascular evacuation of tumour-derived acid is achieved by venules and veins which have thin walls which are susceptible to disruption. As such, increased vascular permeability in venous outflow is a hallmark of acute inflammation (Kumar et al., 2004). Hence, it is possible that the acidic environment created by tumours may disrupt the vasculature, leading to leakiness. With the following model, we explore if increased vessel permeability can account for an acidification of the peritumoural tissue.
4 Mathematical Model
The mathematical model is based on the acid-mediated invasion model of Gatenby and Gawlinski (1996), extended to include excess acid in the tumour vessels. In our model, N1 represents the normal cell density (in cells/cm3), N2 is the tumour cell density (in cells/cm3), LT is the excess H+ ion concentration in the interstitial fluid of the tumour and adjacent tissue (in mol/cm3), and LB is the excess H+ ion concentration in the veins (in mol/cm3), and the governing equations take the form
| (1) |
| (2) |
| (3) |
| (4) |
As in the Gatenby-Gawlinski model (1996), Equation (1) describes the change in normal cell density. They proliferate with growth rate r1 and carrying capacity K1. For simplicity and because it is not the focus of our investigation nor does it change the results found in this study, we do not alter the assumption made in Gatenby and Gawlinski (1996) that the carrying capacities of the tumour and normal cells are uncoupled. The normal cells die in proportion to the excess acid produced by the tumour, at a rate of d1. As the normal tissue is assumed to be well regulated, it does not diffuse in space.
Equation (2) details the tumour cell dynamics. The tumour cells grow at a rate r2 with a carrying capacity of K2. As tumour cells are more resilient to low pH than normal cells, and no decline in growth rate of tumour cells is observed at the pH in our simulations, we neglect tumour cell death from acidification (Gatenby and Gawlinski, 1996). As in the Gatenby and Gawlinski (1996) model, the tumour cells are assumed to diffuse into free space with a rate of D2, but are confined by the presence of normal cells. Hence, if the normal tissue is at its carrying capacity, the tumour cells are confined and unable to spread.
Equation (3) describes excess tumour H+ ions, LT, which are produced by the tumour at a rate r3. The excess acid is exchanged with the vasculature, which is proportional to the difference in concentration of the tumour excess H+ ion concentration LT, and the blood excess H+ ion concentration, LB. The vascular exchange is represented by dv, which incorporates the effects of vessel permeability and surface area for exchange. By varying the vascular exchange parameter, dv, we will be able to examine if increased permeability can contribute to peritumoural acidification. The tumour acid is neutralised by buffers (such as bicarbonate) brought in by the vasculature at a rate κ2g2 where g2 represents the buffering rate in the blood, and κ2 represents the fraction of buffers present in the tissue from that in the blood. In this case, κ2 < 1 as only a proportion of blood buffers reach the tissue. The acid diffuses in the tissue with diffusion rate of D3.
Equation (4) describes excess blood acid, LB, which is exchanged between the tumour and vessels at rate dv (which includes vessel permeability effects), and in proportion to the difference in concentration between the tumour and the blood acid. Interstitial pressures entail that there is no flux of fluid, but there can be a flux of ions across the vessel wall. We assume that the volume of the interstitial fluid is approximately the same volume as the blood vessels in the tumour. Although this volume fraction varies between tumour types, it is approximately the same order of magnitude (Kim et al., 2004). The blood acid is buffered at a rate g2, and is convected with an effective velocity vector field U due to the flow of blood. As our length scale is focused on the microvasculature, we can assume that U is non-pulsatile (Fung, 1990); further, we take it that the velocity vector field is characterised by conservation of mass and incompressibility, so that ∇X · U = 0. Finally, as a first approximation, we assume that the blood transports acid away from the interior of the tumour, neglecting the small amount which may be transported from the tumour rim into the core.
We solve the system assuming spherical symmetry, due to the relative dimensions of the tumour implant and the window chamber over the short timescale of the experiment. Using spherical polar coordinates, with R2 = |x|2, we have
with U constant. Nondimensionalising the model by using the following substitutions: η1 = N1/K1, η2 = N2/K2, , τ= r1t, and , we obtain
| (5) |
| (6) |
| (7) |
| (8) |
where , and .
The initial conditions are calculated from the experimental data in Gatenby et al. (2006), where 2.5 × 106 tumour cells were placed in the window chamber. As the implanted slurry has an initial radius of 0.7 mm (ξ ≈ 0.05), the initial cell density can be calculated as about 1 × 109 cells/cm3, approximately twice the carrying capacity of 5 × 108 cells/cm3. The normal cells were at their carrying capacity, and there was no initial excess acid. Hence, the initial conditions are,
| (9) |
| (10) |
| (11) |
| (12) |
The boundary conditions will be selected from the appropriate equilibrium values of interest, and detailed in the numerical results section. There are four spatially uniform equilibrium points associated with the system, with (η̂1, η̂2, Λ̂T, Λ̂B) denoting the equilibrium values:
FP1= (0, 0, 0, 0), the trivial state with no tumour, tissue, or excess H+ ions, which is linearly unstable to perturbations of normal or malignant tumour cells.
FP2= (1, 0, 0, 0), the normal cell state with no tumour or excess H+ ions which is linearly unstable to perturbations of malignant tumour cells.
, the coexistent state of tumour and tissue, which is linearly stable if 1 > ρ1Λ̃T and unstable if 1 < ρ1Λ̃T.
, the tumour state, which is linearly stable if 1 < ρ1Λ̃T and unstable if 1 > ρ1Λ̃T.
With these equilibrium points, we can see that altering the vessel permeability, ν, will alter the pH in the cases of FP3 and FP4. However, it does not affect the tumour free normal steady state of FP2. Hence, if we look for waves advancing with a tumour state behind the wave, and tumour-free state ahead, there will be no alteration in the acidity far in front of the wave. Nevertheless, the local profiles at the tumour boundary might be altered by the change in vessel permeability, ν, which we will explore through numerical simulations.
5 Numerical results
Equations (5)–(8) were solved on a spatial grid from 0 ≤ ξ ≤ 1, using the Method of Lines with centered finite difference discretisation of the diffusion terms, and an upwind discretisation of the convection term. Parameter values used were obtained from Gatenby and Gawlinski (1996), Gatenby et al. (2006), Torchilin (2006), Jain (2001), and are detailed in Table 1. Initial conditions used were as in Equations (10). Boundary conditions are no flux at ξ = 0 representing the core of the tumour, and (η̂1, η̂2, Λ̂T, Λ̂B) = (1, 0, 0, 0) representing the tumour-free state at ξ = 1.
Table 1.
Parameters used to solve Equations (5)–(8). The carrying capacities of normal and tumour cells (K1,2 respectively), growth rates (r1,2), tumour diffusion (D2), and vascular evacuation (dv) parameters were taken from a previous acid-invasion modelling and experimental study by Gatenby et al. (2006). The diffusion of protons occurs in association with mobile buffer species to ensure charge balance, and the effective diffusion coefficient value used was estimated in Gatenby et al. (2006). From these values, Gatenby et al. (2006) calculate the tumour acid production rate (r3), and a range of values for the normal cell death rate from acid (d1) from which we select. The blood convection rate (U) is determined from the experimental values found in venules (Jain, 2001, Torchilin, 2006). The blood buffering and proportional delivery of buffer from the bloodstream to the tissue is estimated from extensive systemic buffering simulations (Martin et al., A Mathematical Model of Tumour and Blood pH, Submitted). For the increased vascular permeability simulations, we use ν2 which is increased two-fold from the baseline value of vessel permeability, ν1.
| Parameter | Definition | Dimensions | Value | Source | |
|---|---|---|---|---|---|
| K1 | N1 carrying capacity | cells/cm3 | 5 × 108 | Gatenby et al. (2006) | |
| K2 | N2 carrying capacity | cells/cm3 | 5 × 108 | Gatenby et al. (2006) | |
| r1 | N1 growth rate | 1/s | 2 × 10−6 | Gatenby et al. (2006) | |
| r2 | N2 growth rate | 1/s | 3.2 × 10−6 | Gatenby et al. (2006) | |
| D2 | N2 diffusion | cm2/s | 2 × 10−10 | Gatenby et al. (2006) | |
| D3 | Lactic acid diffusion | cm2/s | 5 × 10−6 | Gatenby et al. (2006) | |
| r3 | H+ ion production rate | M · cm3/[s · cell] | 1.1 × 10−17 | fit to Gatenby et al. (2006) | |
| dv | Normal vascular evacuation | 1/s | 1.1 × 10−4 –2.4 × 10−2 | Gatenby and Gawlinski (1996), Gatenby et al. (2006) | |
| d1 | N1 death rate from acid | cells/[M· s] | 0 – 10 | Gatenby and Gawlinski (1996) | |
| U | blood advection | cm/s | 5 × 10−2 | Jain (2001), Torchilin (2006) | |
| κ2 | Proportional delivery buffer | - | 0.25 | estimated | |
| δ6 | g2/r1 | - | 8 × 104 | estimated | |
| ρ1 |
|
- | 3 × 104 | selected from range above | |
| δ2 | r2/r1 | - | 1.6 | from above | |
| α2 | D2/D3 | - | 4 × 10−5 | from above | |
| σ |
|
- | 1.6 × 104 | from above | |
| ν1 | dv/r1 | - | 1.2 × 103 | from above | |
| ν2 | dv/r1 | - | 1.2 × 105 | increased two-fold from normal |
As the window chamber experiments only measure tumours with a radius up to approximately 1.5mm (ξ ≈ 0.1), it is important to examine the dynamics at the tumour front on this length scale. Hence, although we simulate the equations on a domain of 0 ≤ ξ ≤ 1, for some of the figures we display the solution on a domain of 0 ≤ ξ ≤ 0.1. As we are interested in the pH at 6 days (the final measurement in Gatenby et al. (2006)), we simulate 0 ≤ τ ≤ τmax where τmax = 1.05.
5.1 Normal vasculature
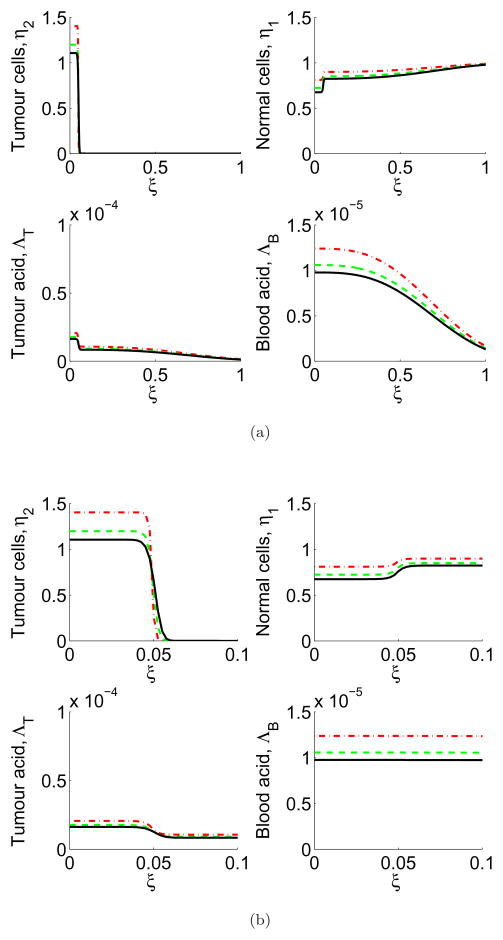
In this section we simulate Equations (5)–(8) where the vessels have normal permeability, so we choose ν = ν1. The simulations are shown in Figure 2, where the tumour and tumour-derived H+ ion profiles advance, killing the normal tissue. In addition, acid is removed from the tumour into the blood, and convected out of the tumour and through the normal tissue in the blood vessels.
Figure 2.
In colour online. (a) Full domain (≈15 mm) and (b) zoomed-in (≈1.5 mm, the scale of the window chamber) simulations of normal vasculature showing tumour cell (top left), normal cell (top right), tumour excess H+ ion (bottom left) and blood excess H+ ion (bottom right) profiles over the course of the simulation. The profiles are shown at 2 days (red dash), 4 days (green dash/dot), and 6 days (black line). Note the initially high level of tumour cells implanted in the window chamber, which die due to the carrying capacity, creating an initially high level of tumour acid which gradually lowers. Simulations are of Equations (5)–(8) with parameters as in Table 1, ν = ν1. Each unit of ξ corresponds to ≈15mm, the radius of the window chamber imaging.
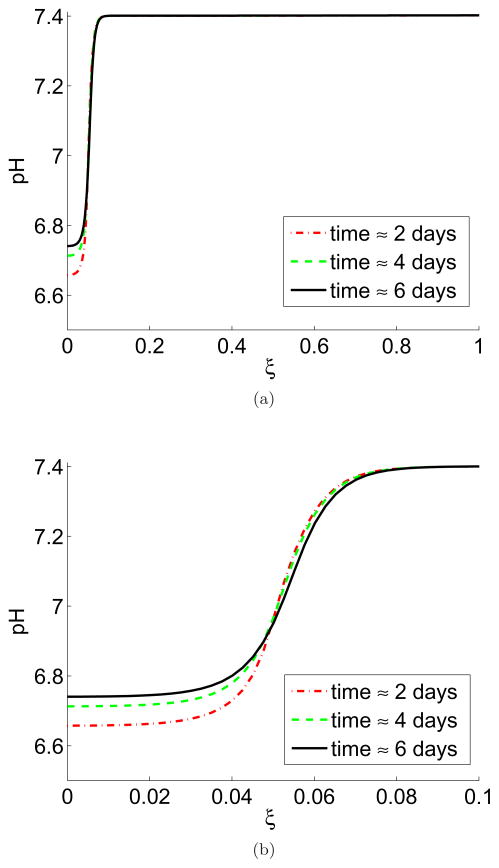
The tumour/tissue pH is shown in Figure 3 where there is a clear acid gradient from the interior of the tumour to the peritumoural tissue. The interior of the tumour has a low pH, rising at the tumour/normal tissue interface until it is normal in the peritumoural tissue. Figure 3 also shows a rise in tumour pH over the time course of the simulation, consistent with the rise in tumour pH found in the window chamber. This is due to the concentration of tumour cells implanted in the chamber initially exceeding the carrying capacity, which produce a large amount of excess acid and then die.
Figure 3.
In colour online. Tumour/tissue pH gradient from interior of the tumour into the peritumoural tissue with no vessel leakiness, shown at 2 days (red dash), 4 days (green dash/dot), and 6 days (black line). Figure (a) shows the whole domain (≈15 mm) and (b) zoomed-in version of (a) on the length scale of the window chamber imaging (≈1.5 mm). Note the expected gradient of acidity from the interior of the tumour (low pH at around 6.7) to normal levels in the peritumoural tissue (normal pH at 7.4). Also note the slight increase in pH inside the tumour over the course of the simulation, which corresponds to the results seen in Figure 1. Simulations are of Equations (5)–(8) with parameters as in Table 1, ν = ν1. The pH is calculated from the excess interstitial tumour/tissue H+ ions, ΛT and with a baseline pH of 7.4. Each unit of ξ corresponds to ≈15mm.
5.2 Leaky vasculature
In Figure 4, we simulate Equations (5)–(8) with the leaky vessels, so we choose ν = ν2, hence increasing vessel permeability by two orders of magnitude.
Figure 4.
In colour online. (a) Full domain (≈15 mm) and (b) zoomed-in (≈1.5 mm, the scale of the window chamber) simulations of the effect of leaky vasculature on tumour cell (top left), normal cell (top right), tumour excess H+ ion (bottom left) and blood excess H+ ion (bottom right) profiles over the course of the simulation. The profiles are shown at 2 days (red dash), 4 days (green dash/dot), and 6 days (black line). The vessel leakiness increases the blood acid levels, and decreases the tumour acid. Simulations are of Equations (5)–(8) with parameters as in Table 1, ν = ν2. Each unit of ξ corresponds to ≈15mm.
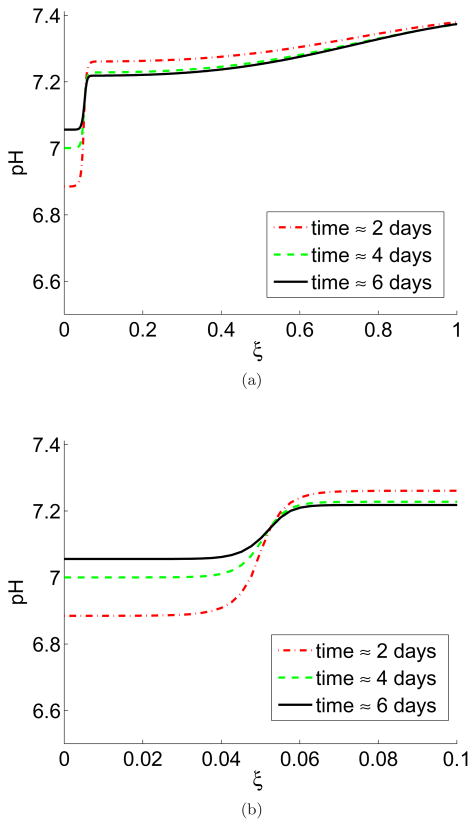
The tumour pH is shown in Figure 5. On the full domain, there is no reduction in the normal tissue pH far from the tumour as predicted by the equilibrium state analysis. However, on the scale of the window chamber, there is an marked absolute reduction of peritumoural pH as compared to the perfect vasculature case (7.20 in the leaky case, 7.40 perfect case at 6 days). Therefore, it is reasonable to conclude that leaky venules (if present) in the direct vicinity of the tumours in the window chamber can act to reduce the acidic gradient from tumour to tissue. However, this effect is not as pronounced as seen experimentally in Figure 1, which shows an acidification of the peritumoural tissue to about pH 7.15.
Figure 5.
In colour online. Tumour/tissue pH gradient from interior of the tumour into the peritumoural tissue with vessel leakiness, shown at 2 days (red dash), 4 days (green dash/dot), and 6 days (black line). (a) Simulations of the whole domain (≈15 mm). Despite the leakiness, the tissue pH returns to a normal 7.4 far away from the tumour (at ξ = 1). (b) A zoomed-in version of (a) on the length scale of the window chamber imaging (≈1.5 mm). In contrast to the perfect vasculature case (Figure 3), there is an absolute reduction in pH in the peritumoural region at the edge of the window chamber (ξ = 0.1) from 7.4 to 7.2 at 6 days, but no progressive acidification over the course of the simulation. The intratumoural pH is higher than the perfect vasculature case (7.07 at 6 days in this figure versus 6.74 in Figure 3), and exhibits an increased alkalinisation over the course of the simulation (from 7.02 to 7.07). Simulations are of Equations (5)–(8) with parameters as in Table 1, ν = ν2. The pH is calculated from the excess interstitial tumour/tissue H+ ions,, ΛT and with a baseline pH of 7.4. Each unit of ξ corresponds to ≈15mm.
Furthermore, although there is a net acidification of the chamber in the leaky versus perfect vasculature simulation, it is important to note that in the leaky simulation there is an increase in peritumoural pH from days 2–6, from 7.16 to 7.20 at ξ = 0.1 (Figure 5b). Hence, although with the leakiness there is a net acidification of the tissue, this acidification is predicted to lessen over time. The increase in peritumoural pH over time is as a result of the initial tumour cell death and reduction of acidity (causing the alkalinisation of the intratumoural pH). This simulated alkalinisation of peritumoural pH is not consistent with the window chamber results, which show a total and progressive acidification of the normal tissue.
With the leaky vasculature, the intratumoural pH is higher than the perfect vasculature case (7.07 at 6 days in Figure 5 versus 6.74 in Figure 3) and still exhibits an increased alkalinisation over the course of the simulation (from 7.01 to 7.07).
5.3 Progressively leaky vasculature
In this section we simulate the situation where the vasculature becomes increasingly leaky over time, hence we use the following function for vessel permeability, . This might occur due to acid damage to the endothelial cells, or another type of tumour disruption of the vessels.
In this case, the tumour and normal cell profiles look similar to the constant vasculature case (not shown), but the pH profiles are slightly altered. Figure 6 shows the pH on the window chamber length scale. This simulation matches the qualitative behaviour seen in the experimental results (Figure 1). Notably, the progressive acidification of the peritumoural tissue over time, in conjunction with the alkalinisation of the intratumoural tissue. Overall, the gradient between tumour and normal tissue is reduced at the tumour boundary.
Figure 6.
In colour online. Tumour/tissue pH with increasing leakiness over time. The figure shows the pH profile at 2 days (red dash), 4 days (green dash/dot), and 6 days (black line). The length scale is (a) ≈ 15 mm and (b) ≈ 1.5 mm, that of the window chamber. Consistent with the experimental data, there is an alkalinisation of the intratumoural region from 6.88 to 7.05. As compared to the leaky vasculature case (Figure 5), there is progressive acidification through time of the peritumoural tissue. As in all the simulations, there is a progressive alkalinisation of the intratumoural tissue. This simulation matches the qualitative behaviour seen in the window chamber (Figure 1), though the magnitude of the acidification is lower. Simulations are of Equations (5)–(8). The parameters used are in Table 1, . The pH is calculated from the excess interstitial tumour/tissue H+ ions, ΛT and with a baseline pH of 7.4.
Although this scenario fits the qualitative experimental results, the magnitude of acidification of the normal tissue is much less pronounced in the simulations, where the simulated pH lowers from 7.26 to 7.22 from days 2 to 6. By contrast, the experimental pH lowers from approximately 7.25 to 7.15 in Figure 1. Furthermore, the increase in the vascular permeability parameter, ν needed to produce such a response is extreme (two orders of magnitude). Additionally, none of the simulations predict the development of a local maximum in pH adjacent to the tumour boundary as seen in Figure 1 by day 6. To conclude, this extreme acidification in the window chambers could not be solely due to vessel leakiness, and the alterations in pH seen in this study would require extremely large increases in vessel permeability.
5.4 Discussion
The efficacy of the tumour vasculature is a critical component for tumour perfusion, acid burden, and drug delivery. A wide body of literature exists on how leaky capillaries affect therapy delivery to the tumour, and mathematical models have increasingly tried to account for this phenomenon (Chapman et al., 2008). However, to our knowledge, no one has mathematically examined how leaky venous outflow from the tumour can act as a source of acid in the peritumoural tissue.
Our analysis indicates that although the tumour free steady state (far ahead of the tumour) will not acidify with increasing leakiness, numerical simulations show that increasing vascular permeability will have a large effect on the spatial intratumoural-peritumoural pH gradients on the millimeter/centimeter scale. In particular, at the tumour boundary, leaky veins will cause a local acidification of the normal tissue. This will have an especially pronounced effect on the length scale of the window chamber experiments, consistent with experimental evidence. Importantly, simulations with leaky vasculature result in a lower peritumoural tissue pH than in normal vasculature, but not a progressive acidification from 2 to 6 days (as seen in the window chamber). However, simulations with increasingly leaky vasculature (such as could be the case with increasing vasculature disruption due to tumour growth) cause both a progressive acidification over time, and also a total decrease in normal tissue pH. All simulations show a slight alkalinisation of the intratumoural tissue due to the initially high concentrations of cells injected in the window chamber, which produce a large amount of acid and then experience cell death towards the tumour carrying capacity. Hence, the initial reduction in tumour cell number serves to reduce the amount of intratumoural acid produced during the timescale of the experiment.
Previous experimental results which showed an acidification of the peritumoural tissue in the window chamber over time, an alkalinisation of the intratumoural tissue, and a breakdown of the intratumoural-peritumoural pH gradient, were hypothesised to be a result of the experimental construct. However, this model indicates the acidification could be as a result of increasing vessel disruption due to the tumour growth. This could be due to a particularly aggressive tumour cell line which actively causes vessel destruction and enhances permeability. Nevertheless it is important to note that in our simulations the permeability had to be substantially increased (by two orders of magnitude) to produce an acidification that was still less than seen in the window chamber. Therefore, it is likely that even if leaky vessels are contributing to acidification, there are additional factors acidifying the window chamber experiments. Futhermore, the window chamber experiments appear to show the development of a local maximum in the pH near the tumour boundary towards the peritumoural stroma which is not predicted by the modelling. As window chambers are one of the primary methods to measure fine spatial tumour pH gradients, it is worthwhile to assess the importance of this effect with different blood vessel co-cultures and also cell lines.
Overall, tumour disruption of local vasculature may aid in stromal acidification and acid-mediated tumour invasion. Hence, in addition to local acidification at the tumour boundary, leaky vessels may cause a longer-range acidification into the peritumoural tissue, which could potentially aid in the invasion of individual cells who alone could not acidify the local environment. Recent experiments have shown that oral administration of the buffer sodium bicarbonate raises tumour pH and prevent metastasis formation Robey et al. (2009). In addition to raising the tumour pH, buffer therapies which increase the buffering capacity of the blood in the tumour vasculature could prevent the vessel disruption and stromal acidification modelled in this study. Therefore, further exploration of the benefits of buffer therapy to prevent vessel disruption is warranted.
Acknowledgments
6.1 Grant Support
NKM: This publication was funded by the National Cancer Institute, NIH grant U56CA113004. EAG: This publication is based on work supported in part by Award No. KUK-C1-013-04, made by King Abdullah University of Science and Technology (KAUST). PKM: This work was partially supported by a Royal Society-Wolfson Research Merit Award. RAG and PKM: This work was partially supported by NIH grant 1U54CA143970-01.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Chapman S, Shipley R, Jawad R. Multiscale modeling of fluid transport in tumors. Bulletin of Mathematical Biology. 2008;70(8):2334–2357. doi: 10.1007/s11538-008-9349-7. [DOI] [PubMed] [Google Scholar]
- Fung Y. Biomechanics: Motion, Flow, Stress and Growth. Springer; 1990. [Google Scholar]
- Gatenby R, Gawlinski E. A reaction-diffusion model of cancer invasion. Cancer Research. 1996;56(24):5745–53. [PubMed] [Google Scholar]
- Gatenby R, Gawlinski E. The glycolytic phenotype in carcinogenesis and tumor invasion: insights through mathematical models. Cancer Research. 2003;63(14):3847–54. [PubMed] [Google Scholar]
- Gatenby R, Gawlinski E, Gmitro A, Kaylor B, Gillies R. Acid-mediated tumor invasion: a multidisciplinary study. Cancer Research. 2006;66(10):5216–5223. doi: 10.1158/0008-5472.CAN-05-4193. [DOI] [PubMed] [Google Scholar]
- Gatenby R, Gillies R. Why do cancers have high aerobic glycolysis? Nature Reviews Cancer. 2004;4(11):891–899. doi: 10.1038/nrc1478. [DOI] [PubMed] [Google Scholar]
- Gatenby R, Gillies R. Glycolysis in cancer: A potential target for therapy. The International Journal of Biochemistry and Cell Biology. 2007;39(7–8):1358–1366. doi: 10.1016/j.biocel.2007.03.021. [DOI] [PubMed] [Google Scholar]
- Gillies R, Robey I, Gatenby R. Causes and consequences of increased glucose metabolism of cancers. Journal of Nuclear Medicine. 2008;49(Suppl 2):24S–42S. doi: 10.2967/jnumed.107.047258. [DOI] [PubMed] [Google Scholar]
- Helmlinger G, Yuan F, Dellian M, Jain R. Interstitial pH and pO2 gradients in solid tumors in vivo: high-resolution measurements reveal a lack of correlation. Nat Med. 1997;3(2):177–82. doi: 10.1038/nm0297-177. [DOI] [PubMed] [Google Scholar]
- Jain RK. Delivery of molecular medicine to solid tumors: lessons from in vivo imaging of gene expression and function. Journal of controlled release. 2001;74:7–25. doi: 10.1016/s0168-3659(01)00306-6. [DOI] [PubMed] [Google Scholar]
- Kim Y, Savellano M, Savellano D, Weisslender R, Bogdanov A. Measurement of tumor interstitial volume fraction: Method and implication for drug delivery. Magnetic Resonance in Medicine. 2004;52:486–94. doi: 10.1002/mrm.20182. [DOI] [PubMed] [Google Scholar]
- Kroemer G. Mitochondria in cancer. Oncogene. 2006;25(34):4630–2. doi: 10.1038/sj.onc.1209589. [DOI] [PubMed] [Google Scholar]
- Kumar V, Abbas A, Fausto N. Pathologic Basis of Disease. Elsevier; 2004. [Google Scholar]
- Robey I, Baggett B, Kirkpatrick N, Roe D, Dosescu J, Sloane B, Hashim A, Morse D, Raghunand N, Gatenby R, Gillies R. Bicarbonate increases tumor pH and inhibits spontaneous metastases. Cancer Research. 2009;69(6):2260–2268. doi: 10.1158/0008-5472.CAN-07-5575. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schornack P, Gillies R. Contributions of cell metabolism and H+ diffusion to the acidic pH of tumors. Neoplasia. 2003;5(2):135–45. doi: 10.1016/s1476-5586(03)80005-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smallbone K, Gatenby R, Gillies R, Maini P, Gavaghan D. Metabolic changes during carcinogenesis: Potential impact on invasiveness. Journal of Theoretical Biology. 2007;244(4):703–713. doi: 10.1016/j.jtbi.2006.09.010. [DOI] [PubMed] [Google Scholar]
- Tannock I, Rotin D. Acid pH in tumors and its potential for therapeutic exploitation. Cancer Research. 1989;49(16):4373–84. [PubMed] [Google Scholar]
- Torchilin V. Nanoparticulates as Drug Carriers. World Scientific Publishing Company; 2006. [Google Scholar]
- Warburg O. On the origin of cancer cells. Science. 1956;123(3191):309–14. doi: 10.1126/science.123.3191.309. [DOI] [PubMed] [Google Scholar]