Abstract
In general, the estimation of the diffusion properties for diffusion tensor experiments (DTI) is accomplished via least squares estimation (LSE). The technique requires applying the logarithm to the measurements, which causes bad propagation of errors. Moreover, the way noise is injected to the equations invalidates the least squares estimate as the best linear unbiased estimate. Nonlinear estimation (NE), despite its longer computation time, does not possess any of these problems. However, all of the conditions and optimization methods developed in the past are based on the coefficient matrix obtained in a LSE setup. In this manuscript, nonlinear estimation for DTI is analyzed to demonstrate that any result obtained relatively easily in a linear algebra setup about the coefficient matrix can be applied to the more complicated NE framework. The data, obtained earlier using non–optimal and optimized diffusion gradient schemes, are processed with NE. In comparison with LSE, the results show significant improvements, especially for the optimization criterion. However, NE does not resolve the existing conflicts and ambiguities displayed with LSE methods.
Keywords: Diffusion tensor imaging, Nonlinear estimation, Least squares estimation
1. Introduction
The magnetic resonance diffusion tensor imaging (MR–DTI) is a methodology that is based on the signal attenuation caused by the diffusion of the spin packets. In a biological setup, the diffusion properties help to infer valuable information otherwise unavailable from standard MR protocols. In recent decades, MR–DTI has been extensively used to investigate tissue structure and pathology caused by or related to injury [1], disease [2], aging [3] and development [4]. The utility of the diffusion weighted imaging (DWI) has been acknowledged for long time. Consequently, MRI scanner manufacturers are including the corresponding pulse sequences as standard protocols making DTI experiments commonly available.
Despite MR–DTI’s wide usage, the tensor algebraic framework initially introduced to describe the model [5, 6], has impeded to a certain extent further developments. Recently, the comprehensive linear algebraic framework described in [7] resulted in the development of new optimal design strategies [8] that brought significant improvements to DTI experiments [8]. The construction of the framework, which contains the application of the logarithm to the measurements, yielded a set of linear equations (see Section 2.1). Furthermore, the objective function of the optimization in [8] was based on the coefficient matrix of these equations (see Section 2.2). Naturally, the solution of the equations is calculated either by matrix inversion or least squares estimation for both non–optimal and optimal cases.
The solution quickly obtained via least squares estimation might not be satisfactory due to the propagation of errors (e.g., due to the application of the logarithm), different types of noise and disturbances. In fact, Section 2.3 shows the deficiency of the least squares estimation by demonstrating how the noise enters the system as a random variable statistically dependant on the signal. The dependence prevents the least squares estimate to be the best linear unbiased estimate. Nonlinear estimation, although computationally more time consuming, is then preferable.
Once this path is taken, it must be guaranteed that the nonlinear estimation problem possesses a unique solution. Although least squares and nonlinear estimation are solving the same problem, there was no proof before this work that relates the non–singularity conditions for these methods. This is indeed one of the goals of this manuscript. By looking at the analysis of Section 3, one can see that the connection is not obvious. Here, the gap left behind is rigorously closed by showing that the coefficient matrix, which must be of full rank by Theorem 1 for least squares estimation, must also have full rank for the case of nonlinear optimization. Otherwise the estimation problem will have either no solution or infinitely many solutions that minimize the residuals. Consequently, the three necessary conditions given in [9] to make the coefficient matrix have full rank are also necessary conditions for the nonlinear estimation. More generally, the derivation of any conditions on the diffusion gradients is accomplished more easily in a least squares estimation environment than in the case of nonlinear estimation.
The manuscript answers the question of whether there exists an equivalence between the mathematical conditions on the choice of gradients for least squares (or linear equations) and for nonlinear estimation or not. What is the role of the coefficient matrix, which is central to least squares estimation, in the case of nonlinear estimation? How do the optimal schemes obtained by minimizing an objective function rooted in the coefficient matrix [8] compare with the non–optimal ones under nonlinear estimation?
These questions are answered by using the experimental data obtained for non–optimal [7] and optimal [8] diffusion gradient schemes. The experimental setup is given in Section 4.1 and the nonlinear estimation results are analyzed in Section 4.2.
2. Overview
2.1. Estimation Equations Under Ideal Conditions
Under ideal conditions, the MR–DTI model, presented in a comprehensive linear algebraic framework in [7], provides the pixel signal intensity at the ith acquisition as
| (1) |
Here Si denotes the signal intensity at each pixel, S0 comes from the reference image and γ is the gyromagnetic ratio. The scalar factor bt (different than the definition of b–value used in the literature) is a factor for the timing of the gradient pulses [8]. It is the double integral of the unit boxcar functions that describe the on and off times of the magnetic field gradients. The magnitude of the gradients are defined in the diffusion gradient vectors, which, therefore are not of unit norm. This setup was essential in generating optimal gradient schemes in [8].
The entries of the row vector vi are the coefficients for the equation that corresponds to the acquisition labeled by the ith diffusion gradient vector. The entries incorporate the effects of all of the gradients. Under noiseless conditions, the logarithm of Eq. 1 is taken for m measurements to obtain a coefficient matrix with ith row equal to vi. The coefficient matrix can be written as a sum of three matrices [7]: V = VD + VC(g) + VI. The matrices represent the effects of the diffusion gradients, the cross terms and the imaging gradients respectively. The diffusion gradient scheme is written as an m × 3 matrix: g. VD, VC are functions of g, whereas VI is a constant matrix defined by the physical position and size of the slices, and pulse sequence parameters [7].
The vector d ∈ IR6 is the representation of the diffusion quadratic form D (3 × 3 symmetric matrix) and it is estimated under ideal conditions (e.g.,noiseless) by solving a set of linear equations:
| (2) |
with p = [ln(S0) − ln(S1) … ln(S0) − ln(Sm)]T . Clearly, the number of diffusion weighted measurements m must at least be 6 and V must have full rank for the experiment to have a unique solution for linear estimation by least squares or matrix inversion [9].
2.2. Optimal Diffusion Gradient Schemes [8]
Aside from the time variables of the pulse sequence, e.g., the echo time, the diffusion gradient vectors are the only variables that the experimenter can modify. The vector space framework, briefly summarized in Section 2.1, makes it possible to pose design problems based on the portions of the coefficient matrix that are functions of the diffusion gradients.
In fact, optimal gradient schemes used in this work were generated by minimizing the objective function given in [8]:
| (3) |
Here ‖ · ‖R is the operator norm corresponding to the Frobenius norm, P is the non–singular matrix that parametrizes the feasible space of diffusion gradients for which V has full rank, and Gmax is the limit for magnetic field gradient amplifiers.
The first portion of the objective function is for bounding the relative difference on the eigenvalues of the diffusion quadratic form obtained by excluding and including the imaging gradients (λi and respectively)
While the left–hand side of this inequality is a function of the sample’s diffusion properties, the bound on the right–hand is calculated from the pulse sequence parameters. It is completely independent from the sample. The bound guarantees the generation of optimal schemes that provide impartial experimental results for two different samples imaged with the same pulse sequence parameters. The second part is the standard condition number for the R–norm that provides stability and robustness for numerical procedures. The last part takes care of the hardware limitations either imposed by the user or the system hardware. The full account of the optimization procedure is given in [8].
2.3. Noisy Conditions and Least Squares Estimation
The equation 1 describes an ideal situation without any perturbations. A more realistic model assumes that noise enters the measurements via Eq. 1. Noisy measurements for m different gradients can be modelled by
| (4) |
where ∊ = [∊1, … , ∊m]T is a random variable independent from the signal.
The propagation of errors for linear estimation methods can be investigated by taking the logarithm of both sides of Eq. 4. Expanding the Taylor series around Si of Eq. 1 results in
| (5) |
with H.O.T. denoting the higher order terms. It is clear from this equation, as also noted in [10], that there must be a high signal to noise ratio (SNR) guaranteeing that |∊i| ⪡ Si in order to use Eq. 5 to estimate D. This may not be always attainable. Specifically, if the diffusion gradients are very strong, Si will have a small magnitude, which makes the error propagate very badly in Eq. 5. Even higher order terms might not be negligible as Si gets smaller.
Nevertheless, linear estimation methods use the left hand side of Eq. 5 to obtain a vector of measurements
and solve for –an estimate of d– using Eq. 2:
It is also assumed that the effects of noise and disturbances can be alleviated by making more than six (possibly repeated) measurements and using weighted least squares estimation [5, 11] to obtain a solution quickly: Theorem 1 (Least Squares Estimate [12]).Suppose and V ∈ IRm×n with linearly independent columns. Let Q be a positive definite matrix (Q > 0), then there is a unique which minimizes over all . Furthermore,
| (6) |
When the noise is an independent random variable and the weight matrix Q is chosen to be equal to the noise covariance, the least square estimate gives the best linear unbiased estimate (BLUE). In addition, if the noise is Gaussian, BLUE is equal to the conditional expectation and thus becomes the optimal estimator over all estimators [13].
Remarkably, these conditions are not met for the linear estimation. Notice that the noise enters Eq. 5 as . Therefore, it is not independent from the signal. Even if the measurements are repeated N times and averaged to transform Eq. 4 into
| (7) |
the remark above is still valid. Averaging improves SNR and changes the covariance of the noise but it does not change the structure of Eq. 5. Setting Q equal to the noise covariance will not provide an optimal solution to the problem because the noise is not independent from the signal in Eq. 5. However, the weight matrix is adjusted to take care of both the noise and the dependence introduced by Eq. 5 (see [5]). This ad hoc procedure is not a definitive solution since it is experiment dependent and might require a lot of guesswork. Moreover, the noise is not the only source of perturbation. There are other issues such as physiologic perturbations and motion artifacts [11, 14].
The remedy is to replace least squares estimation by computationally more time consuming nonlinear estimation, possibly with some variations [11]. The nonlinear estimation described in Section 3 minimizes directly the residual error between the MR–DTI model and the measurements without involving the logarithm.
3. Nonlinear Estimation
In a diffusion weighted imaging experiment, once the gradients are fixed, the noiseless signal Si becomes a function of d in Eq. 1. In the realistic case of Section 2.3, the model does not match the measurements. The mismatch of m measurements forms a vector, χ:
| (8) |
The purpose of the nonlinear estimation is to find out d that minimizes the error between the DTI model of Eq. 1 and the measurements. The natural way to proceed as in [10] is to find minimizers of
| (9) |
The model is fitted to the data directly without applying any logarithms resulting in the reduction of propagation of errors.
To continue with the investigation, there are few useful expressions which need to be computed. Let d0 ∈ IR6 by the mean value version of Taylor’s Theorem [15], given ds ∈ IR6 of small norm, there exists a1 ∈ (0,1) such that χ(d0 + ds) is expressed exactly without any remainders or high order terms as
| (10) |
with
| (11) |
where diag (S(v1 d), … , S(vm d)) denotes the m × m diagonal matrix with the specified entries.
At the heart of this problem lies the gradient of :
| (12) |
and its Hessian
| (13) |
where is the following diagonal matrix
| (14) |
Optimization theory asserts that for a vector to be an extremum, the first necessary condition is that it must be a critical point of , i.e. a vector d0 must satisfy . If a critical point d0 exists, by definition Eq. 13 is equal to zero. To guarantee that the critical point is in fact a strict minimum it is necessary and sufficient that the Hessian is positive definite in a small neighborhood of the critical point with the possible exception of the critical point itself [15]. The real valued functions of a single variable x2 and x4 are standard examples. Their critical point is 0. The Hessian of x2 is positive definite in a neighborhood of 0, the same is true for the Hessian of x4 with the exception of 0 itself. This makes the critical point for both of the functions a strict minimizer. If the Hessian is positive semi–definite, the solution will exist but will not be unique, there will be multiple minimizers.
For the model matching to make sense it must be guaranteed that the estimation problem has a unique solution, a strict minimizer. To demonstrate this, let d0 be a critical point of . Using again Taylor’s Theorem (this time up to the second order expansion), for any ds small enough, there exists a2 ∈ (0, 1) such that can be written exactly as
| (15) |
Under high SNR, the measurements and the model should be close: yielding . This in turn results in 2 implying
Otherwise the Hessian will not be positive definite and the estimation problem will not even have a solution. By the continuity of the entries, is positive definite in a small neighborhood of d0. Assume that V does not have full rank. There exists a non–zero element of Ker V, say ds (meaning ds ≠ 0 and V ds = 0), that can be chosen to have a small norm so that d0 + ds is in the intersection of the neighborhoods of d0 that satisfies the requirements above both for Taylor expansion and positive definiteness of . Therefore Eq. 10 through Eq. 15 imply that
| (16) |
| (17) |
Although the values of ai in the expansions of Eqs. 10, 15 change for a different ds in a small neighborhood of d0, the second expression of the right hand side of those equations will both be equal to zero, as long as ds ∈ Ker V, because of V and its transpose multiply in Eq. 11 and Eq. 13.
In a sufficiently small neighborhood of d0 all of the elements in the set d0 + Ker V will minimize Eq. 9, the uniqueness of the solution will be lost. In essence, the Hessian becomes positive semi–definite because of the rank deficiency of V. This forces the estimation problem to have multiple solutions. Equation 15 illustrates this perfectly: if the Hessian is positive definite, it is obvious that . If it is positive semi–definite, Eq. 17 will hold. As a side remark, one could have argued that Eq. 17 can be directly obtained from Eq. 16 but without Eq. 13 through Eq. 14 the analysis above could not have been accomplished. The most important outcome of this result is that if V has full rank then the Hessian in Eq. 13 will be positive definite.
It follows immediately from these results that the nonlinear estimation problem will be numerically ill conditioned if V is an ill conditioned matrix. In practice, numerical estimation procedures based on descent methods will not converge rapidly if they do converge at all. The issue is addressed in [8] for the optimal design of diffusion gradient schemes by adding the appropriate condition number of V to the objective function of Eq. 3.
In consequence, the full rank condition on V guarantees that the Hessian is positive definite making the critical point a strict minimum. This is equivalent to saying that there exists a unique solution to the model matching problem i.e. the nonlinear estimation will result in a unique diffusion matrix. In the design of the DTI experiments, the diffusion gradients must be carefully chosen in order to make sure that V has full rank. The condition appears as a parametrization of the feasible set of diffusion gradient schemes in [8] for the minimization of imaging gradient effects.
If it is necessary to use a weighted norm, (with K > 0), in Eq. 9, the calculations and the analysis can be extended in a straightforward manner to obtain the same conditions on V.
4. Experimental Setup and Analysis
The type of the estimation method does not affect the way diffusion weighted imaging is carried out. The experimental setup is exactly the same as in [7] and as indicated in [7] the estimation procedures must work properly for the simplest case of diffusion with known characteristics: an isotropic sample. For that reason, a polypropylene centrifuge tube by FisherBrand (Cat. No. 05–539–6) filled with tap water at room temperature, with an inner diameter at the slice of 2.7 cm was chosen as the phantom.
4.1. Experimental Setup
The experiments were carried out on a 4.7 Tesla MR scanner (Varian NMR Systems, Palo Alto, CA, USA) with a gradient system of bore size of 15 cm, maximum gradient strength of 45 gauss/cm and rise time of 0.2 ms using a quadrature birdcage coil (Varian NMR Systems, Palo Alto, CA, USA) with 108/63 mm diameter sizes. DTI data were obtained using the standard spin–echo multi–slice sequence with in–house modifications that store all of the relevant parameters, including the timing and amplitudes of all of the crusher gradients. The images were 128 × 128 pixels with a field of view 64×64 mm2 and 1 mm slice thickness. The repetition time TR = 1 s, echo time TE = 35 ms, diffusion pulse separation Δ = 18 ms, diffusion pulse duration δ = 6 ms were used. All of the experiments were carried out consecutively after leaving the sample in the scanner for approximately 12 hours to reach a stable temperature.
Center–symmetric diffusion gradient schemes with 12 diffusion gradient vectors were used to obtain data. Non–optimal gradient schemes were constructed by appending to the 6 vector gradient schemes [16] their central symmetric part: Tetrahedral (geometrically it is not a tetrahedral and is different from the scheme presented in [17]), Cond6, Jones noniso (without the last vector) renamed as Cond* because it yields to a Vg with a good condition number, Jones (N = 6), Muthupallai, Downhill Simplex Minimization (DSM), Dual Gradient, and also Icosahedron (ICOSA6) scheme from [18]. A maximum diffusion gradient strength of gdiff = 12 gauss/cm was used. With boxcar approximation at maximum diffusion gradient, the value of the scalar coefficient is = 593.61 s/mm2.
4.2. Analysis of the Experimental Results
In–house Mathematica® (Wolfram Research, Champaign, IL USA) code was used to compute components of V as described in [7] using the parameter values written to the hard disk by the pulse sequence. Integrals were computed using trapezoidal shapes rather than rectangular ones. The calculations included all of the crusher gradients. In–house Matlab® (Mathworks, Natick, MA USA) programs were used for the estimation of d at each pixel and the graphical representation and maps of related results. Standard Matlab®Image Processing Toolbox® routines, Sobel edge detection and morphological reconstruction were used to detect the signal region of the phantom in non-diffusion weighted images for each gradient scheme. The edges were removed to obtain a region free of susceptibility artifacts and the intersection of all regions was taken to obtain the circular area with 2022 pixels.
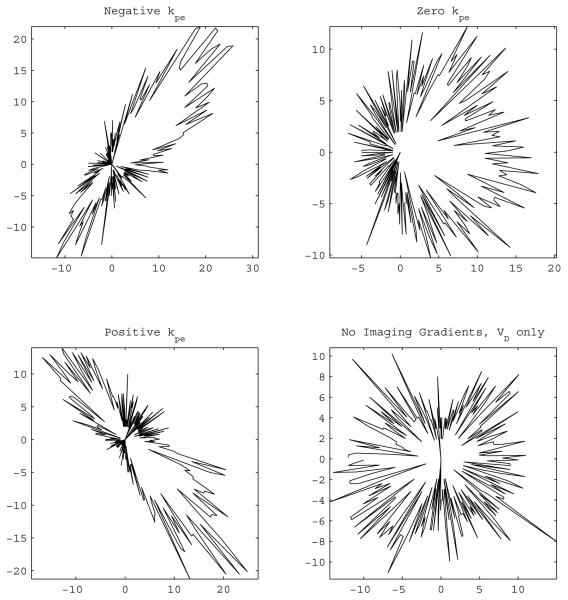
In the computation of VC and VI the phase encoding gradient value of 0 was selected following the same observation described in [7]. The discussion in Section 5 about Fig. 1 and Fig. 2 presents the effects of the choice of the phase encoding gradient values on the results from the non–optimal and optimal schemes with nonlinear estimation.
Figure 1.
Polar histogram of the eigenvector corresponding to the largest eigenvalue for non-optimal diffusion gradient schemes. The distance of each point from the origin is the number of eigenvectors with their slice plane component pointing in the direction of that point. The vertical axis is the phase encoding direction. The eigenvectors align with the phase encode gradient value used in the estimation equations. Under perfect conditions an isotropic sample would result in a circle representing a uniform distribution.
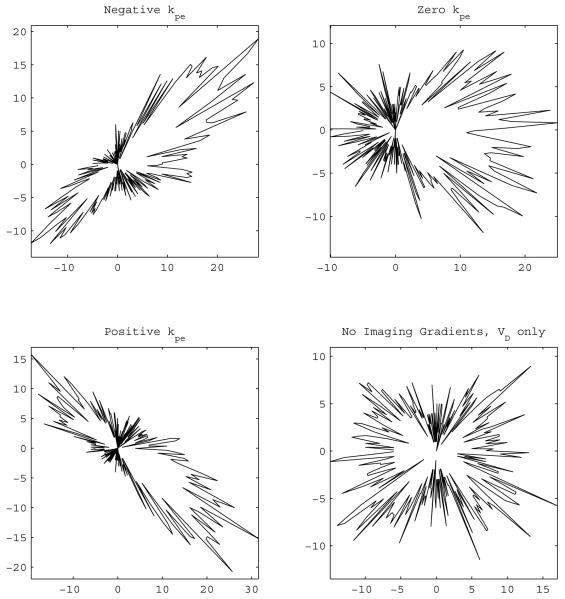
Figure 2.
Polar histogram of the eigenvector corresponding to the largest eigenvalue for optimized diffusion gradient schemes. Qualitatively, the results are similar to the non-optimal versions of the gradient schemes as shown in Fig. 1. In conclusion, neither the optimization nor the nonlinear estimation brings a resolution to the DTI modeling incongruity.
5. Analysis Results
The MR–DTI model was fitted to the data obtained in [7] and [8] from the experiments with non–optimal and optimal diffusion gradient schemes. The numerical calculations was done with the Matlab® Optimization Toolbox® (Mathworks, Natick, MA USA) routine lsqnonlin. The solution of the least squares estimation (LSE) is used as the initial condition for the nonlinear estimation (NE) routines.
Table 1 lists the relative error for the eigenvalue differences with the exclamation point on the left indicating negative eigenvalues for the non–optimal schemes and on the right for the optimal schemes. In the NE case, the difference between the eigenvalues obtained by incorporating all of the imaging gradients and neglecting them goes down in the optimal schemes compared to the values obtained from the non–optimal schemes, except for Cond*. This was one of the aims of the optimization [8] in the specific objective function of Eq. 3. The result is in parallel with LSE [8] demonstrating that the successful optimization goal of [8] also applies to nonlinear estimation.
Table 1.
Difference Between the Eigenvalues, , from VD and V for Least Squares and Nonlinear Estimation
| !cond6! | cond* | dsm | dualgr | icosa | jones6 | muthup | !tetra! | |
|---|---|---|---|---|---|---|---|---|
| Least Squares Estimation from [8] | ||||||||
| Reg. | !−0.668 | 0.032 | 0.0857 | 0.00234 | −1.78 | 0.061 | 0.0622 | −1.06 |
| Opt. | −0.178 | 0.0149 | 0.0787 | 0.0286 | −0.219 | 0.0592 | 0.0604 | −0.561 |
| Reg. | !0.342 | 0.0949 | 0.0999 | 0.0227 | 0.325 | 0.0745 | 0.0739 | −1.06 |
| Opt. | 0.202 | 0.0719 | 0.089 | 0.0528 | 0.247 | 0.0714 | 0.0707 | −0.581 |
| Reg. | !0.751 | 0.185 | 0.203 | 0.358 | 0.685 | 0.247 | 0.244 | 2.06 |
| Opt. | 0.433 | 0.205 | 0.154 | 0.114 | 0.401 | 0.166 | 0.162 | 1.11 |
| Nonlinear Estimation | ||||||||
| Reg. | !−0.755 | −0.0216 | 0.0409 | −0.0504 | −1.99 | 0.0328 | 0.0297 | −1.16 |
| Opt. | 0.866! | 0.0271 | −0.0263 | 0.0118 | 0.0892 | −0.0291 | −0.0202 | 0.84 |
| Reg. | !0.229 | 0.0421 | 0.0674 | −0.026 | 0.282 | 0.0538 | 0.0487 | −1.12 |
| Opt. | 0.289! | −0.0598 | −0.0508 | −0.00199 | 0.0187 | −0.0419 | −0.0364 | 0.4 |
| Reg. | !0.759 | 0.0951 | 0.0974 | 0.288 | 0.693 | 0.123 | 0.131 | 2.11 |
| Opt. | −1.68! | −0.121 | −0.0653 | −0.0218 | −0.222 | −0.0617 | −0.0553 | −1.04 |
When the values from nonlinear and least squares estimation are compared, it is observed that the differences for non–optimal and optimized schemes from NE are lower than the ones from their LSE counterparts with the exception of the largest eigenvalue obtained from the dual gradient scheme. This is a significant improvement at the expense of spending 30 times longer computational time to complete NE versus LSE. Tetrahedron and Cond6 schemes are not considered because they exhibit negative eigenvalues. Nonlinear estimation enhances the benefits of the optimal schemes by reducing the difference between the eigenvalues obtained by full inclusion and exclusion of imaging gradients.
Following the discussions in [8] and [7], about the selection of the phase encoding strength used in the estimation, the polar histograms of the eigenvectors are shown in Figs. 1 and 2. The figures exhibit the tendency of the eigenvectors towards the phase encoding gradient value used in the calculations the same way it happened in [7] and [8] for non–optimal and optimal schemes. This fortifies the claim that the issue originates at a fundamental level of modeling [8] since NE does not remedy the situation neither.
Table 2 represents nonlinear estimation results for the eigenvalues as mean ± standard deviation. The analysis was carried by three different coefficient matrices [7]: V (inclusion of all gradients), NoCroT (No Cross Terms: VD + VI, center–symmetric scheme that removes the cross terms) and VD (exclusion of imaging gradients), which are shown in respective rows. The schemes Cond6 and Tetrahedron exhibit negative eigenvalues with V for both non–optimal and optimized versions. The ratios of the number of pixels with negative eigenvalues to the total number of pixels are 0.00742 for Cond6, 1 for Tetra non–optimal schemes, 0.522 for Cond6, 0.087 for Tetra optimized schemes (nroi = 2022). Although there is improvement for the Cond6 scheme between the non–optimal and optimized schemes with NE, the results of LSE are much better since especially there are no zero eigenvalues for Cond6 optimized scheme with LSE [8].
Table 2.
Summary of Analysis Results for the Eigenvalues
| cond6 | cond* | dsm | dualgr | icosa | jones6 | muthup | tetra | |
|---|---|---|---|---|---|---|---|---|
| Non–optimal Schemes from [7] | ||||||||
| V | !3±0.267! | 2.04±0.0818 | 1.93±0.0544 | 2.01±0.0585 | 4.02±0.256 | 1.91±0.0456 | 1.9±0.0498 | !3.17±0.108! |
| NoCroT | 2.16±0.222 | 1.93±0.0601 | 1.88±0.046 | 1.88±0.0494 | 1.95± 0.13 | 1.86±0.0422 | 1.84±0.0448 | 1.93±0.0959 |
| VD | 2.24± 0.22 | 2.02±0.0612 | 1.97±0.0471 | 1.96±0.0507 | 2.03±0.131 | 1.94±0.0433 | 1.93±0.0459 | 2.02±0.0966 |
| V | !1.7±0.0708! | 1.86±0.0677 | 1.82±0.0431 | 1.9±0.0581 | 1.58±0.0461 | 1.81±0.0437 | 1.8±0.0464 | !2.97±0.102! |
| NoCroT | 1.84±0.0673 | 1.82±0.0491 | 1.8±0.0386 | 1.79±0.0433 | 1.78±0.0462 | 1.77±0.0376 | 1.76±0.0381 | 1.77±0.0773 |
| VD | 1.93±0.0729 | 1.9±0.0503 | 1.88±0.0398 | 1.87±0.0447 | 1.86±0.0471 | 1.86±0.0388 | 1.85±0.0392 | 1.85±0.0786 |
| V | !0.853±0.341! | 1.7±0.0583 | 1.7±0.0539 | 1.5±0.0779 | 1±0.0972 | 1.66±0.0512 | 1.64±0.0537 | !−0.434±0.128! |
| NoCroT | 1.52±0.228 | 1.71±0.056 | 1.71±0.0436 | 1.7±0.0481 | 1.61±0.134 | 1.7±0.0405 | 1.68±0.0411 | 1.59±0.0981 |
| VD | 1.61±0.226 | 1.79±0.057 | 1.8±0.0445 | 1.79±0.0492 | 1.69±0.135 | 1.78±0.0414 | 1.77±0.0419 | 1.68±0.0981 |
| Optimal Schemes from [8] | ||||||||
| V | !2.92±0.396! | 1.97±0.0711 | 1.89±0.0509 | 1.96±0.0657 | 2.06±0.0873 | 1.89±0.0463 | 1.9±0.0479 | !2.91±0.855! |
| NoCroT | 1.99±0.132 | 1.89±0.0565 | 1.85±0.0424 | 1.91±0.058 | 1.92±0.0697 | 1.85±0.0434 | 1.86±0.0425 | 2.04±0.132 |
| VD | 2.06±0.132 | 1.94±0.0556 | 1.92±0.0431 | 1.95±0.0585 | 1.97±0.0697 | 1.92±0.0439 | 1.92±0.0431 | 2.07±0.132 |
| V | !2.12± 0.21! | 1.77±0.0633 | 1.78±0.0405 | 1.83±0.0508 | 1.85±0.0727 | 1.79±0.0414 | 1.8±0.0413 | !2.23±0.208! |
| NoCroT | 1.75±0.0937 | 1.78±0.0464 | 1.76±0.037 | 1.79±0.0461 | 1.77±0.046 | 1.76±0.0377 | 1.77±0.0368 | 1.79±0.0942 |
| VD | 1.83±0.102 | 1.83±0.0467 | 1.83±0.0378 | 1.83±0.0466 | 1.84±0.0456 | 1.83±0.038 | 1.84±0.0375 | 1.83±0.0951 |
| V | !−0.0843± 0.66! | 1.59±0.0875 | 1.68±0.0463 | 1.69±0.0631 | 1.49±0.0975 | 1.69±0.048 | 1.7±0.0468 | !0.554±0.478! |
| NoCroT | 1.52±0.135 | 1.66±0.0537 | 1.67±0.0402 | 1.67±0.0511 | 1.65±0.0573 | 1.68±0.0421 | 1.69±0.0402 | 1.55±0.123 |
| VD | 1.59±0.133 | 1.71±0.0549 | 1.74±0.0408 | 1.72±0.0512 | 1.71±0.0597 | 1.75±0.0418 | 1.75±0.0407 | 1.59±0.123 |
(10−5cm2/s) are the mean eigenvalues from the signal region. Overall, the eigenvalues obtained from the optimal schemes are smaller. The precision, defined by the standard deviation, is better for most of the optimal versions in comparison to the non–optimal schemes. For the non–optimal and optimized schemes the precision is the best for NoCroT and the worst for V consistently. As in the case of non–optimal schemes, VD estimates larger eigenvalues. These facts are again similar to the results observed with LSE.
When the results from the non–optimal schemes with NE and LSE are compared, NE eigenvalues are slightly lower. There is also an increase in the precision for NE. In the case of the optimized schemes, generally NE eigenvalues are very close to LSE. The precision increases slightly again for NE. This is a validation that the optimization criterion of [8] can be successfully used with different estimation methods.
In Table 3, is the mean of the pixel fractional anisotropy index [19] from the signal region. It should be close to zero because the sample is uniform and isotropic. For these experiments, this is the sole criterion that determines the accuracy of the results. With the inclusion of the imaging gradients, optimized schemes show improvements compared to the non–optimal schemes: except for the Cond* scheme, is lower as shown the last row group of Table 3. However, for NoCroT and VD most of the schemes have slightly increased , with the exception of the Icosahedron scheme. As in [7] and [8], is the lowest when all of the imaging gradients are neglected from the calculations (row 3). The standard deviation of the fractional anisotropy does not change drastically between the three methods but the values from VD and NoCroT are much closer to each other than the ones between V and NoCroT as also observed in [7] and [8]. The standard deviation for the optimal schemes increases slightly for all three methods compared to non–optimal ones i.e. there is a decrease in precision after optimization.
Table 3.
Comparison of the Fractional Anisotropy from Nonlinear Estimation
| cond6 | cond* | dsm | dualgr | icosa | jones6 | muthup | tetra | |
|---|---|---|---|---|---|---|---|---|
| Non–optimal Schemes from [7] | ||||||||
| V | !–! | 0.0934±0.0303 | 0.0653±0.0219 | 0.149±0.0314 | 0.624±0.0423 | 0.0724±0.0189 | 0.0763±0.0214 | !–! |
| NoCroT | 0.171± 0.11 | 0.0634±0.0228 | 0.0499±0.0169 | 0.0501±0.0169 | 0.0988±0.0574 | 0.0469±0.0153 | 0.0474±0.0158 | 0.1±0.0518 |
| VD | 0.163±0.105 | 0.0605±0.0218 | 0.0476±0.0161 | 0.0478±0.0161 | 0.0944±0.0548 | 0.0448±0.0146 | 0.0453±0.0151 | 0.0954±0.0495 |
| Optimal Schemes from [8] | ||||||||
| V | !–! | 0.109±0.0407 | 0.0612±0.021 | 0.0759±0.0282 | 0.161±0.044 | 0.058±0.0193 | 0.0589±0.0195 | !–! |
| NoCroT | 0.137±0.0715 | 0.0662±0.024 | 0.051±0.0168 | 0.068±0.0237 | 0.0763±0.0294 | 0.0505±0.0172 | 0.05±0.0163 | 0.138±0.0647 |
| VD | 0.129±0.068 | 0.0646±0.0234 | 0.0488±0.0162 | 0.0662±0.0231 | 0.0716±0.0285 | 0.0474±0.0161 | 0.048±0.0157 | 0.135±0.0633 |
| V | !–! | −16.70 | 6.28 | 49.06 | 74.20 | 19.89 | 22.80 | !–! |
| NoCroT | 19.88 | −4.42 | −2.204 | −35.73 | 22.77 | −7.68 | −5.49 | −38.00 |
| VD | 20.86 | −6.78 | −2.52 | −38.49 | 24.15 | −5.804 | −5.96 | −41.51 |
These observations for are again in concordance with the ones of LSE in [7] and [8]. However, when NE and LSE are compared, generally calculated from NE and its standard deviation are less than the ones from LSE for both non–optimal and optimal schemes. In other words, the precision and accuracy increased with NE. This improvement is due to the fact that logarithm is not applied to the experimental data for NE. Obviously, it comes with the price of increased computation time.
Table 5 shows the model matching error (times , to normalize for the number of acquisitions) from the non–optimal schemes and the optimal ones when NE is used. Table 4 from [8] is also provided for comparison with LSE. is the mean of the pixel residuals from the signal region. The error with NE is slightly less than the error of LSE.
Table 5.
Comparison of the Model Matching Error from Nonlinear Estimation
| cond6 | cond* | dsm | dualgr | icosa | jones6 | muthup | tetra | |
|---|---|---|---|---|---|---|---|---|
| Non–optimal Schemes from [7] | ||||||||
| V | 1139±81.09 | 1089±64.27 | 1049±67.11 | 1036±63.27 | 969.6±66.06 | 1062±68.58 | 1062±64.87 | 845.2±62.04 |
| NoCroT | 632±62.33 | 591.8±52.61 | 561.8±54.15 | 568.9±51.42 | 575.1±54.48 | 570±53.52 | 571.3±51.68 | 649.1±55.72 |
| VD | 632±62.33 | 591.8±52.61 | 561.8±54.15 | 568.9±51.42 | 575.1±54.48 | 570±53.52 | 571.3±51.68 | 649.1±55.72 |
| Optimal Schemes from [8] | ||||||||
| V | 713.4±56.54 | 688.9±55.85 | 952.1±64.98 | 550.3±52.69 | 974.2±70.67 | 933.5± 63.2 | 874.6±58.76 | 383.3± 48.2 |
| NoCroT | 436.4±50.62 | 383.8±49.38 | 506.8±53.57 | 302.3±47.18 | 534.5±57.36 | 499.2±52.78 | 467.3±49.86 | 241.3±46.05 |
| VD | 436.4±50.62 | 383.8±49.38 | 506.8±53.57 | 302.3±47.18 | 534.5±57.36 | 499.2±52.78 | 467.3±49.86 | 241.3±46.05 |
| V | 37.37 | 36.74 | 9.24 | 46.88 | −0.47 | 12.10 | 17.64 | 54.65 |
| NoCroT | 30.95 | 35.15 | 9.79 | 46.86 | 7.06 | 12.42 | 18.20 | 62.83 |
| VD | 30.95 | 35.15 | 9.79 | 46.86 | 7.06 | 12.42 | 18.20 | 62.83 |
Table 4.
Comparison of the Model Matching Error from Least Squares Estimation [8]
| cond6 | cond* | dsm | dualgr | icosa | jones6 | muthup | tetra | |
|---|---|---|---|---|---|---|---|---|
| Non–optimal Schemes from [7] | ||||||||
| V | 1148±81.17 | 1102±64.12 | 1060±66.92 | 1042±63.21 | 975.1±66.1 | 1074±68.68 | 1070±64.76 | 852.3±62.1 |
| NoCroT | 635.3±63.11 | 595.1±53.39 | 564.6±54.83 | 571.3±51.98 | 577.7±55.07 | 572.5±54.1 | 573.9±52.26 | 651.8±56.28 |
| VD | 635.3±63.11 | 595.1±53.39 | 564.6±54.83 | 571.3±51.98 | 577.7±55.07 | 572.5±54.1 | 573.9±52.26 | 651.8±56.28 |
| Optimal Schemes from [8] | ||||||||
| V | 791±60 | 697±55.4 | 966±64.8 | 559±52.1 | 1050±76.5 | 946±62.9 | 886±58.6 | 411±53.4 |
| NoCroT | 438±51.2 | 387±50.4 | 510±54.4 | 305±48.5 | 537±58.1 | 502±53.6 | 470±50.7 | 244±47.6 |
| VD | 438±51.2 | 387±50.4 | 510±54.4 | 305±48.5 | 537±58.1 | 502±53.6 | 470±50.7 | 244±47.6 |
| V | 31.10 | 36.75 | 8.87 | 46.35 | −7.68 | 11.91 | 17.20 | 51.78 |
| NoCroT | 31.06 | 34.97 | 9.67 | 46.61 | 7.045 | 12.31 | 18.10 | 62.56 |
| VD | 31.06 | 34.97 | 9.67 | 46.61 | 7.045 | 12.31 | 18.10 | 62.56 |
In addition, the model matching error reduction achieved by LSE with optimal schemes, is also achieved with very similar figures by NE. Reducing the error in the vicinity of %30 to %45 is highly significant. The model matching error for V, is still larger compared to the less ‘complete’ models, the same way it was in the LSE case [8]. Moreover, there is very slight improvement in NE compared to LSE.
6. Conclusion
The questions that were posed at the introduction about the equivalence of different estimation methods has been investigated using theoretical and experimental results. The bridge between the linear and nonlinear estimation is clearly established: the coefficient matrix V is the common element. The theoretical analysis shows that conditions imposed on V must be respected regardless of the estimation method and its benefits. For example, the nonlinear estimation reduces the propagation of errors but it does not overcome the non–singularity problem or the numerical ill conditioning originating from a poor choice of V. The necessary conditions in [9] must still be respected for V to have full rank. Similarly, the linear parametrization of the feasible set of diffusion gradient schemes [8], which appears as a constraint in the optimization, is also valid for the nonlinear estimation.
On a more general scope, any result obtained with the coefficient matrix V by working in the area of least squares estimation will automatically apply or will be quickly adapted to nonlinear estimation as well. It is easier to demonstrate results in the linear algebra framework of least squares estimation compared to the nonlinear setup.
The nonlinear estimation is computationally more intense and time consuming compared to the least squares estimation. However, the aim of the optimization in [8], to reduce the difference between the eigenvalues obtained with and without the inclusion of the imaging gradients, is attained much more successfully with nonlinear estimation from the experimental data. This is in the same sprit of the general scope described above.
For other criterions , nonlinear estimation yields better results over the least squares estimation but they are mostly in the same vicinity of the least squares estimation. In addition, the conflicts noticed with linear estimation do not disappear: despite the lowering of the residual error in optimal schemes, the fractional anisotropy goes up; the tendency of the eigenvectors to align with the phase encoding gradient value still persists. Moreover, data from optimal Cond6 scheme presents negative eigenvalues with nonlinear estimation.
In the past, diffusion weighted imaging experiments have been modeled more comprehensively [20] even before the introduction of the MR–DTI model. The limitations of the model has forced developments to expand it [21] or to bring in new models [22]. But the simplicity and the speed make the model still popular and viable. So, the efforts of this manuscript and the earlier ones [7, 8] was concentrated on the improvement of the DWI experiments within the DTI model. Although successful results and conclusions were obtained, the unresolved conflicts or ambiguities indicate a necessity to focus on strategies to search for novel methods that will have the right balance of speed and comprehensiveness at the same time.
Acknowledgements
This study was supported, in part, by the Washington University Small Animal Imaging Resource, a National Cancer Institute funded Small Animal Imaging Resource Program facility (U24-CA83060) and the NIH/NINDS grant Biomarkers and Pathogenesis of MS (P01-NS059560). Special thanks to Jim Quirk for kindly reviewing the manuscript. The manuscript is dedicated to Engin Arda Tayşi.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- [1].Kim JH, Loy DN, Liang H-F, Trinkaus K, Schmidt RE, Song S-K. Noninvasive diffusion tensor imaging of evolving white matter pathology in a mouse model of acute spinal cord injury. Magnetic Resonance in Medicine. 2007;58(2):253–260. doi: 10.1002/mrm.21316. [DOI] [PubMed] [Google Scholar]
- [2].Budde MD, Kim JH, Liang H-F, Schmidt RE, Russell JH, Cross AH, Song S-K. Toward accurate diagnosis of white matter pathology using diffusion tensor imaging. Magnetic Resonance in Medicine. 2007;57(4):688–695. doi: 10.1002/mrm.21200. [DOI] [PubMed] [Google Scholar]
- [3].Mielke M, Kozauer N, Chan K, George M, Toroney J, Zerrate M, Bandeen-Roche K, Wang M-C, vanZijl P, Pekar J, Mori S, Lyketso C, Albert M. Regionally-specific diffusion tensor imaging in mild cognitive impairment and Alzheimer’s disease. NeuroImage. 2009;46(1):47–55. doi: 10.1016/j.neuroimage.2009.01.054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Brain Development Cooperative Group. Evans AC. The NIH MRI study of normal brain development. NeuroImage. 2006;30:184–202. doi: 10.1016/j.neuroimage.2005.09.068. [DOI] [PubMed] [Google Scholar]
- [5].Basser PJ, Matiello J, LeBihan D. Estimation of the effective self-diffusion tensor from the NMR spin echo. Journal of Magnetic Resonance Series B. 1994;103:247–254. doi: 10.1006/jmrb.1994.1037. [DOI] [PubMed] [Google Scholar]
- [6].Matiello J, Basser PJ, LeBihan D. Analytical expressions for the B matrix in NMR diffusion imaging and spectroscopy. Journal of Magnetic Resonance Series A. 1994;108:131–141. [Google Scholar]
- [7].Özcan A. Theoretical and experimental analysis of imaging gradients in DTI; Proceedings of the 31st Annual International Conference of the IEEE EMB Society; Minneapolis, MN, USA. 2009; pp. 2703–2706. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Özcan A. Decoupling of imaging and diffusion gradients in DTI; Proceedings of the 31st Annual International Conference of the IEEE EMB Society; Minneapolis, MN, USA. 2009; pp. 2707–2710. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Özcan A. (Mathematical) necessary conditions for the selection of gradient vectors in DTI. Journal of Magnetic Resonance. 2005;172(2):238–241. doi: 10.1016/j.jmr.2004.10.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Conturo TE, McKinstry RC, Aronovitz JA, Neil JJ. Diffusion MRI: Precision, accuracy and flow effects. NMR in Biomedicine. 1995;8:307–332. doi: 10.1002/nbm.1940080706. [DOI] [PubMed] [Google Scholar]
- [11].Chang L, Jones DK, Pierpaoli C. RESTORE: Robust estimation of tensors by outlier rejection. Magnetic Resonance in Medicine. 2005;53:1088–1095. doi: 10.1002/mrm.20426. [DOI] [PubMed] [Google Scholar]
- [12].Luenberger DG. Optimization by Vector Space Methods. 1st Edition John Wiley and Sons; 1969. [Google Scholar]
- [13].Shiryaev AN. Probability. 2nd Edition Springer Verlag; 1995. [Google Scholar]
- [14].Mangin JF, Poupon C, Clark C, Bihan DL, Bloch I. Distortion correction and robust tensor estimation for MR diffusion imaging. Medical Image Analysis. 2002;6(3):191–198. doi: 10.1016/s1361-8415(02)00079-8. [DOI] [PubMed] [Google Scholar]
- [15].Fleming WH. Functions of Several Variables. 2nd Edition Springer Verlag; 1977. [Google Scholar]
- [16].Skare S, Hedehus M, Moseley ME, Li T-Q. Condition number as a measure of noise performance of diffusion tensor data acquisition schemes with MRI. Journal of Magnetic Resonance. 2000;147:340–352. doi: 10.1006/jmre.2000.2209. [DOI] [PubMed] [Google Scholar]
- [17].Conturo TE, McKinstry RC, Akbudak E, Robinson BH. Encoding of anisotropic diffusion with tetrahedral gradients: A general mathematical diffusion formalism and experimental results. Magnetic Resonance in Medicine. 1996;35:399–412. doi: 10.1002/mrm.1910350319. [DOI] [PubMed] [Google Scholar]
- [18].Hasan KM, Parker DL, Alexander AL. Comparison of gradient encoding schemes for diffusion-tensor MRI. Journal of Magnetic Resonance Imaging. 2001;13:769–780. doi: 10.1002/jmri.1107. [DOI] [PubMed] [Google Scholar]
- [19].Basser PJ, Pierpaoli C. Microstructral and physiological features of tissues elucidated by quantitative-diffusion-tensor MRI. Journal of Magnetic Resonance Series B. 1996;111:209–219. doi: 10.1006/jmrb.1996.0086. [DOI] [PubMed] [Google Scholar]
- [20].Callaghan PT. Principles of Nuclear Magnetic Resonance Microscopy. Oxford University Press; 1991. [Google Scholar]
- [21].Özarslan E, Mareci TH. Generalized diffusion tensor imaging and analytical relationships between diffusion tensor imaging and high angular resolution diffusion imaging. Magnetic Resonance in Medicine. 2003;50(5):955–965. doi: 10.1002/mrm.10596. [DOI] [PubMed] [Google Scholar]
- [22].Frank LR. Anisotropy in high angular resolution diffusion-weighted MRI. Magnetic Resonance in Medicine. 2001;45(6):935–1141. doi: 10.1002/mrm.1125. [DOI] [PubMed] [Google Scholar]