Abstract
Transcribed regions in the human genome differ from adjacent intergenic regions in transposable element density, crossover rates, and asymmetric substitution and sequence composition patterns. We tested whether these differences reflect selection or are instead a byproduct of germline transcription, using publicly available gene expression data from a variety of germline and somatic tissues. Crossover rate shows a strong negative correlation with gene expression in meiotic tissues, suggesting that crossover is inhibited by transcription. Strand-biased composition (G+T content) and A → G versus T → C substitution asymmetry are both positively correlated with germline gene expression. We find no evidence for a strand bias in allele frequency data, implying that the substitution asymmetry reflects a mutation rather than a fixation bias. The density of transposable elements is positively correlated with germline expression, suggesting that such elements preferentially insert into regions that are actively transcribed. For each of the features examined, our analyses favor a nonselective explanation for the observed trends and point to the role of germline gene expression in shaping the mammalian genome.
Nucleotide substitution rates, transposable element density, and crossover rates vary dramatically across the human genome for reasons that are poorly understood (Donis-Keller et al. 1987; Kong et al. 2002; McVean et al. 2004; The Chimpanzee Sequencing and Analysis Consortium 2005; Hellmann et al. 2005). Within genes, substitution rates are strand-asymmetric (Green et al. 2003; Polak and Arndt 2008), crossover rates are lower (McVean et al. 2004; Myers et al. 2005; The International HapMap Consortium 2007; Coop et al. 2008), and transposable element density is higher than in intergenic regions (Sela et al. 2007). Each of these features may be a consequence of natural selection, but, alternatively, could be a byproduct of germline gene expression since recombination and mutation events are only passed down to subsequent generations if they occur in germline cells. In this study, we compare these competing hypotheses by examining the correlations between each of these features and gene expression in germline and somatic tissues.
In yeast, several observations link recombination and transcription. Meiotic recombination is initiated by double-strand breaks (DSBs) (Sun et al. 1989), which predominantly occur in the open chromatin regions of promoters (Wu and Lichten 1994; Gerton et al. 2000; Mancera et al. 2008). Regions with very high recombination (recombination “hotspots”) often require the binding of transcription factors to be active (White et al. 1991; Kon et al. 1997; Kirkpatrick et al. 1999a), and genes near hotspots have higher overall expression levels (but also tend to be repressed during meiosis) (Gerton et al. 2000). Despite their association with gene expression, hotspots are not transcription-dependent since disrupting transcription does not necessarily change the recombination rate (Sun et al. 1989; White et al. 1992), and new hotspots can be created by inserting nucleosome-excluding sequences (Kirkpatrick et al. 1999b).
In mammals, the relationship between recombination and transcription is less clear. Across the genome, G+C content is positively correlated with both recombination and gene density (Eyre-Walker 1993; Fullerton et al. 2001; Kong et al. 2002), but crossover rates are lower within genes than in the regions surrounding them (McVean et al. 2004; Myers et al. 2005; The International HapMap Consortium 2007; Coop et al. 2008).
Transcribed regions in many organisms have strand-asymmetric patterns of substitution (Francino et al. 1996; Francino and Ochman 2001; Green et al. 2003). In mammals there is an excess of coding-strand purine transitions (A → G and G → A) compared to coding-strand pyrimidine (T → C and C → T) transitions (Green et al. 2003), and most transversions display a similar asymmetry (Polak and Arndt 2008). The bias also exists in human polymorphism data (Webster and Smith 2004; Qu et al. 2006), and in mutations in some somatic cancers (Rubin and Green 2009; Pleasance et al. 2010). Over time, asymmetrical substitutions give rise to a strand-biased nucleotide composition characterized by an excess of G and T nucleotides on the coding strand (Duret 2002; Green et al. 2003; Touchon et al. 2003). Although the A → G/T → C and transversion substitution biases are uniform over entire genes, the G → A/C → T bias is nonuniform and is, in fact, reversed in the first 1–2 kb downstream from the transcription start site (Polak and Arndt 2008). A similar substitution asymmetry may exist around origins of DNA replication (Touchon et al. 2005; Huvet et al. 2007); however, this asymmetry is very weak after removing the confounding effect of transcription (Necsulea et al. 2009a; Polak and Arndt 2009).
Several studies have examined the relationship between strand biases and gene expression. The coding-strand G+T content of genes is correlated with the average gene expression levels of housekeeping genes (Majewski 2003) and with gene expression levels across several different tissues (Comeron 2004). Additionally, the excess of T over A is strongest for genes with the highest breadth of expression (Duret 2002).
Transposable element density is correlated with gene density in several species, suggesting a possible connection to transcription. In Caenorhabditis elegans, there is an enrichment of LTR retrotransposons near genes (Ganko et al. 2003), while in Arabidopsis, transposable elements are negatively correlated with gene density (Wright et al. 2003). In primates, frequency of the transposable element Alu is positively correlated with both G+C content (Soriano et al. 1983; Smit 1996; International Human Genome Sequencing Consortium 2001) and gene density (Grover et al. 2004). Near genes, the densities of Alu elements in primates and B1 elements in mice are greater than predicted by G+C content (Medstrand et al. 2002) and vary for genes of different functional categories (Grover et al. 2003; Tsirigos and Rigoutsos 2009).
Several investigators have hypothesized that the above differences between transcribed and nontranscribed sequences result from natural selection. For example, selection may act to reduce crossovers within genes if recombination is mutagenic (McVean et al. 2004) and could result in strand-biased composition for efficient splicing (Zhang et al. 2008). Selection could also explain the enrichment of Alus near genes of specific functional categories if selection against transposable elements is weaker for these genes (Grover et al. 2003) or if selection promotes the fixation of Alus with regulatory potential (Tsirigos and Rigoutsos 2009).
In this study, we test whether the differences between genic and intergenic regions in substitution pattern, transposable element density, and crossover rate are, instead, a side effect of transcription, by examining how these features correlate with gene expression in somatic and germ tissues. If these features are a byproduct of transcription, then the strongest correlations should be with gene expression from germline cells. In contrast, natural selection is expected to act on all genes regardless of their tissue of expression. Consistent with the nonselective hypothesis, we find that transposable element density, G+T content, and A → G/T → C substitution asymmetry are all positively correlated with gene expression, and that these correlations are highest for germ tissues. Similarly, crossover rate is most strongly negatively correlated with gene expression from meiotic cells, which suggests that crossover is inhibited by transcription.
Results and Discussion
Crossover rate is negatively correlated with meiotic gene expression
In the human genome, crossover rates within genes are lower than the rates in nearby intergenic regions (Myers et al. 2005; The International HapMap Consortium 2007; Coop et al. 2008). It has been suggested (McVean et al. 2004) that this may be a consequence of selection against mutagenic effects of recombination, but another possibility is that it is a consequence of an interaction between transcription and recombination in meiotic cells. To help distinguish these possibilities, we calculated the pairwise correlation between gene expression for a wide range of tissues (Sato et al. 2003; Su et al. 2004; Barberi et al. 2005; Ge et al. 2005; Perez-Iratxeta et al. 2005; Skottman et al. 2005; Kocabas et al. 2006; Korkola et al. 2006; Looijenga et al. 2006; Chalmel et al. 2007; Houmard et al. 2009; Wu et al. 2009) and fine-scale crossover rate as estimated from linkage disequilibrium (LD) data (Myers et al. 2005; The International HapMap Consortium 2007). Gene expression in most tissues is negatively correlated with crossover rate (Supplemental Figs. S1, S5; Supplemental Table S2); however, the mean correlation of samples containing germ cells ( ) is much stronger than the mean correlation of somatic tissues (
) is much stronger than the mean correlation of somatic tissues (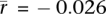 ; P = 2.1 × 10−30; two-sided Welch's t-test). These results are robust to batch effects arising from differences between studies and microarray platform (Supplemental Note S1).
; P = 2.1 × 10−30; two-sided Welch's t-test). These results are robust to batch effects arising from differences between studies and microarray platform (Supplemental Note S1).
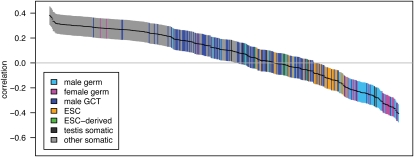
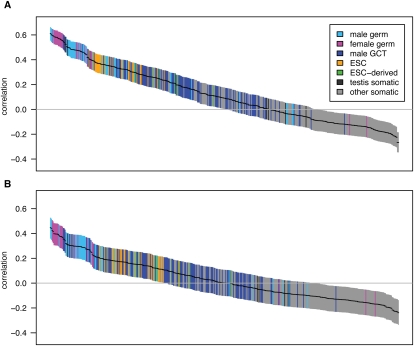
Different tissues tend to have correlated expression patterns due to similar expression levels of “housekeeping” genes. To better distinguish between tissues, we identified the 10% of genes whose expression patterns have the highest tissue differentiation (Schug et al. 2005). These genes have more tissue-specific patterns of expression than housekeeping genes and provide the most power for discriminating between tissues. We recalculated the correlations with crossover rate using this subset of genes and found that the separation between tissues increases (Fig. 1). In fact, the correlation with most somatic tissues becomes positive when the high tissue differentiation genes are used (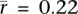 ; P = 1.7 × 10−61; two-sided t-test). Thus, it is gene expression within germ cells, rather than somatic cells, that drives the negative association with crossover rate.
; P = 1.7 × 10−61; two-sided t-test). Thus, it is gene expression within germ cells, rather than somatic cells, that drives the negative association with crossover rate.
Figure 1.
Pairwise correlations between gene expression and crossover rate for a set of genes with high tissue differentiation. Each of the 409 tissue samples is represented by a single bar, colored by tissue type as defined in the key (ESC, embryonic stem cells; GCT, germ cell tumors). Bars are ordered from left to right by the correlation coefficient, r, with the vertical extent of the bar indicating the 95% confidence interval. Only the 507 genes with at least 10 kb of sequence data and the highest tissue differentiation were included in this analysis, as these genes have more tissue-specific patterns of expression and provide the most power for discriminating between tissues; for correlations with the complete gene set see Supplemental Figure S1.
To test whether gene expression during meiotic initiation explains the reduction in crossover rate better than gene expression in other germ tissues, we compared samples containing meiotic cells to other samples from the same studies. We first examined the correlation of crossover rates and fetal ovary gene expression (Houmard et al. 2009), again using the set of tissue-specific genes. Female meiosis begins at ∼12 wk gestation (Houmard et al. 2009), and the mean correlation of samples taken after this time point (12–18 wk;  ; n = 12) is significantly more negative (P = 2.5 × 10−7; two-sided Welch's t-test) than that of samples before this time point (9–11 wk;
; n = 12) is significantly more negative (P = 2.5 × 10−7; two-sided Welch's t-test) than that of samples before this time point (9–11 wk;  ; n = 5). We also find that the mean correlation with expression from purified pachytene spermatocytes (
; n = 5). We also find that the mean correlation with expression from purified pachytene spermatocytes ( , n = 2) is significantly stronger (P = 2.0 × 10−3; two-sided Welch's t-test) than that of all other testis samples from the same study (
, n = 2) is significantly stronger (P = 2.0 × 10−3; two-sided Welch's t-test) than that of all other testis samples from the same study ( ; n = 6) (Chalmel et al. 2007). These results indicate that gene expression in meiotic cells is more strongly associated with a reduction in crossover rate than gene expression in other germ cells.
; n = 6) (Chalmel et al. 2007). These results indicate that gene expression in meiotic cells is more strongly associated with a reduction in crossover rate than gene expression in other germ cells.
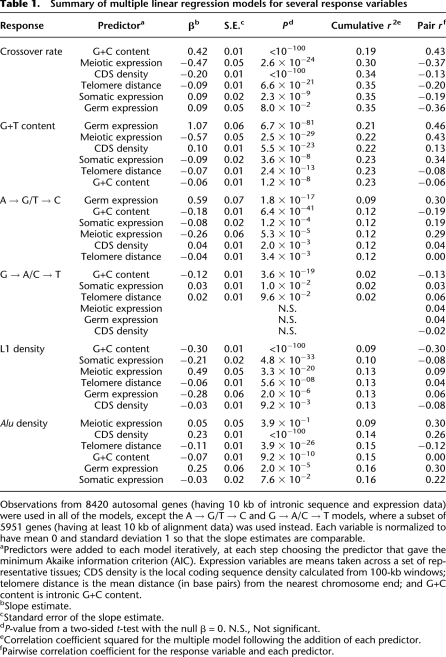
To complement our pairwise correlation analysis, we performed a multiple linear regression using a complete set of autosomal genes. This approach allows confounding effects from covariates to be removed, and the effect of gene expression in different tissues to be compared despite correlation across tissues. We used crossover rate as the response variable and mean expression from meiotic, germline (including both meiotic and non-meiotic cells), and somatic tissues as predictors. We included G+C content, coding sequence density, and telomere distance as potential confounding variables. The regression confirms that meiotic gene expression has a significant negative association with crossover rate (Table 1). In contrast, gene expression from somatic and germ cells show weak positive associations with crossover rate (Table 1).
Table 1.
Summary of multiple linear regression models for several response variables
Observations from 8420 autosomal genes (having 10 kb of intronic sequence and expression data) were used in all of the models, except the A → G/T → C and G → A/C → T models, where a subset of 5951 genes (having at least 10 kb of alignment data) was used instead. Each variable is normalized to have mean 0 and standard deviation 1 so that the slope estimates are comparable.
aPredictors were added to each model iteratively, at each step choosing the predictor that gave the minimum Akaike information criterion (AIC). Expression variables are means taken across a set of representative tissues; CDS density is the local coding sequence density calculated from 100-kb windows; telomere distance is the mean distance (in base pairs) from the nearest chromosome end; and G+C content is intronic G+C content.
bSlope estimate.
cStandard error of the slope estimate.
dP-value from a two-sided t-test with the null β = 0. N.S., Not significant.
eCorrelation coefficient squared for the multiple model following the addition of each predictor.
fPairwise correlation coefficient for the response variable and each predictor.
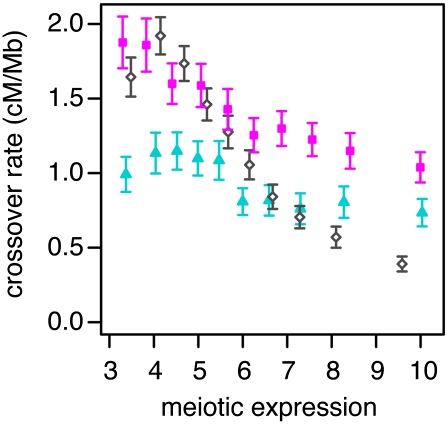
The fine-scale recombination map does not provide information on sex-specific recombination, and it may underestimate crossover rates near genes because it assumes a uniform effective population size over the length of each chromosome, whereas it is now known that natural selection has substantially reduced effective population sizes in genic regions (Cai et al. 2009; McVicker et al. 2009). Therefore, we also estimated rates using inferred crossover locations from a high-resolution linkage study, which are not affected by intrachromosomal variation in the effective population size (Coop et al. 2008). These rates also show a negative dependence on gene expression, and the effect appears somewhat stronger for female crossover rates (Fig. 2). Genes with high fetal ovary expression (upper 10%) have a female crossover rate that is 55.2% (±7.6%; 95% bootstrap confidence interval) that of genes with low expression (bottom 10%). Similarly, genes with high expression have male and sex-averaged LD-based crossover rates that are 73.8% (±12.8%) and 23.8% (±3.6%) that of genes with low expression, respectively. The crossover rate reductions are much stronger for the LD-based map than for the pedigree map, likely because the pedigree map's lower resolution smoothes rate estimates across transcription boundaries.
Figure 2.
Crossover rate as a function of gene expression. Crossover rates for each gene are estimated from male (blue triangles) and female (pink squares) pedigree-based linkage maps or a fine-scale linkage-disequilibrium map (open diamonds). Genes are binned by their meiotic expression (into 10 bins of 1239 genes each); each point gives the mean crossover rate of the genes in a bin. Meiotic expression estimates are from fetal ovaries from 12–18 wk gestation (female map), spermatocytes (male map), or an average of the two (LD-based map). Only autosomal genes of at least 10 kb in length were used in this analysis. Error bars are 95% confidence intervals.
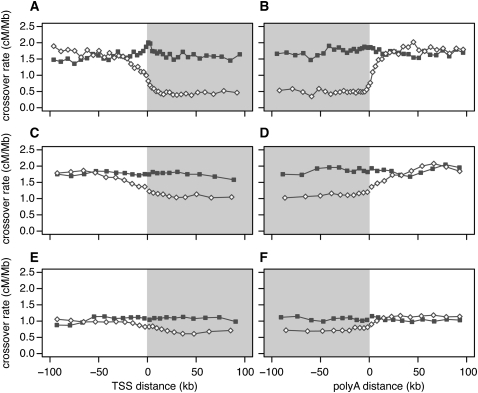
We next examined crossover rates, G+C content, and the density of a recombination hotspot motif as a function of distance from the transcription start site (TSS) or polyadenylation site, considering intergenic and genic regions separately (Fig. 3; Supplemental Fig. S6). Crossover rates are much lower across the entire length of genes with high meiotic expression but are indistinguishable from the flanking upstream and downstream regions for genes with low meiotic expression (Fig. 3). The lower crossover rates in genic regions could potentially be explained by crossover interference if active promoters have higher recombination rates, as in yeast (Wu and Lichten 1994). This does not appear to be the case, however, because crossover rates do not have a well-defined peak near the TSS. Furthermore, interference should reduce crossover rates symmetrically about recombination hotspots, but we do not see lower rates upstream of the TSS.
Figure 3.
Crossover rate as a function of distance from the nearest transcription start site (TSS), and the nearest polyadenylation site. To calculate distances, we used the 5′-most TSS and the 3′-most poly(A) site in genes having more than one such site. Gray shading denotes transcribed regions. (A,B) Linkage disequilibrium–based crossover rates for genes with high (open diamonds) and low (filled squares) meiotic gene expression. (C,D) Pedigree-based female crossover rates for genes with high (open diamonds) and low (filled squares) fetal ovary expression from 12 –18 wk gestation. (E,F) Pedigree-based male crossover rates for genes with high (open diamonds) and low (filled squares) spermatocyte expression.
McVean et al. (2004) proposed that crossover rates within genes may be lower because of selection against recombination-induced mutation; however, this cannot explain the differing correlation trends (negative vs. positive) for high tissue differentiation genes in germline and somatic tissues (or the differing slopes for meiotic vs. somatic expression in the multiple regression model). An alternative explanation for the negative correlation with germline expression could be that recombination during active transcription is deleterious, resulting in selection to cluster meiotically expressed genes in low-recombination regions or to reduce the frequency of recombination-promoting sequence motifs within them. Genes with high meiotic expression do not appear to have relocated to low-recombination regions, however, because their upstream and downstream crossover rates are very similar to those of genes with low meiotic expression (Fig. 3). Furthermore, the density of a known recombination hotspot motif (Myers et al. 2008) does not differ substantially between genes with high or low meiotic expression (Supplemental Fig. S6).
The simplest interpretation of our results is, instead, that gene expression in meiotic cells inhibits crossovers. The positive correlations with somatic expression must reflect a different process, probably selection for the beneficial effect of recombination events that bring together favorable alleles at different sites (Hill and Robertson 1966; Felsenstein 1974). Such selection presumably also acts on germline-expressed genes but is outweighed in these by the interference with transcription. Our results also help to interpret the recent finding (published while this manuscript was in preparation) that crossover rates are higher in genes with monoallelic expression and lower in genes with the greatest expression breadth (Necsulea et al. 2009b) since the latter genes are more likely to be expressed in meiotic cells. Note, however, that the negative correlation with gene expression breadth is not sufficient to reject the selective hypothesis on its own, because broadly or highly expressed genes may also be under the strongest selection (Urrutia and Hurst 2003).
There are three broad mechanisms by which gene expression could inhibit crossover: by suppressing the initial formation of recombination-initiating DSBs, by inducing repair of DSBs before they are processed, or by forcing resolution of recombination intermediates by a noncrossover pathway. The latter hypothesis would predict that noncrossover recombination (gene conversion) is preferred over crossover recombination in genes that are expressed in meiotic cells. Suggestively, in yeast, some genes that are up-regulated during meiosis are biased toward noncrossover recombination (Mancera et al. 2008).
Rather than promoting resolution of DSBs by noncrossover recombination, transcription could prevent the formation of DSBs directly (e.g., by the displacement of the meiotic recombination protein SPO11 by RNA polymerase) or indirectly through epigenetic changes associated with transcription. Two possible epigenetic changes are histone marks (Buard et al. 2009), some of which are associated with active hotspots in mouse, and DNA methylation, which may be associated with crossover rate (Sigurdsson et al. 2009). In C. elegans, condensin has been shown to play a role in the distribution of DSBs, suggesting they may preferentially occur in condensed chromatin (Mets and Meyer 2009). Since transcribed regions tend to be less condensed, they may have fewer DSBs. Another possibility is that the action of transcription-coupled repair (Hanawalt and Spivak 2008) eliminates DNA damage in transcribed regions before it can recruit the recombination machinery (Pauklin et al. 2009).
Strand-asymmetric substitutions are correlated with germline gene expression
Transcribed regions of the human genome have strand-biased compositions and substitution rates, which may be a byproduct of germline transcription (Green et al. 2003). To investigate this possibility, we calculated the G+T content and substitution rate ratios from the coding (nontranscribed) strand of each gene (Supplemental Table S4). The mean G+T content of genes on the autosomes, on the sex chromosomes, and in the pseudo-autosomal region of X and Y are all significantly greater than 50%. The A → G/T → C and G → A/C → T substitution rate ratios are also significantly greater than 1 for the autosomes and for chromosome X.
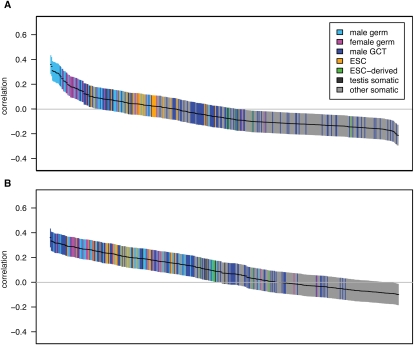
We analyzed the relationship between transcription and strand-biased substitution by calculating pairwise correlations with the genes with high tissue differentiation (Fig. 4). The mean germline tissue correlations are much greater than those from somatic tissues (germ: 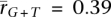 and
and 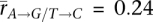 ; somatic:
; somatic: 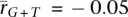 and
and 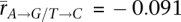 ; PG+T = 1.1 × 10−27, PA→G/T→C = 1.6 × 10−26; two-sided Welch's t-test). The strongest correlation with both G+T content and A → G/T → C asymmetry occurs for spermatogonial stem cells (rG+T = 0.61, rA→G / T→C = 0.45), and is much stronger than the correlations previously observed between G+T content and average housekeeping gene expression (rG+T = 0.28) (Majewski 2003) and G+T content and gene expression in testis (rG+T = 0.16) (Comeron 2004). As spermatogonial stem cells may undergo the greatest number of germ cell divisions (Drost and Lee 1995), gene expression in these cells may contribute disproportionately to the compositional bias. As with crossover rate, these results are consistent across studies and microarray platforms (Supplemental Note S1).
; PG+T = 1.1 × 10−27, PA→G/T→C = 1.6 × 10−26; two-sided Welch's t-test). The strongest correlation with both G+T content and A → G/T → C asymmetry occurs for spermatogonial stem cells (rG+T = 0.61, rA→G / T→C = 0.45), and is much stronger than the correlations previously observed between G+T content and average housekeeping gene expression (rG+T = 0.28) (Majewski 2003) and G+T content and gene expression in testis (rG+T = 0.16) (Comeron 2004). As spermatogonial stem cells may undergo the greatest number of germ cell divisions (Drost and Lee 1995), gene expression in these cells may contribute disproportionately to the compositional bias. As with crossover rate, these results are consistent across studies and microarray platforms (Supplemental Note S1).
Figure 4.
Pairwise correlations between gene expression and strand-biased composition and substitution rates for high tissue differentiation genes. The figure layout is as described in Figure 1. Correlations are between gene expression and G+T content (n = 507) (A) or A → G/T → C substitution asymmetry (n = 346) (B). For correlations with the complete gene set, see Supplemental Figure S2.
In contrast to the A → G/T → C asymmetry, the correlation between gene expression and G → A/C → T substitution asymmetry is very weak (Table 1; Supplemental Fig. S2; Supplemental Tables S2, S4). The mean germ tissue correlation is 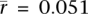 for tissue-specific genes, and only 11 of the 64 germ correlations are significantly greater than 0 (and none of the 182 somatic samples are). This suggests that this asymmetry either arises by a different mechanism or has a more subtle relationship with gene expression.
for tissue-specific genes, and only 11 of the 64 germ correlations are significantly greater than 0 (and none of the 182 somatic samples are). This suggests that this asymmetry either arises by a different mechanism or has a more subtle relationship with gene expression.
We next performed multiple linear regression using G+T content and A → G/T → C asymmetry as response variables (Table 1). Germline gene expression retains a positive slope in both the G+T content and A → G/T → C asymmetry models, whereas the somatic and meiotic slopes become negative. The correlation of the A → G/T → C model is weaker than the G+T content model (r2 = 0.12 vs. r2 = 0.23), but this may at least in part be due to statistical noise from the smaller number of observations.
If the substitution asymmetry within genes arises from natural selection favoring an asymmetric base composition or from a strand-specific gene conversion bias, then it should skew allele frequencies for some bases relative to their complements. Webster and Smith (2004) have previously reported such a strand asymmetry in the allele frequencies of human polymorphisms. We examined derived allele frequencies using several large data sets (The International HapMap Consortium 2007; Keinan et al. 2007; NIEHS SNPs, http://egp.gs.washington.edu/; SeattleSNPs, http://pga.gs.washington.edu), and although we observed the previously reported fixation bias toward G and C alleles (Eyre-Walker 1999), we did not find a significant strand bias in allele frequencies (Supplemental Fig. S7; Supplemental Table S5). As the results in Webster and Smith (2004) are based on much less data and are only marginally significant, they may be spurious. We conclude that the substitution bias in transcribed regions is the result of biased mutation, not biased fixation.
Transposable element density is positively correlated with germline gene expression
To examine the relationship between transposable element insertion and gene expression, we assigned each gene a transposable element density reflecting intronic instances of the two most frequent transposable elements, Alu and L1. We then computed the correlations between Alu or L1 density and gene expression in the subset of genes with high tissue differentiation (Fig. 5). The mean correlation of L1 density and gene expression is positive in germ tissues (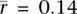 , P = 1.7 × 10−14; two-sided t-test; rmax = 0.36) but is negative in somatic tissues (
, P = 1.7 × 10−14; two-sided t-test; rmax = 0.36) but is negative in somatic tissues ( , P = 4.1 × 10−51; two-sided t-test). Alu density is positively correlated with gene expression in germ tissues (
, P = 4.1 × 10−51; two-sided t-test). Alu density is positively correlated with gene expression in germ tissues (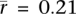 , P = 3.9 × 10−30; two-sided t-test; rmax = 0.36), but the correlation is not significantly different from 0 in somatic tissues (
, P = 3.9 × 10−30; two-sided t-test; rmax = 0.36), but the correlation is not significantly different from 0 in somatic tissues (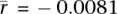 , P = 0.15; two-sided t-test). The difference between somatic and germline correlations appears to explain why Alu density was previously found to be correlated with gene expression breadth but not with expression level (Urrutia et al. 2008).
, P = 0.15; two-sided t-test). The difference between somatic and germline correlations appears to explain why Alu density was previously found to be correlated with gene expression breadth but not with expression level (Urrutia et al. 2008).
Figure 5.
Pairwise correlations between gene expression and transposable element density for high tissue differentiation genes. The figure layout is as described in Figure 1. Correlations are between gene expression and L1 density (A) or Alu density (B) (n = 507). For correlations with the complete gene set, see Supplemental Figure S3.
Multiple linear regression confirms these results (Table 1). L1 density retains a positive association with gene expression in meiotic cells but has a negative association with gene expression in germline and somatic cells once other variables are added to the model. Similarly, in the Alu density model, mean expression in germ cells retains a positive slope, but the slopes for expression in somatic and meiotic cells are not significantly different from 0.
Alu and L1 elements within genes are more often in the antisense orientation (Smit 1999; Medstrand et al. 2002; Glusman et al. 2006). To test whether this pattern reflects an insertional preference related to transcription, we computed correlations between the orientation bias of these elements and gene expression (Supplemental Fig. S4; Supplemental Note S2). We found only a slight correlation with the orientation bias of Alus (and none with L1s), suggesting that this pattern is largely independent of gene expression and may instead reflect selection against elements in the sense orientation, as has been previously suggested (Glusman et al. 2006).
The positive correlation between germline or meiotic gene expression and Alu and L1 densities suggests that transposable elements preferentially integrate into transcriptionally active or open chromatin regions in the germline. This conclusion is supported by the previous observations that most transposable elements are enriched within intronic sequences (Sela et al. 2007) and that Alu density is higher near housekeeping genes than tissue-specific genes (Ganapathi et al. 2005; Eller et al. 2007; Urrutia et al. 2008). In further support of this idea, we find the strongest L1 density correlation in pachytene spermatocytes (r = 0.36), where, in mice, L1 proteins and RNA are specifically coexpressed (Branciforte and Martin 1994). The negative correlations between L1 density and somatic gene expression may result from purifying selection against intronic L1 elements and suggests an antagonistic evolutionary relationship whereby many L1s have become fixed in germline-expressed genes despite selection against them.
Conclusion
Our results reveal that the key evolutionary processes of mutation and recombination are influenced in unexpected ways by gene expression in germline cells. Germline transcription affects mutation by promoting transposable element insertion within the transcribed region and by causing an asymmetry in point mutation patterns. Transcription in meiotic cells suppresses recombination. These effects appear to be consequences of gene expression rather than the result of selection; in fact, our results for somatic genes suggest that selection acts to remove transposable element insertions and to favor crossovers within genes, implying that the observed trends for germline-expressed genes are somewhat deleterious. In combination our findings point to a novel role for germline cell molecular biology in genome evolution.
Methods
Gene annotations
The genomic locations of human transcripts were obtained from the University of California at Santa Cruz (UCSC) “known gene” annotations (Hsu et al. 2006), which we downloaded from the UCSC Genome Informatics website (Kent et al. 2002) in September 2007. Overlapping transcripts (i.e., alternate splice forms) on the same strand were combined into single genes.
Genome sequences and alignments
We downloaded the human genome sequence (hg18) and pairwise human/chimp (panTro2) and human/macaque (rheMac2) alignments from UCSC. The alignments were processed to make them best-reciprocal and were extensively filtered for sequence and alignment quality using the methods described in McVicker et al. (2009). The filtered pairwise alignments were then combined to create a three-species multiple alignment.
G+T content
G+T content was estimated for each gene by counting intronic nucleotides on the coding strand. Sites within 100 bp of any annotated exon were excluded to avoid the effects of selection acting on exons or splice sites. Repetitive sequences identified by RepeatMasker (http://www.repeatmasker.org) were excluded because recently inserted repeats are unlikely to be at compositional equilibrium. CpG islands, defined by annotations downloaded from UCSC, were also omitted because of their unusual sequence composition. Only genes with at least 10 kb of filtered sequence data were used for analyses.
Substitution rates
Substitution rates were estimated by parsimony using the human/chimp/macaque alignment. Each gene was assigned a substitution rate calculated from intronic substitutions that were inferred to be on either the chimpanzee or human branches (using macaque as the outgroup). Rates were calculated from the perspective of the coding strand, and sites in repeats or within 100 bp of any exon were excluded. Sites adjacent to mismatches, Ns, or alignment gaps were also excluded. Sites that were part of a CpG dinucleotide in any of the three species were excluded because CpGs are hypermutable and their substitution rates do not appear to be strand-biased (Polak and Arndt 2008). Substitution rate ratios were log2-transformed because the log ratios are symmetric about 0 and show a stronger linear relationship to other variables such as G+T content. Only genes with at least 10 kb of filtered alignment data were used for analyses.
Allele frequencies
See Supplemental Methods.
Crossover rates
Fine-scale LD-based estimates of crossover rate were obtained from a recombination map constructed from HapMap phase II polymorphism data (The International HapMap Consortium 2007) using the method of Myers et al. (2005) (downloaded from http://www.hapmap.org, last updated June 25, 2008). Crossover rates within map intervals were assumed to be constant, and each site within an interval was assigned the same rate.
Sex-specific pedigree-based crossover rate estimates were calculated using a similar procedure to that of Coop et al. (2008). We obtained genomic intervals of directly inferred crossover events from Coop et al. (2008) and assigned each site within an interval a fractional crossover count, 1/L, where L is the length of the interval. The crossover rate for each site was then calculated by summing fractional counts from overlapping intervals and dividing by the total number of meioses.
For correlation analyses, each gene was assigned an average crossover rate by taking the mean crossover rate of all sites spanned by the gene. To improve the accuracy of the estimates, only genes with a length of at least 10 kb were included in these analyses.
Gene expression
We obtained expression data for 409 microarray experiments in 12 studies representing a wide variety of germ and somatic tissues (Supplemental Table S1; Sato et al. 2003; Su et al. 2004; Barberi et al. 2005; Ge et al. 2005; Perez-Iratxeta et al. 2005; Skottman et al. 2005; Kocabas et al. 2006; Korkola et al. 2006; Looijenga et al. 2006; Chalmel et al. 2007; Houmard et al. 2009; Wu et al. 2009). As these studies used two different microarray platforms (Affymetrix hgu133plus2 and hgu133A), we only considered probesets shared by both arrays (and in some analyses we only used the hgu133plus2 data). The raw intensity data from these studies were background-adjusted, normalized, and summarized using the RMA algorithm (Bolstad et al. 2003; Irizarry et al. 2003a,b) as implemented in the Bioconductor software package (Gentleman et al. 2004).
We assigned probesets to genes using identifiers from version 26 of Affymetrix's array annotation file and UCSC's kgAlias file. Probesets were discarded if they mapped to multiple different genes, failed to map to any genes, were flagged as being incomplete (probesets ending with “i_at”), or were designed with a reduced set of selection rules (probesets ending with “r_at”). In total, 36,675 out of 54,676 probesets were assigned to 17,369 genes for the hgu133plus2 data (19,038 probesets to 11,738 genes when the 22,284 common hgu133A/plus2 probesets were used). Following probeset assignment, each gene was given an expression value by taking the mean RMA value across all probesets assigned to that gene (since RMA values are log2-transformed, this is equivalent to a geometric mean of raw intensities).
For some analyses (e.g., multiple regression and examination of crossover rate as a function of gene expression), it was preferable to use expression data from more genes at the sacrifice of some tissues, so we combined expression data from a subset of the studies that used the hgu133plus2 array (Kocabas et al. 2006; Chalmel et al. 2007; Houmard et al. 2009). In these analyses we also combined replicate experiments by taking the mean of the log2 expression values. Fetal testis data were combined across all gestational time points from 9 to 20 wk because hierarchical clustering revealed that all 17 of these samples have very similar expression patterns (Supplemental Fig. S8). Fetal ovary data were divided into two groups, 9–11 wk gestation and 12–18 wk gestation, and the samples within each group were combined; the ovarian samples were divided this way because meiotic genes are up-regulated beginning at week 12 (Houmard et al. 2009), and hierarchical clustering placed the ovarian samples into two distinct groups (Supplemental Fig. S8). Multiple regression analyses conducted prior to the merging of gene expression replicates yielded results that were very similar to those from the merged expression data set.
To identify genes with high tissue differentiation (i.e., more tissue-specific patterns of expression), we combined replicate experiments by taking the mean expression value, and then calculated the Shannon entropy of each gene's expression across tissues (Schug et al. 2005). We then defined our high tissue differentiation gene set as the 10% of genes with the lowest entropy.
To compare germline and somatic tissues, we considered all tissues that contain germ cells to be “germline” (e.g., whole testis) and all other tissues to be “somatic,” with the exception of germ cell tumors, embryonic stem cells, and immortalized cell lines, which were excluded. We calculated P-values for differences in mean correlations using two-sided Welch's t-tests. To test whether mean correlations were different from 0, we performed two-sided one-sample t-tests.
See Supplemental Note S1 for a discussion of microarray batch effects.
Multiple linear regression
We performed multiple linear regression using a technique similar to that described by Hellmann et al. (2005). We normalized all variables to have a mean of 0 and a standard deviation of 1 so that the estimated slopes are comparable across predictors. We then constructed linear models in a stepwise fashion by adding the predictor variable that gave the minimum AIC at each iteration. To perform this procedure, we used the stepAIC function from R's (R Development Core Team 2008) MASS package (Venables and Ripley 2002).
Each gene was assigned a crossover rate from the LD-based fine-scale recombination map, as described above. These crossover rate estimates were log2-transformed for the regression analyses because this gave a more linear relationship with the other variables in the model. A small value (5.0 × 10−4 cM/Mb, equal to one-half the minimum non-zero crossover rate) was added to all crossover rate estimates to avoid taking the log of 0.
To calculate coding sequence (CDS) density, we first calculated a density for each site in the genome using a sliding 100-kb window. We then defined the CDS density of a gene as the mean taken across all sites spanned by the gene.
G+C content was assigned to each gene using intronic sequences, in the same manner as described for G+T content above.
Mean germ, meiotic, and somatic expression for each gene was estimated using microarray data from three studies, processed as described above (Kocabas et al. 2006; Chalmel et al. 2007; Houmard et al. 2009). Mean germ expression was calculated from seminiferous tubule, spermatid, spermatocytes, whole testis, oocyte, fetal ovary (9–11 wk gestation), fetal ovary (12–18 wk gestation), and fetal testis. Mean meiotic expression was calculated from tissues containing early meiotic cells (oocytes were not included as they are late meiotic cells): spermatocytes, whole testis, fetal ovary (12–18 wk gestation), and seminiferous tubule. Mean somatic expression was calculated from chrondrocytes, vascular smooth muscle, and somatic reference (mRNA from 10 somatic tissues).
Acknowledgments
This work was supported by a Natural Sciences and Engineering Research Council of Canada Postgraduate Scholarship to G.M., and by the Howard Hughes Medical Institute.
Footnotes
[Supplemental material is available online at http://www.genome.org.]
Article published online before print. Article and publication date are at http://www.genome.org/cgi/doi/10.1101/gr.106666.110.
References
- Barberi T, Willis LM, Socci ND, Studer L 2005. Derivation of multipotent mesenchymal precursors from human embryonic stem cells. PLoS Med 2: e161 doi: 10.1371/journal.pmed.0020161 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bolstad BM, Irizarry RA, Astrand M, Speed TP 2003. A comparison of normalization methods for high density oligonucleotide array data based on variance and bias. Bioinformatics 19: 185–193 [DOI] [PubMed] [Google Scholar]
- Branciforte D, Martin SL 1994. Developmental and cell type specificity of LINE-1 expression in mouse testis: Implications for transposition. Mol Cell Biol 14: 2584–2592 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buard J, Barthès P, Grey C, de Massy B 2009. Distinct histone modifications define initiation and repair of meiotic recombination in the mouse. EMBO J 28: 2616–2624 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cai JJ, Macpherson JM, Sella G, Petrov DA 2009. Pervasive hitchhiking at coding and regulatory sites in humans. PLoS Genet 5: e1000336 doi: 10.1371/journal.pgen.1000336 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chalmel F, Rolland AD, Niederhauser-Wiederkehr C, Chung SS, Demougin P, Gattiker A, Moore J, Patard JJ, Wolgemuth DJ, Jégou B, et al. 2007. The conserved transcriptome in human and rodent male gametogenesis. Proc Natl Acad Sci 104: 8346–8351 [DOI] [PMC free article] [PubMed] [Google Scholar]
- The Chimpanzee Sequencing and Analysis Consortium 2005. Initial sequence of the chimpanzee genome and comparison with the human genome. Nature 437: 69–87 [DOI] [PubMed] [Google Scholar]
- Comeron JM 2004. Selective and mutational patterns associated with gene expression in humans: Influences on synonymous composition and intron presence. Genetics 167: 1293–1304 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coop G, Wen X, Ober C, Pritchard JK, Przeworski M 2008. High-resolution mapping of crossovers reveals extensive variation in fine-scale recombination patterns among humans. Science 319: 1395–1398 [DOI] [PubMed] [Google Scholar]
- Donis-Keller H, Green P, Helms C, Cartinhour S, Weiffenbach B, Stephens K, Keith TP, Bowden DW, Smith DR, Lander ES 1987. A genetic linkage map of the human genome. Cell 51: 319–337 [DOI] [PubMed] [Google Scholar]
- Drost JB, Lee WR 1995. Biological basis of germline mutation: Comparisons of spontaneous germline mutation rates among Drosophila, mouse, and human. Environ Mol Mutagen 25: 48–64 [DOI] [PubMed] [Google Scholar]
- Duret L 2002. Evolution of synonymous codon usage in metazoans. Curr Opin Genet Dev 12: 640–649 [DOI] [PubMed] [Google Scholar]
- Eller CD, Regelson M, Merriman B, Nelson S, Horvath S, Marahrens Y 2007. Repetitive sequence environment distinguishes housekeeping genes. Gene 390: 153–165 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eyre-Walker A 1993. Recombination and mammalian genome evolution. Proc Biol Sci 252: 237–243 [DOI] [PubMed] [Google Scholar]
- Eyre-Walker A 1999. Evidence of selection on silent site base composition in mammals: Potential implications for the evolution of isochores and junk DNA. Genetics 152: 675–683 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Felsenstein J 1974. The evolutionary advantage of recombination. Genetics 78: 737–756 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Francino MP, Ochman H 2001. Deamination as the basis of strand-asymmetric evolution in transcribed Escherichia coli sequences. Mol Biol Evol 18: 1147–1150 [DOI] [PubMed] [Google Scholar]
- Francino MP, Chao L, Riley MA, Ochman H 1996. Asymmetries generated by transcription-coupled repair in enterobacterial genes. Science 272: 107–109 [DOI] [PubMed] [Google Scholar]
- Fullerton SM, Bernardo Carvalho A, Clark AG 2001. Local rates of recombination are positively correlated with GC content in the human genome. Mol Biol Evol 18: 1139–1142 [DOI] [PubMed] [Google Scholar]
- Ganapathi M, Srivastava P, Das Sutar SK, Kumar K, Dasgupta D, Pal Singh G, Brahmachari V, Brahmachari SK 2005. Comparative analysis of chromatin landscape in regulatory regions of human housekeeping and tissue specific genes. BMC Bioinformatics 6: 126 doi: 10.1186/1471-2105-6-126 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ganko EW, Bhattacharjee V, Schliekelman P, McDonald JF 2003. Evidence for the contribution of LTR retrotransposons to C. elegans gene evolution. Mol Biol Evol 20: 1925–1931 [DOI] [PubMed] [Google Scholar]
- Ge X, Yamamoto S, Tsutsumi S, Midorikawa Y, Ihara S, Wang SM, Aburatani H 2005. Interpreting expression profiles of cancers by genome-wide survey of breadth of expression in normal tissues. Genomics 86: 127–141 [DOI] [PubMed] [Google Scholar]
- Gentleman RC, Carey VJ, Bates DM, Bolstad B, Dettling M, Dudoit S, Ellis B, Gautier L, Ge Y, Gentry J, et al. 2004. Bioconductor: Open software development for computational biology and bioinformatics. Genome Biol 5: R80 doi: 10.1186/gb-2004-5-10-r80 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gerton JL, DeRisi J, Shroff R, Lichten M, Brown PO, Petes TD 2000. Global mapping of meiotic recombination hotspots and coldspots in the yeast Saccharomyces cerevisiae. Proc Natl Acad Sci 97: 11383–11390 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glusman G, Qin S, El-Gewely MR, Siegel AF, Roach JC, Hood L, Smit AF 2006. A third approach to gene prediction suggests thousands of additional human transcribed regions. PLoS Comput Biol 2: e18 doi: 10.1371/journal.pcbi.0020018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Green P, Ewing B, Miller W, Thomas PJ, NISC Comparative Sequencing Program, Green ED 2003. Transcription-associated mutational asymmetry in mammalian evolution. Nat Genet 33: 514–517 [DOI] [PubMed] [Google Scholar]
- Grover D, Majumder PP, Rao CB, Brahmachari SK, Mukerji M 2003. Nonrandom distribution of Alu elements in genes of various functional categories: Insight from analysis of human chromosomes 21 and 22. Mol Biol Evol 20: 1420–1424 [DOI] [PubMed] [Google Scholar]
- Grover D, Mukerji M, Bhatnagar P, Kannan K, Brahmachari SK 2004. Alu repeat analysis in the complete human genome: Trends and variations with respect to genomic composition. Bioinformatics 20: 813–817 [DOI] [PubMed] [Google Scholar]
- Hanawalt PC, Spivak G 2008. Transcription-coupled DNA repair: Two decades of progress and surprises. Nat Rev Mol Cell Biol 9: 958–970 [DOI] [PubMed] [Google Scholar]
- Hellmann I, Prüfer K, Ji H, Zody MC, Pääbo S, Ptak SE 2005. Why do human diversity levels vary at a megabase scale? Genome Res 15: 1222–1231 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hill WG, Robertson A 1966. The effect of linkage on limits to artificial selection. Genet Res 8: 269–294 [PubMed] [Google Scholar]
- Houmard B, Small C, Yang L, Naluai-Cecchini T, Cheng E, Hassold T, Griswold M 2009. Global gene expression in the human fetal testis and ovary. Biol Reprod 81: 438–443 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hsu F, Kent WJ, Clawson H, Kuhn RM, Diekhans M, Haussler D 2006. The UCSC Known Genes. Bioinformatics 22: 1036–1046 [DOI] [PubMed] [Google Scholar]
- Huvet M, Nicolay S, Touchon M, Audit B, d'Aubenton-Carafa Y, Arneodo A, Thermes C 2007. Human gene organization driven by the coordination of replication and transcription. Genome Res 17: 1278–1285 [DOI] [PMC free article] [PubMed] [Google Scholar]
- The International HapMap Consortium 2007. A second generation human haplotype map of over 3.1 million SNPs. Nature 449: 851–861 [DOI] [PMC free article] [PubMed] [Google Scholar]
- International Human Genome Sequencing Consortium 2001. Initial sequencing and analysis of the human genome. Nature 409: 860–921 [DOI] [PubMed] [Google Scholar]
- Irizarry RA, Bolstad BM, Collin F, Cope LM, Hobbs B, Speed TP 2003a. Summaries of Affymetrix GeneChip probe level data. Nucleic Acids Res 31: e15 doi: 10.1093/nar/gng015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Irizarry RA, Hobbs B, Collin F, Beazer-Barclay YD, Antonellis KJ, Scherf U, Speed TP 2003b. Exploration, normalization, and summaries of high density oligonucleotide array probe level data. Biostatistics 4: 249–264 [DOI] [PubMed] [Google Scholar]
- Keinan A, Mullikin JC, Patterson N, Reich D 2007. Measurement of the human allele frequency spectrum demonstrates greater genetic drift in East Asians than in Europeans. Nat Genet 39: 1251–1255 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kent WJ, Sugnet CW, Furey TS, Roskin KM, Pringle TH, Zahler AM, Haussler D 2002. The Human Genome Browser at UCSC. Genome Res 12: 996–1006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kirkpatrick DT, Fan Q, Petes TD 1999a. Maximal stimulation of meiotic recombination by a yeast transcription factor requires the transcription activation domain and a DNA-binding domain. Genetics 152: 101–115 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kirkpatrick DT, Wang YH, Dominska M, Griffith JD, Petes TD 1999b. Control of meiotic recombination and gene expression in yeast by a simple repetitive DNA sequence that excludes nucleosomes. Mol Cell Biol 19: 7661–7671 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kocabas AM, Crosby J, Ross PJ, Otu HH, Beyhan Z, Can H, Tam WL, Rosa GJ, Halgren RG, Lim B, et al. 2006. The transcriptome of human oocytes. Proc Natl Acad Sci 103: 14027–14032 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kon N, Krawchuk MD, Warren BG, Smith GR, Wahls WP 1997. Transcription factor Mts1/Mts2 (Atf1/Pcr1, Gad7/Pcr1) activates the M26 meiotic recombination hotspot in Schizosaccharomyces pombe. Proc Natl Acad Sci 94: 13765–13770 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kong A, Gudbjartsson DF, Sainz J, Jonsdottir GM, Gudjonsson SA, Richardsson B, Sigurdardottir S, Barnard J, Hallbeck B, Masson G, et al. 2002. A high-resolution recombination map of the human genome. Nat Genet 31: 241–247 [DOI] [PubMed] [Google Scholar]
- Korkola JE, Houldsworth J, Chadalavada RS, Olshen AB, Dobrzynski D, Reuter VE, Bosl GJ, Chaganti RS 2006. Down-regulation of stem cell genes, including those in a 200-kb gene cluster at 12p13.31, is associated with in vivo differentiation of human male germ cell tumors. Cancer Res 66: 820–827 [DOI] [PubMed] [Google Scholar]
- Looijenga LH, Hersmus R, Gillis AJ, Pfundt R, Stoop HJ, van Gurp RJ, Veltman J, Beverloo HB, van Drunen E, van Kessel AG, et al. 2006. Genomic and expression profiling of human spermatocytic seminomas: Primary spermatocyte as tumorigenic precursor and DMRT1 as candidate chromosome 9 gene. Cancer Res 66: 290–302 [DOI] [PubMed] [Google Scholar]
- Majewski J 2003. Dependence of mutational asymmetry on gene-expression levels in the human genome. Am J Hum Genet 73: 688–692 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mancera E, Bourgon R, Brozzi A, Huber W, Steinmetz LM 2008. High-resolution mapping of meiotic crossovers and non-crossovers in yeast. Nature 454: 479–485 [DOI] [PMC free article] [PubMed] [Google Scholar]
- McVean GA, Myers SR, Hunt S, Deloukas P, Bentley DR, Donnelly P 2004. The fine-scale structure of recombination rate variation in the human genome. Science 304: 581–584 [DOI] [PubMed] [Google Scholar]
- McVicker G, Gordon D, Davis C, Green P 2009. Widespread genomic signatures of natural selection in hominid evolution. PLoS Genet 5: e1000471 doi: 10.1371/journal.pgen.1000471 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Medstrand P, van de Lagemaat LN, Mager DL 2002. Retroelement distributions in the human genome: Variations associated with age and proximity to genes. Genome Res 12: 1483–1495 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mets DG, Meyer BJ 2009. Condensins regulate meiotic DNA break distribution, thus crossover frequency, by controlling chromosome structure. Cell 139: 21–23 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Myers S, Bottolo L, Freeman C, McVean G, Donnelly P 2005. A fine-scale map of recombination rates and hotspots across the human genome. Science 310: 321–324 [DOI] [PubMed] [Google Scholar]
- Myers S, Freeman C, Auton A, Donnelly P, McVean G 2008. A common sequence motif associated with recombination hot spots and genome instability in humans. Nat Genet 139: 1124–1129 [DOI] [PubMed] [Google Scholar]
- Necsulea A, Guillet C, Cadoret JC, Prioleau MN, Duret L 2009a. The relationship between DNA replication and human genome organization. Mol Biol Evol 26: 729–741 [DOI] [PubMed] [Google Scholar]
- Necsulea A, Sémon M, Duret L, Hurst LD 2009b. Monoallelic expression and tissue specificity are associated with high crossover rates. Trends Genet 25: 519–522 [DOI] [PubMed] [Google Scholar]
- Pauklin S, Burkert JS, Martin J, Osman F, Weller S, Boulton SJ, Whitby MC, Petersen-Mahrt SK 2009. Alternative induction of meiotic recombination from single-base lesions of DNA deaminases. Genetics 182: 41–54 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perez-Iratxeta C, Palidwor G, Porter CJ, Sanche NA, Huska MR, Suomela BP, Muro EM, Krzyzanowski PM, Hughes E, Campbell PA, et al. 2005. Study of stem cell function using microarray experiments. FEBS Lett 579: 1795–1801 [DOI] [PubMed] [Google Scholar]
- Pleasance ED, Stephens PJ, O'Meara S, McBride DJ, Meynert A, Jones D, Lin ML, Beare D, Lau KW, Greenman C, et al. 2010. A small-cell lung cancer genome with complex signatures of tobacco exposure. Nature 463: 184–190 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Polak P, Arndt PF 2008. Transcription induces strand specific mutations at the 5′ end of human genes. Genome Res 18: 1216–1223 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Polak P, Arndt PF 2009. Long-range bidirectional strand asymmetries originate at CpG islands in the human genome. Genome Biol Evol 1: 189–197 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qu HQ, Lawrence SG, Guo F, Majewski J, Polychronakos C 2006. Strand bias in complementary single-nucleotide polymorphisms of transcribed human sequences: Evidence for functional effects of synonymous polymorphisms. BMC Genomics 7: 213 doi: 10.1186/1471-2164-7-213 [DOI] [PMC free article] [PubMed] [Google Scholar]
- R Development Core Team 2008. R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria [Google Scholar]
- Rubin AF, Green P 2009. Mutation patterns in cancer genomes. Proc Natl Acad Sci 106: 21766–21770 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sato N, Sanjuan IM, Heke M, Uchida M, Naef F, Brivanlou AH 2003. Molecular signature of human embryonic stem cells and its comparison with the mouse. Dev Biol 260: 404–413 [DOI] [PubMed] [Google Scholar]
- Schug J, Schuller WP, Kappen C, Salbaum JM, Bucan M, Stoeckert CJ 2005. Promoter features related to tissue specificity as measured by Shannon entropy. Genome Biol 6: R33 doi: 10.1186/gb-2005-6-4-r33 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sela N, Mersch B, Gal-Mark N, Lev-Maor G, Hotz-Wagenblatt A, Ast G 2007. Comparative analysis of transposed element insertion within human and mouse genomes reveals Alu's unique role in shaping the human transcriptome. Genome Biol 8: R127 doi: 10.1186/gb-2007-8-6-r127 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sigurdsson MI, Smith AV, Bjornsson HT, Jonsson JJ 2009. HapMap methylation-associated SNPs, markers of germline DNA methylation, positively correlate with regional levels of human meiotic recombination. Genome Res 19: 581–589 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Skottman H, Mikkola M, Lundin K, Olsson C, Strömberg AM, Tuuri T, Otonkoski T, Hovatta O, Lahesmaa R 2005. Gene expression signatures of seven individual human embryonic stem cell lines. Stem Cells 23: 1343–1356 [DOI] [PubMed] [Google Scholar]
- Smit AF 1996. The origin of interspersed repeats in the human genome. Curr Opin Genet Dev 6: 743–748 [DOI] [PubMed] [Google Scholar]
- Smit AF 1999. Interspersed repeats and other mementos of transposable elements in mammalian genomes. Curr Opin Genet Dev 9: 657–663 [DOI] [PubMed] [Google Scholar]
- Soriano P, Meunier-Rotival M, Bernardi G 1983. The distribution of interspersed repeats is nonuniform and conserved in the mouse and human genomes. Proc Natl Acad Sci 80: 1816–1820 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Su AI, Wiltshire T, Batalov S, Lapp H, Ching KA, Block D, Zhang J, Soden R, Hayakawa M, Kreiman G, et al. 2004. A gene atlas of the mouse and human protein-encoding transcriptomes. Proc Natl Acad Sci 101: 6062–6067 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun H, Treco D, Schultes NP, Szostak JW 1989. Double-strand breaks at an initiation site for meiotic gene conversion. Nature 338: 87–90 [DOI] [PubMed] [Google Scholar]
- Touchon M, Nicolay S, Arneodo A, d'Aubenton-Carafa Y, Thermes C 2003. Transcription-coupled TA and GC strand asymmetries in the human genome. FEBS Lett 555: 579–582 [DOI] [PubMed] [Google Scholar]
- Touchon M, Nicolay S, Audit B Brodie of Brodie EB, d'Aubenton-Carafa Y, Arneodo A, Thermes C 2005. Replication-associated strand asymmetries in mammalian genomes: Toward detection of replication origins. Proc Natl Acad Sci 102: 9836–9841 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsirigos A, Rigoutsos I 2009. Alu and B1 repeats have been selectively retained in the upstream and intronic regions of genes of specific functional classes. PLoS Comput Biol 5: e1000610 doi: 10.1371/journal.pcbi.1000610 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Urrutia AO, Hurst LD 2003. The signature of selection mediated by expression on human genes. Genome Res 13: 2260–2264 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Urrutia AO, Ocaña LB, Hurst LD 2008. Do Alu repeats drive the evolution of the primate transcriptome? Genome Biol 9: R25 doi: 10.1186/gb-2008-9-2-r25 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Venables WN, Ripley BD 2002. Modern applied statistics with S. Springer, New York [Google Scholar]
- Webster MT, Smith NG 2004. Fixation biases affecting human SNPs. Trends Genet 20: 122–126 [DOI] [PubMed] [Google Scholar]
- White MA, Wierdl M, Detloff P, Petes TD 1991. DNA-binding protein RAP1 stimulates meiotic recombination at the HIS4 locus in yeast. Proc Natl Acad Sci 88: 9755–9759 [DOI] [PMC free article] [PubMed] [Google Scholar]
- White MA, Detloff P, Strand M, Petes TD 1992. A promoter deletion reduces the rate of mitotic, but not meiotic, recombination at the HIS4 locus in yeast. Curr Genet 21: 109–116 [DOI] [PubMed] [Google Scholar]
- Wright SI, Agrawal N, Bureau TE 2003. Effects of recombination rate and gene density on transposable element distributions in Arabidopsis thaliana. Genome Res 13: 1897–1903 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu TC, Lichten M 1994. Meiosis-induced double-strand break sites determined by yeast chromatin structure. Science 263: 515–518 [DOI] [PubMed] [Google Scholar]
- Wu X, Schmidt JA, Avarbock MR, Tobias JW, Carlson CA, Kolon TF, Ginsberg JP, Brinster RL 2009. Prepubertal human spermatogonia and mouse gonocytes share conserved gene expression of germline stem cell regulatory molecules. Proc Natl Acad Sci 106: 21672–21677 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang C, Li WH, Krainer AR, Zhang MQ 2008. RNA landscape of evolution for optimal exon and intron discrimination. Proc Natl Acad Sci 105: 5797–5802 [DOI] [PMC free article] [PubMed] [Google Scholar]