Satellite-based global-ocean mass balance estimates of interannual variability and emerging trends in continental freshwater discharge

Abstract

Freshwater discharge from the continents is a key component of Earth’s water cycle that sustains human life and ecosystem health. Surprisingly, owing to a number of socioeconomic and political obstacles, a comprehensive global river discharge observing system does not yet exist. Here we use 13 years (1994–2006) of satellite precipitation, evaporation, and sea level data in an ocean mass balance to estimate freshwater discharge into the global ocean. Results indicate that global freshwater discharge averaged 36,055 km³/y for the study period while exhibiting significant interannual variability driven primarily by El Niño Southern Oscillation cycles. The method described here can ultimately be used to estimate long-term global discharge trends as the records of sea level rise and ocean temperature lengthen. For the relatively short 13-year period studied here, global discharge increased by 540 km³/y², which was largely attributed to an increase of global-ocean evaporation (768 km³/y²). Sustained growth of these flux rates into long-term trends would provide evidence for increasing intensity of the hydrologic cycle.

Freshwater discharge into the world ocean is a key component of Earth’s global hydrological and biogeochemical cycles, which plays a critical role in supporting the human environment and ecosystem health. It represents an integrated response to natural processes and to anthropogenic activities, exhibiting prominent variability in magnitude, seasonality, and response to future climate warming scenarios (1). Increasing precipitation intensity (2) and greenhouse gas emissions point to significant changes in river runoff, particularly at high latitudes (3). Although human management of water resources, including reservoir storage and excessive groundwater withdrawal, have altered the flow regime of some major river basins (4, 5), global-scale discharge changes remain a key indicator of potential acceleration of the hydrologic cycle (6, 7) and an important input for quantifying rates of global mean sea level rise (8).

Recent discussion of the intensification of the hydrological cycle has included analysis of trends in global freshwater discharge (9–12) that may be occurring in response to increasing evaporation. However, a major limitation in these analyses has been the availability of spatially and temporally consistent, quality-controlled observations of river discharge (13). Methodologies to counter this deficiency are often highly debated (14, 15). Although most global discharge assessments to date have been based on aggregated gauge-based streamflow measurements, strong socioeconomic disincentives for sharing data, a worldwide decline in the number of operational gauging stations, and incomplete measurement of total volume of freshwater discharged along continental margins, combine to severely limit the capacity of gauging networks to characterize the behavior of global freshwater discharge in near real-time (16, 17). Consequently, most prior attempts have focused on climatologic or annual averages taken over historical periods of varying length (18 and references therein).

Recent advances in remote sensing techniques, particularly in the use of interferometric synthetic aperture radar (16) and radar altimetry (19), provide alternatives to overcome some of the limitations of monitoring river discharge and other surface water bodies encountered using ground-based measurements (16). The Gravity Recovery and Climate Experiment (GRACE) satellite mission (20) provides another option for remote sensing of river discharge from large river basin to continental scales. Terrestrial water storage observations from GRACE, when combined with precipitation and evaporation data (or similarly, with the atmospheric moisture storage change and divergence), can be used to solve a water balance for the discharge flux (17, 21). This method presents the most viable means to estimate discharge in near-real time, although it is limited to the period of available land-water storage observations from the GRACE mission (March 2002—present) and its spatial-temporal accuracy range (> 150,000 km²; > 10 days).

Here we present and analyze monthly variations of global freshwater discharge, extending from 1994 to 2006, computed utilizing satellite and in situ observations in a global-ocean mass balance. The length of the computed discharge is primarily governed by the availability of the ocean temperature observations. We emphasize that the computed freshwater discharge estimates do not require additional statistical analysis and/or model (time-integrating) simulations to account for the spatial and temporal inconsistencies or to fill data gaps that are typical of gauge-based river discharge observations. Furthermore, the results presented here are the only available estimates of observation-based global discharge computed on a monthly basis over an extended period (13 y; 1994–2006) from the recent past.

Results and Discussion

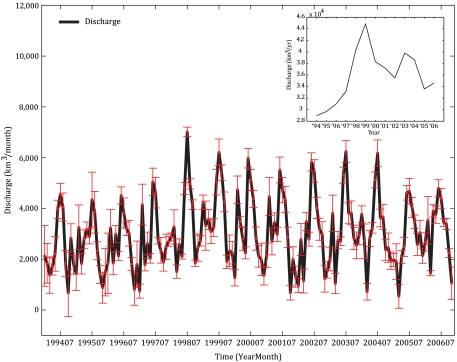
Fig. 1 shows the ensemble mean of monthly global freshwater discharge, computed using different combinations of global-ocean precipitation (P) and evaporation (E) estimates (Fig. S1). Globally, terrestrial freshwater discharge peaks during Northern Hemisphere summer and reaches a minimum during Northern Hemisphere winter. This pattern of variability is intricately linked with the seasonal shifts in the Intertropical Convergence Zone and is also reflected in the peaks of global-ocean mass change during Northern Hemisphere summer (Fig. S2). General agreement between all discharge estimates is evident in their phase and amplitude. Except for a few months, the majority of the monthly discharge estimates fall within one standard deviation of the ensemble mean. Although the lower end members of the global discharge ensemble mostly result from the combination of E from the Special Sensor Microwave Imager-NASA Energy and Water Cycle Study (NEWS) dataset (SSM/I; 2) and P from the Climate Prediction Center (CPC) Merged Analysis of Precipitation (CMAP; 22) (averaging ∼22,000 km³/y), the upper end members are mostly obtained from the combination of E from the Objectively Analyzed Air-Sea Fluxes (OAFlux; 23) and P from the Global Precipitation and Climatology Project (GPCP; 24) (averaging ∼48,000 km³/y). Because E (P) contributes positively (negatively) in the global-ocean mass budget solution for R, the lowest (highest) discharge is produced by the combination of the lowest (highest) E and highest (lowest) P. The average value of global freshwater discharge for the period 1994–2006 is 36,055 km³/y, which is similar to a very recent analysis (25) and is in the middle of the range established by a host of previous studies (e.g., 17, 18). Also shown in Fig. 1, as a conservative estimate of error, are the monthly values of mean absolute deviation about the ensemble mean. These values quantify dispersion among the various estimates of discharge on a month-to-month basis, the average of which for the entire study period is 880 km³/mo. Table 1 lists the mean and standard deviation of the ensemble mean of the global-ocean mass balance for the length of the study.

Fig. 1.

Month-to-month variations in the ensemble mean of global freshwater discharge computed using various combinations of precipitation and evaporation estimates (solid black line). The error bars (in red) shown here are representative of the mean absolute deviation of the various discharge estimates about its mean, at monthly time scales. (Inset) Time series of annual freshwater discharge computed using the ensemble mean of the different freshwater discharge datasets.

Table 1.

Mean, standard deviation, and the emerging trend in the global-ocean mass balance components

Component (data source)	Mean	Standard deviation	Trend
Discharge (R) (ΔM/Δt + E - P)	36,055 km3/y	16,164 km3/y	540 km3/y2
Evaporation (E) (SSM/I, OAFlux, & HOAPS)	409,152 km3/y	10,236 km3/y	768 km3/y2
Precipitation (P) (GPCP & CMAP)	374,220 km3/y	14,221 km3/y	240 km3/y2
Global-ocean mass change (ΔM/Δt) (GMSL minus steric sea surface height)	1,044 km3/y	14,328 km3/y	23 km3/y2

The mean, standard deviation, and the emerging trend estimates for each of the components are based on the ensemble mean, of data obtained from varied sources, for the entire study period (1994–2006).

Note that one of the primary objectives of this study is to establish a method that addresses some of the major limitations for estimating time variations of observation-based freshwater discharge to the global ocean, particularly for the recent past. In order to establish a robust estimate of global discharge, we have utilized a variety of the most commonly used, currently available datasets for each of the individual components of global-ocean mass balance, many of which do not yet include individual error estimates. The uniqueness of the computed discharge estimates therefore necessitated the quantification of uncertainty as a measure of variance in the estimated monthly global discharge values. Hence instrument errors, those due to changes in sensors and retrieval algorithms over time, and other associated errors, may percolate into the computed discharge estimates and are not explicitly represented by the error bars in Fig. 1. The quantification of instrument- and algorithm-specific errors, though important, is beyond the scope of this study,

Differences among ensemble members in Fig. 1 reflect on the current ability to close the global-ocean mass balance. Some monthly discharge values, mostly those estimated using E from SSM/I, are negative and thus unrealistic. Nevertheless, the ensemble mean, in our consideration, is the most robust representation of the seasonal cycle of global freshwater discharge currently available, save for 2 mo in 1994–1995 (see Data and Methods for details).

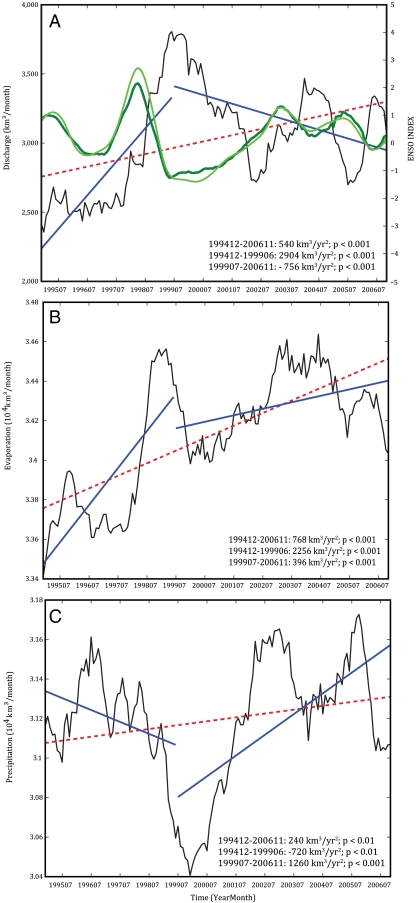
We note here the existence of strong interannual fluctuations in the global hydrological cycle over two consecutive short time periods. We performed a first-order attribution of the variations in global discharge by assessing the coherence of two commonly used climate indices with computed discharge time series. Shown in Fig. 2A is the Bivariate El Niño Southern Oscillation (ENSO) Timeseries (BEST) Index (26) and the most commonly used Niño 3.4 Index (27). Although the “BEST” index is representative of both the temperature and pressure changes associated with the El Niño and La Niña phases of ENSO cycle in the equatorial Pacific Ocean, Niño 3.4 is only related to sea surface temperature (SST) changes in the region. Positive and negative values of these indices are indicative of an El Niño and a La Niña condition, respectively. Results reveal a strong anticorrelated relationship between R and the ENSO indices, BEST (R = -0.48, p < 0.001) and Niño 3.4 (R = -0.44, p < 0.001), such that El Niño events produce less than normal R, whereas La Niña events produce higher than normal R. However, it is likely that warmer SSTs associated with the 1997–1998 El Niño event (the strongest on record; 12) resulted in the strong increase in evaporation, ultimately fueling terrestrial precipitation and a large increase in R during 199412–199906 (Fig. 1, Inset).

Fig. 2.

Monthly time series of (A) global freshwater discharge, (B) global-ocean evaporation, and (C) global-ocean precipitation after smoothing with a 12-month moving average filter. Emerging (short-term) trends in each of the variables, for the periods of 199412–200611 (broken red line), 199412–199906 (solid blue line), and 199907–200611 (solid blue line), and their respective p values (shown as a legend in each of the subplots) are estimated using a linear least-squares regression. Also shown in A are the time series of “BEST” (solid dark green line) and “Nino 3.4” (solid light green line) ENSO indices smoothed as described above.

Previously, estimated trends in discharge into the global ocean were either based on model (time-integrating) simulations (3, 11), combinations of model simulation and observations (12), or on statistical reconstruction of limited gauge-based observations (9, 10). The discharge estimation method presented here will ultimately enable quantification of long-term hydrological trends, in an entirely observation-based framework, as the satellite and in situ data record lengthens. Fig. 2 provides short-term examples of piecewise and study-length trends in the ensemble means of terrestrial freshwater discharge (R), E and P. Here, the magnitudes of the trends are estimated as the slope of the least-squares estimate of best-fit line. We concentrate on the ensemble mean of the various estimates in order to construct a robust time series of global discharge that alleviates some of the discrepancies in each of the six different estimates (see Table S1 for the interannual variations and emerging trends in each of the individual data records). Note that the high frequency variations are removed from each of the time series by using a 12-month moving average filter, prior to trend estimation, to emphasize the interannual variations.

Trends should be interpreted with caution as the record length, although long for an observation-based global discharge, is relatively short considering the high degree of interannual variability apparent in Fig. 1. The trend magnitudes are specific to the time period specified and can be viewed as emerging with respect to the longer term. The identification of longer-term trends clearly requires the availability of extended global discharge estimates, which the methods presented here can ultimately provide.

An increase in the ensemble mean of R is evident from 199412–199906 (2,904 km³/y²; p < 0.001), followed by a decreasing trend (-756 km³/y²; p < 0.001) through the end of the study period (199907–200611). The trend for the entire 199412–200611 study period is 540 km³/y² (p < 0.001). The balance of the trends of E and P explains the piecewise upward, downward, and overall increasing trend in R. For the 199412–199906 period, the upward trend in E (2,256 km³/y²; p < 0.001) is far greater than the decreasing trend in P (-720 km³/y²; p < 0.01). For the period 199907–200611, the downward trend in R is driven by an increase in P (1,260 km³/y²; p < 0.001) relative to insignificant growth in E (396 km³/y²; p < 0.001). The increasing trend in R for the entire study period results from the increase in E (768 km³/y²; p < 0.001) relative to an insignificant increase in P (240 km³/y²; p < 0.01). Although changes in global-ocean water mass (ΔM/Δt) have contributed importantly toward the estimation of monthly R, its contribution to the attribution of an emerging trend in R is statistically insignificant compared to P and E (see Fig. S3). The emerging trends are summarized in Table 1.

The short-term increase in E, and hence R, is primarily attributed to increases in SST, as trends in ocean wind tend to be small (2). Mechanistically, increasing SST leads to increased oceanic evaporation and, consequently, increased precipitation and runoff over land (11). The discharge trend of 540 km³/y² is one to two orders of magnitude greater than those previously estimated by Labat et al. (9) (60.3 km³/y²), Gedney et al. (10) (∼67 km³/y²), and Gerten et al. (11) (30.8 km³/yr²) and strongly contradicts those estimated by Dai et al. (12) (-6.96 km³/y²) and Milliman et al. (28) (no trend). Some of the disagreement stems from the fact that the above-mentioned estimates are based on varied methodology, time span, spatial coverage, and other issues (7, 15). It is also essential to note the holistic nature of our estimates relative to those mentioned above. Because the global, observation-based approach used here includes ocean mass change as a component (see Data and Methods), contributions from melting ice sheets and glaciers are implicitly included in our global discharge estimates. As such, they are consistent with recent observations of ice sheet and glacier mass losses (29–31)

Global changes in river discharge impact fresh water availability. They also point to changes in the intensity of the global hydrologic cycle. Given the aforementioned obstacles to comprehensive discharge monitoring, the methods and estimates presented here offer previously undescribed means to characterize freshwater delivery to the global ocean. Furthermore, as the acquisition and precision of geophysical data continues to improve, the method presented here will become more accurate. And as the length of the satellite data record increases, the method can be used to investigate future rates of water cycle acceleration.

As the Greenland and Antarctic ice sheets continue to melt, and the remaining cryosphere continues to decay, global river discharge could easily continue to increase, further accelerating current rates of sea level rise. Although human management of the water cycle (e.g., by building reservoirs) may significantly mitigate what may be a much greater increase in discharge (32), our work demonstrates that many of these changes can be characterized and understood by analysis of modern satellite data.

Data and Methods

Changes in global-ocean water mass (ΔM/Δt, time derivative of ocean mass) are balanced by the difference of inflows (i.e., P and R) and outflows (E). In this study, monthly ΔM/Δt, P, and E are used to compute monthly global freshwater discharge as the residual of the global-ocean mass balance (R = ΔM/Δt + E - P). We use satellite altimeter observations of global mean sea level (GMSL) along with gridded global-ocean temperature and salinity data to estimate monthly ΔM/Δt. Satellite altimetry provides the best available estimate of GMSL and is now considered the standard of reference (33). Altimeter observations of GMSL integrate both its steric (temperature- and salinity-driven expansion/contraction) and nonsteric (R + P - E, freshwater balance-driven) components. Thus, we compute ocean mass changes by removing the steric variations from altimeter GMSL measurements (34, 35). Since the launch of TOPEX/Poseidon (T/P) and its follow-on Jason-1, GMSL has been continuously monitored with unprecedented accuracy at 10-d intervals (33). We use globally averaged monthly data from the (T/P) and Jason-1 altimeters, aggregated from 10-d estimates, from 1994–2006, subsequent to the application of standard and inverted barometer corrections (available at http://sealevel.colorado.edu).

The satellite radar altimeter data and most ocean flux datasets, except for the precipitation estimates and GRACE observations, have near global (66 °N–66 °S) coverage only. In addition, evaporation over the ocean is computed for ice-free ocean areas only. To make a consistent consideration of the surface area, we have aggregated the fluxes and stores for the ocean area extending from 66 °N–66 °S. This extent covers more than 93% of the global-ocean area and is representative of the entire global ocean. Chambers et al. (34) and Lombard et al. (36) have shown that the Northern Hemisphere high latitude ocean regions have insignificant contributions to the magnitude and trend in global-ocean mass.

In order to estimate the steric contribution to GMSL, depth integrated (0–700 m) specific density anomalies are computed from global-ocean temperature and salinity profiles using the classical expression for the equation of state of the ocean (37). The majority of ocean temperature and salinity profiles are limited in spatial and vertical extent. Hence most ocean temperature and/or salinity datasets often combine different in situ measurements and optimum interpolation techniques in order to make the most accurate estimates. Since its inception, in mid-2003, the ARGO array of profiling floats project has made it possible to make unified measurements of ocean salinity and temperature evenly distributed over the global ocean, including the Southern and Indian oceans, with high levels of accuracy (38). Although ARGO floats have enabled independent observations of the steric component of sea level rise, GRACE has been very effectively used to measure the mass change component (nonsteric) of sea level rise (34). The GRACE mission makes very precise measurements of month-to-month changes in the Earth’s gravity field caused by the redistribution of water mass among the different components of the Earth system (20, 35).

Time series of monthly steric variations for the period of 1994–2006 were computed using gridded global-ocean temperature datasets from Ishii et al. (39) (henceforth, ISHII) and from Ingleby and Huddleston (40) (henceforth, IH). These gridded datasets are based on objective analysis of in situ ocean temperature profiles from a variety of different observational data sources. Details on the processing and analysis scheme can be found in Ishii et al. (39) and in Ingleby and Huddleston (40). Thus, two different time series of global-ocean mass are computed as GMSL minus ISHII (M_ISHII) and GMSL minus IH (M_IH). Month-to-month incremental changes in M_ISHII and M_IH are denoted as ΔM_ISHII/Δt and ΔM_IH/Δt, respectively. Based on the confidence imparted by the comparison to ΔM/Δt computed using the ARGO floats (38) and observed by GRACE (see SI Text 1 and Fig. S2), and the close correspondence between ΔM_ISHII/Δt and ΔM_IH/Δt (R = 0.93, p < 0.01), we consider the monthly mean of ΔM_ISHII/Δt and ΔM_IH/Δt as a consistent estimate of global-ocean mass change, for the period of 1994–2006. Note that, during the winter months of December 1994 and January 1995, the current datasets indicate exceptionally high mass loss over the global ocean. Although it is difficult to isolate the source of this problem, it is most likely due to errors in the measurements of ocean temperature, though errors in the observations of P and E may also contribute The subsurface ocean temperature datasets, before the launch of ARGO, are based on the compilation of a myriad of in situ measurements using various instruments and often involved numerous corrections (35). Because of the high negative values of ΔM, the freshwater discharge values estimated for those months were negative. Negative discharge values were corrected by using the study-period mean ΔM instead of the monthly value in the mass balance for the affected months.

To compute global freshwater discharge we used several different datasets of P and E to establish the range of our estimates. Monthly variations of global-ocean precipitation are from CMAP (22) and GPCP version 2 (24). Both CMAP and GPCP merge satellite and surface radar and gauge-based measurements to provide the best available analysis of global precipitation. Beyond 1987, these datasets benefit significantly from microwave data from SSM/I, particularly over the ocean. In spite of the known regional bias issues in the tropical ocean (41), the overall temporal variability of CMAP and GPCP is in good agreement (R = 0.78, p < 0.01) (see Fig. S4 for comparison). The magnitude of monthly P from CMAP (averaging ∼380,000 km³/y) is consistently higher than that of GPCP (averaging ∼369,000 km³/y) and is comparable to earlier global water cycle studies (18, 41).

Global-ocean evaporation estimates for the period 1994–2006 are obtained from SSM/I (2), OAFlux (23), and the Hamburg Ocean Atmosphere Parameters and Fluxes from Satellite data (HOAPS; 42) version 3, which is available only through 2005. All the evaporation datasets estimate the latent heat flux using the bulk aerodynamic formulation in order to compute ocean evaporation (2). Satellite observations of surface wind speed at the reference height, sea surface temperature and specific humidity of air near the sea surface are the key variables used in the formulation. Despite, the greater variance in the E estimates (see SI Text 2 and Fig. S5), the temporal variability of these datasets is consistent, with all monthly estimates within one standard deviation of their monthly ensemble mean. The average values of global-ocean evaporation ranges between 400,200 km³/y (for SSM/I) and 415,900 km³/y (for OAFlux).