Highly non-planar dendritic porphyrin for pH sensing: observation of porphyrin monocation

Abstract

Metal-free porphyrin-dendrimers provide a convenient platform for construction of membrane-impermeable ratiometric probes for pH measurements in compartmentalized biological systems. In all previously reported molecules, electrostatic stabilization (shielding) of the core porphyrin by peripheral negative charges (carboxylates) was required to shift the intrinsically low porphyrin protonation pK_a’s into the physiological pH range (pH 6–8). However, binding of metal cations (e.g. K⁺, Na⁺, Ca²⁺, Mg²⁺) by the carboxylate groups on the dendrimer could affect the protonation behavior of such probes in biological environments. Here we present a dendritic pH nanoprobe based on a highly non-planar tetraaryltetracyclohexenoporphyrin (Ar₄TCHP), whose intrinsic protonation pK_a’s are significantly higher than those of regular tetraarylporphyrins, thereby eliminating the need for electrostatic core shielding. The porphyrin was modified with eight Newkome-type dendrons and PEGylated at the periphery, rendering a neutral water-soluble probe (TCHpH), suitable for measurements in the physiological pH range. The protonation of TCHpH could be followed by absorption (e.g. ε_Soret(dication)~270,000 M⁻¹cm⁻¹) or by fluorescence. Unlike most tetraarylporphyrins, TCHpH is protonated in two distinct steps (pK_a’s 7.8 and 6.0). In the region between the pK_a’s, an intermediate species with a well-defined spectroscopic signature, presumably a TCHpH monocation, could be observed in the mixture. The performance of TCHpH was evaluated by pH gradient measurements in large unilamellar vesicles. The probe was retained inside the vesicles and did not pass through and/or interact with vesicle membranes, proving useful for quantification of proton transport across phospholipid bilayers. To interpret the protonation behavior of TCHpH we developed a model relating structural changes on the porphyrin macrocycle upon protonation to its basicity. The model was validated by DFT calculations performed on a planar and non-planar porphyrin, making it possible to rationalize higher protonation pK_a’s of non-planar porphyrins as well as the easier observation of their monocations.

Introduction

Over the past decade, porphyrin-dendrimers have been continuously attracting attention in numerous areas of chemistry, including light harvesting, electron transfer, host-guest chemistry, photodynamic therapy and design of biological sensors and imaging agents.¹ Dendritic encapsulation² offers a convenient method for isolation of the porphyrin moiety from components of biological systems, improving solubility and enabling control over the probe distribution in complex biological environments.

As molecular probes, porphyrin-dendrimers have proven particularly useful for imaging of molecular oxygen³ as well as membrane-impermeable pH probes for compartmentalized biological systems.⁴ The latter application makes use of the fact that protonation of the two imine nitrogens in the core of the porphyrin macrocycle leads to dramatic changes of its optical spectra. Yet both protonated and de-protonated forms retain strong absorption and in many cases substantial fluorescence, enabling ratiometric pH measurements. Compared to other macromolecular pH indicators,⁵ porphyrins offer the advantage of very high extinction coefficients (reaching up to ~400,000 M⁻¹cm⁻¹ in the Soret-band region), thereby ensuring high signal-to-noise ratios (SNR) and high measurement accuracy. Once encapsulated inside dendrimers with hydrophilic peripheral groups, porphyrins become highly water-soluble and unable to pass through and/or interact with lipid bilayers - a valuable property for pH measurements in multi-compartment systems.^4b,6

Intrinsic protonation pK_a’s of tetraarylporphyrins⁷ are usually below the physiological pH range (pH 6–8). However, there are several ways by which the proton affinity of the porphyrin macrocycle can be increased, such as substitution with electron-donor groups,⁷ structural deformation⁸ and electrostatic core stabilization.^9,4 In the previously designed dendritic probes, electrostatic stabilization (shielding) of porphyrin cations by peripheral negative charges (carboxylates) was utilized to tune the protonation pK_a’s into the physiological pH range.⁴ Some of these probes proved instrumental in functional studies;^4b,6,10 however, dependence of the protonation state of the sensor on the ionization of the peripheral layer made these probes sensitive to environmental effects. For example, binding of divalent metal cations (Ca²⁺, Mg²⁺ etc) by the carboxylate groups and/or alterations in K⁺ or Na⁺ concentrations influenced the protonation state of the porphyrin, skewing the measurements.

A preferred way to tune the probe’s pK_a would be to modulate the intrinsic proton affinity of the porphyrin. Such modulation can be achieved by altering the geometry of the porphyrin macrocycle, since it is well known that non-planar deformations can dramatically affect porphyrin basicity.⁸ Guided by our previous observation¹¹ that protonation pK_a’s of strongly saddled tetraaryltetracyclohexenoporphyrins (Ar₄TCHP) are several pH units higher than those of regular tetraarylporphyrins, we envisioned using Ar₄TCHP’s as cores of pH probes. Below we describe design, synthesis and properties of a dendritic probe TCHpH, based on Ar₄TCHP, suitable for pH measurements by absorption and/or fluorescence in physiological pH range. TCHpH is an addition to the class of highly non-planar porphyrin-dendrimers, of which there are presently only a few examples.3b,c;3e^;4b;12 The probe was found useful in measurements of proton gradients in micro-compartment systems.

A remarkable feature of TCHpH is the existence of a pH range in which the porphyrin monocation is readily observable in mixtures of the protonated forms. This result is of independent interest, since in the overwhelming majority of cases the two protonations of the pyrrolenine nitrogens of the porphyrin macrocycle are inseparable,¹³ and with rare exceptions^{14,15,16,17,18} porphyrin monocations (or monoacids) are extremely elusive species. To explain this and other properties of TCHpH we developed a model relating acid-base properties of porphyrins to their structural features. The model was validated by DFT calculations, making it possible to rationalize higher protonation pK_a’s of TCHpH and other non-planar porphyrins as well as the presence of their monocations.

Experimental

General

All solvents and reagents were obtained from commercial sources and used as received. Tetrahydroisoindole ethyl ester (pyrrole ester) (1)¹⁹ and di-n-butyl 5-formylisophthalate (aromatic aldehyde)²⁰ were synthesized as described previously. Tris{[2-(tert-butoxycarbonyl)ethoxy]methyl}methylamine (Gen 1 Newkome-type dendron) was synthesized according to the published method.²¹ Thin-layer chromatography was performed on aluminum-supported silica gel plates (Aldrich). Column chromatography was performed on Selecto silica gel (Fisher). Preparative size exclusion chromatography (SEC) was performed on S-X1 beads (Bio-Rad), using THF as a mobile phase. ¹H and ¹³C NMR spectra were recorded on a Brucker DPX-400 spectrometer. The mass spectra were obtained on a MALDI-TOF Voyager- DE^TM RP BioSpectrometry workstation, using α-cyano-4-hydroxycinnamic acid as the matrix.

Quartz fluorometric cells (Starna Cells, Inc., 1 cm optical path length) were used in both UV-Vis and fluorescence experiments. Optical absorption spectra were recorded on a Perkin-Elmer Lambda 40 UV-Vis spectrophotometer and/or an Avantes AvaSpec-2048 fiberoptic spectrometer with a Tungsten Halogen light-source, connected to an in-house constructed titration system.⁶ Steady-state fluorescence measurements were performed on a FS-900 spectrofluorometer (Edinburgh Instruments). The fluorescence quantum yields were determined relative to the fluorescence of Rhodamine 6G (φ_fl=0.95 in EtOH)²² or tetraphenylporphyrin (φ_fl=0.11 in deox. C₆H₆).²³ Time-resolved fluorescence measurements were performed at the Ultrafast Optical Processes Laboratory at the University of Pennsylvania. Dynamic light scattering (DLS) measurements were performed on a Zetasizer Nano-S instrument (Malvern Instruments).

For details of the DFT calculations see Supporting Information. Normal-mode Structural Decomposition (NSD) analysis²⁴ was performed using an on-line Java applet available at the web site of Prof. J. A. Shelnutt: http://jasheln.unm.edu/jasheln/content/nsd/NSDengine/start.htm (S6).

Synthesis

Tetraaryltetracyclohexenoporphyrin octabutyl ester (3)

A mixture of pyrrole ester (1) (300 mg, 1.55 mmol) and potassium hydroxide (~85 %, 140 mg, 2.55 mmol) in ethylene glycol (9 ml) was refluxed under Ar for 1 h. The mixture was cooled to 0 °C and CH₂Cl₂ (20 ml) was added. The organic phase was washed with water and with brine. The product, pyrrole 2, was extracted with CH₂Cl₂. The solution was washed with water and brine, dried over Na₂SO₄, and the solvent was evaporated in vacuum. The residue was purified by column chromatography (Selecto silica gel/CH₂Cl₂). The resulting pyrrole 2 was dissolved in CH₂Cl₂ (150 ml). The flask was protected from ambient light and flushed with Ar, after which dibutyl-5-formylisophthalate (430 mg, 1.41 mmol) was added in one portion. The solution was stirred for 10 min, after which BF₃·Et₂O (40 mg, 0.28 mmol) was added, and the mixture was stirred at r.t. for 2 h. DDQ (350 mg, 1.55 mmol) was added, and the mixture was stirred overnight. The resulting green solution was washed with 10% aq Na₂SO₃, 10% aq Na₂CO₃, 5% aq HCl, and finally with brine. The organic layer was dried over Na₂SO₄ and reduced in volume by rotary evaporation. The green colored residue was purified by column chromatography on silica gel using CH₂Cl₂/EtOAc (85:15 by volume) as a mobile phase. After evaporation of the solvent, and drying in vacuum, porphyrin 3 was isolated as a green-brown solid. Yield: 230 mg, 10% (based on 1). UV-vis (CH₂Cl₂-TFA, 9:1) λ_max (log ε ) 464 (5.29), 611 (4.08), 671 nm (4.29); ¹H NMR (CDCl₃) δ 8.40–8.37 (m, 12H), 4.90 (s, 16H), 2.64–2.44 (m, 32H), 1.86–1.84 (m, 16H), 1.68–1.65 (m, 16H), 0.89 (s, 24H), 0.31 (br s, 2H); ¹³C NMR (CDCl₃) δ 159.6, 140.6, 135.0, 131.1, 127.7, 124.1, 123.7, 88.8, 56.1, 39.1, 28.9, 24.0, 15.6, 12.3; MALDI, m/z for C₁₀₀H₁₁₈N₄O₁₆ calcd. 1630.8, found 1630.8.

Tetraaryltetracyclohexenoporphyrin octacarboxylic acid (4)

Porphyrin 3 (46 mg, 0.028 mmol) was dissolved in THF (6 ml) at 0 ºC, and two-three pellets of NaOH and MeOH (~0.5 ml) were added to the mixture. The mixture was left to stir at r.t. overnight, after which it was concentrated in vacuum, and several drops of water were added to dissolve the brown precipitate. The solution was stirred for 1 h at r.t., and THF was removed by rotary evaporation. The solution was acidified with conc. HCl. The precipitate was isolated by centrifugation and washed with water three times to give 4 as a dark green powder. Yield: 33 mg, 94%. ¹H NMR (DMSO-d₆) δ 8.33–8.05 (m, 12H), 1.45–0.94 (m, 32H), 0.39 (br s, 2H); MALDI, m/z for C₆₈H₅₄N₄O₁₆ calcd. 1182.3, found 1182.7.

Porphyrin-dendrimer poly-^tBu-ester (5)

Porphyrin 4 (52 mg, 0.044 mmol) and HBTU (250 mg, 0.66 mmol) were dissolved in dry NMP (25 ml). DIPEA (520 mg, 4.05 mmol) was added to the solution at r. t., immediately followed by the addition of the Newkome G1 dendron (334 mg, 0.66 mmol). The resulting mixture was stirred for 4 days at r.t., after which it was poured into aq. NaCl (3%). The resulting precipitate was collected by centrifugation, washed with water by suspension/centrifugation cycles (3×30 ml) and dried in vacuum. The green-brown viscous solid was re-dissolved in THF and purified by SEC (Bio-Rad S-X1 Beads, 200–400 mesh, THF) to yield the porphyrin-dendrimer 5. MALDI, m/z for C₂₆₈H₄₁₄N₁₂O₈₀ calcd. 5080.9, found 5080.3. The MALDI spectrum revealed that the resulting product contained ~15% of the porphyrin modified with 7 Newkome dendrons.

Porphyrin-dendrimer polycarboxylic acid (6)

To a well-stirred solution of 5 (198 mg, 0.039 mmol) in CH₂Cl₂ (12 ml), TFA (10 ml) was added dropwise at 0°C over a period of 20 min. The solution was allowed to react for 2 h, after which the solvent and the excess TFA were evaporated in vacuum at r.t. The residual TFA was removed by re-dissolving the precipitate in CH₂Cl₂ (10 ml) and evaporating it in vacuum. This procedure was repeated several times, leaving polyacid 6 as a dark green viscous material. Yield: 142 mg, 98%. MALDI, m/z for C₁₇₂H₂₂₂N₁₂O₈₀ calcd. 3735.4, found 3735.4. The MALDI spectrum revealed that the resulting product contained ~15% of the porphyrin modified with 7 Newkome dendrons. Porphyrin-dendrimer poly-PEG-ester (TCHpH). Polyacid 6 (129 mg, 0.035 mmol) was dissolved in CH₂Cl₂ (10 ml), monomethoxyoligoethyleneglycol (Av. MW 750, 3 ml) was added, and the solution was left under stirring for 15 min at r.t., after which it was cooled on an ice bath. sym-Collidine (8–10 drops), HOBt (1.18 g, 8.75 mmol) and DCC (1.81 g, 8.75 mmol) were added to the mixture, and it was left to react under stirring for 4 days at r.t. Ice-cold 0.05 M aq. HCl (50 ml) was added to the mixture to quench the reaction, and the mixture was stirred for 30 min in order to decompose the unreacted DCC. The mixture was filtered through a Whatman 55 filter paper. The filtrate was extracted with CH₂Cl₂ and the solvent was removed in vacuum. The product was purified by size-exclusion column chromatography (Bio-Rad S-X1 beads, 200–400 mesh, THF) to yield the target TCHpH probe as a green viscous solid. Yield: 396 mg, 53%.

pH titrations

Bulk titrations of TCHpH were performed at 22°C using 50 mM potassium phosphate buffer or 25 mM HEPES buffer. pH was adjusted by addition of HCl, H₂SO₄ or KOH. K₂SO₄, Ca(OAc)₂ and Mg(OAc)₂ were used to test the influence of metal ion concentrations. In the titrations by absorption, absorbances of solutions at Soret peak maxima were kept below 1.0 OD. In titrations by fluorescence, absorbances at the excitation wavelengths were kept below 0.1 OD.

The titration curves were constructed by plotting absorbances at selected wavelengths, or, in the case of fluorescence titrations, integrated fluorescence vs pH. In ratiometric titrations, ratios of the integrated fluorescence spectra upon excitation at selected wavelengths (e.g. at the Soret peaks corresponding to the free-base and dication forms) were plotted vs pH. The titration data were fitted to the Henderson-Hasselbalch-type equation derived for the case of two sequential protonations (S2):

$${\text{S}}_{\lambda }(\text{pH})=\frac{P_3\times {10}^{-2\text{pH}}+P_2\times {10}^{-\text{pH}}+P_1}{{10}^{-2\text{pH}}+P_4\times {10}^{-\text{pH}}+P_5},$$ (1)

where S_λ(pH) designates the absorbance at a selected wavelength λ and fitting parameters P₁–P₅ are the functions of the equilibrium constant(s), probe concentration and molar extinction coefficients of the free-base, monocation and dication. In eq. 1, P₄=K₄ and P₅=K₃K₄ (S2). Similar treatment was used previously to extract protonation constants K₃ and K₄ of other water-soluble porphyrins.²⁵ Fitting was performed using Microcal Origin software (Origin 7.0).

Liposome experiments

Large unilamellar liposomes containing TCHpH were prepared from palmitoyl-oleoyl phosphatidylcholine (Avanti Polar Lipids) according to the protocol described previously.⁶ The buffer was potassium phosphate (20 mM, pH 7) with addition of EDTA (250 μM) and K₂SO₄ to bring the total K⁺ concentration to 50 mM. This procedure is designed specifically for the preparation of proteoliposomes, and, therefore, it includes the step of partial liposome solubilization after their initial formation. The solubilization was performed using octylglucoside (Avanti Polar Lipids) as a detergent, which was subsequently removed by adsorption on hydrophobic beads (Bio-Beads, SM-2, Bio-Rad). TCHpH was added to the mixture prior to the step of detergent removal to a total concentration of 4.67 mg/ml. After vesicle formation, the probe not enclosed into liposomes was removed by centrifugation of the liposomes at 40,000 rpm for 2 h, discarding the supernatant and re-suspending the formed pellet in a fresh buffer (6 ml). This procedure was repeated three times. Based on the DLS measurements, the liposomes were characterized by homogenous size distributions with the average diameter of ~200 nm.

For calibration of the signal from the encapsulated probe, gramicidin (Sigma) solution in DMSO was added to liposome suspensions to make up the final concentration of ~1 μg/ml. The bulk pH was titrated, and the absorption spectra were corrected for the scattering background arising from the turbidity of the liposome suspension. The normalized quantity R_fb, used for fitting in these experiments, was determined using absorbances at 430 nm (on the blue edge of the Soret band of the free-base) and 459 nm (λ_max of the Soret band of the dication):

$$R_{fb}=\frac{{\text{S}}_{430}-{\text{S}}_{459}\times a}{{\text{S}}_{430}\times b+{\text{S}}_{459}\times a},$$ (2)

where constants a and b account for the difference in the extinction coefficients of differently protonated forms and their spectral overlap.

The pH-jump experiment (Fig. 7) was performed using a suspension of liposomes in a mixture of Mes buffer (20 mM), potassium phosphate buffer (20 mM) and EDTA (250 μM). The pH in the extraliposomal (bulk) solution was set to 4.75. The spectra were recorded every 5 s during ~16 min, after which gramicidin in DMSO was added to make a final concentration of 1 μg/ml.

Figure 7.

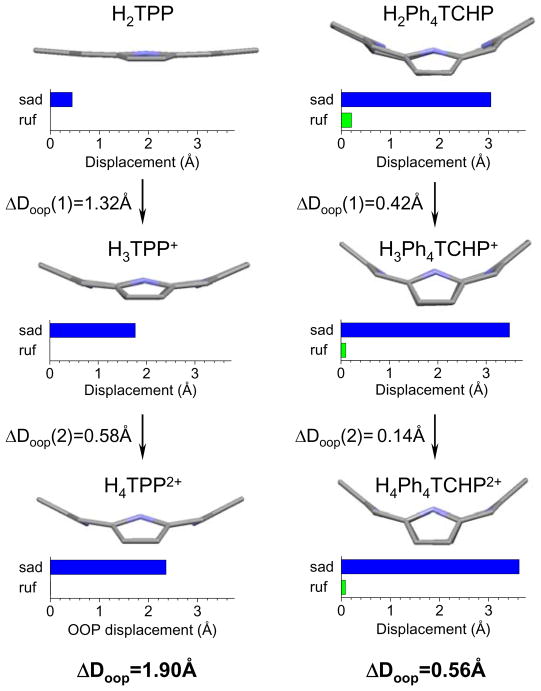
Structural changes upon protonation of TPP (left) and Ph₄TCHP (right). Side views of the tetrapyrrole macrocycles are shown. Structures of cations were calculated for the corresponding chloride salts. Charts graphically depict the degrees of two main out-of-plane (oop) displacements: saddling (sad) and ruffling (ruf). ΔD_oop designates the difference between the mean square oop displacements (sum of all non-planar modes) among differently protonated forms.²⁴

The passive proton permeability of the liposome bilayer was calculated from the difference in pH between times t₁ (pH₁) and t₂ (pH₂) during the initial period prior to the addition of gramicidin (Fig. 6), taking into account the capacity of the buffer inside the liposomes (20 mM, pK_a 6.87):

$$\mathrm{\Delta }[{\text{H}}^{+}]=\frac{20·{10}^{(6.87-{\text{p}H}_2)}}{1+{10}^{(6.87-{\text{p}H}_2)}}-\frac{20·{10}^{(6.87-{\text{p}H}_1)}}{1+{10}^{(6.87-{\text{p}H}_1)}}$$ (3)

Figure 6.

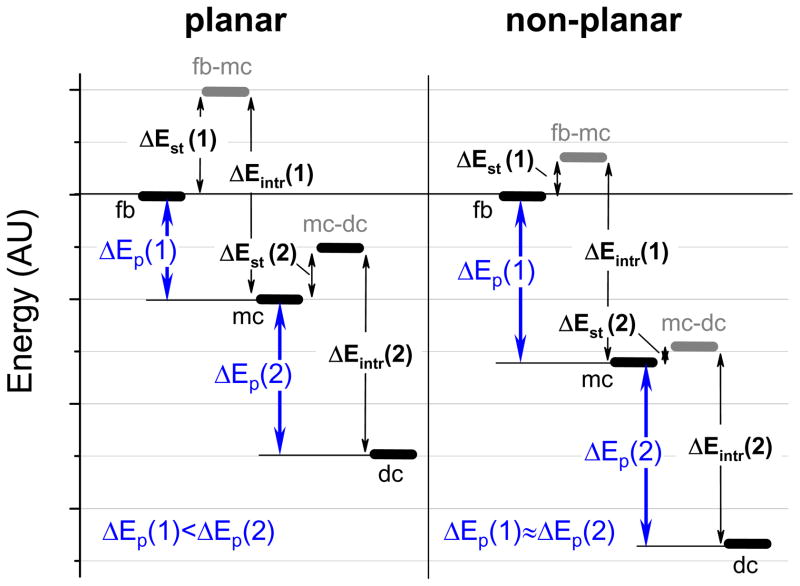
Energy diagram depicting two sequential protonations of planar (left) and non-planar (right) porphyrins.

Expression (3) gives the change in the proton concentration [H⁺] (in mM) inside the liposomes between times t₁ and t₂. When multiplied by the total internal liposome volume, this quantity gives the total amount of protons that traversed the phospholipid membrane.

Adhesion of TCHpH to polystyrene beads (SM-2, Bio-Rad) was tested by adding the beads (100 mg) to a solution of the probe in the buffer (1 ml, 8.5 mg/ml of TCHpH, pH 7.2), incubating the suspension under stirring for 1 h, adding more beads (50 mg) and continuing stirring for additional 1 h.

Results and Discussion

Choice of the porphyrin core and probe synthesis

Free-base porphyrins (H₂P) are able to bind two protons by the core imine nitrogens with formation of mono- (H₃P⁺) and di- (H₄P2⁺) cations. Traditionally, these two proton dissociation reactions are described by equilibrium constants K₃ and K₄, while constants K₁ and K₂ are reserved for formation of porphyrin anions.⁷

$${\text{H}}_4{\text{P}}^{2+}\underset{+{\text{H}}^{+}}{\overset{{\text{K}}_4}{\rightleftharpoons }}{\text{H}}_3{\text{P}}^{+}\underset{+{\text{H}}^{+}}{\overset{{\text{K}}_3}{\rightleftharpoons }}{\text{H}}_2\text{P}\left(\underset{+{\text{H}}^{+}}{\overset{{\text{K}}_2}{\rightleftharpoons }}{\text{HP}}^{-}\underset{+{\text{H}}^{+}}{\overset{{\text{K}}_1}{\rightleftharpoons }}{\text{P}}^{2-}\right)$$ (4)

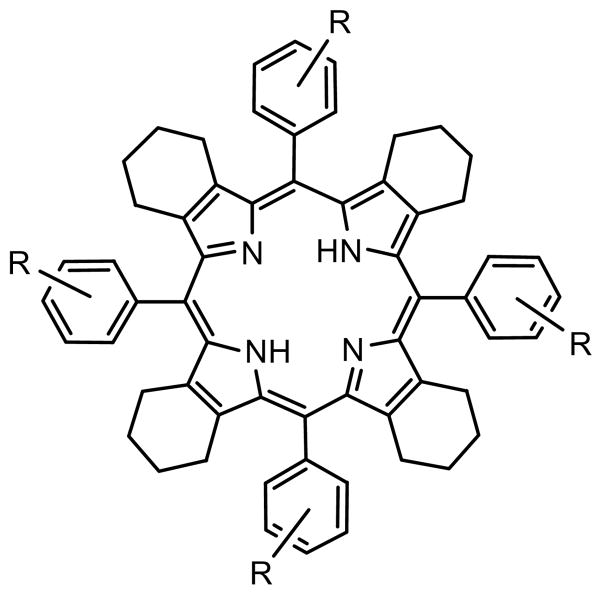
The choice of Ar₄TCHP (Chart 1) as a core for the dendritic probe was motivated by our previous measurements of pK_a’s (pK₃ and pK₄) of water-soluble Ar₄TCHP’s¹¹ and subsequent studies of Ar₄TCHP photophysics.²⁶ It is well known that pK_a’s of non-planar porphyrins are typically higher than pK_a’s of their planar counterparts.⁸ Ar₄TCHP’s belong to the class of highly non-planar porphyrins; and in addition, their proton affinities are increased due to the σ-electron-donor effect of the cyclohexeno-substituents in the β-pyrrolic positions. As a result, pK_a’s of Ar₄TCHP’s may become too high, i.e. higher than the physiological pH range. To counterbalance the effect of the cyclohexeno-substituents we introduced electron-withdrawing carboxyl groups into the meta-positions of the meso-aryl rings, which simultaneously provided anchor points for linking the solubilizing dendrons.

Chart 1.

Structure of Ar₄TCHP.

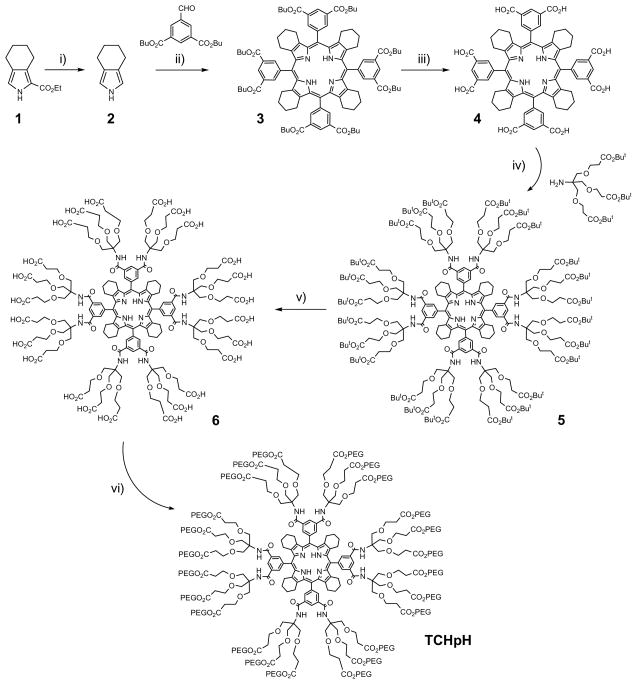
The synthesis of probe TCHpH (Scheme 1) followed the path developed previously for the synthesis of phosphorescent Pt and Pd porphyrin dendrimers.^3e Pyrrole 2 with fused cyclohexene rings was obtained by decarboxylation of pyrrole-ester 1, which was synthesized by the modified Barton-Zard method, as reported previously.¹⁹ Octabutoxycarbonyltetracyclohexenoporphyrin 3 was synthesized by the Lindsey method²⁷ and converted into the corresponding octacarboxylic acid 4 by way of base-mediated hydrolysis. The eight carboxylic groups on 4 were modified with Newkome-type dendrons using HBTU/DIPEA coupling chemistry, and the resulting porphyrin-dendrimer 5 was purified by SEC on polystyrene beads using THF as a mobile phase. The product was found to contain 10–15% of the porphyrin modified with seven Newkome dendrons, which is quite typical for modification of porphyrins with many anchor points.

Scheme 1.

Synthesis of probe TCHpH.

Reagents and conditions: (i) KOH, HOCH₂CH₂OH, reflux, 1 h; (ii) a) BF₃·Et₂O, CH₂Cl₂, r.t., 2 h; b) DDQ, r.t., 12h, 10% for two stages; (iii) NaOH, THF, r.t., 12 h, 94%; (iv) HBTU, DIPEA, NMP, r.t., 4 days, 86%; (v) TFA, 0°C, 20 min, 98%; (vi) PEG750, DCC, HOBt, Sym-collidine, CH₂Cl₂, r.t., 4 days, 53%.

Abbreviations: NMP=N-methylpyrrolidone; HBTU=2-(1H-benzotriazol-1-yl)-1,1,3,3-tetramethyluronium hexafluorophosphate; DIPEA=N,N-diisopropylethylamine; TFA=Tri fluoroacetic acid; PEG750=oligoethyleneglycol monomethyl ether, Av. MW 750; DCC=N,N-dicyclohexylcarbodiimide; HOBt = 1-hydroxybenzoytriazole.

Newkome-type ester-amide dendrons²⁸ were chosen because they possess a trifurcated branching junction, thereby producing 24 peripheral functionalities already at the first generation. Newkome-type dendrons are easily accessible²⁹ and have been used previously for constructions of porphyrin-dendrimers.^30,4b The peripheral tert-butyl ester groups on 5 were cleaved by TFA, giving polyacid 6, whose peripheral carboxyl groups were subsequently esterified with monomethoxyoligo(ethylene glycol) (Av. MW 750) using the DCC/HOBt method.30a,b The final PEGgylated porphyrin-dendrimer (TCHpH) was purified twice by SEC on polystyrene beads. TCHpH was isolated as a dark green viscous material, exhibiting very high aqueous solubility.

Spectroscopic properties of TCHpH

The changes in the optical absorption spectra of TCHpH upon changes in pH are shown in Fig. 1. The free-base probe (pH 10.5) has its Soret band (S₀→S₂) at 442 nm (Fig. 1b) and shows the characteristic four-band pattern in the Q-band (S₀→S₁) region (Q_y(1,0), Q_y(0,0), Q_x(1,0), Q_x(0,0)) (Fig. 1c), which is typical for tetraarylporphyrins.³¹ All bands are broadened and red-shifted compared to TPP, which is consistent with the high non-planarity its conformational flexibility of the Ar₄TCHP skeleton.^26,32,33 The red-most absorption (Q_x(0,0)) has its maximum at 676 nm.

Figure 1.

Changes in the absorption spectra of probe TCHpH upon changes in pH (pH is shown in the legend, upper graph). Buffer: phosphate, 50 mM. a - Full spectrum; b - Soret band region; c - Q-band region. Arrows indicate the direction of the intensity changes with increase in pH.

The spectrum of the fully protonated species (porphyrin dication, pH 4.0) exhibits a narrower and higher intensity Soret band (λ_max=459 nm), which is 838 cm⁻¹ lower in energy than the peak of the free-base Soret band (Fig. 1b). This is a much smaller shift compared to what is typically encountered in planar tetraarylporphyrins.^33d,e For example, the corresponding difference between the Soret peaks of the free-base and dication of water-soluble probe Glu³, based on tetracarboxyphenylporphyrin, is 1317 cm⁻¹.⁶

Due to the higher symmetry of the dication, the four bands of the free-base merge into the single Q(1,0)-Q(0,0) pattern (λ_max=605 nm, 659 nm), shifted blue relative to the lower energy Q_x(0,0) band of the free-base. This behavior is different from tetraarylporphyrins, where the protonation is accompanied by large red shifts, which occur because of the induced strong non-planar deformations.^33d

The extinction coefficients were measured for the dication of porphyrin 3 in CH₂Cl₂/TFA at 22°C (ε_Soret=197,000 M⁻¹cm⁻¹, λ_max(Soret)=464 nm). It was assumed that for the same transitions the oscillator strengths of the dendritic porphyrin (TCHpH probe) in water and of the parent porphyrin 3 in CH₂Cl₂ would be similar. The extinction coefficients of TCHpH in an aqueous buffer were calculated to be ε₄₅₉(dication)=272,000 M⁻¹cm⁻¹ and ε₄₄₂(free-base)=163,000 M⁻¹cm⁻¹. These values are somewhat lower than the extinction coefficients of the previously reported porphyrin-based pH probes,^4,6 but still are more than adequate for analytical applications.

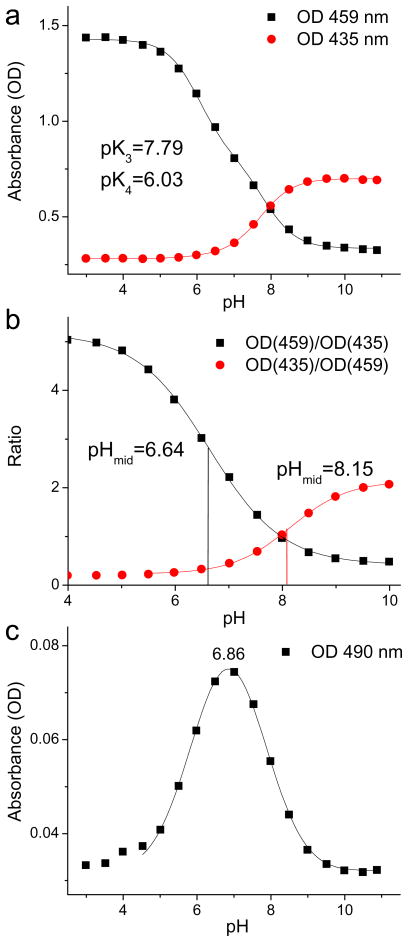
Examination of the absorption changes during protonation revealed the presence of several isosbestic points. For example, in the Soret band region two such points (446 and 473 nm) occur in the pH range 3.0–6.5 and one (451 nm) in the range 7.5–10.0, suggesting two distinct protonation processes. In order to evaluate the dissociation pK_a’s, absorbances at selected wavelengths were plotted as a function of pH and fitted to equation (1), which describes two sequential protonations (Fig. 2) (S2).

Figure 2.

Changes in absorbances of TCHpH with pH: a) OD at 435 nm and OD at 459 nm and their fits to equation (1); b) ratios of absorbances and their fits to the Boltzman type sigmoidal curves (S3–S5); c) OD at 490 nm and its fit to a Gaussian form (pH_max=6.86).

The two wavelengths were chosen to be 435 nm - the blue edge of the Soret peak of the free-base, and 459 nm - λ_max of the Soret peak of the dication. Independent least-squares fitting of the two data sets revealed nearly the same pK_a’s: pK₃=7.79 and pK₄=6.03 (Fig. 2a). As expected for non-planar porphyrins, these values are shifted significantly towards higher pH compared to pK_a’s of regular tetraarylporphyrins.⁷ The optical spectra were found to be practically unaffected by the choice of the buffer (for example, HEPES (25 mM) vs 50 mM phosphate) in the physiological pH range (S9).

For the purpose of practical pH determination it is useful to use ratiometric curves, whose mid-point values (pH_mid) can be tuned by changing measurement wavelengths (S3). An example of such curves is shown in Fig. 2b. Ratios of absorbances at 435 and 459 nm were plotted against pH and fitted to Boltzmann-type sigmoidal curves (S5). The midpoints of the two fits, pH_mid=6.64 and pH_mid=8.15, make these curves optimally suited for measurements in two overlapping, but different pH ranges, ca 4.5–8.5 and 6.5–10.

A remarkable feature of the titrations shown in Fig. 1b is that a distinct spectral pattern emerges and then disappears again with a monotonic increase in pH. For example, the absorbance at ~632 nm rises and then falls back, and the absorbance at the red edge of the Soret band (490 nm) undergoes similar changes, reaching the maximum around pH 6.9 (Fig. 2c). This behavior indicates the presence of an intermediate species, which was tentatively assigned to the porphyrin monocation.

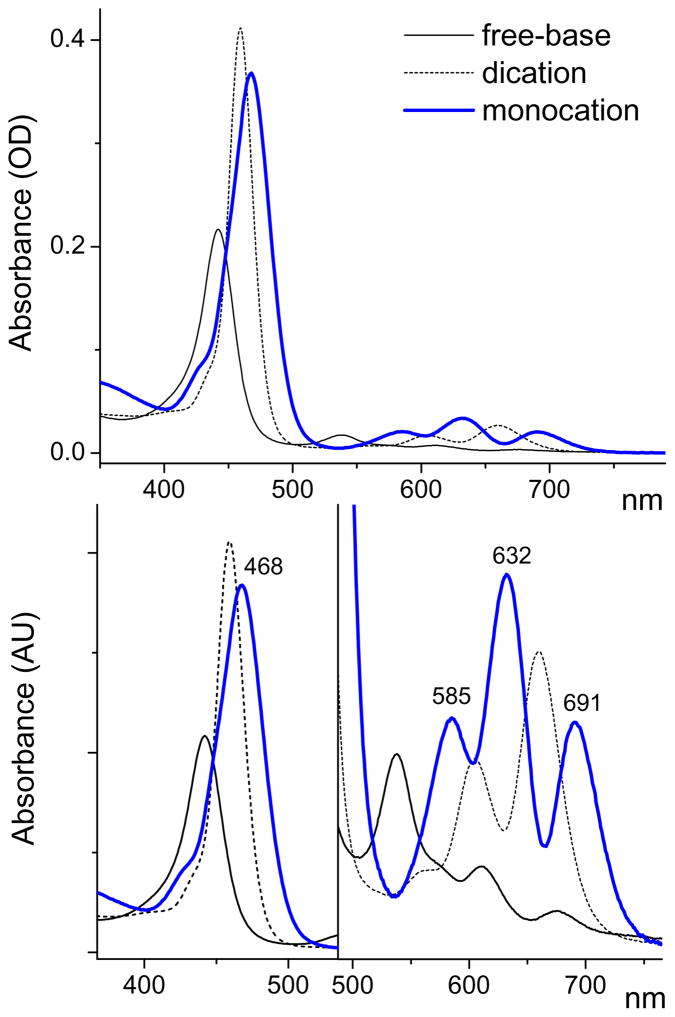
In order to obtain the spectral signature of the monocation, the absorption spectrum recorded at pH 7.01 was fitted with a linear combination of the spectra of the free-base and the dication a (recorded at pH 10.0 and 3.5, respectively) and the sum of parameters, each representing the absorbance at its own individual wavelength (see Supporting Information, S12). The fitting was performed by the linear least-squares, implemented as a positively-constrained quadratic optimization algorithm.³⁴ The result is depicted in Fig. 3, together with the weighted spectra of the dication and the free-base. The original experimental spectrum (the sum of all three components) can be seen in Fig. 1 (also see Fig. S6). Very similar results were obtained by fitting the spectra of the probe recorded at other pH values between 6.5 and 7.5.

Figure 3.

Optical absorption spectra of the three absorbing species: TCHpH monocation (blue), free-base and dication. The spectrum of the monocation was obtained by deconvolution of the experimental spectrum recorded at pH 7.01.

The spectrum of the monocation is distinctly different from the spectra of the free-base and dicationic forms. It exhibits a red shift of the Soret band vs the Soret bands of both the free-base (by 1257 cm⁻¹) and the dication (by 419 cm⁻¹). The Soret band of the monocation is broadened and, in fact, it may well be a superposition of two or more overlapping bands resulting from splitting due to the monocation asymmetry.

In the Q-band region, the absorption spectrum of the monocation consists of three peaks: 585, 632 and 691 nm. A similar three-band pattern was observed previously for the monocation of octaethylporphyrin (H₃OEP⁺), stabilized by a large transition-metal based anionic complex.¹⁴ Since the monocation is an asymmetrical species, it is expected to possess two orthogonal transition dipoles, Q_x and Q_y, just like the parent free-base;^31,33e however, the Q_x, Q_y transitions of the monocation may be closer in energy, and their Q_y(0,0) and Q_x(1,0) components may overlap, giving rise to the observed three-band pattern. The lowest energy Q_x(0,0) band of the monocation (λ_max=691 nm) is red-shifted by 321 cm⁻¹ relative to the Q_x(0,0) band of the free-base, which may be due to the monocation’s non-planar distortion.^33d

The fluorescence quantum yield of the parent porphyrin 3 (dication) in CH₂Cl₂/TFA was found to be 0.0050±0.0007 when measured against fluorescence of Rhodamine 6G in EtOH (φ_fl=0.95)²² and 0.010±0.001 when measured against fluorescence of H₂TPP in deoxygenated benzene (φ_fl=0.11).^23,35 This low yield is a result of rapid internal conversion of the S₁ state - a process well documented for non-planar porphyrins,³³ including Ar₄TCHP’s.²⁶ The fluorescence quantum yield of TCHpH dication was found to be approximately twice as high when measured in aqueous buffer (φ_fl=0.012±0.0008, measured against Rhodamine 6G), which suggests lower conformational flexibility of the porphyrin skeleton and could in part result from the modification of the porphyrin with bulky dendritic substituents. The fluorescence decay of the dication in aqueous buffer (S16) could be approximated by a single-exponential function with the time constant of 0.59 ns, which resembles S₁ lifetimes of other distorted porphyrins.³³ The fluorescence quantum yield of TCHpH free-base (pH 10.2) is ca. two times lower than that of the dication (φ_fl=0.006±0.0008, measured against Rhodamine 6G).

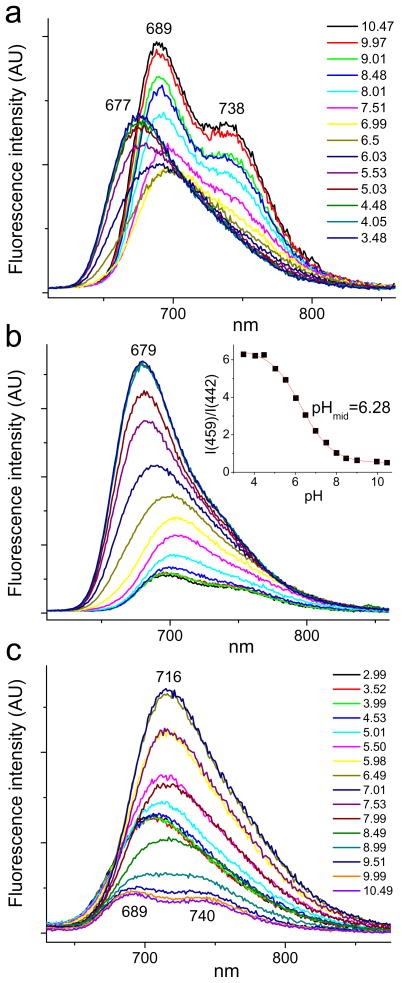
In spite of its low quantum yield, fluorescence of TCHpH still can be useful as a pH indicator, especially for bulk ensemble measurements. Changes in the emission spectra with varying pH are shown in Fig. 4. Fluorescence was excited at either 442 nm (λ_max(Soret) of the free-base) or at 459 nm (λ_max(Soret) of the dication), while the absorbances were kept below 0.1 OD.

Figure 4.

Changes in fluorescence spectra of TCHpH upon changes in pH (pH is shown in the legend, upper graph). Buffer: phosphate, 50 mM. a - λ_ex=442 nm; b - λ_ex=459 nm; c - λ_ex=490 nm. Inset: ratio of integrated fluorescence intensities vs pH: R=I(459)/I(442), where I(459) - fluorescence spectrum integrated from 600 to 860 nm, λ_ex=459 nm; I(442) - fluorescence spectrum integrated from 700 to 860 nm, λ_ex=442 nm.

Similar to other non-planar porphyrins, TCHpH exhibits broad featureless emission spectra, whose changes upon protonation follow the changes in absorption (Fig. 1). Since the emission signal is weak, the most practical method for pH measurements would be dual-wavelength excitation with collection of the entire integrated fluorescence output. For example, a ratiometric curve could be constructed by plotting the ratio of the integrated fluorescence intensities upon excitation at the Soret peaks of the free-base and dication forms (Fig. 4, inset), showing suitability of the fluorescent signal for physiological pH measurements.

Attempts to isolate the excitation spectrum of the monocation by taking measurements of a sample equilibrated at pH 6.9 resulted in spectra with maxima varying with the emission wavelength, but all the spectra were superpositions of all three emitting species (free-base, monocation and dication). Similarly, emission spectra obtained at different excitation wavelengths showed shifts in the emission maxima (S15). Further, a series of emission spectra was recorded at different pH values for the excitation at 490 nm (Fig. 4c), i.e. at the red-shoulder of the monocation absorption (Fig. 3). Near pH 7.0, the fluorescence has its maximum at 715 nm, which is significantly red-shifted relative to the emission peaks of the dication (Fig. 4b). The emission at pH 7.0 originates mostly from the porphyrin monocation.

Probe performance in micro-compartment systems - liposome experiments

In order to evaluate the suitability of TCHpH for measurements in micro-compartment biological systems, we first investigated the dependence of the probe read-out on the concentration of metal cations. Titrations of TCHpH were performed at several K⁺ concentrations, showing no apparent difference in the calibration plots (S10). In contrast, carboxyl-terminated dendritic probes, e.g. Glu³, were shown to be sensitive to ionic strength.⁶ Between pH 6 and 8 in HEPES buffer (25 mM) the spectra of TCHpH did not show any visible changes upon addition of up to 28 mM of Ca or Mg acetates (S10). However, at lower pH values (e.g. pH 5.0) absorbances at the Soret bands’ maxima somewhat decreased at higher cation concentrations.

A useful quality of dendritic probes for proton translocation measurements is the lack of adsorption to hydrophobic beads, which are typically used in preparation of proteoliposomes. The adsorption of TCHpH was found to be somewhat higher than that of polycarboxylated probes,⁶ but significantly below that of commercial pH probes. For example, after 90 min of incubation with polystyrene beads, 89% of TCHpH remained in solution, whereas 72% of commercial macromolecular probe SNARF-dextran (10 kDa) remained in solution under the same conditions.

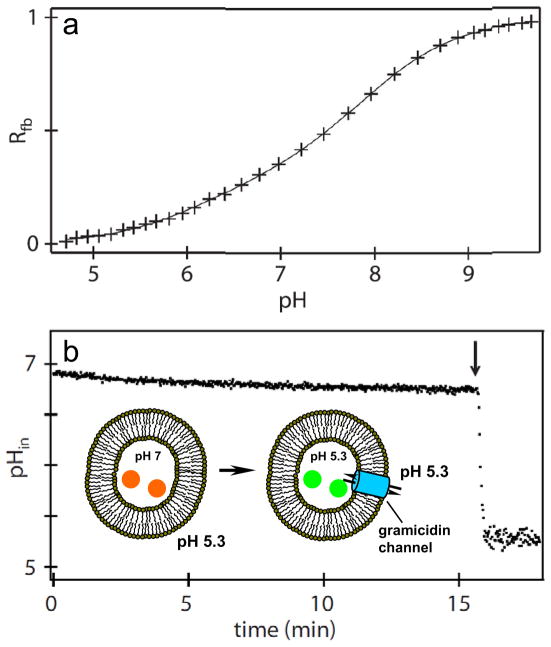
The performance of TCHpH in pH gradient measurements was evaluated by incorporating the probe into large unilamellar vesicles made of phosphatidyl choline. The vesicles were prepared by sonication, extrusion, solubilization by detergent and detergent removal using beads, followed by the removal of the bulk probe by ultra-centrifugation.⁶ The average liposome diameter was 200 nm, as determined by dynamic light scattering. The concentration of the probe inside vesicles was kept high, 0.22 mM, to insure high signal-to-noise ratios in absorbance measurements. In order to calibrate the pH response of the encapsulated probe, the liposomes were treated with a non-specific ionophore gramicidin. Gramicidin forms channels in phospholipid bilayers, making them permeable for small ions, including protons,³⁶ but impermeable to large molecules, such as TCHpH. The absorption spectra of the probe encapsulated inside the liposomes were collected at different pH values, and a calibration curve was constructed (Fig. 8a) by fitting the normalized absorbance (R_fb) (eq. (2)) to a sigmoidal curve. This curve was found to be nearly identical to the one obtained in bulk titrations, showing that the liposomal entrapment of the probe and its high local concentration have no effect on the calibration parameters.

A pH gradient across the phospholipid bilayer was created by mixing one part of the liposomes’ suspension in a buffer at pH 7.0 with nine parts of a buffer at pH 4.75 (Fig. 5). Mixing of the two buffers brought the extraliposomal pH to 5.3, while the intraliposomal pH right after mixing was 7.0. The probe was encapsulated inside the liposomes. Its absorption spectra were recorded continuously, and absorbances at selected wavelengths were converted into pH values using the calibration curve shown in Fig. 5a.

Figure 5.

Probe inside phospholipid vesicles. a) pH titration plot obtained by measuring absorption spectra of the probe inside liposomes with channels made by gramicidin. b) pH-jump experiment. pH_in - pH inside liposomes, as measured by absorbance, converted into pH values using the calibration curve in the upper graph. Gramicidin added after 16 min (arrow), resulting in an abrupt decrease in pH_in due to the rapid mixing of internal and external volumes.

During the initial period, pH inside the liposomes (pH_in) showed a slow drift, reflecting passive transport of protons across the phospholipid bilayer. The internal liposome volume was calculated to be ca 1.5% of the total volume of the suspension. Taking into account the average liposome size and the buffer concentration, the change in pH_in in the absence of gramicidin (Fig. 5b) could be converted into the average passive permeability of the liposome bilayer, giving the value of ~30 protons/s·μm² under the pH gradient of 1.7. This permeability agrees well with previous estimations.⁶

After approximately 16 min, gramicidin was added, instantly forming pores and permitting free proton flow along the concentration gradient, i.e. from the outside into the liposomes. As a result, pH_in abruptly dropped, reflecting fast equilibration of the external and internal volumes. This experiment demonstrates that TCHpH is a membrane-impermeable probe, capable of reporting pH in internal liposomal compartments.

Acid-base properties of TCHpH - structural analysis

In view of the observed behavior of TCHpH it is interesting and relevant to discuss acid-base properties of non-planar porphyrins. Traditionally, higher protonation pK_a’s (pK₃ an pK₄ in Eq. 4) of non-planar porphyrins are attributed to easier accessibility of the core nitrogens to protons in distorted macrocycles.³⁷ However, easy accessibility does not explain the relative thermodynamic stability of protonated forms, but rather implies faster protonation reactions. The rate of protonation may or may not correlate with the protonation free-energy ΔG_p,³⁸ and hence the question still needs to be answered: why are non-planar porphyrins more basic than planar porphyrins, i.e. ΔG_p(non-planar)<ΔG_p(planar)?

In our discussion below we focus on electronic effects. Therefore, instead of using ΔG_p (Gibbs free energy of protonation), we consider only internal electronic energy ΔE_p (also see [45]). We divide ΔE_p into two parts, the intrinsic proton affinity ΔE_intr and the structural term ΔE_st:¹¹

$$\mathrm{\Delta }{\text{E}}_{\text{p}}=\mathrm{\Delta }{\text{E}}_{\text{intr}}+\mathrm{\Delta }{\text{E}}_{\text{st}}$$ (5)

It is well known that protonation of porphyrins leads to their non-planar, typically saddling, deformations.³⁷ With only rare exceptions,^39,40 porphyrin cations are known to be strongly non-planar species.^37a,c;41 We define ΔE_intr as the energy of the protonation of a free-base porphyrin, whose geometry matches that of the corresponding cation (i.e. mono- or dication). ΔE_intr encompasses all the electronic effects of the substituents as they affect the proton affinity. Thus, electron-donating substituents make ΔE_intr more negative, favoring protonation, while electron-withdrawing substituents do just the opposite. Importantly, the effect of a particular substituent on ΔE_intr may depend on the structure of the porphyrin. For example, electron-withdrawing and electron-donating meso-aryl groups would have a stronger effect on ΔE_intr if they would be more aligned and thus better conjugated with the tetrapyrrole macrocycle.⁴²

The structural term ΔE_st in turn consists of the two parts: ΔE_st=ΔE_st(d)+ΔE_st(c). ΔE_st(d) represents the energetic cost of the protonation-induced distortion of the macrocycle relative to its free-base conformation. Since non-planar distortion destabilizes the macrocycle,⁴² it disfavors the protonation (ΔE_st(d)>0). The second term, ΔE_st(c), is related specifically to meso-aryl-substituted porphyrins, for which it has been shown⁴² that saddling distortion is coupled to the rotation of the meso-aryl groups relative to the macrocycle mean plane. This rotation increases the conjugation between the meso-aryls and the macrocycle π-system, stabilizing porphyrin cations⁴³ and thus favoring protonation (ΔE_st(c)<0). Notably, meso-aryl substituents always prefer to align with the macrocycle plane; however, starting from a certain angle their rotation begins to force the macrocycle out of planarity, thereby costing energy. The fact that tetraarylporphyrins, such as tetraphenylporphyrin (TPP), remain planar as free-bases suggests that the benefit of the conjugation (ΔE_st(c)) is not large enough to overcome the structural penalty associated with distortion, i.e. |ΔE_st(c)|<|ΔE_st(d)|.⁴⁴

Considering the above formalism, it is possible now to contemplate the porphyrin protonation reaction as a sequential process (Fig. 6). At first, the free-base (fb) is distorted to match the geometry of the monocation, forming the hypothetical species fb-mc. This process raises the energy by the structural penalty term ΔE_st(1). A proton is then added to fb-mc, producing the monocation (mc) and lowering the energy by ΔE_intr(1). In the second step, the monocation is first distorted to match the geometry of the dication (dc), producing the hypothetical species mc-dc and raising the energy by ΔE_st(2), followed by the addition of the second proton and release of ΔE_intr(2).

Assuming the intrinsic proton affinities ΔE_intr (for example ΔE_intr(1)) are equal for the planar and non-planar porphyrins under comparison, it is now easy to see why the protonation of non-planar macrocycles is more energetically favorable. The attachment of protons to already non-planar free-bases requires less extra-distortion, and, therefore, it is associated with a smaller structural penalty term ΔE_st(d). At the same time, the component associated with the energetic benefit of increased conjugation (ΔE_st(c)), which in principle may be larger for planar porphyrins, is still smaller in its absolute value than ΔE_st(d) (see above). Thus, we first of all can conclude that all other terms being equal, higher basicity of non-planar porphyrins is due to the lesser energetic penalty associated with protonation-induced distortion of the macrocycle: ΔE_st(planar)>ΔE_st(non-planar).

The second conclusion from the diagram in Fig. 6 is related to the existence of monocation of TCHpH, which is an interesting and unusual property. In the overwhelming majority of cases two sequential protonations of porphyrins are inseparable, and with only rare exceptions^14–18 porphyrin monocations (monoacids) are extremely elusive species. To rationalize this behavior we recall that normally the attachment of the first proton to a neutral species disfavors the second protonation because of the electrostatic repulsion between the monocation and the second proton, i.e. ΔE_p(2)>ΔE_p(1). This leads to a difference in protonation pK_a’s and makes detection of the monocations feasible in the pH range between these pK_a’s. However, in porphyrins the situation is different presumably because of the cooperativity effect. In general, cooperativity entails a mechanism by which the first protonation assists the second protonation, thereby reducing the difference between ΔE_p(1) and ΔE_p(2) and, in extreme cases, making ΔE_p(2) more negative than ΔE_p(1), i.e. ΔE_p(2)<ΔE_p(1). The latter situation has been computationally demonstrated, for example, for the case of TPP,¹⁷ and it is shown in Fig. 6. In general, the smaller the difference [ΔE_p(2)-ΔE_p(1)], the less monocation is present in the mixture under equilibrium.

The cooperative enhancement of the second protonation in porphyrins can be explained by the structural effect: the protonation of the first imine nitrogen induces already strong enough deviation of the macrocycle from planarity, so that the attachment of the second proton requires much less structural deformation, reducing the associated structural penalty term ΔE_st(2). This scenario is illustrated in Fig. 6. The intrinsic proton affinities for the first and second protonations, ΔE_intr(1) and ΔE_intr(2), were considered equal to more clearly show that the structural effect alone may be responsible for more negative ΔE_p(2) than ΔE_p(1). Most relevant to our discussion is the fact that a decrease in ΔE_st(1) and ΔE_st(2), which occurs in non-planar porphyrins, leads to an increase in the difference [ΔE_p(2)-ΔE_p(1)]. As a result, cooperativity decreases, and the monocation becomes more readily observable.

Because of electrostatic and other reasons, intrinsic proton affinities ΔE_intr(1) and ΔE_intr(2) in real systems are most certainly not the same. For example, the values of ΔE_intr may be affected significantly by counterions. The effect of counterions on the detectability of porphyrin monocations has been discussed in the literature.¹⁷ Nonetheless, the above conclusions regarding the structural effect should hold true as long as ΔE_intr themselves are not strongly influenced by planar deformations. The limitations of this assumption will have to be evaluated separately, but the calculations performed so far on model porphyrins (see below) suggest that ΔE_intr’s indeed depend only slightly on the degree of non-planar deformations.

To apply the described structural model to interpret the experimentally observed properties of TCHpH, we performed calculations on two model systems: planar tetraphenylporphyrin (TPP), which has been modeled previously,^17,42,43 and highly non-planar Ph₄TCHP (Chart 1, R=H), which is a close analog of the core in TCHpH. The σ-electron donor effect of tetracyclohexeno-rings in Ph₄TCHP could be estimated by comparing proton affinities of unsubstituted porphine (P) and meso-unsubstituted tetracyclohexenoporphyrin (TCHP), since in the absence of meso-aryl substituents tetracyclohexeno-groups do not induce structural deformations (S6). Unsubstituted meso-phenyl groups were chosen in this model study because regardless of their orientation with respect to the macrocycle, orthogonally or at an angle, they presumably do not significantly affect intrinsic proton affinities (ΔE_intr). Of course, the electron-withdrawing carboxyl groups in meso-aryl rings of TCHpH decrease its intrinsic proton affinity compared to that of Ph₄TCHP. However, this effect is not structural, and it is apparently much weaker than the structural effect, since TCHpH still exhibits higher pK_a’s than the majority of tetraarylporphyrins.⁷

The calculations were performed by the DFT methods using B3LYP/6-31G(d) model chemistry (S6). All structures were analyzed by the Normal Mode Structural Decomposition (NSD) method,²⁴ which provides a convenient tool for quantification of porphyrin distortions. The difference in the total mean out-of-plane displacements (D_oop), as calculated by the NSD program, between free-base and protonated forms (ΔD_oop) was used as a measure of the macrocycle distortion induced by protonation (S6). The results of the calculations are summarized in Fig. 7 and Table 1.

Table 1.

Energies^a (kcal mol⁻¹) for Gas Phase Protonations of TPP and Ph₄TCHP. Cl⁻ was used as counterion in calculations of mono- and dications.

	TPP	Ph4TCHP	Ph4TCHPcorrb
ΔEp(1)	−10.5848	−23.0291	−20.6710
ΔEp(2)	−26.8487	−33.1956	−29.9947
ΔEp	−37.4335	−56.2247	−50.6657
[ΔEp(2)-ΔEp(1)]	−16.2639	−10.1665	−9.3237
ΔEst(1)	24.9494	16.4256	16.4256
ΔEst(2)	8.4672	6.8071	6.8071
[ΔEst(2)-ΔEst(1)]	−16.4822	−9.6185	−9.6185
ΔEintr(1)	−35.5342	−39.4547	−37.0966
ΔEintr(2)	−37.0966	−40.0027	−36.8018

^aAll energies shown are derived from the pure uncorrected electronic energies of the corresponding components (see Supporting Information for details);

^bEnergies in this column were corrected by the differences in the corresponding proton affinities of TCHP and P to account for the σ-donor effect of tetracyclohexenogroups in Ph₄TCHP.

It can be clearly seen that the overall protonation-induced deformation (Fig. 7), going from free-bases to dications, is significantly larger for TPP (ΔD_oop=1.90Å) than for Ph₄TCHP (ΔD_oop=0.56Å); and that the magnitudes of the deformations, which are in all cases dominated by saddling, correlate with the calculated proton affinities (ΔE_p).⁴⁵ Total ΔE_p of Ph₄TCHP, for the two protonation steps combined, is ~18.8 kcal/mol more negative than that of TPP (S6).⁴⁶ Based on the comparison between porphine (P) and unsubstituted TCHP, only ~5.5 kcal/mol of this difference is due to the σ-donor effect of the cyclohexeno substituents in Ph₄TCHP. The remaining ~13.3 kcal/mol is mostly accounted for by the difference between the structural terms: |ΔE_st(TPP)-ΔE_st(Ph₄TCHP)|~10.2 kcal/mol, suggesting that the decrease in the structural penalty indeed plays the central role in defining high proton affinity of Ph₄THCP and presumably of other non-planar porphyrins.

As expected, after correction for the σ-donor effect of the cyclohexeno substituents in Ph₄TCHP, the intrinsic proton affinities ΔE_intr of TPP and Ph₄TCHP are indeed very similar. This indicates that the degree of non-planar distortion and the orientation of unsubstituted meso-phenyls with respect to the macrocycle, which are different in fb-mc and mc-dc structures of TPP and Ph₄TCHP, have only a minor effect on the intrinsic proton affinities. In other words, the intrinsic proton affinity of the porphyrin macrocycle is only weakly affected by its distortion.

The calculations confirmed that the overwhelming part of the non-planar deformation occurs with the first protonation, and that the absolute values of the distortions (ΔD_oop’s) in both protonation stages are significantly higher in the case of TPP (Fig. 7). The associated structural terms ΔE_st( 1) and ΔE_st(2) (Table 1) follow these trends, making the difference between the free energies of the first and second protonations [ΔE_p(2)-ΔE_p(1)] substantially lower in the case of TPP, resembling the situation shown in Fig. 6. This enables us to conclude that the relative ease of detectability of the monocation of TCHpH is due to the high non-planarity of its core porphyrin. Notably, one of the recent reports on porphyrin monocations also describes highly non-planar dodecasubstituted porphyrin.¹⁸

Several spectroscopic properties of TCHpH can also be rationalized using the described above structural model. First, we note that red shift of the Soret band of TCHpH is smaller than the corresponding shifts typically observed for regular porphyrins. This is consistent with a smaller extra-distortion of the non-planar core of TCHpH induced by protonation, taking into account that non-planar deformations cause red shifts in the spectra of porphyrins.^32,33 Secondly, the red-most Q-band of the TCHpH dication is shifted blue relative to the Q_x(0,0) transition of the free-base, unlike in regular porphyrins where the corresponding shift occurs in the opposite direction. Symmetrization of the porphyrin upon protonation causes its Q_x and Q_y bands to coalesce, and in the case of regular porphyrins, strong non-planar distortion causes the resulting band to move beyond the Q_x(0,0) band of the free-base. In the case of TCHpH the distortion is much smaller, and the band is red-shifted significantly less.

Calculations performed by the ZINDO/S method (S8),⁴⁷ using the structures shown in Fig. 7, were able to qualitatively reproduce the relative shifts of the bands of Ph₄TCHP dication vs the free-base, positions of Q_x and Q_y bands of the monocation vs those of the free-base, and the merging of the Q_x and Q_y transitions into the single Q-band of the dication. However, both the Soret and the Q-bands of the dication were predicted to be red-shifted relative to the bands of the free-base and the monocation, which does not agree with the experiment. Higher level calculations, such as performed recently on monocations of other tetraarylporphyrins,¹⁷ will be required to fully delineate the spectral features of TCHpH.

Conclusions

The newly developed dendritic probe TCHpH is a macromolecular porphyrin-based pH-sensitive dye suitable for measurements in microcompartmentalized systems, including dynamic measurements of proton gradients. The probe consists of a polyfunctionalized non-planar porphyrin, modified with eight trifurcated Newkome-type dendrons. The latter together with peripheral PEG residues serve to increase the probe’s solubility, control its size and prevent its interactions with components of the measurement system. In the present version of the probe, PEG residues with an average molecular weight of 750 Da were used; however, larger probes can be easily constructed by modifying terminal groups on the dendrimer with larger methoxypolyethyleneglycol or methoxypolyethyleneglycol amine residues, which are readily available. Such alterations will not change the protonation pK_a’s, but may appear instrumental in optimizing the probe’s distribution in microcompartmentalized systems.

To rationalize acid-base properties of TCHpH we further developed a proposed earlier¹¹ structural model that relates electronic effects of macrocycle deformation to porphyrin basicity. The predictions of this model were validated by DFT calculations on a planar and non-planar porphyrin - a structural analog of the core of TCHpH. One relevant prediction is the relative ease of observations of monocations of strongly out-of-plane distorted porphyrins, which was experimentally confirmed in the case of TCHpH. The unique monocation spectrum was identified in the spectra of the mixture of variously protonated forms by spectral deconvolution and could be partly interpreted in terms of the classic porphyrin electronic structure model.