Risk Prediction using Genome-Wide Association Studies

Abstract

Over the last few years many new genetic associations have been identified by Genome-Wide Association Studies (GWAS). There are potentially many uses of these identified variants: a better understanding of disease etiology, personalized medicine, new leads for studying underlying biology, and risk prediction. Recently there has been some skepticism regarding the prospects of risk prediction using GWAS, primarily motivated by the fact that individual effect sizes of variants associated with the phenotype are mostly small. However, there have also been arguments that many disease associated variants have not yet been identified so prospects for risk prediction may improve if more variants are included.

From a risk prediction perspective, it is reasonable to average a larger number of predictors, of which some may have (limited) predictive power, and some actually may be noise. The idea being that when added together, the combined small signals results in a signal that is stronger than the noise from the unrelated predictors.

We examine various aspects of the construction of models for the estimation of disease probability. We compare different methods to construct such models, examine how implementation of cross-validation may influence results, and examine which SNPs are most useful for prediction. We carry out our investigation on GWAS of the Welcome Trust Case Control Consortium. For Crohn’s disease we confirm our results on another GWAS. Our results suggest that utilizing a larger number of SNPs than those which reach genome-wide significance, for example using the lasso, improves the construction of risk prediction models.

It is the hope that genome-wide association studies (GWAS) not only identify regions in the genome (e.g. SNPs) that are associated with phenotypes, but also that the genetic variants that are identified can contribute to (risk-)prediction models for those phenotypes. In some GWAS publications there have been initial attempts to look at the predictive power of the few identified “top-SNPs” [e.g. Zheng et al, 2008; Lin et al. 2009; Miyaki et al. 2009; Myocardial Infarction Genetics Consortium. 2009]. A recent commentary suggested that more and larger studies would help yield more effective prediction models [Kraft and Hunter, 2009]. The results of Gail [2009] are in line with the commentary. In Evans et al. [2009] it was investigated how models, combining marginal results for SNPs in a sensible way, can be used to compute a prediction score. Wu et al. [2009] recently carried out a similar experiment using Support Vector Machines. In our paper we take this several steps further: (i) we use sparse regression models, which deal with correlation between SNPs, and yield estimates of the probability of disease; (ii) by varying some aspects of the cross-validation we critically examine the effect of selecting significant SNPs in the same study as on which the prediction models are constructed; and (iii) we evaluate one of the constructed prediction models on an entirely different GWAS.

Most published GWAS have identified one to a few SNPs associated with a phenotype. Further meta-analyses of GWAS studies with the same phenotype often identify additional SNPs, but for most phenotypes the number of consistently confirmed SNPs is less than a dozen. Exceptions are some continuous phenotypes, such as lipids, for which GWAS have more power. The lack of power of GWAS suggests that there may very well be many more SNPs associated with some phenotypes that have smaller effect sizes. It would be expected that such SNPs are among the SNPs that have larger, but statistically insignificant, test-statistics. Another argument for the existence of more SNPs that are associated with a disease is that often the Q-Q plots for the P-values start showing deviations from the identity (diagonal) well before the effects are significant. The International Schizophrenia Consortium [2009] also combined large numbers of variants; in the current paper we are exploring more systematically different ways to combine large numbers of variants.

Sparse regression methods, such as the lasso [Tibshirani, 1996] and the elastic net [Zou and Hastie, 2005] are increasingly used in high-dimensional settings [Hastie et al., 2001]. The advantage of those approaches is that in regression models they simultaneously carry out variable selection, and provide estimates of the coefficients of the selected variables. In this paper we explore the use of such methods for the construction of risk prediction models using GWAS data. In Wu et al. [2009] the lasso is used for finding significant SNPs in GWAS data. In Park and Hastie [2008] sparse regression methods are used to identify gene × gene interactions in smaller genetic association studies. However, to the best of our knowledge, sparse regression methods have not yet been used to construct prediction models in GWAS to estimate the probability of disease and validate these probabilities on an independent data set.

When constructing such models, it is important to keep the “training data” and “test data” strictly separate. As such, we cannot start from the consensus list of disease associated SNPs, as typically all data sets were used to obtain such a list. Instead we need to use the training data to select the set of SNPs that will be used in constructing the prediction model and the actual construction of that model. Additionally, the high bar that typically exists for a SNP to be declared genome-wide significant (e.g. p < 10⁻⁷) is not necessary for a SNP to be useful in risk prediction. In particular, a group of SNPs that have promising False Discovery Rates, but are not genome-wide significant will likely make a positive contribution to a risk prediction model, as some of these SNPs will predict, while the other ones just add some noise.

Our experiments consist of two parts. In the initial phase we used the Welcome Trust Case Control Consortium (WTCCC) GWAS data for several diseases with about 3000 controls and 2000 cases [Welcome Trust Case Control Consortium, 2007], and split those in a training and a test data set. Model selection (based on cross-validation) was performed on the training data, and the selected model was evaluated on the test data. This paper contains the results for the Crohn’s disease GWAS; the results for type 1 diabetes and type 2 diabetes data are mostly similar; we refer to the results for these phenotypes in a few places. It should be noted that Wu et al. [2009] used a Support Vector Machine approach for the WTCCC type 1 diabetes data. Test data log-likelihood, receiver operator characteristic curves (ROC) and the area under the ROC curve (AUC) are used to evaluate the models. In addition we check whether estimated probabilities of “a subject being a case” correspond to the fraction of subjects that are a case. Other methods for assessing risk models, such as positive and negative predicted value and misclassification rate exist [e.g. Pepe 2003], though it has been argued that well calibrated probabilities are of critical importance in individual risk prediction [Cook, 2007].

As a confirmation experiment, we used the complete WTCCC Crohn’s disease data, consisting of UK subjects, as our training data, and the National Institute of Diabetes and Digestive and Kidney diseases (NIDDK) GWAS data on Crohn’s disease, consisting of US subjects, as our test data. We should note here that the NIDDK data was genotyped on the Illumina platform, and the WTCCC data on the Affymetrix platform, thus to apply the WTCCC derived model to the NIDDK data we needed to impute the Affymetrix SNPs on the NIDDK data.

Overall our results suggest that prediction models (when applied to GWAS cohort data) like the one we develop may provide well calibrated risk estimates. But the predictive value overall is somewhat limited, as demonstrated by the overall AUC of these risk models; they may be most useful for designing trials, and weighing risk-benefits for preventive treatments. For individual risk prediction the genetic factors would presumably be more useful if combined with other established risk-factors.

METHODS

DATA PROCESSING

We obtained GWAS data from the Welcome Trust Case Control Consortium [Welcome Trust Case Control Consortium, 2007], and data from the NIDDK GWAS on Crohn’s disease [Duerr et al. 2006, Rioux et al 2007] from dbGaP. We refer to these data sets as the WTCCC and the NIDDK data, respectively.

WTCCC DATA

The WTCCC data consists of 2000 cases for each of seven diseases and 3000 shared controls. The subjects in this study, from the UK, were genotyped on the Affymetrix 5.0 platform. Separately for the Crohn’s disease data, the type 1 diabetes data, and the type 2 diabetes data, we removed all samples with call rate smaller than 0.95, removed SNPs that had a Hardy Weinberg P-value smaller than 10⁻⁵, SNPs that had more than 10% missing data, SNPs that were in the WTCCC list of “bad SNPs” that was provided with the data, and SNPs with minor allele frequency smaller than 0.05.

The small amount of remaining missing data was imputed using a probabilistic imputation based on a three SNP sliding window. That is, if SNP i was missing for participant j, we calculated the probability distribution of SNP i given the values of SNP i − 1 and i + 1 (for the appropriate case or control portion of the data) and imputed a random realization of this probability distribution. This imputation was quick and easy, and allowed us to carry out initial experiments using multiple imputation (not reported here). Other more sophisticated imputation methods, such as MACH [Li et al., 2006] could have been used as well. Given the small amount of missing data this would not have had any qualitative effect on our results.

NIDDK DATA

The NIDDK GWAS consists of 792 cases of Crohn’s disease and 932 controls. These subjects, Caucasians in the US, were genotyped on the Illumina HapMap300. As for the WTCCC data, we removed subjects with large percentages of missing data, and SNPs that had high missingness rates, or very small Hardy Weinberg P-values. SNPs with small minor allele frequency were retained.

All prediction models that were applied on the NIDDK data used (a subset of) the 3000 marginally most significant SNPs in the WTCCC Crohn’s disease data. As most of the SNPs that were part of the Affymetrix 5.0 panel of SNPs are not part of the HapMap300 panel of SNPs, we used MACH [Li et al., 2006] to impute the data. In particular, we used ten sets of probabilistic inputs based on the CEPH HapMap data, using MACH options --greedy --phase. Since some of the SNPs in the prediction models may be in the same haplotype blocks, we did not want to impute either the “best” imputation, or use marginal posterior probabilities, as those approaches do not acknowledge joint imputation probabilities between two SNPs. The results reported in this paper are based on the average posterior probability of a subject being a case over the ten imputed data sets.

PREDICTION METHODS

Let Y_i, be a binary indicator for the phenotype of subject i = 1, … , n, and let X_ij be the value of SNP j = 1, … , p for subject i, coded as 0,1,2 for the number of minor alleles. We write Y = (Y₁, … , Y_n)^t, X_j = (X_1j, … , X_nj)^t, and x_i = (X_i1, … , X_ip)^t. All approaches that we consider are carried out on data sets of the p most significant SNPs (p ≤ 3000). These most significant predictors are consistently pre-selected on just the training data, and this selection is repeated each of the cross-validation steps. (As the results we report here typically do not change beyond p ~ 2000 and computations are getting increasingly slow, we did not systematically investigate p > 3000.) For the remaining, assume that we have ordered the SNPs, and that X₁ is the marginally most significant SNP, X₂ the next most significant one, and so on.

Since for most phenotypes that are studied in GWAS the signal is small, and often other risk factors are known, we focus on modeling the probability that a subject is a case using logistic regression, rather than looking at classification. We also believe that a probabilistic risk estimate can convey more subtilty than a simple classification. If a classification rule is needed probabilistic estimates can be thresholded taking miss-classification costs in consideration. The simplest approach to model the probabilities is to fit a linear logistic regression model on the p pre-selected SNPs:

$$\mathrm{logit}\left(P\right(Y_i=1\mid x_i\left)\right)={\beta }_0+\sum _{j=1}^p{\beta }_j{X}_{ij}.$$

Traditionally parameters in this model are estimated using maximum likelihood. When large numbers of predictors are used, the logistic regression model is known to overfit the data. Instead, we consider the lasso and the elastic net, two examples of penalized regression methods. Let ℓ(β; Y_i, x_i, i = 1, … , n) be the logistic log-likelihood. The lasso and elastic net estimates of β are the maximizers of

$$\ell (\beta ;Y_i,x_i,i=1,\dots ,n)-{\lambda }_1\sum _{j=1}^p\mid {\beta }_j\mid ,$$

and

$$\ell (\beta ;Y_i,x_i,i=1,\dots ,n)-{\lambda }_1\sum _{j=1}^p\mid {\beta }_j\mid -{\lambda }_2\sum _{j=1}^p{\beta }_j^2,$$

respectively, where λ₁ and λ₂ are estimated using cross-validation. Both of these approaches effectively carry out model selection, as the l₁ penalty ${\lambda }_1{\sum }_{i=1}^p\mid {\beta }_i\mid$; will set many of the coefficients β_j to 0. The potential advantage of the elastic net is that when many of the predictors are highly correlated the l₂ penalty ${\lambda }_2{\sum }_{i=1}^p{\beta }_i^2$ encourages averaging of multiple correlated predictors, while the lasso would select just a single predictor. The elastic net penalty can be viewed as a combination of the lasso penalty and the l₂ penalty form ridge regression, an early penalized regression method [Hoerl and Kennard, 1970]. We applied both approaches, using the R [R Development Core Team, 2009] package glmnet. The implementation of this package has the advantage that computation time does not significantly increases even when 1000s of values of λ₁’s are used in the lasso, making the optimization over this parameter using cross-validation straightforward.

In addition to these penalized regression methods, we considered traditional (stepwise) fitting of logistic regression models. In particular, we considered fitting models of the p marginally most significant predictors (referred to as “GLM”), fitting models of the p marginally most significant predictors, omitting any predictor that is correlated with correlation larger than R = 0.9 to a more significant predictor (referred to as “filtered GLM”), stepwise addition of predictors (considering the top p marginally most significant SNPs) using AIC and BIC to select the number of SNPs (referred to as “stepwise GLM-AIC” and “stepwise GLM-BIC”). The parameter p for GLM and filtered GLM was selected using cross-validation of the log-likelihood. We investigated alternative cut-offs for the correlation between predictors for the filtering and found that the actual value has little influence over a range of about (0.7, 0.95).

CROSS-VALIDATION

There are two model selection steps in our procedure: selecting the parameters λ₁ (lasso and elastic net), λ₂ (elastic net), and p (stepwise glm), and pre-selecting the marginally most significant SNPs that will be considered by the modeling approaches. The parameters were all selected using 10-fold cross-validation on the training data. We considered three approaches to pre-selecting the marginally most significant SNPs:

1. Pre-select those SNPs based on the training and test data combined.

2. Pre-select those SNPs based on the complete training data.

3. Re-select those SNPs for each cross-validation step, using only nine-tenth of the training data that are used to fit the model. After the parameters are selected, the SNPs are once more selected using the complete training data, and the final model is estimated using the complete training data.

In the model selection literature the consensus is that such a pre-selection of SNPs should only use the data that is trained for in a particular validation run (as in Approach 3), and that it should not include the 10% of the training data used for validation (as in Approach 2), and definitely not the test data (as in Approach 1) [Hastie et al. 2001]. Since we noted that each of these approaches to pre-selection have occurred frequently in the GWAS literature we wanted to quantify the magnitude of the problem that using Approaches 1 or 2 causes. For example, in Evans et al. [2009] the AUC values in their Table 1 appear to follow the strict selection rules of Approach 3, but the AUC values in their Table 2, which include variants that were identified in the same study as the one on which they are evaluated, would be considered closer to Approach 1. The International Schizophrenia Consortium [2009] used a separate training and test set when constructing their model, more in line with Approach 2. The model developed in Myocardial Infarction Genetics Consortium [2009] is a mixture of Approaches 1 and 3, as some of the included variants were identified in the study on which the risk model was evaluated, while others were identified in other studies.

Table 1.

Number of SNPs used in the prediction models with non-zero foefficients, log-likelihoo, and AUC (area under the curve) for the test data (n = 1878: 1175 controls and 703 cases) for the WTCCC Crohn’s disease data using the lasso.

method	SNPs used	Log-likelihood	AUC
no SNPs used	0	−1241.77	0.500
GLM	18	−1223.12	0.606
filtered GLM1	26	−1224.94	0.626
stepwise GLM AIC	38	−1287.68	0.631
stepwise GLM BIC	14	−1236.35	0.614
lasso 1 top SNPs considered	1	−1239.33	0.528
lasso 2 top SNPs considered	2	−1231.84	0.551
lasso 5 top SNPs considered	4	−1232.09	0.569
lasso 10 top SNPs considered	6	−1232.71	0.568
lasso 25 top SNPs considered	14	−1207.98	0.612
lasso 50 top SNPs considered	25	−1197.59	0.630
lasso 100 top SNPs considered	33	−1193.20	0.637
lasso 250 top SNPs considered	91	−1196.24	0.634
lasso 500 top SNPs considered	155	−1195.61	0.635
lasso 1000 top SNPs considered	176	−1195.04	0.636
lasso 2000 top SNPs considered	177	−1194.78	0.637

¹For filtered GLM SNPs with correlation larger than 0.9 with a more significant SNP were omitted. The highest rank SNP among the selected SNPs for filtered GLM was 58.

EVALUATION

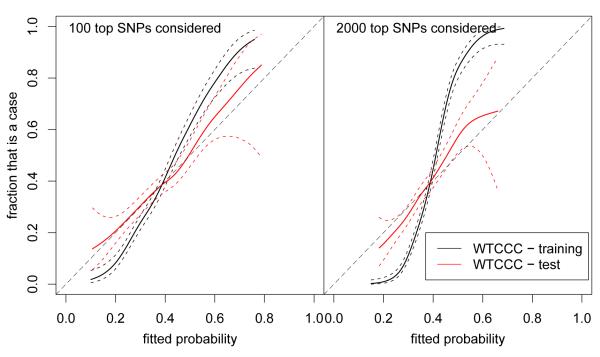
For each of the models, we evaluated the predicted probability of disease using the logistic regression model for the selected model on test data. We summarize these fitted probabilities using test data log-likelihoods, receiver operating characteristic (ROC) curves, and the area under the curve (AUC). For Figures 5 and 7 we fitted a generalized additive model with smoothing splines for logistic regression, using default settings in the R package gam, of fitted probability on case-control status.

Figure 5.

Smoothed estimates of the probability of being a case as a function of the predicted probability of being a case with 95% confidence intervals for the WTCCC Crohn’s disease data. The steeper curves for the training data suggest some overfitting, while the test data appears better calibrated.

RESULTS

After the initial data processing described in the METHODS section, there were 4686 subjects (1748 cases, 2938 controls) in the WTCCC data, which we divided in a training set of 2808 subjects (1045 cases, 1763 controls) and a test set of 1878 subjects (703 cases, 1175 controls).

CROSS-VALIDATION AND THE SELECTION OF SIGNIFICANT PREDICTORS

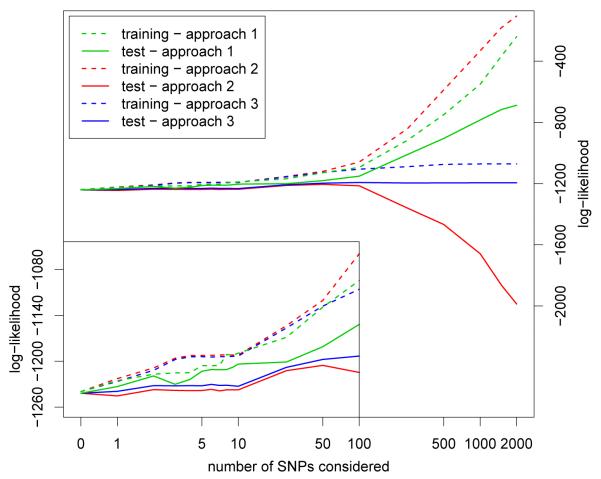
In Figure 1 we show the log-likelihood for the lasso with the three approaches to pre-select the most significant predictors in conjunction with cross-validation for the WTCCC Crohn’s disease data. For Approach 1 all training and test data is used to pre-select the most significant predictors. The effect of this is that the test data is more similar to the training data than would be the case for new independent data. As a result, when the number of SNPs considered increases substantially, even the test results show overfitting. This overfitting, which is very apparent when the number of SNPs considered is larger than 100, is already evident from comparing to Approach 3 when the number of SNPs reaches 10. This result raises concern regarding predictive models for GWAS, where the same data is used to discover the SNPs and to construct the prediction models, even if only the “top established hits” are used.

Figure 1.

Log-likelihood for the WTCCC Crohn’s disease data using three different ways to carry out the pre-selection of significant SNPs in relation to the cross-validation. The training data log-likelihood was rescaled by a factor of 1878/2808 to be on the same scale as the test data log-likelihood.

Approach 2 uses the complete training data but not the test data to pre-select the most significant SNPs. As a result, the 90% learning part of the training data during cross-validation is more similar to the 10% validation part of the training data than to the test data. The effect is that because of this similarity between the validation data and the training data the selected model is larger than it is in Approach 3 (i.e. the λ₁ in the lasso is smaller than what it is in Approach 3), as a result the training data overfits more, the model is too big, and the test data, which is more different from the training data, performs worse. Since the cross-validation results are used to select the model size, this would results in a too complex prediction model being selected.

Approach 3 pre-selects the top SNPs for each cross-validation fold. The effect of this is that the validation 10% of the data is as (dis)similar to the training data as the test data is to the training data. The results for Approach 3 start to deviate from Approach 2 when more than about 50 SNPs are considered. As a result we do not get the incorrect picture that model fits keep on improving with increased model size (such as for Approach 1), or overfitting (such as for Approach 2).

When we compare the test data log-likelihood results that are displayed in Figure 1 with what we would obtain if we used the test data to select the best parameters after the most significant SNPs are pre-selected on the complete training data we find that the difference of this approach, which would generally be considered “cheating”, with the “correct” Approach 3 is much smaller than the differences between Approaches 1 and 3 or the differences between Approaches 2 and 3 (data not shown), suggesting that incorporating pre-selection of the significant SNPs in cross-validation is in fact very important.

CHOICE OF MODELING METHOD

When larger numbers of predictors (SNPs) are used to model a regression outcome, sparse regression methods, such as the lasso [Tibshirani, 1996] and the elastic net [Zou and Hastie, 2005] can be used both to carry out model selection, and for estimation of the parameters in a (generalized) linear model. These sparse regression methods are alternatives to standard generalized linear models (GLM), where model selection is implicitly included by either restricting the generalized linear model to the most significant SNPs, or by using stepwise regression, where at each step of the algorithm the most significant SNP is selected for inclusion in the model.

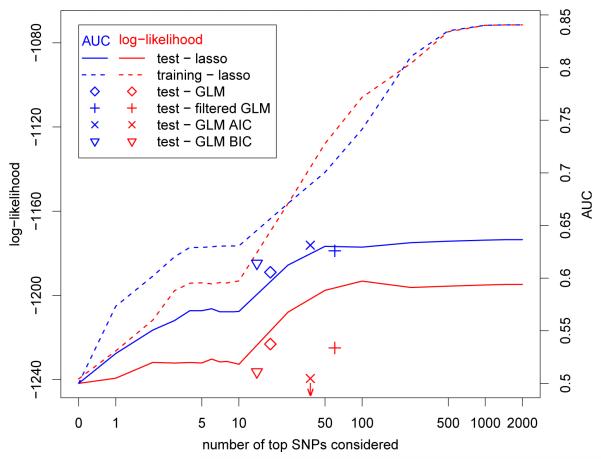
We obtained prediction models using the lasso, the elastic net, GLM, filtered GLM, and stepwise GLM on a training data set of 60% of the WTCCC data. When we applied these models to the remaining 40% of the WTCCC data as test data, leading to test-sample validated predictions, we noted that the lasso and the elastic net gave very similar results, both with respect to the test data log-likelihood and area under the curve (AUC) (Table 1 and Figure 2; the results for the diabetes data are similar).

Figure 2.

Log-likelihood and AUC for the WTCCC Crohn’s disease data for prediction models for test and training data. The training data log-likelihood was rescaled by a factor of 1878/2808 to be on the same scale as the test data log-likelihood. Note that not all SNPs considered have nonzero coefficients, see Table 1. The log-likelihood for stepwise GLM using AIC (GLM-AIC) is −1287.7. The insert figure at the left bottom vertically expands the curves for the models with 100 SNPs or less.

For Crohn’s disease the results for the lasso compare favorably to a standard GLM which, when using the best 18 SNPs selected by cross-validation, had a test data log-likelihood of −1223.1 and an AUC of 0.606. When highly correlated SNPs were omitted a larger model of 26 SNPs (out of the top 58 SNPs) was selected with a log-likelihood of −1224.9 and an AUC of 0.626. A standard stepwise algorithm using the Akaike Information Criterion (AIC) selected 38 SNPs and had a log-likelihood of −1287.7 and an AUC of 0.631, and using the Bayesian information Criterion (BIC) selected 14 SNPs and had a log-likelihood of −1236.3 and an AUC of 0.614. (The maximum number of SNPs considered in the stepwise procedures was 100; when we used a larger maximum virtually no SNPs beyond number 100 were selected.) The AIC selected model has a much worse likelihood because on a few of the test samples some of the correlated SNPs that perform well in the training data yield very bad results. (a few estimated probabilities of a cases close to 0 “sink” the log-likelihood which is all that AIC uses to select the model). This does not effect the AUC, which is comparable to results obtained by the lasso. The filtered GLM, which could be considered as a very simple regularization method for the regression, performs the best of the GLM methods, considering both AUC and log-likelihood.

For most of the elastic net models displayed the λ₂ penalty parameter selected by cross-validation was 0; for models using these number of SNPs the elastic net results are thus the same as the lasso results. For the few models that were different between the lasso and the elastic net the differences in log-likelihood were small, and the differences in AUC negligible. Therefore we do not display the results obtained using the elastic net. Use of the lasso and cross-validation limits the amount of over-fitting, but while the test-data results flatten off when more than 100 SNPs are considered, the training data results still improve, suggesting some over-fitting (Figure 2). For type 2 diabetes there is much less signal in the WTCCC data. The results for type 1 diabetes are somewhat better than for Crohn’s disease because of the strong dependence of type 1 diabetes on the HLA genes. In fact, on the test data for type 1 diabetes we achieved an AUC of 0.88, very similar to the AUCs of between 0.87 and 0.89 that Wu et al. [2009] achieved on the validation part of the training data using Support Vector Machines.

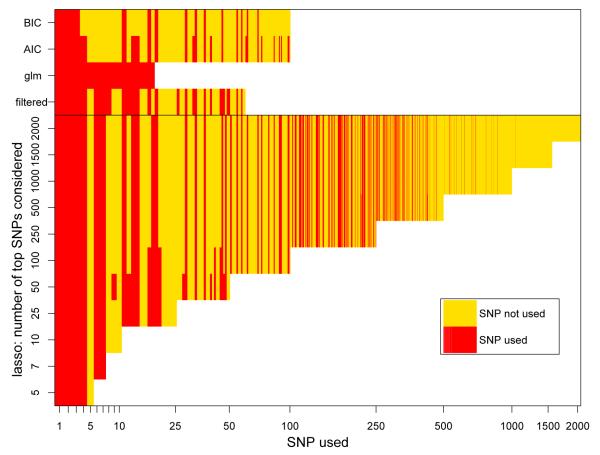
The number of SNPs that have non-zero coefficients in the lasso models levels off at about 175 for Crohn’s disease (Table 1). When 100 of the top SNPs were considered as predictors, 33 ended up having nonzero coefficients in the lasso models. A paired t-test on the likelihoods of the test set, suggests that the model where the top 100 SNPs were considered was significantly better than the model where the top 25 SNPs were considered (p ~ 0.025). While in meta-analysis with other Crohn’s disease data sets such a number of disease associated SNPs in GWAS have been identified, this is a much larger number than what was identified using just the WTCCC data. Similar results were obtained for the WTCCC data for type 1 and 2 diabetes. An advantage of the lasso over other machine learning techniques, such as support vector machines, is the effective selection of SNPs when some parameters corresponding to SNPs get set to zero. In Figure 3 we display for several of the lasso models which of the SNPs that were considered were used with nonzero coefficients, and which SNPs were not used. We note that most SNPs used in models where fewer SNPs are considered are also used in the models where more SNPs are considered, as is evident from the vertical stripes in Figure 3. Some of the highly significant SNPs are not used in a prediction model: for example, the column for SNP 5 is completely yellow, indicating that this SNP is not used in any model. Typically these SNPs are highly correlated with more significant SNPs. (For example, SNP 5 has correlation larger than 0.99 with SNP 4.) On the other hand, a few SNPs that are less significant are used: for example three SNPs with ranks larger than 500 have nonzero coefficients. These SNPs maybe less significant in marginal models, but are more significant in models where the other SNPs are already included.

Figure 3.

Which SNPs are and are not used with nonzero coefficients for the lasso model and other prediction models for the WTCCC Crohn’s disease data. The SNPs are ordered on the horizontal axis by significance. The vertical stripes suggest that frequently the same SNPs are selected.

Receiver Operating Characteristic (ROC) curves based on the test data also improve until approximately 100 SNPs are used for Crohn’s disease (Figure 4) and type 1 diabetes. For type 2 diabetes there is no improvement after about 5 SNPs.

Figure 4.

ROC curves for the WTCCC Crohn’s disease data for prediction for lasso models considering different numbers of SNPs. The AUCs for these models are displayed in Table 1.

CALIBRATION OF PREDICTION PROBABILITIES

In Figure 5 we show the results of a smoothed regression estimate of the fraction of the data that is a case as a function of the estimated probability. We would like the curves for the test data to follow the dashed diagonal; if there was no signal in the data the curves would be horizontal. For the lasso model considering 100 SNPs, and the model considering 2000 SNPs this is the case for the test data, while the curves for the training data become much worse when the number of SNPs that is considered increases. The WTCCC data is case-control data, but we here treat it as cohort data, which is reasonable as both cases and controls are samples of the UK population of cases and controls (be it obtained in different ways). As such, the “incidence” in this data is 40% by design. The population incidence in the US is between 1 in 500 and 1 in 1000; with different population probabilities the axes in Figure 5 would both be rescaled, but the angle of the curve would remain unchanged. To practically use a prediction model, we would want to combine this prediction model with established risk factors, such as age, ethnicity, smoking, and family history. A prediction model using genetics could be seen as a refinement of the family history risk factor.

APPLYING A MODEL OBTAINED FROM ONE GWAS TO ANOTHER POPULATION

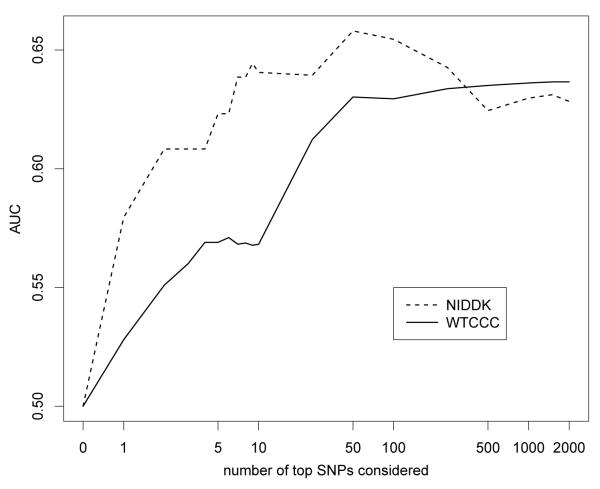
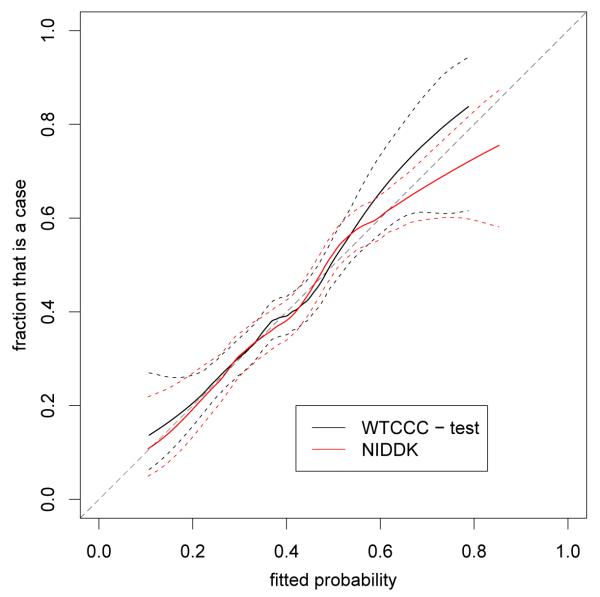
We applied the results from the lasso on the WTCCC data to the data from a GWAS on Crohn’s disease carried out by the NIDDK. While the populations for both GWAS studies are Caucasian, the population for the WTCCC GWAS is from the UK, and the one for the NIDDK GWAS from the USA. There are also many technical differences between these two GWAS; for example, since the NIDDK data were generated on a different platform, genotypes were imputed. See the methods section for details. Figure 6 compares the AUC for models considering different numbers of SNPs for the test data part of the WTCCC data and the NIDDK data. We note that, surprisingly, the AUC for the NIDDK data is larger than for the WTCCC data. Figure 7 shows the results of a smoothed regression estimate of the fraction of the data that is a case as a function of the estimated probability for models considering 100 SNPs, arguably the best model size for the WTCCC data. We note that the probabilities appear well calibrated. (In fact, the models using both 50 and 250 SNPs appeared even better calibrated.)

Figure 6.

Comparison of test data AUC for the NIDDK and WTCCC data. The model for the NIDDK data is trained on the complete WTCCC data, the model for the test part of the WTCCC data is trained on the training part of the WTCCC data.

DISCUSSION

We believe the results from our experiments on three of the diseases studied in the WTCCC GWAS (using a 40% test sample for validation) and full test data from the NIDDK Crohn’s disease GWAS convincingly support the feasibility for constructing multi-SNP risk models from GWAS (albeit with modest predictive strength). These models include SNPs that would have failed a genome-wide significance test. We obtained similar results for the WTCCC GWAS of type 1 diabetes and type 2 diabetes, suggesting that our results are generalizable to other diseases.

Our model building strategy incorporated several important but generally accepted statistical components.

1. The genotyped SNPs were first filtered with respect to missingness, Hardy-Weinberg equilibrium, and minor allele frequency.

2. Smaller numbers of SNPs <3000 were pre-selected for more model building; this step controls the variability of subsequent regression analysis.

3. The penalized regression modeling (e.g. lasso) incorporates variable selection and estimation properties that further controls the variability of the risk estimates.

4. To avoid models which are overly optimistic “the winners curse” (with too many SNPs ) we used cross-validation of the entire model building process, including the pre-selection of the larger number of SNPs that are considered by the penalized regression modeling, to obtain relatively unbiased estimates of prediction error.

In other words, our GWAS risk model statistical recipe includes a small number of ingredients: quality control, variance control, well structured SNP combinations and prediction optimism adjustment via cross-validation.

We believe that applying the model fit on the WTCCC GWAS to the NIDDK GWAS provides a strong confirmation of our approach because of the differences between the two studies: (i) the WTCCC GWAS and NIDDK GWAS were carried out on different genotyping platforms, so that the NIDDK prediction is for more than 90% based on imputed SNPs; (ii) both studies were carried out on different populations, the WTCCC GWAS was carried out in the UK, the NIDDK GWAS within the US; (iii) there is no information whether other important characteristics, such as disease adjudication for the cases and risk profile of the controls, was comparable. Notwithstanding these differences, the estimated probabilities from the WTCCC GWAS derived model, calibrated well on the NIDDK cohort. It has been argued that whether a probability estimate is well calibrated is more important for individual risk prediction than a focus on classification methods or AUC [Cook, 2007].

The predictive ability of the models that we derive, as measured by the area under the curve (AUC) is modest and the greatest utility of these models is probably for risk calculation in research studies. However, we should put that in perspective in that these genetic factors can be used in addition to already established other risk factors. Also, many frequently used risk prediction models have modest AUCs. For example, the often used Gail model for prediction of breast cancer risk [Gail et al. 1989] has an AUC of only about 0.58-0.6 [Rockhill et al., 2001], nevertheless it is used frequently for identifying risk groups for research studies and even sometimes for individual risk prediction, see for example www.cancer.gov/bcrisktool.

Constructing risk prediction models with many predictors requires some form of regularization, as well as careful model selection using, for example, cross-validation. The lasso and the elastic net achieve this in an automated way, but the relatively good performance of the filtered GLM suggests that even some simpler regularization can do a decent job. The lack of regularization in (unfiltered) GLM and the less careful model selection using stepwise GLM can sometimes lead to less impressive results.

We think the success of the lasso algorithm for risk prediction in GWAS is not surprising. The performance of the lasso and several variants has been studied in considerable theoretical detail in the statistics literature. For instance, in early work, Donoho and Johnstone [1994] showed near-minimax risk of the predictions for case of orthogonal predictors. And while orthogonality is not true for GWAS SNPs (since p > n) there is typically small correlation between SNPs that are not close together in the genome.

Theorem 2 in [Zou and Hastie, 2005] implies that the elastic net is a stabilized version of the lasso. It also suggests that if the predictors that are considered are uncorrelated the elastic net solution should be similar to the lasso. Thus, the observation that most of the top SNPs in a GWAS are fairly uncorrelated explains the fact that the elastic net and the lasso perform equivalently in our experiments.

More recently, mathematical studies have shown success of the adaptive lasso algorithm [Zou, 2006], which adaptively weights the penalty function based on initial estimators of the regression coefficients. Such a strategy directly relates to our pre-selection of a smaller number of SNPs to include in the regression based on univariate regression p-values. As the sample size gets large, good performance of the procedure (for both correctly selecting SNPs associated with outcome and prediction error) is obtained if the SNPs that are associated to the phenotype have low only correlation to those SNPs that are not associated with the phenotype. We believe this is a reasonable assumption for most SNPs in GWAS.

We also establish that to get unbiased prediction results it is critical to have a strict separation of training and test data: cases in the test data should not even be used to identify the most significant SNPs. In estimating odds ratios related to the most significant SNPs this effect is generally accepted as the “winners curse” [Zöllner and Pritchard, 2007; Zhong and Prentice, 2008]. Unfortunately, in risk prediction models we have noted that many GWAS publications publish small “prediction models” on the hand-full of SNPs implicated in the same publication.