GPU-enabled FREALIGN: Accelerating single particle 3D reconstruction and refinement in Fourier space on graphics processors

Abstract

Among all the factors that determine the resolution of a three-dimensional reconstruction by single particle electron cryo-microscopy (cryoEM), the number of particle images used in the dataset plays a major role. More images generally yield better resolution, assuming the imaged protein complex is conformationally and compositionally homogeneous. To facilitate processing of very large datasets, we modified the computer program, FREALIGN, to execute the computationally most intensive procedures on Graphics Processing Units (GPUs). Using the modified program, the execution speed increased between 10 and 240-fold depending on the task performed by FREALIGN. Here we report the steps necessary to parallelize critical FREALIGN subroutines and evaluate its performance on computers with multiple GPUs.

Introduction

Single particle electron cryo-microscopy (cryoEM) is a versatile tool for studying the three-dimensional (3D) structures of biological macromolecules at high resolution. Recently, this technique has been used to determine near-atomic resolution structures of icosahedral viruses (Zhang et al., 2008; Yu et al., 2008; Chen et al., 2009; Wolf et al., 2010; Zhang et al., 2010) and large asymmetric protein complexes (Cong et al., 2010). In single particle cryoEM, a 3D reconstruction is calculated from a large number of individual images representing different views of the same molecule. The resolution of a 3D reconstruction is improved iteratively by refining the geometric parameters of each particle, including three Euler angles and two in-plane shifts, and microscope parameters, including defocus and magnification. To reach high resolution, especially when a particle exhibits little or no symmetry, a large number of images are needed to improve the signal-to-noise ratio (SNR) of the 3D reconstruction and to provide finer sampling in Fourier space. With the development of advanced electron microscope systems and large format digital image recording devices, it is now feasible to acquire very large single particle datasets. The time required to process these datasets depends almost linearly on the number of particles in the datasets. Therefore, shortening the time needed for data processing becomes one of the key issues in high-resolution single particle cryoEM.

A commonly used method in single particle cryoEM data processing is to split a dataset into many smaller subsets and distribute them over a cluster of many computer nodes with single Central Processing Units (CPUs), or to parallelize the algorithm to take advantage of a multi-CPU architecture (Bilbao-Castro et al., 2009; Fernandez, 2008; Yang et al., 2007). The data processing speed on this kind of multi-CPU architecture depends on the number of CPUs. An alternative approach is to use Graphics Processing Units (GPUs), which, unlike CPUs, have hundreds of vector processing cores, integrated into one unit. With a large number of cores in one processor, a GPU is capable of performing massively parallelized scientific computing by concurrently applying a single instruction to multiple data (the so-called SIMD architecture) that is commonly used in vector supercomputing. For cryoEM, the idea of using GPUs for data processing has been extensively evaluated and tested in the past few years (Castano-Diez et al., 2008; Schmeisser et al., 2009). Many recent efforts of using GPUs to accelerate cryoEM data processing have shown some significant speed increases (Castano Diez et al., 2007; Schmeisser et al., 2009; Tan et al., 2009).

FREALIGN is a stand-alone program for very efficient refinement and 3D reconstruction (Grigorieff, 2007). A number of subnanometer resolution (Cheng et al., 2004; Fotin et al., 2006; Rabl et al., 2008) or near-atomic resolution (Chen et al., 2009; Wolf et al., 2010; Zhang et al., 2008; Zhang et al., 2010) structures were reconstructed and refined using this program. In FREALIGN, refinement can easily be implemented on a multi-CPU cluster for distributed computing. The time needed to complete a cycle of refinement depends on the number of particles in the dataset and the number of CPUs used for the refinement. The 3D reconstruction step is often carried out on a single CPU. The latest version of FREALIGN (version 8.08) offers some parallelization of the reconstruction step using OpenMPI to accelerate 3D reconstruction (about 3-fold on an 8 core CPU system).

We have modified FREALIGN to utilize the parallel computing power of GPUs. Using a test dataset of images of 20S proteasome, we have achieved a ~10-fold speed increase in the search and refinement steps and a ~240-fold speed increase in calculating a 3D reconstruction. While the detailed computational procedures are modified to enable GPU enhancement, the algorithms for single particle refinement and 3D reconstruction used by the original FREALIGN code were unaltered. Thus, the results obtained with our GPU-enabled FREALIGN code are essentially the same compared to those obtained from the original code. Here we report the computational procedures of our modification to FREALIGN, hardware configurations and test results.

Parallelization of FREALIGN procedures

The general concept and technical details of utilizing the CUDA language to program GPUs for cryoEM image processing have been described in detail, for examples (Castano-Diez et al., 2008; NVIDIA, 2009; Schmeisser et al., 2009). Our current study aims to specifically accelerate FREALIGN on NVIDIA GPUs using CUDA.

The mode of operation in FREALIGN is controlled by an integer called IFLAG. In each mode, the computational procedures can be divided into various subroutines (Grigorieff, 2007). A primary function evaluated multiple times during a search or refinement (IFLAG ≠ 0) is the weighted correlation coefficient, or its inverse cosine (FREALIGN's phase residual). It is calculated between the Fourier transform (FT) of a two-dimensional (2D) particle image and a central section through the FT of the 3D reference. During an iterative search (IFLAG = 4) and refinement (IFLAG = 1) a Powell optimization function is used for maximizing the correlation coefficient of each individual image by optimizing all geometric and microscopy parameters. In a 3D reconstruction (IFLAG = 0), the FTs of all particle images, weighted by using their phase residuals, are inserted into the 3D FT of the new 3D reconstruction using an interpolation function. Thus, two major procedures in FREALIGN are used to calculate correlation coefficients and to interpolate between grid points.

During a search or refinement, the correlation coefficient is calculated by accumulating the co-variances between two images or their FTs. One image is the particle image shifted to the image origin and multiplied by the CTF. The other is a central section of the 3D FT of the reference volume masked by a cosine-edged mask and multiplied by the square of the CTF. To calculate a central section of the 3D volume the value of each pixel in the resulting 2D image is calculated as the sum of the contributions from the nearest n×n×n neighbors (n = 1, 3, or 5). To calculate a 3D reconstruction the contribution of each 2D image pixel is added to its 8 nearest neighbors according to the view presented by the particle in the image.

Table 1 lists the major FORTRAN subroutines in FREALIGN that make use of the correlation coefficient or interpolation functions. Supplementary Table 1 lists the execution times in microseconds needed to complete each subroutine for a particular image size, and Supplementary Table 2 lists the percentage of total runtime taken by each subroutine. Subroutines cc3m() and ccp() are used in search and refinement. Both include three parts: extracting a central section from the 3D FT, applying the cosine mask and CTF to the section, and computing the correlation coefficient. The total time used by these two subroutines in a search or refinement cycle depends on the parameter setting, because they are executed more than once, but together they account for more than 95% of the execution time. The main function of subroutine pinsert_s() is the interpolation used in the 3D reconstruction procedure. It accounts for most of the execution time used for 3D reconstruction and is invoked N times for each contributing image, where N is the symmetry of the particle. The other three subroutines are used less often in a search/refinement/reconstruction cycle.

Table 1.

List of primary FREALIGN subroutines that can be parallelized

	Subroutine	Description
Refinement	cc3m()	Calculate overall phase residue in Fourier space
	ccp()	Calculate cross-correlation in Fourier space
Reconstruction	pinsert_s()	Interpolate a particle image into 3D Fourier transform of the volume being reconstructed
Other	sigma2()	Calculate correlation coefficient in real space
	presb()	Calculate amplitude correlation coefficient in Fourier space
	ccoef()	Calculate correlation coefficient in real space

In the original version of FREALIGN, the subroutines listed in Table 1 consist of calculating FTs and loops over each pixel in a 2D image for interpolation, masking and summation. These loops execute the same computation for each pixel and can, therefore, be parallelized following the SIMD architecture. The computations within a loop are first cast into a function to be executed on a GPU, named kernel in CUDA (NVIDIA, 2009). Furthermore, a thread array is created according to the dimension of the pixel array of the 2D image. All threads in the array execute the kernel concurrently, one for each pixel in the image. For the computation in real space, the dimension of both thread array and image array is m×m, where m is the dimension of the particle image. In Fourier space, FREALIGN uses reduced image arrays to save memory. Thus, the dimension of both the image and thread arrays is m×(m/2+1). The entire thread array needs to be divided into many blocks in order to run on multiple processors (MPs) of the GPU. In the current version, the dimension of blocks for computing the correlation and interpolation is 32 × 16 and 16 × 16 threads, respectively, following recommendations by the manufacturer (NVIDIA, 2009).

Most loops in FREALIGN's procedures can be parallelized following the method mentioned above except those involving summation. In CUDA, the addition operation includes three individual steps: an argument is read from memory, a number is added to it, and the result is written back to the same memory location. If executed by multiple threads concurrently, there are two potential problems that are commonly known as data hazard. First, when an argument is read by one thread for addition, the same argument could be read by another thread for the same operation before it is updated from the result of the first thread. Second, if more than one thread writes their results to the same address at the same time, CUDA only guarantees one of the writes to succeed (NVIDIA, 2009). In both cases, CUDA will return an undefined result. In the parallelized FREALIGN subroutines, a potential data hazard occurs in two places: one is the interpolation for the 3D reconstruction, when the contributions from different image pixels are added simultaneously to the same pixels of the FT of the new reconstruction; the other is the summation of co-variances for calculating the correlation coefficient.

The first situation occurs infrequently, but the memory address accessed by multiple threads is usually unpredictable. We avoid data hazard by setting a barrier to prevent the addition operation to be interrupted. Although this approach effectively converts the addition to the same address into a sequential operation, it does not have a serious impact on the performance due to its rare occurrence. The second situation is more complicated because all threads calculate additions to the same address. With the barrier directive, the resulting sequential addition would slow execution substantially. To overcome this problem, we adopted a parallel tree-structured summation algorithm as shown in Figure 1A. The summation between every two pixels is carried out in a synchronized manner to get a new set of data with half the size. This procedure is repeated until the final result is obtained. According to CUDA, the synchronization is only available for the threads in the same blocks and blocks in the same grid. Therefore, the tree-structured summation is at first calculated within blocks. The result from each block is written to global memory. After all blocks have finished, the results are summed up using the same method again until the final result is obtained.

Figure 1. Implementing parallelization of FREALIGN.

(A) Tree-structured parallel summation algorithm. The sums between every two pixels within the same block are computed in synchronization, and repeated until the final result is obtained. (B) Dividing and distributing subsets of the data on multiple GPUs for search and refinement. (C) Dividing and distributing subsets of the data on multiple GPUs for 3D reconstruction.

In order to minimize data transfer between host and GPU all data are stored in the global memory of the GPU whenever possible. When a FREALIGN job is launched, either for a search/refinement or a 3D reconstruction, the 3D reference volume and/or the new 3D reconstruction are loaded into the global memory of the graphics card at the beginning. A 2D particle image is loaded when it is used for the first time. In addition, all temporary arrays are allocated in the global memory at the beginning of FREALIGN to avoid the time needed by dynamic memory allocation during the execution.

Because of the relatively high latency of the global memory, we adopted the following strategies to improve execution performance. First, the temporary arrays used in the summation, which will be accessed many times, are loaded from the global memory into the in-chip shared memory of the GPU at the beginning of the kernel launch. Only the final results are written back to the global memory. Second, the pixel arrays for the 2D images and CTF are accessed following a sequential pattern, thus enabling the GPU to coalesce many accesses to a single access. Third, the FT of the 3D reference is bound to the read-only texture memory space. When sectioning the FT of the 3D reference map, only pixels of the 3D FT along a defined orientation are accessed by the threads. The random orientation of all 2D images leads to a random memory access pattern. By using the texture hardware, which is designed for such random access, the high latency of the global memory is avoided. However, the size of this texture memory limits the size of the volume it can handle. Currently, we limit the image size that can be handled by the GPU-enabled FREALIGN to 500 × 500.

In this study, we used two computer systems with four or eight GPU devices (Table 2) for our testing. The parallelization of FREALIGN discussed above was expanded to a multi-GPU architecture by partitioning and distributing the dataset evenly between multiple devices, i.e. each GPU device processes only a few particles of the whole dataset. Figures 1B and C show schematic diagrams of parallelization on a multi-GPU setup, in which the POSIX thread library is used to create host threads on each CPU that controls GPU devices. Each CPU thread then launches corresponding GPU kernel/threads to process a subset of the data.

Table 2.

Configurations of the computer systems used for the test

System	I	II
Operating system	Fedora 11	Centos 5
Motherboard	Asus P6TD Deluxe	SuperServer 7046GT-TRF
CPU	1 × Intel i7 920 quad core, 2.66 GHz	2 × Intel Xeon X5550 quad core, 2.66 GHz
RAM	12GB DDR3-1333	24GB DDR3-1333
Graphic Card	2 × NVIDIA GeForce GTX 295	4 × NVIDIA GeForce GTX 295
Total number of GPUs1	4	8

¹Each GTX 295 graphic card was connected through a PCI-E 2.0 16X expansion slot. In both systems, all GPUs were used for computation only (no display). In System I, a third NVIDIA graphic card, GeForce 8400 GS was used to drive a display. In System II, an onboard VGA controller is used for the display.

In a multi-CPU/GPU architecture, the entire dataset is split sequentially into a number of subsets for the search/refinement. The number of subsets is equal to the total number of GPU devices available. Each subset is then processed independently on each CPU/GPU device and the output parameter files are merged when completed (Fig. 1B). For calculating a 3D reconstruction, assuming there are N GPU devices (N must be an even number), the dataset is split into N subsets in such a way that the particles assigned to the nth subset (n = 1, 2, ..., N) have the particle numbers of mN+n, where m is an integer variable (Fig. 1C). In FREALIGN, a 3D reconstruction is calculated from a 3D FT of a 3D volume in Fourier space where each sample point is calculated as following (Grigorieff, 2007):

$$R_i=\frac{\sum _j{w}_j^2{b}^2{c}_j{P}_{ij}}{f+\sum _j{\left(w_{j}b{c}_j\right)}^2}.$$

Here, R_i represents sample i in the 3D FT of the reconstruction, P_ij is a sample from the FT of particle image j (before CTF correction) contributing to sample R_i, c_j is the CTF for image j corresponding to that point in the image, b is the interpolation function (for example, box transformation), and w_j is a weighting factor describing the quality of the image. f is a constant, similar to a Wiener filter constant, that prevents over-amplification of terms when the rest of the denominator is small. Thus, a total of N numerator and denominator arrays are calculated in Fourier space from particles of N subsets by N GPUs concurrently. Next, two numerator and denominator arrays are calculated by merging N/2 corresponding arrays from the even and odd numbered GPUs respectively. Two 3D reconstructions are calculated from these two sets of numerator and denominator arrays respectively, corresponding to all odd and even numbered particles. These two 3D reconstructions are used to calculate a Fourier Shell Correlation (FSC) curve. The final 3D reconstruction is then calculated by merging the two 3D reconstructions from odd and even numbered particles. Figure 1C shows an example of calculating a 3D reconstruction using 4 GPU devices.

Test and results

We have parallelized the code of FREALIGN (version 8.06) as described above and tested its performance with two single particle cryoEM datasets. One test dataset contained a total of 44,794 images of archaeal 20S proteasome with 224 × 224 pixels size. Previously, we published a 3D reconstruction calculated from this dataset at a resolution of ~6.8Å using the unmodified version of FREALIGN. Acquisition and processing of this dataset is described in (Rabl et al., 2008). We also generated a series of new test datasets of yeast 20S proteasome with image sizes between 100 ~ 500. We tested the GPU-enabled FREALIGN on two different multi-GPU systems (System I and II in Table 2). To compare the performance of the unmodified (non-GPU) version of FREALIGN running on a single CPU core with the performance of the GPU-enabled code running on a single GPU, we used System I with only one GPU enabled. This ensured that the hardware configuration remained the same in these tests. The performance of the GPU-enabled FREALIGN was characterized by measuring the speed enhancement factors with respect to the single core CPU reference (Fig. 2 and 3, Supplementary Table 3 and 4). Furthermore, we determined the additional acceleration gained by using multiple GPUs (four on System I and eight on System II).

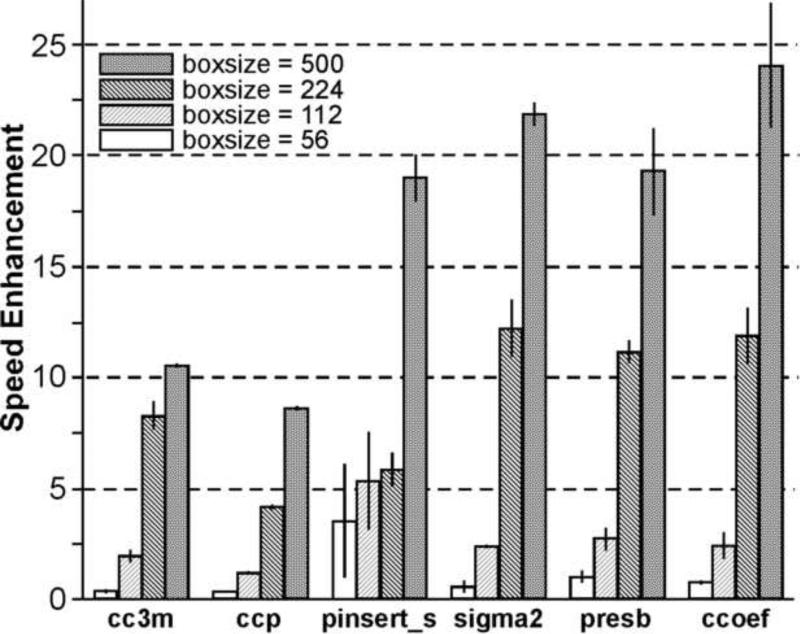
Figure 2. Speed enhancement factors of individual FREALIGN subroutines.

Acceleration of individual subroutines with different image sizes: 56 × 56 to 500 × 500 pixels. For the measurement of the speed enhancement factors, only one GPU on system I was used.

Figure 3. Acceleration of search and refinement by GPU-enabled FREALIGN with various image sizes.

(A) Search and (B) refinement. The accelerations factors were measured on a single GPU on System I vs. a single i7 CPU core on the same system. The corresponding execution times are listed in Supplementary Table 3 and 4. (C) Reconstruction. The acceleration factors were measured on 4 and 8 GPUs on System I and II, respectively, vs. a single CPU core on the same systems.

The GPU-enabled version of FREALIGN is a mixture of CUDA, C/C++ and FORTRAN77 code. The parts that control data flow and computations were coded in C/C++ and CUDA as described above. All code was compiled and linked using G77, GCC 3.4 and CUDA 2.3. The CPU version of FREALIGN v8.06 was compiled using default flag of the original package, and the same flags were also used to compile the GPU-enabled version.

We first evaluated the speed increase of six major FREALIGN subroutines listed in Table 1 when processed on a single GPU on System I. For the tests we used a number of different image sizes of the archaeal 20S proteasome dataset, 56 × 56, 112 × 112, 224 × 224 and 500 × 500 pixels (Fig. 2 and Supplementary Table 1). The speed enhancement factor increases steeply with the increase of the image size. A ~25-fold speed increase was achieved in subroutine “ccoef()”, and a ~20-fold speed increase was observed for subroutine pinsert_s(). The highest speed gain is obtained for 500 × 500 pixel images, the largest image size we have tested. However, the acceleration factor is less than 1 for images of 56 × 56 pixels and, therefore, the GPU-enabled FREALIGN is slower than the original version for such small images. The overall dependency of the GPU-enabled FREALIGN on image size is consistent with other reports on similar algorithms (Castano-Diez et al., 2008; Tan et al., 2009).

The overall performances of three different FREALIGN modes, i.e. search (IFLAG = 4), refinement (IFLAG = 1) and reconstruction (IFLAG = 0) were evaluated for various image sizes of yeast 20S proteasome dataset (Fig. 3, Supplementary Table 3 and 4). The acceleration factors for search and refinement were evaluated as the ratios of execution times of the original and CPU-enabled version of FREALIGN to complete processing of the same number of particles (Fig. 3A and B, Supplementary Table 3). Because the GPU-enabled FREALIGN requires an even number of GPUs for 3D reconstruction (see above), the speed enhancement factors of 3D reconstruction were evaluated by comparing execution times on a single CPU core on System I and System II with execution times using 4 and 8 GPUs on System I or II, respectively. This resulted in speed enhancements of ~130 or ~240-fold for the 4 and 8 GPU systems, respectively (Fig. 3C, Supplementary Table 4).

We also evaluated the acceleration of search and refinement when using multiple GPUs vs. a single GPU (Fig. 4, Supplementary Table 5), and 3D reconstruction when using 8 GPUs vs. 4 GPUs. For all tasks, the acceleration with multiple GPUs is approximately proportional to the total number of GPUs used. The linear behavior parallels the acceleration observed when distributing the parameter search and refinement for particles in a stack as smaller stacks across multiple CPUs in a cluster (see above). One minor difference is that the GPU-enabled FREALIGN handles parallelization over multiple GPUs automatically while job distribution on a cluster is usually handled by a shell script running multiple instances of FREALIGN.

Figure 4. Acceleration of GPU-enabled FREALIGN on multiple GPUs.

(A) Search, (B) refinement and (C) 3D reconstruction. Solid lines are the speed enhancement factors obtained for System I while dashed lines apply to System II. All corresponding data are listed in Supplementary Table 5.

Except for parallelization, we did not alter the original algorithms of FREALIGN. Thus, the results of the GPU-enabled FREALIGN and the original CPU version of FREALIGN are essentially the same (Supplementary Figure 1).

Conclusion

In our current study, the time-critical subroutines of the single particle reconstruction and refinement program FREALIGN were parallelized using CUDA. The goal of this work is to accelerate the iterative refinement-reconstruction cycles performed by FREALIGN using GPUs without changing the accuracy of the result. We focused on parallelizing subroutines that involve mostly computations in Fourier space, and kept the data structure and all the data processing algorithms unchanged. We achieved between 10 ~ 25-fold speed enhancements in individual procedures, and a ~10-fold acceleration in the overall performance of the search and refinement operations. Similar to the original (non-GPU) version of FREALIGN, the search and refinement tasks can be distributed over multiple GPUs. We also parallelized the 3D reconstruction on multiple GPUs and achieved an acceleration of ~240-fold on an 8-GPU system compared with calculations on a single CPU core. This factor is likely to increase further with more GPUs. Speed enhancement will be smaller when compared to multithreaded 3D reconstruction on a multi-core CPU system using the latest version of FREALIGN (version 8.08), which is OpenMPI-enabled. As expected, comparison of the final reconstructions from all tests show that the results from the GPU-enabled FREALIGN are essentially the same as those obtained from the original FREALIGN running on CPUs. Our current work represents an important step towards a high-performance data processing system for large single particle cryoEM dataset using FREALIGN.