The contribution of individual subunits to the coupling of the voltage sensor to pore opening in Shaker K channels: effect of ILT mutations in heterotetramers

Abstract

Voltage-gated ion channels couple conformational change(s) of the voltage-sensing domain to those of the opening of an intracellular gate to allow ionic conduction. Much larger positive potentials are required to couple these conformational changes to the opening of the gate of Shaker K⁺ channels with the concurrent mutations V369I, I372L, and S376T (ILT) at the N-terminal end of the S4 segment. We used cut-open oocyte voltage clamp to study the biophysical and thermodynamical properties of heterotetrameric concatemerized channels with different stoichiometries of ILT mutations. The voltage-sensing domains of ILT mutant channels require smaller depolarization to activate but their intracellular gate does not immediately follow the movement of the voltage-sensing domain, requiring larger depolarization to open. Our results demonstrate that each subunit contributes equally to the rightward shift of the conductance–voltage relationship and that a single ILT-containing subunit is sufficient to induce a large enthalpic and entropic barrier, limiting opening of the intracellular gate.

INTRODUCTION

Opening of voltage-dependent K⁺ channels repolarizes the cell membrane during the falling phase of the action potential (Hodgkin and Huxley, 1952). Displacement of the channels’ voltage sensors through the membrane electric field produces small currents, known as gating currents (Armstrong and Bezanilla, 1973, 1974; Keynes and Rojas, 1973), that precede the large ionic currents through the pore of the channels. Several studies have established that both the gating and ionic currents have complex kinetics (for review see Bezanilla, 2000), suggesting that multiple conformational changes occur in the channel’s structure during these processes. The non(fast-)inactivating voltage-dependent K⁺ channel Shaker (Δ6-46) has provided a powerful tool to establish fine details of activation processes (Hoshi et al., 1991, 1994; Zagotta et al., 1994a,b). However, the relation between conformational changes and the ionic and gating currents are still not fully understood.

From a structural standpoint, the gating currents arise principally from the displacement of four charged arginine residues in the S4 segment from each of the four subunits within the membrane electric field (Aggarwal and MacKinnon, 1996; Seoh et al., 1996; Starace et al., 1997; Starace and Bezanilla, 2001, 2004; Asamoah et al., 2003; Chanda et al., 2005). After movement of the voltage sensor (or of the voltage-sensing domain comprising transmembrane segments 1–4), the inner bundle crossing helices (lowest part of S6, which forms the intracellular gate) must undergo a conformational change to allow ion permeation through the pore (Holmgren et al., 1998; Liu et al., 2001; Ding and Horn, 2002, 2003; Webster et al., 2004; Jogini and Roux, 2005). However, the mechanism of coupling between these conformational changes is yet to be solved (Hackos et al., 2002; Lu et al., 2002; Sukhareva et al., 2003; Long et al., 2005a,b, 2007; Soler-Llavina et al., 2006; Sadovsky and Yifrach, 2007).

The concurrent conservative mutations in the S4 segment of Shaker, V369I, I372L, and S376T have been shown to modify the voltage-dependent reactions of the channel, inducing a large separation of the charge distribution and the open probability along the voltage axis (Smith-Maxwell et al., 1998a,b; Ledwell and Aldrich, 1999). This uncoupling between gating and opening is believed to represent an effect on the last concerted step that opens the channel after all four voltage sensors have moved (Zagotta et al., 1994a; Schoppa and Sigworth, 1998a; Ledwell and Aldrich, 1999) independently (Gagnon and Bezanilla, 2009).

Analysis of the functional characteristics of an engineered heterotetrameric single voltage sensor Shaker, with one wild-type subunit and three neutral (i.e., carrying neutral residues in place of the four Arg) S4 subunits has allowed the isolation of single voltage sensor functioning, refinement of previously proposed gating models, and demonstration of independence in voltage sensor movement (Gagnon and Bezanilla, 2009). As the ILT mutations affect the concerted (i.e., nonindependent) movement(s) of the four subunits that follows the independent activation of four voltage sensors, it appears important to address the effect of disrupting the symmetry of ILT mutations on channel gating. In this report, we explore the mechanism by which the ILT mutations produce their effect in Shaker by studying the biophysical and thermodynamic properties of heterotetramers with different ILT stoichiometries. Our results show that the right shift of the conductance in the voltage axis is the result of equal contribution of each of the ILT-bearing subunits. In addition, we provide evidence that the overall opening transition in the ILT mutant involves an increase in free energy with similar contributions by each subunit.

MATERIALS AND METHODS

Site-directed mutagenesis

Site-directed mutations were introduced according to Fisher and Pei (1997) and confirmed by dideoxy DNA sequencing (University of Chicago Cancer Research Center, DNA Sequencing Facility). For simplifying the notation throughout the paper, Shaker zH4 Δ6–46, or noninactivating (IR) (Hoshi et al., 1990), and the quadruple mutant (R362Q/R365Q/R368N/R371Q) will be referred to as wild type (or wt) and neu, respectively (Gagnon and Bezanilla, 2009). The mutations V369I, I372L, and S376T will be referred to as ILT. Fig. S1 A shows the comparison of the amino acids of the S4 segment in Shaker, neu, and Shaker ILT.

Concatenated cDNA construction

The tandem tetramer cDNA constructs were designed as described previously (Gagnon and Bezanilla, 2009). In brief, as illustrated in Fig. S1 B, the tetramer constructs have a unique six-base restriction site between each protomer to allow cDNA sequencing. The C terminus of domain I was linked to the N terminus of domain II by a proline residue, creating an AvrII restriction site. Domain II C terminus and domain III N terminus were linked with a histidine residue and are thus separated by an NdeI restriction site, and domains III and IV with an aspartic acid, which gives an AatII restriction site. The first methionine residue of domains II and IV were mutated into arginine and valine, respectively. For the sake of simplicity, the tandem tetramer wt_ILT/wt/wt_ILT/wt will be referred to as 2ILT/2wt.

Expression in Xenopus oocytes

cDNA was linearized using NotI (New England Biolabs, Inc.), and in vitro mRNA transcription was performed using mMESSAGE mMACHINE T7 kit (Applied Biosystems). 50 ng mRNA was injected in Xenopus oocytes and measurements were done 1–3 d after injection. The oocytes were kept at 18°C (or 12°C) in a solution containing (in mM) 100 NaCl, 2 KCl, 1 MgCl₂, 1.8 CaCl₂, 5 HEPES, 0.1 EDTA, supplemented with penicillin 100 U/ml and streptomycin 0.1 mg/ml (or 50 mg/ml gentamicin).

Electrophysiology

Cut-open voltage clamp measurements were performed to asses the function of heterologously expressed tetramer tandem channels and were performed at room temperature unless otherwise noted. Room temperature was around 19–20°C. Otherwise, the temperature was set with an in-house fabricated temperature controller (or TC-10, Dagan Corporation) and verified in the top chamber using a temperature probe (HH-25, Omega Engineering, Inc.). The variation of the temperature in the top chamber was approximately ±0.5°C. All concatemer constructs carried ionic currents of similar amplitude as compared with Shaker 1–2 d after injection.

Cut-open recording was essentially performed as described previously (Cha and Bezanilla, 1998; Gagnon and Bezanilla, 2009). In brief, the agar bridges were filled with 1 M N-methyl-d-glucamine-methanesulfonic acid (NMG-MS); the current microelectrode was filled with 3 M CsCl and had resistance of ∼0.1–0.3 MΩ. Data were filtered at 10 kHz and sampled at 50 kHz. The linear leak and the remaining noncompensated capacitance were either subtracted online using the standard P/−4 (unless otherwise noted) protocol with subtracting pulses from holding potential (HP) of −120 mV or analogically compensated for capacitance but nonsubtracted, as noted in the figure legends.

The cell-attached configuration of the patch clamp technique was used to record single channel activity (or macroscopic currents), using 2–5 MΩ pipettes with borosilicate glass (WPI, Inc.), in symmetrical 120 K⁺, using the Axopatch 200B amplifier (Axon Instruments). Data were filtered at 20 kHz and sampled at 100 kHz for macroscopic currents or filtered at 5 kHz and sampled at 50 kHz for single channel measurements. The HP was set to −100 mV. Single channel transitions were measured on patches containing macroscopic amount of channels (current >50 pA at +100 mV) but studied in the range of voltage at which few channels open. Blank traces (containing no activity) were averaged for offline subtraction of linear capacitance. All points’ histograms were constructed and fitted with Gaussian distributions to determine the single channel current.

Solutions

In the cut-open oocyte technique, the solutions were composed, respectively, of (in mM) internal solution, 120 potassium methanesulfonate (MS), 20 HEPES, 2 EGTA (120 K⁺), and external solutions, 103 NMDG-MS, 12 K-MS, 20 HEPES, 2 Ca-(MS)₂ (12 K⁺), or 120 K-MS, 20 HEPES, 2 Ca-(MS)₂ (120 K⁺), or 70 NMDG-MS, 50 K-MS, 20 HEPES, 2 Ca-(MS)₂ (50 K⁺), as noted. When specified as so, the solutions for gating current measurements were composed, respectively, of (in mM): 115 NMG-MS, 20 HEPES, and 2 EGTA (internal) and 115 NGM-MS, 20 HEPES, and 2 Ca(OH)₂ (external).

In patch-clamp experiments, the pipette (external) solution was (in mM): 120 K-MS, 20 HEPES, and 2 CaCl₂. The oocytes were bathed with 120 mM K-MS and 20 mM HEPES. The pH of each solution was 7.4.

Data analysis

The conductance–voltage (G-V) curves were obtained from the amplitude of the tail currents at a constant return potential or calculated as G = I/(E − E_r). The G-V (or Q-V) curve were fitted with Origin version 7 or 8 (Microcal Software, Inc.) with a Boltzmann (i.e., G = [1/(1 + exp(V − V_1/2)zF/RT)]). The fits with Origin were performed using the Levenberg-Marquardt algorithm and the instrumental weighting method.

Time constants of activation and deactivation were obtained by fitting single or double exponentials with an in-house program (or Clampfit 10.2, Molecular Devices) using the Levenberg-Marquardt algorithm, which is a minimization of the χ² to the currents. When more than one time constant was necessary for the fit, weighted time constants were shown and calculated as τ = (ΣA_iτ_i)/(ΣA_i), where A_i is the exponential coefficients and τ_i the time constants. Uncertainty on weighted τ was calculated using propagation of error.

The thermodynamic parameters were calculated based on the transition state theory. The chemical component of the free energies (ΔG = G_α − G_β) is related to the rate constants α (forward) and β (backward), respectively, by the following equations:

$$\begin{array}{c}\alpha ={\alpha }_0\exp \left(\frac{z_{\alpha }FV}{RT}-\frac{G_{\alpha }}{RT}\right)\hspace{1em}\text{and}\\ \beta ={\beta }_0\exp \left(\frac{-z_{\beta }FV}{RT}-\frac{G_{\beta }}{RT}\right),\end{array}$$ (1)

where α and β are the rates of activation and deactivation (α = 1/τ_act and β = 1/τ_deact), and F, V, R, and T are the Faraday constant, the voltage, the gas constant, and the temperature, respectively. A global fitting was performed using SCoP (simulation control program) version 3.5 (http://www.simresinc.com/scopinfo.html) with the ratio of the forward and backward rates measured at the different temperatures to determine ΔG, z_α, and z_β. The activation energy (E_a) was calculated from the slope of the Arrhenius plot (−E_a/R). The enthalpy and the entropy (ΔH and TΔS) changes can be calculated from the other parameters with the following equations:

$$\Delta H=\left(E_{\alpha }-E_{\beta }\right)+\left(z_{\alpha }-z_{\beta }\right)FV$$ (2a)

$$\Delta G=\Delta H-T\Delta S.$$ (2b)

Kinetic model

The kinetic model was programmed using SCoP. For the fitting, SCoP searches for the lowest standard error value; it is a least square or χ² fit. The optimization algorithm is called PRAXIS for principal axis method. The global fitting routine was used to fit the data to the model.

Statistics

The experiments were performed on at least three oocytes obtained for a minimum of two different donors. Data are reported as mean ± SEM. Statistical difference was tested using ANOVA test in Origin, which assumes a normal distribution of error. Statistical significance was set at P < 0.05.

Online supplemental material

Fig. S1 provides the color code used for identifying the concatemer constructs in the figures and more details about their construction. Online supplemental material is available at http://www.jgp.org/cgi/content/full/jgp.201010487/DC1.

RESULTS

Functional effect of changing the number of ILT mutant subunits

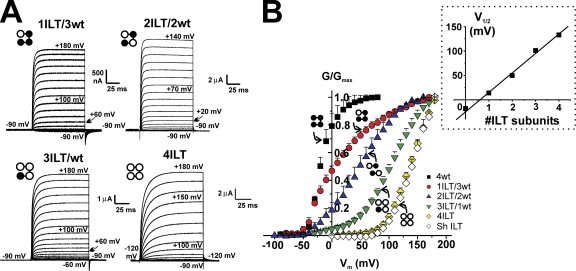
We created concatemerized Shaker tetramers with different stoichiometries of the ILT mutation-containing subunit to further understand the mechanism by which these mutations produce their effect. The homotetramers and heterotetramers with different stoichiometries of ILT were expressed in Xenopus oocytes and studied under cut-open voltage clamp. We measured no functional difference between Shaker ILT expressed as monomers or as a concatemer (4ILT) either in the ionic currents (Fig. 1 B, white and yellow diamonds) or gating currents (see Fig. 8 A, below). Thus, as shown previously for concatenation of wt Shaker (Gagnon and Bezanilla, 2009), our concatenation of the four subunits has no effect on the ILT homotetramer function. Typical family of current traces elicited by pulses from −90 mV (or −120 mV, see figure legend) to the indicated voltages in oocytes injected with each construct are shown in Fig. 1 A. The traces show the influence of ILT stoichiometry on activation kinetics (see below). Fig. 1 B depicts the normalized conductance (G/G_max)–voltage (V) curve for the homotetramer constructs 4wt, 4ILT, and Shaker ILT together with that of the heterotetramers 1ILT/3wt and 3ILT/1wt, and the average of the dimers wt/ILT and ILT/wt. It is noteworthy that the curves for the concatemerized 4ILT and that of Shaker ILT expressed as monomers superimpose. Two striking differences between the hetero- and homotetramers emerge. (1) There is an incremental shift of the G-V curve toward positive voltages as more ILT-containing subunits are added. The inset of Fig. 1 B shows the linear relationship between the midpoint (V_1/2) of the G-V curve and the number of ILT subunits. (2) There is a complex change in the slope of the G-V curves that is steep on both homotetramers and shallower in the heterotetramers. This second effect is complex because the G/G_max-V for one of the constructs does not follow a simple Boltzmann distribution. However, this is in line with the known effect that the transition from the deep closed states to the open state is a multi-state process (Zagotta et al., 1994a; Schoppa and Sigworth, 1998a).

Figure 1.

Functional effect of the stoichiometry of ILT subunits on Shaker. (A) Typical recordings of family of ionic currents from oocytes expressing heterotetramer constructs. The pulses were applied from an HP of −90 mV (with or without prepulse to −120 mV, as noted) to membrane potentials varying from −90 to +180 mV, by 10-mV step for each heterotetramers. The external and internal solutions contained 12 and 120 mM K⁺, respectively. (B) Normalized G-V curves for each heterotetramer. The conductance was calculated using the peak tail currents measured in symmetrical 120 mM K⁺ for the concatemers 4wt (black squares, n = 4), 1ILT/3wt (red circles, n = 7), averaged of dimers wt/wt_ILT and wt_ILT/wt (blue up triangles, n = 9 total), 3ILT/1wt (green down triangles, n = 5), 4ILT (yellow diamonds, n = 5), and Shaker zH4 Δ6-46 ILT (open diamonds, n = 5), respectively. The inset shows the V_1/2 of the G-V curves plotted against the number of ILT subunits. The straight line represents a linear fit to the data. The values for 4wt were taken from Fig. 4 of Gagnon and Bezanilla (2009).

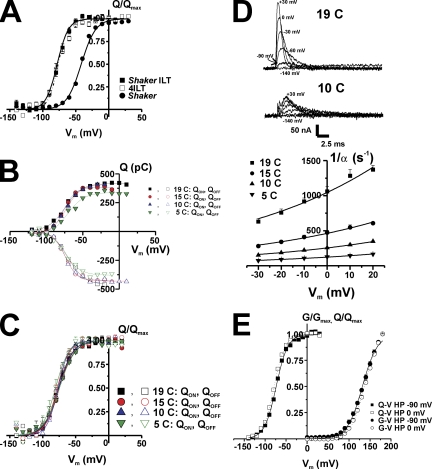
Figure 8.

Temperature and HP effects on 4ILT. (A) The voltage dependence of the charge movement in Shaker ILT, 4ILT compared with that of Shaker. Gating currents were measured in oocytes expressing Shaker, Shaker ILT, and 4ILT, integrated over time to get the transferred charge at different V_m and obtain the Q-V curve. HP was −90 mV, subtraction was made online with the P/−4 protocol, and subtracting HP was −120 mV. Each oocyte’s Q-Vs were individually fitted with a Boltzmann relationship (Q = Q_min + Q_max/(1 + exp[−z(V_1/2 − V_m)F/RT]) in which z, F, R, and T have their usual meanings. The curves were normalized and baselined so that the charge at hyperpolarizing V_m is null. The V_1/2 have values of −50 ± 2, −77 ± 2, and −77 ±1 mV and z of 2.6 ± 0.3, 2.3 ± 0.5, and 2.4 ± 0.4 for Shaker (filled circles, n = 4), Shaker ILT (filled squares, n = 4), and 4ILT (open squares, n = 4), respectively. The external and internal solutions for gating current measurement were used and both contained 115 mM NMG⁺. (B and C) No effect of temperature on the steady-state charge movement in 4ILT. Q-V curves (Q_ON and Q_OFF) at various temperatures, as indicated, for a typical oocyte expressing 4ILT (B). Filled symbols correspond to the Q_ON and the open symbols to the Q_OFF; squares (19°C), circles (15°C), up triangles (10°C), and down triangles (5°C). Averaged Q/Q_max-V curves (n = 4) for 4ILT (C). The averaged V_1/2 were −76 ± 1 and −75 ± 1 (Q_ON and Q_OFF, 19°C, squares), −75 ± 1 and −78 ± 1 (Q_ON and Q_OFF, 15°C, circles), −76 ± 1 and −77 ± 1 (Q_ON and Q_OFF, 10°C, up triangles), −75 ± 1 and −80 ± 1 mV (Q_ON and Q_OFF, 5°C, down triangles), respectively. The slope factors were all comprised between 2.1 and 3.1 ± 0.1–0.3. The external and internal solutions contained 12 and 120 mM K⁺, respectively. (D) Temperature decrease slows the kinetics of ON gating charge in 4ILT. Traces from −140 mV to +30, 0, −30, −60, and −90 mV are shown, as indicated, at 19 and 10°C (top). The rates (1/α) of ON gating currents measured at different temperatures are plotted against V_m (bottom). The lines represent the global fit of the data, with a z of 0.4 and ΔG of 2 kCal/mol. (E) No effect of the HP on the charge movement or conductance in 4ILT. Q/Q_max-V (squares) curves for a typical oocyte expressing 4ILT when held at two HP. G/G_max-V (circles) curves measured for 4ILT (n = 6) when measured at two HP. When HP was −90 mV, subtraction was made with the P/−4 protocol, and subtracting HP was −120 mV. When HP was 0 mV, subtraction was made using the P/−8 protocol, and the subtracting HP was +10 mV (no ionic current are observed at this V_m). The solutions contained both 115 mM NMG⁺ for charge movement measurement but under 12 and 120 mM K⁺ in the external and internal solutions, respectively, for ionic current measurements.

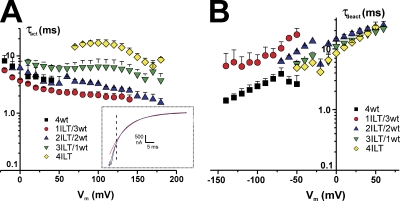
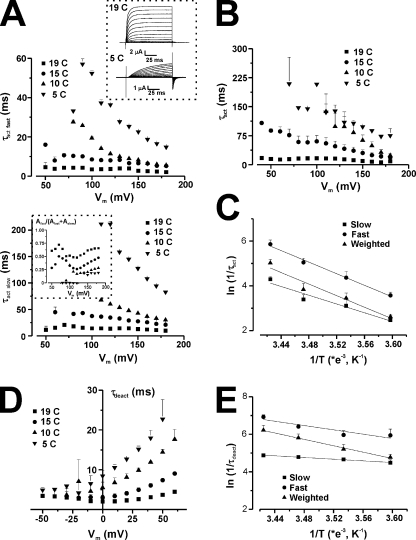
As indicated by visual inspection of the traces, the activation kinetics varies with ILT stoichiometry. The time constants for both activation (τ_act) and deactivation (τ_deact) were analyzed with two exponentials, and the weighted time constants are shown in Fig. 2. The inset illustrates the current traces at +160 mV from a HP of −90 mV with a prepulse to −120 mV from an oocyte expressing 4ILT superimposed with two traces corresponding to fits with a single (red) and a double (blue) exponential function to the curve. The higher the number of ILT subunits, the slower the activation kinetics (Fig. 2 A), but compared with 4wt, τ_act significantly differs (P < 0.05) only with a minimum of three ILT subunits in the range of voltages where 4wt was measured. No significant difference in kinetics of deactivation measured at 5–7°C (or 19°C, not depicted) can be correlated with the number of ILT subunits (Fig. 2 B).

Figure 2.

Effect of the stoichiometry of ILT subunits on Shaker activation and deactivation kinetics. (A) Activation time constants (τ_act) and (B) deactivation time constants (τ_deact) of the heterotetramers compared with that of 4ILT. The weighted τ_act as a function of the activating membrane potential is shown. The inset illustrates a current trace (black) at +160 mV from an oocyte expressing 4ILT, a fit with a single (red) and double (blue) exponential function. The vertical dotted line indicates the time position for the beginning of the fit. The internal and external solutions contained 120 and 12 mM K⁺, respectively. The weighted τ_deact from an activating pulse at +160 mV plotted against the returning membrane potential. The internal and external solutions contained 120 and 50 mM K⁺, respectively. 4wt (black squares, n = 5), 1ILT/3wt (red circles, n = 3), 2ILT/2wt (blue up triangles, n = 3), 3ILT/1wt (green down triangles, n = 3), 4ILT (yellow diamonds, n = 4). Data from 4wt was taken from Fig. 4 of Gagnon and Bezanilla (2009).

Single channel conductance is not affected by the stoichiometry of ILT subunits

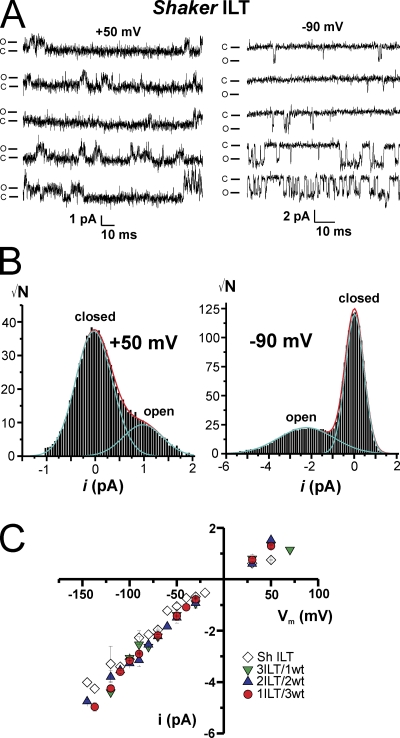
To evaluate whether the observed change in slope in the G-V curve with the different stoichiometries may reflect a modification of the single channel activity and/or conductance by the ILT mutations, we measured single channel conductance in cell-attached patches with 120 mM K⁺ in the pipette in oocytes expressing ILT constructs. Due to the large positive shift in open probability as a function of voltage (Smith-Maxwell et al., 1998a,b; Ledwell and Aldrich, 1999), we could measure single channel activity in patches that exhibit macroscopic currents above +50 mV. Fig. 3 A shows five representative traces from a patch displaying single channel transitions for Shaker ILT at +50 (left) and −90 mV (right). Even though Shaker ILT open probability is near 0 at −90 mV, we could measure short (1–10 ms) and fewer longer (20–30 ms) periods of activity in ∼20 traces over 160, which represent an overall open probability of ≤0.01. The single channel current amplitude (i) determined through all point histograms of a few selected traces in which there is activity (Fig. 3 B) was plotted against voltage for Shaker ILT and the heterotetramers as illustrated in Fig. 3 C. All constructs had similar conductance (γ) that displayed some rectification (∼20 pS for outward currents at +50 mV and ∼30–35 pS for inward currents). Thus, consistent with previous results (Solc et al., 1987; Heginbotham and MacKinnon, 1993; Shao and Papazian, 1993; Hoshi et al., 1994; Li and Correa, 2001), the ILT mutations do not modify the conductance, even at different stoichiometry, suggesting that the characteristics of the pore conductance for K⁺ ions are not affected by these S4 mutations.

Figure 3.

Single channel conductance is not modified by the stoichiometry of ILT subunits. (A) Representative traces of single channel activity measured in an oocyte expressing Shaker ILT at +50 mV (left) and −90 mV (right). The closed and open channel current levels are indicated as c and o, respectively. (B) All point histograms of single channel group of selected traces at +50 mV (left) and −90 mV (right). (C) Single channel current amplitude versus voltage relationship for the heterotetramers and Shaker ILT. Shaker ILT (open diamonds, n = 4), 3ILT/1wt (green down triangles, n = 3), 2ILT/2wt (blue up triangles, n = 3), and 1ILT/3wt (red circles, n = 3). The internal and external (pipette) solutions both contained 120 mM K⁺. Patch-clamp experiment.

Temperature dependence of the kinetics of activation/deactivation of 4ILT

By measuring temperature dependence and performing thermodynamical analysis of Shaker ionic and gating currents, Rodriguez and colleagues (Rodriguez and Bezanilla, 1996; Rodriguez et al., 1998) determined the enthalpic and entropic contributions to the main energetic barrier along the activation pathway and upon opening, and showed that opening required a reordering of the channels’ structure. As the conformational changes that open the ILT Shaker channel pore are more separated in the voltage axis from the main movement of the voltage sensor, it allowed us to determine the energy of activation of the opening and closing transitions (E_af and E_ab), assuming a simple transition. We measured activation/deactivation kinetics at temperatures ranging from 5 to 20°C to estimate the chemical components of the free energy (ΔG) and of the enthalpy (ΔH) and the entropy (ΔS) changes.

The simplest observation is the temperature dependence of the ionic currents. Upon a reduction of temperature from 19 to 5°C, ionic current amplitude decreased by an average of ∼75% (see Fig. 4, top panel, inset), in a reversible manner. This gives a Q₁₀ value of ∼2.7.

Figure 4.

Temperature and voltage dependence of the activation and deactivation kinetics of 4ILT. (A) Voltage dependence of τ_act at four temperatures, as indicated, for a typical oocyte expressing 4ILT. The top and bottom panels represent the fast and slow component of the activation, respectively. The error bars are the error on the fit. The top panel inset shows family of ionic current traces measured at 19 (top) and 5°C (bottom), for a typical oocyte expressing 4ILT (oocyte 3, 11/03/09). The bottom panel inset shows the proportion of the fast component (oocyte 2, 05/02/09). Averaged voltage dependence of the weighted τ_act (B) and τ_deact (D) at four temperatures for 4ILT. Data from all the oocytes combined, each oocyte was tested for at least two temperatures. For τ_act, 19°C (n = 8), 15°C (n = 4), 10°C (n = 4), and 5°C (n = 3) and for τ_deact, 19°C (n = 6), 15°C (n = 5), 10°C (n = 4), and 5°C (n = 4). In both cases, the internal solutions contained 120 mM K⁺; the external solutions contained 12 and 50 mM K⁺ for activation and deactivation, respectively. The error bars are the SEM. Arrhenius plot of the ln of rate of activation (ln(1/τ_act)) (C) at +180 mV and that of the rate of deactivation (ln(1/τ_deact)) (E) at 0 mV for 4ILT. The slow (squares), fast (circles), and weighted (triangles) components are shown. For activation, the slopes and intercepts for a linear fit to the data were −9800 ± 1800 (s⁻¹/K⁻¹) and 38 ± 6 (s⁻¹), −13000 ± 800 (s⁻¹/K⁻¹) and 50 ± 3 (s⁻¹), and −12900 ± 2200 (s⁻¹/K⁻¹) and 49 ± 8 (s⁻¹) for the three components, respectively. For deactivation, the slopes and intercepts for a linear fit to the data were −8500 ± 500 (s⁻¹/K⁻¹) and 35 ± 2 (s⁻¹), −5700 ± 1600 (s⁻¹/K⁻¹) and 26 ± 6 (s⁻¹), and −2200 ± 100 (s⁻¹/K⁻¹) and 12.6 ± 0.5 (s⁻¹) for the three components, respectively. The activation energy (E_af) for the forward transition was calculated from the slope (−E_a/R) at 19.5, 25.8, and 25.6 kCal/mol and that of the backward transition (E_ab) at 16.9, 11.3, and 4.4 kCal/mol.

As the kinetics of the currents at 5°C is extremely slow, this value may not be representative of the temperature dependence of the open channel conductance. A detailed study of the time constants is then required.

Fig. 4 A illustrates the voltage and temperature dependence of the time constant of activation (τ_act) for an oocyte expressing 4ILT. For both the fast (Fig. 4 A, top) and the slow (Fig. 4 A, bottom) components, a ∼15°C decrease in temperature slows down the kinetics of activation by a factor of ∼8-10. This is clear in an individual oocyte (Fig. 4 A) as well as in the averaged data (n = 3–8) for the weighted τ_act, as depicted in Fig. 4 B. The inset in Fig. 4 A (bottom) depicts the threefold decrease in the proportion of the fast component from ∼60% at 19°C to ∼20% at 5°C. Similarly, Fig. 4 D represents the averaged voltage and temperature dependence of the deactivation time constant (τ_deact) for 4ILT. Arrhenius plots for activation (at +180 mV) and deactivation (at 0 mV) rates are shown respectively in Fig. 4, C and E, which give values of activation energy, E_af, of 19.5, 25.8, and 25.6 kCal/mol for the fast, slow, and weighted rates of activation, respectively. Table I provides the energetic parameters for each construct.

TABLE I.

Activation energy (E_a) calculated from Arrhenius plots of the rate of activation (f)/deactivation (b) (slow, fast, and weighted components) for heterotetramers with different stoichiometries of ILT mutations

Shakera	Eaf fast	Eaf slow	Eaf weighted	Eab fast	Eab slow	Eab weighted
	kCal/mol	kCal/mol	kCal/mol	kCal/mol	kCal/mol	kCal/mol
	−	−	−5.4	−	−	24.8
1ILT/3neu	17.5	18.1	25.8	20.1	0.6	12.9
1ILT/3wt	29.3	23.6	35.3	14.3	15.1	18.5
2ILT/2wt	23.2	16.5	20.4	10.5	13.3	16.9
3ILT/1wt	21.8	19.6	25.8	8.5	15.9	14.3
4ILT	25.8	19.5	25.6	11.3	4.4	16.9

^aRodriguez and Bezanilla, 1996.

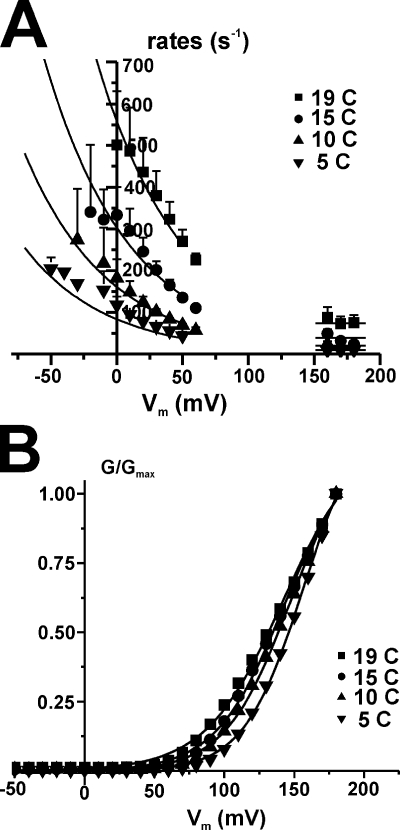
To separate the chemical from the electrical components of the energy difference between the states in the last transition, we performed a global fitting of the ratio of the voltage dependence of the rates of activation (α = 1/τ_act) over that of deactivation (β = 1/τ_deact) measured at the four different temperatures (5, 10, 15, and 19°C), where

$$\alpha ={\alpha }_0\exp \left(\frac{z_{\alpha }FV}{RT}-\frac{G_{\alpha }}{RT}\right)\hspace{1em}\text{and}$$

$$\beta ={\beta }_0\exp \left(\frac{-z_{\beta }FV}{RT}-\frac{G_{\beta }}{RT}\right)$$

Since we cannot separate the preexponential term from G, taking the ratio of the fitted rates eliminates the preexponential terms (which are assumed to be the same for forward and backward, i.e., α₀ = β₀), allowing the estimation of the parameters z_α, z_β, and ΔG = G_α − G_β, which are shown in Table II. The data for 4ILT overlapped with the global fit results as continuous lines is shown in Fig. 5 A. The data for deactivation were taken below +60 mV and those of activation above +150 mV, which represent the region of voltage where the G-V saturates or is near saturation for the 4ILT construct. As described previously for Shaker (Rodriguez and Bezanilla, 1996; Rodriguez et al., 1998), the activation rate is voltage independent (z_α = 0). In contrast, the deactivation rate of the mutant was voltage dependent, with z_β ∼ 0.35e₀, slightly lower than the ∼0.51e₀ for Shaker. Finally, the global fit gave a ΔG of +1.1 kCal/mol. Comparing this value to the −0.6 kCal/mol obtained for normal Shaker (Rodriguez and Bezanilla, 1996; Rodriguez et al., 1998), this indicates a higher free energy barrier for opening of 4ILT compared with Shaker.

TABLE II.

Thermodynamic parameters for the opening transition for heterotetramers with different stoichiometries of ILT mutations

Shakerb	zα	zβ	ΔG	ΔHa	TΔS
	e0	e0	kCal/mol	kCal/mol	kCal/mol
	0	0.51	−0.6	−30.2	−29.6
1ILT/3neu	0	0.35	−0.4	13.3	13.7
1ILT/3wt	0	0.39	−0.5	18.5	19.0
2ILT/2wt	0	0.34	0	6.8	6.8
3ILT/1wt	0	0.30	0.4	10.9	11.3
4ILT	0	0.38	1.1	8.1	7

^aComputed at V = 0.

^bRodriguez and Bezanilla, 1996.

Figure 5.

Determination of the chemical component of the free energy and effect of the temperature on the conductance in 4ILT. (A) Global fitting of the voltage dependence of weighted 1/τ_act and 1/τ_deact for 4ILT. The data were fitted globally with the ratio of the forward and backward components of Eq. 1, α for activation and β for deactivation (see Materials and methods for full equations), assuming that α₀ = β₀. z_α was found to be null. The lines represent the curve from the best fit. The results of z_β, ΔG for 4ILT, and the heterotetramers are listed on Table II. ΔH was calculated from E_a and z (ΔH = (E_af − E_ab) + (z_α − z_β)FV) for V = 0, and TΔS was calculated from ΔG and ΔH (see Table II). (B) Right shift of the G-V with a decrease in temperature in 4ILT. Normalized G-V curve for a typical oocyte measured at temperatures of 19, 15, 10, and 5°C. The shift from 19 to 5°C was in averaged 7 ± 3 mV (n = 4). The conductance was calculated using the peak tail currents. The external and internal solutions contained 12 and 120 mM K⁺, respectively.

The enthalpic component (at V = 0) of the opening transition was computed from the activation energies of the forward and backward transitions and the electric component with $\Delta H=\left(E_{af}-E_{ab}\right)+\left(z_{\alpha }-z_{\beta }\right)FV$ for V = 0 while the change in free energy is given by $\Delta G=\Delta H-T\Delta S$. By using these equations, it is possible to determine the changes in enthalpy (ΔH) and entropy (TΔS), which are included in Table II. The equilibrium thermodynamic parameters are thus all the zero-voltage values, and TΔS was calculated at room temperature. In contrast to the large negative change in entropy previously calculated for Shaker (TΔS = −29.6 kCal/mol) (Rodriguez and Bezanilla, 1996; Rodriguez et al., 1998), the entropic change for the 4ILT is large and positive (TΔS ∼7 kCal/mol). The difference reflects a large enthalpy barrier for activation of the mutant (ΔH is 8.1 kCal/mol vs. −30.2 for Shaker).

As the negative TΔS value determined for Shaker was associated with a small leftward shift in the G-V curve as temperature is lowered, we estimated the G-V as a function of temperature for 4ILT with the limitation that a precise value is difficult to obtain due to the extreme potentials at which the curve is centered. We observed a rightward shift of ∼5–10 mV when the temperature was reduced from 19 to 5°C (n = 4) (Fig. 5 B). However, the value coming from the fit seems underestimated if one considers the larger shift (∼30 mV) observed when comparing the foot of the G-V curve at 5°C with the corresponding foot of the G-V curve at 19°C. This difference in the estimation is probably because the G-V curves do not show clear saturation in the voltage range reached experimentally. The large shift to the left when increasing the temperature is the expected result of an increase in entropy when opening the ILT mutant, as determined by the ratio of the rates shown above (see Correa et al., 1992, Eq. 2).

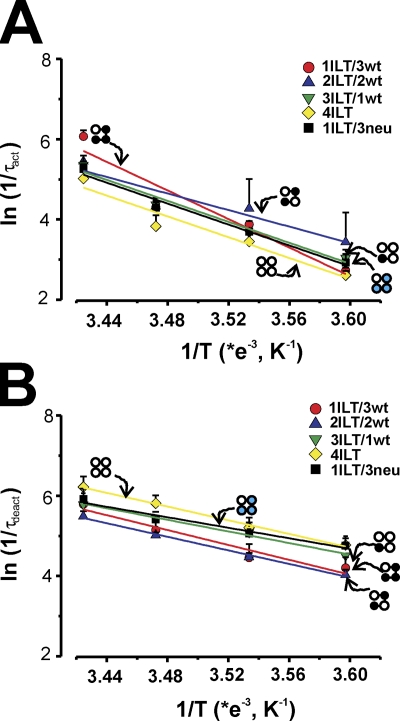
Thermodynamic parameters for heterotetramers with different stoichiometries of ILT mutations

Fig. 6 shows the Arrhenius plots of the weighted rates of activation (Fig. 6 A) and deactivation (Fig. 6 B) for all the heterotetramer constructs superimposed with that of 4ILT. The most striking difference between the homotetramer 4ILT and the heterotetramers’ thermodynamic value (see Table II) is that ΔG increases slightly with the number of ILT subunits. ΔG was determined at −0.6 kCal/mol for Shaker, and this value increases by 0.43 ±0.06 kCal/mol for each ILT subunit. Apart from ΔG, none of the other thermodynamic parameters seems to have a clear trend with the number of ILT subunits: the z_β was found between 0.3 and 0.39; the ΔH varies between 6.8 and 18.5 kCal/mol; and the TΔS varies between 6.8 and 19.0 kCal/mol. It seems clear though that one ILT subunit (ILT/3wt or ILT/3neu) is enough to generate a positive enthalpy barrier and a positive entropy change.

Figure 6.

Arrhenius plots of the forward and backward transition for the ILT heterotetramers. The ln(1/τ_act) (A) and ln(1/τ_deact) (B) are plotted against 1/T (K⁻¹). The slopes of the curve (−E_a/R), in which R is the gas constant (1.985 Cal·mol⁻¹·K⁻¹), are used to calculate E_a for each heterotetramer (see Table I). 1ILT/3wt (red circles), 2ILT/2wt (blue up triangles), 3ILT/1wt (green down triangles), 4ILT (yellow diamonds), and 1ILT/3neu (black squares). Data for activation were taken at +70, +60, +150, +180, and +100 mV for 1ILT/3wt, 2ILT/2wt, 3ILT/1wt, 4ILT, and 1ILT/3neu, respectively, and at +60, +10, 0, 0, and +30 mV for deactivation for 1ILT/3wt, 2ILT/2wt, 3ILT/1wt, 4ILT, and 1ILT/3neu, respectively.

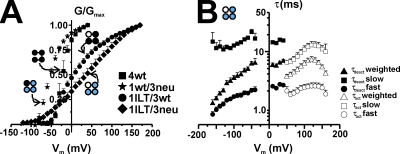
Effect of the ILT mutations on channels with a single voltage sensor

We have shown that a single functional voltage sensor can gate Shaker channels (Gagnon and Bezanilla, 2009). We used this heterotetramer with only one voltage-sensitive subunit (the others do not have gating charges) as a tool to further characterize the effect of the ILT mutations by introducing these residues in the only subunit with a functional voltage sensor. Fig. 7 A illustrates the G-V curve of the 1ILT/3neu (diamonds) as compared with that of 4wt (squares), 1wt/3neu (stars) (Gagnon and Bezanilla, 2009), and 1ILT/3wt (circles) (see also Fig. 1). Whereas the shift in the G-V produced by the ILT mutations in one subunit when the four voltage sensors are functional was +30 mV, the shift produced when they are made in the wt subunit in the single voltage sensor Shaker was +90 mV. The dramatic change in slope of the G-V (now spread on the full voltage range) is consistent with the reduced gating charge, now present in only one subunit. Fig. 7 B shows the slow, fast, and weighted components of the kinetics of activation and deactivation measured at room temperature. Following the procedure described above for 4ILT we determined the thermodynamic parameters (see Tables I and II) of the 1ILT/3neu (and other heterotetramers), and we used kinetic modeling of 1ILT/3neu and 4ILT to determine the transitions affected by the ILT mutations (see below) (Gagnon and Bezanilla, 2009).

Figure 7.

Conductance and kinetics of the single voltage sensor Shaker ILT. (A) Normalized G-V curve for the single voltage sensor Shaker ILT. Data from 4wt (squares), 1wt/3neu (stars), 1ILT/3wt (circles, n = 7), and 1ILT/3neu (diamonds, n = 4) are shown. The ones from 4wt and 1wt/3neu were taken from Gagnon and Bezanilla (2009). The internal and external solutions contained both 120 mM K⁺, respectively. (B) Kinetics of activation (τ_act, open symbols) and deactivation (τ_deact, filled symbols) of 1ILT/3neu measured at room temperature. The slow (squares), fast (circles), and weighted (top triangles) components are shown. In both cases, the internal solutions contained 120 mM K⁺; the external solutions contained 12 and 50 mM K⁺ for activation and deactivation, respectively.

Temperature does not affect steady-state charge movement of 4ILT

The thermodynamic analysis described above is a simplification that assumes a single step between closed and opened states. A more precise description includes several voltage-dependent transitions between closed states before channel opening. These transitions can be studied by measuring gating currents, which in the case of the 4ILT, can be studied under the same ionic conditions as ionic currents (Smith-Maxwell et al., 1998a; Ledwell and Aldrich, 1999) (see also Fig. 8 A). Therefore, we studied the effect of temperature on steady-state charge movement of Shaker ILT (Fig. 8, B and C). Fig. 8 A shows the transferred charge (Q-V) curves of the 4ILT together with that of Shaker ILT injected as monomers. The midpoint is located at −77 ± 2 mV and the slope factor is ∼2.3, which is similar to the values provided by Ledwell and Aldrich (1999) for Shaker ILT W434F. Fig. 8 B shows that the Q-V curve (Q_ON and Q_OFF) does not vary with temperature between 19 and 5°C in a typical oocyte expressing 4ILT. The slight decrease in total charge at 5°C is probably due to the difficulty of integrating the slowest component of the gating currents at this temperature. The averaged normalized Q-V curves from four oocytes in Fig. 8 C demonstrate that neither V_1/2 nor the slope of the curve is affected by temperature. However, as illustrated with the gating current traces (Fig. 8 D, top) measured at two temperatures, the rate of decay of the gating currents decreases with a reduction in temperature from 1060 ± 70 s⁻¹ (19°C) to 255 ±9 s⁻¹ (10°C), at 0 mV (n = 4). From its temperature (at 0 mV) and voltage dependence (Fig. 8 D, bottom), we found an activation energy of the ON gating, E_ag of 23.8 kCal/mol, a z of 0.4, and a ΔG of 2 kCal/mol. This is consistent with the analysis described above for the temperature and voltage dependence of the rate of activation of ionic currents.

No effect of holding potential on steady-state charge movement and conductance in 4ILT

Shaker Q-V curve exhibits hysteresis with HP, reflected as a shift to the left in the midpoint of the Q-V curve when the HP is maintained at depolarized potentials, a process referred to as relaxation (Villalba-Galea et al., 2008). Although this property has been typically associated with C-type inactivation (Bezanilla et al., 1982; Olcese et al., 1997), it is now clear that it is a property of the voltage sensor that may not always be associated with slow inactivation (Villalba-Galea et al., 2008). Hysteresis and C-type inactivation occur in the same range of voltage in Shaker since the voltage dependence of the Q-V and G-V is in the same voltage range. In contrast, we did not observe displacement of the Q-V curve in the ILT mutant whether the charge movement is measured from HP of −90 (voltage at which the channels are closed) or 0 mV (voltage at which most of the charge is moved) (Fig. 8 E), nor whether do we measure it in the presence or absence of external and internal K⁺ in the solutions (not depicted). Also, the G-V curve measured when the HP was set to 0 or −90 mV was not significantly different (Fig. 8 E). This indicates that relaxation of the voltage sensor does not occur in the ILT mutant at voltages at which most of its charge has saturated and suggests that relaxation may only proceed after the channel undergoes the last step that leads to the concerted transition that opens the conduction pathway. It is important to note that in the positive voltage range where the channel conducts, there is a small fraction of the gating charge (Ledwell and Aldrich, 1999) that may be a requisite to induce relaxation.

DISCUSSION

The ILT mutant has been used as a tool to study the last transition in the activation pathway since it drastically affects the coupling between gating and ionic conduction (Smith-Maxwell et al., 1998a,b; Ledwell and Aldrich, 1999; Sack et al., 2004; del Camino et al., 2005; Pathak et al., 2005; Laitko et al., 2006; Vaid et al., 2008). We found that (1) each subunit contributes equally to the displacement of the G-V by the ILT (Fig. 1), suggesting that indeed, voltage sensors do not influence each other; (2) the ILT mutations do not affect the single channel conductance either in the homo- or heterotetramers (Fig. 3); (3) the gating and the last opening transition are highly temperature dependent (Figs. 4, 5, 7, and 8, Tables I and II) as soon as one ILT subunit is present, supporting the idea of a cooperative opening. We interpret our results using the conventional kinetic model.

Independence of the voltage sensors

Independent and cooperative models of voltage sensor movement have been proposed to account for the biophysical properties of Kv channels as well as those of some mutants (Hodgkin and Huxley, 1952; Tytgat and Hess, 1992; Zagotta et al., 1994a; Schoppa and Sigworth, 1998a; Ledwell and Aldrich, 1999; Gagnon and Bezanilla, 2009; Tombola et al., 2010). We observed linearity in the relationship between the V_1/2 of the G-V and the number of ILT subunits (Fig. 1) in a background with all the gating charge present. We interpret this result as evidence of the independence of the voltage sensors. Indeed, if this perturbation introduced in the second, third, or fourth subunit were to produce more (or less) effect than when it was done in a single subunit, it would deviate from linearity and it would be interpreted as positive (or negative) cooperativity.

Understanding the reason for the change in the G-V slope with the number of ILT subunits is not straightforward because the charge of the sensor is not the only determinant factor for the slope of the G-V. The peculiarity of the ILT mutations is that they produce a perturbation in the S4 segment without affecting the S4 charge content. Mutation of other hydrophobic residues in S4 and the S4–S5 linker have been shown to modify the charge movement, namely by modifying the center and the slope of the G-V curve (Lopez et al., 1991; McCormack et al., 1991, 1993; Schoppa and Sigworth, 1998b; Yifrach and MacKinnon, 2002). These effects can be explained by a change in the chemical interactions and/or a change in the local field and they do not require any changes in the formal charged groups.

High temperature dependence of the opening transition with minimally one ILT subunit

Classically, an ion channel with a Q₁₀ > 2 is considered highly temperature dependent (Hille, 2001). In general, channels have a Q₁₀ for gating processes comprised between 2 and 4 but lower (1.2–1.5) for ion conductance, similar to a diffusion-like process in the gramicidine channels (E_a = 5 kCal/mol, Q₁₀ = 1.35). Our estimate of the Q₁₀ for 4ILT based on ionic current amplitude change with temperature is 2.7. In patch experiments, Rodriguez et al. (1998) found that temperature has little effect on Shaker elementary charge or in the number of active channels, but that the single channel conductance was reduced by 45% when going from 18 to 5°C. It is then not surprising that it is also the case for the ILT mutant since its single channel conductance is identical to that of Shaker (Fig. 3).

The detailed analysis of the temperature dependence of homotetrameric 4ILT (Figs. 4–6) and heterotetrameric channels (Fig. 6–7) revealed an unexpected property. In contrast to observation with Shaker (Rodriguez and Bezanilla, 1996; Rodriguez et al., 1998), the small zero-voltage free energy of opening measured for the ILT homotetramer (and heterotetramers) arises from a large unfavorable enthalpy almost balanced out by a favorable entropy (Table II), which makes the chemical component of the free energy change to be small and positive (1.1 kCal/mol for 4ILT or ∼2 RT). The ΔG increased by 0.43 ± 0.06 kCal/mol for each additional ILT subunit, which is in the order of magnitude of thermal motion. One ILT subunit is enough to change from a large negative enthalpy change (−30.2 kCal/mol) in Shaker to a positive value of ∼18.5 kCal/mol in the background with all the gating charges or 13.3 kCal/mol in the single voltage sensor Shaker (ILT in wt subunit). By comparison, in Shaker mutants P475C and P475S in which ionic current begins to appear with depolarization above +100 mV, the ΔG₀ value solely calculated from the G-V (V_1/2 and z) gave ∼7.5 kCal/mol (Sukhareva et al., 2003).

We provide supporting evidence that these enthalpy and entropy changes come from the opening transition. Indeed, we have not observed any shift of the steady-state charge movement voltage dependence in 4ILT with temperature (Fig. 8), similar to Shaker (Rodriguez et al., 1998). In short, the early transitions (between the deep closed states) are affected equally by temperature. Structurally, these results indicate that upon opening in ILT mutants, the channel/water complex becomes more disordered, or has more degrees of freedom. As these thermodynamic measurements refer to the whole system, at present we cannot infer the exact nature of these structural changes.

ILT eases the gating charge movement but does not present hysteresis

An intriguing feature of the ILT mutant is that its Q-V curve is left shifted (approximately −25 mV) but that its G-V is right shifted (∼150 mV) compared with Shaker (Fig. 1 B and Fig. 8 A). Based on mutagenesis, kinetic modeling, and MTS reagents, Cd²⁺, or toxin binding (BrMT), this behavior can be explained if, at 0 mV, the ILT mutant is stabilized in the activated-not-opened state (Smith-Maxwell et al., 1998a; Ledwell and Aldrich, 1999; Sack et al., 2004; del Camino et al., 2005). In addition to that, ILT is the only Shaker mutant characterized so far that presents no hysteresis of the Q-V curve with HP (−90 vs. 0 mV) (Fig. 8 E). This provides evidence that the relaxation of the voltage sensor (Villalba-Galea et al., 2008) and C-type inactivation do not arise from the activated-not-opened state where the ILT resides at 0 mV. Indeed, the ionic currents measured from HP −90 mV (ILT channels closed) or HP 0 mV (activated-not-opened state) are nearly identical (Fig. 8 E).

All transitions are modified by the ILT

We performed global fitting of the 4ILT and single voltage sensor Shaker ILT (1ILT/3neu) current traces at voltages describing their voltage dependency with the conventional model (Gagnon and Bezanilla, 2009), illustrated in Scheme 1. As described before, it was assumed that a neutral S4 subunit would be in state A while a wt subunit would undergo voltage-dependent transitions according to the values of alphas and betas. In the present case, the wt subunit carries the ILT; thus, the best fit will provide the valence of the charge and rate constants of each transition, which are actually only due to the ILT subunit(s) movement. The rate constants and elementary charge valence found to best fit our data are noted in Table III (see Fig. 9).

TABLE III.

Parameters of the kinetic model

Rate constant	k0 ILT	zk ILT	k0(a)	zka
	ms−1	e0	ms−1	e0
α00	17.3	0.20	0.3659	0.3965
β00	0.00006	3.4	0.0001	2.5084
α10	0.17	0.04	2.9902	0.0037
β10	0.00003	0.97	0.4255	1.1015
α20	1.19	1.02	0.2586	0.0001
β20	1.43	0.000004	2.4364	0.0261

The rate constants are given for the model presented in Scheme 1. Forward and backward rate constants are α and b, respectively, and follow exponential voltage dependence as α₀ = α₀₀*e^{(z0f*Vm*F/RT)} and β₀ = β₀₀*e^{(-z0b*Vm*F/RT)}. The k₀ column gives each of the rates at 0 mV, and the z_k column indicates the equivalent valence in electronic charge units assigned to the transition. F is the Faraday constant, V_m is voltage, R is the universal gas constant, and T is temperature in Kelvin.

^aGagnon and Bezanilla, 2009.

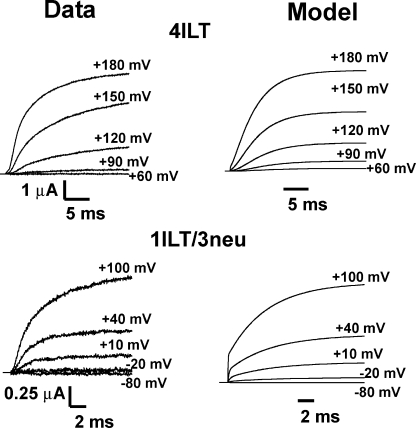
Figure 9.

Predictions of the model for ionic currents in symmetrical 120 mM K⁺ at room temperature (19–20°C) for 4ILT and 1ILT/3neu compared with experimental data. Experimental data are shown on the left, and the right panel illustrates the predictions of the kinetic model illustrated in Scheme 1. The HP was −90 mV, and steps were elicited to the annotated V_m. The rate constants and equivalent valence in electronic charge units are shown in Table III.

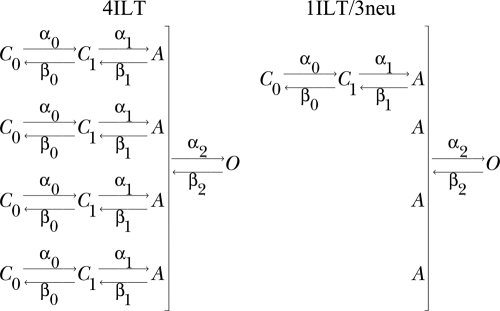(SCHEME 1)

All the rate constants and valences had to be modified to fit our data, suggesting that the ILT modifies most steps in the activation pathway. This type of model has difficulties in predicting the delay for activation of 1ILT/3neu but, overall, the conductance of both 4ILT and 1ILT/3neu is very well accounted for with the parameters found. We found that a strong voltage dependency (z_2f = 1.02) of the last concerted step was required to account for the conductance of 4ILT (Zagotta et al., 1994a; Ledwell and Aldrich, 1999). One striking aspect of the model is that contrary to that proposed before (Ledwell and Aldrich, 1999), it is not the last but rather the previous to last step that is rate limiting. This is in line with the results presented here because the additivity of the ILT mutation points to an effect in each of the subunits and not in the concerted step. Also, one can estimate the open probability with the ratio α₂₀/β₂₀, which should be close to 0 and 0.3–0.4 in the case of 4ILT and 1ILT/3neu, respectively, at 0 mV. Our best fit gave a value of 0.8 for this ratio, which still predicts very small currents at +60 mV in the case of 4ILT.

The ILT mutant can be compared with the so-called V2 mutant (Shaker L382V) as 80% of its charge can be transferred without appearance of ionic conduction (Schoppa and Sigworth, 1998a), though the gap between the Q-V and G-V curves is only of 50 mV versus close to 200 mV in ILT. V2 mutation was described to affect mostly two concerted transitions in the proposed model, consistent with the absence of shift in the Q-V and the right shift of the G-V compared with Shaker wt. It seems logical that the ILT modifies most transitions, considering the large shift of both the Q-V and G-V curves in opposite directions. A better model that accounts for all the known characteristics of the 4ILT (left shift of the gating currents and right shift of the conductance) will probably require one more voltage-dependent transition before the concerted step.

Possible structural interpretation of the uncoupling

As observed in the Kv1.2 and Kv1.2/Kv2.1 chimera crystal structures (Long et al., 2005a; 2007), the residues VIS present in Shaker and Kv1.2 are facing the lipids or the S5 segment of the adjacent subunit in the putatively closed and open-inactivated states, respectively. It has been shown that Shaker gating charge movement was also facilitated (left shift of the Q-V) by conversion of sphingomyelin into ceramide-1-phosphate after a treatment with bacterial sphingomyelinase D (Xu et al., 2008). Even though the substitutions V→I, I→L, and S→T do not change by more than 15% the hydrophobic index of the residue nor their isoelectric point, both V→I and S→T modify the residues’ volume and surface area by 20–30% and 13–22%, respectively (Zamyatnin, 1972), and mutations V→I and I→L both change the solubility by a factor of two. These changes in amino acid residue properties might be enough to affect interaction of the S4 segment with the lipid bilayer and promote the gating alteration. Modification of these interactions actually facilitates the voltage sensor movement because the gating charges move with smaller depolarization than in Shaker but prevents the final movement that opens the bundle crossing. The angle separating the S4 and S4–S5 segments changes from nearly parallel in the putative closed to nearly perpendicular in the opened channel’s pore structure (Long et al., 2005a, 2007), respectively. That suggests that some interactions must be broken from one conformation to the other. During gating, one can speculate that if the S4 and S4–S5 linker move as a rigid body (Nishizawa and Nishizawa, 2009) in the case of the ILT mutant, the bundle crossing opening becomes more difficult because it has a stronger interaction.

We aimed at deciphering the mechanism by which the ILT mutations act and transform Shaker into a channel for which the gating charges move at voltages more negative than Shaker but for which ionic conduction only arises with very large positive potentials. We found by introducing the ILT mutations stoichiometrically, or in one subunit at a time, that each subunit contributes equally to the displacement of the G-V, but that one ILT subunit is sufficient to raise a high entropy and enthalpy barrier for the opening step. The mechanistic interpretation of the present results is that the ILT mutation is not directly involved in the concerted step. Rather, when compared with the wt channel, this mutant channel seems to have a more stabilized state just before the last step of the voltage sensor activation, thus requiring a larger voltage to overcome this final transition. Overall, our results support independence of the voltage sensor in the gating process and cooperativity on the final opening step.