Image Guided Small Animal Radiation Research Platform: Calibration of Treatment Beam Alignment

Abstract

Small animal research allows detailed study of biological processes, disease progression, and response to therapy, with the potential to provide a natural bridge to the clinical environment. The Small Animal Radiation Research Platform (SARRP) is a portable system for precision irradiation with beam sizes down to approximately 0.5 mm and optimally planned radiation with on-board cone-beam CT (CBCT) guidance. This paper focuses on the geometric calibration of the system for high-precision irradiation. A novel technique for calibration of the treatment beam is presented, which employs an x-ray camera whose precise positioning need not be known. Using the camera system we acquired a digitally reconstructed 3D “star shot” for gantry calibration, and then developed a technique to align each beam to a common isocenter with the robotic animal positioning stages. The calibration incorporates localization by cone-beam CT guidance. Uncorrected offsets of the beams with respect to the calibration origin ranged from 0.4 mm to 5.2 mm. With corrections, these alignments can be brought to within < 1 mm. The calibration technique was used to deliver a stereotactic-like arc treatment to a phantom constructed with EBT Gafchromic films. All beams were shown to intersect at a common isocenter with a measured beam (FWHM) of approximately 1.07 mm using the 0.5 mm collimated beam. The desired positioning accuracy of the SARRP is 0.25 mm and the results indicate an accuracy of 0.2 mm. To fully realize the radiation localization capabilities of the SARRP, precise geometric calibration is required, as with any such system. The x-ray camera-based technique presented here provides a straightforward and semi-automatic method for system calibration.

1. Introduction

Preclinical models using small laboratory rodents are a key means for understanding and developing treatments for a wide spectrum of diseases from psychiatric disorders to cancer. It has become apparent that much can be gained in this regard from advanced technology such as in vivo imaging. Micro-animal imaging systems capable of very high resolution have been developed in positron emission tomography (Jacob & Cherry 2001, Rubins et al. 2001), X-ray CT (Medynsky et al. 1998, Wan et al. 2002), magnetic resonance imaging (Allport & Weissleder 2001, Franconi et al. 2000), magnetic resonance spectroscopic imaging (Zhang et al. 2001), ultrasound imaging (Turnbull et al. 1996) and optical imaging (such as IVIS Spectrum, Caliper Life Sciences, Hopkinton, MA). To date, however, there have been no radiation systems available with commensurate quality and precision, even though irradiation is frequently employed in a variety of preclinical contexts including cancer therapy.

The small animal radiation research platform (SARRP) developed by our laboratory aims to address these issues by providing a platform that can perform high-resolution imaging and accurate conformal beam therapy on standard animal models for human cancers (Wong et al. 2008). The system consists of a kilovoltage x-ray tube mounted on a rotating gantry. The tube provides a low-energy beam for cone-beam CT imaging (with a flat panel detector) and a high-energy beam for radiotherapy. The animal is placed on a four-axis robotic positioner that provides rotary motion for cone-beam CT and translation and rotation for radiotherapy targeting. The SARRP offers several advantages over previous generation systems, including the ability to deliver small and/or conformal radiation beams from a variety of angles as well as practical advantages such as portability and the absence of radioactive isotopes. By combining cone-beam CT imaging and radiotherapy, the SARRP offers capabilities similar to modern clinical systems which integrate linac and x-ray imaging system (see e.g. (Sharpe et al. 2006)).

The central goal of this paper is to present the method for calibrating the system alignment as a function of the gantry angle. While many systems simply quantify the amount that beams of different gantry angles deviate from an ideal isocenter (e.g. “star shots” used in clinical radiation oncology physics assessments), we adopt the approach here of robotically correcting for the misalignment of each beam at each gantry angle in order to provide a more precise overall system alignment. The calibration method uses an x-ray camera, and a visual servoing method, to measure and correct for errors in the position and orientation of the treatment beam. This method has some similarity to the calibration method of the Cyberknife (Accuracy, Inc. Sunnyvale, CA.) system, which uses a light-sensitive crystal (Murphy & Cox 1996). Their method uses a 2 mm laser beam that is assumed to be coaxial with the treatment beam.

2. Methods and Materials

2.1. System Overview

The SARRP employs an isocentric design for imaging and irradiation (see Fig. 1). The entire assembly is portable to facilitate ease in deployment. A dual-focus constant voltage x-ray source operating up to 225 kVp is mounted on a gantry with a nominal source-to-isocenter distance of 35 cm. Gantry rotation is limited to 120° from vertical at fixed 15° increments. Computer controlled robotic translation and rotation stages are used to position the animal. The animal is put under anesthesia and immobilized using fixtures (a mouse bed is shown in Fig. 3). A novel CBCT imaging method is devised where the prone animal is rotated between the stationary x-ray source and a two dimensional (2D) digital flat-panel detector in a horizontal setup (Wong et al. 2008). Radiation beams with dimensions ranging from 0.5 mm in diameter to 200×200 mm are delivered with regularly and irregularly shaped collimators or blocks. Simple and complex three dimensional (3D) dose distributions are delivered using a combination of gantry and robotic stage motions.

Figure 1.

Different components of the Small Animal Radiation Research Platform.

Figure 3.

The mouse bed designed for immobilization and registration.

SARRP integrates imaging, radiation delivery and treatment planning capabilities. The mechanical structure is designed to meet the system requirements, which are to attain CT voxel resolution of 0.5 mm or better with 1cGy imaging dose, localized radiation dose whose exact beam size can be controlled with interchangeable collimators, and a dose rate of approximately 200 cGy per minute. In the following sections, different components of the SARRP are briefly described:

2.1.1. Robotic Positioner

The robotic positioner θXYZ consists of three modular off-the-shelf subassemblies: rotating table, X-Y cross table and vertical stage, Fig. 1. The rotary table is a preloaded, anti-backlash worm assembly that provides exceptional angular accuracy (0.05 degrees) and repeatability (0.007 degrees) (RTR-6, Danaher Motion, Salem, MA). It is actuated by an encoded DC motor. This stage provides unlimited angular positioning but, because of the chain that carries the other cables (for the XYZ axes), the range of motion is limited to ±190° via software. The X-Y motions are realized with a cross table X-Y (XY- 6060, Danaher Motion, Salem, MA). Each axis consists of a table actuated by an encoded DC motor driven lead-screw (65 µm/axis accuracy), with a monolithic center. The unit incorporates anti-backlash friction nuts to achieve a high repeatability (6 µm). The motion range for each axis is ±50 mm. For the vertical (Z) motion, we employed a stage with a scissors mechanism, motorized with an encoded DC motor (Servo Systems Co., Montville, NJ). The travel length is 38 mm and the anti-backlash lead-screw assembly has good repeatability (0.125 mm). Although this repeatability is worse than the other axes, it is sufficient for the design.

2.1.2. X-Ray Tube and Gantry

The X-ray source has a variable output with maximum beam energy of 225kVp. Images are acquired using 100 kVp setting and a focal spot size of 0.4mm. In treatment mode, 225 kVp setting is used with a 3.0mm focal spot with up to 13 mA beam current to deliver clinically useful dose rates (~2 Gy/min).

The X-ray source is mounted on a rotary gantry with source to center nominal distance of 35 mm, which can be manually set at nine different positions. These positions are located 15 degrees apart to create a 120 degree motion range. Any location of the gantry can be used for radiation treatment, whereas cone-beam CT acquisition is accomplished with the gantry in the horizontal position (= 90°).

2.1.3. Collimator and Shutter

Two collimator sets have been designed: “large” and “small”. The large collimator set is most useful for beam sizes larger than 10×10 mm, while the smaller collimator set is designed for higher accuracy and is most useful for beam sizes smaller than approximately 10×10 mm. Both sets contain three collimators aligned with the x-ray beam axis. The primary collimator, fixed to the x-ray source, reduces the size of the beam to 200×200 mm at the isocenter and is permanently attached. In the large collimator set, the secondary collimator has a telescopic design and can be removed; it reduces the beam size to 60×60 mm at the isocenter, Fig. 2(a). The third collimator has a variable position along the x-ray axis (minimum 230 mm, maximum 310 mm), is removable (together with the second one), and can be chosen to set beams with the following sizes: 0.5, 1 mm diameter and 3 × 3, 5 × 5mm, Fig. 2(c). Due to the finite size of the focal spot, the beam penumbra can be substantial, and is especially noticeable for smaller beam sizes. For the smallest beam (0.5 mm diameter), the beam is dominated by penumbra and becomes peaked. Even though the beam deviates from the ideal shape of a step function, however, it can still be used if one accepts some inhomogeneity in the target dose. This is similar to the clinical stereotactic radiosurgery scenario, where in one sets a prescription line at 50% of the maximum dose for example.

Figure 2.

(a) Collimator with a telescopic design, suitable for larger beam sizes, (b) Collimator designed for higher accuracy, suitable for smaller beam sizes and (c) Removable collimators to set beam size down to 0.5mm.

The smaller collimator set has a cylindrical design and is attached to the primary collimator in a fixed position. The distal end of the nozzle has a nominal 5 cm distance to isocenter. Like the larger collimator set, the third collimator can be chosen to set the beam diameter as low as 0.5 mm, Fig. 2(b). The shutter is a motor driven linear stage carrying two brass pieces to block the x-ray radiation during the tube power-up phase.

2.1.4. Fixation and Alignment

The SARRP provides a laser alignment system to facilitate accurate, reproducible setup of subjects. Three lasers, two mounted on the standing frame and the third mounted on the gantry pivot, converge at the nominal isocenter. This enables visual setup of large treatment fields, where an accuracy of several millimeters is sufficient.

While the laser system is intended for relatively coarse alignment, several mouse carriers are being developed for immobilization and registration, where millimeter or submillimeter accuracy is required. The mouse carriers incorporate gas anesthesia, temperature control to prevent hypothermia, and stereotactic frames for accurate delivery of treatment beams to the cranium, Fig. 3. The devices are MR compatible, and provide fiducials for coregistration of PET, MR and CBCT volumes.

Moreover, the SARRP provides integrated imaging using an x-ray camera box mounted below the subject in the anterior-posterior plane. The image captured by the camera may be used to perform the initial setup as well as to confirm setup accuracy post treatment.

2.1.5. Imaging subsystem

Acquisition of images is accomplished with a flat panel digital x-ray detector. The current system is the Model XRD digital x-ray panel from Perkin Elmer Inc. (Waltham, MA), a 512×512 pixel array with 0.4 mm² pixel size and 16 bit resolution. The detector frame rate is 7 Hz, providing rapid acquisition of images for cone beam tomography. Preprocessing of acquired images is performed in hardware on the frame grabber card to maximize the acquisition rate, and allow concurrent reconstruction of CT volumes while images are acquired on a standard PC workstation. Dark current and gain correction images are acquired at least once per day and used to correct pixel intensities as each image is acquired.

The imaging system uses a novel geometry to acquire cone-beam CT. The animal rests on a rotating platform, and is rotated around a dorsal-ventral axis. This is in contradistinction to the more traditional CT geometry in which the rotation is about the cranial-caudal axis. Images are acquired with the x-ray source in the horizontal position. As the subject is rotated, a series of projection radiographs are acquired. Volumetric reconstruction is accomplished using filtered back projection (Feldkamp et al. 1984). Because of the imaging geometry there is a large path length difference between the beams that traverse the long axis of the subjects vs. the lateral axis, but the resulting reconstruction image quality is nevertheless similar to a more traditional geometry.

The SARRP imaging beam operates at 100 kVp with 1 mm Al filtration. The aim of the imaging subsystem is not high resolution CT, but rapid, low dose acquisition and quantitative CT for dose calculation and treatment planning.

2.2. Treatment Calibration

Radiation treatment is often delivered from multiple poses that are intended to intersect at a specified point (the isocenter). Using beams from multiple angles results in a confined dose distribution that limits dose to surrounding areas. With the SARRP, rotation about a target can be obtained via the rotary (θ) axis or the x-ray gantry (ϕ). In reality, there is no single isocenter because the two axes of rotation do not (in general) intersect and even if they did, physical factors such as gravity loading on the mechanical structure would cause the x-ray beam to deviate from its ideal positions. Thus, x-ray beams delivered from multiple gantry angles will not intersect at a single point. One common solution is to find a single “best-fit” isocenter, but this approach does not yield sufficient accuracy for our system. Our solution is to define nine different isocenters – one for each position of the x-ray gantry. This is particularly appropriate for the SARRP because the gantry is manually rotated to one of nine distinct orientations; more generally, for systems with continuous gantry rotation, this approach can be used at a finite set of angles and a complete solution can be obtained by model-fitting or interpolation. For convenience, it is only necessary for the user to position the target at the image origin – the system will move it to the gantry-specific isocenter and will also adjust for any rotation (θ) of the target.

Fig. 4 depicts the two translations that are required to move the target from the image origin to the gantry-specific isocenter. It is assumed that the imaging system calibration aligns the image (CT) and robot coordinate systems, with the Z axis defined by the axis of rotation (θ) and the origin lying along this axis (i.e., X = Y = 0). We define the calibration origin as the point on the axis of rotation that is closest to the beam axis when the gantry is in the horizontal position (ϕ = 90°). Ideally, the translation A from the image origin to the calibration origin should consist only of a Z component (because the image origin should already lie on the axis of rotation), but in practice small X and Y values can compensate for inaccuracies in the image calibration. Second, the vector G(θ) translates from the calibration origin to the gantry-specific isocenter, which is obtained by using methods in described in Sections 2.2.2 – 2.2.5. Thus, the overall offset to each gantry-specific isocenter is given by:

$$\mathrm{\Delta }P=A+G(\varphi )$$ (1)

Figure 4.

Steps of defining isocenter, as seen in robot X-Y plane. Calibration origin is the point on the axis of rotation that is closest to the horizontal x-ray beam.

2.2.1. Measuring the offset to the calibration origin

The translation vector A (from image origin to calibration origin) is obtained by placing a ball bearing (BB) on the robotic positioner and performing a CBCT scan. The BB is then moved to the origin of the image coordinate system and a collimator (e.g., 3×3 or 5×5 mm) is installed, with the gantry still at the horizontal (imaging) position. The robot Z axis is adjusted until the BB appears vertically centered in the collimator, as measured on a 2D projection image, Fig. 5. The robot X and Y axes are adjusted to ensure that the BB does not move as the θ axis is rotated. The vector A is given by the amount that the robot X, Y, and Z axes were adjusted.

Figure 5.

Ball Bearing at the center of 5 × 5 mm collimated beam.

2.2.2. Measuring relative offsets to the gantry-specific isocenters

To measure the offsets G(ϕ), it is necessary to find the axis of rotation of the robotic positioner and the beam axes for each gantry angle. This is accomplished by placing an x-ray camera on the robotic stages in a position that can intersect the x-ray beam for as many gantry angles as possible. We found that a good x-ray camera position is when it makes a 45° angle with the horizon as shown in Fig. 6. This method does not require precise positioning or calibration of the x-ray camera. It does require a visual servoing method, described in the following section, which enables the system to automatically find the axis of rotation and the beam axes, as described in subsequent sections.

Figure 6.

Radiation calibration setup. The x-ray camera is placed at 45° with respect to the horizon to intercept the beam for as many gantry angles as possible.

2.2.3. Visual servoing method

Visual servoing is a technique that uses feedback information extracted from a vision sensor to control the motion of a robot (Hutchinson et al. 1996). In our application, the controller should be able to read the x-ray camera image, find the appropriate feature in the image (e.g. center of gravity of x-ray beam spot) and command the robot to move the image feature to a specified target position. A block diagram representing the control method is shown in Fig. 7. It is necessary to calculate the image Jacobian inverse to convert errors in image coordinates (u, v) to incremental robot motions (dx, dy, dz). We are currently using a precomputed image Jacobian that is based on our camera configuration. In particular, our x-ray camera is mounted at a 45° angle. This enables us to keep the camera in the same position for gantry angles between 0° and 105° degrees, which is a requirement for our calibration procedure. Also, the camera is mounted so that the robot x axis is approximately aligned with the camera v axis. The robot y and z axes then affect only the camera u axis, so it is straightforward to geometrically derive the non-trivial elements of the Jacobian, as shown in Fig. 8, when the x-ray arm is positioned ϕ° from vertical:

$$\frac{\mathit{\text{du}}}{\mathit{\text{dy}}}=\frac{\mathit{\text{tan}}(90-\varphi )}{\mathit{\text{sin}}(45)(1+\mathit{\text{tan}}(90-\varphi ))},\frac{\mathit{\text{du}}}{\mathit{\text{dz}}}=-\frac{\mathit{\text{tan}}(\varphi )}{\mathit{\text{sin}}(45)(1+\mathit{\text{tan}}(\varphi ))}$$ (2)

Figure 7.

Control block diagram of visual servo procedure.

Figure 8.

Relation between motion in robot y and z-axes and image u coordinate.

Of course, our controller requires the inverse of this Jacobian. For this simple case, the inverse terms are given by:

$$\begin{array}{ccccc}\hfill \left[\begin{array}{c}\hfill \mathit{\text{dx}}\hfill \\ \hfill \mathit{\text{dy}}\hfill \\ \hfill \mathit{\text{dz}}\hfill \end{array}\right]\hfill & \hfill =\left[\begin{array}{cc}\hfill 0\hfill & \hfill 1\hfill \\ \hfill \frac{1}{K}\left(\frac{\mathit{\text{du}}}{\mathit{\text{dy}}}\right)\hfill & \hfill 0\hfill \\ \hfill \frac{1}{K}\left(\frac{\mathit{\text{du}}}{\mathit{\text{dz}}}\right)\hfill & \hfill 0\hfill \end{array}\right]\hfill & \hfill \left[\begin{array}{c}\hfill \mathit{\text{du}}\hfill \\ \hfill \mathit{\text{dv}}\hfill \end{array}\right]\hfill & & \hfill K={\left(\frac{\mathit{\text{du}}}{\mathit{\text{dy}}}\right)}^2\hfill \end{array}+{\left(\frac{\mathit{\text{du}}}{\mathit{\text{dz}}}\right)}^2$$ (3)

We found that controller performance is not very sensitive to the image Jacobian inverse, so our nominal matrix worked well in all practical situations. It is also possible to empirically estimate the image Jacobian by moving the robot a fixed distance along each axis and measuring the corresponding image change. This would require computation of a matrix pseudo-inverse to obtain the desired image Jacobian inverse.

We obtained excellent performance from a simple proportional controller. Note that our controller inherently includes an integrator because we sum the incremental motions obtained by applying the image Jacobian inverse to the errors measured in image coordinates.

2.2.4. Measuring the axis of rotation

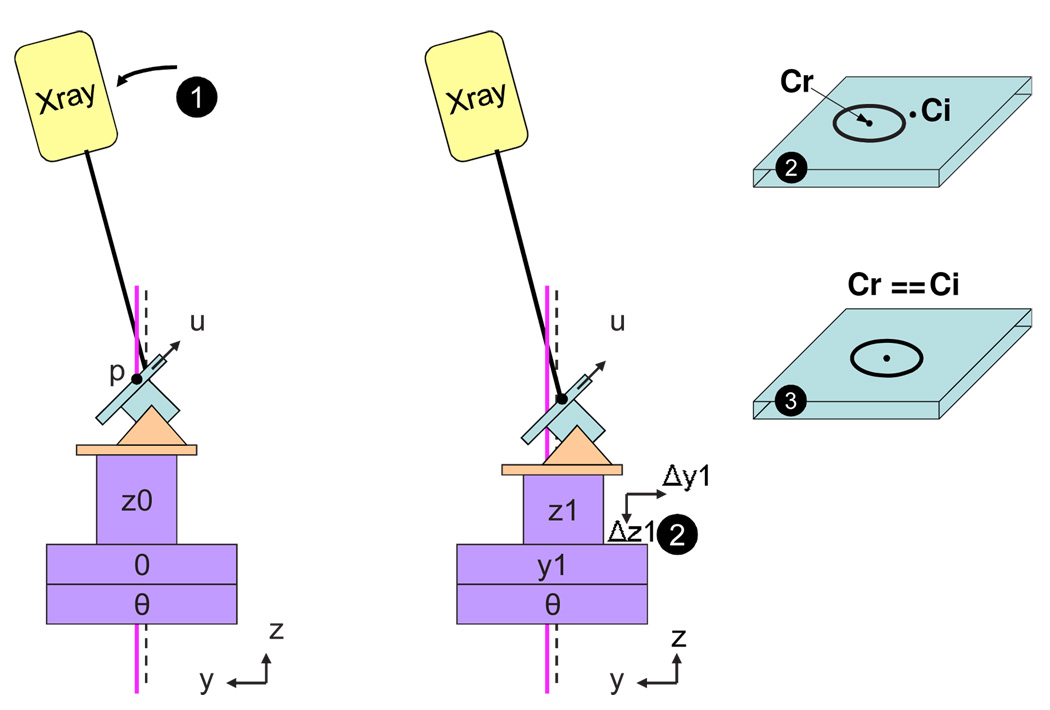
As a first step, we measure the axis of rotation of the robotic positioner because it is needed to determine the calibration origin. The measurement is performed by placing the x-ray gantry in the vertical position and rotating the stage through a set of angles, with X = Y = 0 and Z = Z₀, where Z₀ is an arbitrary value that places the camera near the expected isocenter. The x-ray camera captures an image at each angle; these images are superimposed (added), as shown in Fig. 9(a). The center of rotation, C_r (in camera coordinates), is given by the center of gravity of the final image. Effectively, C_r defines the coordinates of a specific camera pixel that we will use for all subsequent measurements. This pixel corresponds to the point (0,0,Z₀), in robot coordinates, through which the axis of rotation passes. The axis of rotation is determined by moving the robot Z axis to a second position, Z₁, and then using the visual servoing to move the robot X and Y axes until the measured center of rotation, C_r1, is equal to C_r. The axis of rotation is given by the vector (Δx, Δy, Z₁ − Z₀), where Δx and Δy are the amounts that the X and Y axes were moved, respectively. The point on the axis of rotation that is closest to the horizontal x-ray beam (to be measured below) defines the calibration origin in robot coordinates.

Figure 9.

(a) X-ray images used to find the axis of rotation (b) Calibration of the axis of rotation.

2.2.5. Measuring beam axes

Once C_r is determined, we measure the beam axis at each x-ray arm position as follows (see Fig. 10):

1. Move the x-ray gantry to the angle α.

2. Capture an image with the x-ray camera and compute center of gravity, C_i.

3. Use visual servoing to move the robot and capture images until C_i is equal to C_r. The amount of XYZ motion provides the coordinates of one point on the x-ray beam.

4. Move the robot to a new position and repeat the procedure. This provides a second point on the x-ray beam which, along with the first point, defines the direction of the x-ray beam.

Figure 10.

2D illustration of procedure to find the vector describing an x-ray beam.

The two points collected above define the coordinates of a unit vector along the beam axis. We compute the calibration origin by finding the point on the axis of rotation that is closest to beam axis at 90°. Then each G(ϕ) in equation (1) is given by solving the least-squares optimization:

$$\begin{array}{cc}\text{min}{\displaystyle \sum _{\varphi }{\Vert P(\varphi )+D(\varphi )s(\varphi )-C\Vert }^2}\hfill & \varphi =0°,15°,\dots \hfill \end{array}$$ (4)

where P(ϕ) and D(ϕ) are the (measured) point and direction vector that define the beam axis at the gantry angle ϕ, C is the (unknown) “best fit” isocenter, and s(ϕ) is the (unknown) parameter that defines the point on the line that is closest to C. Specifically, for each gantry angle ϕ, the calibration offset G(ϕ) is given by P(ϕ) + D(ϕ)s(ϕ).

A graphical user interface has been developed to implement the above procedure. For each gantry location, the program derives the corresponding image Jacobian, finds the center of gravity of the image and controls the robot motion to accurately determine the point and normal vector that define the beam axis. Then, the interface displays all of these data and performs the least-squares optimization given by equation (4).

3. Results and Discussion

3.1. Results

Based on the methods described in Section 2.2, a set of experiments were carried out to find the calibration offsets. For the different gantry angles, the coordinates of a unit vector along the beam axis and a point on the beam axis were found. Fig. 11 shows these data when they are plotted in the YZ-plane (which is the plane spanned by the ideal beam axes). This corresponds to a digitally constructed “star shot” image. The offsets from the calibration origin to the gantry-specific isocenters are given in Table 1.

Figure 11.

Digitally constructed “star shot” showing x-ray beams for each gantry angle. Plot shows both nominal gantry angles (right) and measured angles (on each line), AOR=Axis of rotation, other symbols indicate gantry-specific isocenter.

Table 1.

Isocenter offsets relative to calibration origin. The large y-axis offset indicates that the mechanical calibration was not able to align the CBCT origin with the robot origin.

	Isocenter Offsets (mm)
Gantry Angle	x	y	z
0	1.07	−5.18	−0.54
15	0.94	−4.33	−0.62
30	0.82	−3.99	−0.84
45	0.77	−3.96	−1.01
60	0.75	−4.13	−0.94
75	0.56	−4.32	−0.57
90	0.41	−4.27	0.16

To validate the calibration results, we constructed a phantom with three radiographic films in a vertical stack, as shown in Fig. 12. Using cone-beam CT we identified a target on the center film and delivered a collimated beam (1 mm diameter) from multiple gantry angles (45 and 15 degrees from horizontal) and at 45 degree increments of the rotary θ stage. The center film shows the spot where all x-rays intersect. To emphasize the importance of calibration, we used the same phantom with a 0.5 mm beam to compare a calibrated beam with an uncalibrated one. Fig. 13 shows the scanned EBT films for this experiment. It is clear that unless the offsets are applied for each rotary stage motion, the beams do not intersect. All beams intersect at a common isocenter with a measured beam (FWHM) of approximately 1.07 mm.

Figure 12.

Validation using radiographic films at gantry angles (ϕ) of 45° and 15°, with 45° stage rotations (θ) with 1 mm beam.

Figure 13.

0.5 mm uncalibrated (left) and calibrated (right) beam over 360° arc of robot rotational stage at isocenter for gantry at 45°. As clearly observed, beams at different gantry angles intersect each other only if offsets for each robot axes are applied.

To quantify the calibration error and repeatability, we performed an additional three trials, using just the 45 degree gantry angle. This produced films similar in appearance to Fig. 12, minus the smaller circle of spots on the top and bottom films due to irradiation at the 15 degree gantry angle. We collected a set of data for each film (bottom, center and top), as shown in Fig. 14 for the first sample. Here, the spot on the bottom film is wider than the one on the top film, as would be expected due to beam divergence. The expected diameter in the center film is given by the average of the top and bottom diameters (because the films are equidistant). The calibration error is the difference between the measured radius (on the center film) and the expected radius (i.e., one half of the difference in diameters).

Figure 14.

Data profiles for bottom, center and top films. Ideally, the full width of center spot would be midway between full width of top and bottom spots. The fact that the center spot width is slightly larger indicates some error (~ 0.2mm) in targeting accuracy.

Table 2 depicts the measurements of the spot diameters for three samples. These measurements are the full width of the beam, rather than the FWHM, because the FWHM would underestimate the calibration error due to its higher maximum value. For the center film, the measurement is oriented so that it covers the longest dimension of the star shape. All of the calibration errors were ±0.20 mm or lower.

Table 2.

X-ray beam diameter measurement in radiographic films (in mm) for 1mm beam. The desired positioning accuracy of the SARRP is 0.25mm and the results indicate an accuracy of 0.2mm.

	Beam Diameters (mm)
	Top Film	Center Film	Bottom Film	Error(mm)
Sample 1	2.39	2.85	2.58	±0.18
Sample 2	2.17	2.62	2.55	±0.13
Sample 3	2.15	2.80	2.65	±0.20

3.2. Discussion

Our results have demonstrated that SARRP can provide focal irradiation of a target volume with submillimeter accuracy, which is a critical capability for small animal radiation research. Radiation can be delivered to the isocenter from multiple gantry angles, and at different orientations of the target, over a 360° arc. The error in alignment of the beam from multiple angles measured to be less than 0.20 mm.

Our calibration method uses an x-ray camera, mounted on the robotic positioner, to measure the center of rotation and the beam axes. The method uses visual servoing to achieve automated measurement of these parameters. From these parameters, we define a set of gantry-specific isocenters and obtain the offsets from our calibration origin to each isocenter. The technique is easy to perform and takes less than one hour for all gantry angles, as it does not require calibration or precise placement of the x-ray camera. Thus, it can easily be performed as a periodic quality assurance procedure.

Other investigators have discussed the need for highly accurate radiation delivery for small animal research. DesRosiers et al. (2003) note that most clinical systems, such as a linear accelerator (Linac), have an accuracy of about ±2 mm, whereas small animals (with correspondingly smaller structures) require an accuracy that is an order of magnitude higher (e.g., ±0.2 mm). They demonstrated the feasibility of using a Gamma Knife (R) (Elekta Inc., Stokholm, Sweden), with a localization accuracy of about ±0.5 mm, for small animal research. Similar studies have also used the Gamma Knife for irradiation of a rat brain (Bartolomei et al. 1998). The disadvantage of the Gamma Knife, the Gammacell ®(MDS Nordion Inc., Ottawa, Canada) and other related irradiation systems is that the minimum size of the deliverable beam is rather large (4 mm diameter in the case of Gamma Knife) and there is no established method for localizing the subject with sub-millimeter accuracy.

Development efforts for small animal radiation systems similar to ours are being undertaken by a handful of groups in North America. The laboratory of Jaffray (Lindsay et al. 2008) built a system that shows many similarities to the one presented here, with the exception that the animal bed does not rotate. Instead, the gantry rotates over a 360° range around the cantilevered animal. Moros et al. (2008) also reported the construction of a system wherein the animal is positioned by a 6DOF robotic arm. In many respects, including the collimator design, the system provides identical capabilities to the one presented here. Graves et al. (2007) constructed a variable aperture collimator for shaping the beam of a microCT scanner that can image small animal subjects at high resolution, and is capable of delivering therapeutic doses with reasonable exposure times. Rodriguez & Jeraj (2008) designed a micro-irradiator to irradiate partial bodies in zebrafish embryos 3 – 4 mm in length. Through an automatic image-based specimen recognition, they move a computer controlled table to position the embryos and cell cultures underneath a 1 mm pencil beam. Wang et al. (2007) prototyped a CNT field emission cathode array chip with 5 × 5 cathode pixels to generate a dose rate on the order of 100 cGy/min at the center of the chip. Another ¹⁹²Ir-based small animal conformal irradiator has been designed by Stojadinovic et al. (2007) that utilizes aluminum and tungsten collimators to shape the beam for four orthogonal directions (0°, 90°, 180°, 270°). Their system is equipped with a three-axis computer-controlled stage to position the animal relative to the radiation beam. The definition of the collimator assembly coordinate system is done using an animal stage with fiducial markers and a phantom with three embedded ball bearings.

The main difference between the SARRP and other systems mentioned above is the capability of SARRP for doing non-coplanar stereotactic-like treatment. This may provide advantages for applications that require restricted beam entry angles. All mechanical systems require some geometric calibration; we note that although it may be relatively straightforward to produce a < 1mm delivery beam, it is challenging to make all these beams intersect at the same point from a large mechanical system like SARRP. Our calibration method is based on the premise that higher accuracy can be achieved by defining multiple points (in our case, one for each of the fixed gantry angles) and moving the robotic positioner to place the target at the appropriate isocenter.

4. Conclusion

In this paper, we presented a novel system for small animal radiation with advanced imaging and irradiation capabilities that mimic methods employed in modern human treatment. The design incorporates three important component parts: focal irradiation of a target volume to within 1 mm resolution; on-board tomographic imaging; and volumetric treatment planning to design high-precision pre-clinical irradiation experiments.

Currently we are constructing a second system with a motorized gantry. Future improvements include development of coordinated robot motion to achieve a virtual center of rotation for conformal therapy, rather than just the “step and shoot” approach shown in Fig. 12. Ongoing validation studies are focusing on determining the system repeatability and recommended calibration intervals.