Compensating Inhomogeneities of Neuromorphic VLSI Devices Via Short-Term Synaptic Plasticity

Abstract

Recent developments in neuromorphic hardware engineering make mixed-signal VLSI neural network models promising candidates for neuroscientific research tools and massively parallel computing devices, especially for tasks which exhaust the computing power of software simulations. Still, like all analog hardware systems, neuromorphic models suffer from a constricted configurability and production-related fluctuations of device characteristics. Since also future systems, involving ever-smaller structures, will inevitably exhibit such inhomogeneities on the unit level, self-regulation properties become a crucial requirement for their successful operation. By applying a cortically inspired self-adjusting network architecture, we show that the activity of generic spiking neural networks emulated on a neuromorphic hardware system can be kept within a biologically realistic firing regime and gain a remarkable robustness against transistor-level variations. As a first approach of this kind in engineering practice, the short-term synaptic depression and facilitation mechanisms implemented within an analog VLSI model of I&F neurons are functionally utilized for the purpose of network level stabilization. We present experimental data acquired both from the hardware model and from comparative software simulations which prove the applicability of the employed paradigm to neuromorphic VLSI devices.

Introduction

Software simulators have become an indispensable tool for investigating the dynamics of spiking neural networks (Brette et al., 2007). But when it comes to studying large-scale networks or long-time learning, their usage easily results in lengthy computing times (Morrison et al., 2005). A common solution, the distribution of a task to multiple CPUs, raises both required space and power consumption. Thus, the usage of neural networks in embedded systems remains complicated.

An alternative approach implements neuron and synapse models as physical entities in electronic circuitry (Mead, 1989). This technique provides a fast emulation at a maintainable wattage (Douglas et al., 1995). Furthermore, as all units inherently evolve in parallel, the speed of computation is widely independent of the network size. Several groups have made significant progress in this field during the last years (see for example Indiveri et al., 2006; Merolla and Boahen, 2006; Schemmel et al., 2007, 2008; Vogelstein et al., 2007; Mitra et al., 2009). The successful application of such neuromorphic hardware in neuroscientific modeling, robotics and novel data processing systems will essentially depend on the achievement of a high spatial integration density of neurons and synapses. As a consequence of ever-smaller integrated circuits, analog neuromorphic VLSI devices inevitably suffer from imperfections of their components due to variations in the productions process (Dally and Poulton, 1998). The impact of such imperfections can reach from parameter inaccuracies up to serious malfunctioning of individual units. In conclusion, the particular, selected emulation device might distort the network behavior.

For that reason, designers of neuromorphic hardware often include auxiliary parameters which allow to readjust the characteristics of many components. But since such calibration abilities require additional circuitry, their possible extent of use usually has to be limited to parameters that are crucial for the operation. Hence, further concepts are needed in order to compensate the influence of hardware variations on network dynamics. Besides increasing the accuracy of unit parameters like threshold voltages or synaptic time constants, a possible solution is to take advantage of self-regulating effects in the dynamics of neural networks. While individual units might lack adequate precision, populations of properly interconnected neurons can still feature a faultless performance.

Long-term synaptic potentiation and depression (Morrison et al., 2008) might be effective mechanisms to tailor neural dynamics to the properties of the respective hardware substrate. Still, such persistent changes of synaptic efficacy can drastically reshape the connectivity of a network. In contrast, short-term synaptic plasticity (Zucker and Regehr, 2002) alters synaptic strength transiently. As the effect fades after some hundred milliseconds, the network topology is preserved.

We show that short-term synaptic plasticity enables neural networks, that are emulated on a neuromorphic hardware system, to reliably adjust their activity to a moderate level. The achievement of such a substrate on a network level is an important step toward the establishment of neuromorphic hardware as a valuable scientific modeling tool as well as its application as a novel type of adaptive and highly parallel computing device.

For this purpose, we examine a generic network architecture as proposed and studied by Sussillo et al. (2007), which was proven to feature self-adjustment capabilities. As such networks only consist of randomly connected excitatory and inhibitory neurons and exhibit little specialized structures, they can be found in various cortical network models. In other words, properties of this architecture are likely to be valid in a variety of experiments.

Still, the results of Sussillo et al. (2007) not necessarily hold for neuromorphic hardware devices: The referred work addressed networks of 5000 neurons. As the employed prototype hardware system (Schemmel et al., 2006, 2007) only supports some hundred neurons, it remained unclear whether the architecture is suitable for smaller networks, too. Furthermore, the applicability to the specific inhomogeneities of the hardware substrate have not been investigated before. We proof that even small networks are capable of leveling their activity. This suggests that the studied architecture can enhance the usability of upcoming neuromorphic hardware systems, which will comprise millions of synapses.

The successful implementation of short-term synaptic plasticity into neuromorphic hardware has been achieved by several work groups, see, e.g., Boegershausen et al. (2003) or Bartolozzi and Indiveri (2007). Nevertheless, this work presents the first functional application of this feature within emulated networks. It is noteworthy, that the biological interpretation of the used hardware parameters is in accord with physiological data as measured by Markram et al. (1998) and Gupta et al. (2000).

Since the utilized system is in a prototype state of development, the emulations have been prepared and counter-checked using the well-established software simulator Parallel neural Circuit SIMulator (PCSIM; Pecevski et al., 2009). In addition, this tool allowed a decent analysis of network dynamics because the internal states of all neurons and synapses can be accessed and monitored continuously.

Materials and Methods

The applied setup and workflow involve an iterative process using two complementary simulation back-ends: Within the FACETS research project (FACETS, 2009), the FACETS Stage 1 Hardware system (Schemmel et al., 2006, 2007) and the software simulator PCSIM (Pecevski et al., 2009) are being developed.

First, it had to be investigated whether the employed network architecture exhibits its self-adjustment ability in small networks fitting onto the current prototype hardware system. For this purpose, simulations have been set up on PCSIM which only roughly respected details of the hardware characteristics, but comprised a sufficiently small number of neurons and synapses. Since the trial yielded promising results, the simulations were transferred to the FACETS Hardware. At this stage the setup had to be readjusted in order to meet all properties and limitations of the hardware substrate. Finally, the parameters used during the hardware emulations were transferred back to PCSIM in order to verify the results.

In Sections “The Utilized Hardware System” and “The Parallel neural Circuit SIMulator” both back-ends are briefly described. Section “Network Configuration” addresses the examined network architecture and the parameters applied. In Section “Measurement”, the experimental setup for both back-ends is presented.

The utilized hardware system

The present prototype FACETS Stage 1 Hardware system physically implements neuron and synapse models using analog circuitry (Schemmel et al., 2006, 2007). Beside the analog neural network core (the so-called Spikey chip) it consists of different (mostly digital) components that provide communication and power supply as well as a multi-layer software framework for configuration and readout (Grübl, 2007; Brüderle et al., 2009).

The Spikey chip is built using a standard 180 nm CMOS process on a 25-mm² die. Each chip holds 384 conductance-based leaky integrate-and-fire point neurons, which can be interconnected or externally stimulated via approximately 100,000 synapses whose conductance courses rise and decay exponentially in time. As all physical units inherently evolve both in parallel and time-continuously, experiments performed on the hardware are commonly referred to as emulations. The dimensioning of the utilized electronic components allows a highly accelerated operation compared to the biological archetype. Throughout this work, emulations were executed with a speedup factor of 10⁵.

In order to identify voltages, currents and the time flow in the chip as parameters of the neuron model, all values need to be translated between the hardware domain and the biological domain. The configuration and readout of the system has been designed for an intuitive, biological description of experimental setups: The Python-based (Rossum, 2000) meta-language PyNN (Davison et al., 2008) provides a back-end independent modeling tool, for which a hardware-specific implementation is available (Brüderle et al., 2009). All hardware-specific configuration and data structures (including calibration and parameter mapping), which are encapsulated within low-level machine-oriented software structures, are addressed automatically via a Python Hardware Abstraction Layer (PyHAL).

Using this translation of biological values into hardware dimensions and vice versa which is performed by the PyHAL, all values given throughout this work reflect the biological interpretation domain.

Short-term synaptic plasticity

All synapses of the FACETS Stage 1 Hardware support two types of synaptic plasticity (Schemmel et al., 2007). While a spike-timing dependent plasticity (STDP) mechanism (Bi and Poo, 1997; Song et al., 2000) is implemented in every synapse, short-term plasticity (STP) only depends on the spiking behavior of the pre-synaptic neuron. The corresponding circuitry is part of the so-called synapse drivers and, thus, STP-parameters are shared by all synaptic connections operated by the same driver. Each pre-synaptic neuron can project its action potentials (APs) to two different synapse drivers. Hence, two freely programmable STP-configurations are available per pre-synaptic neuron. The STP mechanism implemented in the FACETS Stage 1 Hardware is inspired by Markram et al. (1998). But while the latter model combines synaptic facilitation and depression, the hardware provides the two modes separately. Each synapse driver can either be run in facilitation or in depression mode or simply emulate static synapses without short-term dynamics. Despite this restriction, these short-term synapse dynamics support dynamic gain-control mechanisms as, e.g., reported in Abbott et al. (1997).

In the Spikey chip, the conductance g(t) of a synapse is composed of a discrete synaptic weight multiplier w_n, the base efficacy w₀(t) of a synapse driver and the conductance course of the rising and falling edge p(t):

g(t) = w_n·w₀(t)·p(t) =: w(t)·p(t)

with w_n ∈ {0,1,2,…,15}. In this framework, STP alters the base efficacy w₀(t) while the double-exponential conductance course of a single post-synaptic potential is modeled via p(t) ∈ [0,1]. Whenever an AP is provoked by the pre-synaptic neuron, p(t) is triggered to run the conductance course. To simplify matters, the product w_n·w₀(t) often is combined to the synaptic weight w(t) or just w in case of static synapses.

Both STP-modes, facilitation and depression, alter the synaptic weight in a similar manner using an active partition I(t) ∈ [0,1]. The strength w_stat of a static synapse is changed to

$$\begin{array}{l}{w}_{\text{fac}}(t)=w_{\text{stat}}\cdot \left[1+\lambda \cdot \left(I(t)-\beta \right)\right],\\ w_{\text{dep}}(t)=w_{\text{stat}}\cdot \left[1-\lambda \cdot I(t)\right]\end{array}$$ (1)

in case of facilitation and depression, respectively. The parameters λ and β are freely configurable. For technical reasons, the change of synaptic weights by STP cannot be larger than the underlying static weight. Stronger modifications are truncated. Hence, 0 ≤ w_fac/dep ≤ 2·w_stat.

The active partition I obeys the following dynamics: Without any activity I decays exponentially with time constant τ_STP, while every AP processed increases I by a fixed fraction C toward the maximum,

$$\frac{dI}{dt}=-\frac{I}{{\tau }_{\text{STP}}}+C\cdot \left(1-I\right)\cdot \delta \left(t-t_{AP}\right).$$

For C ∈ [0,1], I is restricted to the interval mentioned above. Since the active partition affects the analog value w₀(t), the STP-mechanism is not subject to the weight-discretization w_n of the synapse arrays but alters weights continuously.

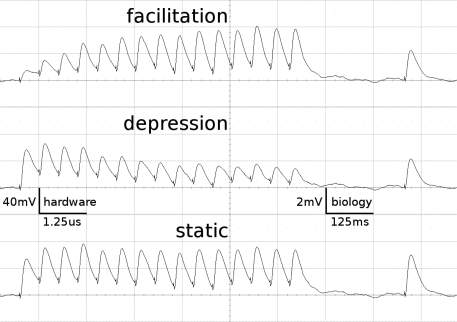
Figure 1 shows examples of the dynamics of the three STP-modes as measured on the FACETS Stage 1 Hardware. The applied parameters agree with those of the emulations presented throughout this work.

Figure 1.

Short-term plasticity-mechanism of the FACETS Stage 1 Hardware. A neuron is excited by an input neuron that spikes regularly at 20 Hz. Three hundred milliseconds after the last regular spike a single spike is appended. Additionally, the neuron is stimulated with Poisson spike trains from further input neurons. The figure shows the membrane potential of the post-synaptic neuron, averaged over 500 experiment runs. As the Poisson background cancels out, the EPSPs provoked by the observed synapse are revealed. Time and voltage are given in both hardware values and their biological interpretation. The three traces represent different modes of the involved synapse driver. Facilitation: The plastic synapse grows in strength with every AP processed. After 300 ms without activity the active partition has partly decayed. Depression: High activity weakens the synapse. Static: The synapse keeps its weight fixed.

Hardware constraints

Neurons and synapses are represented by physical entities in the chip. As similar units reveal slightly different properties due to the production process, each unit exhibits an individual discrepancy between the desired configuration and its actual behavior. Since all parameters are controlled by voltages and currents, which require additional circuitry within the limited die, many parameters and sub-circuits are shared by multiple units. This results in narrowed parameter ranges and limitations on the network topology.

Beyond these intentional design-inherent fluctuations and restrictions, the current prototype system suffers from some malfunctions of different severity. These errors are mostly understood and will be fixed in future systems. In the following, the constraints which are relevant for the applied setup will be outlined. For detailed information the reader may refer to the respective literature given below.

Design-inherent constraints

• As described above, synaptic weights are discrete values w = w_n·w₀ with w_n ∈ {0,1,2,…,15} (Schemmel et al., 2006). Since biological weights are continuous values, they are mapped probabilistically to the two closest discrete hardware weights. Therefore, this constraint is assumed to have little impact on large, randomly connected networks.

• Each pre-synaptic neuron allocates two synapse drivers to provide both facilitating and depressing synapses. Since only 384 synapse drivers are available for the operation of recurrent connections, this restricts the maximum network size to 384/2 = 192 neurons. After establishing the recurrent connections, only 64 independent input channels remain for excitatory and inhibitory external stimulation via Poisson spike trains (see Bill, 2008, Chapter VI.3).

• Bottlenecks of the communication interface limit the maximum input bandwidth for external stimulation to approximately 12 Hz per channel when 64 channels are used for external stimulation with Poisson spike trains. Future revisions are planned to run at a speedup factor of 10⁴ instead of 10⁵, effectively increasing the input bandwidth by a factor of 10 from the biological point of view (see Grübl, 2007, Chapter 3.2.1; Brüderle, 2009, Chapter 4.3.7).

Malfunctions

• The efficacy of excitatory synapses was found to be unstable. A frequent global activity of excitatory synapses has been shown to decrease EPSP amplitudes up to a factor of two. Presumably, this effect depends on both the configuration of the chip and the overall spike activity. We refer to this malfunction as load-dependency of the synaptic efficacy in the following. Since the error cannot be counterbalanced by calibration or tuning the configuration, it is considered crucial for the presented experimental setup (see Brüderle, 2009, Chapter 4.3.4).

• The current system suffers from a disproportionality between the falling-edge synaptic time constant τ_syn ≈ 30 ms and the membrane time constant τ_mem ≈ 5 ms, i.e., a fast membrane and slow synapses. This was taken into consideration when applying external stimulation, as presented in Section “Applied Parameters” (see Brüderle, 2009, Chapter 4.3.5; Kaplan et al., 2009).

• Insufficient precision of the neuron threshold comparator along with a limited reset conductance result in a rather wide spread of the neuron threshold and reset voltages V_thresh and V_reset. As both values are shared by multiple neurons, this effect can only be partially counterbalanced by calibration. The used calibration algorithms lead to ${\sigma }_{V_{\text{thresh}}}\approx 3\text{\hspace{0.17em}mV}$ and ${\sigma }_{V_{\text{reset}}}\approx 8\text{\hspace{0.17em}mV}$ (see Bill, 2008, Chapter IV.4; Brüderle, 2009, Chapter 4.3.2).

• Insufficient dynamic ranges of control currents impede a reasonable configuration of the STP parameters λ and β in Eq. 1 without additional technical effort. The presented emulations make use of a workaround which allows a biologically realistic setup of the STP-parameters at the expense of further adjustability. The achieved configuration has been measured and is used throughout the software simulations, as well (see Bill, 2008, Chapter IV.5.4).

• An error in the spike event readout circuitry prevents a simultaneous recording of the entire network. Since only three neurons of the studied network architecture can be recorded per emulation cycle, every configuration was rerun 192/3 = 64 times with different neurons recorded. Thus, all neurons have been taken into consideration in order to determine average firing rates. But since the data is obtained in different cycles, it is unclear to what extent network correlation and firing dynamics on a level of precise spike timing can be determined (see Müller, 2008, Chapter 4.2.2).

A remark on parameter precision

The majority of the parameter values used in the implemented neuron model are generated by complex interactions of hardware units, as transistors and capacitors. Each type of circuitry suffers from different variations due to the production process, and these fluctuations sum up to intricate discrepancies of the final parameters. For that reason, both shape and extent of the variances often cannot be calculated in advance. On the other hand, only few parameters of the neuron and synapse model can be observed directly. Exceptions are all kind of voltages, e.g., the membrane voltage or reversal potentials. The knowledge of all other parameters was obtained from indirect measurements by evaluating spike events and membrane voltage traces. The configuration given in Section “Applied Parameters” reflects the current state of knowledge. This means that some specifications – especially standard deviations of parameters – reflect estimations which are based on long-term experience with the device. But, compared to the above-described malfunctions of the prototype system, distortions arising from uncertainties in the configuration can be expected to be of minor importance.

The parallel neural circuit simulator

All simulations were performed using the PCSIM simulation environment and were set up and controlled via the associated Python interface (Pecevski et al., 2009).

The neurons were modeled as leaky integrate-and-fire cells (LIF) with conductance-based synapses. The dynamics of the membrane voltage V(t) is defined by

$$\begin{array}{ll}{C}_{\text{m}}\frac{\text{d}V(t)}{\text{d}t}\hfill & =g_{\text{leak}}\cdot (V(t)-V_{\text{rest}})\hfill \\ \hfill & -{\displaystyle \sum _{k=1}^{N_{\text{e}}}{g}_{\text{e},k}(t)\cdot (V(t)-E_{\text{e}})}\hfill \\ \hfill & -{\displaystyle \sum _{k=1}^{N_{\text{i}}}{g}_{\text{i},k}(t)\cdot (V(t)-E_{\text{i}})}\hfill \\ \hfill & +I_{\text{noise}}(t),\hfill \end{array}$$

where C_m is the membrane capacity, g_leak is the leakage conductance, V_rest is the leakage reversal potential, and g_e,k(t) and g_i,k(t) are the synaptic conductances of the N_e excitatory and N_i inhibitory synapses with reversal potentials E_e and E_i, respectively. The white noise current I_noise(t) has zero mean and a standard deviation σ_noise = 5 pA. It models analog noise of the hardware circuits.

The dynamics of the conductance g(t) of a synapse is defined by

$$\frac{\text{d}g(t)}{\text{d}t}=-\frac{g(t)}{{\tau }_{\text{syn}}}+w\cdot \delta \left(t-t_{\text{AP}}\right),$$

where g(t) is the synaptic conductance and w is the synaptic weight. The conductances decrease exponentially with time constant τ_syn and increase instantaneously by adding w to the running value of g(t) whenever an AP occurs in the pre-synaptic neuron at time t_AP. Modeling the exponentially rising edge of the conductance course of the FACETS Stage 1 Hardware synapses was considered negligible, as the respective time constant was set to an extremely small value for the hardware emulation.

If we used static synapses the weight w of a synapse was constant over time. Whereas for simulations with dynamic synapses, the weight w(t) of each synapse was modified according to the short-term synaptic plasticity rules described in Section “Short-Term Synaptic Plasticity”.

The values of all parameters were drawn from random distributions with parameters as listed in Table 1.

Table 1.

Full set of parameters.

Description	Name	Unit	Mean μ	σ/μ	π/μ	Comment
NETWORK ARCHITECTURE
Number of exc neurons	Ne		144
Number of inh neurons	Ni		48
Conn prob from exc to exc neurons	pee		0.1
Conn prob from exc to inh neurons	pie		0.2
Conn prob from inh to exc neurons	pei		0.3
Conn prob from inh to inh neurons	pii		0.6
NEURONS (EXCITATORY AND INHIBITORY)
Membrane capacitance	Cm	nF	0.2	0	0	by definition
Leakage reversal potential	Vrest	mV	−63,…,−55			variable parameter
Firing threshold voltage	Vthresh	mV	−55.0	0.05	0.1
Reset potential	Vreset	mV	−80.0	0.1	0.2
Excitatory reversal potential	Ee	mV	0.0	0	0	−20 mV in some simulations
Inhibitory reversal potential	Ei	mV	−80.0	0	0
Leakage conductance	gleak	nS	40.0	0.5	0.5	*)
Refractory period	τref	ms	1.0	0.5	0.5
RECURRENT SYNAPSES
Weight of exc to exc synapses	wee	nS	1.03	0.6	0.7	*) values refer to
Weight of exc to inh synapses	wie	nS	0.52	0.6	0.7	*) static synapses
Weight of inh to exc synapses	wei	nS	3.10	0.6	0.7	*)
Weight of inh to inh synapses	wii	nS	1.55	0.6	0.7	*)
Cond time constant for all synapses	τsyn	ms	30.0	0.25	0.5
Conversion factor for facilitation			1.10			to match with static syns
Conversion factor for depression			1.65			at regular firing of 20 Hz
Strength of STP	λ		0.78	0.1	0.2
Bias for facilitation	β		0.83	0.1	0.2
STP decay time constant	τSTP	ms	480	0.2	0.4
Step per spike for facilitation	Cfac		0.27	0.1	0.2
Step per spike for depression	Cdep		0.11	0.1	0.2
EXTERNAL STIMULUS: POISSON SPIKE TRAINS
Number of exc external spike sources	Next,e		32
Number of inh external spike sources	Next,i		32
Number of exc inputs per neuron			4–6			uniform distribution
Number of inh inputs per neuron			4–6			uniform distribution
Firing rate per input spike train	νinp	Hz	11.8	0.2	0.2	*)
Weight of exc input synapses	winp,e	nS	0.26,…,1.29	0.6	0.7	*) varied via Winput and
Weight of inh input synapses	winp,i	nS	0.77,…,3.87	0.6	0.7	*) refer to Vrest = −60 mV
Cond time constant for all synapses	τsyn	ms	30.0	0.25	0.5
EXPERIMENT
Simulated time per exp run	Texp	ms	4500			only t ≥ 1000 ms evaluated
Number of exp runs per param set	nrun		20			×64 in hardware with same network

All values given in biological units. If not stated otherwise, values are drawn from a bound normal distribution with mean μ, standard deviation σ, and bound π. Parameters marked by a *) have been spread for the hardware emulations by configuration.

Network configuration

In the following, the examined network architecture is presented. Rather than customizing the configuration to the employed device, we aimed for a generic, back-end agnostic choice of parameters. Due to hardware limitations in the input bandwidth, a dedicated concept for external stimulation had to be developed.

Network architecture

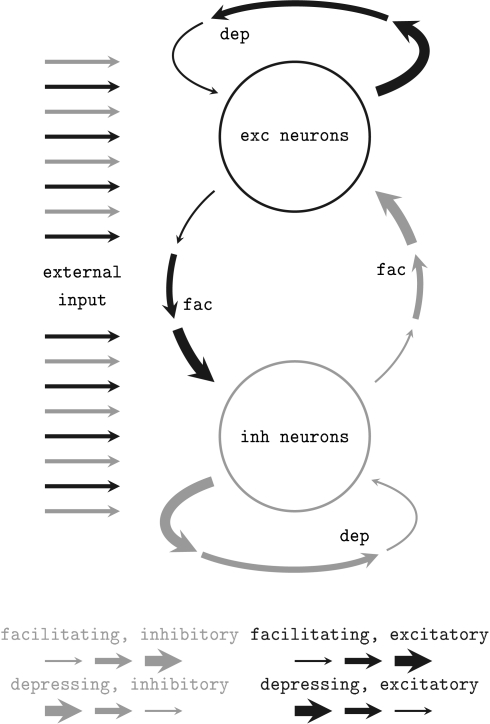
We applied a network architecture similar to the setup proposed and studied by Sussillo et al. (2007) which was proven to feature self-adjustment capabilities. A schematic of the architecture is shown in Figure 2. It employs the STP mechanism presented above. Two populations of neurons – both similarly stimulated externally with Poisson spike trains – are randomly connected obeying simple probability distributions (see below). Connections within the populations are depressing, while bridging connections are facilitating. Thus, if excitatory network activity rises, further excitation is reduced while inhibitory activity is facilitated. Inversely, in case of a low average firing rate, the network sustains excitatory activity.

Figure 2.

Schematic of the self-adjusting network architecture proposed in Sussillo et al. (2007). Depressing (dep) and facilitating (fac) recurrent synaptic connections level the network activity.

Sussillo et al. (2007) studied the dynamics of this architecture for sparsely connected networks of 5000 neurons through extensive computer simulations of leaky integrate-and-fire neurons and mean field models. In particular, they examined how the network response depends on the mean value and the variance of a Gaussian distributed current injection. It was shown that such networks are capable of adjusting their activity to a moderate level of approximately 5–20 Hz over a wide range of stimulus parameters while preserving the ability to respond to changes in the external input.

Applied parameters

With respect to the constraints described in Section “Hardware Constraints”, we set up recurrent networks comprising 192 conductance-based leaky integrate-and-fire point neurons, 144 (75%) of which were chosen to be excitatory, 48 (25%) to be inhibitory. Besides feedback from recurrent connections, each neuron was externally stimulated via excitatory and inhibitory Poisson spike sources. The setup of recurrent connections and external stimulation is described in detail below.

All parameters specifying the networks are listed in Table 1. Most values are modeled by a bound normal distribution which is defined by its mean μ, its standard deviation σ and a bound π: The random value x is drawn from a normal distribution N(μ,σ²). If x exceeds the bounds, it is redrawn from a uniform distribution within the bounds.

In case of hardware emulations, some of the deviations σ only reflect chip-inherent variations, i.e., fluctuations that remain when all units are intended to provide equal values. For other parameters – namely for all synaptic efficacies w, the leakage conductance g_leak and the input firing rate ν_inp – the major fraction of the deviations σ was intentionally applied by the experimenter. If present, the variations of hardware parameters are based on Brüderle et al. (2009).

In case of software simulations, all inhomogeneities are treated as independent statistical variations. Especially, systematic effects, like the load-dependency of the excitatory synaptic efficacy or the unbalanced sensitivity between the neuron populations (see “Self-Adjustment Ability”), have not been modeled during the first simulation series.

Recurrent connections

Any two neurons are synaptically connected with probability p_post,pre and weight w_post,pre. These values depend only on the populations the pre- and post-synaptic neurons are part of.

Synaptic weights always refer to the strength of static synapses. When a synapse features STP, its weight is multiplicatively adjusted such that the strengths of static and dynamic synapses match at a constant regular pre-synaptic firing of 20 Hz for t → ∞. This adjustment is necessary in order to enable dynamic synapses to be both stronger or weaker than static synapses according to their current activity.

Although the connection probabilities and synaptic weights used for the experiments do not rely on biological measurements or profound theoretical studies, they follow some handy rules. The mean values of the probability distributions are determined by three principles:

1. Every neuron has as many excitatory as inhibitory recurrent input synapses: p_post,e·N_e = p_post,i·N_i.

2. Inhibitory neurons receive twice as many recurrent synaptic inputs as excitatory neurons. This enables them to sense the state of the network on a more global scale: p_i,pre·N_pre = 2·p_e,pre·N_pre.

3. Assuming a uniform global firing rate of 20 Hz and an average membrane potential of V = −60 mV, synaptic currents are well-balanced in the following terms:

• (a)For each neuron the excitatory and inhibitory currents have equal strength,
• (b)each excitatory neuron is exposed to as much synaptic current as each inhibitory neuron.

Formally, we examine the average current induced by a population pre to a single neuron of the population post:

I_post,pre ∝ p_post,pre·N_pre·w_post,pre·|E_pre − V|.

Principle 3 demands that I_post,pre is equal for all tuples (post, pre) under the mentioned conditions. Given the sizes of the populations and the reversal potentials, the Principles 1 and 2 determine all recurrent connection probabilities p_post,pre and weights w_post,pre except for two global multiplicative parameters: one scaling all recurrent connection probabilities, the other one all recurrent weights. While the ratios of all p_post,pre as well as the ratios of the w_post,pre are fixed, the scaling factors have been chosen such that the currents induced by recurrent synapses exceed those induced by external inputs in order to highlight the functioning of the applied architecture.

External stimulation

In order to investigate the modulation of activity by the network, external stimulation of different strength should be applied. One could think of varying the total incoming spike rate or the synaptic weights of excitation and inhibition. In order to achieve a biologically realistic setup, one should choose the parameters such that the stimulated neurons will reach a high-conductance state (see Destexhe et al., 2003; Kaplan et al., 2009). Neglecting the influence of recurrent connections and membrane resets after spiking, the membrane would tune in to an average potential μ_V superposed by temporal fluctuations σ_V.

As mentioned above, the FACETS Stage 1 Hardware suffers from a small number of input channels if 2 × 192 synapse drivers are reserved for recurrent connections. At the same time, even resting neurons exhibit a very short membrane time constant of τ_mem ≈ 5 ms. Due to these limitations, we needed to apply an alternative type of stimulation to approximate appropriate neuronal states:

Regarding the dynamics of a conductance-based leaky integrate-and-fire neuron, the conductance course toward any reversal potential can be split up into a time-independent average value and time-dependent fluctuations with vanishing mean. Then, the average conductances toward all reversal potentials can be combined to an effective resting potential and an effective membrane time constant (Shelley et al., 2002). In this framework, only the fluctuations remain to be modeled via external stimuli.

From this point of view, the hardware neurons appear to be in a high-conductance state with an average membrane potential μ_V = V_rest without stimulation due to the short membrane time constant τ_mem. Ex post, the available input channels can be used to add fluctuations. The magnitude σ_V of the fluctuations is adjusted via the synaptic weights of the inputs.

Throughout all simulations and emulations, 32 of the 64 input channels were used for excitatory stimulation, the remaining 32 input channels for inhibitory stimulation. Each neuron was connected to four to six excitatory and four to six inhibitory inputs using static synapses. The number of inputs was randomly drawn from a uniform distribution for each neuron and reversal potential. The synaptic weights of the connections were drawn from bound normal distributions. The mean value of these distributions was chosen such that the average traction w·(E_rev − μ_V) was equal for excitatory and inhibitory synapses. The values listed in Table 1 refer to μ_V = V_rest = −60 mV. In case of other resting potentials, the synaptic weights were properly adjusted to achieve an equal average current toward the reversal potentials: In case of excitatory inputs the weight was set to w_inp,e·|[E_e − (−60 mV)]/E_e − V_rest|. Similarly, inhibitory input weights were adjusted to w_inp,e·|[E_i − (−60 mV)]/E_i − V_rest|.

Thus, neglecting the influence of recurrent connections and resets of the membrane after APs, the average input-induced membrane potential μ_V always equals V_rest. The magnitude of the fluctuations was controlled via a multiplicative weight factor W_input affecting all input synapses.

Measurement

In order to study the self-adjustment capabilities of the setup, three types of networks were investigated:

• –unconnected All recurrent synapses were discarded (w = 0) in order to determine the sole impact of external stimulation.
• –dynamic All recurrent synapses featured STP. The mode (facilitating, depressing) depended on the type of the connection as shown in Figure 2.
• –static The STP-mechanism was switched off in order to study the relevance of STP for the self-adjustment ability.

Rather than on the analysis of the dynamics of a specific network, we aimed at the investigation of the universality of application of the examined network architecture.

Therefore, random networks were generated obeying the above described probability distributions. Besides the three fundamentally different network types (unconnected, dynamic and static), external stimulation of different strength was applied by sweeping both the average membrane potential V_rest and the magnitude of fluctuations W_input.

For every set of network and input parameters, n_run = 20 networks and input patterns were generated and run for T_exp = 4.5 s. The average firing rates of both populations of neurons were recorded. To exclude transient initialization effects, only the time span 1 s ≤ t ≤ T_exp was evaluated. Networks featuring the self-adjustment property are expected to modulate their activity to a medium level of about 5–20 Hz over a wide range of external stimulation.

This setup was both emulated on the FACETS Stage 1 Hardware system and simulated using PCSIM in order to verify the results.

Results

First we present the results of the hardware emulation and compare them with the properties of simulated networks. Beside the capability of adjusting network activity in principle, we examine to what extent the observed mechanisms are insusceptible to changes in the hardware substrate. Finally we take a look at the ability of such networks to process input streams.

Self-adjustment ability

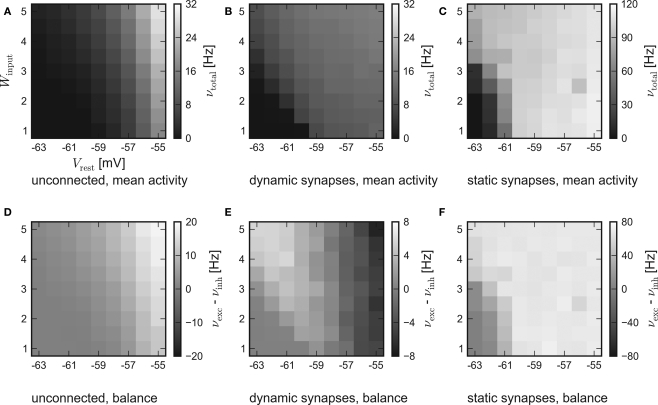
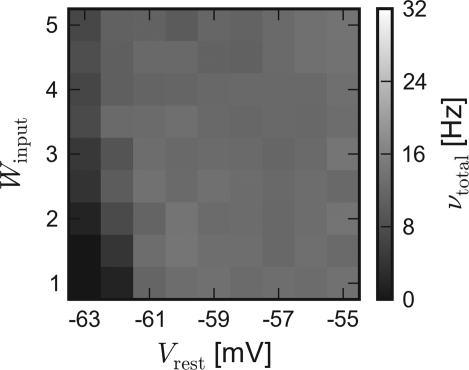
The results of the hardware emulation performed according to the setup description given in Sections “Network Configuration” and “Measurement” are shown in Figure 3. The axes display different input strengths, controlled by the average membrane potential V_rest and the magnitude of fluctuation W_input. Average firing rates are indicated by the shade of gray of the respective tile.

Figure 3.

Results of the emulations on the FACETS Stage 1 Hardware. External stimulation of diverse strength is controlled via V_rest and W_input. For every tile, 20 randomly connected networks with new external stimulation were generated. The resulting average firing rates are illustrated by different shades of gray. Inevitably, differing saturation ranges had to be used for the panels. HORIZONTAL: different types of recurrent synapses. (A,D) Solely input driven networks without recurrent connections. (B,E) Recurrent networks with dynamic synapses using short-term plasticity. (C,F) Recurrent networks with static synapses. VERTICAL: Mean activity of the entire network (A–C) and the balance of the populations, measured by the difference between the mean excitatory and inhibitory firing rates (D–F).

The average response of networks without recurrent connections is shown in Figure 3A. Over a wide range of weak stimulation (lower left corner) almost no spikes occur within the network. For stronger input, the response steadily rises up to ν ≈ 29 Hz. In Figure 3D the activity of the excitatory and the inhibitory population are compared. Since external stimulation was configured equally for either population, one expects a similar response ν_exc − ν_inh ≈ 0, except for slight stochastic variations. Obviously, the used hardware device exhibits a strong and systematic discrepancy of the sensitivity between the populations, which were located on different halves of the chip. The mean firing rate of excitatory neurons is about three times as high as the response of inhibitory neurons.

The mid-column – Figures 3B,E – shows the response of recurrent networks featuring dynamic synapses with the presented STP mechanism. Over a wide range of stimulation, the mean activity is adjusted to a level of 9–15 Hz. A comparison to the solely input driven setup proves that recurrent networks with dynamic synapses are capable of both raising and lowering their activity toward a smooth plateau. A closer look at the firing rates of the populations reveals the underlying mechanism: In case of weak external stimulation, excitatory network activity exceeds inhibition, while the effect of strong stimuli is attenuated by intense firing of inhibitory neurons. This functionality agrees with the concept of depressing interior and facilitating bridging connections, as described in Section “Network Architecture”.

In spite of the disparity of excitability between the populations, the applied setup is capable of properly adjusting network activity. It is noteworthy that the used connection probabilities and synaptic weights completely ignored this characteristic of the underlying substrate.

To ensure that the self-adjustment ability originates from short-term synaptic plasticity, the STP-mechanism was switched off during a repetition of the experiment. The respective results for recurrent networks using static synapses are shown in Figures 3C,F. The networks clearly lack the previously observed self-adjustment capability, but rather tend to extreme excitatory firing. It must be mentioned that such high firing rates exceed the readout bandwidth of the current FACETS Stage 1 Hardware system. Thus, an unknown amount of spike events was discarded within the readout circuitry of the chip. The actual activity of the networks is expected to be even higher than the measured response.

Comparison to PCSIM

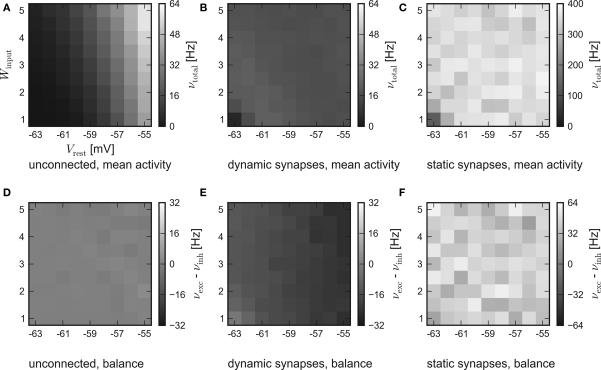
While the results of the hardware emulation draw a self-consistent picture, it ought to be excluded that the observed self-adjustment arises from hardware-specific properties. Therefore, the same setup was applied to the software simulator PCSIM. The results of the software simulation are shown in Figure 4. The six panels are arranged like those of the hardware results in Figure 3.

Figure 4.

Results of the software simulation. The experimental setup and the arrangement of the panels are equal to Figure 3. Also, the general behavior is consistent with the hardware emulation, though the average network response is more stable against different strengths of stimulation and all firing rates are higher. Accordingly, in case of dynamic recurrent synapses, the plateau is located at ν_total ≈ 17 Hz.

In agreement with the hardware emulation, the average response of networks without recurrent connections rises with stronger stimulation, see Figure 4A. But as the disparity in the population excitability was not modeled in the simulation, their balance is only subject to statistical variations, see Figure 4D.

Generally, the software simulation yields significantly higher firing rates than the hardware emulation. Two possible causes are:

• The load-dependency of the excitatory synaptic efficacy (see Hardware Constraints) certainly entails reduced network activity in case of the hardware emulation.

• The response curve of hardware neurons slightly differs from the behavior of an ideal conductance-based LIF model (Brüderle, 2009, Figure 6.4).

Consistently, an increased activity is also observed in the simulations of recurrent networks. Figures 4B,E show the results for networks with synapses featuring short-term synaptic plasticity. Obviously, the networks exhibit the expected self-adjustment ability. But the plateau is found at approximately 17 Hz compared to 12 Hz in the hardware emulation. Finally, in case of static recurrent synapses – see Figures 4C,F – the average network activity rises up to 400 Hz and lacks any visible moderation.

In conclusion, the hardware emulation and the software simulation yield similar results regarding the basic dynamics. Quantitatively, the results differ approximately by a factor of 2.

In order to approximate the influence of the unstable excitatory synaptic efficacy, which is suspected to be the leading cause for the inequality, the excitatory reversal potential was globally set to E_e = −20 mV during a repetition of the software simulation. Indeed, the results of the different back-ends become more similar. The average activity of networks with dynamic synapses (corresponding to Figures 3B and 4B) is shown in Figure 5.

Figure 5.

Software simulation: Lower excitatory reversal potential. Average network response of recurrent networks with dynamic synapses. In order to approximate the load-dependency of the excitatory synaptic efficacy in the chip, E_e was set to −20 mV for subsequent software simulations. Compare with Figure 3B.

Due to the obviously improved agreement, all further software simulations have been performed with a lower excitatory reversal potential E_e = −20 mV.

Robustness

We show that the observed self-adjustment property of the network architecture provides certain types of activity robustness that are beneficial for the operation of neuromorphic hardware systems.

Reliable and relevant activity regimes

By applying the network architecture presented in Section “Network Architecture”, we aim at the following two kinds of robustness of network dynamics:

• A high reliability of the average network activity, independent of the precise individual network connectivity or stimulation pattern. All networks with dynamic synapses that are generated and stimulated randomly, but obeying equal probability distributions, shall yield a similar average firing rate ν_total.

• The average firing rate ν_total shall be kept within a biologically relevant range for a wide spectrum of stimulation strength and variability. For awake mammalian cortices, rates in the order of 5–20 Hz are typical (see, e.g., Baddeley et al., 1997; Steriade, 2001; Steriade et al., 2001).

The emergence of both types of robustness in the applied network architecture is first tested by evaluating the PCSIM data. Still, it is not a priori clear that the robustness is preserved when transferring the self-adjusting paradigm to the hardware back-end. The transistor-level variations discussed in Section “Hardware Constraints” might impede the reliability of the moderating effects, e.g., by causing an increased excitability for some of the neurons, or by too heterogeneous characteristics of the synaptic plasticity itself. Therefore, the robustness is also tested directly on a hardware device and the results are compared with those of the software simulation.

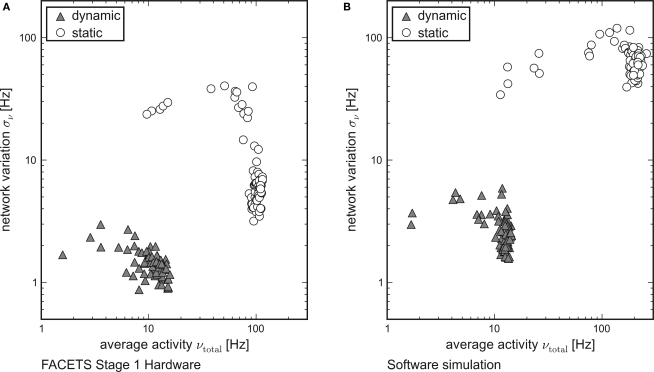
While each tile in Figure 3 represents the averaged overall firing rate ν_total of 20 randomly generated networks and input patterns, Figure 6 shows the standard deviation σ_ν of the activity of networks obeying equal probability distributions as a function of ν_total. Networks using dynamic synapses are marked by triangles, those with static synapses by circles. Only setups with ν_total > 1 Hz are shown.

Figure 6.

Reliable and realistic network activity. Each point is determined by 20 random networks generated from equal probability distributions. The average firing rate of all networks is plotted on the x-axis, the standard deviation between the networks on the y-axis. Recurrent networks featuring short-term plasticity (triangles) can reliably be found within a close range. Setups with static synapses (circles) exhibit both larger average firing rates and larger standard deviations. (A) Emulation on the FACETS Stage 1 Hardware. (B) Software simulation with lowered excitatory reversal potential E_e.

For both the hardware device and the software simulation, the data clearly show that the required robustness effects are achieved by enabling the self-adjusting mechanism with dynamic synapses. The fluctuation σ_ν from network to network is significantly lower for networks that employ dynamic recurrent connections. Moreover, only for dynamic synapses the average firing rate ν_total is reliably kept within the proposed regime, while in case of static synapses most of the observed rates are well beyond its upper limit.

This observation qualitatively holds both for the hardware and for the software data. In case of networks with static synapses emulated on the hardware system, the upper limit of observed firing rates at about 100 Hz is determined technically by bandwidth limitations of the spike recording circuitry. This also explains the dropping variation σ_ν for firing rates close to that limit. If many neurons fire at rates that exceed the readout bandwidth, the diversity in network activity will seemingly shrink.

While the software simulation data prove that the self-adjusting principle provides the robustness features already for networks as small as those tested, the hardware emulation results show that the robustness is preserved despite of the transistor-level variations. Even though the different biological network descriptions are mapped randomly onto the inhomogeneous hardware resources, the standard deviation of firing rates is similar in hardware and in software.

Independence of the emulation device

Besides the ambiguous mapping of given biological network descriptions to an inhomogeneous neuromorphic hardware system as discussed above, the choice of the particular emulation device itself imposes another source of possible unreliability of results. Often, multiple instances of the same system are available to an experimenter. Ideally, such chips of equal design should yield identical network dynamics. But due to process-related inhomogeneities and due to the imperfections as discussed in Section “Hardware Constraints”, this objective is unachievable in terms of precise spike timing whenever analog circuitry is involved. Nevertheless, one can aim for a similar behavior on a more global scale, i.e., for alike results regarding statistical properties of populations of neurons.

All previous emulations have been performed on a system which was exclusively assigned to the purpose of this work. In order to investigate the influence of the particular hardware substrate, a different randomly chosen chip was set up with the same biological configuration. In this context, biological configuration denotes that both systems had been calibrated for general purpose. The high-level pyNN-description of the experiment remained unchanged – only the translation of biological values to hardware parameters involved different calibration data. This customization is performed automatically by low-level software structures. Therefore, the setup is identical from the experimenter's point of view.

In the following, the two devices will be referred to as primary and comparative, respectively. Just as on the primary device, networks emulated on the comparative system featured the self-adjustment ability if dynamic synapses were used for recurrent connections. But network activity was moderated to rather low firing rates of 2–6 Hz. The response of networks without recurrent connections revealed that the used chip suffered from a similar disparity of excitability as the primary device. But in this case, it was the inhibitory population which showed a significantly heightened responsiveness.

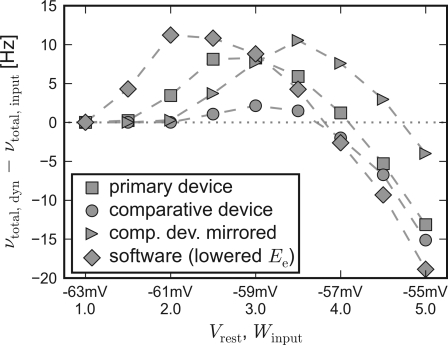
Apparently, the small networks were not capable of completely compensating for the systematic unbalance of the populations. Nevertheless, they still were able to both raise and lower their firing rate compared to input-induced response. Figure 7 shows the difference of the activity between recurrent networks with short-term synaptic plasticity and solely input driven networks without recurrent connections,

Figure 7.

Self-adjusting effect on different platforms. The difference Δν := ν_total,dyn − ν_total,input is plotted against an increasing strength and variability of the external network stimulation. The diamond symbols represent the data acquired with PCSIM. The square (circle) symbols represent data measured with the primary (comparative) hardware device. Measurements with the comparative device, but with a mirrored placing of the two network populations, are plotted with triangle symbols. See main text for details.

Δν := ν_total,dyn − ν_total,input.

For this chart, the V_rest − W_input diagonal of Figure 3 has been mapped to the x-axis, representing an increasing input strength. Δν is plotted on the y-axis. Independent of the used back-end, recurrent networks raise activity in case of weak external excitation, while the effect of strong stimulation is reduced.

To allow for the inverse disparity of excitability of the comparative device, the mapping of the excitatory and the inhibitory population, which were located on different halves of the chip, was mirrored during a repetition of the emulation. Thus, the excitatory population exhibited an increased responsiveness resembling the disparity of the primary device. The Δν-curve of the mirrored repetition on the comparative system can also be found in Figure 7. As expected, with this choice of population placing, the moderating effect of the applied self-adjusting paradigm matches better the characteristics of the primary device.

These observations suggest that differing emulation results rather arise from large-scaled systematic inhomogeneities of the hardware substrate than from statistically distributed fixed pattern noise of individual units.

Therefore, it can be stated that the applied architecture is capable of reliably compensating statistical fluctuations of hardware unit properties, unless variations extend to a global scale. But even in case of large-scale deviations, the applied construction principle preserves its self-adjustment ability and provides reproducible network properties, albeit at a shifted working point.

Responsiveness to input

While it was shown that the applied configuration provides a well-defined network state in terms of average firing rates, it remains unclear whether the probed architecture is still able to process information induced by external input. It can be suspected that the strong recurrent connectivity “overwrites” any temporal structure of the input spike trains. Yet, the usability of the architecture regarding a variety of computational tasks depends on its responsiveness to changes in the input. A systematic approach to settle this question exceeds the scope of this work. Therefore, we address the issue only in brief.

First, we determine the temporal response of the architecture to sudden changes in external excitation. Then, we look for traces of previously presented input patterns in the current network state and test whether the networks are capable of performing a non-linear computation on the meaning assigned to these patterns.

For all subsequent simulations the input parameters are set to V_rest = −59 mV and W_input = 4.0 (cf. Figure 5). Only networks featuring dynamic recurrent connections are investigated. Due to technical limitations of the current hardware system as discussed in Section “Hardware Constraints”, the results of this section are based on software simulations, only. For example, the additional external stimulation, as applied in the following, exceeds the current input bandwidth of the prototype hardware device. Furthermore, the evaluation of network states requires access to (at least) the spike output of all neurons, simultaneously. The current hardware system only supports the recording of a small subset of neurons at a time.

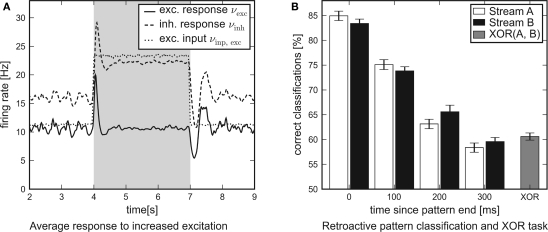
In Figure 8A the average response of the excitatory and inhibitory populations to increased external excitation are shown. For this purpose, the firing rate of all excitatory Poisson input channels was doubled from 11.8 to 23.6 Hz at t = 4 s. It was reset to 11.8 Hz at t = 7 s, i.e., the applied stimulation rate was shaped as a rectangular pulse. In order to examine the average response of the recurrent networks to this steep differential change in the input, n_run = 1000 networks and input patterns have been generated. While the network response obtained from a single simulation run is subject to statistical fluctuations, the influence of the input pulse is revealed precisely by averaging over the activity of many different networks. For analysis, the network response was convolved with a box filter (50 ms window size). In conclusion, the temporal response of the recurrent networks is characterized by two obvious features:

Figure 8.

Network traces of transient input. Results of software simulations testing the response of recurrent networks with dynamic synapses to transient input. (A) Firing rate of the excitatory input channels and average response of either population to an excitatory input pulse lasting for 3 s. The steep differential change in excitation is answered by a distinct peak. After some hundred milliseconds the networks attune to a new level of equilibrium. (B) Average performance of the architecture in a retroactive pattern classification task. The network states contain information on input spike patterns which were presented some hundred milliseconds ago. The latest patterns presented are to be processed in a non-linear XOR task.

1. Immediately after the additional input is switched on or off, the response curves show distinct peaks which decay at a time scale of τ ≈ 100 ms.

2. After some hundred milliseconds, the networks level off at a new equilibrium. Due to the self-adjustment mechanism, the activity of the inhibitory population clearly increases.

These findings confirm that the investigated networks show a significant response to changes in the input. This suggests that such neural circuits might be capable of performing classification tasks or continuous-time calculations if a readout is attached and trained.

We tested this conjecture by carrying out a computational test proposed in Haeusler and Maass (2007). The 64 external input channels were assigned to two disjunct streams A and B. Each stream consisted of 16 excitatory and 16 inhibitory channels. For each stream two Poisson spike train templates (referred to as +s and −s,S ∈ {A,B}) lasting for 2400 ms were drawn and partitioned to 24 segments ±s,i of 100 ms duration. In every simulation run the input was randomly composed of the segments of these templates, e.g.,

Stream A: +_A23−_A22…−_A1 + _A0

Stream B: −_B23+_B22…−_B1 − _B0

leading to 2²⁴ possible input patterns for either stream. Before the input was presented to the network, all spikes were jittered using a Gaussian distribution with zero mean and standard deviation 1 ms. The task was to identify the last four segments presented (0 ≤ i ≤ 3) at the end of the experiment. For that purpose, the spike response of the network was filtered with an exponential decay kernel (τ_decay = τ_syn = 30 ms). The resulting network state at t = 2400 ms was presented to linear readout neurons which were trained via linear regression as in Maass et al. (2002). The training was based on 1500 simulation runs. Another 300 runs were used for evaluation. In order to determine the performance of the architecture for this retroactive pattern classification task, the above setup was repeated 30 times with newly generated networks and input templates.

The average performance of networks with recurrent dynamic synapses is shown in Figure 8B. The error bars denote the standard error of the mean. Obviously, the network state at t = 2400 ms contains significant information on the latest patterns presented and preserves traces of preceding patterns for some hundred milliseconds. For comparison, recurrent networks using static synapses performed only slightly over chance level (not shown). In addition to the pattern classification task, another linear readout neuron was trained to compute the non-linear expression XOR(±_A0,±_B0) from the network output. Note that this task cannot be solved by a linear readout operating directly on the input spike trains.

Summing up, the self-adjusting recurrent networks are able to perform multiple computational tasks in parallel. Since the main objective of this work was to verify the self-adjustment ability of small networks on a neuromorphic hardware device, both connection probabilities and synaptic weights of recurrent connections had been chosen high compared to the strength of external stimulation. Still, the networks significantly respond to changes in the input and provide manifold information on present and previous structure of the stimulus.

Recent theoretical work (Buesing et al., 2010) stressed that the computational power of recurrent networks of spiking neurons strongly depends on their connectivity structure. As a general rule, it has been shown to be beneficial to operate a recurrent neural network in the edge-of-chaos regime (Bertschinger and Natschläger, 2004). Nevertheless, as addressed in Legenstein and Maass (2007), the optimal configuration for a specific task can differ from this estimate. Accordingly, task-dependent recurrent connectivity parameters might be preferable to achieve good experimental results (see, e.g., Haeusler et al., 2009). While networks of randomly connected neurons feature favorable kernel qualities, i.e., they perform rich non-linear operations on the input, theoretical studies of Ganguli et al. (2008) prove that networks with hidden feedforward structures provide superior memory storage capabilities. Future research might identify such connectivity patterns in seemingly random cortical circuits and improve our understanding of working memory.

While the examined recurrent network architecture was not optimized for computation, neither regarding its kernel quality nor its memory traces, the cited studies suggest that the performance will increase if network parameters are attuned to particular tasks. Further research is needed to explore under which conditions the examined architecture provides a stable operating point, a high responsiveness to stimuli, and appropriate memory traces.

Discussion

We showed that recurrent neural networks featuring short-term synaptic plasticity are applicable to present neuromorphic mixed-signal VLSI devices. For the first time dynamic synapses play a functional role in network dynamics during a hardware emulation. Since neuromorphic hardware devices model neural information processing with analog circuitry, they generally suffer from process-related fluctuations which affect the dynamics of their components. In order to minimize the influence of unit variations on emulation results, we applied a self-adjustment principle on a network level as proposed by Sussillo et al. (2007).

Even though the employed prototype system only supports a limited network size, the expected self-adjustment property was observed on all used back-ends. The biological description of the experimental setup was equal for all utilized chips, i.e., the configuration was not customized to characteristics of the specific hardware system. Beyond the validation of the basic functioning of the self-adjusting mechanism, we addressed the robustness of the construction principle against both statistical variations of network entities and systematic disparities between different chips. We showed that the examined architecture reliably adjusts the average network response to a moderate firing regime. While congeneric networks emulated on the same chip yielded a widely similar behavior, the operating point achieved on different systems still was affected by large-scale characteristics of the utilized back-end.

All outcomes of the hardware emulation were qualitatively confirmed by software simulations. Furthermore, the influence of a major imperfection of the current revision of the FACETS Stage 1 Hardware, the load-dependency of the excitatory synaptic efficacy, was studied by the accompanying application of the simulator PCSIM.

Presumably, the performance of the applied architecture will improve with increasing network size. Upcoming neuromorphic emulators like the FACETS Stage 2 Wafer-scale Integration system (see Fieres et al., 2008; Schemmel et al., 2008) will comprise more than 100,000 neurons and millions of synapses. Even earlier, the present chip-based system will sustain the interconnection of multiple chips and thus provide a substrate of some thousand neurons. As such large-scale mixed-signal VLSI devices will inevitably exhibit variations in unit properties, detailed knowledge of circuitry design is required by the user to reduce distortions of experimental results on the level of single units. On the other hand, the beneficial application of neuromorphic VLSI devices as both neuroscientific modeling and novel computing tools will require that it does not demand an expert in electronic engineering to run the system. We showed that self-regulation properties of neural networks can help to overcome disadvantageous effects of unit level variations of neuromorphic VLSI devices. The employed network architecture might ensure a highly similar network behavior independent of the utilized system. Therefore this work displays an important step toward a reliable and practicable operation of neuromorphic hardware.

The applied configuration required strong recurrent synapses at a high connectivity. The results of Sussillo et al. (2007) show that even sparsely connected networks can manage to efficiently adjust their activity, provided they comprise a sufficiently large number of neurons which will be sustained by future hardware systems. Thereby, the examined construction principle will become applicable to a variety of experimental setups and network designs. As touched upon in Section “Responsiveness to Input”, the presented self-adjusting networks still are sensitive and responsive to changes in external excitation. Furthermore, we verified that even networks with disproportionately strong recurrent synapses can perform simple non-linear operations on transient input streams. By applying biologically more realistic connectivity parameters, it has been shown that randomly connected networks of spiking neurons are able to accomplish ambitious computational tasks (Maass et al., 2004) and that short-term synaptic plasticity can improve the performance of such networks in neural information processing (Maass et al., 2002). Thus, this architecture provides a promising application for neuromorphic hardware devices while the high configurability of novel systems as well supports the emulation of circuits tailored to specific tasks.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.