Surgeon and Hospital Volume as Quality Indicators for CABG in Taiwan: Examining Hazard to Mortality and Accounting for Unobserved Heterogeneity

Abstract

Objective

To investigate whether provider volume has an impact on the hazard of mortality for coronary artery bypass grafting (CABG) patients in Taiwan.

Data Sources/Study Setting

Multiple sources of linked data from the National Health Insurance Program in Taiwan.

Study Design

The linked data were used to identify 27,463 patients who underwent CABG without concomitant angioplasty or valve procedures and the surgeon and hospital volumes. Generalized estimating equations and hazard models were estimated to assess the impact of volume on mortality. The hazard modeling technique used accounts for bias stemming from unobserved heterogeneity.

Principal Findings

Both surgeon and hospital volume quartiles are inversely related to the hazard of mortality after CABG. Patients whose surgeon is in the three higher volume quartiles have lower 1-, 3-, 6-, and 12-month mortality after CABG, while only those having their procedure performed at the highest quartile of volume hospitals have lower mortality outcomes.

Conclusions

Mortality outcomes are related to provider CABG volume in Taiwan. Unobserved heterogeneity is a concern in the volume–outcome relationship; after accounting for it, surgeon volume effects on short-term mortality are large. Using models controlling for unobserved heterogeneity and examining longer term mortality may still differentiate provider quality by volume.

There is a long-standing interest in the relationship between surgical procedural volume and patient outcomes dating back to early work by Luft, Bunker, and Enthoven (1979) and Luft (1980). Meta-analysis of earlier studies suggests there is a positive association between volume and outcomes in a variety of surgical and treatment settings (Halm, Lee, and Chassin 2002). As a result of this literature, there is a push to use surgical volume as a measure of provider quality, particularly for prevalent or high-risk procedures, including coronary artery bypass grafting surgery (CABG) (Peterson et al. 2004). Researchers, policy makers, hospital managers, physicians, and patients have continued interest in whether volume should be used as a quality indicator for major surgery, including CABG (Birkmeyer 2000; Birkmeyer, Finlayson, and Birkmeyer 2001; Birkmeyer et al. 2002; Epstein 2002; Shahian and Normand 2003; Birkmeyer and Dimick 2004; Shahian 2004;). Given that this procedure is still performed more than 100,000 times each year in the United States and an estimated 800,000 times per year globally and is invasive and expensive, this interest and efforts to address the extent to which volume continues to impact the outcomes of CABG surgery in different settings are warranted.

Over time, a variety of methodological and empirical concerns have been raised in the volume–outcomes literature (Sfekas 2009). Some have suggested that further probing the mechanisms through which volume affects mortality would be of additional value (Huesch and Sakakibara 2009). Previously stated and investigated concerns about the observed relationship between volume and outcomes range from issues of patient selection and the causality of the observed relationship (Luft, Hunt, and Maerki 1987) to whether administrative data are detailed enough to account for differences in patient severity of illness (Hannan et al. 1992, 1997; Ho 2005; Tsai et al. 2006) to which modeling methods are appropriate in estimating this relationship (Austin, Tu, and Alter 2003; Hannan et al. 2005; Sfekas 2009;) and whether superior processes of care, which are generally unmeasured by researchers, may be correlated with volume and are at the root of the volume–outcome relationship (Shahian 2004). In spite of these concerns, studies using modern statistical analysis has found a relationship between both hospital (Sfekas 2009) and surgeon volume and outcomes (Hannan et al. 2003), though there is evidence these associations may have grown weaker over time in the United States (Peterson et al. 2004; Marcin et al. 2008; Ricciardi et al. 2008; Boudourakis et al. 2009;).

In this study we reiterate the original question, “Does provider volume impact patient health outcomes?” We address this question by first clarifying what it means for volume to impact outcomes. Better technology and strategic efforts to improve immediate postoperative care reduce the likelihood of short-term mortality following CABG, meaning that measurable differences in mortality outcomes may not occur within 30 days, but at a later time point. Rather than simply estimate the impact of volume on a binary mortality outcome of whether a patient survives to a particular time point shortly after surgery, we consider what the impact of volume is on the postoperative hazard of mortality. We show that only looking at binary short-term mortality outcomes may not provide a complete picture of the volume–outcome relationship for CABG, particularly as it applies to Taiwan.

We also address an important methodological issue with our choice of models; we consider whether unobserved heterogeneity of the patients or providers could be impacting the estimated relationship between volume and outcomes. We use a model rarely applied in this literature to address the issue of unobserved heterogeneity. While this estimation technique does not allow us to separate the impacts of the unobserved characteristics from one another (i.e., we cannot separate referral effects from organizational process effects, for example), it yields estimates of the impact of provider (hospital and surgeon) volume net of this unobserved heterogeneity on the hazard of mortality. We obtain estimates of the impact of surgeon and hospital volume on the hazard to mortality that are more statistically robust than those that would be derived from standard hazard estimation using administrative claims data in a study such as this.

METHODS

Background

Taiwan launched a Universal Health Insurance Program in March of 1995. The reimbursement system under the Taiwan's National Health Insurance (NHI) is generous, and the uptake of insurance is quite high, with more than 95 percent of the population being enrolled during any given year across our period of interest (Cheng 2003). From the patient perspective, the contribution to insurance is relatively minimal and uniform when compared with the United States, so the choice of provider is based on the willingness of a patient to travel, and the information available to them about the quality of each provider. Thus, patient preference is not complicated by differing levels and generosity of insurance coverage that is inherit in the U.S. system. Hospitals and clinics that are to be reimbursed under the NHI Program must have a contract with Taiwan's Bureau of NHI, but the hospitals themselves are not state owned. The labor market for surgeons in Taiwan still operates as a private market, with better surgeons able to negotiate higher salaries, bonuses, work preferences, etc. However, unlike some cases in the United States, the surgeons in Taiwan contract to work as an employee of a specific hospital, and therefore practice at only one hospital instead of potentially having admitting privileges at multiple hospitals. This mitigates concerns about facility-specific surgeon volume effects found in previous work by Huckman and Pisano (2006).

Data

The data for this study were gathered from four different sources in the National Health Insurance Data (NHID), which is maintained by the National Health Research Institutes in Taiwan. We first collected the longitudinal medical claims of patients who have undergone CABG between 1998 and 2007. The patient claims records are similar to those found in the United States in that they include ICD-9 codes for both primary and secondary disease diagnoses as well as procedures. Our patient population consists of those who have been admitted and undergone CABG (ICD-9 codes 36.10-36.16) during the current admission without also having a percutaneous intervention or a valve procedure in that admission. Those with concurrent percutaneous coronary intervention (PCI) are omitted from our sample because we are unable to determine whether this was planned coincidence of the procedures or if the CABG was performed in an emergency as a result of complication from PCI. Those having valve procedures are omitted because they represent a subsample of patients with distinctly different disease and risk.

Since nearly the entire population of Taiwan is covered by NHI (varies between 95 and 97 percent over the period), and CABG would be expensive to pay for with one's own resources in the absence of insurance, it is likely that we are observing nearly all of the CABG patients having this procedure performed in Taiwan. The ICD-9 procedure codes combined with facility and surgeon identifiers allow us to construct the volume variables for each of the providers. In addition, ICD-9 diagnoses codes in the claims were used in the construction patient risk adjustment using the method developed by Elixhauser et al. (1998).

These claims data have detailed admission dates, discharge dates, and detailed descriptions of actual medical expenses broken down by category (i.e., room, food, surgery, etc). Another important feature of this data set is that each patient, surgeon, and hospital has a unique ID code which enables linkage of these data to other NHID sources. We linked the medical claims to datasets containing NHID health provider information and to patient eligibility files which both span the period of interest. From the provider datasets we extract location, ownership status, accreditation and number of beds of hospitals, and the ages of the surgeons. We use patient eligibility files to extract patient demographics.

Finally, because NHI is compulsory we use disenrollment dates to impute the date of death. Lien, Chou, and Liu (2009) compare the ending date of coverage with actual death records of stroke patients and demonstrate the validity for calculating death dates. Specifically, for those who died within 1 year after discharge, 90 percent of the sample contains no differences between these two dates, <5 percent have differences larger than a week, and <2 percent have differences larger than a month.

Empirical Strategy

We begin by estimating the model using one of the standard measures of outcome in this literature, 1-month mortality after surgery. We use the model frequently used in this literature, generalized estimating equations (GEE). In our GEE model we use a logit link function with an exchangeable correlation structure which has been shown to have desirable properties in modeling the volume–outcome relationship (Panageas et al. 2007). We then use the GEE model to consider other binary outcomes of mortality: 3-, 6-, and 12-month mortality. While these models are not the focus of our study, the intent in presenting them is to provide the reader a context for comparing the results of the subsequent hazard models we estimate given these data are from Taiwan and the previous literature on volume and outcomes has focused on the United States, Canada, and Europe.

We proceed to use a duration model to assess the volume–outcome relationship. Rather than measuring whether volume of a provider leads to patient survival for a particular fixed, short-term postoperative period, this will capture whether volume extends postoperative patient survival time. A practical statistical advantage to using the duration model we use is the ease of identifying whether there is unmeasured heterogeneity and being able to account for it in the estimation.

Suppose the hazard is parameterized using a proportional hazard form h(t)=h₀(t)e^X′β, where h₀(t) is the baseline hazard at time t and is parameterized as Weibull hazard h₀(t)=αt^α−1, X is a vector of explanatory variables which are assumed to be time invariant, and β is a vector of parameters to be estimated. In the presence of unobserved heterogeneity (v), such as providers' quality and patients' severity of illness, the conditional hazard is written as

where v is a random variable that is assumed to be independent of X. In order to obtain consistent estimates of parameters of the conditional hazard, v should be integrated out over its distribution g(v).

Given h(t|v), the likelihood contribution from an individual who is observed having a failure time t is

and the probability of surviving at least to t is

We adopt the method used in Butler, Anderson, and Burkhauser (1989), which originates from Heckman and Singer (1984), to estimate the semiparametric duration model. The Heckman and Singer (1984) version of this model has been applied previously by Hamilton and Hamilton (1997) to the question of the impact of hospital volume on outcomes for hip fracture patients.

Instead of making any assumption about the function form for v, the distribution of v can be approximated by a step function.

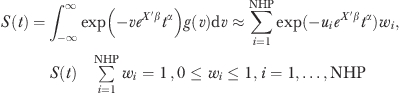where NHP is number of semiparametric points. The value of integration points (u_i) is fixed in advance, and only weights (w_i) are estimated. In the absence of unmeasured heterogeneity, NHP=1 and w₁=1. Thus, rejecting a restriction to one point using the likelihood ratio test is evidence for the presence of unmeasured heterogeneity.

Suppose δ_i if individual i is observed to have a failure time t and δ_I=0 if individual i survives at least to t, then the likelihood function for a sample of N individuals can be written as 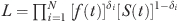. The primary interest lies not in the parameters β and α, but in the effects of the covariates X on the probability of failure between t_s and t_e, where 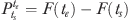. The marginal effect of a dummy variable can be expressed as .

Dependent Variable

The dependent variable T in the duration model is defined as min{t_d−t_n, t_c−t_n}, where t_d is the date of death, t_n is the admission date, and t_c is the censored date (we are able to track mortality up to January 1, 2008 in our data). The mean and standard deviation of the dependent variable are given in Table 1. Out of the sample of 27,463 CABG patients and the average survival time for all patients was 54.64 months; 30.77 percent of the sample died and the mean survival time of those who died in the sample was 30.28 months.

Table 1.

Sample Statistics

	Mean	Standard Deviation
Provider characteristics
Patients treated at hospitals with 250–600 beds (%)	31.9	46.6
Patients treated at hospitals with 600+ beds (%)	67.8	46.7
Patients treated at nonprofit hospitals (%)	56.9	49.5
Surgeon age (at time of procedure)	44.6	8.3
Surgeon had a recent patient die in-hospital (%)	1.7	13.0
Patient characteristics
Patient age at admission	65.5	10.4
Male (%)	76.3	42.5
Had a PCI in the past 12 months (%)	10.6	30.8
Elixhauser comorbidities (%)
CHF	10.7	30.9
Valve	4.0	19.6
Peripheral vascular disease	4.1	19.7
Hypertension	38.6	48.7
Chronic pulmonary disease	4.7	21.2
Diabetes	31.4	46.4
Diabetes with complication	5.9	23.5
Deficiency anemia	1.7	12.9
Other comorbid condition*	6.9	26.5
12-month volume summary statistics	Surgeon	Hospital
Mean	59.6	166.1
Standard deviation	42.8	97.3
25th percentile	28.0	87.0
Median	51.0	159.0
75th percentile	84.0	234.0

^*This is an indicator equal to one if the patient had at least one of the Elixhauser conditions, which affect <1% of this population.

CHF, congestive heart failure; PCI, percutaneous coronary intervention.

Explanatory Variables

The explanatory variables of interest are the volumes of both the hospital and surgeon. We enter the volumes of both of these providers into our model simultaneously. Because we are interested in comparing the impacts of volume not at the conditional mean but rather between providers of different volume levels, we created a series of indicators for volume quartiles for the hospitals and for the surgeons. This approach facilitates comparisons of mortality hazards between different patients whose provider volumes at the time of the procedure were in different quartiles of the volume distribution. This provides insight into the comparison of outcomes between those who underwent a procedure at a hospital or by a surgeon with volume at a different point on the volume distribution than simply examining the impact at the conditional mean using a continuous volume measure. It is analogous to the low-, medium-, high-, and very high-volume hospital classification used in previous research such as Peterson et al. (2004).

Because our data are from Taiwan and those volume categories developed for use in the U.S. data by Peterson et al. (2004) may not be the best characterization of the distribution of provider volumes, we simply use the distribution of volume as present in the sample to create our volume categories. Specifically we divide the distribution into approximate quartiles by the providers 12-month volume at the time of the procedure, thus each quartile group contains approximately the same number of patient observations (the number of observations is only approximately equal in each quartile because the provider volume for some observations is on the cutoff between two quartiles and must be assigned to one quartile or the other). The lowest volume quartile for surgeons and hospitals serve as the reference groups. There are 660 surgeons and 69 hospitals observed in the study. Summary statistics for both hospital and surgeon annual volumes are in Table 1.

Other than surgeon volume we have little outside data on surgeons beyond their age at the time of the procedure. However, this is a proxy measure for experience, so it is included in our model. We include an indicator for whether a patient had a CABG patient die in-hospital in the last 30 days; this raises the likelihood of 30-day patient mortality (Hockenberry, Lien, and Chou 2008).

To account for hospital characteristics that may impact patient outcomes the model includes indicator variables for hospital size classified as those treated in hospital with 250–600 beds and those treated in a >600 bed hospital. The reference group is those treated at <250 bed hospital. Because Taiwan has NHI, as opposed to a nationalized health care system, hospitals also operate as either for-profit or not-for-profit as in the Unites States and we include a not-for-profit hospital indicator. Summary statistics of surgeon and hospital characteristics are listed in Table 1.

The model is patient risk adjusted using the method described by Elixhauser et al. (1998) with some slight modifications, as well as patient age at the time of the surgery and gender. The modification is necessary because of our hazard estimation technique. Convergence in this model is sensitive to the presence of a profusion of indicator variables in which a very small percentage of the observations are equal to one. Thus, we have summarized all comorbidities affecting <1 percent of the patient population into a single indicator of whether the patient had at least one of these conditions. We also have an indicator variable for whether the patient underwent a PCI in the year before the CABG to adjust for potential failed attempts to treat the patient's coronary artery disease. Summary statistics of patient characteristics are listed in Table 1.

RESULTS

We present the results of the GEE models in Table 2. Mortality within 1 month is the measure that has been most frequently used in this line of literature; however, we extend our models to also consider 3-, 6-, and 12-month mortality. Rather than raw coefficients we calculate the marginal effects and p-values resulting from those estimations. We do so to provide both easy comparisons and context for the hazard model estimates that we also present. In addition, for perspective on the overall mortality rates we include the mean mortality rate overall, for the surgeon volume quartile reference group and hospital volume quartile reference group.

Table 2.

Adjusted GEE Model Estimates of the Impact of Provider Quartile of Volume on Patient Mortality at Select Time Points^*

Outcome	1-Month Mortality		3-Month Mortality		6-Month Mortality		1-Year Mortality
Overall	Mean Mortality=0.058		Mean Mortality=0.091		Mean Mortality=0.112		Mean Mortality=0.135
among Surgeons in the Lowest Volume Quartile (Reference Group)	Mean Mortality=0.091		Mean Mortality=0.144		Mean Mortality=0.178		Mean Mortality=0.208
among Hospitals in the Lowest Volume Quartile (Reference Group)	Mean Mortality=0.090		Mean Mortality=0.132		Mean Mortality=0.158		Mean Mortality=0.185
	Marginal Effect	p-value	Marginal Effect	p-value	Marginal Effect	p-value	Marginal Effect	p-value
Surgeon volume quartiles
2nd	−0.010	.002	−0.022	.000	−0.032	.000	−0.008	.027
3rd	−0.019	.000	−0.034	.000	−0.045	.000	−0.015	.001
4th	−0.019	.003	−0.032	.000	−0.044	.000	−0.012	.040
Hospital volume quartiles
2nd	−0.021	.000	−0.023	.000	−0.024	.001	−0.020	.000
3rd	−0.013	.012	−0.016	.027	−0.017	.060	−0.009	.136
4th	−0.021	.000	−0.027	.000	−0.031	.001	−0.018	.003
Patient characteristics
Patient age	0.002	.000	0.003	.000	0.004	.000	0.002	.000
Male	−0.009	.002	−0.014	.001	−0.020	.000	−0.010	.001
PCI in last 12 months	0.005	.238	0.001	.797	−0.001	.864	0.006	.184
Elixhauser comorbidities
CHF	0.038	.000	0.059	.000	0.074	.000	0.044	.000
Valve	−0.014	.004	−0.022	.001	−0.027	.000	−0.017	.001
Peripheral vascular disease	0.033	.000	0.051	.000	0.057	.000	0.035	.000
Hypertension	−0.036	.000	−0.060	.000	−0.070	.000	−0.043	.000
Chronic pulmonary disease	−0.018	.000	−0.030	.000	−0.028	.000	−0.021	.000
Diabetes	−0.015	.000	−0.016	.000	−0.016	.000	−0.017	.000
Diabetes with complication	−0.007	.102	0.006	.285	0.022	.003	−0.009	.046
Deficiency anemia	−0.020	.002	−0.037	.000	−0.047	.000	−0.024	.001
Other comorbid condition†	0.006	.195	0.016	.021	0.032	.000	0.008	.142
Surgeon characteristics
Age	−0.001	.022	−0.001	.041	−0.001	.061	−0.001	.018
Recent patient died in-hospital	0.008	.390	0.005	.667	0.002	.896	0.010	.308
Hospital characteristics
Not-for-profit	0.002	.612	0.004	.497	0.007	.377	0.005	.289
250–600 beds	0.013	.711	0.028	.595	0.019	.708	0.012	.760
600+ beds	0.018	.497	0.033	.383	0.031	.462	0.016	.627
N=	27,463		27,463		27,463		27,463

^*Estimated using a logit link with exchangeable correlation structure.

^†This is an indicator equal to one if the patient had at least one of the Elixhauser conditions, which affect <1% of this population.

CHF, Congestive heart failure. GEE, generalized estimating equations; PCI, percutaneous coronary intervention.

The results of the GEE models suggest that having a procedure by a surgeon in the higher quartiles of volume reduces 1-month mortality between 1.0 and 1.9 absolute percentage points, 3-month mortality between 2.2 and 3.4 absolute percentage points, and 6-month mortality between 3.2 and 4.5 absolute percentage points relative to those who had the procedure performed by a surgeon in the lowest quartile of volume. However, by 12 months, mortality differences are only much lower and range from 0.8 to 1.5 absolute percentage points lower than those patients who had a procedure by a surgeon in the lowest quartile. The estimate of the coefficient on the third quartile of surgeon volume had a larger point estimate than the indicator on the fourth quartile, though a t-test of the equivalence of these two coefficients failed to reject the null at conventional levels.

The GEE estimates of the impact of having a CABG performed at a hospital in a higher volume quartile follow a similar pattern to the surgeons. The range of mortality reduction are 1.3–2.1, 1.6–2.7, 1.7–3.1, and 0.9–2.0 in estimations 1-, 3-, 6-, and 12-month mortality outcomes, respectively. Of note is that in the 6- and 12-month mortality equations having a surgery performed at a hospital in the third quartile of volume is not statistically different from having it performed at a hospital in the first quartile of volume at conventional levels.

In Table 3, we report both sets of coefficients from our hazard model estimated with and without controlling for unobserved heterogeneity. Column one of the first panel of Table 3 contains the estimates of the impact of surgeon and hospital volume-by-volume quartile, with the lowest volume quartile being the omitted reference group for both surgeons and hospitals.

Table 3.

Hazard Model Coefficient Estimates of Time to Mortality for Patients Undergoing Isolated CABG in Taiwan 1998–2007

	Time to Mortality		Time to Mortality
Dependent Variable	Coefficient	p-value	Coefficient	p-value
Surgeon volume quartiles
2nd	−0.231	.030	−0.200	.035
3rd	−0.337	.033	−0.307	.038
4th	−0.265	.035	−0.222	.040
Hospital volume quartiles
2nd	−0.087	.033	−0.027	.039
3rd	−0.067	.036	−0.033	.042
4th	−0.195	.038	−0.151	.044
Patient characteristics
Patient age	4.932	.123	5.457	.149
Male	−0.069	.025	−0.031	.029
PCI in last 12 months	−0.046	.038	−0.043	.044
Elixhauser comorbidities
CHF	0.616	.029	0.664	.035
Valve	−0.045	.055	0.018	.061
Peripheral vascular disease	0.500	.044	0.519	.052
Hypertension	−0.426	.026	−0.358	.029
Chronic pulmonary disease	−0.064	.050	0.020	.054
Diabetes	0.161	.026	0.253	.029
Diabetes with complication	0.550	.039	0.696	.044
Deficiency anemia	−0.213	.086	−0.136	.091
Other comorbid condition	0.420	.039	0.504	.043
Surgeon characteristics
Age at time of surgery	−1.062	.146	−1.106	.168
Recent patient died in-hospital	−0.027	.080	−0.032	.089
Hospital characteristics
Not-for-profit	0.018	.024	0.005	.028
250–600 beds	0.031	.210	−0.117	.226
600+ beds	0.113	.210	−0.051	.227
Point 1			0.059	.003
Point 2			0.941	.003
Maximum likelihood	−47189.670		−46942.570
Does the likelihood ratio test reject the null hypothesis of no unobserved heterogeneity?	N/A		Yes
Controlling for unobserved heterogeneity?	No		Yes
N=	27,463		27,463

CABG, coronary artery bypass grafting; CHF, congestive heart failure; PCI, percutaneous coronary intervention.

The second panel in Table 3 contains the results of the hazard model controlling for unobserved heterogeneity. There are two pieces of evidence suggesting the presence of unobserved heterogeneity, that is, the presence of more than one mass point. First, the estimates of two mass points are statistically significant. Second, the likelihood ratio test rejects the null hypothesis that the unobserved heterogeneity is absent, that is, there is a single mass point.

While the results in Table 3 indicate the presence of unobserved heterogeneity, these are only raw coefficients and give little indication as to the magnitude of the impact of surgeon and hospital volume on mortality at different time points after surgery. To facilitate ease of comparison with the volume quartile impacts in the GEE models, in Table 4 we report the marginal effects on 1-, 3-, 6-, and 12-month mortality rates of having a surgery performed by surgeons and hospitals in the different volume quartiles.

Table 4.

Marginal Effects of Adjusted Hazard Model Estimates of the Impact of Provider Quartile of Volume on Patient Mortality at Select Time Points for Patients Undergoing Isolated CABG in Taiwan 1998–2007

Outcome	1-Month Mortality				3-Month Mortality				6-Month Mortality				12-Month Mortality
Overall	Mean Mortality=0.058				Mean Mortality=0.091				Mean Mortality=0.112				Mean Mortality=.0135
among Surgeons in the Lowest Volume Quartile (reference group)	Mean Mortality=0.091				Mean Mortality=0.144				Mean Mortality=0.178				Mean Mortality=0.208
among Hospitals in the Lowest Volume Quartile (reference group)	Mean Mortality=0.090				Mean Mortality=0.132				Mean Mortality=0.158				Mean Mortality=0.185
	Marginal Effect	p-value	Marginal Effect	p-value	Marginal Effect	p-value	Marginal Effect	p-value	Marginal Effect	p-value	Marginal Effect	p-value	Marginal Effect	p-value	Marginal Effect	p-value
Surgeon volume quartiles
2nd	−0.012	<.001	−0.057	<.001	−0.015	<.001	−0.031	<.001	−0.018	<.001	−0.013	<.001	−0.023	<.001	−0.003	.003
3rd	−0.017	<.001	−0.089	<.001	−0.021	<.001	−0.051	<.001	−0.026	<.001	−0.022	<.001	−0.033	<.001	−0.005	.003
4th	−0.013	<.001	−0.063	<.001	−0.017	<.001	−0.035	<.001	−0.021	<.001	−0.015	<.001	−0.026	<.001	−0.003	.008
Hospital volume quartiles
2nd	−0.005	.008	−0.007	.489	−0.005	.054	−0.004	.492	−0.007	.008	−0.002	.498	−0.009	.008	0.000	.510
3rd	−0.004	.055	−0.009	.439	−0.006	.008	−0.005	.444	−0.006	.053	−0.002	.451	−0.007	.054	0.000	.467
4th	−0.010	<.001	−0.042	<.001	−0.013	<.001	−0.023	<.001	−0.016	<.001	−0.010	.006	−0.019	<.001	−0.002	.029
Controlling for unobserved heterogeneity?	No		Yes		No		Yes		No		Yes		No		Yes

CABG, coronary artery bypass grafting.

In the model controlling for unobserved heterogeneity, the impacts of surgeon volume on 1-month mortality range from 5.7 to 8.9 percentage points. The relative impact of surgeon volume tapers off up to the 12-month mark, where the range of volume effects is between 0.3 and 0.5 absolute percentage points.

A different pattern emerges when looking at the effect of controlling for unobserved heterogeneity on the estimated impact of increased hospital volume on reductions in patient mortality at different points after CABG. Once we control for unobserved heterogeneity, only those having their procedure performed at hospitals in the highest volume quartile have a statistically significant lower likelihood of mortality than those in the lowest quartile for each mortality outcome time point. The estimated mortality advantage of having surgery at the highest volume hospital rather than the lowest volume hospital is 4.2, 2.3, 1.0, and 0.2 absolute percentage points at the respective mortality outcomes of interest.

DISCUSSION

Over the period from 1998 to 2007 in Taiwan, we find there is a relationship between surgeon and hospital volumes and the duration to patient mortality. Higher volume quartile surgeons and hospitals have a reduced probability of a patient experiencing mortality at 1, 3, 6, and 12 months. Using a duration modeling approach based on Butler, Anderson, and Burkhauser (1989), which is based upon Heckman and Singer (1984), to deal with unobserved heterogeneity reveals that indeed unobserved heterogeneity is likely a concern, as suspected previously.

Overall, the results of both our GEE and hazard modeling suggest the marginal effect of having CABG performed by a higher volume surgeon are larger in the short term. While the impact of surgeon volume remains statistically significant in the long run, the impact relative to the mean mortality is rather small, suggesting less of a clinical significance than at the earlier time points. The estimated impact of hospital volume is similar to surgeon volume at 1 month in our GEE model, though the advantage is not monotonically increasing as volume increases, suggesting some potential nonlinearity to the hospital volume–outcome relationship or potentially some unobserved heterogeneity. Indeed, the later appears to be the case once we turn to our hazard modeling strategy, which adjusts for this unobserved heterogeneity.

After adjusting for unobserved heterogeneity in our hazard model, the impact on 1-month mortality of having surgery performed by a higher volume surgeon becomes quite large. With respect to the impact of hospital volume, this model suggests that there is only a mortality advantage if a patient undergoes his/her procedure in the highest quartile of volume. In both the case of surgeon and hospital volume, it appears that the hazard to mortality and unobserved heterogeneity may be an important consideration in the modeling of short-term outcomes.

Focusing on the hazard model results that adjust for unobserved heterogeneity (Table 4), one can see that the effect of surgeon and hospital volume wanes as we transition to longer term outcomes. The surgeon volume effects calculated from our model controlling for unobserved heterogeneity are still statistically significant at the time periods we considered, though one could argue that the impact is much less significant clinically by the 6- and 12-month mark, where the relative reduction in mortality compared with the mean of the reference group is at most 12.4 percent at 6 months and 2.4 percent at 12 months. With respect to the impact of having CABG performed at a higher volume hospital on the impacts on 3-, 6-, and 12-month mortality, the results are qualitatively similar to the hospital impact on 1-month mortality, that is, the mortality advantage is concentrated in the highest quartile of volume hospitals. In both the case of surgeon and hospital volume, the transition to examining longer term outcomes reveals that outcome differences at those points are still observable in Taiwan. Unsurprisingly, unobserved heterogeneity is a concern with regard to the exact magnitudes of the volume impacts at those later time points.

While there is a mortality advantage concentrated at the highest of volume hospitals, the clinical significance of this advantage is smaller than simply avoiding having CABG performed by the lowest volume surgeons. This last point suggests that surgeon volume is at least as important as hospital volume as a measure of quality in Taiwan. Similar approaches to this question using data from the United States, Canada, and Europe, from where most of the current evidence in the literature is derived, might further the understanding of the volume–outcome relationship across all systems.

More generally, our results suggest using methods that examine the hazard to a particular outcome may be an important consideration when estimating the impact of volumes on mortality. From a methodological standpoint it appears that the GEE models with binary endpoints potentially understate the impacts of surgeon volume on mortality while overstating the impacts of hospital volume on mortality. In addition, our hazard model estimates suggest that unobserved heterogeneity is present in this relationship as estimated. Unfortunately, our methodology does not allow us to specifically identify the source(s) of the unobserved heterogeneity. However, the implication of our results is that surgeon volume has a more clinically significant impact on the hazard to mortality in Taiwan.

With regard to examining longer term outcomes, one could argue that mortality outcomes further into the future are based on other factors and not attributable to the quality of the procedure or postoperative care. To a large extent we agree there are other factors that impact longer term outcomes that are beyond the control of the provider and therefore not attributable to quality differences but may be due to unobserved factors. Our hazard to mortality estimates support this assertion to a large extent, though controlling for unobserved heterogeneity in these models does not completely mitigate the long-term differences in mortality attributable to volume level.

If measures of provider quality such as volume have absolutely no impact, the estimate of the volume impact on the longer term outcomes should not be statistically different from zero. If the estimated impact of volume and other quality indicators on longer term outcomes or time to these outcomes are not zero, then there are some potential explanations. These quality indicators, such as volume, do in fact impact these other longer term measures of outcome. For example, patient behavior after discharge may have large impacts on mortality differences, and one might argue that experienced surgeons may give more effective counsel on the behavior changes a patient needs to make, which improves their patients' outcomes. Alternatively, patients who are going to change their health behaviors and preferences ex post are also differentially sorting to providers by quality indicators such as volume ex ante. A priori both explanations seem implausible, but these are empirical questions to be addressed by future research.

Our study does have limitations. The most important is that our data are drawn from Taiwan, where rates of CABG are much lower than in the United States, Canada, and Europe, even though in Taiwan there are still high-volume providers by U.S. standards. Specific estimates of the impact of provider volume by quartile may differ in other systems. Similar research using the methods suggested here on data from the United States, Canada, or Europe would be needed before drawing any definitive conclusions or making policy recommendations in these systems. Lastly, because we do not know the clinical cause of death for those who die, we are limited to using disenrollment. This has been shown to be a valid imputation in the data from Taiwan; however, the ability to focus on related causes of death might improve the evidence base. Of course, accurate data on cause of death are not easy to obtain in any nation, so this is more of a measurement limitation than a limitation specific to our data.

Supporting Information

Additional supporting information may be found in the online version of this article:

Appendix SA1: Author Matrix.

Please note: Wiley-Blackwell is not responsible for the content or functionality of any supporting materials supplied by the authors. Any queries (other than missing material) should be directed to the corresponding author for the article.