Dual interference channel quantitative phase microscopy of live cell dynamics

Abstract

We introduce and experimentally demonstrate a new fast and accurate method for quantitative imaging of the dynamics of live biological cells. Using a dual-channel interferometric setup, two phase-shifted interferograms of nearly-transparent biological samples are acquired in a single digital camera exposure, and digitally processed into the phase profile of the sample. Since two interferograms of the same sample are acquired simultaneously, most of the common phase noise is eliminated, enabling the visualization of millisecond-scale dynamic biological phenomena with sub-nanometer optical path length temporal stability.

Imaging live cells requires a system that is able to visualize mostly transparent three-dimensional objects with very little inherent absorption, imposing almost no change on the light amplitude reflected from or transmitted through them. Conversely, the phase of the light transmitted through these transparent objects can give a good indication of the optical path delays associated with them. Phase imaging can be performed by several well-known microscopy techniques, such as phase contrast and differential interference contrast microscopy [1]. However, these conventional microscopy techniques do not yield quantitative phase measurements. In addition, they suffer from various artifacts that make it hard to correctly interpret the resulting phase images in terms of optical path delays.

Digital holography, on the other hand, yields quantitative measurement of the phase distribution [2-6]. Therefore, it is possible to reshape the captured complex wave front and, for example, compensate for optical aberrations. Digital holography, however, requires interferometric setups, typically yielding phase images that are not free from phase noise. “Elimination of most of the phase noise, originating from the common perturbations in the interferometer arms and from the DC background, can be accomplished by acquiring two or more interferograms of the same sample [5,6].”

Still, certain biological processes, such as cell membrane fluctuations and neuron activity, occur faster than the scanning rates of most optical systems. Therefore, this paper suggests a new optical system for obtaining dynamic quantitative phase measurements with high precision and a low degree of phase noise. The method, called dual interference channel quantitative phase microscopy (DQPM), is based on a new dual-channel interferometric setup that is able to simultaneously obtain two phase-shifted interferograms of the same sample. These interferograms are digitally processed to yield the phase profile of the sample. Due to the fact that two interferograms of the same sample are acquired, it is possible to eliminate most of the common phase noise in the final phase image. Additionally, due to the simultaneous manner of the acquisition, one can capture rapid cell phenomena with sub-nanometer temporal stability, with the only limit being the true full frame rate of the digital camera used.

Ikeda et al. [7] have suggested another dynamic quantitative phase microscopy method which is based on the acquisition of a single interferogram. This method is able to avoid the temporal phase noise between successive frames, but since only one interferogram is acquired, common phase noise due to the sample is not eliminated. Various attempts for simultaneous phase imaging have been performed in the optical testing field [8-12]. However, these methods are not implemented for microscopy of biological cells as performed in the current paper.

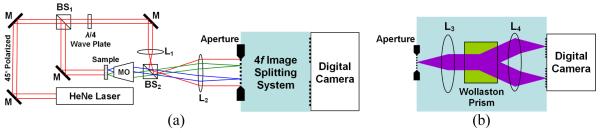
Figures 1 illustrates the DQPM system. This system includes an off-axis digital holographic microscopy setup based on a Mach Zehnder interferometer, followed by an image splitting system. Light from a HeNe laser source, linearly-polarized at 45°, is split into sample and reference beams by beam splitter BS₁. The sample arm includes a sample, and microscope objective MO that is in a 4f configuration with lens L₂. Lens L₁ in the reference arm is in a 4f configuration with lens L₂ as well. BS₂ combines the sample and reference beams, and the interference pattern of interest appears one focal length behind lens L₂. This interference pattern is spatially restricted by an aperture to an area that is not bigger than half of the digital camera sensor size. The interference pattern at the aperture plane is then imaged, through the 4f image splitting system shown in Fig. 1(b), onto the digital camera. This 4f image splitting system includes two identical lenses, L₃ and L₄, creating a one to one image of the aperture plane onto the camera. A Wollaston prism is positioned between these two lenses to create two spatially-separated and phase-shifted interferograms on the camera.

Figure 1.

The DQPM system: dual-channel, single exposure interferometer for obtaining phase profiles of live dynamic biological cells: (a) The entire interferometer; (b) The 4f image splitting system.

The phase shift between the interferograms is explained as follows. In the reference arm, a quarter (λ/4) wave plate is oriented along the horizontal axis, so that the light transmitted through it has a 90° phase difference between the horizontal and vertical components. On the other hand, in the sample arm the light remains 45° linearly-polarized, so there is 0° phase difference between the horizontal and vertical components. When the beams are combined by BS₂, there is α = 90° shift between the interference pattern formed by the horizontal component and the interference pattern formed by the vertical component. Due to its ability to output two perpendicularly-polarized beams, the Wollaston prism separates the horizontal or vertical components for each of the interferograms, yielding a phase shift of α between the interferograms.

The two interferograms, I₁ and I₂, acquired by the digital camera in a single exposure, can be mathematically expressed as follows:

$$I_1=I_R+I_s+2\sqrt[]{I_s{I}_R}\left[\text{cos}({\varphi }_{OBJ}+{\varphi }_C)\right];I_2=I_R+I_s+2\sqrt[]{I_s{I}_R}\left[\text{cos}({\varphi }_{OBJ}+{\varphi }_C+\alpha )\right],$$ (1)

where I_R and I_S are the reference and sample intensity distributions, respectively; ϕ_OBJ is the spatially-varying phase associated with the object; and ϕ_C is the spatially-varying phase of the interferometer without the presence of the object. Note that ϕ_C and α can be digitally measured, based on the fact that off-axis holographic geometry is used, by fitting the background interference (interference pattern observed without the presence of the sample) in each of the interferograms to a sine wave. The wrapped object phase ϕ_OBJ is computed as follows:

$$F=\frac{\text{exp}(-j{\varphi }_c)}{1-\text{exp}\left(j\alpha \right)}[I_1-I_2+jHT\{I_1-I_2\}];{\varphi }_{OBJ}=\text{arctan}\left\{\frac{\text{Im}F}{\text{Re}F}\right\})$$ (2)

where HT denotes a Hilbert transform. Next, an unwrapping algorithm is applied to obtain the final unwrapped object phase. Note that the process described above removes most common noise and background elements, enabling reliable phase measurement. In addition, since the interferograms I₁ and I₂ are acquired simultaneously, in a non-scanning manner, fast phenomena can be visualized. Using Eq. (1) and recalling that $HT\left\{\text{cos}\left(\varphi \right)\right\}=\text{sin}\left(\varphi \right)$, that $\text{cos}\left(\varphi \right)=0.5[\text{exp}\left(j\varphi \right)-\text{exp}(-j\varphi )]$, and that $\text{sin}\left(\varphi \right)=0.5j[\text{exp}(-j\varphi )-\text{exp}\left(j\varphi \right)]$, one can easily show that $F=2\sqrt[]{I_s{I}_R}\text{exp}\left(j{\varphi }_{OBJ}\right)$, and thus Eq. (2) holds.

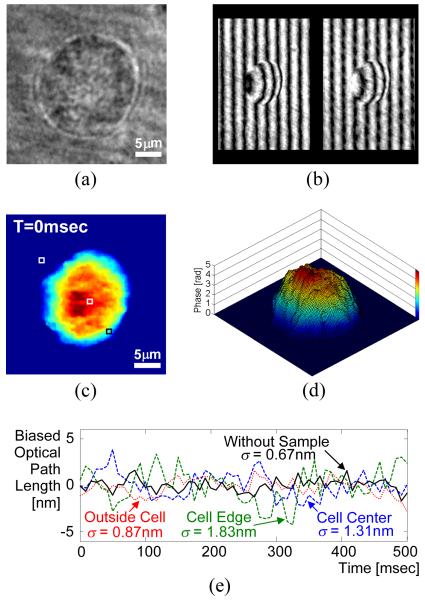
To demonstrate the DQPM system shown in Fig. 1, we have imaged a live, unstained MDA-MB-468 human breast cancer cell in standard phenol red growth medium. Figure 2(a) shows the regular microscopic image of the sample through the optical system, demonstrating the very low visibility achieved with simple imaging of this sample. A HeNe laser (5 mW, 633 nm) was used as the source in the interferometric setup. In both interferometer arms, 40x, 0.65 NA achromatic objective lenses were used. Each of these lenses created 33x magnification when paired with lens L₂ (15 cm focal length). The resulting complex amplitude was spatially restricted by a 3.2 mm × 2.3 mm aperture. The 4f image splitting system shown in Fig. 1(b) used two similar lenses L₃ and L₄, each with a focal length of 7.5 cm. The Wollaston prism (crystal quartz, 2° of angular separation), positioned between these two lenses, split the pattern from the aperture plane so that the CCD camera (AVO Pike F032-B, 640×480 pixels) captured the two phase-shifted interferograms I₁ and I₂ shown in Fig 2(b), spatially separated by about 2.4 mm. To determine the coordinate mapping between the two different interferograms in the single CCD image, a test target (USAF resolution chart) was used as a preprocessing sample. The frequency q and the actual phase shift α were extracted by fitting each of the interferograms to a sine wave. Based on the fact that the background interference fringes in each of the interferograms are vertical, we get ϕ_C = qx, where x is the horizontal coordinate in each interferogram frame. Figures 2(c) and (d) show the final unwrapped phase profile of the sample as obtained by applying Eq. (2) and a phase unwrapping algorithm. The same cell was acquired every 8.3 milliseconds [120 frames per second (fps)] for a duration of 500 milliseconds. As can be seen from the movie linked from Fig. 2(c), the temporal phase stability is excellent even in the presence of a sample containing fluid media.

Figure 2.

MDA-MB-468 human breast cancer cell: (a) Regular microscopic imaging through the system; (b) The two phase-shifted interferograms captured in a single camera exposure; (c) Final unwrapped phase profile (media 1); (d) Temporal phase stability without the sample, and with the sample in the three points marked in (c); (e) Surface plot of the phase profile shown in (c). Viewing this figure in color is highly recommended.

To quantify this temporal phase stability, we recorded the temporal path-length fluctuations associated with a diffraction-limited spot defined by the imaging optics at millisecond rates. The stability was first assessed without the presence of a sample, and then with the presence of the sample in the three marked points in Fig. 2(c): on the cell center, on the cell edge, and at the background (through the medium only). The fluctuations standard deviations in these four cases were 0.67 nm, 1.31 nm, 1.83 nm, and 0.87 nm, respectively, as shown in Fig. 2(e). The first result above, representing the true temporal stability of the optical system, indicates that sub-nanometer path-length sensitivity can be achieved for imaging on the millisecond time scale. We attribute the slightly lower stability in the three latter cases to small vibrations occurring inside the entire sample.

To illustrate the utility of DQPM for imaging dynamic cell phonemena, the movie (120 fps acquired for 2 seconds) linked from Fig. 3 presents the phase profiles of a rat beating myocyte (myocardial cell taken from rat heart muscles) in phenol red growth medium.

Figure 3.

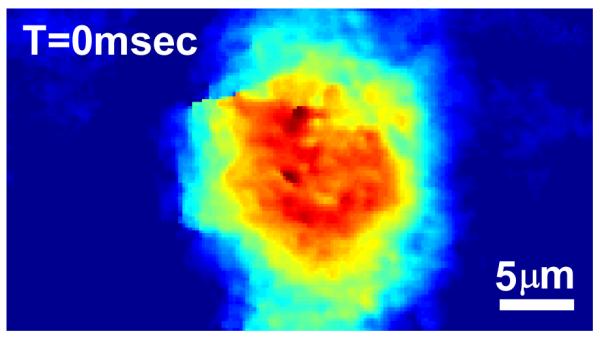
The final unwrapped phase profile of a rat beating myocyte (media 2). Viewing this figure in color is highly recommended.

In summary, we have demonstrated a new method for imaging fast biological phenomena with high accuracy. Experimental results show good spatial resolution for dynamic cell phase imaging and excellent temporal phase stability. Due to its simultaneous acquisition, the system’s ability to observe fast cellular phenomena is only limited by the true full frame rate of the camera, and thus this method provides a powerful tool for dynamic studies of biological cells.