A Simulation Study of Cellular Hypertrophy and Connexin Lateralization in Cardiac Tissue

Abstract

Many cardiac diseases coincide with changes in cell size and shape. One example of such a disease is cardiac hypertrophy. It is established that cardiac impulse propagation depends on the cell size, as well as other factors, but interrelations between conduction velocity (CV), cell size, and gap junction (GJ) conductance (g_GJ) are complex. Furthermore, cardiac diseases are often accompanied by connexin (Cx) lateralization. To analyze the effects of cell size and Cx lateralization in cardiac disease, a two-dimensional computer simulation of ventricular myocytes based on the Luo-Rudy model was used. Control cells (80 μm/20 μm (length/diameter)), long cells (160 μm/20 μm), and wide cells (80 μm/40 μm) were simulated as was a redistribution of lateral GJs (constant lateral g_GJ and increased lateral g_GJ). CV in long cells showed high stability, i.e., it declined very slowly when g_GJ was gradually reduced. Wide cells, however, were more affected by reduced g_GJ, resulting in early transition to discontinuous propagation and low CV. Conduction block occurred earlier in enlarged cells than in control cells due to increased cell capacitance. Increased lateral g_GJ stabilized longitudinal CV, which was a result of two-dimensional effects during planar wave propagation. Therefore, Cx lateralization may compensate for cardiac inhomogeneities. High lateral g_GJ and enhanced cell diameter increased the susceptibility to conduction block at tissue expansion, providing a substrate for arrhythmia.

Introduction

Hypertrophic heart diseases coincide with ventricular arrhythmia and increased mortality due to sudden cardiac death (1–6). Arrhythmogenesis depends on multiple factors, because the electrophysiological behavior of cardiac tissue is a result of active and passive properties. Active properties include transmembrane ionic currents and channel kinetics, and passive properties include intercellular and intracellular resistances, gap junction (GJ) distribution, degree of fibrosis, and cell geometry. Electrical remodeling, of K⁺ channels, e.g., in hypertrophied and failing hearts can result in prolonged duration of action potentials (7–9), widening the vulnerable window for unidirectional conduction block and increasing the risk of arrhythmia. Hypertrophied hearts tend to prolonged QT intervals (10), which are known to be associated with sudden cardiac death (11). However, effects of increased cell size and GJ distribution in hypertrophied hearts are difficult to study experimentally. It is known that cell size can have a strong effect on impulse propagation (12–15). In a study by Spach et al. (13), an increase in cell size resulted in higher conduction velocity (θ),in accordance with findings of Ghali et al. (15), who showed that decreased cell size can negatively affect θ. In contrast, McIntyre et al. (16) found a negative correlation between cell diameter and θ in human ventricular tissue, which seems paradoxical, because an increase in cell diameter reduces the intracellular resistance. This indicates that the effects of cell size may be complex and are not completely understood. This study shall therefore provide a systematic analysis of effects of cell size on cardiac impulse propagation. Since impulse propagation strongly depends on GJ conductance (g_GJ), it was appropriate to take into account the finding that hypertrophic, ischemic, and inflammatory cardiac diseases are often accompanied by altered cellular GJ distribution, with an increased number of connexin43 GJs (Cx43s) at cell sides (17–24), leading to an increased ratio of lateral to polar Cx43s (lateralization). Atrial fibrillation can also be accompanied by Cx lateralization (25). However, it is difficult to assess whether lateralized Cx builds a functional GJ. There are few studies of this issue. Polontchouk et al. (26) have shown that after stimulating rat atria for 24 h at a stimulation rate of 10 Hz, Cx43 was lateralized together with an increase in transverse θ (θ_T), giving evidence of functionality, whereas longitudinal θ (θ_L) was unchanged. In this study, we provide experimental evidence that this may also occur in human atria, although there are studies showing that Cx lateralization can be accompanied by decreased θ (19,27). Besides quantitative alterations, a more uniform spatial distribution of lateral Cx is observed (28). It is hardly possible to investigate separately the effects of altered cell size and GJ distribution in experiment, because usually they are accompanied by additional alterations, e.g., altered transmembrane currents (7–9) or fibrosis (29). Computer simulations make it possible to vary isolated parameters. Therefore, a two-dimensional (2D) computer model based on the Priebe-Beuckelmann (9) and Luo-Rudy (30) models was used. Different types of hypertrophy and different degrees of GJ lateralization were simulated and analyzed under normal and pathological conditions.

Methods

Mapping and immunostaining of atrial human tissue

A detailed description of Cx43 immunostaining and mapping experiments can be retrieved from the Supporting Material.

Computer model

For details, see the Supporting Material. A 2D computer simulation model with each cell composed of several cell segments 10 μm × 10 μm in size was used (Fig. 1). Different degrees of overlapping are discussed in Fig. S2 in the Supporting Material. Control cells were assigned a length and diameter of 80 μm and 20 μm, respectively (23,24,31), polar and lateral g_GJ of 3.7 μS and 2.6 μS, respectively, and cytoplasmatic resistivity of 1.5 Ωm (32,33). Throughout the simulations, transmembrane current densities and kinetics were assumed to be unaltered. It is known that θ in elliptic waves can be smaller than in planar waves (34). Both were simulated, revealing a difference of 3–7%. If not otherwise specified, all results obtained were for planar waves.

Figure 1.

Schematic illustration of the bricklike cell arrangement and GJ distribution used in the simulations. Squares represent cell segments of 10 μm × 10 μm. Horizontal and vertical bars between blocks of cell segments indicate longitudinal and transverse GJs, respectively. Control cells had a nonuniform lateral GJ distribution, i.e., 90% of the lateral conductance was restricted to GJs near the cell poles (black vertical bars). Under simulation conditions of uniform connexin distribution, gray and black GJs had the same conductance.

Simulating hypertrophy and Cx lateralization

Junctional conductance

Hypertrophied cells have a greater membrane area (A_m) and, thus, a higher cell capacitance. If GJ density (number of GJs/A_m) remains constant, g_GJ will increase proportionally to A_m. If the number of GJs remains constant, g_GJ will remain constant. Because experimental data indicate that both situations may occur (35,17–19,23,24,36), both were simulated. Increased g_GJ is simulated under assumption I, and constant g_GJ under assumption II. Regarding Cx lateralization, it was necessary to decide whether a lateralization of Cx involves creation of new GJs or only redistribution of the existing GJs. Experimental studies suggest that both occur (19,27,24,26,37), so both were simulated. GJs were simulated as passive ohmic resistors.

Cellular parameters

Hypertrophy is often accompanied by increased cell diameter (31,38). To examine this effect, cell diameter was increased from 20 μm to 40 μm. Because cell length may also be increased (31) or decreased (27) in hypertrophy, it was increased from 80 μm to 160 μm (see Table 1). Cell capacitance increased from 113 pF in control cells to 214 pF in long and 251 pF in wide cells, corresponding well with experimental data (29,38). Table 2 shows the electrophysiological parameters.

Table 1.

Geometrical parameters of control cells and enlarged cells

	l	d	Am	V	C	Am/V
Control	80 μm	20 μm	5655 μm2	25133 μm3	113pF	0.225 μm−1
Increased width	80 μm	40 μm	12566 μm2	100531 μm3	251pF	0.125 μm−1
Increased length	160 μm	20 μm	10681 μm2	50265 μm3	214pF	0.213 μm−1

Parameters represented are as follows: l, length; d, diameter; A_m, geometrical membrane area; V, volume, C, capacitance; A_m/V, area/volume ratio.

Table 2.

Electrophysiological parameters of simulated conditions

	gIC		gGJ		gGJ/CnS/pF	RGJ/RIC		ρ
	L (μS)	T (μS)	L (μS)	T (μS)		L	T	L (Ω cm)	T (Ω cm)
Control	2.6	42	3.7	2.6	111	0.7	16	256	2575
Increased width I	10.5	42	8.2	5.8	111	1.3	7	341	1242
Increased width II	10.5	42	3.7	2.6	50	2.8	16	575	2575
Increased length I	1.3	84	7.0	4.9	111	0.2	17	178	2716
Increased length II	1.3	84	3.7	2.6	59	0.4	32	203	5000
GJ lateralization	2.6	42	3.7	13.0	295	0.7	3	256	635

Parameters are for 100% of coupling. L, longitudinal; T, transverse; g_IC, intracellular conductance; g_GJ, gap junction conductance; g_GJ/C, ratio of total cellular g_GJ in two dimensions to cell capacitance; R_GJ/R_IC, ratio of junctional to intracellular resistance; ρ, tissue resistivity.

Cx lateralization

Some studies have shown that Cx lateralization is accompanied by increased θ_T in ventricular and atrial tissue from rats (26,37), indicating functional Cx and increased lateral g_GJ. In this study we provide evidence that this is also possible in human cardiac tissue (Fig. 2). Recent experimental findings show that in diseased hearts, lateral Cx can be increased up to fivefold (24,27). Human tissue samples indicated an even more pronounced increase in atrial fibrillation (Fig. 2). Therefore, Cx lateralization was simulated by a fivefold increase in lateral g_GJ. However, since some studies show that Cx lateralization can coincide with unchanged or diminished total Cx (18,19,23,27), we also simulated a redistribution with constant lateral g_GJ (Fig. 1).

Figure 2.

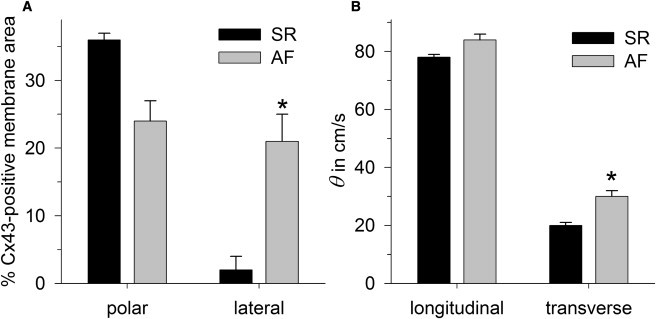
Experimental data obtained from atrial tissue samples from patients with sinus rhythm (SR) and atrial fibrillation (AF). (A) Percentage of the Cx43-positive membrane area, detected by immunostaining at cell poles (polar) and cell sides (lateral). (B) Conduction velocities (θ) obtained from mapping in longitudinal and transverse directions. An asterisk indicates a significant difference (p < 0.05) between SR and AF.

Conduction block

Polar and lateral g_GJ were gradually reduced from 100% until the conduction block. Conductance was defined as 100% of coupling (Table 2). Maximum sodium channel conductivity (g_Na) was gradually reduced from 100% (16 mS/μF) to 10% (1.6 mS/μF). A common method for assessing susceptibility to conduction block is the tissue expansion model (39,40). The critical width (h_c) of a 4-mm-long cell strand (current source) sufficient to maintain propagation in the bulk area (4 mm × 4 mm; current sink) was determined.

Limitations

See the Supporting Material.

Results

Mapping and immunostaining of atrial human tissue

Atrial tissue samples (10 mm × 10 mm) of patients with sinus rhythm (SR) and atrial fibrillation (AF) were paced at a central electrode (1 Hz, 0.6 mA, 1-ms pulses) and simultaneously mapped using 64 electrodes. Immunohistological and morphometric analysis revealed that in SR, 36 ± 1% of the polar membrane length was positive for Cx43, whereas only 2 ± 2% of the lateral membrane was Cx43-positive. In AF, lateral Cx43 expression was strongly increased to 21 ± 4% (p < 0.05), whereas polar expression was slightly diminished to 24 ± 3% (Fig. 2 A). Mapping data revealed that θ_L was 78 ± 1 cm/s in SR and 84 ± 2 cm/s in AF (not significant). θ_T, which was 20 ± 1 cm/s in SR, significantly increased to 30 ± 2 cm/s (p < 0.05) in AF (Fig. 2 B). Micrographs of immunostaining are given in Fig. S1.

Effects of increased cell size

Assumption I: increased g_GJ

In control cells (length/diameter of 80 μm/20 μm), θ_L was 59 cm/s and θ_T was 16 cm/s. When we assumed that g_GJ increases proportionally to A_m (Fig. 3 A), both enhanced length (160 μm/20 μm) and enhanced diameter (80 μm/40 μm) led to a comparable increase in θ_L: +22% in long cells (72 cm/s) and +15% in wide cells (68 cm/s). However, wide cells showed a much faster reduction of θ_L during gradual uncoupling. As a result, θ_L in wide cells dropped below θ_L in control cells when coupling was ≤15% and θ_L ≤30 cm/s. In contrast, θ_L in long cells declined very slowly. At 12.5% of coupling, θ_L was reduced to 51% (30 cm/s) in control cells, only to 68% (49 cm/s) in long cells, and to 44% (30 cm/s) in wide cells (Fig. 3 C). One explanation for this is that the increase in θ_L in wide and in long cells is based on different mechanisms. Increased cell length prolongs the distance between GJs, i.e., the proportion of intracellular resistance (R_IC) to total resistance becomes greater. Accordingly, longitudinal tissue resistivity (ρ) and the ratio of GJ resistance (R_GJ) to R_IC are lower than in the control, i.e., the effect of g_GJ on ρ is smaller. An increase in diameter, however, increases longitudinal ρ. Higher θ_L is the result of an approximately twofold lower ratio of A_m to cell volume (A_m/V). See Tables 1 and 2 for details. Since a twofold increase in diameter results in a fourfold smaller R_IC, the R_GJ/R_IC ratio is greater in wide cells. As a result, θ_L decreases faster in wide cells than in control cells. θ_T was considerably higher in wide cells (31 cm/s) than in control cells (16 cm/s), because apart from lowering the A_m/V, the longer distance between GJs decreases transverse ρ. Long cells revealed a θ_T similar to that of control cells (15 cm/s vs. 16 cm/s), because transverse ρ and A_m/V were almost unchanged. In contrast to θ_L, the relative decrease of θ_T during gradual uncoupling was comparable in all groups (Fig. 3 C), a result of the higher R_GJ/R_IC ratios in the transverse direction: R_GJ represents almost 100% of the transverse ρ, i.e., an increase in R_GJ by a given factor increases transverse ρ by the same factor in all groups. Note that this is a reason why anisotropy (θ_L/θ_T) becomes greater at lower g_GJ (see Fig. S3).

Figure 3.

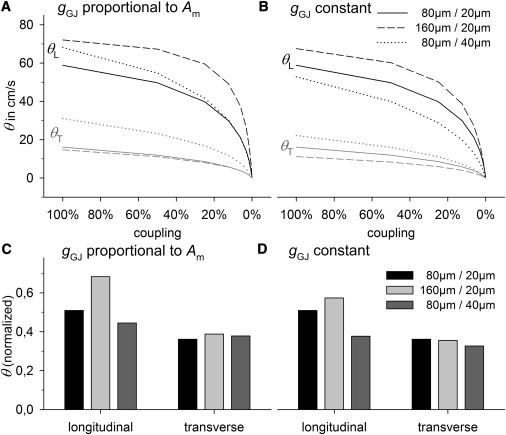
θ_L and θ_T in control cells (80 μm/20 μm (length/width)), long cells (160 μm/20 μm), and wide cells (80 μm/40 μm) with gradual reduction in coupling. Cell size was increased, assuming that g_GJ is proportional to A_m (left) and that g_GJ remains constant (right). (A and B) Plots of absolute values of θ_L and θ_T versus coupling. (C and D) θ_L and θ_T at 12.5% of coupling, normalized to their values at 100% of coupling.

Assumption II: constant g_GJ

When we assumed constant g_GJ, the ratio of g_GJ to cell capacitance was lower in enlarged cells (Table 2). Accordingly, θ was lower than under assumption I (Fig. 3 B). However, θ_L in long cells was higher (68 cm/s) than in control cells (59 cm/s), which was a result of a still lower longitudinal ρ (Table 2). The R_GJ/R_IC ratio was also still lower than in control cells, i.e., θ_L decreased more slowly during gradual uncoupling, but less significantly compared to assumption I (Figs. 3 C and D). Regarding θ_T, there was a considerable reduction to 11 cm/s (−30%). Wide cells at constant g_GJ revealed decreased θ_L (52 cm/s) and higher θ_T (22 cm/s). θ_L declined even faster than under assumption I (Fig. 3 D). It is interesting to note that long cells under assumption II had the same θ_L (68 cm/s) as did wide cells under assumption I (compare Fig. 3, A and B), although g_GJ was more than twofold higher in wide cells and cell capacitance was similar. At lower g_GJ (25% of coupling), θ_L was even higher in long cells compared to wide cells (50 cm/s vs. 41 cm/s).

Gradual uncoupling

As indicated by Fig. 3, cell size affected the sensitivity to uncoupling: θ_L declined faster in wide cells with both increased and constant g_GJ, suggesting a mechanism independent of g_GJ. To analyze cell-size effects independent of θ, in the following simulations, g_GJ was adapted in enlarged cells to obtain the same θ (±5%) as in control cells. Fig. 4 gives insight into the basic effects of uncoupling. At high coupling (Fig. 4 A), the membrane potential (ϕ) spreads almost continuously, because R_IC and R_GJ are in the same order of magnitude. As a result, there is a steady spatial curve at the wave front, leading to continuous impulse propagation, indicated by continuous activation time curves (Fig. 4 A, inset). There were no differences among the different cell sizes, and the curve of discrete cells corresponded well to the ideal curve of a continuous model with the same average ρ. The distance over which ϕ spreads is characterized by the space (also the length) constant (λ), which is the distance from the point of maximum ϕ (ϕ_max) to the point where ϕ = ϕ_max/e, i.e., where ϕ is ∼37% of ϕ_max. At 100% of coupling and θ_L ∼ 60 cm/s, λ was ∼300 μm, which was almost fourfold longer than the length of control cells. Thus, the discrete tissue character did not interfere with the impulse propagation. However, at low coupling (Fig. 4 B), λ becomes smaller because of increased ρ. Cable theory predicts that λ is proportional to 1/√ρ. An eightfold increase of ρ would lead to an approximately threefold decrease in λ. Accordingly, at 12.5% of coupling and a velocity of ∼30 cm/s, λ was ∼100 μm in the continuous model. This was in the range of the cell length. Fig. 4 B shows that when λ was equal to or smaller than the cell length, impulse propagation became discontinuous. Low coupling, with R_GJ >> R_IC, does not allow a steady spatial spread of ϕ. In contrast, cells become equipotential with high ϕ gradients along GJs. Each cell acts as a minimum discrete capacitance, being depolarized and activating at once. As a result, λ cannot drop below the cell length and θ becomes lower than predicted by the cable theory (where θ is proportional to 1/√ρ). As an indicator for discontinuous propagation we calculated junctional and intracellular activation time delays (JD and ID). A high JD/ID ratio indicates discontinuity. During longitudinal propagation, control cells and cells of increased length revealed similar values: their respective JD/ID ratios were 0.7 and 0.6 at 100% of coupling and 4.6 and 3.9 at 12.5% of coupling. In contrast, wide cells showed significantly higher values: 1.4 at 100% of coupling and 13.5 at 12.5% of coupling, i.e., propagation in wide cells became discontinuous earlier. This is an additional explanation of why θ_L decreased most rapidly in wide cells (Fig. 3). During transverse propagation, ID was already negligible at 100% of coupling, with very high JD/ID ratios (between 27 and 37), indicating that in the transverse direction there is always discontinuous propagation. This fits with the result that θ_T showed a similar decay during gradual uncoupling in all cell size groups and that θ_T was more affected than θ_L by uncoupling (Fig. 3) (for details, see Fig. S4).

Figure 4.

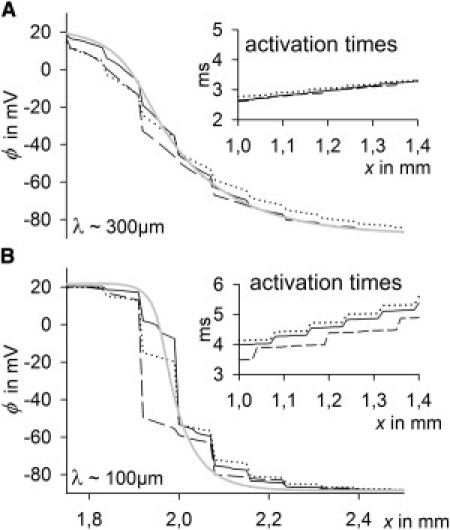
Membrane potential (ϕ) curves in the x-direction during longitudinal impulse propagation of control cells (black solid line), long cells (dashed line), and wide cells (dotted line), and a continuous model (gray solid line) in which resistivity is that same as in the control cell. g_GJ was adapted in enlarged cells to obtain the same θ_L and θ_T at 100% of coupling as in the control (±5%). (Insets) Activation times in the x-direction (right), and λ (left), the space constant. (A) 100% of coupling. (B) 12.5% of coupling.

Conduction block

As described above, λ cannot drop below a certain value in a medium with discrete capacitive units, i.e., below cell length in longitudinal and below cell width in transverse propagation. A consequence would be that the whole-cell capacitance must be charged until its activation threshold, i.e., the lowest charge (Q) that must be provided by already-activated cells is proportional to the cell size. To verify this prediction, we calculated the Q accumulated by nonactivated tissue in front of the activation wave (Fig. 5 A). At 100% of coupling, equal values were obtained from different cell sizes and a continuous model with the same ρ. At 12.5% of coupling, tissue with discrete elements (cells) accumulated more Q than did the continuous model and enlarged cells accumulated more than did control cells. This was more pronounced at 1.56% of coupling. As expected, long cells, having the highest discrete capacitance/tissue width in the longitudinal direction, revealed the highest Q accumulation. Accordingly, in the transverse direction, wide cells showed the highest Q values (not shown). Coupling was further reduced until conduction block occurred (Fig. 5 B). Minimum θ_L and θ_T correlated well with the cell length and width, respectively. Block occurred at ∼5 nS in control cells, ∼10 nS in long cells, and ∼12 nS in wide cells, corresponding well to the minimum discrete capacitance (C), i.e., C_cell (113 pF, 214 pF, and 251 pF, respectively). Thus, g_GJ/C_cell was constant (∼45 pS/pF). Note that in a continuous model there is no conduction block. If block occurs, a smaller value of Δx or Δy, reducing the minimum capacitive unit, always allows conduction to be maintained.

Figure 5.

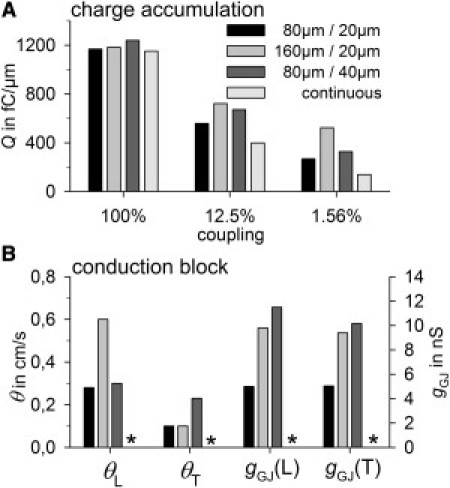
(A) Charge accumulated by nonactivated cells during longitudinal impulse propagation at 100%, 12.5%, and 1.56% of coupling in control cells (80 μm/20 μm), long cells (160 μm/20 μm), and wide cells (80 μm/40 μm), and in a continuous model with the same resistivity as the control. Note that this charge corresponds to the area under the curve (ϕ) in Fig. 4 within the x-interval from the point where ϕ ∼ –40 mV to x_max, multiplied by the specific membrane capacity (in pF/μm²). For details, see Fig. S5, Fig. S6, and Fig. S7. (B) Minimum longitudinal (L) and transverse (T) θ and minimum g_GJ directly before conduction block due to uncoupling. There is no block in a continuous model (asterisks).

Reduced excitability

To analyze the influence of reduced membrane excitability on different cell sizes, g_Na was reduced gradually from 100% (16 mS/μF) to 10% (1.6 mS/μF). The effect of reduced g_Na on the spatial curve of ϕ is contrary to the effect of reduced g_GJ. Whereas a reduction of g_GJ decreased the space constant (λ), a reduction of g_Na led to an increase in λ. As a consequence, the effects of low g_Na did not differ from those in a continuous model and did not reveal differences in enlarged cells. Conduction block occurred at 13% of g_Na in all groups (Fig. S8).

GJ lateralization

Fig. 6 shows the effects of fivefold-enhanced lateral g_GJ (from 2.6 to 13 μS) under conditions of normal lateral GJ distribution (Fig. 6 A) and uniform lateral GJ distribution (Fig. 6 B). It is interesting to note that under normal distribution conditions, enhanced lateral g_GJ increased not only θ_T, from 16 cm/s to 30 cm/s, but also θ_L, from 59cm/s to 63cm/s. Furthermore, it stabilized both θ_L and θ_T against uncoupling (Fig. 6 C). Under conditions of uniform GJ distribution, enhanced lateral g_GJ had a negligible effect on θ_L but increased θ_T to 40 cm/s, 33% higher than with normal GJ distribution, but lower lateral g_GJ (2.6 μS) effected an increase in θ_T of only 12% (from 16 to 18 cm/s) under uniform compared to normal distribution. Hence, at a given θ_T, uniform distribution is more strongly affected by g_GJ. The reason is that if lateral GJs are concentrated near the cell poles (normal distribution), currents must flow in the longitudinal cell direction also to activate the downstream cell (zig-zag-like), whereas this is not necessary if GJs are uniformly distributed (for better understanding, see Fig. 6, A and B, insets, or Fig. 1). As a result, longitudinal intracellular resistance (R) contributes to total R during transverse impulse propagation. Thus, if lateral g_GJ is changed, the resulting change in total R is higher in cells with uniform lateral GJ distribution.

Figure 6.

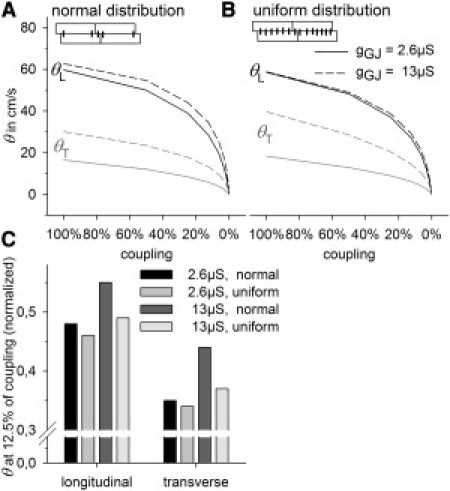
Effects of increased lateral g_GJ on θ_L and θ_T. Lateral g_GJ was increased from 2.6 μS to 13 μS. (A) Normal lateral GJ distribution with 90% of lateral g_GJ near the poles (see inset). (B) Uniform lateral GJ distribution. (C) θ_L and θ_T at 12.5% of coupling, normalized to their values at 100% of coupling.

Microscopic effects

Increased lateral g_GJ was able to stabilize θ_L against uncoupling (Fig. 6 C), i.e., it enhanced θ_L more when coupling and θ_L were low. This effect is a result of overlapping cells and the decrease of the space constant λ at low g_GJ (Fig. 7). As a consequence of cell arrangement, the activation wave front is not completely planar (Fig. 7 A, inset). Thus, there is a ϕ gradient in the transverse direction, which is the driving force for lateral currents. A smaller λ in the longitudinal direction (low coupling) causes higher transverse ϕ gradients, i.e., the driving force for lateral currents increases as coupling decreases. Accordingly, high lateral g_GJ had more of an effect at low polar g_GJ (Fig. 7 B). Note that high lateral g_GJ was able to partially counteract cell-size effects at low polar g_GJ. At polar g_GJ 0.06 μS and lateral g_GJ 0 μS, control cells, long cells, and wide cells had θ_L values of 8 cm/s, 23 cm/s, and 4 cm/s, respectively. That is, θ_L was around sixfold higher in long than in wide cells. If lateral g_GJ was 3.7 μS, θ_L values were 32 cm/s, 41 cm/s, and 23 cm/s, respectively, i.e., θ_L was less than twofold higher in long than in wide cells.

Figure 7.

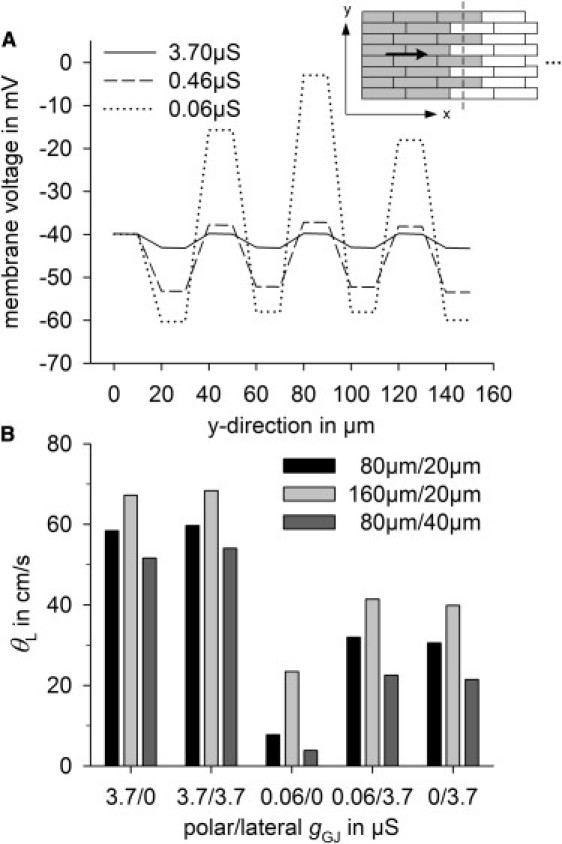
(A) Membrane potential gradients in the transverse direction (y) during longitudinal impulse propagation (see inset, where activated cells are gray) at 100%, 12.5%, and 1.56% of coupling in control cells, with polar and lateral g_GJs of 3.7 μS, 0.46 μS, and 0.06 μS, respectively. (B) Effects of polar and lateral g_GJ on θ_L in control cells (80 μm/20 μm), long cells (160 μm/20 μm), and wide cells (80 μm/40 μm).

Macroscopic effects

Similar effects of increased lateral g_GJ were observed on a more macroscopic scale (Fig. 8). To simulate heterogeneity, a tissue stripe of 4 mm × 1 mm was initialized with differing polar g_GJ and stimulated to obtain longitudinal propagation. In the upper half of the stripe, polar g_GJ was decreased to 12.5% (0.5 μS), whereas it was normal in the lower half (3.7 μS) (Fig. 8 A). A fivefold increase in lateral g_GJ from 2.6 μS to 13 μS was able to smooth the activation wavefront (Fig. 8 B) and to enhance θ_L in the partially uncoupled area from 33 cm/s to 42 cm/s, whereas θ_L was unchanged in the well-coupled area (58 cm/s). Furthermore, the tissue activation time was reduced from 10.2 ms to 8.8 ms (Fig. 8 C).

Figure 8.

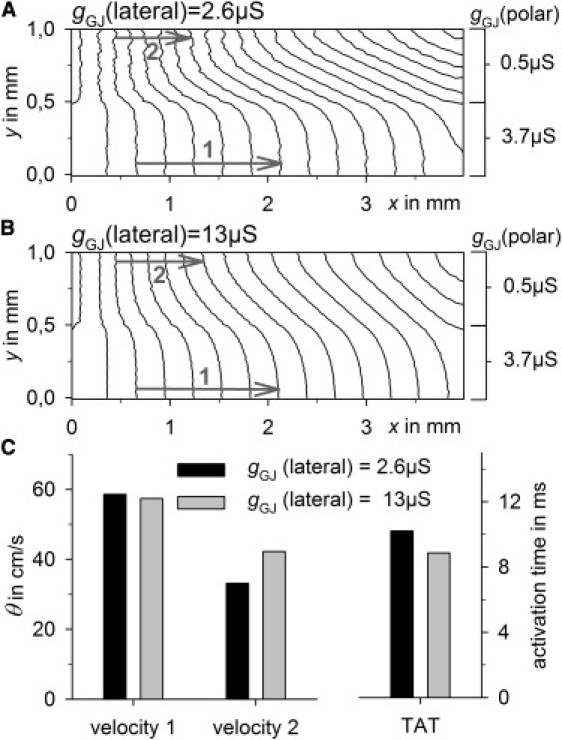
A tissue stripe of 4 mm × 1 mm was simulated with different polar g_GJs (3.7 μS and 0.5 μS). θ was measured in the areas of high polar coupling (velocity 1) and low polar coupling (velocity 2) (gray arrows). (A) Isochrones of tissue activation for a lateral g_GJ of 2.6 μS. (B) Isochrones of tissue activation for a lateral g_GJ of 13 μS. Distance between isochrones is 0.5 ms. (C) Velocity 1, velocity 2, and tissue activation time (TAT) at normal (black) and increased (gray) lateral g_GJ.

Conduction block at tissue expansion

We concluded by investigating the susceptibility of different cell sizes and degrees of GJ lateralization to conduction block at elliptic wave propagation, using a tissue expansion model (see Fig. 9 A, inset). The critical width of a cell strand at which propagation could be maintained in the expanded area, h_c,was determined. Fig. 9 A plots h_c at different cell sizes against g_Na, showing that with increased cell diameter, h_c increases from 50 μm (control) to 80 μm (+60%) if g_GJ is proportional to A_m (assumption I). A reduction of g_Na to 40% potentiated this, leading to an h_c of 120 μm in control and 220 μm (+83%) in wide cells. If g_GJ was constant (assumption II), the effects were similar but less significant. In long cells, however, h_c was equal to or smaller than the control cell value at both increased and constant g_GJ. GJ lateralization (Fig. 9 B) was able to increase h_c strikingly. Whereas at normal lateral g_GJ (2.6 μS), a uniform lateral GJ distribution had no effect, at fivefold-higher g_GJ (13 μS), h_c increased from 50 μm to 80 μm (+60%) with normal GJ distribution and 110 μm (+120%) with uniform GJ distribution. When g_Na was reduced to 40%, this effect became more pronounced: h_c increased from 120 μm in control to 220 μm (+83%) with normal and 280 μm (+133%) with uniform GJ distribution.

Figure 9.

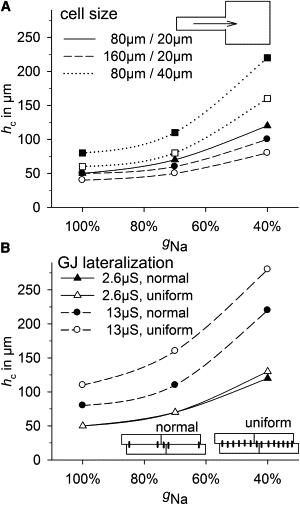
Susceptibility to conduction block determined by a tissue expansion model. The critical width (h_c) of a 4-mm-long source strand at which propagation can be maintained in the 4 mm × 4 mm bulk area (see inset in A) was determined at 100%, 70%, and 40% of the maximum sodium channel conductance (g_Na). (A) h_c versus g_Na in control cells (80 μm/20 μm; solid line), long cells (160 μm/20 μm; dashed lines), and wide cells (80 μm/40 μm; dotted lines). Assumption I (g_GJ proportional to A_m) is represented by solid symbols, and assumption II (constant g_GJ) by open symbols. (B) h_c versus g_Na in control cells with normal (solid symbols) or uniform (open symbols) GJ distribution (insets) while lateral g_GJ was 2.6 μS (solid lines) or 13 μS (dashed lines).

Discussion

This study demonstrates that there is a complex interplay between cell size, cell arrangement, and gap junction (GJ) distribution, showing that cell size, shape, and lateral GJ conductance (g_GJ) are important factors in modulating the influence of uncoupling on conduction velocity (θ).

Cell size not only affected θ at normal conditions, but also modulated the effects of partial uncoupling on θ. Increasing the cell diameter or the cell length led to an approximately twofold-higher cell capacitance (C_cell) but resulted in significant differences in θ_L and θ_T. θ_L in long cells was high and showed a very slow decline during uncoupling, whereas θ_L in wide cells decreased much more quickly. We were able to show that there are two underlying mechanisms. On the one hand, long cells have a lower R_GJ/R_IC ratio, i.e., total R is less affected by increased R_GJ, contrary to the situation in wide cells. On the other hand, impulse propagation in wide cells becomes discontinuous more rapidly, also reducing θ_L. Spach et al. (13) supposed that increasing cell size at a given g_GJ increases discontinuity. The results of this study confirm that supposition for increased diameter but not for increased length. However, θ_T was significantly greater in wide cells, resulting in lower anisotropy and higher risk of conduction block at tissue expansion (Fig. 9), which is a result of mismatches between current sources and sinks (34,39,40). It was also shown that C_cell is directly related to the occurrence of conduction block at very low g_GJ, since C_cell/g_GJ was constant. The discontinuous nature of propagation does not allow capacitive units smaller than the cell size, leading to earlier block (at higher θ and at higher g_GJ) in enlarged cells. In summary, small cells and cells with a high length/width ratio seem to have advantageous properties regarding θ_L, anisotropy (θ_L/θ_T), effects of uncoupling, and conduction blocks. This fits well with the results of Ghaly et al. (15) and Nygren et al. (27), who found a “reduced conduction reserve”, together with Cx lateralization and shorter cells, in diabetic hearts. Unfortunately, they did not discriminate between θ_L and θ_T and did not measure g_GJ. This study explains that reduced conduction reserve (Fig. 3 and Table 2), since shorter cells are more affected by uncoupling due to an increased R_GJ/R_IC ratio. The aforementioned studies (15,27) also found higher sensitivity to reduced g_Na, which cannot be explained by altered cell size (Fig. S8). Spach et al. (29) demonstrated a positive correlation between cell size and θ, whereas McIntyre et al. (16) found a negative correlation. Both can be explained by the results of this study. Increased diameter reduces θ_L if g_GJ remains constant, whereas it increases θ_L if g_GJ is proportional to A_m, suggesting that g_GJ/C_cell and A_m/V (Tables 1 and 2) are more important in analyzing cardiac disease than is g_GJ.

Lateral GJ distribution proved to be crucial not only for θ_T but also for θ_L. It has been shown by other authors (41,42) that a bricklike cell arrangement can increase θ_L, but those studies lacked a detailed explanation of why this would be the case. This study provides a systematic insight and explains this mechanism, showing that the 2D effects present in planar wave propagation cannot be taken into account by one-dimensional models (Fig. 7). High lateral g_GJ can stabilize θ_L against uncoupling (Figs. 6 and 7) and can balance out inhomogeneities on a microscopic and a macroscopic scale, decreasing activation time (Fig. 8). Therefore, GJ lateralization may be a compensating mechanism in cardiac disease, which is often accompanied by increased inhomogeneity, e.g., due to fibrosis (29). However, there may also be negative effects of increased lateral g_GJ. As indicated by Fig. 9, the susceptibility to conduction block at tissue expansion becomes significantly higher, as do the effects of reduced g_Na. Cx lateralization with constant g_GJ decreased θ_L slightly and increased θ_T by up to 30%, in accordance with other studies (28), but also allowed much higher θ_T (Fig. 6). The question remains whether lateralized Cx increases lateral g_GJ. Experimental data show that Cx43 lateralization coincides with enhanced θ_T in human atria (Fig. 2), giving a rationale for the simulations. However, the findings discussed here refer to ventricular hypertrophy. In vivo, hypertrophy is often accompanied by fibrosis, with collagen separating lateral cell strands, reducing θ_T (29), i.e., θ_T can hardly be used as an indicator of lateral g_GJ in hypertrophied ventricles. However, fibrotic strands are not evenly distributed, i.e., areas showing the changes obtained from simulations of high lateral g_GJ may be adjacent to areas with transverse uncoupling.

Conclusions

The g_GJ/C_cell ratio and the cell shape can be more important than absolute values, indicating a lack of experimental data regarding the combination of geometrical and functional measurements, because there are very few data on the functionality of lateralized Cx and on specific alterations of cell size, shape, and g_GJ in cardiac diseases. This study required several assumptions. Some effects of increased cell size and GJ lateralization found in this study, e.g., the higher risk of conduction block in wide cells and cells with GJ lateralization, as well as the faster decline of θ_L in wide cells, are proarrhythmic. It is important to note that cardiac diseases often coincide with altered transmembrane currents (7–9,43), higher degrees of inhomogeneity, and fibrosis (29,44–46), which may further increase the risk of arrhythmia. Taking this into account together with cell-size effects could be the subject of further studies.