Abstract
Single-molecule FRET (smFRET) has long been used as a molecular ruler for the study of biology on the nanoscale (∼2–10 nm); smFRET in total-internal reflection fluorescence (TIRF) Förster resonance energy transfer (TIRF-FRET) microscopy allows multiple biomolecules to be simultaneously studied with high temporal and spatial resolution. To operate at the limits of resolution of the technique, it is essential to investigate and rigorously quantify the major sources of noise and error; we used theoretical predictions, simulations, advanced image analysis, and detailed characterization of DNA standards to quantify the limits of TIRF-FRET resolution. We present a theoretical description of the major sources of noise, which was in excellent agreement with results for short-timescale smFRET measurements (<200 ms) on individual molecules (as opposed to measurements on an ensemble of single molecules). For longer timescales (>200 ms) on individual molecules, and for FRET distributions obtained from an ensemble of single molecules, we observed significant broadening beyond theoretical predictions; we investigated the causes of this broadening. For measurements on individual molecules, analysis of the experimental noise allows us to predict a maximum resolution of a FRET change of 0.08 with 20-ms temporal resolution, sufficient to directly resolve distance differences equivalent to one DNA basepair separation (0.34 nm). For measurements on ensembles of single molecules, we demonstrate resolution of distance differences of one basepair with 1000-ms temporal resolution, and differences of two basepairs with 80-ms temporal resolution. Our work paves the way for ultra-high-resolution TIRF-FRET studies on many biomolecules, including DNA processing machinery (DNA and RNA polymerases, helicases, etc.), the mechanisms of which are often characterized by distance changes on the scale of one DNA basepair.
Introduction
Biological systems studied by single-molecule FRET (smFRET) are often characterized by distance changes at the nanometer scale. In DNA replication and transcription, for example, the characteristic distance scale is one DNA basepair (1 bp), just 0.34 nm (1). Because the resolution of smFRET is fundamentally determined by the noise and error on the measurement, a complete understanding of all major sources of heterogeneity and error is required for studies at this scale.
A fundamental advantage of smFRET is the ability to resolve sample heterogeneity. A sample may contain static heterogeneity, i.e., differences between molecules within the sample (e.g., the sample may contain a mixture of distinct, noninterconverting species), or dynamic heterogeneity, i.e., time-dependent changes of individual molecules (e.g., conformational changes). In addition to these heterogeneity sources related to biomolecular function, the resolution of measurements is limited by heterogeneity introduced by experimental noise and error, which must be carefully investigated to accurately quantify smFRET resolution.
Total internal reflection fluorescence (TIRF) microscopy, combined with smFRET (TIRF-FRET, hereafter tFRET), allows multiple surface-immobilized molecules to be imaged simultaneously, allowing static and dynamic heterogeneity to be monitored in complex systems. To characterize the limits of spatial and temporal resolution in tFRET, we require theoretical predictions for heterogeneity and robust experimental characterization of the technique using well-understood standards. Although such characterization has been reported for confocal smFRET (2–7), to our knowledge this has never been reported for tFRET: a significant omission given the general importance of the method.
A tFRET measurement involves acquisition of a sequence of images of surface-immobilized molecules (8), followed by extraction of FRET data by image analysis. This imaging step adds complexity to the analysis and theoretical description of smFRET heterogeneity compared to diffusion-based smFRET or surface-immobilized confocal smFRET measurements, but careful designing and testing of custom-built analysis software allowed us to minimize the effects of these complications.
Building on previous work (2–4,9,10), we derived a theoretical description of the heterogeneity expected on a tFRET measurement for a homogeneous, static sample (heterogeneity due to experimental sources of noise). We compared predictions against simulations and experimental data, considering results for static and dynamic heterogeneity separately (we term these analysis methods “dynamic heterogeneity analysis” and “static heterogeneity analysis”, respectively). We then characterized the current limits of spatial and temporal resolution of tFRET. Our analysis paves the way for measurement of molecular dynamics within immobilized molecules at timescales inaccessible to dwell time analysis and for design of experiments involving multiple static or molecular subpopulations.
Theory
For a surface-immobilized molecule with constant donor-acceptor separation excited at constant intensity, the donor and acceptor fluorescence photon counts are well approximated by independent Poisson distributions (4), with the ratio of the mean acceptor to the sum of donor and acceptor photon counts determined by the accurate (i.e., true) FRET efficiency,
| (1) |
where RDA is the donor-acceptor separation and R0 is the Förster radius (usually ∼5–7 nm (11)).
Emitted photons are collected and focused onto an electron-multiplying charge-coupled device (emCCD) camera (12), producing two images containing the point spread functions (PSFs) of immobilized molecules in the donor and acceptor emission channels. We measure the photon counts from the molecular PSFs in the donor and acceptor emission channels, and calculate the apparent FRET efficiency,
| (2) |
where D, A, and N are the donor, acceptor, and total photon counts, respectively. E reports on the separation of the donor-acceptor pair and can be related to ET upon application of correction factors (8,13). Although derivations presented here are for apparent (uncorrected) FRET, the same expressions hold for accurate FRET ET on substitution of corrected photon counts and variances.
We measure the acceptor photon count upon direct acceptor excitation (AA) via alternating laser excitation (14–16), and calculate the stoichiometry S,
| (3) |
We use S and AA to select exclusively molecules labeled with one donor and one acceptor, and to monitor photophysical fluctuations of either fluorophore.
We derived predictions for heterogeneity on a static homogeneous sample with mean FRET, E0, in the presence of the heterogeneity sources inherent to a tFRET measurement: shot noise from stochastic photon emission (12), background photons and noise due to the electron-multiplying gain register (17), read-out noise (12), dark noise (12), and noise due to finite spatial resolution of the camera (pixelation effects) (9,10,18). We use the standard deviation σ(E) of the observed FRET distribution as the metric for measurement of heterogeneity. Building upon previous work (2,4,5,9,10), we derived expressions for limiting heterogeneity in a tFRET measurement based on χ2-minimization. For data distributed independently and normally about their true values (a reasonable assumption for a sample with constant donor-acceptor separation (4)), this approach is the maximum-likelihood method (19), and resulting predictions are approximately the optimal signal/noise achievable in a measurement.
We modeled the molecular PSF in each channel as a circular two-dimensional Gaussian (9),
| (4) |
| (5) |
where (i,j) are the pixel coordinates; (x0, y0) is the position of the molecule; Dij, D, and Aij, A are the photon counts for a single pixel and for the entire PSF, in the donor and acceptor channels respectively; sD and sA are the widths of the PSF in the donor and acceptor channel; and BD and BA are the expected background levels in the donor and acceptor channels.
We performed χ2-minimization (9,10) in the donor and acceptor channels for Eqs. 4 and 5, and performed error propagation (5,20) for Eq. 2, to obtain an expression for σ(E) (see the Supporting Material). (For the full theoretical prediction, see Eq. S21 and Eq. S22 in the Supporting Material.)
Assuming that, where the magnitudes of shot noise and background noise are similar, σ(E) is well approximated by interpolation between the separate results for high photon counts and high background, and neglecting pixilation effects (9), we obtained an analytic expression for σ(E),
| (6) |
where E0 is the mean apparent FRET value; bD and bA are the observed standard deviations (photons per pixel) of the background noise in each channel; a is the pixel size; and fG is the excess noise factor (), accounting for noise introduced by the emCCD (17).
We also derived predictions of σ(E) for aperture photometry, a commonly used photon-counting method (8,21–23), wherein a small aperture is placed around a molecule, and the total within-aperture photon count is measured. Pixels outside the aperture are used to measure local background. The prediction for limiting heterogeneity using aperture photometry is given by Eq. S22 in the Supporting Material. An investigation of the photon-counting accuracy of different photon-counting methods is included in the Supporting Material.
Materials and Methods
DNA
We used dsDNA FRET standards labeled with a donor fluorophore, Cy3B (GE Healthcare, Little Chalfont Buckinghamshire, UK) and acceptor fluorophore, ATTO647N (ATTO-TEC, Hannover, Germany) (see Fig. 1 and see sequences in the Supporting Material). The ssDNAs were prepared by automated synthesis (IBA, Munich, Germany), labeled with fluorophores, and purified using denaturing polyacrylamide gel electrophoresis. The ssDNAs were annealed to produce final dsDNAs. Labeling at the 5′ end was to a 5′-amino-C6; internal labeling was to an amino-modified-dT.
Figure 1.
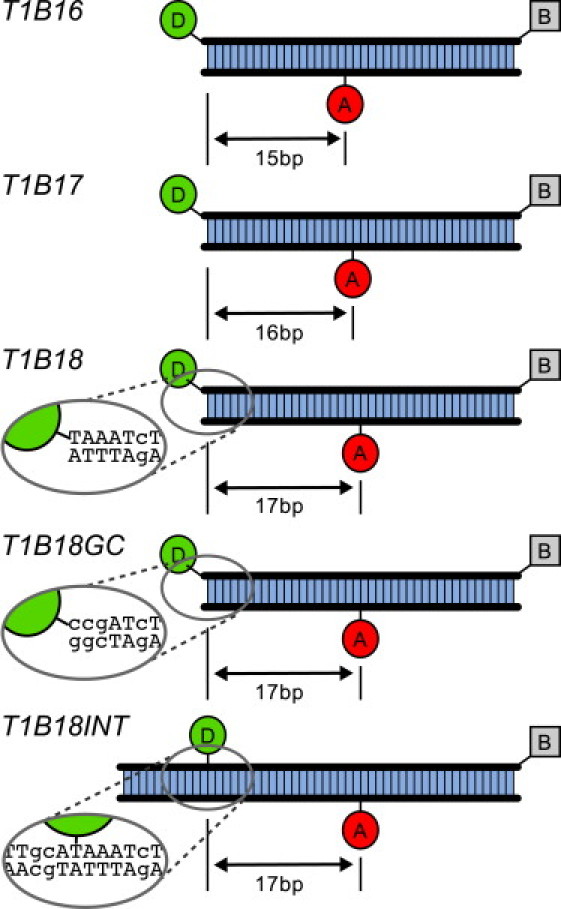
DNA FRET standards used for heterogeneity analysis. D, donor fluorophore; A, Acceptor fluorophore; B, biotin. T1B16, T1B17, T1B18: 15-, 16-, and 17-bp donor-acceptor separation, respectively, with an end-labeled donor, and an internally labeled acceptor. T1B18GC: 17-bp donor-acceptor separation, sequence adjacent to donor changed to CCG, as shown. T1B18INT: 17-bp donor-acceptor separation, internally labeled donor, modified sequence as shown. Full sequences included in the Supporting Material.
smFRET data acquisition
Our experimental apparatus has been previously reported (24) and is presented in detail in the Supporting Material. Briefly, an objective-type TIRF microscope (24) was used to excite surface-immobilized dsDNAs at 532 nm (donor excitation) and 635 nm (acceptor excitation), using alternating laser excitation (14). Fluorescence emission was imaged using an emCCD camera (Andor Technologies, Belfast, Northern Ireland), with pixel size measured as 94 nm. A motorized xy-scanning stage (MS-2000; ASI Imaging, Vista, CA) was used to control the coverslip position relative to the objective.
Simulations
Monte Carlo simulations of surface-immobilized fluorescent molecules included the effects of shot noise, electron-multiplying gain, digitization noise, pixelation noise, and Gaussian background noise. For results in the main text, we simulated isolated immobilized molecules, neglecting complications due to random PSF overlap. This approximation is supported by results presented in the Supporting Material for multiple randomly distributed surface-immobilized molecules, which showed that our filtering algorithm (discussed below) is effective at excluding the effects of PSF overlap. Simulated PSFs were modeled as circular two-dimensional Gaussian PSFs (Eqs. 4 and 5). For comparison to theory, mean background level photons and background noise photons was used in both channels; and sD and sA were 132 nm and 150 nm, respectively, matching typical experimental values. For comparison to experiment, all simulation parameters were chosen to match the experimentally observed mean values for each dataset.
Data analysis: image analysis
Image analysis was carried out using custom-built software (see the Supporting Material; this software will be released to the community). Briefly, molecules were automatically identified by convolution of an averaged image of the first five recorded frames with a Gaussian kernel, and selection of above threshold pixels (18,25). Photon counts in each channel were measured by fitting molecular PSFs with an elliptical two-dimensional Gaussian (26),
| (7) |
where Mij and M indicate the expected photon count for a single pixel and for the entire PSF, respectively; and BM is the expected background level. The values y′ and x′ are the pixel coordinates in the coordinate system aligned to the major axis,
and the minor axis,
of observed elliptical PSF, where (x0,y0) is the expected position of the molecule, (i,j) are the pixel coordinates, and θ is the angle between the (i,j) and (x′,y′) coordinate systems. The values sy and sx are the PSF widths along each elliptical axis. Recent work (27) showed that fitting to molecular PSFs using a Gaussian model ignores ∼40% of a PSF's photons, mainly those contained in its power-law tail, which is ignored or treated as background by the Gaussian model. However, the Gaussian model is still appropriate for FRET measurements because the mean of the FRET ratio is unaffected by the addition of a fixed fraction to the photon counts. Equation 6 remains valid as an estimator of FRET heterogeneity for Gaussian profile fitting, but in principle, if the 40% extra photons could be measured and included in the photon count entirely uncontaminated by real background (a nontrivial task), this ideal situation could reduce observed FRET heterogeneity by 20% (H. Flyvbjerg, Technical University of Denmark, personal communication, 2010).
Fitting was carried out by ordinary-least-squares (OLS) minimization (28), i.e., by minimizing,
| (8) |
where mij is the observed photon count and Eq. 7 defines Mij.
The apparent FRET E and the stoichiometry S were calculated (Eqs. 2 and 3). Only molecules detected in both emission channels (indicating the presence of a single donor and acceptor) were included in the analysis. Molecules with close nearest-neighbors were excluded from the analysis. Data were filtered on a per-frame basis to exclude molecules too dim, too bright, or with large eccentricity (i.e., a very asymmetric PSF; see Eq. S23 in the Supporting Material) to minimize errors introduced by overlapping PSFs.
Data analysis: heterogeneity analysis
We separately performed two types of analysis: heterogeneity analysis on the distributions of individual molecules, which we term “dynamic heterogeneity analysis”, and heterogeneity analysis on the combined distributions of many molecules, which we term “static heterogeneity analysis”. Both include intrinsic heterogeneity due to photon-counting shot noise and background noise (determined by Eq. 6). In addition to intrinsic heterogeneity, dynamic heterogeneity is sensitive to conformational changes of individual molecules, whereas static heterogeneity is sensitive to constant differences between individual molecules; these latter heterogeneity sources are typically of interest in terms of biomolecular function. Any additional heterogeneity must arise from unexpected experimental noise or error, which we term excess heterogeneity. In particular, because we expect our dsDNA standards to be static and homogeneous, any heterogeneity larger than intrinsic heterogeneity may be identified as excess heterogeneity.
For dynamic heterogeneity analysis, it is important to separate the timescales at which different sources of heterogeneity are significant. To achieve this, we calculated the standard deviation of the difference series (9), formally known as the Allan deviation (29),
| (9) |
where i indicates the index in an n data-point time-series. This time-series metric is standard in metrology (29,30) and is now finding use in biophysics (31,32) because, unlike the standard deviation, σAD is sensitive only to noise sources on the timescale of the integration time for a measurement, and not to longer timescale variations. To test for the presence of longer timescale variations, we simply recalculated the Allan variance after increasing the integration time post hoc by software binning (32). Additionally, in the presence of drifts (i.e., any time-correlated variation in mean value), the conventional standard deviation is rather counterintuitively dependent on the duration of the measurement, whereas the Allan deviation is not (29). In the absence of drifts, the Allan deviation converges exactly to the conventional standard deviation (29).
For static heterogeneity analysis, because it is not possible to calculate the Allan deviation when combining data from multiple molecules, we calculated the standard deviation from the fit of a one-dimensional Gaussian to the combined histogram of the data.
For heterogeneity analysis of simulated data, the mean and standard deviation was calculated directly from the raw data rather than from a fit to the data. Errors on measurements in all cases represent the standard error on the mean.
Results and Discussion
Simulations
To test the validity of our theoretical heterogeneity predictions, we compared them to heterogeneity seen in simulated data (Fig. 2). For the simplest case where only shot noise is included, FRET heterogeneity decreases as for increasing photon count N (see Fig. 2 A, black line). The heterogeneity has a parabolic dependence on mean FRET, E0, reaching a maximum at E0 = 0.5 and decreasing for lower or higher FRET (see Fig. 2 B, black line). If we include background noise in the predictions, we see similar behavior, except that heterogeneity is significantly increased for low photon counts (21% for E0 = 0.5, N = 390 photons) or extreme FRET values (27% for E0 = 0.1, N = 2000 photons), demonstrating the importance of incorporating background noise into predictions (see Fig. 2, A and B, red line).
Figure 2.
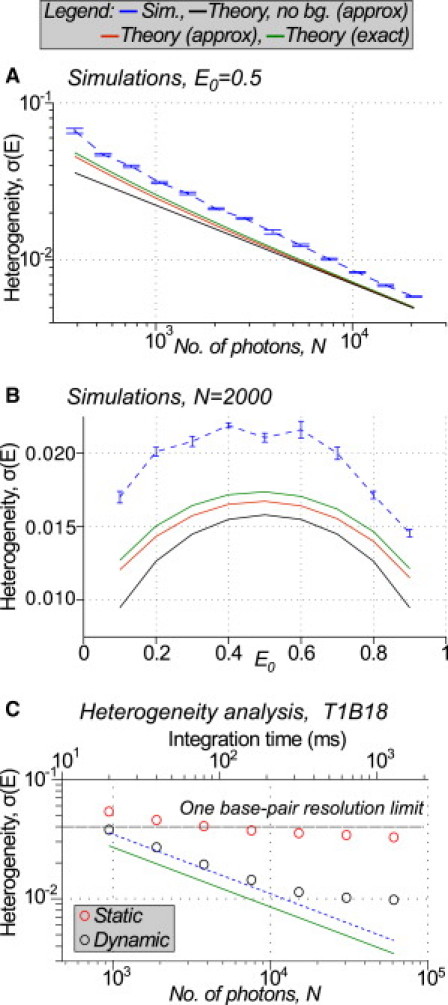
(A and B) Simulated datasets (blue line, simulation) compared to theoretical predictions for a wide range of number of collected photons N (A) and mean FRET efficiencies E0 (B). Theoretical predictions presented for numerical integration of full theoretical prediction (theory (exact), green line); for analytic result, Eq. 6, with approximations discussed in main text (theory (approximate), red line); and for analytic result, neglecting background noise in the prediction (theory, no background (approximate), black line). Results in panel A for E0 = 0.50, results in panel B for N = 2000 photons per molecule per frame. (C) Heterogeneity analysis for 17-bp donor-acceptor separation dsDNA (T1B18, E0 = 0.45). Results of dynamic heterogeneity analysis (dynamic, black circles) and static heterogeneity analysis (static, red circles) compared to predictions from simulation (blue dashed line) and theory (green line). Heterogeneity σ < 0.04 is required for 1-bp resolution (see text). Integration time at acquisition was 20 ms; duration of each measurement, 20 s. Each data point combines results for all molecules observed for >5 frames at that integration time in a 648-molecule dataset from 18 combined FOVs. Simulation parameters matched experimentally observed values at the original 20 ms integration time. Simulation values for longer integration times, τ, were calculated as .
We tested the validity of the assumptions made in derivation of Eq. 6 (see Theory) by performing numerical integration of Eq. S10 and Eq. S11 from the Supporting Material (see Fig. 2, A and B, green line). The numerical predictions are only 6% larger than those from Eq. 6 at low photon counts (E0 = 0.5, N = 390 photons), becoming negligible for large photon counts, showing that Eq. 6 is an acceptable approximation in most cases. For accuracy, we compared subsequent experimental results with the numerical expression.
Simulations showed good agreement with theoretical predictions for all values of FRET and photon counts, even outside the linear range of FRET (see Fig. 2, A and B, blue dashed line); however, the simulations showed constant ∼30% excess heterogeneity. This arises because the PSF fitting algorithm used (OLS minimization) does not account for shot noise in the image, but assumes constant Gaussian background noise only (9,27) (see the Supporting Material). This excess heterogeneity is not a serious issue for the analysis of experimental data; to verify that our experimental results agreed with the theoretical description of the system, we simply compared observed heterogeneity to predictions based on simulation rather than theory alone, thereby incorporating excess fitting heterogeneity into our predictions.
Heterogeneity analysis of dsDNA FRET standards
Dynamic heterogeneity analysis
To test whether dynamic heterogeneity present on individual static molecules (with constant donor-acceptor separation) was consistent with theory, we carried out dynamic heterogeneity analysis for 648 dsDNA molecules labeled with donor and acceptor at 17-bp separation (T1B18 standard, E0 = 0.45; see Fig. 2 C, black circles). When the integration time (and thus photon count per molecule per frame) is increased by post hoc software binning, dynamic heterogeneity decreases, eventually leveling off toward σAD(E) = 0.01. Consistent with results in Fig. 2, A and B, both experimental results and simulations (see Fig. 2 C, black circles and blue dashed line, respectively) showed excess heterogeneity of 30% compared to theory (due to noise introduced by the OLS fitting algorithm).
For timescales below 200 ms, we observed good agreement between experimental data and simulation (from 6% excess heterogeneity at 20 ms up to 14% excess heterogeneity at 160 ms), validating our description of the major sources of heterogeneity affecting a static sample on short timescales. Furthermore, our results confirm that for timescales between 20 and 200 ms, doubly labeled dsDNA indeed behaves as a static FRET standard, with measured heterogeneity arising solely from shot noise, background noise, and the OLS algorithm, rather than dynamic fluctuations of the dsDNA or of the fluorophores (previously a topic of some debate (2,3,7)).
Above 200 ms, we observed significantly excess heterogeneity compared to simulations (see Fig. 2 C; black circles deviate from blue dashed line, 27% excess heterogeneity at 320 ms, increasing to 119% excess heterogeneity at 1280 ms). We investigated the source of this heterogeneity by analyzing and manually classifying the individual fluorescence trajectories of all molecules in the dataset (Fig. 3). Of the 648 molecules, 119 contained too few frames for analysis of dynamics at the longest integration times and were excluded from analysis. The remaining molecules appeared to be separated into three distinct subpopulations (Fig. 3).
Figure 3.
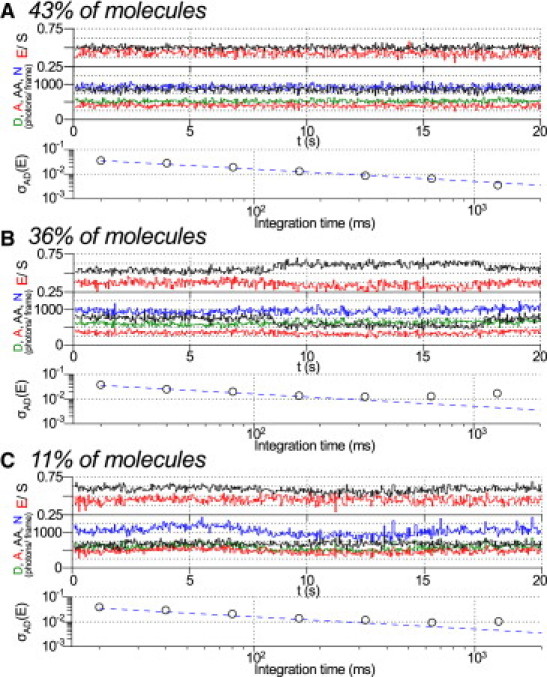
Excess dynamic heterogeneity investigated by manual analysis and classification of molecular subpopulations. Example of single-molecule time-traces from 648-molecule dataset used for heterogeneity analysis (T1B18, Fig. 2C). A set of 119 molecules with too few above-threshold frames were excluded from manual analysis. (Top) Apparent FRET (E, red line) and stoichiometry (S, black line). (Middle) D, donor excitation donor emission (green); A, donor excitation acceptor emission (red); AA, acceptor excitation acceptor emission (black); and total emission during donor excitation, N, (cyan). (Bottom) Observed Allan deviation, σAD (black circles); predictions from simulation (blue dashed line). (A) A set of 227 molecules (43%) show stable fluorescence, FRET, and stoichiometry for the duration of the measurement. (B) A set of 191 molecules (36%) show steplike E fluctuations with a corresponding sharp change in AA emission and without a corresponding change in N emission, characteristic of acceptor photophysics. (C) A set of 58 molecules (11%) show slow E fluctuations with corresponding slow change in total emission intensity under donor excitation, characteristic of focal drift. Fifty-three molecules (10%) could not be clearly classified into any of the three populations.
The major population (Fig. 3 A; 227 molecules, 43%), showed steady FRET, stoichiometry, and fluorescence intensities for the entire measurement, resulting in small excess heterogeneity for all measured integration times (Fig. 3 A). A second population (Fig. 3 B; 191 molecules, 36%), showed steplike fluctuations in FRET coincident with significant changes in stoichiometry and acceptor photon count upon acceptor excitation, but without changes in total photon count under donor excitation. This resulted in large excess heterogeneity for integration times >200 ms. A third population (Fig. 3 C; 58 molecules, 11%), showed slow fluctuations in FRET and total photon count under donor excitation, again resulting in large excess heterogeneity for integration times >200 ms. Finally, 53 molecules (10%) could not be clearly classified into any of the three populations.
The first population is consistent with static molecules, with heterogeneity as predicted by theory. The second population most likely arises from stochastic photophysical fluctuations in quantum yield and emission or absorption spectra of the acceptor, resulting in a transient change in R0 for the FRET pair (7). The first and second populations likely reflect two snapshots of the same underlying population; if the first population were observed for sufficient duration, we expect that stochastic photophysical fluctuations would have been observed. These results establish that acceptor photophysics is the major limiting factor on FRET resolution at long timescales (>200 ms) for the FRET pair used in this study.
The most likely source of the third population, which showed slow fluctuations in FRET and fluorescence intensity, is focal drift (variation in the distance between the coverslip and the objective lens). Although raw images do not show visually detectable focal drift, intensity fluctuations are correlated for a significant minority of the molecules within affected movies (e.g., 13 of 42 molecules for the movie presented in Fig. S1 in the Supporting Material). The fact that intensity fluctuations are not observed for all the molecules within affected movies excludes laser power fluctuations as the source of this behavior. For a stable measurement apparatus and acquisition times of 20 s, the fraction of molecules affected by focal drift was relatively small (10%), but clearly, focal drift is a significant potential source of excess dynamic heterogeneity for timescales >200 ms.
Static heterogeneity analysis
To investigate the static heterogeneity present within ensembles of molecules, we carried out static heterogeneity analysis on the same dataset analyzed via dynamic heterogeneity analysis. Static heterogeneity analysis revealed large excess heterogeneity compared with simulations (see Fig. 2 C; red circles deviate from blue dashed line, from 50% at 20 ms to 634% at 1280 ms). We considered four possible sources of static heterogeneity to explain these deviations:
-
1.
Intrinsic heterogeneity, which we use to describe the dynamic heterogeneity on an individual molecule, which largely agreed with theoretical predictions.
-
2.
Location-dependent heterogeneity, i.e., heterogeneity across the field of view (FOV), e.g., due to chromatic aberration or image distortion.
-
3.
Focal drift on combination of data from multiple fields of view, due to stage drift and manual refocusing between acquisitions of images for each FOV.
-
4.
Intermolecular heterogeneity, i.e., differences between individual molecules which remained constant over the duration of the measurement.
To measure the magnitude of the different heterogeneity sources, we carried out static heterogeneity analysis on ensembles of molecules subject to different combinations of static heterogeneity (Fig. 4). We first measured the heterogeneity on a single individual molecule in a single position on the FOV (see Fig. 4 A, single position, σA), which should reflect only intrinsic heterogeneity. We next measured the heterogeneity on an individual molecule moved to multiple different positions within the FOV using an xy-scanning stage (see Fig. 4 A, multiple positions, σB) which should include intrinsic heterogeneity, location-dependent heterogeneity, and focal drift. We also measured the heterogeneity for multiple different molecules in a single FOV (see Fig. 4 A, multiple molecules, σC) which should include intrinsic heterogeneity, location-dependent heterogeneity, and intermolecular heterogeneity. Finally, the heterogeneity on multiple molecules in multiple FOVs was measured (see Fig. 4 A, multiple FOV, σD), which should include all four heterogeneity sources.
Figure 4.
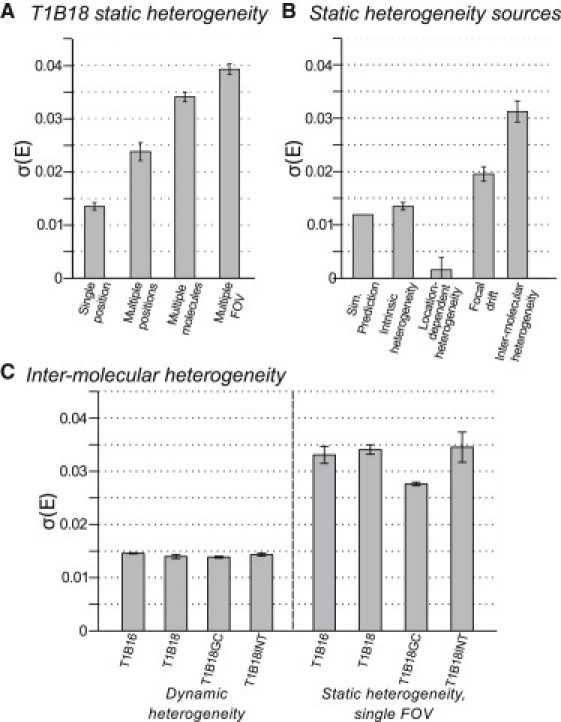
Sources of static heterogeneity. (A) Sources of static heterogeneity on T1B18 dsDNA standard probed in the presence of different heterogeneity sources. Single position: static heterogeneity on a single molecule in a single position on the FOV. Multiple positions: single molecule moved between multiple different positions on the field of view (FOV) using a scanning stage. Multiple molecules: multiple molecules from a single FOV only. Multiple FOV: multiple molecules from multiple FOVs. Measurement parameters: Integration time, 100 ms; duration of measurement, 5 s; 80 photons/ms per molecule. Results for multiple molecules and multiple FOV from three separately prepared samples, >400 molecules per sample, ∼20 FOV per sample. Results for single position and multiple positions are from 19 molecules, each measured for 5 s in ≥4 different positions within an area of ∼1 FOV, yielding in total 84 distinct, randomly distributed positions across the FOV. This dataset is necessarily small, because only molecules within a small area could be used, and all molecules retained in the analysis were excited for >20 s without bleaching. (B) Magnitudes of static heterogeneity sources calculated using results from panel A. (C) Intermolecular heterogeneity investigated using dsDNA FRET standards shown in Fig. 1. Measurement parameters: Integration time, 100 ms; duration of measurement, 5 s; 80 photons/ms per molecule; three sample repeats for each measurement; >20 FOV per sample; >190 molecules per sample.
Assuming linear addition of the variances (20), we extracted estimates for the magnitude of the individual heterogeneity sources using the simple model of
| (10) |
| (11) |
| (12) |
| (13) |
where σA, σB, σC, and σD are the measured heterogeneities, as above, and σI, σL, σF, and σM are the heterogeneity sources: intrinsic heterogeneity, location-dependent heterogeneity, focal drift, and intermolecular heterogeneity, respectively. Solving this model yields estimates for the contribution of each heterogeneity source (Fig. 4 B):
-
1.
Intrinsic heterogeneity, σI = 0.0135 ± 0.0007;
-
2.
Location-dependent heterogeneity, σL = 0.0016 ± 0.0023;
-
3.
Focal drift, σF = 0.0195 ± 0.0013;
-
4.
Intermolecular heterogeneity, σM = 0.031 ± 0.002.
Intrinsic static heterogeneity is close to predictions from simulations (σsim = 0.0119), consistent with the results of dynamic heterogeneity analysis. Intermolecular heterogeneity was the largest heterogeneity source, with focal drift also being significant. Location-dependent heterogeneity was not observed, even though some image distortion was visibly present.
Intermolecular heterogeneity very likely arises due to the slowly-interconverting photophysically distinct states of the acceptor (6,7), or possibly from slow fluctuations in donor-acceptor separation, e.g., due to DNA-fluorophore interactions (33). We investigated whether intermolecular heterogeneity was specific to the DNA sequence, FRET values, or fluorophore local environment of the sample using four different dsDNA standards (Fig. 1). All four samples showed near identical dynamic heterogeneity (Fig. 4 C). Three of the samples (T1B18, T1B16, and T1B18INT) showed similar static heterogeneity, measured for a single FOV to exclude focal drift (σ = 0.0341 ± 0.0009, 0.0331 ± 0.0016, and 0.0345 ± 0.0002, respectively). In contrast, the sample with a more GC-rich local environment in the region of the donor (T1B18GC) showed a statistically significant reduction in noise (σ = 0.0276 ± 0.0003). Although the source of this difference is unclear, all the samples showed very similar low steady-state anisotropies (0.15–0.22; see Table S1 in the Supporting Material), insufficient to indicate restricted rotational freedom on timescales resolvable by tFRET measurements (34). Additionally, the variation on total photon count upon donor excitation (D) and acceptor photon count upon acceptor excitation (AA) for the different samples was small compared to the error on the measurements, suggesting that sample-specific reduction of donor quantum yield (quenching), or acceptor photophysics, are not responsible for the reduction in heterogeneity.
Photophysical fluctuations caused a much larger increase in static heterogeneity than dynamic heterogeneity, indicating that the ensemble and single molecule averages of this process are not equivalent; this is likely an example of nonergodicity on the timescale of observation (35). Our results also show that recent efforts to reduce static heterogeneity via accurate FRET correction on a single-molecule basis (36) may indeed reduce the effects of a major broadening source (focal drift); however, this approach cannot reduce the largest broadening source, i.e., intermolecular, position-independent heterogeneity (due to photophysics).
Defining the limits of resolution
To quantify the current practical limits of tFRET spatial resolution, we compared the observed experimental resolution (Fig. 2 C) with the resolution required to resolve a 1-bp distance difference. After measuring the Förster radius, R0, for Cy3B-A647N on dsDNA as 6.2 nm (11), we estimated that a distance difference equivalent to a 1-bp step (0.34 nm) corresponded to a FRET difference of ΔE = 0.08 in the range of maximum FRET resolution (0.4 ≲ E ≲ 0.6) for this pair. Using a Rayleigh-limit approximation (37), ΔEmin ∼ 2σ(E), we obtained a limit on the FRET resolution required to resolve a single basepair step: σ1bp(E) < 0.04.
For studies of dynamic heterogeneity, σ1bp(E) < 0.04 is observed even at an integration time of 20 ms (60 photons/ms per molecule) (see Fig. 2 C, black circles), showing that 1-bp resolution is possible for measurements of dynamic heterogeneity even at very short integration times and moderate photon counts.
For studies of static heterogeneity, greater excess heterogeneity places 1-bp resolution on the limit of our measurement capability (see Fig. 2 C, red circles). To investigate whether we could achieve this resolution, we prepared a mixture of two static dsDNA samples with a D-A separation of 15 bp (T1B16; see Fig. 5 A, top, E0 = 0.53 when measured alone) and 16-bp (T1B17; see Fig. 5 A, middle, E0 = 0.47 when measured alone). We maximized resolution by using software binning to extend integration time to 1000 ms and by sampling a large number of molecules (1236 molecules).This revealed a main peak at E = 0.47 and a secondary peak at E = 0.53 (Fig. 5 A, bottom), matching the positions of the peaks for the pure T1B17 and T1B16 samples, respectively. However, the separation of the two peaks is clearly at the limit of resolution of the measurement; we conclude that 1-bp resolution represents a best-case for static heterogeneity studies, at the limit of current experimental capabilities.
Figure 5.
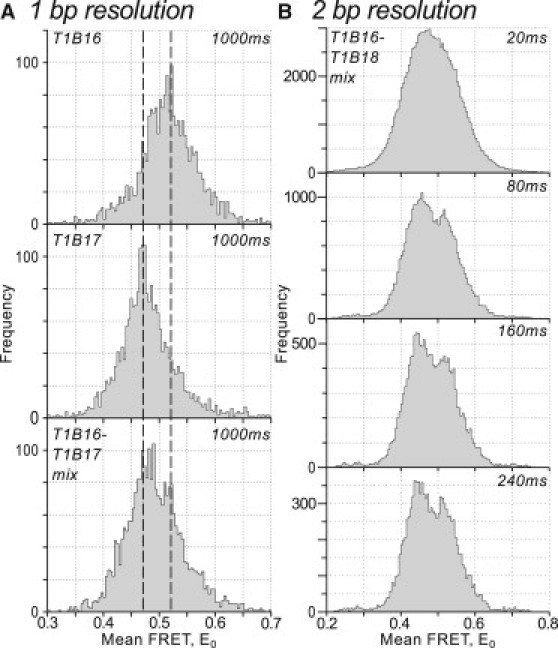
High-resolution static heterogeneity analysis. (A) One-basepair resolution with 1000-ms time resolution. Measured FRET distributions for dsDNA with 15-bp (T1B16) and 16-bp (T1B17) donor-acceptor separation, and for an equimolar mixture of each (T1B16-T1B17 mix). (B) Two-basepair resolution with 80-ms time resolution. Measured FRET distribution at increasing integration times for an equimolar mixture of dsDNA with 15-bp and 17-bp D-A separation (T1B16-T1B18 mix). Measurement parameters, 1-bp data: integration time at acquisition, 100 ms; duration of measurement, 5 s; ∼50 photons/ms per molecule; >1200 molecules; ∼45 combined FOV. Measurement parameters, 2-bp data: integration time at acquisition, 20 ms; duration of measurement, 20 s; 55 photons/ms per molecule; 335 molecules; 11 combined FOV.
To test the minimum distance difference which could be unambiguously resolved, we prepared a mixture of dsDNA standards with a 2-bp distance difference, using dsDNAs with a separation of 15 bp (T1B16; E0 = 0.53) and 17 bp (T1B18; E0 = 0.45) (Fig. 5 B). We analyzed the observed FRET distributions for the presence of peaks at these E0 values, acquiring data at 20-ms integration time, using software binning to analyze longer integration times. At 20 ms, the two species were not resolved; however, on increasing the integration time to 80 ms (55 photons/ms per molecule) we could clearly resolve the two species, demonstrating clear 2-bp spatial resolution with high temporal resolution. Increasing the integration time to 160 ms and 240 ms further increased resolution.
The resolution limits which we report should be achievable on any apparatus with similar photon detection rates and focal stability to those we reported, using gel-purified dsDNA standards and the Cy3B-ATTO647N FRET pair.
Conclusions
Despite the importance and popularity of tFRET, a theoretical and experimental characterization of the limits of resolution of the technique has not been previously reported. This is a significant omission, particularly for the ultra-high-resolution studies required for the study of DNA processing machinery such as polymerases and helicases. To address this, we derived a theoretical description of the maximum signal/noise achievable for a tFRET measurement, and observed good agreement among theory, simulation, and experimental measurements of dynamic heterogeneity at short timescales (<200 ms). Significant excess heterogeneity was observed for dynamic heterogeneity analysis at long timescales (>200 ms) and for static heterogeneity analysis over all timescales measured. In both cases, the excess heterogeneity was identified as arising primarily from acceptor photophysics, with focal drift also being significant. Excess static heterogeneity was also dependent on dsDNA sequence adjacent to the donor fluorophore, which merits further investigation.
We quantified the current limits of tFRET resolution. For studies of dynamic heterogeneity, e.g., conformational changes of individual molecules, we can clearly achieve 1-bp resolution for short integration times (20 ms, 60 photons/ms per molecule). Results using switchable FRET (38), a method that allows monitoring of two FRET efficiencies and corresponding distances within one molecule, have already demonstrated this capability (S. Uphoff, S .J. Holden, and A. N. Kapanidis, unpublished). For studies of static heterogeneity, i.e., resolution of multiple species within a single sample, we established that 2-bp resolution is possible even at short integration times (80 ms, 55 photons/ms per molecule). Previous FRET measurements of distance changes on the order of 1-bp were either based on analysis of the mean values of FRET histograms (3,39), or exploited the coupling of a small distance change to a larger observable (39,40). Our quantification of FRET resolution for direct measurements will provide a useful reference for experimental design and analysis, and indicates the feasibility of single basepair translocation studies for helicases and DNA/ RNA polymerases via tFRET, consistent with recent reports (39).
Clearly, the exact magnitudes of different excess heterogeneity sources will be unique to the tFRET apparatus, FRET pairs, and imaging buffers of an individual lab. However, for an optimized tFRET apparatus, we expect that acceptor photophysics and focal drift will be the limiting factors for FRET resolution. Importantly, the methods described here can be applied to any surface-immobilization-based smFRET apparatus (including prism-type TIRF and wide-field smFRET) to quantify its performance, and determine its FRET-resolution limit; the magnitude of excess heterogeneity and the dsDNA standards reported here may be used as initial reference standards.
We identified the major limiting factor to FRET resolution as acceptor photophysics, emphasizing the fundamental importance of understanding and controlling fluorophore photophysics, and designing more photostable fluorophores. Focal stability of tFRET apparatus was also a limiting factor to FRET resolution even where focal drift was not visibly apparent on raw images, making high focal stability an important consideration in experimental design, particularly for measurements over extended periods (facilitated by optimized fluorophores and buffers (8,41,42)). Finally, FRET resolution is also limited by the OLS fitting algorithm used for data extraction. At present, the OLS algorithm does not achieve optimal signal/noise, introducing ∼30% excess heterogeneity into measurements. Recent work (27) showed that it should be possible to improve the fitting algorithm by use of maximum-likelihood methods rather than OLS, allowing near-optimal signal/noise to be achieved.
Our results demonstrate that we have a good predictive understanding of tFRET dynamic heterogeneity at short timescales. Conformational changes in biological systems often occur on the timescale of 1–10 ms, currently at the limit of tFRET temporal resolution (at ∼5 ms; S. Uphoff and A. N. Kapanidis, unpublished). Our work paves the way for the extension of probability distribution analysis (2–4,43,44) and burst variance analysis ((43) and J. P. Torella, S. J. Holden, Y. Santoso, J. Hohlbein, and A. N. Kapanidis, unpublished) to tFRET measurements, which should allow analysis of unresolved dynamic heterogeneity at or just below the temporal resolution of the measurement, extending the utility of the technique.
Acknowledgments
We thank J. P. Torella and Y. Santoso for editorial assistance and M. Little for helpful technical discussions.
S.J.H., S.U., J.H, L.L.R., and A.N.K. were supported by a UK Bionanotechnology Informatics Research Center grant No. GR/R45659/01, Engineering and Physical Sciences Research Council grant No. EP/D058775, Biotechnology and Biological Sciences Research Council grant No. BB/H0179SX/1, European Community Seventh Framework Programme grant No. FP7/2007-2013, and Revolutionary Approaches and Devices for Nucleic Acid grant No. HEALTH-F4-2008-201418. S.U. was supported by the German National Academic Foundation, the SAP, and MathWorks. D.Y. was supported by the Wellcome Trust.
Contributor Information
Seamus J. Holden, Email: s.holden1@physics.ox.ac.uk.
Achillefs N. Kapanidis, Email: a.kapanidis1@physics.ox.ac.uk.
Supporting Material
References
- 1.Berg J., Tymoczko J., Stryer L. WH Freeman; New York, NY: 2002. Biochemistry. [Google Scholar]
- 2.Nir E., Michalet X., Weiss S. Shot-noise limited single-molecule FRET histograms: comparison between theory and experiments. J. Phys. Chem. B. 2006;110:22103–22124. doi: 10.1021/jp063483n. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Antonik M., Felekyan S., Seidel C.A.M. Separating structural heterogeneities from stochastic variations in fluorescence resonance energy transfer distributions via photon distribution analysis. J. Phys. Chem. B. 2006;110:6970–6978. doi: 10.1021/jp057257+. [DOI] [PubMed] [Google Scholar]
- 4.Gopich I.V., Szabo A. Single-molecule FRET with diffusion and conformational dynamics. J. Phys. Chem. B. 2007;111:12925–12932. doi: 10.1021/jp075255e. [DOI] [PubMed] [Google Scholar]
- 5.Deniz A.A., Laurence T.A., Weiss S. Ratiometric single-molecule studies of freely diffusing biomolecules. Annu. Rev. Phys. Chem. 2001;52:233–253. doi: 10.1146/annurev.physchem.52.1.233. [DOI] [PubMed] [Google Scholar]
- 6.Chung H.S., Louis J.M., Eaton W.A. Distinguishing between protein dynamics and dye photophysics in single-molecule FRET experiments. Biophys. J. 2010;98:696–706. doi: 10.1016/j.bpj.2009.12.4322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Kalinin S., Sisamakis E., Seidel C.A.M. On the origin of broadening of single-molecule FRET efficiency distributions beyond shot noise limits. J. Phys. Chem. B. 2010;114:6197–6206. doi: 10.1021/jp100025v. [DOI] [PubMed] [Google Scholar]
- 8.Roy R., Hohng S., Ha T. A practical guide to single-molecule FRET. Nat. Methods. 2008;5:507–516. doi: 10.1038/nmeth.1208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Thompson R.E., Larson D.R., Webb W.W. Precise nanometer localization analysis for individual fluorescent probes. Biophys. J. 2002;82:2775–2783. doi: 10.1016/S0006-3495(02)75618-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.King I.R. Accuracy of measurement of star images on a pixel array. Pub. ASP. 1983;95:163–168. [Google Scholar]
- 11.Lakowicz J.R. 2nd Ed. Kluwer Academic/Plenum; New York; London, UK: 1999. Principles of Fluorescence Spectroscopy. [Google Scholar]
- 12.Howell S.B. Cambridge University Press; Cambridge, UK: 2006. Handbook of CCD Astronomy. [Google Scholar]
- 13.Lee N.K., Kapanidis A.N., Weiss S. Accurate FRET measurements within single diffusing biomolecules using alternating-laser excitation. Biophys. J. 2005;88:2939–2953. doi: 10.1529/biophysj.104.054114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Kapanidis A.N., Lee N.K., Weiss S. Fluorescence-aided molecule sorting: analysis of structure and interactions by alternating-laser excitation of single molecules. Proc. Natl. Acad. Sci. USA. 2004;101:8936–8941. doi: 10.1073/pnas.0401690101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Santoso Y., Hwang L.C., Kapanidis A.N. Red light, green light: probing single molecules using alternating-laser excitation. Biochem. Soc. Trans. 2008;036:738–744. doi: 10.1042/BST0360738. [DOI] [PubMed] [Google Scholar]
- 16.Holden S.J., Kapanidis A.N. Single Particle Tracking and Single Molecule Energy Transfer: Applications in the Bio and Nano Sciences. Wiley-VHC; Berlin, Germany: 2009. Alternating-laser excitation and pulsed-interleaved excitation of single molecules; pp. 131–162. [Google Scholar]
- 17.Basden A.G., Haniff C.A., Mackay C.D. Photon counting strategies with low-light-level CCDs. Mon. Not. R. Astron. Soc. 2003;345:985–991. [Google Scholar]
- 18.Irwin M.J. Automatic analysis of crowded fields. Mon. Not. R. Astron. Soc. 1985;214:575–604. [Google Scholar]
- 19.Baker S., Cousins R.D. Clarification of the use of χ-square and likelihood functions in fits to histograms. Nucl. Instrum. Methods. 1984;221:437–442. [Google Scholar]
- 20.Taylor J. University Science Books; Herndon, VA: 1997. An Introduction to Error Analysis: the Study of Uncertainties in Physical Measurements. [Google Scholar]
- 21.Schluesche P., Stelzer G., Meisterernst M. NC2 mobilizes TBP on core promoter TATA boxes. Nat. Struct. Mol. Biol. 2007;14:1196–1201. doi: 10.1038/nsmb1328. [DOI] [PubMed] [Google Scholar]
- 22.Solomatin S.V., Greenfeld M., Herschlag D. Multiple native states reveal persistent ruggedness of an RNA folding landscape. Nature. 2010;463:681–684. doi: 10.1038/nature08717. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Howell S.B. Two-dimensional aperture photometry—signal-to-noise ratio of point-source observations and optimal data-extraction techniques. Pub. ASP. 1989;101:616–622. [Google Scholar]
- 24.Lymperopoulos K., Crawford R., Kapanidis A.N. Single-molecule DNA biosensors for protein and ligand detection. Angew. Chem. Int. Ed. 2010;49:1316–1320. doi: 10.1002/anie.200904597. [DOI] [PubMed] [Google Scholar]
- 25.Crocker J.C., Grier D.G. Methods of digital video microscopy for colloidal studies. J. Colloid Interface Sci. 1996;179:298–310. [Google Scholar]
- 26.Rust M.J., Bates M., Zhuang X. Sub-diffraction limit imaging by stochastic optical reconstruction microscopy (STORM) Nat. Methods. 2006;3:793–795. doi: 10.1038/nmeth929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Mortensen K.I., Churchman L.S., Flyvbjerg H. Optimized localization analysis for single-molecule tracking and super-resolution microscopy. Nat. Methods. 2010;7:377–381. doi: 10.1038/nmeth.1447. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Dennis J., Schnabel R. Society for Industrial and Applied Mathematics; Philadelphia, PA: 1996. Numerical Methods for Unconstrained Optimization and Nonlinear Equations. [Google Scholar]
- 29.Zhang N.F. Allan variance of time series models for measurement data. Metrologia. 2008;45:549–561. [Google Scholar]
- 30.Allan D. Statistics of atomic frequency standards. Proc. IEEE. 1966;54:221–230. [Google Scholar]
- 31.Gibson G.M., Leach J., Padgett M.J. Measuring the accuracy of particle position and force in optical tweezers using high-speed video microscopy. Opt. Express. 2008;16:14561–14570. doi: 10.1364/oe.16.014561. [DOI] [PubMed] [Google Scholar]
- 32.Czerwinski F., Richardson A.C., Oddershede L.B. Quantifying noise in optical tweezers by Allan variance. Opt. Express. 2009;17:13255–13269. doi: 10.1364/oe.17.013255. [DOI] [PubMed] [Google Scholar]
- 33.Iqbal A., Arslan S., Lilley D.M.J. Orientation dependence in fluorescent energy transfer between Cy3 and Cy5 terminally attached to double-stranded nucleic acids. Proc. Natl. Acad. Sci. USA. 2008;105:11176–11181. doi: 10.1073/pnas.0801707105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Clegg R.M. Fluorescence resonance energy transfer and nucleic acids. Methods Enzymol. 1992;211:353–388. doi: 10.1016/0076-6879(92)11020-j. [DOI] [PubMed] [Google Scholar]
- 35.Brokmann X., Hermier J., Dahan M. Statistical aging and nonergodicity in the fluorescence of single nanocrystals. Phys. Rev. Lett. 2003;90:120601. doi: 10.1103/PhysRevLett.90.120601. [DOI] [PubMed] [Google Scholar]
- 36.McCann J.J., Choi U.B., Bowen M.E. Optimizing methods to recover absolute FRET efficiency from immobilized single molecules. Biophys. J. 2010;99:961–970. doi: 10.1016/j.bpj.2010.04.063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Hecht E. Addison-Wesley; Reading, MA: 1998. Optics. [Google Scholar]
- 38.Uphoff S., Holden S.J., Kapanidis A.N. Monitoring multiple distances within a single molecule using switchable FRET. Nat. Methods. 2010;7:831–836. doi: 10.1038/nmeth.1502. [DOI] [PubMed] [Google Scholar]
- 39.Christian T.D., Romano L.J., Rueda D. Single-molecule measurements of synthesis by DNA polymerase with base-pair resolution. Proc. Natl. Acad. Sci. USA. 2009;106:21109–21114. doi: 10.1073/pnas.0908640106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.McKinney S.A., Joo C., Ha T. Analysis of single-molecule FRET trajectories using hidden Markov modeling. Biophys. J. 2006;91:1941–1951. doi: 10.1529/biophysj.106.082487. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Cordes T., Vogelsang J., Tinnefeld P. On the mechanism of Trolox as antiblinking and antibleaching reagent. J. Am. Chem. Soc. 2009;131:5018–5019. doi: 10.1021/ja809117z. [DOI] [PubMed] [Google Scholar]
- 42.Aitken C.E., Marshall R.A., Puglisi J.D. An oxygen scavenging system for improvement of dye stability in single-molecule fluorescence experiments. Biophys. J. 2008;94:1826–1835. doi: 10.1529/biophysj.107.117689. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Santoso Y., Joyce C., Kapanidis A. Conformational transitions in DNA polymerase I revealed by single-molecule FRET. Proc. Natl. Acad. Sci. USA. 2010;107:715–720. doi: 10.1073/pnas.0910909107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Santoso Y., Torella J.P., Kapanidis A.N. Characterizing single-molecule FRET dynamics with probability distribution analysis. ChemPhysChem. 2010;11:2209–2219. doi: 10.1002/cphc.201000129. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


