A Structurally Relevant Coarse-Grained Model for Cholesterol

Abstract

Detailed atomistic computer simulations are now widely used to study biological membranes, including increasingly mixed lipid systems that involve, for example, cholesterol, which is a key membrane lipid. Typically, simulations of these systems start from a preassembled bilayer because the timescale on which self-assembly occurs in mixed lipid systems is beyond the practical abilities of fully atomistic simulations. To overcome this limitation and study bilayer self-assembly, coarse-grained models have been developed. Although there are several coarse-grained models for cholesterol reported in the literature, these generally fail to account explicitly for the unique molecular features of cholesterol that relate to its function and role as a membrane lipid. In this work, we propose a new coarse-grained model for cholesterol that retains the molecule's unique features and, as a result, can be used to study crystalline structures of cholesterol. In the development of the model, two levels of coarse-graining are explored and the importance of retaining key molecular features in the coarse-grained model that are relevant to structural properties is investigated.

Introduction

Cholesterol (CHOL) plays an important role in the properties of biological membranes and in determining membrane dynamics. Specifically, it is known that CHOL is required for cellular viability and proliferation (1,2) and that similar sterols, such as ergosterol, cannot replace CHOL in mammalian cells (3). As a membrane lipid, CHOL has a unique molecular structure with both a rigid multi-ring arrangement and a flexible tail. Additionally, within the ring structure, the presence of chiral methyls on one plane of the molecule results in contrasting smooth and rough faces, while the alcohol group contributes to the hydrophilic component of the molecule's amphiphilic properties and drives the orientation of CHOL in bilayers (4). Several studies (5–7) have shown that CHOL acts as a molecular rigidifier to increase order and decrease molecular motion in model membranes (commonly referred to as the “condensing effect” (5–7)), while also acting as an impurity to prevent bilayers from becoming too structured through the mismatch in shape between CHOL and typical membrane lipids (such as sphingomyelin or other phospholipids).

Experimentally, in the pure state, cholesterol exhibits a triclinic crystal structure that undergoes a phase transition at 304.8 K (8,9) to a less symmetric structure (rather than a more symmetric one), making cholesterol somewhat of an oddity among biological molecules (9). At room temperature (298 K), the unit cell contains eight unique molecules (labeled A–H), but at body temperature (310 K), the unit cell contains 16 unique molecules, decreasing its level of symmetry relative to the room temperature cell. In each unit cell, cholesterol displays a degree of pseudosymmetry, in that the molecules exist in similarly structured pairs throughout the cell with the alcohol groups directed toward the center of the unit cell, allowing the formation of hydrogen bonds both within and across the molecular pairs.

In an effort to provide further insight into the role of CHOL in membranes, several simulation studies have been reported that elucidate the importance of the unique molecular features of CHOL with respect to its effects on bilayer structure and mechanics (10–17). For example, to investigate the ordering and fluidizing effect of CHOL, Chiu et al. (10) performed a series of simulations on dipalmitoyl phosphatidyl choline (DPPC) bilayers that showed while changing the CHOL concentration from 0 to 4 mol % induces a high degree of structure in the lipid tails, increasing the concentration up to 50% had little additional effect. Additionally, the area per lipid was found to increase in a linear fashion with respect to the amount of CHOL, indicating that the CHOL was fluidizing the bilayer. The importance of CHOL's molecular structure was further emphasized by Zhang et al. (17) in an investigation of the effects of unsaturation in the bilayer lipid tails; the smooth face of CHOL was found to preferentially align with fully saturated tails, while the rough face packed more efficiently with monounsaturated tails. These results were further supported by the work of Pandit et al. (14), who observed CHOL to pack most efficiently in bilayers with a mix of saturated and unsaturated phospholipids tails. In related work, Róg and co-workers have performed simulations to explore the importance of the chiral methyl groups and double-bonds in the ring structure (16,18,19), finding that molecules with only smooth faces or more double bonds do not induce the same degree of bilayer structure as CHOL. Additionally, independent of which chiral methyls are removed, saturated DPPC tails were found to have a preference for the smooth CHOL face, resulting in preferential van der Waals contacts with other tails and a higher degree of order.

While it has been shown that atomistic simulations, such as those described above, can provide a wealth of information on the molecular level and be used to study self-assembly in simple lipid bilayers (see, for example, (20)), the timescale for self-assembly of mixed lipid systems is expected to be prohibitively long. Although many interesting phenomena occur on the nanosecond timescale, processes like phase separation in lipid mixtures occur on much longer timescales. As a result, coarse-grained (CG) models, in which some of the atomistic detail is sacrificed, are commonly used in studies of biological membranes (21–29). Several CG models have been developed for membrane lipids, most commonly for phospholipids, and have been used to study, for example, lipid self-assembly (24,30), membrane dynamics (31), and phase behavior (24,30). Although a myriad of different techniques (21–29,32) can be used to develop CG models, they all share the aim of reducing the number of degrees of freedom in the model whilst matching specific behavior or attributes of the atomistic or experimental system on the CG level. For an overview of coarse-graining techniques and their applications, the reader is directed to several excellent reviews (29,33–35). Here we briefly discuss the CG models developed for CHOL as they relate to the current work.

Although several very CG (i.e., single-site) models for lipids have been developed and used to model phospholipid bilayers containing CHOL (25,36), generally only qualitative agreement with experiment is observed. In work more closely related to the current study, Izvekov and Voth (37) have developed four-site and seven-site models for CHOL for use in molecular dynamics simulations using the force-matching algorithm. In the four-site model, the molecule is essentially linear, with two beads representing the multi-ring structure and the flexible tail mapped to the remaining two beads. In the seven-site model, although the flexible tail is mapped in the same way, the ring structure is described by five separate beads to duplicate the planar nature of CHOL. Both models were found to be able to match radial distribution functions measured from atomistic simulations, indicating that the packing of the CHOL within the bilayer is retained, though the authors preferred the four-site model due to its computational efficiency. A similar degree of coarse-graining is used in the CHOL model developed by Marrink et al. (30) within the Martini force field; the ring structure and four carbons of the flexible tail are described using six beads in a cross-linked multi-ring structure while the last four carbons of the flexible tail are modeled as a separate bead. As such, the single-site tail does not have the same flexibility as that found in the Izvekov and Voth model. Although these CG models with two smooth faces can induce a degree of order into bilayers (25,30, 37,38), we anticipate that, to retain accurate bilayer structuring and the condensing effect observed experimentally, a CG model that maintains an explicit rough and smooth face in the ring structure should be used.

Although most lipid bilayers containing CHOL are in an ordered-liquid phase, some, such as those found within the stratum corneum, are in a more solid-like crystalline state. Therefore, in this work, we have developed a CG model for CHOL that captures the unique structural features of the CHOL molecule and is capable of reproducing the CHOL crystal structure. As such, the focus of this article is on pure CHOL; its effect in mixed lipid systems will be explored in future work.

Coarse-Grained Model and Force-Field Development

Since the goal of this work is to develop a model for CHOL that is capable of mimicking the structuring properties of CHOL observed experimentally and in atomistic simulations, the target data for the CG force field optimization are radial distribution function (RDF) data taken from atomistic simulations of CHOL using the CHARMM force field for cholesterol developed by Cournia et al. (39). Trajectories from the atomistic simulations were mapped to the CG level using the center of mass of the atoms within a CG bead on the atomistic level as the center of mass of the CG bead. The CG potential was then parameterized using the method developed by Reith, Pütz, and Müller-Plathe (RPM) (40,41) in which the bonded potential is derived using Gaussian-based potentials (41), and results in harmonic potentials to describe bond stretching and bond-angle bending, and the nonbonded potential is iteratively parameterized through comparison of the target and CG RDFs.

Because RDF data from atomistic simulations is used to parameterize the CG model, the atomistic force field was first validated against experimental data to ensure accurate results on the CG level. The CHARMM atomistic force field for CHOL (39,42) was developed by Cournia et al. (42) by fitting to the vibrational spectra and dynamics of the alcohol group, to capture the hydrogen-bonding capabilities of CHOL (39). The force field has been shown to predict the experimental room temperature crystal structure of CHOL accurately; therefore, as an additional test of the force field, the crystal structure at body temperature (310 K), which is relevant to most biological membranes, was also studied in this work.

When mapping CHOL to the CG level, the number of beads employed was minimized, while still retaining the key structural features of CHOL, as described below. The first mapping scheme considered will be referred to as the full CG CHOL model, and as shown in Fig. 1, retains the rigid multi-ring structure through the connectivity of five beads (denoted ALC, 1RNG, 2RNG, 3RNG, and 4RNG), with the ALC bead also representing the hydrophilic component of the molecule. The chiral methyls on the planar ring are mapped as their own explicit beads (denoted CHM) to distinguish between the rough and smooth faces in the CG model. Finally, the CHOL tail is described by two beads (TAILC and TERC) of four carbons each that are separate from the rigid ring structure to allow for the tail's flexible nature.

Figure 1.

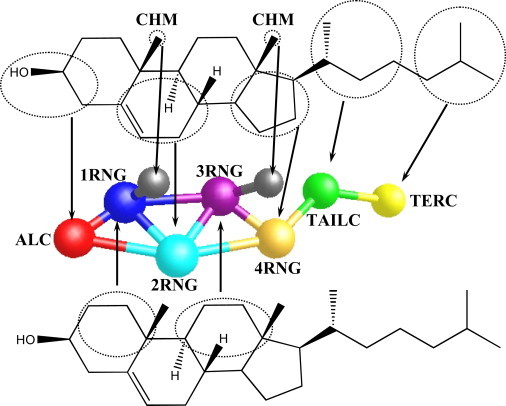
The mapping scheme proposed for cholesterol.

As discussed in detail in the Results and Discussion section below, the inclusion of explicit chiral methyls is the major distinction between our CG CHOL model and those proposed in the literature to date (25,30,36,37), and were found to be critical to obtaining the crystalline structure of CHOL. We also note that in contrast to the models optimized to date for CHOL in the literature, the proposed mapping scheme would be able to distinguish different sterol molecules on the CG level and so would be suitable to study sterols such as lanosterol, which has extra methyl groups creating a rough face on both sides of the molecule, and ergosterol and desmosterol, which have additional double bonds.

A possible drawback of this mapping is the large number (eight) of different bead types, which results in a total of 36 interactions that need to be optimized in a pure CHOL system. Although the ALC, CHM, and flexible tail beads have unique interactions and roles within the model, the four-ring beads could be replaced by four beads that share the same nonbonded potential. Therefore, in a second model, only one type of ring bead (RING) is used, resulting in a model with only five different bead types and 15 interactions to optimize. We refer to this model as the homogenized CG CHOL model. The benefits and drawbacks of both models are discussed in the Results and Discussion section.

Simulation Details

Molecular dynamics simulations were performed in the NσT ensemble, in which the stress σ on each face of the cell containing a fixed number of molecules N is maintained at a constant temperature T. The NσT ensemble was used in the simulations to allow the shape of the simulation cell to change to the most stable repeat structure. In the atomistic simulations, 96 CHOL molecules were initially arranged according to the crystal structure of Sheih et al. (43) and the system equilibrated. Simulations were performed over a range of temperatures to estimate the melting point of CHOL to compare with experimental data. The self-diffusion coefficient and average system density were measured during each simulation and used to determine the approximate temperature at which a phase-change is observed. In subsequent simulations with the CG model, the same simulation conditions and initial configurations were used as in the atomistic counterparts. Additional simulation details are provided in the Supporting Material.

Methodology

The parameters for the bond stretching (and bond-angle bending) potentials were determined from a normalized distribution of the distance between two bonded sites (or the angle between three angled sites) measured from the target atomistic trajectory mapped to the CG level. From this the force constant for a harmonic oscillator and the equilibrium bond length (or angle) can be determined as described in the Supporting Material. As in earlier work by the authors on the development of a CG model for fatty acids (44), a dihedral potential taken from the atomistic CHARMM force field for hydrocarbons was applied to the beads associated with the flexible tail. The bond and angle potentials between the beads in the ring structure are sufficient to maintain the correct molecular architecture (i.e., planar) on the CG level and so dihedral parameters were not needed to maintain a planar ring structure.

The intermolecular interactions between CG beads were determined using numerical potentials iteratively optimized against RDF data, the initial guesses for which were either a Lennard-Jones potential or a previously optimized potential for a similar interaction type. In the RPM method, a CG simulation is performed using the initial potential, and the RDFs determined from the simulation trajectory compared to the atomistic target RDFs. The initial potential is then updated via a modified Boltzmann inversion,

$$V_{j+1}\left(r\right)=V_j\left(r\right)+\delta kT\ln \frac{g_j\left(r\right)}{g_{\ast }\left(r\right)},$$ (1)

where V_j(r) is the potential, g_j(r) is the CG RDF at iteration number j, g^∗(r) the target RDF, r the interatomic distance, and δ a damping factor. These steps are iteratively repeated in simulations each lasting 1.0 ns until the changes in the potentials are negligible. As described in earlier work (44), fitting RDFs for crystalline systems is an ill-defined optimization due to the sharp peaks and high repeatability of the system; however, the diverging oscillatory response seen using the original RPM method (40) can be prevented by using the damping factor in Eq. 1.

Results and Discussion

The average crystal structure parameters, including lattice vectors and cell density, determined from atomistic simulations at 298 K and 310 K, are reported and compared to the experimental results (8,9,43) for CHOL in Tables 1 and 2, respectively. From the tables, we find that the predicted density and unit cell angles are in very good agreement with experiment, with the unit cell lengths showing deviations of <3% compared to the experimental values, and are consistent with those obtained by Cournia et al. (39) at 298 K. Furthermore, we qualitatively observe the rotation along the molecular axis of the CHOL molecules within the unit cell in the 310 K crystal compared to that at 298 K, as seen experimentally (8,9).

Table 1.

Crystallographic data for cholesterol taken from experiment (43), atomistic simulation, and coarse-grained simulation at 298 K

	Experimental∗	Atomistic		Full CG model		Homogenous CG model
Density (g/cm3)	1.021	1.018	± 0.006	1.007	± 0.028	1.030	± 0.024
a (Å)	14.172	14.149	± 0.062	14.133	± 0.226	13.949	± 0.212
b (Å)	34.209	33.614	± 0.250	34.315	± 0.763	33.823	± 0.598
c (Å)	10.481	10.743	± 0.088	10.748	± 0.077	10.749	± 0.086
α	94.64°	94.50°	± 0.58	94.40°	± 1.65	97.51°	± 3.72
β	90.67°	90.32°	± 0.49	89.82°	± 0.83	89.99°	± 0.99
γ	96.32°	97.61°	± 0.84	99.24°	± 5.60	94.93°	± 3.29

^∗Data from Hsu et al. (9).

Table 2.

Crystallographic data for cholesterol taken from experiment and atomistic simulation at 310 K

	Experimental∗	Atomistic
Density (g/cm3)	1.0119	1.0117 ± 0.0053
a (Å)	27.565	28.204 ± 0.140
b (Å)	38.624	37.859 ± 0.430
c (Å)	10.748	10.770 ± 0.064
α	93.49°	91.10° ± 0.53
β	90.90°	90.32° ± 0.55
γ	117.15°	117.56° ± 1.33

^∗Data from Hsu et al. (9).

To estimate the melting point of the high temperature crystal, simulations were performed over a range of temperature from 100 K to 725 K and the self-diffusion coefficient and density calculated to provide an estimation of the melting point. The results for the self-diffusion coefficient as a function of temperature are reported in Fig. 2, from which the melting point is determined to be the point at which a distinct change in the slope of the self-diffusion coefficient as a function of temperature is observed. The estimate of the melting point, determined from the intersection of these two lines, occurs at 519 K, which is almost 100 K higher than the experimental value of 422 K; however, the determination of the melting point from a molecular simulation using periodic boundary conditions is known to lead to an overestimation of the melting point because of periodic effects (45). The gradual change in magnitude of the self-diffusion coefficients at temperatures below the observed melting transition is presumably due to the flexible and more mobile nature of the CHOL tail compared to the rigid multi-ring structure. As a result, the distinction between the solid phase and the liquid phase is less sharp than that seen for simpler molecules. For example, in simulations of atomistic fatty acids (44), in which in the crystalline state the hydrocarbon tails are elongated in mainly trans-gauche conformations and are relatively motionless (i.e., have low diffusivities), a sharp transition is observed at the melting point. In contrast, although the CHOL tails behave similarly to the fatty acid tails, the rigidity and general bulkiness of the CHOL ring structure inhibits motion of the molecule as a whole at all temperatures.

Figure 2.

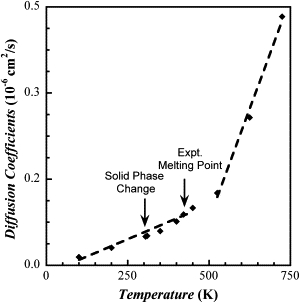
Diffusion coefficients for cholesterol as a function of temperature. The dashed lines are a fit to the simulation data (diamonds). The experimental melting point and temperature at which the cholesterol undergoes a structural transition are also indicated.

Having validated the atomistic force field, the atomistic simulation trajectories were then mapped to the CG level using the mapping scheme shown in Fig. 1. To determine the parameters for the bond-length potentials, the distribution of bond lengths was measured and fitted to a single-peak Gaussian. Utilizing the RPM method, the parameters for the harmonic bond potential can be extracted from the distribution as described in the Supporting Material. Similarly, the parameters for the angle potential can be extracted from a distribution of angles between sites. The rigid nature of the ring structure is reflected in the force constants obtained for the bond and angle potentials, as reported in Table 3; compared to the potentials found, for example, for the bond between the TERC and TAILC beads in the flexible tail, the ring force constants are almost an order-of-magnitude higher.

Table 3.

Force constants for bonds and angles in the coarse-grained cholesterol models proposed

Bond	Force constant (kcal/mol/Å2)	Equilibrium distance (Å)
ALC-1RNG	355.1	2.591
ALC-2RNG	141.4	4.200
1RNG-2RNG	204.0	3.347
1RNG-3RNG	124.8	4.008
1RNG-CHM	132.9	2.402
2RNG-3RNG	319.4	3.394
2RNG-4RNG	155.6	4.180
3RNG-4RNG	366.8	3.041
3RNG-CHM	145.3	2.622
4RNG-TAILC	155.8	3.717
TAILC-TRMC	10.8	4.227
Angle	Force constant (kcal/mol)	Equilibrium angle
1RNG-ALC-2RNG	1070	52.8
ALC-1RNG-2RNG	631.0	89.1
ALC-1RNG-3RNG	356.7	142.6
ALC-1RNG-CHM	127.1	107.1
2RNG-1RNG-3RNG	1835	54.0
2RNG-1RNG-CHM	218.1	62.7
3RNG-1RNG-CHM	367.3	62.8
ALC-2RNG-1RNG	2379	38.1
ALC-2RNG-3RNG	457.0	110.8
ALC-2RNG-4RNG	284.4	155.9
1RNG-2RNG-3RNG	864.4	73.0
1RNG-2RNG-4RNG	628.8	118.6
3RNG-2RNG-4RNG	2647	45.9
1RNG-3RNG-2RNG	1324	52.9
1RNG-3RNG-4RNG	485.5	133.4
1RNG-3RNG-CHM	113.9	129.3
2RNG-3RNG-4RNG	1040	80.8
2RNG-3RNG-CHM	280.7	98.1
4RNG-3RNG-CHM	778.5	53.9
2RNG-4RNG-3RNG	1913	53.3
2RNG-4RNG-TAILC	363.8	149.1
3RNG-4RNG-TAILC	495.7	96.1
4RNG-TAILC-TRMC	68.0	135.8

To illustrate the accuracy with which the RPM method with a damping factor can optimize the nonbonded interactions, in Fig. 3 we present RDFs for the ALC-ALC (panel a) and CHM-CHM (panel b) bead interactions, which are common to both CHOL models. In both figures, the high degree of structure can be verified by the existence of multiple regularly spaced sharp peaks. If we focus on the ring potentials, which differentiate the two proposed models, we can see from Fig. 4 a, that the RDFs for the 1RNG, 2RNG, 3RNG, and 4RNG beads are more structured than that for the homogenized model; the individual ring RDFs (Fig. 4 b) are more structured because there is only one bead of the same type at specific interaction distances, whereas with the homogenous model, the nearest-neighbor CHOL molecules contain four beads of the same type all at different interaction distances and so the structuring becomes more generalized (and less localized), resulting in a broader less structured RDF.

Figure 3.

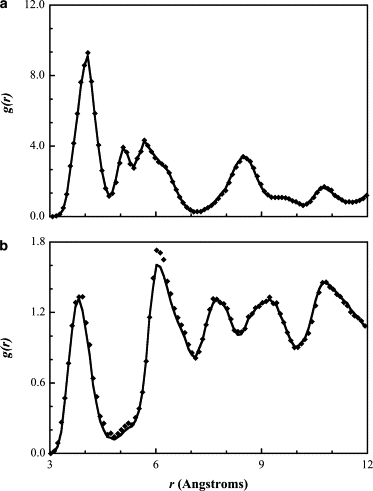
Radial distribution function between (a) alcohol (ALC-ALC) and (b) chiral methyl (CHM-CHM) beads from a coarse-grained simulation (diamonds) and from the target atomistic simulation (solid line).

Figure 4.

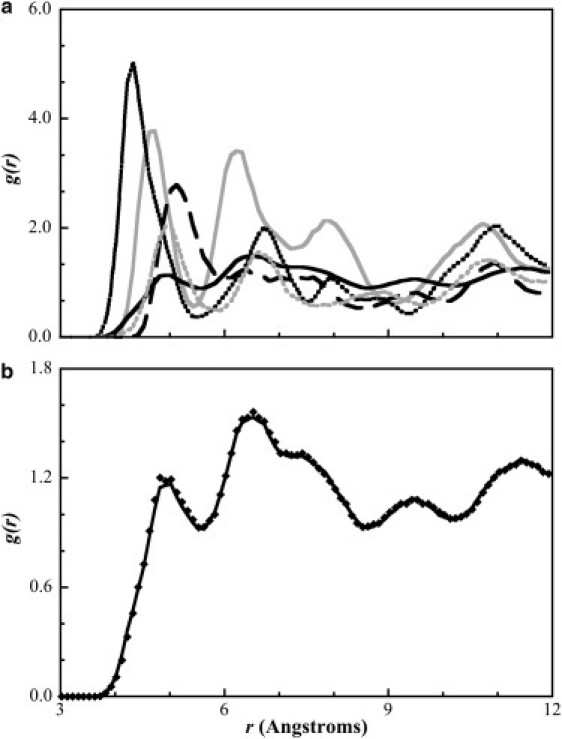
(a) Comparison between the target radial distribution functions for the cholesterol ring beads in the full and homogenized coarse-grained models: 1RNG-1RNG (solid shaded line), 2RNG-2RNG (dashed black line), 3RNG-3RNG (long dashed black line), 4RNG-4RNG (dashed shaded line), and RING-RING (solid black line) and (b) comparison of the radial distribution function between ring beads (RING-RING) from a crystalline coarse-grained simulation with the homogenized model (diamonds) and the target atomistic simulation (solid line).

Although the RPM method is able to optimize both the full and homogenized CG ring models, it was found during the optimization process that a smaller damping factor was needed for the full model (∼0.01 compared to a value of ∼0.1 to optimize the homogenized model). This effect is presumably due to the large number of coupled interactions that need to be simultaneously optimized in the full model, which adds additional complexity to an already ill-defined optimization and forces the optimization steps to be smaller. A similar effect was observed by Peter et al. (46), who found that convergence could not be achieved with the original RPM method when developing a nine-site CG potential for a liquid crystal molecule if all of the interactions were optimized simultaneously; to overcome the issue, fragments of the molecule were optimized in turn based on simpler, smaller molecules. In comparing the full and homogenized model, we therefore find that the homogenized model is more computationally efficient, because there are fewer interactions to optimize and, because the optimization for each individual interaction is more stable as there are less interdependent potentials being optimized at once, it converges more rapidly.

During the optimization process, when testing different CG mapping schemes, we found that a crystalline structure could not be retained without the explicit mapping of the chiral methyl groups. In an initial mapping, the methyls were subsumed into the site that they are attached to, namely the 1RNG bead and the 3RNG bead in the explicit ring model. Using this approach the optimization did not converge and the average density of the system was found to be that of a liquid. The inclusion of the chiral methyl beads had a significant effect on the optimization: if the CHM-CHM interaction was optimized while keeping the other interactions constant, the agreement between the CG and atomistic target RDFs for the CHM-CHM interaction was very good and the density of the system increased dramatically toward the target density. On the other hand, if all of the interactions in the full CG model were optimized simultaneously from the same starting point in the optimization process, the agreement between the CG and target atomistic RDFs for the CHM-CHM interaction and the density improved only slightly. In other words, focusing on the CHM-CHM interaction, while keeping all others constant was the key to achieving a solidlike density; the accuracy of this interaction appears to have a stronger effect on the molecular packing than all of the interactions as a whole. In addition, we observed that although the molecules in a given unit cell had minimal movement within the cell, the repeat crystal structure, as measured from the simulation cell parameters, changed by a large degree as the accuracy in the RDFs improved throughout the optimization. Although anecdotal, these qualitative observations suggest CHOL cannot maintain a crystal structure without the explicit mapping of the chiral methyls to describe the rough face of the molecule; the CHM beads presumably prevent the molecules from slipping past each other easily and ensures the system remains in a solid crystalline state.

In Table 1, we report the unit cell parameters obtained from both the full and homogenized CG models compared to the atomistic and experimental data (43). If we consider first the full model, we see that the unit cell parameters from the CG simulations not only match the atomistic target well, but are also in good agreement with the experimental data. The largest percentage differences between the CG crystal and the experimental values are a 3% difference between the γ-angles and a 2.5% differences for the length of the c vector. Compared to the atomistic results, the discrepancies observed are smaller, with only three of the parameters (density, γ-angle, and b-vector length) having a percentage difference between 1% and 3%. We can see from Figs. 5 and 6 that the overall shape of the crystal is retained with the full CG model and the spacing between the molecules and their orientations are in good agreement with that seen atomistically. In Fig. 6, in particular, we can see that the CG molecules maintain sheets, as observed in the atomistic simulations with similar spacing between the sheets. As further support for the accuracy of the predicted crystal structures, in Fig. 7 we show part of the hydrogen-bonding network from both the CG simulation and target trajectory. In both cases, hydrogen-bonding is measured solely by the distance between hydrogen-bonding sites. From the figure, we can see that the alcohol groups hydrogen-bond with two different sites, one within the molecular pair and one across the crystal unit cell in the y direction, as described in the experimental crystal structure (43). Within a pair, the average hydrogen-bonding distance is measured as 5.68 ± 0.24 and 5.73 ± 0.41 Å in the atomistic and CG simulations, respectively. Between molecular pairs, an average distance of 4.09 ± 0.22 Å is observed in the atomistic trajectory and 4.10 ± 0.44 Å in the CG simulation, giving a difference of only 0.33%. We note that the hydrogen-bonding network in sphingomyelin/CHOL bilayers was found by Róg and Pasenkiewicz-Gierula (15) to be much more extensive than that seen in bilayers containing phospholipids like DPPC and CHOL (11,13,15); the ability of the model to retain hydrogen-bonding networks will therefore be important.

Figure 5.

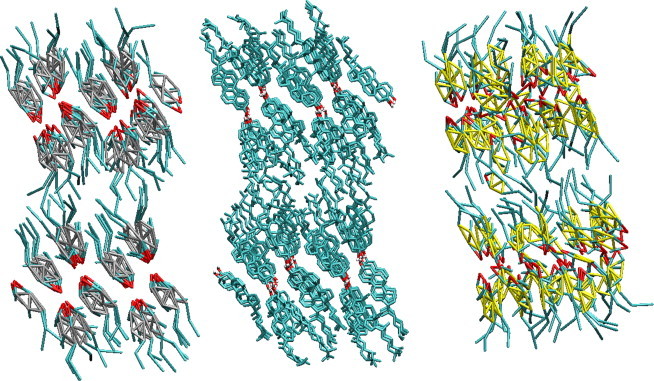
Snapshots taken of the cholesterol crystal in the xy-plane from the atomistic simulation (center) and simulations with the full (left) and homogenized (right) coarse-grained models.

Figure 6.

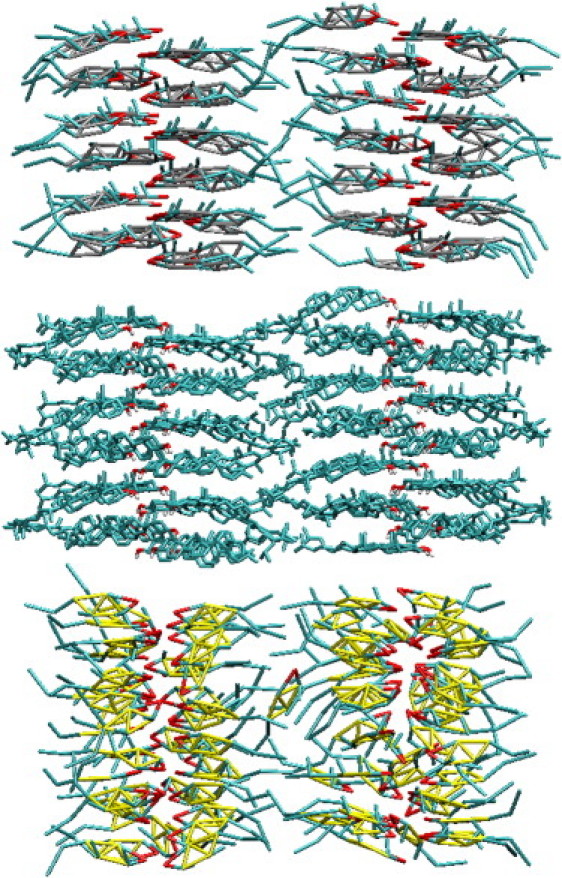
Snapshots taken of the cholesterol crystal in the yz-plane from the atomistic simulation (center) and simulations with the full (top) and the homogenized (bottom) coarse-grained models.

Figure 7.

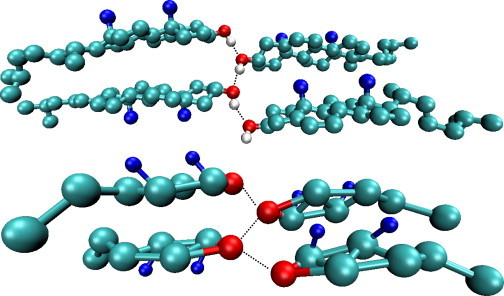
Closeup of the hydrogen-bonding network in the cholesterol crystal (indicated by the dashed lines) from the atomistic (top) and full coarse-grained model simulations (bottom).

If we now consider the homogenized CG model, we can see, from Table 1, that the crystal density and lattice lengths are also in good agreement with experiment, indicating that the correct volume, length, and cross-sectional area is predicted; however, with the homogenous ring structure, the molecules can arrange themselves within the crystal structure in multiple ways that produce the same RDFs, but represent different molecular arrangements within the unit cell. Whereas, in the full CG model, by fitting the 10 separate RDFs that are associated with the four different ring beads, the available molecular arrangements of CHOL are minimal and so the molecules exhibit a packing arrangement that is very similar to that seen in the atomistic simulation (as seen in Figs. 5–7).

Although molecular motions in a crystalline state are minimal, changes in the crystal structure will occur if the initial configuration is not at equilibrium (44). This is seen directly with the homogenous CG model simulations, where we find that the molecules rotate along the axis of the molecule, so that although the ALC groups are arranged as in the atomistic model, the specific packing of the molecules is different. This can be seen most clearly in Fig. 6, in which the rings in the homogenized CG model are seen to have a significantly different tilt than in the atomistic model, but the spacing of the molecules along both axes is similar to that seen in the atomistic target. Additionally, from Figs. 5 and 6, we also note that while the hydrogen-bonding between ALC beads is retained in the homogenized model, the molecules change hydrogen-bonding partners from the original crystal structure. The change in hydrogen-bonding pairs is not systematic and so it is difficult to track to perform a numerical analysis; however, although different from the hydrogen-bonding network seen in the atomistic simulations and in the experimental crystal, a hydrogen-bonding network is retained. This can be verified from both the ALC-ALC RDF and Fig. 8, where we show a closeup of the hydrogen bonding within a unit cell for both CHOL models. The hydrogen bonding exists in the homogenous model, but the specific molecules of the unit cell involved in the hydrogen-bonding network in this example are different (i.e., molecules A, B, E, and H versus molecules A, B, G, and H) than that seen in the experimental crystal structure. In addition, the hydrogen-bonding network does not have the zig-zag pattern seen in the atomistic crystal shown in Fig. 7.

Figure 8.

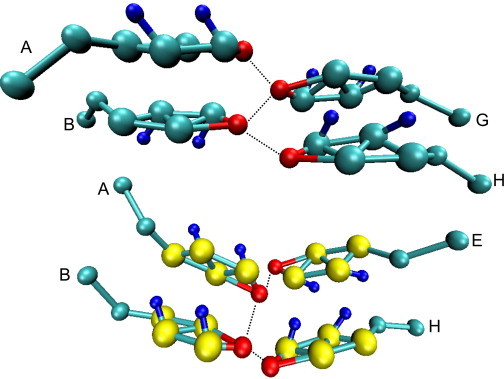
Closeup of coarse-grained hydrogen-bonding network (indicated by the dashed lines) in simulations of the full (top) and the homogenized (bottom) coarse-grained cholesterol models. The letters identify the specific molecule within the unit cell of the crystal.

Conclusions

CHOL has unique structural features that have been shown in the literature to play an important role in its interactions with other molecules in biological membranes. In this work, two CG models for CHOL have been developed that retain these unique features, to ensure that simulations with the CG models exhibit the same structural effects as seen in experimental studies and atomistic simulations. Specifically, the models proposed have a rigid multi-ring structure attached to a flexible tail, with amphiphilic properties and an explicit rough and smooth face on the ring structure.

The models were developed based on atomistic simulations of CHOL using the CHARMM force field for cholesterol developed by Cournia et al. (39,42). To validate further the atomistic model, we studied the CHOL crystal structure at body temperature and found good agreement with experimental data. Additionally, the melting point of the atomistic model was investigated through the calculation of the self-diffusion coefficient and density (not shown). Although an over-prediction of the melting point was observed, the calculations highlighted the effect of the dualistic rigid/flexible nature of CHOL on its melting-point behavior.

In developing the CG models, we found that the chiral methyls play an important role in retention of the crystal structure. Using our unique mapping, a CG CHOL model was optimized that is capable of predicting the structural properties of atomistic CHOL as seen by the agreement obtained in the RDFs, the crystal parameters, and configuration snapshots comparing the atomistic and CG simulations. This mapping could also be used in the study of similar sterols that differ from CHOL in the number of chiral methyls or double bonds. Although accurate and ∼180 times faster than its atomistic counterpart, the full CG model contains nine beads (eight different types), which requires the optimization of 36 interdependent interactions, resulting in a complex optimization process. A simpler model in which the four different ring beads were replaced by four identical homogenized ring beads was therefore also studied. With this simpler homogenized model, the optimization was better defined and although the relative conformations of the molecules are altered in the homogeneous model, the important structural features of CHOL are retained. This is attributed to fitting the specific ALC-ALC interaction, as the positions of the molecules cannot change significantly without the ALC-ALC RDF containing large deviations. This interaction therefore allows the homogenized CHOL model to retain the important aspects of its structure in the same manner as the specific ring bead interactions achieve for the full CG model. Although in the context of modeling the pure crystal structure of CHOL the full model is clearly more appropriate, it is anticipated that when studying CHOL's effect on the structure of a bilayer, the homogenous ring model will be adequate and its computational benefits (in terms of the CG force-field optimization process in the study of mixed lipid systems) should outweigh the slight loss in accuracy.

In future work, we will report the results of mixed lipid self-assembly simulations involving the homogenized cholesterol model and water ((47); K. R. Hadley and C. McCabe, unpublished). Preliminary results indicate that the model demonstrates the condensation effect seen atomistically as measured by the area/lipid in a self-assembled CG bilayer.