The Diffusion Coefficient for PGK Folding in Eukaryotic Cells

Abstract

We compare the folding kinetics of a fluorescent phosphoglycerate kinase construct in 30 mammalian cells with that in aqueous buffer. In both environments, the kinetics can be fitted to the functional form exp[−(t/τ)^β]. A histogram of τ shows that the average folding relaxation time in cells is only twice as long as in aqueous buffer. Consideration of the folding free energy and of β reveals that only some of the variation in τ arises from perturbation of the protein's energy landscape. Thus, the diffusion that controls barrier crossing during protein folding is nearly as fast in cells as in vitro, even though translational diffusion of phosphoglycerate kinase in the cell is slow compared to in vitro.

Translational diffusion of proteins in eukaryotic cells is affected by the viscosity of the solvent, by binding to macromolecules and organelles, and by large crowders that sterically restrict motion (1). Studies with fluorescence-labeled proteins have shown that they undergo slightly anomalous diffusion 〈Δx²〉 ∼ t^α (α = 0.75–1) due to crowding (2). On the 1-μm length scale, enzymes such as phosphoglycerate kinase (PGK) have a translational diffusion coefficient $D_{cell}^{\left(trans\right)}$ ≈ 0.04 × $D_{water}^{\left(trans\right)}$ in mammalian cells (1). The rotational diffusion coefficient $D_{cell}^{\left(rot\right)}=0.7D_{water}^{\left(rot\right)}$ of a native protein is much closer to the aqueous value (3).

Diffusion also plays a key role in protein folding (4). The prefactor τ₀ of the folding time

$${\tau }_f={\tau }_0\left(D^{\left(fold\right)}\right)e^{\Delta G_f^{†}\left(T\right)/RT}$$ (1)

depends inversely on the diffusion coefficient D^(fold) of the protein chain in the transition state ensemble. Within the crowded cell, a rotating native protein explores much less interstitial space than a translationally diffusing protein. The folding reaction is intermediate in terms of the volume explored by the denatured state, so one might expect an intermediate value for the diffusion coefficient D^(fold). The value $D_{cell}^{\left(fold\right)}/D_{water}^{\left(fold\right)}$ has not been measured before, to our knowledge. We need to know its value to answer the question: How much is the prefactor of in vitro studies likely to differ from the prefactor in the natural folding environment within the cell?

Here we compare the folding relaxation time of PGK in mammalian (U2OS) cells with that in aqueous solution. To make sure that a single anomalous cell does not skew the results, we studied the relaxation of PGK in 30 different cells to obtain an average folding relaxation time $\overline{\tau }$= 4.1 s, only twice our measured in vitro value of 2.0 s. The value τ is affected by two influences: Local viscosity modulates the prefactor in Eq. 1 (5,6). Crowding, binding, and chemical variations modulate the protein's folding free energy landscape, and hence the activation barrier in Eq. 1. To estimate the effect of the latter, we measured the variation of ΔG for folding within cells and from cell to cell to estimate the variation of ΔG^†. The correction turns out to be small, and we calculate that $D_{cell}^{\left(fold\right)}/D_{water}^{\left(fold\right)}$= 0.6 on average, with a standard deviation of σ_D = 25% among cells. Thus diffusion of the folding polypeptide chain occupies a middle ground between near-aqueous rotational diffusion, and slower (considerably slower for metabolic enzymes) translational diffusion in the eukaryotic cell.

We measured PGK folding/unfolding kinetics by fast-relaxation imaging (7). The same instrument configuration with the same Förster resonance energy transfer (FRET)-labeled mutant was used for in cell and in vitro measurements to allow a direct comparison of relaxation times τ (Fig. 1). Fluorescent PGK was expressed in U2OS (bone tissue cancer) cells. The mutant, which has enzymatic activity nearly identical to the wild-type (8), unfolds at ∼41°C in U2OS cells. The 30 cells we measured were picked at random and differed in size, expression level, and cytoplasm/nuclear area ratio c/n (see Fig. S1 in the Supporting Material). FRET-labeled PGK in aqueous solution or in cells was subject to a millisecond temperature jump of 39–43°C (Fig. 1) centered on the thermal unfolding transition. Thus, folding and unfolding relaxation times are about the same, as implied by Eq. 1. Folding relaxation kinetics were read out as the change in donor-acceptor fluorescence intensity ratio, P(t) ∼ D(t)/A(t). By studying kinetic lifetimes instead of absolute amplitudes, our results are insensitive to deactivated acceptor labels, cell thickness variations, or similar artifacts. We previously showed that FRET-labeled PGK that could be unfolded and then refolded reversibly in <15 s (7). Our small temperature jumps did not affect cell viability, as evidenced by cell morphology (9). The FRET labels unfold only above 70°C (7), outside our measurement range.

Figure 1.

Fast-relaxation imaging measures protein folding relaxation in cells. Relaxation kinetics are induced by a programmable infrared laser pulse shape. The temperature in the cell is obtained from the fluorescence quantum yield of the red mCherry label attached to the C-terminus of PGK, and calibrated against thermocouples. A blue LED (470 nm) excites the green AcGFP1 at the N-terminus of PGK, resulting in either green donor (D) fluorescence (unfolded) or energy transfer to the acceptor (A) and red fluorescence (folded), changing D/A.

Fig. 2 shows the normalized relaxation kinetics of PGK in three representative cells (full set in the Supporting Material). All data were well fitted by stretched exponentials $P\left(t\right)=\exp [-{(t/\tau )}^{\beta }]$ (β = 1: folding is two-state, β < 1: folding is on a rough free energy landscape). Fig. 3 shows a histogram of τ for the ensemble of 30 U2OS cells and for 30 in vitro data points that characterize the measurement uncertainty (see the Supporting Material for β). The in vitro distributions yield $\overline{\tau }$= 2.03 ± 0.11 s and $\overline{\beta }$ = 0.72 ± 0.02. The uncertainties (±SD) characterize the measurement error. The in vivo distributions are accounted for by $\overline{\tau }$= 4.1 s with a standard deviation of σ_t = 1.2 s, and $\overline{\beta }$= 0.7, with a standard deviation of 0.13 (see the Supporting Material). The relaxation time is typically slower in cells (2–7 s) than in vitro, and twice as long on average. The width of the histogram in the cell is much greater than the measurement error deduced from the in vitro measurement (compare widths of blue and black histograms in Fig. 3).

Figure 2.

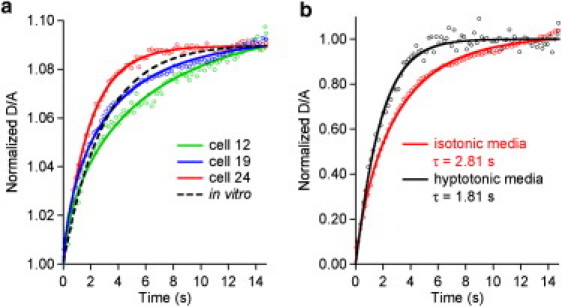
(a) Protein folding/unfolding relaxation monitored near the denaturation midpoint (jump starting at 39°C) in three of the 30 studied cells compared to aqueous solution (dotted black line). The parameter obtained from fits to stretched exponentials are summarized in the Supporting Material. (b) Cells with greater water content (hypotonic) promote faster protein folding.

Figure 3.

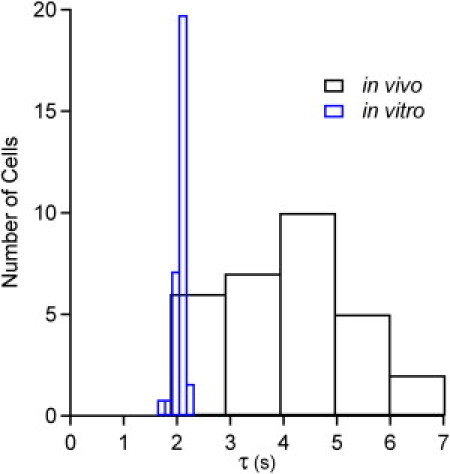
Histogram of folding lifetime in vitro and in cells. The in vivo distribution (black bars) is much wider and slower than the variation among in vitro measurements (blue bars).

We verified that the relaxation time has the correct qualitative dependence when viscosity and crowding in the cell are reduced by dilution of the cytoplasm. Fig. 2 b shows the speed-up of the relaxation rate when a cell is treated with hypotonic media, increasing its size (and hence water content) approximately by a factor of 2.

If the only factor affecting τ were the viscosity of the cellular matrix, one could conclude from the histogram in Fig. 3 that $D_{cell}^{\left(fold\right)}/D_{water}^{\left(fold\right)}$= 0.5 on average, and that its relative standard deviation among cells is σ_D = 30%. However, τ is also affected by changes in the protein's folding free energy landscape. Crowding could destabilize the unfolded state (10), and hence reduce the folding barrier. Chemical variations and protein binding could further modulate the free energy barrier and vary the folding time τ.

We first considered the effect of protein stability on τ. We measured thermal melts as described in Ebbinghaus et al. (7) for several cells (see the Supporting Material). PGK on average melts 2°C higher in U2OS cells than in vitro. The average stabilization at the in vitro T_m of 39.5°C was $\overline{\Delta G}$= −4.0 kJ/mole, with a cell-to-cell standard deviation σ_ΔG = 1.8 kJ/mole. The average ϕ-value of 0.3 for proteins (11,12) yields correspondingly smaller $\Delta {\overline{G}}^{†}$ and σ_ΔG, if we assume that the same ϕ-values apply for free energy variations in the cell as for in vitro mutation. Based on this shift and variability of the free energy barrier in cells, we estimate that energy landscape modulation increases the average τ in the histogram of Fig. 3 by a factor ≈ 1.3 compared to in vitro (see the Supporting Material). We also estimate it contributes ∼15% of the 30% cell-to-cell variation of τ (see the Supporting Material).

Energy landscape roughness could have a direct kinetic effect on τ as well. In the U2OS cells we observed, β ranges from 0.4 to 1, from energy landscapes rougher than in vitro to two-state landscapes. We found a weak correlation between β and τ (see the Supporting Material): PGK folds a little faster in cells closest to two-state behavior (β ≈ 1). Thus, we compared only those cells with β = 0.7 ± 0.1 with the in vitro result (β = 0.72 ± 0.02). As it turns out, these 16 (out of 30) cells have $\overline{\tau }$ = 4.2 s, close to the average for the whole ensemble.

Therefore, the corrected value for the folding diffusion coefficient in cells lies very close to the value deduced directly from Fig. 3: $D_{cell}^{\left(fold\right)}/D_{water}^{\left(fold\right)}$≈ (1.3 × 2.03/4.2) ≈ 0.6, with a 25% cell-to-cell variation. The average diffusion coefficient for folding of our construct lies between the typical value for rotational diffusion of folded proteins (ratio of 0.7) and the value for diffusion of dye-labeled PGK injected into mammalian cells (ratio of 0.04, $D_{cell}^{\left(trans\right)}$ ≈ 0.004 nm²/ns) from Verkman (1).

The discrepancy between $D_{cell}^{\left(fold\right)}$ and $D_{cell}^{\left(trans\right)}$ is rather larger for the enzyme PGK than for a protein such as GFP ($D_{cell}^{\left(trans\right)}$ ≈ 0.025 nm²/ns). Such slow diffusion has been observed for several metabolic enzymes, and Verkman (1) has proposed that binding of metabolic enzymes to cell components is responsible, being part of metabolic regulatory activity.

It is worth mentioning that some effects of crowding are not included in our corrections. For example, translational diffusion of PGK in Verkman (1) was studied without large fluorescent protein labels. Labeled PGK might diffuse even more slowly than unlabeled PGK, or diffusion could be similar if binding interactions are causing the slowdown. Also, tethered labels deplete freely diffusing cellular components near PGK, which could affect the folding diffusion coefficient (10). This effect could be quantified in the future by injecting dye-labeled PGK into the cell, rather than expressing fluorescent protein in the cell.

In summary, we have shown that the local diffusion coefficient for folding in eukaryotic cells is similar to the value obtained in aqueous solution. Our results suggest that the prefactor for the folding rate coefficient in vivo is only a factor-of-two slower than in vitro. Crowding does affect folding in the cell: average protein stability differs among cells by as much as 1.7 RT (4.3 kJ/mole), and folding times vary by greater than a factor of 3. Yet the frictional properties of water in the interstitial space between crowders sampled during folding are similar to the bulk.

Given the unusually slow translational diffusion of PGK, we speculate that cells may affect the function of their proteins by at least three nongenetic mechanisms: variations in expression level (13), posttranslational modifications (14), and now modulation of the protein energy landscape and viscosity in the cell.