A binding free energy decomposition approach for accurate calculations of the fidelity of DNA polymerases

Abstract

DNA polymerase β (pol β) is a small eukaryotic enzyme with the ability to repair short single-stranded DNA gaps that has found use as a model system for larger replicative DNA polymerases. For all DNA polymerases, the factors determining their catalytic power and fidelity are the interactions between the bases of the base pair, amino acids near the active site, and the two magnesium ions. In this report, we study effects of all three aspects on human pol β transition state (TS) binding free energies by reproducing a consistent set of experimentally determined data for different structures. Our calculations comprise the combination of four different base pairs (incoming pyrimidine nucleotides incorporated opposite both matched and mismatched purines) with four different pol β structures (wild type and three separate mutations of ionized residues to alanine). We decompose the incoming deoxynucleoside 5′-triphosphate-TS, and run separate calculations for the neutral base part and the highly charged triphosphate part, using different dielectric constants in order to account for the specific electrostatic environments. This new approach improves our ability to predict the effect of matched and mismatched base pairing and of mutations in DNA polymerases on fidelity and may be a useful tool in studying the potential of DNA polymerase mutations in the development of cancer. It also supports our point of view with regards to the origin of the structural control of fidelity, allowing for a quantified description of the fidelity of DNA polymerases.

Introduction

Prior to cell division, replicative DNA polymerases make exact copies of DNA molecules, enabling the cell to divide and pass on a complete set of DNA to both daughter cells.¹ These enzymes catalyze the incorporation of nucleotides at the 3′ end of the newly synthesized DNA (primer) strand opposite of the parental template DNA strand. In this process, a deoxynucleoside 5′-triphosphate (dNTP) enters the active site of the DNA polymerase and base pairs with the template base, forming the nascent Watson-Crick base pair.² Then, a nucleophilic attack of the deprotonated primer 3′ OH on the α-phosphorus (P_α) of the dNTP occurs and the pyrophosphate leaving group is eliminated.³ It has yet to be determined whether the mechanism of the reaction is of stepwise or concerted nature.⁴ For a more detailed discussion of the possible reaction pathways, see References 5 and 6. Two bivalent active-site metal ions, usually Mg²⁺, facilitate the reaction; one [Mg(b)] binds the incoming dNTP, the other one [Mg(c)] catalyzes the reaction by stabilizing the pentacoordinated transition state (cf. Figure 1).⁷ The accuracy of DNA replication is remarkable: the rate of misincorporation (incorporation of an incorrect nucleotide opposite the template nucleotide) of replicative DNA polymerases is in the order of 10^-4 to 10^-5.⁸ This already low rate of misincorporation is further decreased by several orders of magnitude through the proofreading exonuclease activity⁹ of DNA polymerases (to about 10^-6 to 10^-8)⁸ and by two to three additional orders of magnitude by the mismatch repair mechanism (to about 10^-9 to 10^-10)^8,10. Occasionally, misincorporations by DNA polymerase pass these proofreading and repair mechanisms and can then lead to mutations and cancer. The higher the original rate of misincorporation is, the higher the likelihood that this may happen. Therefore, the molecular basis for the fidelity of DNA polymerases has been the subject of intensive studies.^4,11-17 DNA polymerase fidelity is defined as the sum of the catalytic efficiency for incorporation of the correct nucleotide and the catalytic efficiency for incorporation of an incorrect nucleotide divided by the catalytic efficiency for the incorporation of the incorrect nucleotide.¹⁷ Mutations in DNA polymerases usually compromise their fidelity and are employed to study the molecular mechanism of misincorporation.^17-23 It should be noted that the outcome of the trade-off between efficiency and precision of DNA polymerases, leading to a certain probability of mutations in an organism's genome, is not limited to negative effects, e.g., cancer. These mutations also allow for the adaptation of the organism to its environment, and thus can benefit its fitness to survive in a changed environment, allowing for an evolution of the species.²⁴

Figure 1.

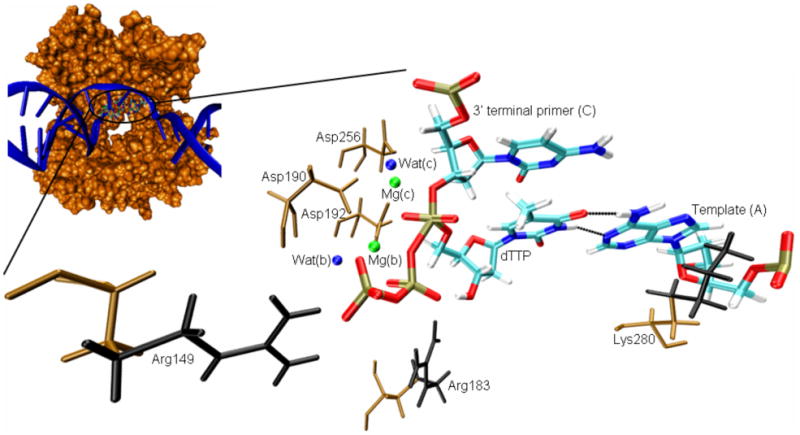
Transition state model of the active site of DNA polymerase β, including relevant residues in its vicinity. dTTP was generated by mutating the imide group between P_α and P_β of the dUTP analogue present in the crystal structure (2FMS³⁶) to a phosphoanhydride oxygen, followed by a mutation of the nucleic base from uracil to thymine. A bond was added between the deprotonated O3′ of the primer cytidine and P_α of the deoxythymidine triphosphate. For improved representation, the protein-DNA complex (small image) was rotated horizontally by approximately 180°, compared to the representation of the active site residues. Nucleotides are shown as sticks, colored based on atom type (cyan [C], white [H], blue [N], red [O], light brown [P]). The hydrogen bonds between the bases of template (A) and incoming dTTP are represented by dotted lines. Amino acids are shown as sticks, colored in brown. The amino acid side chain parts removed in the mutations of Arg149, Arg183, and Lys280 to alanine are colored in black. For simplicity, water oxygens are represented as blue spheres and magnesium ions are shown as green spheres.

DNA polymerase β (pol β), a small enzyme involved in base-excision repair, consists of 335 amino acids arranged in a single polypeptide chain and lacks exonuclease activity. Because of its relatively simple structure, it is a popular model enzyme for the larger replicative DNA polymerases.¹² Pol β has previously been used to computationally study the effects of mutations on catalytic efficiencies by calculating the binding free energy of transition state (TS) models (cf. Figure 1)^15,16, or by finding critical structural parameters that correlate with the observed mutation effects²⁵. We have hypothesized that the fit or misfit in the base binding site supports or interferes, respectively, with the chemical reaction in the catalytic site.¹⁵ The simulation studies have been carried out both using a conventional point-charge representation (Mg²⁺)¹⁵ or a cationic dummy atom model (MD₆²⁺)¹⁶ for the magnesium ions. Using the MD₆²⁺ model, we were able to computationally reproduce the experimentally observed effect of mutations on the incorporation efficiency of correct dNTPs, giving rise to the Watson-Crick base pairs A:T and G:C (in our notation the first letter designates the template base and the second letter the base of the incoming dNTP).¹⁶ However, we could not reproduce the experimentally observed fidelities (preference for the incorporation of the correct over the incorrect pyrimidine nucleotides opposite purine nucleotides, giving rise to transition mutations). Part of the problem are most likely the strong electrostatic interactions between the triphosphate part of the dNTP-TS model (bearing a formal charge of -5) with the two magnesium ions (formal charge of +2 each), whose contribution to the dNTP-TS model binding free energy overshadows the interactions between the bases in the nascent base pair.

In this report, we explore the utility of decomposing the dNTP-TS into smaller subunits that contribute individually to the binding free energy. Specifically, we ran independent scaled protein dipole/langevin dipole simulations in the linear response approximation version (PDLD/S-LRA)^26,27 to calculate the binding of the triphosphate-TS model and the incoming base separately for different enzyme variants (wild type [WT] as well as three different mutants) and different matched (G:C and A:T) and mismatched (G:T and A:C) nascent base pairs. We decompose the dNTP-TS into the triphosphate part and the base part and account for the different dielectric environments generated by either the charged metal ions and the triphosphate-TS, or the uncharged nascent base pair. Overall, we obtained a good correlation between our calculated binding free energies and a consistent experimental data set of catalytic efficiencies¹⁷ (correlation coefficient R of 0.93 [MD₆²⁺ model] and 0.91 [Mg²⁺ model], respectively). The implication of this finding will be discussed in the Concluding Remarks.

Background

As discussed in our previous work^14,15,28,29, in the likely situation that the chemical step is rate limiting we expect the rate of polymerization divided by the dissociation constant (k_pol/K_d) to determine the overall of DNA polymerases. In other words, if the dynamical effects are considered as the motions between the open and closed conformations, then it is difficult to see how it would be advantageous to use these as a mechanism to control replication fidelity. Fidelity is determined by the ratio between k_pol/K_d of wrong (W) and right (R) base pairs. If the rate-limiting step is the conformational transition between the open and closed conformations and the barrier for these states is much larger for W than for R, then there could, in principal, be conformational control of fidelity. However, this mechanism is in conflict with the chemical step being rate-limiting (see References 15^,16,30). If the chemical step is rate limiting, then it seems that the only way for conformational changes to control fidelity is that the TS for both W and R must occur in a different conformation than the reactant state (RS), and the barrier along the conformational axis in Figure 8 of Reference 29 is higher than the chemical barrier, and that this barrier will be higher in W than in R. Although we have not determined the conformational barriers (in part because it is not clear what, if any, conformational transition occurs in pol β.), our calculations are consistent with R having both the TS and RS in the same closed conformational region. As argued earlier, the situation with W is such that a barrier for the transition to the TS will only push the fidelity above its observed value.

Now some readers may wonder why we use k_pol/K_d, rather than k_cat/K_M (the catalytic constant divided by the Michaelis constant) or some other descriptor. First, we would like to clarify that we view the discussion of the exact selection (in particular when it is emphasized as crucial issue (e.g., ^31,32) as a major problem in the field. That is, the key issue in enzymology is how the enzyme reduces k_cat (or the rate constant for the chemical step), and to a much lesser extent the control of K_d.³³ In the case of k_cat, we frequently find an enormous effect of the enzyme. Thus, focus on the trivial difference between K_d and K_M (which is completely understood and rigorously formulated) diverts the community from the major role of the enzyme and from the puzzles of enzyme catalysis. In the case of large changes in k_pol/K_d, which occur in DNA replication fidelity, the question is what determines the change in this parameter and what it is related to in the protein sequence and structure, and not the trivial issue of how the rate will change with change in the substrate concentration.

At any rate, our task is to relate k_pol/K_d to the protein structure and this is done by calculating the TS binding free energy, obtaining (see supporting information of Reference 34):

$$\Delta G_{\mathit{\text{bind}}}^{\mathit{\text{TS}}}=\Delta g_{\mathit{\text{protein}}}^{‡}-\Delta g_{\mathit{\text{water}}}^{‡}=-\mathit{\text{RT}}ln\frac{k_{\mathit{\text{pol}}}}{K_d(\mathit{\text{RS}})}+\mathit{\text{RT}}ln{k}_{\mathit{\text{water}}}$$ (1)

where Δg^‡ is the activation barrier for the reaction in water or when catalyzed by the protein, respectively, R is the gas constant, T is the temperature, k_pol is the rate of polymerization, K_d (RS) is the equilibrium dissociation constant of dNTP in the reactant state, and k_water is the rate constant for the reference reaction in water.

Finally, before we move into the actual calculations we would like to clarify again what we view as the molecular origin of fidelity and how to look on this issue (cf. schematic representation given in Figure 2). That is, in order to quantify the origin of the structural control of fidelity, it is necessary to consider the interplay between the stabilization of the TS in the catalytic site and the binding site of the incoming base. Our previous work^13,14,28 suggests that it is the preorganization energy provided by the binding site that determines the binding of the incoming base. In the case of a matched base pair, the protein provides both a perfect base binding and catalytic site (cf. Figure 2a). The binding of an incorrect dNTP to the binding site leads to suboptimal binding of the incoming base to the template base (cf. Figure2b). The nucleotide can relax in order to achieve better binding between the bases, resulting in a reorganization of the environment at the base binding site. This leads to a disruption of the preorganization in the catalytic site, which results in a suboptimal interaction between the TS and the catalytic site, reducing the TS binding free energy (cf. Figure 2c). We include Figure 2 in view of the continuing discussion of fidelity in rather wage terms (e.g., ³⁵), and find the present study to provide major support to our point of view with regards to fidelity, allowing for the quantification and prediction of the fidelity of DNA polymerases.

Figure 2.

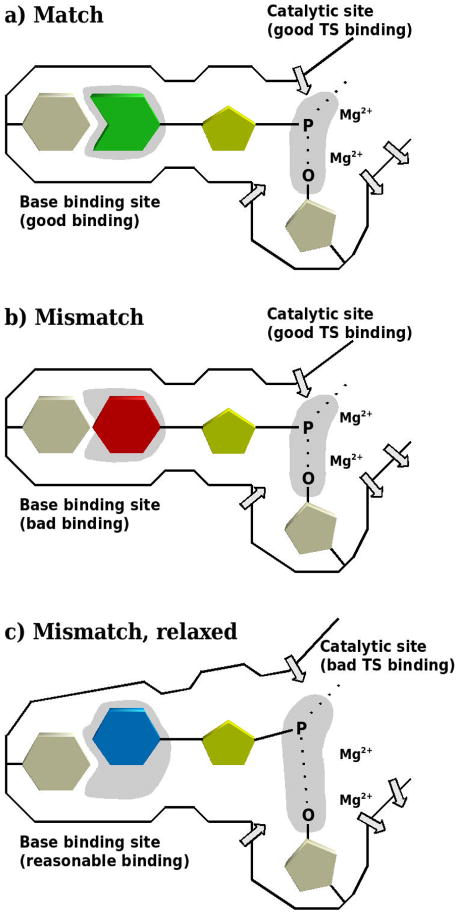
Schematic description of our point of view with regards to the molecular origin of the fidelity of DNA polymerases. In the case of a correct base pair (a), the protein provides both a perfect base binding and catalytic site (indicated as light gray areas). The binding of an incorrect nucleotide leads to suboptimal binding of the incoming base (b). This causes the protein to relax, thereby destroying the preorganization in the chemical part (c). Protein dipoles are indicated by arrows.

Computational Procedures

The X-ray crystal structure of human pol β (PDB accession code 2FMS³⁶) used for this study is in the closed conformation. It includes two Mg²⁺ ions in complex with a gapped DNA substrate and a nonhydrolyzable dUTP analogue (2′-deoxyruridine-5′[α,β]-imido triphosphate) opposite a template adenine. Deoxythymidine triphosphate (dTTP) was generated by mutating the imide group between P_α and P_β of the dUTP analogue to a phosphoanhydride oxygen, followed by the mutation of the base from uracil to thymine. Transition mutations of the template and the incoming base of the A:T matched nascent base pair were generated to yield the G:C matched base pair as well as the two mismatches A:C and G:T. It is useful to note that the A:C mismatch may be stabilized by protonation on the N1 position of adenine³⁷. However, in the present study neutral adenine is used as a template both for the A:T and the A:C base pairs. A better agreement between computational and experimentally observed results for the incorporation of the correct and the incorrect dNTPs may be obtained by considering a closed structure of pol β for correct incorporations and one or more partially open conformations for misincorporations.²⁹ Here, however, we investigate both matches and mismatches in the closed conformation (see Concluding Remarks for our rationale). It should be noted that purin:purin mismatches and pyrimidine:purin mismatches result in considerable structural rearrangements of the template DNA strand.³⁸ Therefore, we did not investigate such mismatches here.

Three mutants of pol β were generated by truncating the side chains of one of three charged amino acids (Arg149, Arg183, or Lys280) to C_β, yielding alanine. Self-consistent kinetic constants, all stemming from the same experimental study, have been determined for these mutants of rat pol β¹⁷ which shares 96% sequence identity with human pol β. All 14 amino acids differing between these two polymerases are located on the surface of the enzymes, which are identical in the active site.^39-41 The available experimental catalytic efficiencies (k_pol/K_d) were converted to the corresponding TS binding free energies (ΔG^TS_bind) using Equation 1 (k_water was taken from Reference 42). The resulting ΔG^TS_bind,obs as well as the original k_pol/K_d for the systems considered are summarized in Table I.

Table I.

Observed catalytic efficiencies (k_pol/K_d) and resulting TS binding free energies (ΔG^TS_bind,obs).^a

Pol β variant	A:T		G:C
	kpol/Kd [M-1s-1]	ΔGTSbind,obs [kcal/mol]	kpol/Kd [M-1s-1]	ΔGTSbind,obs [kcal/mol]
wild type	4,100,000	-14.6	6,600,000	-14.9
R149A	685,000	-13.5	920,000	-13.7
R183A	43,000	-11.8	440,000	-13.2
K280A	n.a.b	n.a.b	2,000,000	-14.1
Pol β variant	A:C		G:T
	kpol/Kd [M-1s-1]	ΔGTSbind,obs [kcal/mol]	kpol/Kd [M-1s-1]	ΔGTSbind,obs [kcal/mol]
wild type	1,200	-9.6	570	-9.1
R149A	312	-8.7	n.a.b	n.a.b
R183A	14.6	-6.8	2.6	-5.8
K280A	n.a.b	n.a.b	220	-8.5

^aThe pre-steady state experiments for the incorporation of T or C opposite A (A:T and A:C) or G (G:T and G:C) were all conducted in the same laboratory under the same conditions, allowing for a consistent set of data.¹⁷ Binding free energies were calculated using Equation 1; the rate constant for the reference reaction in water (k_water = 2.8 × 10^-4 M^-1s^-1) was taken from Reference 42.

^bn.a., not available.

The pentacoordinated TS models are based on the regular force field rather than on empirical valence bond (EVB) parameters, but are constrained to give EVB structures¹⁴. This simplified approach was used since our study focuses on LRA adiabatic charging and PDLD/S calculations, where the exact nature of the TS internal energy does not play a significant role (we basically compare the solvation energy of the TS in the protein and in water)

The TS models were generated by deleting the proton of the primer 3′ hydroxyl, adding a bond between the primer O3′ and P_α of the dNTP, and by extending the bond between P_α and the oxygen bridging to P_β to 2.2 Ź⁴, using a force constant of 1,000 kcal mol^-1 Å^-2, as described previously¹⁶. The charges of the TS complex were the same as in our previous study, that is, a formal charge of -4.5 for the triphosphate-TS part of the dNTP, and -0.5 for the deoxyribose of the primer.¹⁶ The partial charges stem from calculations at the B3LYP/6-31G* level using a PCM solvation model⁴³ implemented in Gaussian03⁴⁴ and are the same as those summarized in Table 1 of Reference 15, with the following exceptions: both in the present study and in Reference 16 P_α and the primer O3′ bear charges of 0.955 and -0.655, respectively. Two different models were used to represent the octahedrally coordinated Mg²⁺ ions. In addition to the conventional one-atom model, a magnesium-cationic dummy atom model was used as reported recently, consisting of a central atom carrying a charge of -1, surrounded by six dummy atoms, each with a formal charge of 0.5 (see Table 1 of Reference 16 for relevant force field parameters). In our previous work, this model allowed for a more accurate representation of the structure and energetics of pol β than the conventional one-atom representation.¹⁶

All calculations were carried out at 310 K (which is the same temperature used in the experiments the catalytic efficiencies were obtained from¹⁷ using either the all-atom LRA method^27,30, or the PDLD/S-LRA method^26,27. Region I contained either the full dNTP-TS model (incoming dNTP and attacking O3′ of the primer), or – where two separate calculations were run – the triphosphate-TS part or the base part of the model, respectively. All other atoms included in the explicitly treated simulation sphere were contained within region II. In order to maintain the structure of the DNA during the calculations, a positional restraint of 0.5 kcal mol^-1 Å^-2 was applied on all atoms both in region I and II. This restraint is extremely small and simply helps the stability of the calculations by preventing excursions, which is particularly important for the typically short PDLD/S calculations. Like in our previous study¹⁶, the structures were equilibrated for 101 ps at 30 K and for 100 ps at 310 K. Then, the POLARIS module of MOLARIS²⁶ was used to automatically generate 30 molecular dynamics configurations for the uncharged and charged states at 310 K, totaling a simulation length of 150 ps.

Results and Discussion

In our previous work, we examined the effect of mutations on the catalytic efficiencies of pol β. The magnesium cations involved were represented either as conventional one-atom Mg²⁺ ions¹⁵, or by a dummy atom model¹⁶, which was found to reproduce experimental data with higher accuracy for both Michaelis and TS complexes. For purine:pyrimidine matches (A:T and G:C) in TS structures of wild-type pol β and three of its mutants (R149A, R183A, and K280A), an excellent correlation (R=0.97) between experimentally determined binding free energies and the calculated values was reported.¹⁶ Here, this study is extended to the two purine:pyrimidine mismatches A:C and G:T for TS structures of the same pol β variants. The availability of experimental data, stemming from the same study and measured under the same conditions in the same laboratory, provides a self-consistent set of reference values.¹⁷

The three mutations were selected based on their location near the active site (cf. Figure 1) and their significant effect on the catalytic efficiency of pol β (cf. Table I). Arg149 interacts with P_γ of the incoming dNTP (4.6 Å away), stabilizing the ground state complex. Its mutation to alanine (R149A) results in a lowered catalytic efficiency by a factor of about 6 (A:T), 7 (G:C), and 4 (A:C), respectively, compared to wild-type pol β. Arg183 helps to stabilize the transition state by interacting with P_β (over a distance of 3 Å). In R183A, k_pol/K_d is lowered 95-fold (A:T), 15-fold (G:C), 82-fold (A:C), and 219-fold (G:T), respectively. Lys280 is located 3.4 Å away from the template base and helps to stabilize the template purines.⁴⁵ Its mutation to alanine (K280A) lowers the catalytic efficiency to about a third in both G:C and G:T. In three cases (R149A/G:T, K280A/A:T, and K280A/A:C), no kinetic parameters were measured during the experiments the reference data was taken from.¹⁷ The deduced values for the TS binding free energies in the mutants differ between 0.6 and 3.4 kcal/mol from the wild-type enzyme (cf. Table I).

At first, calculations were run for the pol β structures with mismatched base pairing (A:C and G:T), using the same procedures as outlined in our previous work¹⁶, where we presented the results for the matched base pairs (A:T and G:C). A clear deviation can be found between the matched and mismatched structures, resulting in two parallel correlations separated by approximately 5 kcal/mol (cf. Figure 3). While excellent correlations were obtained individually for both the structures with the matched (R=0.97, as reported in our previous study¹⁶) and the mismatched base pairs (R=0.96), the overall correlation coefficient of 0.55 is poor. As discussed and demonstrated in Reference 15, the different magnitude of our results, compared to the experimentally determined free energies, is mainly due to the fact that no dielectric constant was used in our all-atom LRA calculations. The dielectric is needed to account (implicitly) for major protein reorganization and water penetration effects that are not captured within reasonable simulation time for such highly charged systems. As reported previously¹⁶, the MD₆²⁺ model allows for significantly better agreement between experimental and calculated free energies (Mg²⁺ data not shown), even though it still leads to overestimated absolute free energies.

Figure 3.

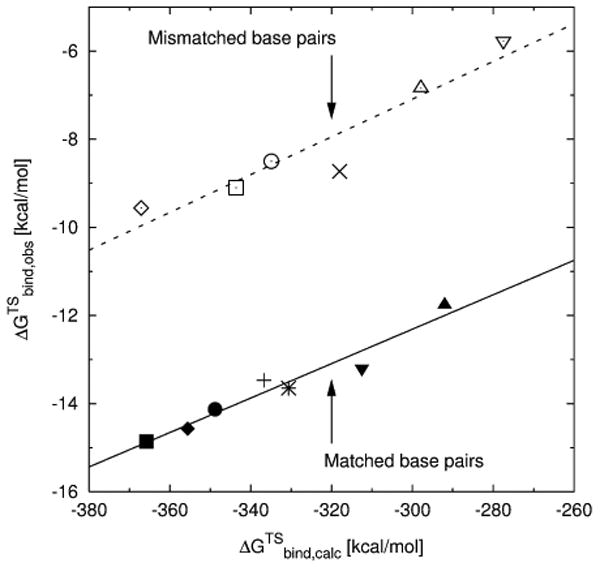
Plot of the experimentally determined TS binding free energies (ΔG^TS_bind,obs) versus the calculated TS binding free energies (ΔG^TS_bind,calc) with the entire dNTP-TS in region I, using the LRA method and the MD₆²⁺ magnesium model. The correlation for the mismatches (dashed line) is shifted by about 5 kcal/mol, compared to the matches (solid line, taken from Reference 16). The nascent base pairs for wild-type pol β are: (◆) A:T, (■) G:C, (◊) A:C, (□) G:T; for the R149A mutant: (+) A:T, (✳) G:C, (×) A:C; for R183A: (▲) A:T, (▼) G:C, (△) A:C, (∇) G:T; and for K280A: (●) G:C, (○) G:T.

It is useful to note that the relative binding free energies of the base-moiety of incoming mismatched dNTPs have previously been calculated for wild-type pol β-DNA-dNTP ternary complexes, using the LRA method.²⁸ Apparently, the current work gave larger differences in the binding of W and R than those obtained in Reference 28 (the differences are 5 kcal/mol and 8 kcal/mol, respectively, for the A:C and G:T mismatches). This may be due to the fact that the LRA calculations of Reference 28 involved more extensive simulations and thus obtained larger explicit compensation by the environment.

In any case, the microscopic LRA calculations resulted in a major overestimation of the observed trend, indicating that the current simulations do not provide a major part of the compensation by reorganization effects and that introducing proper dielectric constants can provide the missing effect. Furthermore, considering our experience from previous studies it appears that the dielectric constant should be different for the highly charged phosphate part and the neutral base part. Thus, we studied the contributions and specific environments of the different parts of the incoming dNTP-TS. It can be broken up into three separate parts: base, sugar and triphosphate-TS (which includes O3′ of the primer, cf. Figure 4).

Figure 4.

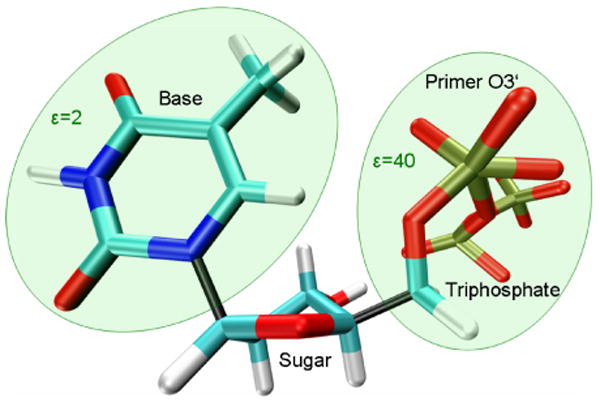
Breaking up the dNTP-TS (dTTP-TS shown) for calculating the contributions of the base and the triphosphate part separately, taking into consideration the different dielectric environments. The dielectric constant ε used for the calculations with the base in region I was 2. The sugar contribution was found to be negligible and thus included as part of the “protein” (region II), rather than as substrate (region I). Due to the highly charged environment of the triphosphate-TS fragment, a dielectric constant of 40 was used for this part of the molecule; note that the O3′ atom of the primer was included in region I and thus is also shown in this representation. The color scheme is according to atom type (cyan [C], white [H], blue [N], red [O], light brown [P]); the bonds connecting the three parts of the dNTP are represented in black.

Our calculations revealed that the contribution of the sugar, which interacts neither with the template base nor with the highly charged magnesium ions, is insignificant (data not shown). This leaves us with the base, forming hydrogen bonds with the template base, and the triphosphate-TS that carries a formal charge of -5 and interacts with the two Mg²⁺ ions. These strong electrostatic interactions, which overshadow the interaction between incoming and template base of the nascent base pair, were accounted for by using different dielectric constants for the base and the triphosphate-TS in our calculations: separate calculations for the base (calculated with a dielectric constant ε of 2) and the triphosphate-TS (ε=40) were run. While the chosen dielectric constants allow for the best agreement between observed and calculated data, there are also other combinations of dielectric constants that give only slightly less accurate results (e.g., ε=2 for the base and ε=20 for the triphosphate-TS). The PDLD/S-LRA method was chosen because in this specific case it yields calculated data that is in slightly better agreement with the experimentally observed data (cf. Table II; see Supplementary Material for a more detailed discussion). The results for base and triphosphate-TS were combined and then compared to consistent experimental catalytic efficiencies¹⁷. A good correlation between the calculated values and the experimental values was obtained, both when using the MD₆²⁺ (R = 0.93, Figure 5a) and the Mg²⁺ model (R=0.91, Figure 5b). Based on calculations with structures stemming from different initial equilibrations, the average standard deviation is about 0.7 kcal/mol (MD₆²⁺ model) and 0.4 kcal/mol (Mg²⁺ model), respectively. Compared to the magnesium-cationic dummy atom model, using the one-atom model resulted in a small shift by about 1.5 kcal/mol, while mostly showing the same pattern (see Supplementary Material for more details). In both cases, when using this new approach, the triphosphate-TS no longer overshadows the base pairing. The base part of the dNTP-TS represents the main contribution toward the correlation between experimental and calculated data, which is additionally strengthened by the triphosphate-TS results (cf. Table II). The optimal dielectric constants used in the calculations of the contributions of the base and the triphosphate-TS are smaller than the values that would reproduce the observed values. However, using larger dielectric constants (e.g., 4 for the base and 80 for the triphosphate-TS) would result in a slightly reduced correlation. At any rate, the correlation obtained here is quite encouraging.

Table II.

Correlation coefficients between experimentally determined and calculated TS binding free energies.^a

	Base		Triphosphate-TS		Sum
	MD62+	Mg2+	MD62+	Mg2+	MD62+	Mg2+
PDLD/S-LRA	0.84	0.86	0.46	0.41	0.93	0.91
LRA	0.82	0.79	0.24	0.14	0.50	0.44

^aThe correlations between ΔG^TS_bind,obs and ΔG^TS_bind,calc for the base and the triphosphate part of the dNTP-TS, as well as the sum of their contributions, were obtained for the PDLD/S-LRA and the LRA method and for two different magnesium models (MD₆²⁺ and Mg²⁺). Note that the weak correlation for the sum of base and triphosphate-TS when using the LRA method is due to not using a dielectric constant during the calculations.

Figure 5.

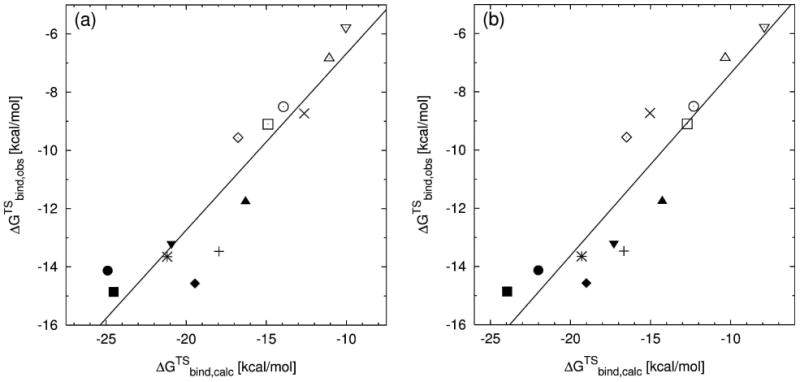
Plot of the experimentally determined TS binding free energies (ΔG^TS_bind,obs) versus the calculated TS binding free energies (ΔG^TS_bind,calc) from separate PDLD/S-LRA calculations of the triphosphate (using a dielectric constant of 40) and the base part (at ε=2) of the dNTP-TS. The magnesium ions are represented by the MD₆²⁺ (a), and the Mg²⁺ (b) model, respectively. The nascent base pairs for wild-type pol β are: (◆) A:T, (■) G:C, (◊) A:C, (□) G:T; for the R149A mutant: (+) A:T, (✳) G:C, (×) A:C; for R183A: (▲) A:T, (▼) G:C, (△) A:C, (∇) G:T; and for K280A: (●) G:C, (○) G:T.

Based on our results, we believe that we can use the current approach to predict the catalytic efficiencies for various enzyme/nascent base pair combinations that have not been determined yet (see Table III and Supplementary Material for more details). These predictions could be tested using the same methodology as in the experiments (carried out by Kraynov et al.¹⁷) this study is based on.

Table III.

Predicted TS binding free energies (ΔG^TS_bind,pred) and catalytic efficiencies (k_pol/K_d).^a

Nascent base pair	Pol β variant	MD62+ model			Mg2+ model
		ΔGTSbind,calc [kcal/mol]	ΔGTSbind,pred [kcal/mol]	kpol/Kd [M-1s-1]	ΔGTSbind,calc [kcal/mol]	ΔGTSbind,pred [kcal/mol]	kpol/Kd [M-1s-1]
A:T	K280A	-18.0	-11.6	32,600	-19.3	-13.6	847,300
A:C	K280A	-15.9	-10.1	2,800	-16.6	-11.6	31,700
G:T	R149A	-13.0	-8.1	107	-12.9	-8.8	342

^aThe predicted free energies are based on the correlation between ΔG^TS_bind,calc and available ΔG^TS_bind,obs shown in Figure 4. Catalytic efficiencies based on ΔG^TS_bind,pred were calculated using Equation 1.

Concluding Remarks

The approach of decomposing the dNTP-TS and calculating the contributions of the base and triphosphate parts separately improves our ability to predict the effect of matched versus mismatched base pairing in the nascent base pair, as well as that of mutations in DNA polymerases, on fidelity. It enables us to account for the base-base interactions, without them being overshadowed by the electrostatic interactions between the highly charged triphosphate-TS and magnesium ions.

The crystal structure of pol β used in this report is in a closed conformation and contains a purine:pyrimidine matched Watson-Crick base pair. Based on this structure, we generated all matched and mismatched structures for both wild-type and mutant pol β. While there are some interesting structural changes upon change from matched to mismatched base pairs^29,38, the protein remains at a partially closed conformation and the TS energy at the closed conformation is always higher than that at the TS. Since our relaxation process for the structures with mismatched base pairs, which starts at the closed structure with the matched base pair, does not force the protein to fully move to the relaxed protein structure, our calculations provide an upper limit to the relevant estimate. Nevertheless, the excellent agreement between the calculated and observed fidelity indicates that our dielectrics treatment probably captures the missing relaxation process.

The effect of MD₆²⁺, allowing for a more accurate reproduction of the crystal structure than the conventional magnesium model (see Reference 16), has also been observed in the current study (slightly smaller distances for Mg(b)-Mg(c), Mg(b)-O1A, and Mg(b)-O2B). Nevertheless, this does not affect our ability to reproduce experimental TS binding free energies, when using PDLD/S-LRA calculations for the decomposed dNTP-TS. Due to the advantages the cationic dummy atom model offers with regards to structural effects and its ability to reproduce experimentally observed free energies equal to, or better than the conventional Mg²⁺, it remains our magnesium model of choice.

As clarified in our previous work (e.g., ^15,29), DNA polymerase fidelity is controlled by the interplay between the poor preorganization (and the corresponding poor binding) in the base binding site and the binding of the chemical part of the transition state at the chemical site. This compensation reflects a complex balance of forces where the accommodation of the incorrect base results in structural rearrangements in the chemical site that reduce the TS binding energy (cf. Figure 2). Here, the focus in the analysis of the information transfer can be on the exact nature of the conformational changes, or on the prediction of the resulting energy changes. Our previous work¹⁵ introduced fidelity matrixes that allow to relate the information transfer to the corresponding network of interaction. However, this instructive approach does not yet provide a quantitative prediction of the corresponding fidelity. The present work, on the other hand, focuses on obtaining a less rigorous but more reliable way of predicting the fidelity by using effective dielectrics that approximate the effect of the conformational changes. Remarkably, this simple approach seems to provide a very effective way of predicting DNA polymerase fidelity. This finding provides further support to the idea that fidelity represents mainly an electrostatic effect, as is the case with many other allosteric systems (e.g. ^46-48).

It may be useful to comment here on the implication of Reference 49 that pre-chemistry steps can have a major effect on fidelity. Apparently, as long as the barriers for the pre-chemistry steps (e.g., the open to closed conformational change) are significantly lower than the chemical barrier they cannot change the kinetics and the corresponding fidelity (except in some particular substrate saturation conditions). That is, the reaction rate is determined by the difference between the energy of the enzyme plus substrate (E + S) state and the TS for the chemical step. Having many barriers between the open and closed configurations in the binding step of Figure 8 of Reference 29 is not going to change the kinetics as long as these barriers are smaller than the TS barrier. An additional insight is obtained for example from inspection of Figure 1 of Reference 27. This figure describes the calculated barriers for the pre-chemistry steps. Since the barriers for W are smaller than that for R, it is very hard to see how these barriers could account for the observed fidelity. The obvious answer is that the real difference is in the chemical step. It seems to us that the fact that we were able to reproduce the observed change in fidelity can be considered as a verification of the above arguments, since it is extremely unlikely that calculations based on pre-chemistry control of fidelity can reproduce the observed trend.

Finally, we believe that the present study provides major support to our point of view concerning the molecular origin of fidelity as represented in Figure 2 and discussed in the Background section. As demonstrated by our TS binding free energy decomposition approach, the theory behind Figure 2 allows for the quantification and prediction of the fidelity of DNA polymerases.