Lung Dosimetry for Radioiodine Treatment Planning in the Case of Diffuse Lung Metastases

Abstract

The lungs are the most frequent sites of distant metastasis in differentiated thyroid carcinoma. Radioiodine treatment planning for these patients is usually performed following the Benua– Leeper method, which constrains the administered activity to 2.96 GBq (80 mCi) whole-body retention at 48 h after administration to prevent lung toxicity in the presence of iodine-avid lung metastases. This limit was derived from clinical experience, and a dosimetric analysis of lung and tumor absorbed dose would be useful to understand the implications of this limit on toxicity and tumor control. Because of highly nonuniform lung density and composition as well as the nonuniform activity distribution when the lungs contain tumor nodules, Monte Carlo dosimetry is required to estimate tumor and normal lung absorbed dose. Reassessment of this toxicity limit is also appropriate in light of the contemporary use of recombinant thyrotropin (thyroid-stimulating hormone) (rTSH) to prepare patients for radioiodine therapy. In this work we demonstrated the use of MCNP, a Monte Carlo electron and photon transport code, in a 3-dimensional (3D) imaging–based absorbed dose calculation for tumor and normal lungs.

Methods

A pediatric thyroid cancer patient with diffuse lung metastases was administered 37MBq of ¹³¹I after preparation with rTSH. SPECT/CT scans were performed over the chest at 27, 74, and 147 h after tracer administration. The time–activity curve for ¹³¹I in the lungs was derived from the whole-body planar imaging and compared with that obtained from the quantitative SPECT methods. Reconstructed and coregistered SPECT/CT images were converted into 3D density and activity probability maps suitable for MCNP4b input. Absorbed dose maps were calculated using electron and photon transport in MCNP4b. Administered activity was estimated on the basis of the maximum tolerated dose (MTD) of 27.25 Gy to the normal lungs. Computational efficiency of the MCNP4b code was studied with a simple segmentation approach. In addition, the Benua–Leeper method was used to estimate the recommended administered activity. The standard dosing plan was modified to account for the weight of this pediatric patient, where the 2.96-GBq (80 mCi) whole-body retention was scaled to 2.44 GBq (66 mCi) to give the same dose rate of 43.6 rad/h in the lungs at 48 h.

Results

Using the MCNP4b code, both the spatial dose distribution and a dose–volume histogram were obtained for the lungs. An administered activity of 1.72 GBq (46.4 mCi) delivered the putative MTD of 27.25 Gy to the lungs with a tumor absorbed dose of 63.7 Gy. Directly applying the Benua–Leeper method, an administered activity of 3.89 GBq (105.0 mCi) was obtained, resulting in tumor and lung absorbed doses of 144.2 and 61.6 Gy, respectively, when the MCNP-based dosimetry was applied. The voxel-by-voxel calculation time of 4,642.3 h for photon transport was reduced to 16.8 h when the activity maps were segmented into 20 regions.

Conclusion

MCNP4b–based, patient-specific 3D dosimetry is feasible and important in the dosimetry of thyroid cancer patients with avid lung metastases that exhibit prolonged retention in the lungs.

Lungs are the most frequent distant metastasis site in thyroid cancer, occurring in 7% of all papillary thyroid carcinoma patients and >80% of those with disseminated diseases (1,2). Furthermore, nearly half of the fatalities in thyroid cancer are caused by pulmonary failure (3). Past studies have suggested that small repeated doses tend to cause loss of iodine avidity in metastases, which develop into highly malignant anaplastic carcinoma. On the other hand, large ¹³¹I doses have the potential to induce radiation pneumonitis and pulmonary fibrosis (4). Clinically, one widely adopted dose-planning method developed by Benua and Leeper constrains the therapeutic administered activity so that absorbed dose to blood does not exceed 200 cGy and the whole-body retention does not exceed 4.44 or 2.96 GBq (120 or 80 mCi) at 48 h after administration in the absence or presence of iodine-avid diffuse lung metastases, respectively (5). Implementation of the Benua–Leeper method has reduced, if not eliminated, fatalities associated with radiation-related side effects such as bone marrow suppression and radiation pneumonitis after radioiodine therapy of thyroid cancer. However, it is possible to envision cases in which more precise estimates of the absorbed dose to normal organs and tumors could be critical for planning radioiodine therapy (6), particularly in patients with iodine-avid lung metastases.

Several approaches for estimating absorbed dose have been developed. The most commonly adopted approach is based on the MIRD schema using tabulated whole-organ dose conversion coefficients (S values). Computer software packages, such as MABDOSE and OLINDA, have been developed for standard phantom-based dosimetry (7,8). In calculating absorbed dose to tumor and normal organs, where the normal organ anatomy is influenced by the presence of tumor, a standard phantom-based approach is not easily applicable and, instead, patient-specific 3-dimensional (3D) imaging–based methodologies are appropriate.

Combined-modality imaging technologies such as PET/CT and SPECT/CT, by providing the spatial activity distribution in the context of anatomic information, have significantly advanced the ability to perform 3D imaging–based, patient-specific dosimetry (9–19). New iterative reconstruction methodologies that incorporate anatomic information from CT have led to improved image quantification and resolution by applying more accurate compensation for attenuation, scatter, collimator–detector response, and septal penetration. These advances have resulted in image-derived spatial activity distributions with substantially improved resolution and accuracy (12,17,20–22). Repeated imaging over several time points after tracer injection enables reconstruction of the time–activity curve within the region of interest (ROI), and the cumulated activity in each ROI can be obtained by integrating this curve. Such 3D data are collected in a voxel format according to the resolutions of the imaging modalities and converted into appropriate input format for further absorbed dose calculation.

Several patient-specific dose calculation codes have been developed using either a dose point-kernel convolution technique (8,23) or Monte Carlo–based simulation packages, such as EGS4 or MCNP (10,13,19). The MCNP4b code was developed at Los Alamos National Laboratory and is capable of neutron, electron, and photon transport (24). The repeated structure and lattice features of the MCNP4b package are well suited to describe the complex geometry and composition of human tissues on a voxel basis (25). Tallies of the energy deposited in ROIs, such as lung tissue or tumors, during photon and electron transport are then used to calculate dose distributions in theses regions.

Lungs bearing diffuse metastases often are dose limiting after the bone marrow in patients undergoing radioiodine therapy for thyroid cancer. Accurate calculation of lung absorbed dose, however, is difficult in the presence of disseminated tumors because the disseminated disease leads to a heterogeneous tissue density and composition that complicated dose calculation. The assumption that electron energy is locally deposited also becomes invalid due to low density of normal lung tissue. Furthermore, because of the arborizing anatomic structure of the lungs, dose deposition at different locations, such as at bronchi versus alveoli, will likely have different consequences in terms of toxicity. Accurate dose calculation in the lungs, therefore, favors the use of 3D imaging–based, patient-specific Monte Carlo calculations.

In this work, we compared treatment planning using different dosimetry approaches for determining absorbed doses to lungs and tumors in thyroid cancer patients with iodine-avid lung metastases. A specific clinical case is used to demonstrate these methodologies. It is important to note that dosimetry-based planning of administered activity has not yielded superior tumor control compared with standard fixed activity of 3.8–5.6 GBq (26,27). This may reflect the state of sophistication of dosimetry at the time; the issue needs to be reexamined in light of recent innovations in dosimetry methodology and advances in instrumentation and reconstruction software.

MATERIALS AND METHODS

Study Patient

The patient is a female who presented at 11 y of age with a 4-cm follicular variant of papillary thyroid cancer. She initially underwent near-total thyroidectomy, with histopathologic findings of a diffusely infiltrating tumor with capsular and vascular invasion. The postoperative serum thyroglobulin concentration was 5,790 ng/mL. An empiric 3.7-GBq (100 mCi) ¹³¹I dose was administered without preceding diagnostic imaging at another center, where the posttreatment scan demonstrated intense activity diffusely in both lungs; a chest CT scan revealed diffuse bilateral small pulmonary nodules. At 13 y of age she was referred for repeat ¹³¹I therapy, and she had been withdrawn from her chronic thyroxine therapy for >4 wk. She had dyspnea on mild exertion, requiring supplemental portable oxygen. On examination, the patient was clinically euthyroid and comfortable at rest with a well-healed thyroidectomy scar, no palpable thyroid tissue or cervical adenopathy, and lungs that were clear to percussion and auscultation. Her serum thyrotropin (thyroid-stimulating hormone) (TSH) concentration was 8 mU/L, presumably due to her burden of functioning metastatic thyroid tumor tissue; and her serum thyroglobulin was 4,654 ng/mL. Pulmonary function testing revealed a normal carbon monoxide diffusing capacity but significant exertional arterial oxygen desaturation consistent with a right-to-left arterial shunt, presumably due to her extensive lung metastases.

Dosimetric Studies

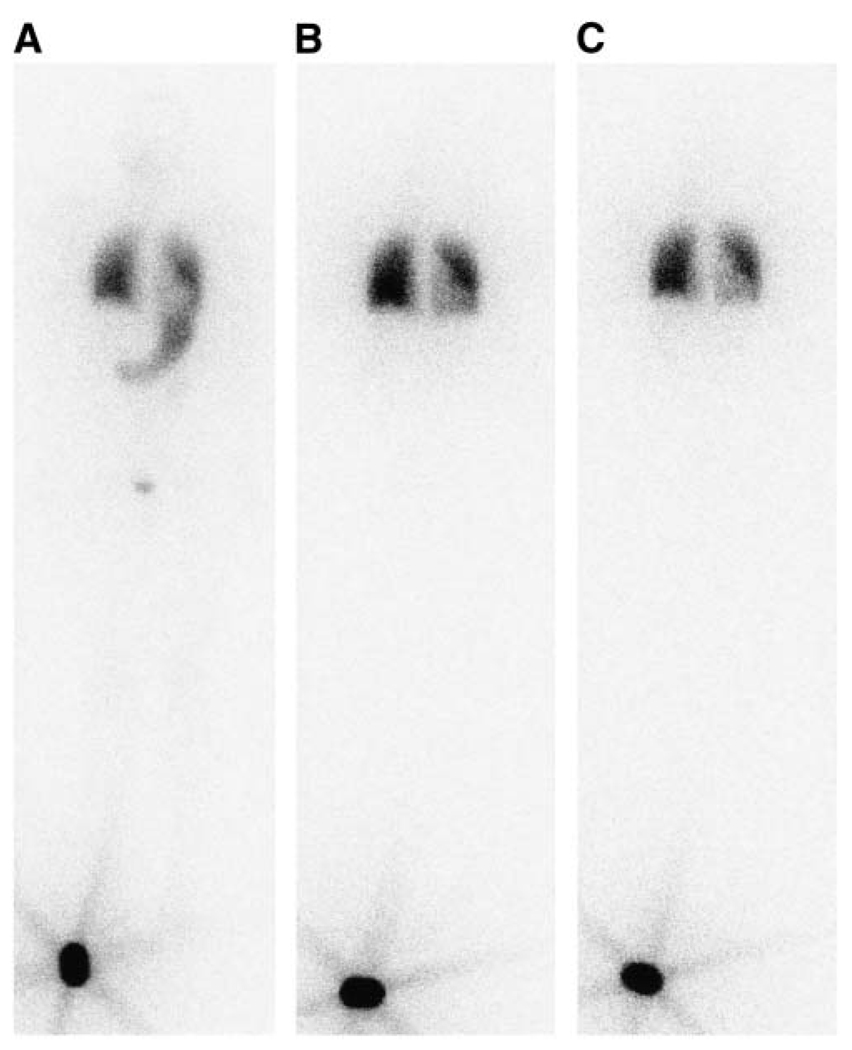
The patient was administered 37 MBq (1.0 mCi) of ¹³¹I after recombinant TSH (rTSH), 0.9 mg/d intramuscularly for 2 d with the latter rTSH dose 24 h earlier. Tracer uptake was followed by whole-body probe measurement (Captus 2000 Thyroid Uptake System) and planar imaging for 4 consecutive days. The whole-body clearance and effective half-life were obtained by fitting to a monoexponential curve. The time–activity curve and the percentage of activity retained in the lungs were determined by drawing ROIs over the lungs on the whole-body planar images. Anterior and posterior counts were corrected for attenuation using distance measurements obtained from CT. A calibration standard was placed beside the patient during the scan (Figs. 1A–1C, bottom left). SPECT/CT images over the patient’s chest were obtained at 27, 74, and 147 h after tracer injection with a Millennium VG Hawkeye system (GE Healthcare). Blood (1.0 mL) was collected at 2, 4.3, 26, 48.4, 72.5, and 95.2 h after tracer injection and counted. The blood clearance of radioiodine for this patient was rapid, and the blood dose was not a constraint on recommended administered activity.

FIGURE 1.

Whole-body planar projection (anterior view) of radioactive iodine distribution 3 h (A), 26 h (B), and 146 h (C) after diagnostic administration of 37 MBq. A standard (~18.5 MBq) was placed by the patient’s right foot during scan. Stomach and bladder can be seen on 3-h scan. Activity is localized to both lungs and retained there 146 h after injection. Gray level intensity in part of left lung is weaker due to overlap of heart.

Dose-Rate–Based “80-mCi Rule”

To estimate the administered activity using the Benua–Leeper constraints on whole-body activity at 48 h, the 80-mCi rule (no more than 2.96 GBq (80 mCi) retained in whole body at 48 h after administration if diffuse lung disease is present) was converted to a dose-rate rule (28). This was accomplished by using the adult female lung-to-lung S value (OLINDA) to convert 2.96 GBq (80 mCi) in lungs to a dose rate. The calculated lung dose rate was then converted to a corresponding activity by using the lung-to-lung S values for this patient scaled with body weight from the standard phantom modeling a 15-y old (OLINDA) (7). The 48-h activity thus calculated was extrapolated back to time zero using the measured lung kinetics to give equivalent administered activity for this patient. This approach is based on the assumption that the 2.96 GBq (80 mCi) at 48 h actually represents a dose-rate limit and this limit also applies to pediatric cases.

Whole-Organ, S-Value–Based Dosimetry

An estimate of the recommended administered activity was obtained using the maximum tolerated dose (MTD) to the lungs. An MTD of 27.25 Gy to the lungs was chosen on the basis of a myeloablative radioimmunotherapy study of B-cell lymphoma (29). A lung-to-lung S value of 5.16 ×10⁻⁵ mGy/MBq-s for a phantom modeling a 15-y old was used (7). Because >80% of the whole-body activity was in the lungs, lung kinetics derived from planar whole-body imaging were used to estimate the cumulated activity and absorbed dose per unit administered activity. This value was then used to estimate the recommended administered activity based on a lung MTD constraint.

Monte Carlo, 3D Imaging–Based Dosimetry

The recommended administered activity was also estimated using a fully 3D patient-specific, Monte Carlo–based dose calculation. SPECT was used to define the spatial distribution of decays at each of the 3 time points collected. The CT portion of the study at each time point was used to generate a density matrix for use in the Monte Carlo calculation. The SPECT reconstruction and CT/SPECT coregistration were performed with the commercially available Millennium VG Hawkeye system (GE Healthcare) with a 1.59-cm-thick crystal.

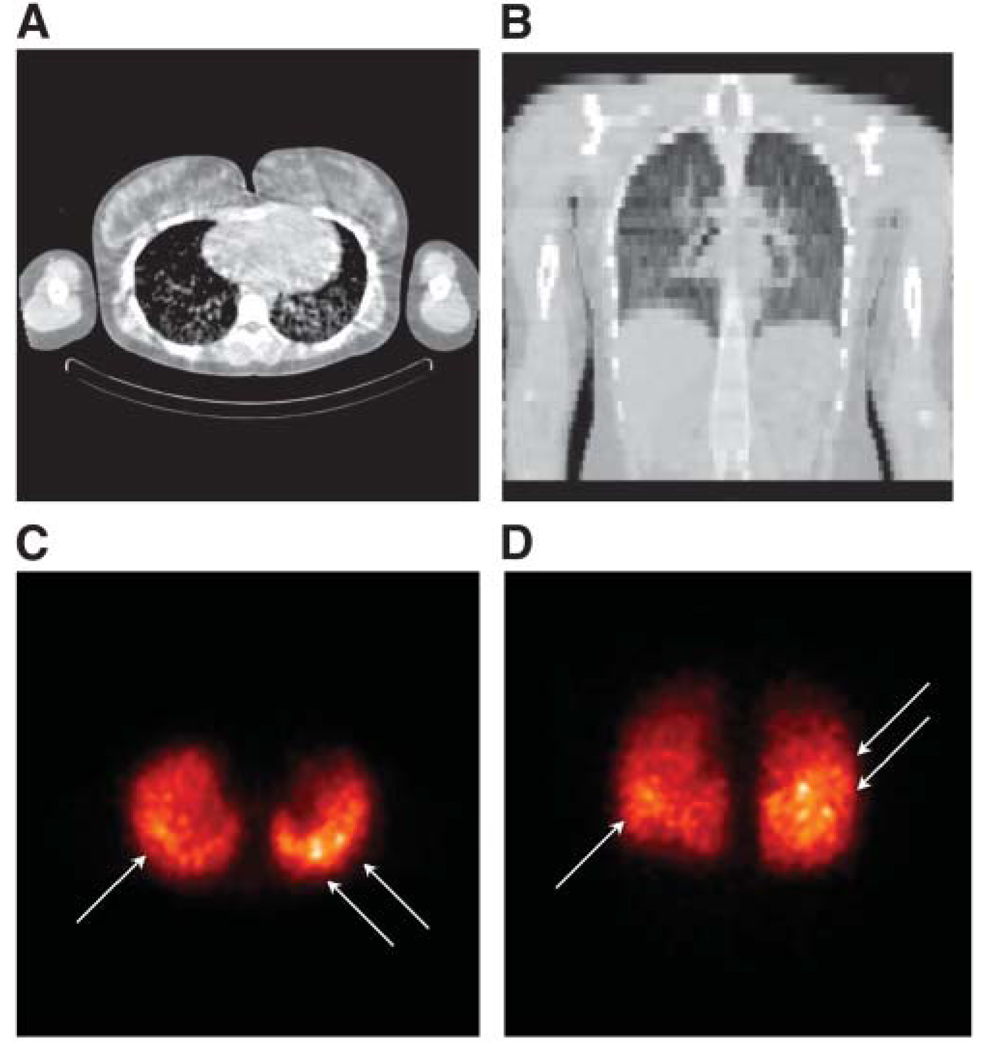
The images were reconstructed using ordered-subsets expectation maximization with compensation for attenuation, patient scatter, and the collimator–detector response, including septal penetration and scatter. Ten iterations with 24 subsets for iteration were used (21). Compensation for collimator–detector response results in improved image resolution and reduced high-frequency noise but introduces a correlated noise with a lumpy texture. This correlated noise can be seen in the lungs in the images shown in Figure 2. However, the hot spots indicated by the arrows (Figs. 2C and 2D) have an intensity that is much greater than that of the noise, indicating that they reflect tumors with high-activity uptake.

FIGURE 2.

Selected transverse (A) and coronal (B) CT images (obtained from CT portion of SPECT/CT study and, therefore, of low resolution) and corresponding maximum-intensity-projection (MIP) images of transverse (C) and coronal (D) SPECT slices are shown. Loci with strong activity uptake are indicated by arrows. MIP images were generated using the MIAU software package.

Reconstructed images were converted to units of activity per voxel by dividing the reconstructed pixel value by the measured sensitivity of the collimator–detector system and the acquisition time. Using an algorithm that recognizes the density difference between lungs and surrounding tissues, both CT and SPECT images were cropped so that the view was limited to only the lungs (21). Final coregistered lung images from the 3 time points consisted of 50,000, 46,069, and 43,872 voxels within a 71 × 64 × 46 matrix. The corresponding activity map for each time point was subsequently represented with an activity probability density matrix that is suited for MCNP4b input. The cumulated activity within each voxel can be obtained by integrating the monoexponential clearance curve in each voxel obtained from the 3 SPECT/CT examinations (11,30). However, due to the effect of breathing motion during the scans and imperfect registration, voxel-by-voxel cumulated activity estimation was not used because it could lead to errors in cumulated activity calculation. An alternative approach was taken in which the specific absorbed doses were calculated for each density/activity map obtained from the 3 SPECT/CT images. Cumulated activity was divided into 3 parts using the clearance curve, and each part was multiplied with the corresponding specific absorbed dose and was summed to get total doses to tumors and the normal lungs:

$$D(T)={\displaystyle \sum _{i=1}^3{S}_i(T,LV)\frac{A_0}{\lambda }(\mathit{\text{Exp}}(-\lambda t_{i-1}))-(\mathit{\text{Exp}}(-\lambda t_i)),}$$ Eq. 1

$$D(L)={\displaystyle \sum _{i=1}^3{S}_i(L,LV)\frac{A_0}{\lambda }(\mathit{\text{Exp}}(-\lambda t_{i-1}))-(\mathit{\text{Exp}}(-\lambda t_i)),}$$ Eq. 2

where S_i(T,LV) and S_i(L,LV) are the MCNP-derived specific absorbed doses to the tumor and lungs (mGy/MBq-s), respectively, for each SPECT/CT scan, with the total activity in the lung volume (LV) as source; A₀ is the initial activity within the lungs, obtained as the product of injected activity and the percentage lung retention; λ is the lung clearance rate (h⁻¹) obtained from the planar images; t_i is the middle time point between 2 scan times (T1, T2, or T3), where t₁ is T₁ + 0.5(T₂ − T₁), t₂ is T₂ + 0.5(T₃ − T₂), t₀ is 0, and t₃ is ∞. D(T), D(L) are the absorbed dose to tumors and lungs, respectively.

MCNP4b Package

The MCNP4b package provides a rich collection of commands, referred to as cards, for users to adapt its standard features—including geometry, source, materials, energy tally, and so forth—to their own applications (24). Its lattice and repeated structure cards were used here to communicate the composition and activity in the voxels of either phantom or SPECT/CT data to the MCNP4b simulation. The cuboid boundary of the hexahedral lattice was defined by lattice and surface cards. Voxels were represented by lattice cells assigned to a specific universe number with the fill card. A FORTRAN subroutine was developed to convert the voxels containing lung tissue, tumors, and air into universe numbers suitable for MCNP4b input. Activity levels from SPECT images were converted to universes in MCNP. The density of every voxel was obtained from CT. The density of each universe was calculated by averaging densities of all voxels belonging to the same universe. SPECT image can be analyzed by a 3D internal dosimetry (3D–ID) thresholding algorithm to distinguish tumor and normal lung tissue. Two standard compositions were used for tumor (soft tissue) and normal lung tissues. On each universe card, composition and density of the tissue can thus be defined (10).

After the geometry was described, the source card defined the photon and electron sources, including activity distribution between cells, distribution of activity within each cell, energy spectrum of the electron and photon sources, particle types, and the sampling efficiency. The activity probability distribution was obtained from SPECTand normalized. The full photon and electron spectra of ¹³¹I were obtained from The Lund/LBNL Nuclear Data Search (http://nucleardata.nuclear.lu.se/nucleardata/toi/, version 2.0, 1999). A *F8 energy deposition tally was then used along with the repeated structure chains to accumulate energy deposited in the ROIs, which could be either a single voxel or combined voxels with the same universe number. Subsequent peripheral cards determined the number of histories (NPS), initial random number seeds, and output of the tallies. The MCNP4b code was executed on a 60-node Beowulf cluster, with dual AMD (Advanced Micro Devices) Athlon MP(Multiprocessor) processors (1,800–2,100 MHz) on each central processing unit CPU). The tally results along with the relative errors were combined after simulations using independent sequences of random numbers. Sufficient histories were generated in each case to reduce the relative errors to <10% for each tally result. Output in ASCII files was analyzed with a FORTRAN postprocessing sub-routine. The absorbed dose to each ROI was calculated and summed for tissues (tumors or lungs) corresponding to ROIs. A binary file was generated for imaging processing by previously developed software, Multiple Image Analysis Utility (MIAU, version 3.10) (31).

Validation

The electron and photon transport in the MCNP4b code was validated by comparing calculated absorbed fractions to literature values (32,33). The absorbed fraction of ¹³¹I β-rays and photons in mathematically defined and voxelized spheres filled with water agreed very well with the published results (Table 1). The largest relative differences were <2% for β-rays and 0.2% for photons. At these dimensions and for this geometry, voxelized representation did not significantly impact the estimated absorbed fractions. The adult male lung phantom from the Cristy–Eckerman model (34) was used to evaluate the lung-to-lung specific absorbed fraction (SAF) and compared with the values from the MIRD Pamphlet No. 5 for monoenergetic photons with energy from 0.01 to 4.0 MeVand ¹³¹I (Table 2) (35). The adult male lung phantom was voxelized as follows with 0.4-cm voxels. Cubic voxels were generated and, using the mathematic description of the adult lung, any voxel with its center located within the lung phantom was included in the voxel phantom. The voxelized adult lung phantom thus constructed contains 52,700 voxels with a total mass of 998 g. The differences of SAFs from the MIRD Pamphlet values varied from 0.3% to 13% with larger differences at smaller energies. The assumption that electrons are deposited locally could be the cause of the difference as electrons are explicitly transported in MCNP4b. Mass and geometric changes of lungs after voxelization might also contribute to such differences (25). The lung-to-lung self-absorbed fraction for ¹³¹I was found to be approximately 6.0% different from published data using this voxelized lung phantom.

TABLE 1.

Absorbed Fraction of Uniformly Distributed ¹³¹I Source in Various Sizes of Spheres Filled with Water as Medium

Sphere R (cm)	131I β*	Voxel sphere*	Ref. A†	Sphere R (cm)	131Iγ‡	Voxel sphere‡	Ref. B§
0.1	0.71	—∥	0.73	1.0	0.025	0.028	0.025
0.2	0.85	0.87	N/A	2.0	0.049	0.048	0.049
0.25	0.88	0.90	0.89	4.0	0.099	0.101	0.099
0.5	0.94	0.96	0.94	6.0	0.149	0.149	0.151
1.0	0.97	0.98	0.97	8.0	0.197	0.197	0.197
2.0	0.99	0.98	0.98	10.0	0.244	0.244	0.244
				12.0	0.287	0.288	0.288
				14.0	0.329	0.328	0.329

^*NPS = 10,000; relative errors < 10%.

^†Akabani et al. (32).

^‡NPS = 50,000; relative errors < 10%.

^§Furhang et al. (33).

^∥Sphere with 0.1-cm radius is below resolution of (0.4 cm)³ voxel.

NPS = number of histories; N/A = not applicable.

TABLE 2.

Absorbed Fraction of Photons and ¹³¹I in Adult Lung Phantom by MCNP4b

Photons (MeV)	Voxel phantom*	MIRD Pamphlet No. 5	Fractional difference
0.01	9.18E–04†	8.17E–04†	0.12
0.05	8.04E–05	8.99E–05	0.11
0.1	4.38E–05	5.05E–05	0.13
0.5	4.68E–05	5.01E–05	0.07
1.0	4.37E–05	4.55E–05	0.04
2.0	3.66E–05	3.92E–05	0.07
4.0	3.07E–05	3.08E–05	0.003
131I	4.32E–04‡	4.50E–04§	0.06

^*Voxelized lung phantom is obtained from Cristy–Eckerman model (34).

^†Lung-to-lung self-absorbed doses are reported as SAF (g⁻¹).

^‡Absorbed fraction from both γ-rays and β-rays of ¹³¹I are tallied in voxel phantom calculation.

^§131I absorbed fraction is obtained from MIRD pamphlet No. 11 and reported in rad/µCi-h (36).

Segmentation Studies

Because voxel-by-voxel input and energy tallies are computationally intensive, the MCNP4b calculations were also performed on a segmented dataset. The rationale for segmentation is that statistical significance can be improved by pooling activity regions, especially in regions of lower activity concentration. This was accomplished by numerically dividing activity into 5, 10, or 20 equally sized activity bins on the 3D lung activity map. Correspondingly, the voxels belonging to the same bin on the activity map were merged on the density map and assigned the same universe number in the MCNP4b input file. The lung tumor burden was estimated using the 3D–ID thresholding algorithm (23,37), which was applied to the activity map and used to discriminate between tumor and normal lung tissue based on a threshold activity value. The effect of segmentation on estimated tumor and lung absorbed dose was studied. This simple segmentation method is solely intended to show that computational efficiency can be greatly improved.

RESULTS

The whole-body anterior planar images at 3 different time points are shown in Figure 1. Correcting for physical decay, close to 96% of the injected activity was retained in the whole body at 146 h The time–activity curve in the lungs gave a residence time of 270 h, with 82.2% of whole-body activity in the lungs at 26 h after injection. The lung residence time calculated from quantitative SPECT/CT images acquired over 3 time points was 238 h. The SPECT/CT image of this patient’s lungs taken 27 h after tracer injection is shown in Figure 2. On both transverse and coronal projections of the CT, diffuse disease was discernable throughout the lungs (Figs. 2A and 2B). Intense focal uptake of ¹³¹I was found in multiple foci in the right and left lower lobes of the lungs (Figs. 2C and 2D).

Following the standard Benua–Leeper method, the prescribed activity was 4.3 GBq (116.2 mCi). The standard Benua–Leeper method, however, does not take into account the differences in patient weights and organ sizes. The method was modified to account for the difference in lung weight and anatomy. This was accomplished by estimating the dose rate to the lungs at 48 h. The 48-h whole-body retention of 2.96 GBq (80 mCi) gives a dose rate of 43.6 rad/h to the lungs with the standard adult female phantom. A 48-h lung activity retention of 2.44 GBq (66 mCi) is required to deliver the same dose rate if the S value for the phantom of a 15-y old is used. Adjusting for this patient’s body weight and lung clearance kinetics, the recommended administered activity for this patient became 3.89 GBq (105.0 mCi).

Accounting for lung clearance, the whole-organ S value– based approach gave an initial administered activity of 0.66 GBq (17.8 mCi) when the total absorbed dose to the lungs reaches the MTD. If the same S value approach was applied to the initial administered activity planned with the dose-rate method, the absorbed doses to normal lungs would be 160.3 Gy, approximately 5-fold higher than the MTD of normal lungs.

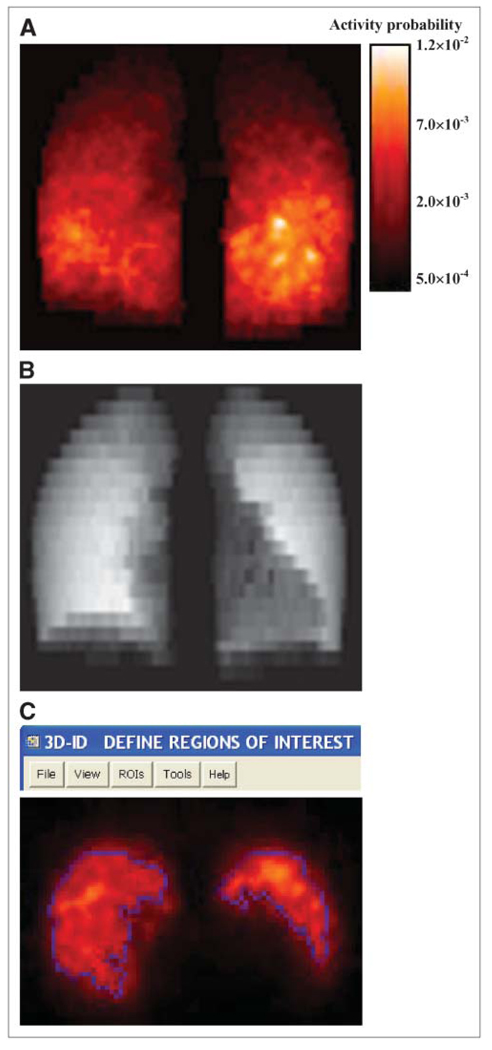
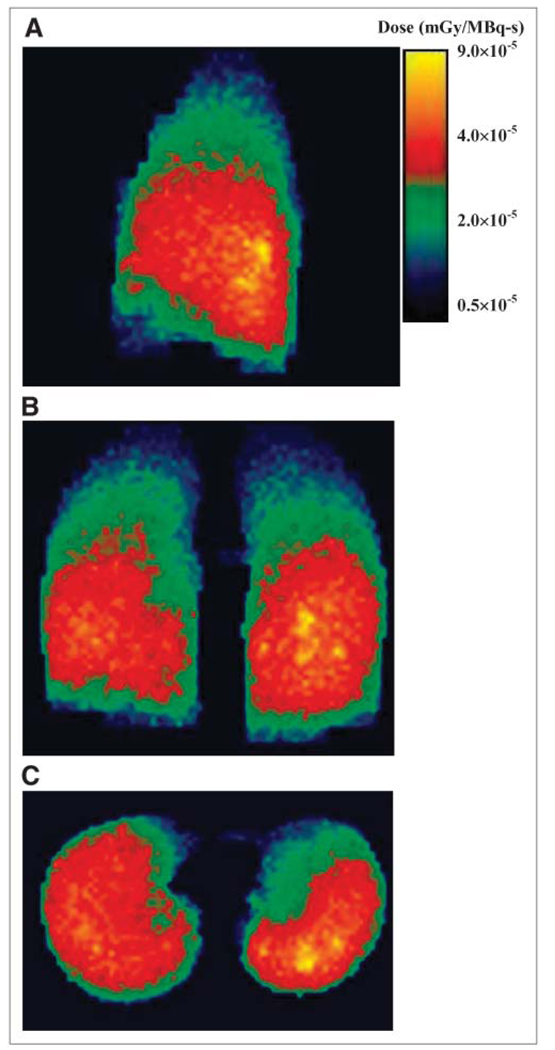
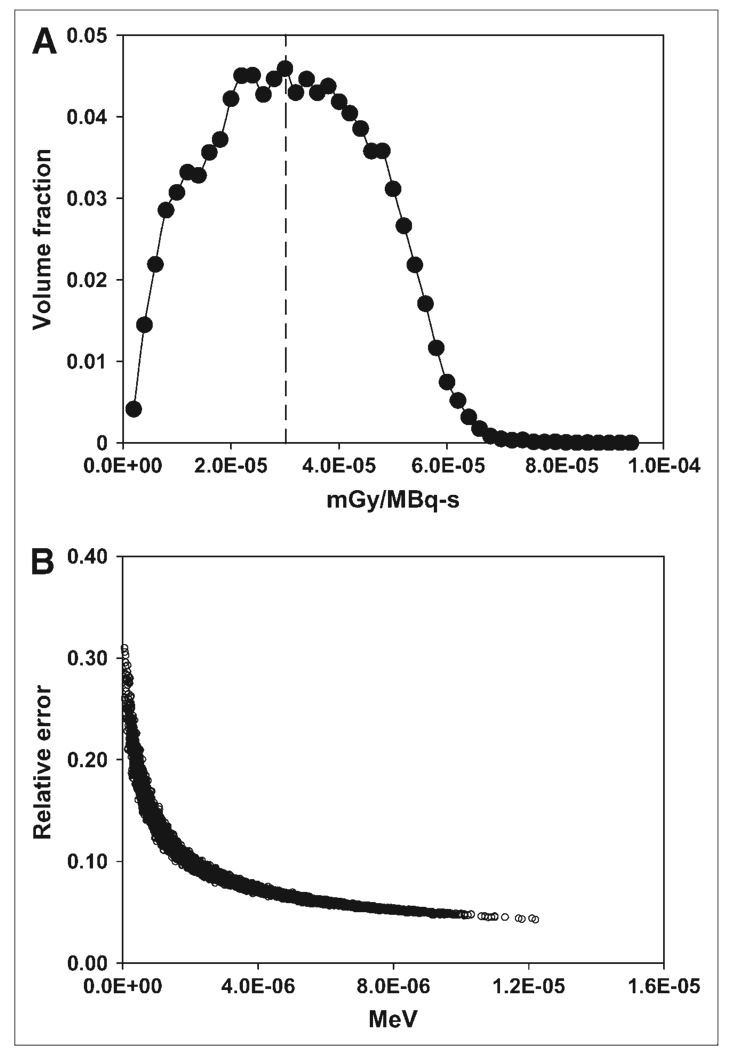
Figure 3 shows the coronal maximum-intensity-projection (MIP) image of the activity probability map (Fig. 3A) obtained from SPECT/CT at 27 h. The projection image of the lung density map is also shown (Fig. 3B). SPECT/CT images obtained at 74 and 147 h were processed in the same way. A lung tumor burden of about 650 cm³ was estimated from the 3D–ID package using a thresholding algorithm that determines the boundary of tumor and normal lungs (37). Figure 3C shows a representative SPECT slice taken at 27 h with contours outlining the tumor voxels with high uptake. The Monte Carlo–derived absorbed dose distribution in the lungs is shown in Figure 4. Note that the areas with higher energy deposition were strongly correlated with the areas showing high activity on SPECT (Fig. 3). The dose–volume histogram corresponding to Figure 4 is depicted in Figure 5A. There were 50,000 voxels with specific absorbed doses ranging from 3.93 × 10⁻⁷ to 9.06 × 10⁻⁵ mGy/MBq-s and a mean of 3.01 × 10⁻⁵ mGy/MBq-s per voxel. To achieve relative error <10% in the tally values in each voxel, a large number of histories for electron and photon transport were needed. Figure 5B plots the energy tallied per voxel against its corresponding relative error after 10 million histories of electron transport. The energy deposited in the voxels with relative errors of <0.10 accounts for 91.7% of the total energy deposited in the lungs. The 90% threshold was set so that computational resources were not spent unnecessarily on voxels within regions of much lower activity. The energy–volume histogram was then divided into regions considered to be tumors and the rest as normal lung tissues. The absorbed dose to tumor and normal lung per disintegration in the entire lung volume was 3.89 × 10⁻⁵ and 1.43 × 10⁻⁵ mGy/MBq-s, respectively. Absorbed doses for tumors and normal lung tissues using activity distributions obtained at 74 and 147 h were calculated in the same way. As noted, cumulated activity in the lungs was obtained from planar imaging–derived lung clearance kinetics. The absorbed dose to tumor and normal lung obtained using different treatment-planning protocols are summarized in Table 3. As shown in Table 3, the recommended administered activity, based on a MTD of 27.25 Gy (29), was 1.72 GBq (46.4 mCi) when the Monte Carlo calculation was applied. Direct application of the Benua–Leeper approach would lead to a recommended administered activity of 4.30 GBq (116.2 mCi). After adjusting for the patient’s body weight, the recommended administered activity was 3.89 GBq (105.0 mCi). Because of the presence of extensive disease in the patient’s lungs, both activities were greater than that estimated by Monte Carlo and resulted in estimated lung absorbed doses much higher than the lung MTD when a whole-lung self-dose S value was applied. However, if the lung MTD was implemented together with the lung self-dose S value, the recommended activity would have been 0.66 GBq (17.8 mCi) in this case. Given that a large fraction of lung activity was actually in thyroid cancer metastases, this approach would have overestimated the lung dose, leading to a recommended administered activity that would underdose the tumor. The MCNP-based approach gave a recommended administered activity of 1.72 GBq (46.4 mCi) at lung MTD, which would have lead to 63.7 Gy to the tumor metastases.

FIGURE 3.

(A) MIP slices of processed lung activity probability map obtained from corresponding SPECT study. Color bar indicates intensity for normalized activity probability. (B) Representative slice of lung density map obtained from 27-h SPECT/CT scan. Density map and activity probability maps are direct inputs for MCNP4b dose calculation. (C) ROIs of tumors in a representative transverse slice, generated by 3D-ID, are shown.

FIGURE 4.

MIP slices of absorbed doses in lungs after MCNP4b electron and photon transports. Sagittal (A), coronal (B), and transverse (C) views of dose rates (mGy/MBq-s) calculated for activity and density maps at 27 h after tracer administration. Color bar indicates intensity for absorbed dose per disintegration.

FIGURE 5.

(A) Absorbed dose–volume histogram corresponding to dose-rate images shown in Figure 4. Average absorbed dose rate per unit activity per voxel is 3.01 × 10⁻⁵ mGy/MBq-s (dashed line). (B) Relative errors after 10 million histories of electron transport are plotted against voxel energy deposited.

TABLE 3.

Recommended Administered Activities and Absorbed Doses to Tumors and Lungs Using Different Treatment Planning Methods

Activity or absorbed dose	Benua–Leeper	Dose-rate method	S value	MCNP4b
Administered activity, GBq (mCi)	4.30 (116.2)	3.89 (105.0)	0.66 (17.8)	1.72 (46.4)
Absorbed dose to lungs (Gy)	177.4*	160.3* (61.6†)	27.25‡	27.25
Absorbed dose to tumors (Gy)	—§	—§ (144.2†)	—§	63.7

^*Absorbed dose to lungs was calculated using ¹³¹I lung-to-lung S value from OLINDA (7).

^†Absorbed dose in parentheses is calculated using dose conversion factor from MCNP4b transport.

^‡MTD to lung tissue was obtained from Press et al. (29).

^§Absorbed doses to tumors were not calculated with conventional approach.

The largest hurdle for clinical implementation of MCNP-based, patient-specific dosimetry is its computational efficiency (10). A voxel-by-voxel tally is unnecessarily computationally expensive, with most of the computational time spent on voxels with lower activity values in order to reach statistically reliable tallies. As shown in Figure 5B, Figure 91.7% of the energy deposited in the lungs was in the voxels with relative errors of <10% after 10 million electron transport histories. With half of that number of histories, 60.8% of deposited energy was in the reliable voxels, whereas voxels of lower activity consumed half of the computing power. Rational segmentation of regions with similar activity levels and compositions can greatly optimize the use of limited computing resources. The most favorable segmentation method would be fully automated and based on algorithms that not only recognize the boundaries between normal tissue and tumors but also partition regions with appropriate weight. For example, tumors could be segmented into a much larger amount of regions, possibly down to a single voxel, so that the non-uniform distribution of absorbed doses within tumors could be quantified at high resolution (38,39).

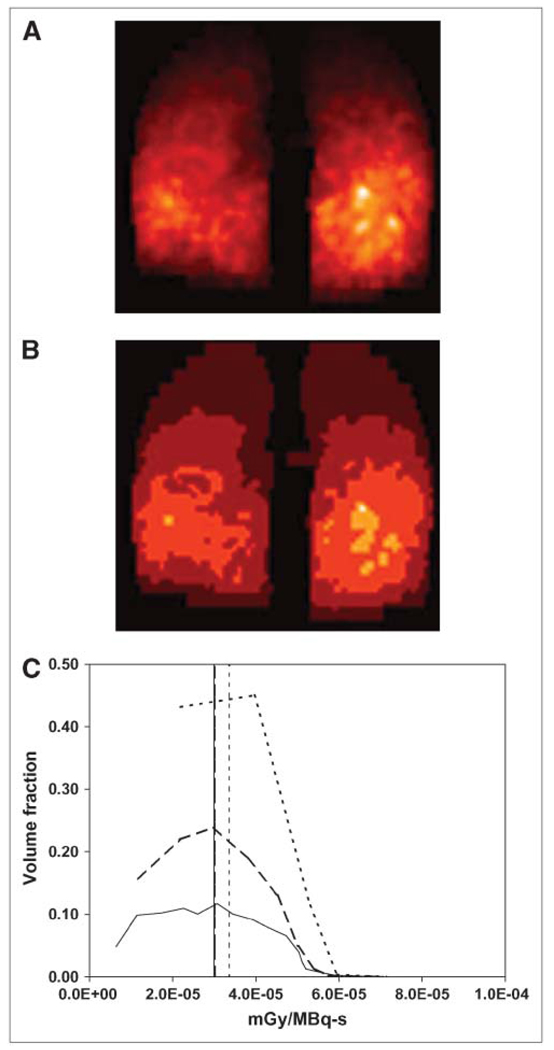
Here, a simple segmentation method, where the activity map was evenly divided into multiple levels, was used to demonstrate the value of segmentation for MCNP-based dosimetry. Figure 6 shows the activity map that has been segmented into 10 (Fig. 6A) and 5 (Fig. 6B) regions based on activity values. Segmentation of the activity map into 20 levels was also performed. Dose–volume histograms calculated for the 3 segmented activity maps are shown in Figure 6C. The dose distribution for the 10- and 20-level segmentation map was similar to the fully voxel-based calculation (Fig. 5A). The difference in volume fraction was caused by the fact that more segmentation levels result in smaller volume bins. Most notably, segmentation dramatically reduced the computing time required to generate statistically reliable tallies (Table 4). When 50,000 voxels were tallied and 4 millions photon histories were performed, the computations consumed a clinically prohibitive 4,642.3 h of CPU time. Segmented activity maps, with far fewer tallies and improved statistics in each tally, consumed much more manageable CPU times of 16.8, 4.0, and 0.5 h, respectively. Such a major improvement in computational efficiency highlights the critical role of rational segmentation in the development of MCNP-based, patient-specific dosimetry.

FIGURE 6.

MIP coronal slice images of segmented activity maps. Activity was evenly divided into 10 (A) and 5 (B) levels. (C) Dose–volume histograms calculated from segmented activity maps: 20 (solid line), 10 (dashed line), and 5 (dotted line) levels; horizontal lines depict mean absorbed doses per disintegration.

TABLE 4.

Segmentation of Activity Maps Improves Computational Efficiency

Tallies	No. of histories*	CPU time† (h)	Tumor mean dose‡ (Gy)
50,000	4,000,000	4,642.3	63.7
20	200,000	16.8	60.6
10	30,000	4.0	60.4
5	4,000	0.5	53.5

^*Photon transport for activity and density maps from SPECT/CT scan at 27 h.

^†CPU time is sum of all CPU time spent on each node of Beowulf cluster.

^‡Absorbed doses to tumors are calculated using MTD of 27.25 Gy to normal lungs.

The mean absorbed doses to tumors after segmentation were also compared. With the same MTD to normal lungs, both 10- and 20-level segmentation resulted in deviations of on the order of 5% in the mean tumor absorbed dose, whereas 5-level segmentation produced a 16% difference in the mean tumor absorbed dose.

DISCUSSION

Thyroid cancer patients with iodine-avid lung metastases represent a potential challenge in planning radioiodine treatment. Estimating the absorbed dose to tumor foci and normal lungs can define the administered activity that adequately treats the malignancy while minimizing the risk of lung toxicity. Accurate dosimetry is difficult, however, because of highly heterogeneous tissue density and activity distribution within the lungs. In this work, we compared different treatment-planning approaches in a thyroid cancer patient with diffuse iodine-avid lung metastases to illustrate the different methodologies.

Compared with the simplest whole-organ S-value–based dose estimation, the planned administered activity from the MCNP-based calculation was 2.6-fold higher (1.72 vs. 0.66 GBq). This was foreseeable because the whole-organ S-value approach did not account for the fact that a large proportion of the activity and energy deposited within the lungs was actually distributed and deposited in tumor instead of lung parenchyma. This inevitably overestimated the lung dose and lead to suboptimal therapy.

The Benua–Leeper method has been adopted by several institutions as a rational approach to planning radioiodine therapy of thyroid cancer patients while preventing serious side effects of radiation-related bone marrow suppression and pneumonitis (4,5). In the current analysis, the recommended administered activity, estimated from the MCNP calculation, was approximately 60% lower than that obtained using the dose-rate method. This is, perhaps, not surprising as the 80-mCi rule is empiric and accounts only for the variability in activity retention, whereas the dosimetry-based approach provides the additional information needed to identify an administered activity that reaches the tolerable lung absorbed dose. Implementation of Benua–Leeper is usually associated with clinical prognosis and, rarely, actual doses to normal organs and tumors are estimated. Lack of dose–response correlation and widely adopted fixed dosing approach further complicated the issue. It is interesting to note that the dose-rate method gave a dose that was about 5 times higher than that obtained from the S-value–based estimation. Such discrepancy highlights the necessity of more studies to correlate between the Benua–Leeper dosing method and absorbed doses to normal organs and tumors.

The 3D imaging–based, patient-specific dosimetry, however, also has several technical limitations. The intermixture of high- and low-density regions (i.e., tumor and lung tissue) places a substantial burden on accurate matching of the radioactivity with the density distribution. Any misregistration that places a high-activity voxel over a low-density lung tissue voxel, or vice versa, will lead to large errors because the low mass assigned to a lung voxel will increase the estimated absorbed dose artificially (i.e., mass is in the denominator of the absorbed dose equation and mass values near zero can lead to very high absorbed doses). In this study, the software available on the SPECT/CT system (Millennium VG Hawkeye) was used without correction for patient breathing motion. The impact of this can be evaluated by examining the dose calculations that used segmented activity distributions. Lung activity segmentation calculations did not give substantially different mean absorbed doses or dose–volume histograms (Table 4), suggesting that the loss of activity resolution associated with lung motion is unlikely to change the estimates significantly.

In addition to the intermixture of low- and high-density tissue, another dosimetric challenge arises when the tumor lesions, as seen on CT and SPECT images, are diffusely disseminated throughout the lungs, making it difficult to delineate tumor versus normal lung tissue. Such delineation is necessary to obtain absorbed dose parameters (e.g., mean absorbed dose or dose–volume histograms) for tumor and normal lungs. In this work, we applied an activity threshold to delineate tumor tissue from normal lung, implicitly making the assumption that regions with higher iodine uptake shown on SPECT represent tumors, whereas those with lower uptake are normal lung tissues. The resulting ROIs thus drawn might assign activity from tumors to normal lung tissue, especially if the tumor nodules were smaller than the SPECT resolution of 3.45 mm. That this probably has occurred is suggested by the observation that the average density of the normal lung tissue regions obtained by an activity-based threshold segmentation of the tumor and calculated from the corresponding CT was 0.486 g/cm³ instead of the expected lung density value of 0.296 g/cm³ (40). It is worth noting, however, that the increase in energy deposition to normal lung regions is offset somewhat by the corresponding increase in density, thereby minimizing the sensitivity of the absorbed dose calculation to segmentation errors.

Although we have previously applied 3D imaging–derived voxel-based kinetics for patient-specific dosimetry calculations (30), this was not done in the current calculations; instead, the kinetics was derived from planar imaging. Use of voxel-based kinetics requires the voxel-by-voxel alignment of lungs from CTs of multiple time points, the spatial transformations of which are applied to the corresponding SPECTs (12). The diffuse nature of the disease imposed an uncertainty on the dose calculation that was deemed too high. A study is underway to investigate the impact of such voxel-by-voxel integration and its sensitivity to misregistration.

CONCLUSION

MCNP-based, patient-specific dosimetry was performed in the radioiodine treatment of a thyroid patient with lung metastases. The study showed the feasibility of using MCNP in 3D imaging–based dosimetry, whereas rational segmentation is critical for its practical implementation in clinical settings due to limited computing resources. This work also highlights the impact that a detailed dosimetric analysis can have on treatment optimization and patient management.