A Combined Molecular Dynamics and Experimental Study of Doped Polypyrrole

Abstract

Polypyrrole (PPy) is a biocompatible, electrically conductive polymer that has great potential for battery, sensor, and neural implant applications. Its amorphous structure and insolubility, however, limit the experimental techniques available to study its structure and properties at the atomic level. Previous theoretical studies of PPy in bulk are also scarce. Using ab initio calculations, we have constructed a molecular mechanics force field of chloride-doped PPy (PPyCl) and undoped PPy. This model has been designed to integrate into the OPLS force field, and parameters are available for the Gromacs and TINKER software packages. Molecular dynamics (MD) simulations of bulk PPy and PPyCl have been performed using this force field, and the effects of chain packing and electrostatic scaling on the bulk polymer density have been investigated. The density of flotation of PPyCl films has been measured experimentally. Amorphous X-ray diffraction of PPyCl was obtained and correlated with atomic structures sampled from MD simulations. The force field reported here is foundational for bridging the gap between experimental measurements and theoretical calculations for PPy based materials.

Introduction

Polypyrrole is an amorphous, conducting polymer that is easily synthesized either chemically or electrochemically. PPy is made conductive by oxidizing some fraction of the pyrrole rings and conjugating them with anions, which greatly reduces the band gap in a process called doping. This phenomenon has been well described by several review papers [1, 2]. Studies have shown that structural re-arrangement of PPy upon doping is not limited to the oxidized ring, but rather the charge spreads to neighboring rings [3]. It has been shown that doped polypyrrole (PPy) performs well as a biomaterial or implant coating in the nervous system [4]. Its electrical conductivity makes it well suited to detect endogenous electrical signals from the nervous system or to deliver therapeutic electrical stimulation to the body. PPy’s surface chemistry has also been modified to promote different biological responses by “tethering” relevant molecules or peptides to the material surface through covalent attachment[5], through inclusion as dopant ions [6], or through affinity binding [7]. Yet despite tremendous advances in the experimental characterization and synthesis of various types of doped PPy, much remains unknown about its nano-scale structure and surface properties.

A large number of experimental studies and several computational studies of PPy precede this work. The early computational work has mostly been performed with low-level ab initio methods. Ford et al. analyzed UV photoemission and optical absorption of polypyrrole using a semi-empirical CNDO/S3 method [3]. It was suggested, based on the calculated density of valence states, that a photoexcited pyrrole cation could span over 4–6 repeat units. Bredas et al. performed Hartree-Fock calculations of quaterpyrrole with and without Na⁺ dopants (n-type) using the STO-3G basis set [8]. Even though the small basis set was inadequate for accurate description of electronic structure, this work demonstrated an almost complete charge separation between the doping ions and pyrrole rings. It was also proposed that at high-doping levels, 33% and above, the bipolaron (two doping ions located adjacent to each other) was the dominant state [8]. The conformational energy of undoped pyrrole oligomers was previously investigated using Möller Plesset energy perturbation (MP2) and density functional theory (DFT) methods [9]. That study found that the anti-gauche conformation was lowest in energy, and the rotational energy barrier of ca. 4 kcal/mol was reduced slightly from di- to tetrapyrrole. Thus undoped oligo or polypyrrole have non-planar structures and are likely to be rather flexible. Most recently, a quantum mechanics (QM) study of the equilibrium structures of oligomers up to 24 rings in length showed that higher doping ratios produce more planar chains [10]. They also showed that explicitly including dopant ions in QM calculations with oxidized PPy chains increased the localization of positive charge near the doping sites. To ensure that this effect is captured in this study, all QM calculations of PPyCl explicitly included a dopant ion.

Molecular mechanical studies of PPy are scarce. An early molecular dynamics simulation of crystalline PPy was made using a generic polymer force field [11]. The OPLS-AA force field was reported for liquid pyrrole, but not the polymer form [12]. More recently Cascales and Otero performed dynamics simulations of Cl-doped films in an aqueous environment [13–15]. However, the charges and the torsional parameters in the force field were not fully substantiated. The atomic charges from the results of CNDO quantum mechanical calculations were reduced by 50%, which made them very small in comparison to other studies. In addition, the exact approach used to generate the chain packing was unclear and the bulk properties were not fully validated. Finally, the fairly short simulations of 1–2 ns were likely insufficient. For efficient computation, a coarse-grain model of PPy was reported [16]. However, the fidelity of electrostatic representation is questionable in such a model. This coarse-grain study also reported QM results for the backbone conformational energy of oxidized and undoped PPy. The torsional energy barrier of oxidized PPy was estimated to be around 20 kcal/mol, but no attempt was made to fit a model to these results. No previously reported model of doped PPy has rigorously parameterized both the charge distribution and the conformational flexibility, which has limited the use of computational simulations to explore PPy based materials and their interactions with other molecules.

In this work, by using ab initio QM methods, we have investigated the charge distribution and backbone flexibility of PPy oligomers, with and without doping. On the basis of QM calculations, a new classical molecular mechanics potential has been developed and utilized in the molecular dynamics simulations of condensed-phase polypyrrole matrices. Both simulated annealing and potential scaling schemes were compared in producing representative PPy bulk structures. In addition to comparing the model’s performance against gas phase QM structures and conformational energies, the bulk densities and atomic structures sampled from condensed-phase simulations using the force field have been directly compared to our experimental density and amorphous X-ray diffraction data. This potential was specifically developed to be compatible with the OPLS-AA force field [17, 18] for future study of protein interactions.

Methods

Quantum mechanics calculations

QM geometry optimization calculations were performed on PPy trimers, pentamers, and septamers using the HF/6-31G* level basis set and the Gaussian03 software package [19]. The final structures were used to define equilibrium bond lengths and angles. For doped PPy, a chloride ion was placed near an oxidized (polaron) polypyrrole oligomer. To ensure that the initial placement of the chloride ion was near the global minimum, we first performed twelve geometry optimizations of doped PPy trimers with the chloride ion in various positions around the chain. Eleven of the twelve converged to the same location, whereas one stopped in a local minimum of much higher energy. After choosing the initial placement of the chloride ion, geometry optimization of trimers, pentamers, and septamers was performed as in the undoped case.

To quantify the backbone flexibility for both doped and undoped PPy, the backbone conformational energy profile was calculated by rotating and constraining the central bond of PPy quatermers in 15° increments from 0° to 360°. The geometry was optimized with the constraint in place using the HF/6-31G* basis set, and a single point calculation of the energy was performed using the MP2/6-311++G(2d,2p) basis set. Again, doped PPy quatermers were modeled with a single chloride doping ion.

Potential energy function and parameterization

Parameters for our molecular mechanics model were chosen to complement the OPLS-AA force field, which describes the potential energy with the following components:

$$E(r^N)=E_{\mathit{bond}}+E_{\mathit{angle}}+E_{\mathit{dih}}+E_{\mathit{elec}}+E_{\mathit{VdW}}$$

Equilibrium bond lengths and bond angles were computed by averaging the QM minimum energy structures of PPy trimers, pentamers, and septamers. The force constants for bond lengths and bond angles were transferred over from similar, existing aromatic parameters such as pyrrole in the OPLS-AA force field. Atomc partial charges for the electrostatic potential energy term were derived using the ChelpG method [20] on the HF/6-31G* QM minimum energy structures. The values were then rounded slightly up or down to ensure that the net charge of the model was exactly zero. Van der Waals parameters were also transferred from corresponding pyrrole atom types in the OPLS-AA force field. The dihedral angle energy contribution was calculated by comparing the QM conformational energy scan to equivalent MM structures using all energy terms except the dihedral angle term. The differences in energy between the QM and MM results were then fit to a Fourier series and an equivalent Ryckaert-Belleman function [21] for the dihedral angle parameters. These two functional forms are used by TINKER [22] and Gromacs [23], respectively.

Amorphous matrix formation

The developed force field has been incorporated into the TINKER [22] and Gromacs [23] software packages. All molecular dynamics (MD) simulations were performed using Gromacs v4.0. Undoped, amorphous PPy matrices were formed by placing 75 randomly-oriented PPy chains 4 nm apart in a 20 × 20 × 12 nm periodic box. The PPy chains were between 8 and 16 pyrrole rings in length to match experimental measurements [24]. The boxes were then slowly compressed under a pressure of 1000 bars using MD simulations with a constant number of atoms, controlled pressure, and controlled temperature (i.e., NPT ensemble) over approximately 40 ns. During the pressurization either simulated annealing or potential scaling was performed to sample the chain packing (see below). Once the box volume stabilized, the pressure was reduced to 1 bar and room temperature, and an additional 20 ns of NPT simulation data were recorded. The average density and radial distribution function for each of the matrices were measured from the last 15 ns of each simulation at increments of 10 ps.

A total of six in silico amorphous matrices were generated. For three matrices, thermal annealing up to 1000 K was performed during the high pressure phase of the simulation. For the other three matrices, a potential scaling approach was used in which van der Waals parameters were slowly turned on first, followed by electrostatic parameters. The scaling, or “turning on,” of the parameters was done linearly at every step of a 10 ns simulation. For each matrix, the same initial, dilute structure was used, but velocities were assigned by using different seed values to ensure different trajectories. Doped PPy matrices were created by starting with a final undoped film structure, randomly placing chloride ions, and slowly mutating the force field parameters from undoped PPy to doped PPy over 10 ns. The van der Waals parameters of the chloride ions were initially turned off, which allowed the ions to move to energetically favorable locations as their van der Waals the charge parameters were slowly scaled up. We found this was most effective in distributing the ions across the matrix while promoting the “sharing” of ions between more than one PPy chain.

Crystalline matrix formation

Two in silico crystalline matrices were created to examine how different chain packing affects bulk material properties. The first crystalline matrix was assembled by placing 75 chloride-doped PPy chains all parallel to each other in 5 rows of 15 pi-stacked chains. The chains were placed close together (i.e., pre-packed) in a 4.7 × 4.7 × 4.5 nm box. All the chains were 12 repeat units in length. The second crystalline matrix was also created from 5 rows of 15 pi-stacked chains, but the 2^nd and 4^th rows of chains were turned 90° so that they were perpendicular to their neighboring rows. After the initial structure was created, both matrices were pressurized as described in the amorphous matrix formation section and were thermally annealed at 800 K, although the backbone rearrangement from thermal annealing was limited by the already dense packing. As with the amorphous matrices, a 20 ns room temperature, atmospheric pressure simulation was performed, and data points were taken every 10 ps over the last 15 ns of the simulation.

When uniformly scaling the charge parameters up or down, additional 10 ns trajectories were simulated for each matrix starting from the final frame of the simulations described above. Data points were extracted every 10 ps for the last 5 ns of this trajectory. When testing previously published parameters, additional 20 ns trajectories were simulated, and data points were extracted every 10 ps for the last 15 ns.

Radial distribution functions

Radial distribution functions (RDFs) were created using the built-in “g_rdf” command in Gromacs 4. As in our density calculations, we used snapshots that were 10 ps apart over the last 15 ns of the simulation at room temperature and atmospheric pressure. For the nitrogen-nitrogen RDF, all intramolecular nitrogen atoms were excluded so that only intermolecular distances are counted. Excluding intramolecular distances prevents the peaks associated with chain packing from being hidden by the peaks that are characteristic of single molecules.

X-ray diffraction experiment

A thick polypyrrole film was electrochemically synthesized onto indium tin oxide (ITO)-coated glass slides (Delta Technologies) from a solution of 0.1 M pyrrole (98%, Sigma-Aldrich) and 0.1 M NaCl (Sigma-Aldrich) in distilled, de-ionized (DDI) water. Pyrrole was purified using an aluminum oxide column before use. A 3-electrode configuration was used for electrochemical deposition with an oxidizing potential of 720 mV versus a saturated calomel electrode (SCE). The temperature of the solution was maintained near 273 K during synthesis by packing ice around the beaker. The surface area of the working electrode (the ITO slide) was controlled at 3 cm² and 6 Coulombs of charge were passed. The resulting film was gently rinsed with DDI water and dried overnight under vacuum. X-ray diffraction was performed on the dry film using a Phillips θ - 2θ Cu Kα powder diffractometer. The sample was scanned in increments of 0.02° with a dwell time of 10 seconds between 2θ angles of 3 and 40°, which corresponds to d spacing between 2.25 and 29.4 Angstroms using Bragg’s law ( d=nλ/2sinθ ).

Flotation density

We performed flotation density experiments to determine the density of PPyCl based on methods previously published [25, 26]. Dichloromethane (Sigma Aldrich) and chloroform (Sigma Aldrich) were used as the solvents. Using standard protocol, the composition of the solvents was adjusted until small PPyCl fragments remained suspended in solution. The 2 ml glass vials holding the samples were capped between adjustments to prevent evaporation, and the samples were allowed ample time to reach equilibrium. Density was calculated from the volumes of the solvents added and the known density values of the solvents provided by Sigma Aldrich. Most previously published values for the density of PPy were measured using the density of flotation method and range from 1.37 to 1.48 g/cm³ [25, 26]; however, the closest dopant to chloride that was measured was perchlorate.

Results and Discussion

Gas phase properties from QM and MM calculations

As discussed in the introduction, several previous studies have examined the molecular and electronic structure of PPy oligomers using a range of ab initio theory [3, 8–10]. Earlier works were limited by computational cost and used less accurate basis sets. More recent studies used high level, accurate basis sets to explore the equilibrium structure of polypyrrole at various chain lengths, but detailed information regarding electrostatics or backbone flexibility of the polymer is still lacking. In this study, we examined PPy oligomers up to septamers in both the undoped and chloride-doped (PPyCl) states. We have calculated the charge distribution of PPyCl to generate atomic charge parameters and have performed conformational energy scans of undoped and chloride-doped PPy quatermers to derive the torsion potentials. We have used these data to construct a new molecular mechanics force field for doped and undoped PPy.

From the minimum-energy structures of doped PPyCl pentamers and septamers, we found that at least 80% of the charge from oxidation is localized to the three PPy rings closest to the dopant ion. This finding, combined with the fact that many studies report PPy doping ratios (the ratio of dopant ions to PPy rings) around 33%, supports the approximation of confining charge spreading to the three rings closest to the dopant ion. Also, we found that averaging the charge equally across these three rings produced better fits to QM torsion data, simplified the number of parameters in the model, and probably more accurately reflects bulk environments where chloride ions are dispersed through the film, such as the lattice structures proposed by Veluri et al. [27]. As a practical matter, dividing the charge across three pyrrole rings required us to round the atomic charge of chloride from −1.000 to −0.999 to preserve charge neutrality in the system. The HF/6-31G* basis set, which we used for fitting partial charges, is known to overestimate the dipole moment (and thus the partial charges) for a molecule in gas phase. This overestimation, however, helps account for the increased polarization expected in condensed-phase simulations, since fixed-charge models do not explicitly include a polarization term [12]. The ChelpG charge fitting method was used largely for consistency with the OPLS-AA force field.

Bond lengths, bond angles, and partial charges obtained from QM calculations are shown graphically in Figure 1 and also listed in Table 1. The alternating single bonds and double bonds within the ring structure are apparent, and the bond order switches across the PPy backbone upon doping. Bond lengths and angles for undoped PPy match closely with previously reported QM studies [28]. Atomic charges for undoped PPy have similar trends to ab initio QM charges reported for pyrrole [29]. The largest difference is the Cα atom, which has a slightly negative atomic charge for pyrrole and has a positive atomic charge in polypyrrole since the C-H bond is replaced with the backbone C-C bond. Previously reported atomic charges derived using the CNDO method [13] are much smaller in magnitude. In the following section, we explore how scaling atomic charges to account for polarization affects the density of the bulk material.

Figure 1. Bond length, bond angle, and partial charges for (a) undoped and (b) doped PPy.

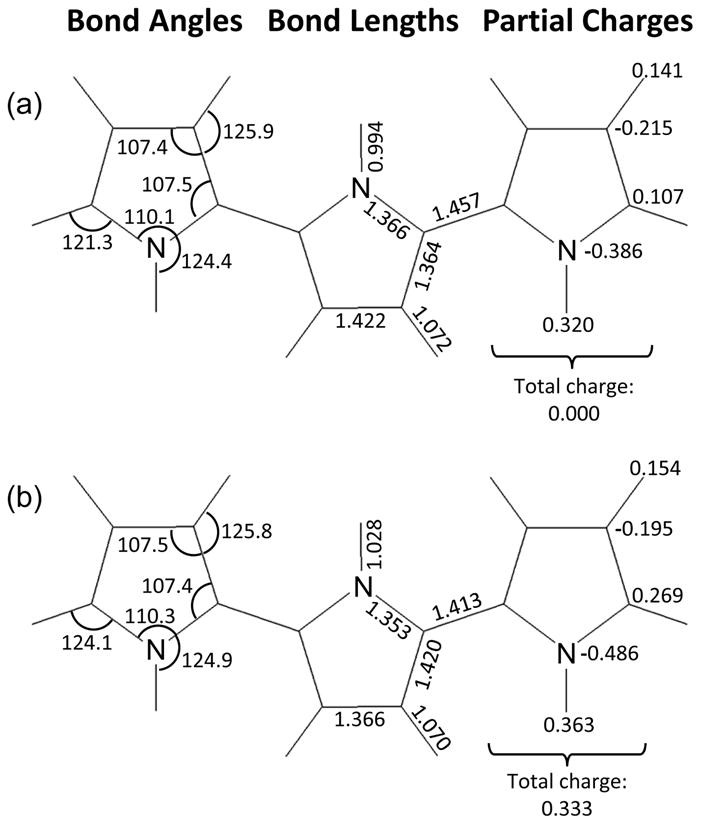
The minimized structure for (a) undoped and (b) doped PPy provides the equilibrium values for bond length and bond angles as well as the partial charges of the atoms. Although displayed across three PPy rings for clarity, all parameters are for a single PPy ring.

Table 1.

Parameters for undoped PPy and doped PPyCl

Undoped Polypyrrole
Atom Type	Charge (e−)	σ (Å)	ε(kcal/mol)
NA opls_542	−0.386	3.250	0.170
CW opls_543	0.107	3.550	0.070
CS opls_544	−0.215	3.550	0.070
H opls_545	0.320	0.000	0.000
HA opls_547	0.141	2.420	0.030

Bonds	bo(Å)	kb (kcal/mol/Å2)
NA-H	0.9937	434
NA-CW	1.3657	427
CW-CW	1.4567	469
CW-CS	1.3644	546
CS-CS	1.4223	469
CS-HA	1.0715	367
CW-HA	1.0698	367

Angles	θ0(degrees)	kθ(kcal/mol/rad2)
H-NA-CW	124.42	35
NA-CW-CW	121.34	70
NA-CW-CS	107.49	70
NA-CW-HA	121.04	35
CW-NA-CW	110.12	70
CW-CW-CS	131.17	70
CW-CS-CS	107.44	70
CW-CS-HA	125.93	35
CS-CW-HA	130.85	35
CS-CS-HA	126.54	35

N-C-C-N Torsion Parameter*		(kcal/mol)
Ryckaert-Bellemans function		Fourier series
C0	2.797	V0	0.000
C1	−0.718	V1	1.093
C2	−4.557	V2	2.307
C3	0.228	V3	−0.114
C4	2.250	V4	−0.563

Doped Polypyrrole
Atom Type	Charge (e−)	σ (Å)	ε(kcal/mol)
NA opls_542	−0.486	3.250	0.170
CW opls_543	0.269	3.550	0.070
CS opls_544	−0.195	3.550	0.070
H opls_545	0.363	0.000	0.000
HA opls_547	0.154	2.420	0.030
Cl-opls_401	−0.999	4.417	0.118

Bonds	bo(Å)	kb(kcal/mol/Å2)
NA-H	1.0280	434
NA-CW	1.3526	427
CW-CW	1.4127	469
CW-CS	1.4197	546
CS-CS	1.3660	469
CS-HA	1.0700	367
CW-HA	1.0698	367

Angles	θ0(degrees)	kθ (kcal/mol/rad2)
H-NA-CW	124.86	35
NA-CW-CW	124.09	70
NA-CW-CS	107.38	70
NA-CW-HA	121.04	35
CW-NA-CW	110.28	70
CW-CW-CS	128.54	70
CW-CS-CS	107.49	70
CW-CS-HA	125.82	35
CS-CW-HA	130.85	35
CS-CS-HA	126.68	35

N-C-C-N Torsion Parameter*		(kcal/mol)
Ryckaert-Bellemans function		Fourier series
C0	5.042	V0	0.000
C1	2.466	V1	−1.233
C2	15.57	V2	5.042
C3	−2.466	V3	1.233
C4	−20.612	V4	5.153

^*Ryckaert-Bellemans (R-B) function is used in Gromacs [23] and Fourier series is used in TINKER [22].

All values are shown in units of kcal/mol. The R-B parameters listed use the Gromacs convention where 0° is the trans configuration (i.e., the “polymer convention”). The Fourier series parameters listed use the Tinker convention where 0° is the cis configuration.

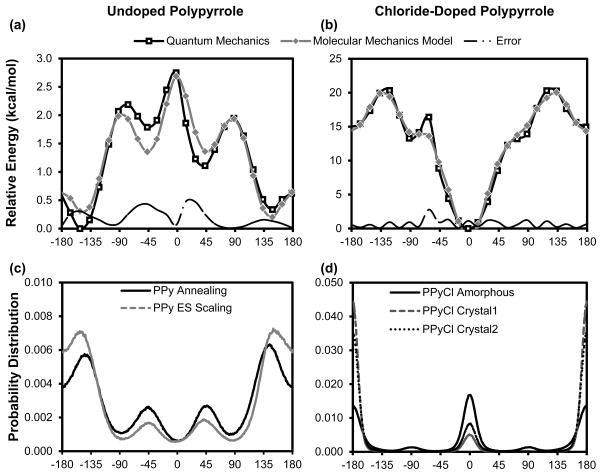
The conformational energy profile of undoped PPy (Figure 2a) shows energy minima at the anti-gauche position around ±148°, with a relatively small torsional energy barrier of approximately 3 kcal/mol. A low energy barrier is consistent with the single carbon-carbon bond (i.e., longer bond length) that connects the pyrrole rings along the backbone of the polymer and again matches previously reported values for PPy [28]. Small energy wells in the syn-gauche configuration are also observed. The asymmetry in the conformational energy profile of PPy has not been reported before, since previous studies used bipyrrole rather than quaterpyrrole. From our observation, this asymmetry reflects the long-range electrostatic interaction between non-neighboring PPy rings such that they prefer to be out of plane from each other. Within the MM force field, the torsion energy parameter must be symmetrical, and asymmetry in the conformational energy profile must be captured in the other non-bonded energy terms. Since the torsion energy term also serves as an error function, using a PPy quatermer in the torsion energy scan allowed us to quantify how well we capture both torsional and non-bonded energy terms. Although using bipyrrole as the model system causes the conformational energy scan to always be symmetrical, it provides no information about the non-bonded contribution to conformational energy in a longer chain. For doped PPyCl (Figure 2b), QM results showed a much more rigid backbone, indicative of a double carbon-carbon bond across the backbone. One asymmetric high-energy data point at around −60° was observed in the QM results, which was the result of out-of-plane bending at one of the hydrogen atoms near the dopant ion. It is important to note that for PPyCl QM calculations, we explicitly included a chloride dopant ion. The energy difference between the 0° and ±180° backbone conformations is primarily due to electrostatics. In bulk PPyCl, this bias is not present, since chloride ions would be present on both sides of the PPy chain.

Figure 2. Conformational energy profile and probability distribution for (a, c) undoped PPy and (b, d) doped PPyCl.

Torsion angle is defined such that zero is the cis configuration with the nitrogens on the same side. In a relaxed state, (a) undoped PPy does not adopt a planar backbone conformation, but rather an anti configuration at ±148°. (b) PPyCl, however, has a very rigid backbone with minima at 0° and 180°. Note that the 15 kcal/mol energy difference between 0° and 180° for PPyCl is from electrostatic interactions with the dopant, not from a torsion contribution. As shown in (d), bulk amorphous PPyCl adopts a roughly equal torsion angle distribution between cis and trans conformations. The torsional energy barrier of doped PPy is an order of magnitude greater than that of undoped PPy. For comparison, the condensed phase backbone distribution (c, d), which should be inversely proportional to the torsion energy, is also shown here. Potential scaling and thermal annealing approaches yielded similar backbone distributions for undoped PPy. For PPyCl, pre-packed crystals were mostly constrained to the trans configuration.

Using the final force field parameters, we have minimized the energy of undoped and doped PPy quatermer structures and compared them to QM results. Figure 3 shows the superimposed structures. The root-mean-square deviation (RMSD) between QM and MM structures (including hydrogen atoms) for undoped PPy was 0.145 Å, and for doped PPy was 0.043 Å, showing good agreement. As a note, the PPyCl quatermer shown in Figure 3b has a central backbone angle of 0° and is the lowest energy structure in Figure 2b. A torsion energy scan comparing QM results and the complete MM force field (Figure 2) also showed excellent agreement, with maximum error values less than 0.5 kcal/mol for undoped PPy. For PPyCl, a few data points had an error greater than 1 kcal/mol, but the shapes of the important energy wells were well reproduced. The 14.96 kcal/mol energy difference between the optimized structures at 0 and ±180° was captured by the MM force field within 0.4 kcal/mol without a torsion energy term (data not shown), which further demonstrates the adequacy of the electrostatic parameters to capture the non-bonded interactions.

Figure 3. Minimum energy structures of PPy quatermers.

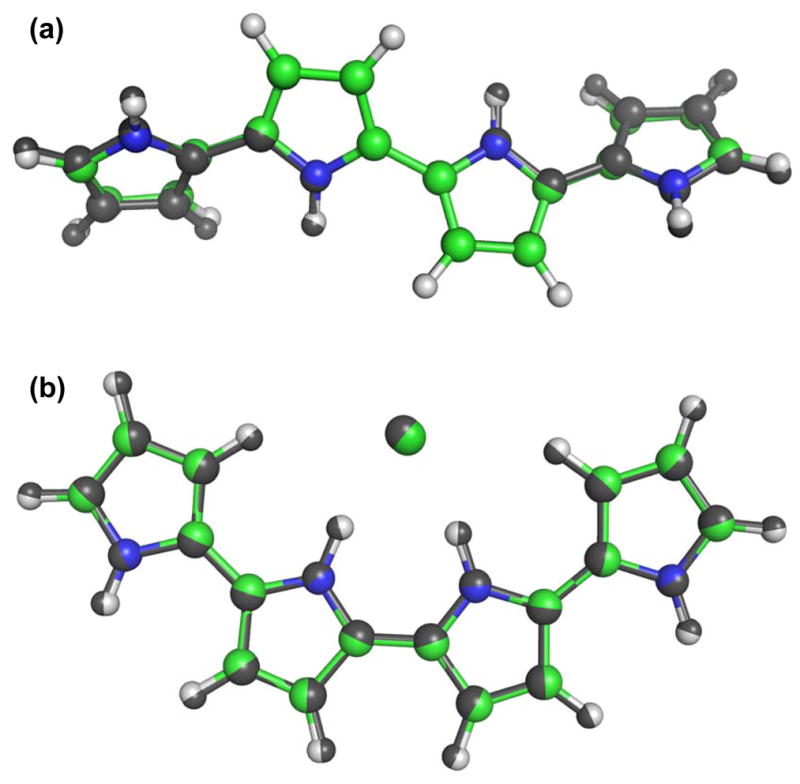
Quantum mechanics (QM) minimum energy structures are shown in dark gray. Molecular mechanics (MM) structures are in color (available online). RMSD of undoped PPy structures is 0.145 Å, and RMSD of PPyCl is 0.043 Å. Tight agreement between QM and MM minimum energy structures serves as one validation of the MM model.

Condensed-phase simulation of polypyrrole matrices

With the molecular mechanics model, we have performed condensed-phase simulations of PPyCl and undoped PPy in bulk environment. For PPy specifically, the average chain length for PPy electrochemically synthesized with low current density at lower temperatures is reported to be around 12 repeat units [24], which is short compared with other polymers. Experimental studies describing the chain packing of PPy are limited, but previous X-ray diffraction data show that PPy is mostly amorphous with small crystalline peaks detected under certain synthesis conditions [30].

Amorphous polymer simulations pose challenges not present in most small molecule or biomolecule calculations. For polymers with flexible backbones, like PPy, each chain has a large number of low-energy conformations. When expanded to a system of many chains, the result is a very large conformational space with a large number of structures that all represent the most probable structures. This is in contrast to protein folding problems, where a single global minimum is expected (the native structure). To create the PPy polymer matrices, we sought to sufficiently sample the energy landscape to find representative low-energy structures that yielded consistent density values, torsion angle distributions, and radial distribution functions. Both molecular dynamics and Monte Carlo methods are suitable for this problem. We chose to use two molecular dynamics approaches: thermal annealing and potential scaling. Thermal annealing is a commonly used approach because of its simplicity and broad software support, but the potential scaling approach offered a greater level of control. As previous work has already mentioned [31], both approaches have mathematically equivalent effects on lowering the energy barrier to allow efficient sampling of the conformational space.

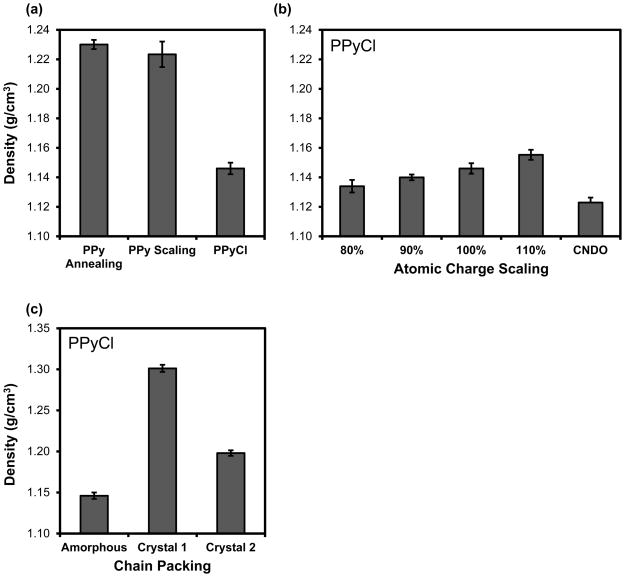
For undoped PPy, we found that both thermal annealing and potential scaling produced PPy matrices of similar density, which suggests that both approaches are able to sufficiently sample the conformational space of the system. The final average density values, also shown in Figure 4a, were 1.230 g/cm³ for thermally annealed, undoped PPy and 1.223 g/cm³ for potential-scaled, undoped PPy. These density values are in good agreement with the reported density of undoped PPy of 1.25 g/cm³ [11]. The probability distribution of the backbone torsion angles (Figure 2c) of the relaxed matrices were similar between the two approaches, with the annealing method resulting in a slightly higher percentage of torsion angles in the higher energy well around +/−45°. In both cases, however, the backbone torsion angle probability distribution agrees with the conformational energy scan (Figure 2a), which suggests that the matrix was able to form a relaxed, condensed phase structure.

Figure 4. Density measurements for undoped and doped PPy.

(a) Average density measurements (n=3 matrices, 1500 snapshots for each matrix) for undoped PPy matrices generated by thermal annealing, undoped PPy matrices generated by potential scaling, and PPyCl matrices made through a mutation process. Both thermal annealing and potential scaling approaches consistently produced matrices of similar density. For doped PPy, we observed a swelling in the material that caused a slight decrease in density. (b) Average density measurements (n=3 matrices, 500 snapshots for each matrix) for PPyCl where electrostatic charge parameters have been scaled up or down. CNDO charges taken from Cascales et al. [13] were also used for comparison. For fixed charge models, scaling charge parameters is one way to account for polarization. We found that scaling the electrostatics of PPyCl has a non-trivial effect on polymer density, with larger charge parameters producing denser films. (c) Average density for crystalline PPyCl (n=1 matrix, 1500 snapshots) demonstrates that chain packing greatly affects bulk density.

When attempting to construct doped PPy matrices, thermal annealing did not effectively sample the energy landscape, because the intermolecular forces between PPyCl chains were too strong. Initially, we attempted to form matrices the same way we formed undoped PPy matrices: starting with the full system in gas phase and slowly condensing the system at high temperature and high pressure. In these simulations, the charged PPy chains quickly wrapped around chloride ions and then aggregated together, forming very stable but very non-physical structures. Even at 1000° Kelvin, the chains remained clustered and wrapped. Using the potential scaling method, we were able to initially turn off the electrostatic parameters for the system and slowly increase them over time. This solved the aggregation problem, but we found that the packing was still dominated by individual chains wrapped around their chloride ions. In the end, we found that by starting with the undoped PPy matrix, adding “ghost” chloride ions, and slowly scaling the parameters from undoped PPy to PPyCl, we were able to produce amorphous matrices with a proper backbone torsion angle distribution and chloride ions shared between chains. This approach is similar to free energy perturbation calculations, where a molecule is very slowly mutated to a slightly different molecule, and the system is give time to adapt and relax [32]. This approach, however, has the limitation that, when applied to a densely packed system, large scale backbone rearrangement is mostly prohibited. The torsion angle distribution for PPyCl (Figure 2d) agrees well with the conformational energy profile shown in Figure 2b when the electrostatic contributions are taken into account. As mentioned in the discussion of the gas phase QM results, the ~15 kcal/mol difference between 0 and ±180° in the conformational energy profile is the result of explicitly including a chloride ion on one side of the PPy chain. An equal probability of 0 and ±180° conformations was expected and observed in bulk, amorphous PPyCl.

Upon doping PPy, we found that the in silico matrix expanded slightly to give a lower average density value of 1.146 g/cm³. Previous computational studies of PPy also report a swelling or decrease in density upon doping [15]. These density results fall somewhat below experimental measurements. Experimentally determined density values for doped PPy films previously reported using the flotation method range from 1.37 to 1.48 g/cm³ [25, 26], but given the sensitivity of PPy’s properties to synthesis conditions and dopant selection [30, 33], relevant values may also fall outside this range. In the current study, we have performed our own density of flotation experiments on PPyCl and obtained a density of 1.46 g/cm³. For in silico PPy matrices, low density values can be caused by partial charges that do not capture the polarization effects of the local environment or by non-optimal chain packing, so we have further examined the effects on bulk density of scaling atomic charges and different chain packing.

Partial charge calculations from gas phase QM calculations do not account for polarization of the molecules in the bulk phase. Other molecules in the OPLS force field use gas phase QM as a starting point [34] and uniformly scale the magnitude if necessary to match experimental data [12] for liquid simulations. Although charge fitting using the HF/6-31G* basis set slightly overestimates the dipole moment in pyrrole monomers, this overestimation is often a closer approximation for molecules in an aqueous environment [12]. Nevertheless, the lack of transferability of fixed-charge models across different environments makes it a challenge to calculate electrostatic parameters. To investigate the effect of atomic charges on density, we scaled the partial charges of doped PPy final structures to 80%, 90%, and 110% of the values reported in Figure 1. The results are shown in Figure 4b. The results show that scaling up the atomic charge leads to an increased density of PPyCl. This was not expected, since a previous theoretical study with PPyCl by Cascales et al. used very low partial charge values but reported final density values around 1.32 g/cm³ [15]. We have applied the charge and united-atom van der Waals parameters used by Cascales et al. in our protocol, but the resulting density values we calculated were only 1.12 g/cm³ (also shown in Figure 4b). Switching from our all-atom van der Waals parameters to the united-atom parameters without changing the atomic charges led to a negligible increase in the PPyCl density of 0.03 g/cm³. The doping ratio we used (~30% in this study vs. ~10% previously) could also attribute some to the difference. Another difference between this and the previous study may lie in chain packing. In the previous study, Cascales et al. placed PPy chains in a packed configuration and allowed the system to relax. In this work, we started with a very dilute system of PPy chains and performed molecular dynamics simulations to relax and sample the chain packing. The current approach is more rigorous, as the results are independent of the initial conditions, but there is no guarantee that the level of crystallinity matches the properties of experimentally fabricated PPyCl. It is likely that PPyCl contains small crystalline regions at the microscopic level due to the rigid backbone. To test the effect of crystallinity on bulk density, we performed additional simulations with crystalline chain packing (shown in Figure 4c) and observed a significant increase in the density of the matrix to over 1.3 g/cm³. This shows that chain packing greatly affects density, and experimentally measured densities for PPy may have such large variation because different synthesis conditions result in different amounts of crystallinity [30].

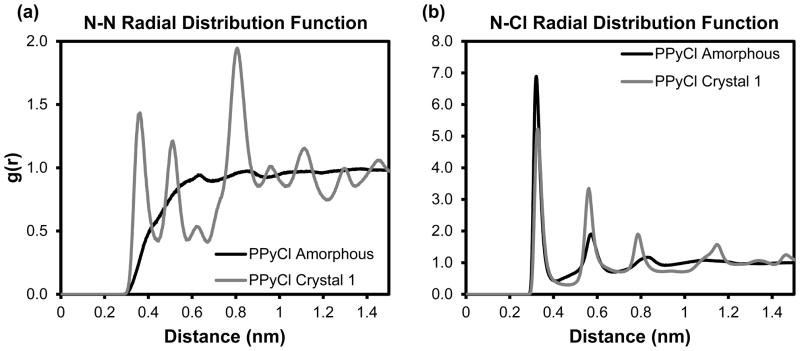
Simulations provide a wealth of information about atomic structure and molecular interactions that is not easily gathered experimentally. In addition to comparing the bulk density, we have also compared the radial distribution functions (RDF) of our in silico matrices to experimental x-ray diffraction data we gathered for PPyCl. Interchain radial distribution functions for PPyCl are shown in Figure 5. For the nitrogen-chloride RDF, the sharp peak at 0.32 nm in both amorphous and crystalline PPyCl shows a stable, well-defined electrostatic interaction between chloride and oxidized PPy. The nitrogen-nitrogen RDF, which does not include intramolecular nitrogen distances, has a shoulder around 0.4 nm and rounded peaks at 0.61 nm and 0.81 nm for amorphous PPyCl. In contrast, crystalline PPyCl has pronounced peaks at 0.35 nm and 0.506 nm. From the simulated structures, we observed that PPy chains in a π-stacked configuration were between 0.33 and 0.43 nm apart, which accounts for the shoulder observed at 0.4 nm in amorphous PPyCl and the peak at 0.35 in crystalline PPyCl. The distances between nitrogen atoms of different chains surrounding the same chloride ion are between 0.61 and 0.66, corresponding to the first rounded peak in the amorphous RDF.

Figure 5. Radial distribution functions for PPyCl.

Normalized radial distribution functions for (a) nitrogen-nitrogen and (b) nitrogen-chloride. Nitrogens within the same molecule were excluded. (a) The peak at 0.35 nm for crystalline PPyCl shows an increase in pi stacking versus amorphous PPyCl. (b) In both crystalline and amorphous PPyCl, dopant ions are consistently 0.32 nm from the nitrogen atom with which they interact.

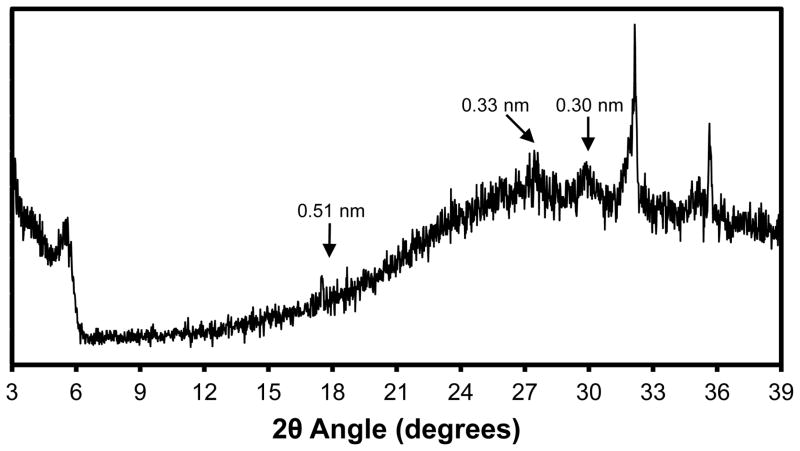
We performed amorphous X-ray diffraction experiments on electrochemically synthesized thick PPyCl films to examine peaks associated with chain packing. As shown in Figure 6, the reflections associated with average chain packing distance are concentrated around a 2θ angle of 27°, which may correspond to the N-N separation of pi-stacked PPy chains observed in the simulated RDFs (Figure 5). Previous studies using perchlorate-doped PPy report chain packing 2θ angles of 22° (0.40 nm) for an amorphous PPy film and 24° (0.37 nm) for a slightly more crystalline PPy film, as controlled by synthesis conditions [30]. These previously reported distances are in agreement with the N-N separation in our simulated amorphous PPyCl matrix (Figure 5a). In our X-ray diffractogram, we also observed peaks at 2θ angles of 29.5° and 32° and a small peak at 17.5°. The peak at 32° may indicate the presence of residual NaCl crystals on the surface of the film. Even after rinsing, we have occasionally observed some residual salt crystals on the surface of our PPyCl films. The peak at 29.5° corresponds to an interatomic distance of 0.30 nm and the small peak at 17.5° corresponds to 0.506 nm. Given that our simulated films had slightly lower densities, the experimentally observed peak at 0.30 nm may be related to the average N-Cl distance of 3.2 nm in our simulated films. The small X-ray diffraction peak at 0.506 nm matches perfectly with the second peak of the N-N RDF for our simulated crystal structure.

Figure 6. X-ray diffractogram of electrochemically synthesized PPyCl.

Experimentally synthesized PPyCl films were analyzed for comparison with computationally generated PPyCl matrices. The broad rounded peak associated with chain packing centered around a 2θ angle of 27°, which corresponds to a d-spacing of 0.33 nm. The sharp peak around 32° likely represents residual NaCl crystals on the surface of the film that were not fully removed from rinsing.

Conclusions

We have analyzed polypyrrole’s structure, charge distribution, and backbone flexibility in both the doped and undoped state using quantum mechanics calculations. We found that over 80% of the net positive charge of oxidized PPy stays within the three rings closest to the dopant ion. We also observed a dramatic increase in backbone stiffness upon doping. From these QM calculations, we have parameterized a fixed-charge force field suitable for studying the properties of bulk PPy. We examined the performance of this model by comparing the minimum energy structure with quantum mechanics results, by comparing the backbone torsion energy scan with quantum mechanics results, and by comparing bulk density measurements and RDFs to our own experimental data and previously reported data from flotation density and X-ray diffraction. The force field performed well when compared to QM results. Our simulated density values were slightly below reported experimental values, but after attempting to repeat the work with a previously reported model, we conclude that the force field itself performs well and that there is room for improvement in chain packing approaches. We believe this work presents the most rigorously parameterized and accurate force field to date, especially with respect to the electrostatics and torsion potential. As future work, the parameterization and incorporation of bipolarons would strengthen the model and may also improve the recreation of bulk material properties. Polypyrrole has many promising applications in biomedical and electronic fields, and an accurate computational model of this material creates opportunities for us and others to investigate its behavior and interactions with other molecules.