Quantitative understanding of cell signaling: The importance of membrane organization

Abstract

Systems biology modeling of signal transduction pathways traditionally employs ordinary differential equations, deterministic models based on assumptions of spatial homogeneity. However, this can be a poor approximation for certain aspects of signal transduction, especially its initial steps: the cell membrane exhibits significant spatial organization, with diffusion rates approximately two orders of magnitude slower than those in the cytosol. Thus, to unravel the complexities of signaling pathways, quantitative models must consider spatial organization as an important feature of cell signaling. Furthermore, spatial separation limits the number of molecules that can physically interact, requiring stochastic simulation methods that account for individual molecules. Herein, we discuss the need for mathematical models and experiments that appreciate the importance of spatial organization in the membrane.

Introduction

Cell signaling is an essential, ubiquitous process that living systems use to respond to the environment. Cell signaling underlies critical cellular decisions such as development, cell growth and division, differentiation, migration, apoptosis, and it essentially provides the coordination required for the functionality of multicellular organisms. Understanding cell signaling is critical, due to its importance in cellular fate decisions and because malfunctions in cellular signaling are at the heart of many diseases such as cancer, autoimmune disease and others. To further the understanding of cellular signaling, traditional biological reductionist research is now complemented with a systems biology approach. It is the focus of this opinion article to discuss the importance of an often neglected aspect of cell signaling—the spatial organization of the cell membrane.

Signal propagation is controlled in part by spatial and temporal organization of the proteins involved in the subsequent protein-protein and protein-lipid interactions. The challenge is to understand the mechanisms that regulate the efficiency, specificity and duration of cell signaling, and how interactions among proteins in the signaling network alter signal strength and the nature of the physiological response. These are all not simply functions of the biochemical properties of the proteins involved. For example, if two components of a signaling pathway occupy separate and distinct regions of the cell membrane, there will essentially be a block in the signaling pathway. In contrast, if two proteins in the same signaling pathway exist at very low concentrations, the signal can still be transmitted effectively, if the proteins are co-clustered in the same microdomain on the cell membrane. It is likely that the cell uses spatial organization to control and regulate signaling. Therefore, the spatial and temporal complexities of cell membranes must be fully resolved, in order to properly understand cell signaling and its regulation. Furthermore, additional features in the membrane such as signaling microdomains, lipid rafts, cytoskeletal corrals and lipid shells, must be addressed [1–7].

Systems biology for signal transduction

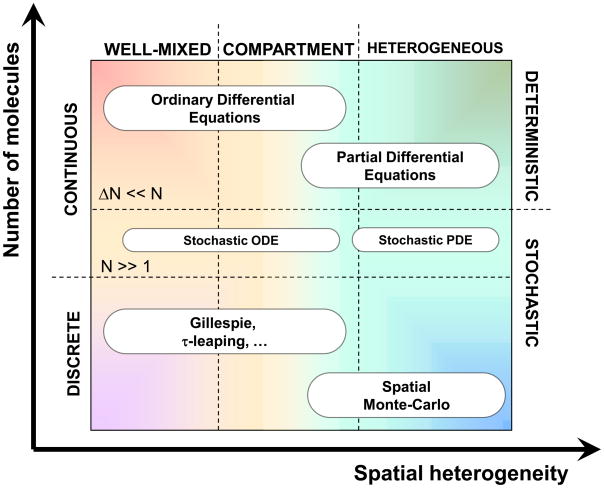
Mathematical modeling of signaling pathways has traditionally been divided into two types, deterministic and stochastic (Figure 1). In reality, biochemical reacting systems are stochastic; however, when the numbers of molecules are large, the stochastic fluctuations are insignificant relative to the absolute molecule number. This is the justification for the deterministic approach used in the vast majority of systems biology models. Another simplification that is inherent to many systems biology studies is the well-mixed assumption. In other words, these models do not consider spatial organization of the cells, tissues, organs, etc. Nonetheless, deterministic models continue to provide useful insight [8,9]. On the other hand, given the heterogeneous organization of biological systems, we view the spatial organization as an important aspect of cell biology to be included. Therefore, over the past decade we have been developing systems biology simulation tools that include realistic spatial organizations [10–14]. We have started with the plasma membrane, given its central role in signal transduction, and are extending our tools and approaches inward to the cytosol [14] and outward to the tissue level. This manuscript focuses on the systems biology tools for studying spatially non-homogeneous systems and the needs for future developments.

Figure 1.

Classes of mathematical models for biochemical processes in cells and their applicability and assumptions. Well-mixed systems: The underlying biochemical processes with cells are stochastic transformations. However, a deterministic mathematical description may be applicable depending on the number of molecules N of each molecular species in the volume (or area) of interest. This number must be large (N≫1) for a deterministic approach to provide an accurate representation. Basically, the expected stochastic fluctuations of the molecule number (ΔN, the magnitude of intrinsic fluctuations is on the order of N^1/2) must be small relative to the absolute number for a deterministic description to be an acceptable assumption. Spatially heterogeneous systems: The well-mixed assumption implies that there is no significant spatial heterogeneity in the system. If this is not true but there are well-defined spatial regions that are homogeneous, then a compartment-based model may be used instead of a fully spatial model.

Spatial simulations

The majority of discrete, stochastic simulations have been limited to well-mixed (also called spatially uniform or homogeneous) systems [15–24]. The assumption of a well-mixed condition may be justified in some biological systems, whereas for other conditions spatial modeling may be necessary. The introduction of powerful microscopy methods (Figure 2)[25] has enabled the construction of spatially distributed (nonuniform) models that can impact significantly our understanding and control of biological systems at the molecular level.

Figure 2.

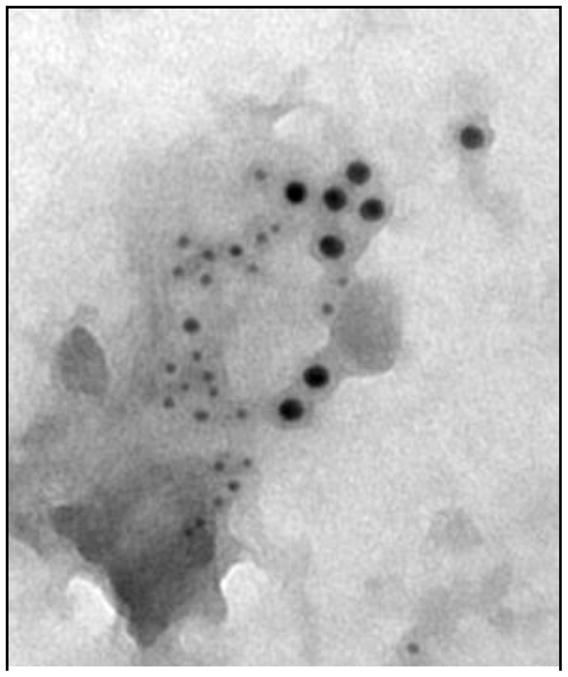
Electron micrograph of a membrane sheet as prepared by Wilson et al [75]. The figure shows colocalization of the formyl peptide receptor (FPR)(5 nm) and FcεRI (10 nm) within 1 min of simultaneous addition of their ligands.

Recent studies have emphasized the necessity of stochastic spatial, as opposed to well-mixed deterministic or partial differential equation (PDE), models for accurate quantitative analysis of biological systems; see [17,26–35] and reviews [27,28,36]. The inclusion of a spatial description is of great importance in biology [27], and spatial modeling has conventionally been performed with PDE methods. PDEs have been used to study receptor-ligand dynamics [37–46], intracellular processes [47,48], signaling processes in the plasma membrane [49,50] and other biological problems [51]. Furthermore, Fickian diffusion and Smoluchowski models have been used to study diffusion aspects of synaptic transmission [52,53]. An excellent software tool, VCell, has been developed for PDE-based spatial simulations [54].

PDE-based approaches usually have difficulty capturing the transients of bimolecular reactions, for example, receptor-receptor interactions. Two excellent examples underscoring the limitations of PDEs are found in [26,55]. These limitations arise because tracking the transient evolution of bimolecular reactions with reactants is a many-body problem [56–59], whereas most of the PDE-based efforts are based on the Smoluchowski [60,61] and Collins-Kimball [62] models which only include two-particle interactions, and are valid in the diffusion-limited regime [11]. Our intent here is not to review these efforts; rather, to point out that an exact relation between the effective reaction rate constant and diffusivity is difficult to obtain for a general two-dimensional bimolecular reaction, especially if one is interested in the transient behavior of the system.

Stochastic PDEs, such as the Langevin equation, are also used to capture the effect of noise in spatiotemporal dynamics [63]. However, these approaches rely on the idealized notion of white noise, with fluctuations on all scales. This is unrealistic and may lead to difficulties when the number of copies of proteins is small, as is often the case with plasma membrane proteins. A brief overview of the types of continuum equations that have been used for this purpose see [63] and references therein.

Kinetic or dynamic Monte Carlo (MC) based spatial modeling involves first-principles stochastic simulations of the movement, collisions and chemical transformations of individual molecules in a finite sized volume or area. It is an attractive alternative to PDE-based approaches for modeling cell surface receptor dynamics, because its computational implementation can explicitly consider (1) the creation of a spatially non-random distribution of proteins due to bimolecular reactions [26], (2) the spatial heterogeneity such as microdomains in the plasma membrane [7,64–67] and (3) the noise and correlations resulting from a small number of copies of activated receptors. The major limitation of Kinetic MC based approaches is that they are computationally demanding. Attempts at acceleration of spatial algorithms have primarily focused on algorithmic aspects: fast update and search methods. For example, the work of Bortz et al. on the n-fold or continuous time MC (CTMC) method [68] is a significant achievement in computational speedup. However, improvements are needed for stiff problems, to overcome the one event per iteration issue and to reach large length scales.

Rationale for spatial stochastic modeling: Application to the FcεRI and Formyl Peptide Receptor (FPR) systems

The rapidly growing body of simulation studies has clearly demonstrated that stochastic modeling is essential in spatially well-mixed systems when the population size of one or more key intermediates is small [22,24]. Under such conditions, large noise and significant departure of average rates from their deterministic counterparts are encountered. However, as the population size increases the noise is reduced, and for large systems deterministic behavior is recovered. In the FcεRI and FPR systems it is estimated that there are 50–200 receptors and 1–5 coated pits (diameter of 60–80 nm) in each 1 μm² of plasma membrane [25]. Such small population sizes require a stochastic method [11].

Many microscopic-scale biological systems, including several spatial features in the FcεRI and FPR system, have yet to be evaluated by spatial stochastic models. Important spatial features of membrane systems include: (1) the necessary proximity of two receptors for dimerization to occur (nonlinear chemical events can cause significant spatial correlations and lead to pattern formation such as clustering, even in the absence of direct attractive intermolecular forces [29,69]) (Figure 3); (2) the possible attractive interactions between receptors and membrane microdomains that render Fickian diffusion structurally incorrect [70]; (3) the directional‘ or uphill‘ diffusion of receptors toward pits; and (4) the observed hop diffusion of membrane proteins [67,71–74]. With such spatial effects, the stochastic solution differs from the deterministic solution even in the infinite, macroscopic size limit. Thus, this situation is very different from spatially homogeneous systems. Consequently, we propose that the spatial multi-resolution MC framework will provide a protein-level model that can provide much insight into signal transduction.

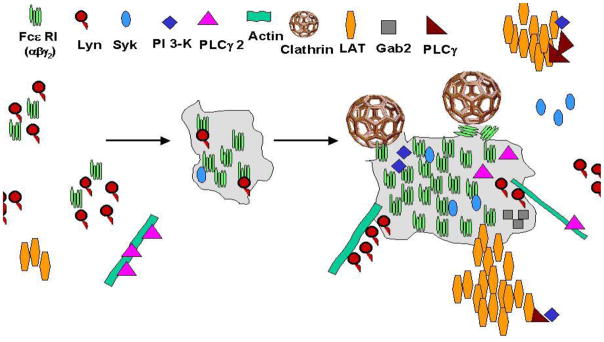
Figure 3.

Membrane organization of a subset of signaling proteins in the FcεRI (High-affinity IgE receptor) cascade, based on immunogold labeling experiments. This figure features new added complications that must be addressed by systems biology. Abbreviations used: PLCγ2 (Phospholipase C-γ2), PLCγ (Phospholipase C-γ), LAT (linker for activation of T cells), Syk (Spleen Tyrosine Kinase), Lyn (Yamaguchi sarcoma viral related oncogene homolog – a Src family tyrosine kinase), Gab2 (Grb2 associated binding protein 2), PI3K (Phosphoinositide 3-Kinase).

Need for more detailed spatial models focusing on the membrane

The fluid mosaic model portrays protein movement as Brownian motion in a sea of lipids. Although this model is the foundation of membrane biology, it has been beset by two inconsistencies: (1) the diffusion coefficients for both proteins and lipids are 5 to 50 times smaller in the plasma membrane than in artificial membranes and (2) oligomers or molecular complexes exhibit a much lower diffusion coefficient (by a factor of 40) in the plasma membrane than in artificial membranes. Also, direct observation has revealed that proteins are not randomly distributed. These discrepancies between the fluid mosaic model and experimental findings are indicative of the necessity for an improved model, and have lead researchers on an almost 40-year journey to uncover the true nature of the plasma membrane.

Associated with this lipid-based architecture arises a landscape of complexity, ranging from the coalescence of phospholipids into “lipid rafts” to the hindering interactions caused by the cytoskeleton. Thus this almost 40-year journey has enlightened the membrane biology community, and provides a new direction for systems biology as a whole. What has been established is that the plasma membrane is a highly compartmentalized surface, which affects the diffusion of signaling proteins in the membrane, and hence the initiation and activation of signal transduction pathways. These developments highlight a need for computational algorithms that take into account the observed biological complexity occurring within the cell membrane.