Impact of Ignoring Extraction Ratio When Predicting Drug-Drug Interactions, Fraction Metabolized, and Intestinal First-Pass Contribution

Abstract

Many mathematical models for in vitro to in vivo prediction of drug-drug interactions (DDIs) of orally administered victim drugs have been developed. However, to date, none of these models have been applicable to all intravenously administered victim drugs. We derived and conducted a sensitivity/error analysis of a modification to the existing multiple mode interaction prediction model such that it is applicable to all intravenously administered victim drugs. Using this model we showed that ignoring the hepatic extraction ratio (EH) (as low as 0.3) of intravenously administered victim drugs can result in 1) substantial underestimation of f_{m, CYPi} (the fraction of hepatic clearance of the victim drug via a given enzymatic pathway) and 2) error in dissecting the contribution of intestinal and hepatic components of DDIs for orally administered drugs. Using this model we describe DDI boundaries (degree of inhibition or induction) at which ignoring the EH of commonly used victim drugs results in ≥30% error in the predicted area under the concentration-time curve (AUC) ratio or contribution of intestinal interaction to a DDI (CYP3A probes only). For the most widely used victim drug midazolam, these boundaries for AUC ratio are net inhibition (I/K_i or λ/k_deg) ≥1.3 or fold induction ≥2.1; for intestinal contribution the boundaries are 0.37 and 1.5, respectively. To accurately predict the intravenous AUC ratio, intestinal contribution, or f_{m, CYPi} 1) for all induction DDIs irrespective of EH of the victim drug and 2) for modest to potent inhibition DDIs even when the EH is moderate (≥0.3), we propose that our model be used.

Introduction

The concept of hepatic clearance has been described by either a well stirred or a parallel tube model (Rowland et al., 1973; Pang and Rowland, 1977). Through many iterations (Ito et al., 1998; Mayhew et al., 2000; Ernest et al., 2005; Venkatakrishnan and Obach, 2005; Obach et al., 2006; Shou et al., 2008), this concept has been applied to predict the change in clearance and, therefore, AUC of a victim drug in the presence and absence (AUC ratio, AUC′/AUC) of a perpetrator drug operating via enzyme inhibition, inactivation, and/or induction. The culmination of these iterations has resulted in a combined model that accounts for all three of these mechanisms in both the intestine and the liver (Fahmi et al., 2008). All of these models have been derived for oral administration of the victim drug, for which the AUC ratio is directly proportional to the change in intrinsic clearance. This type of model can be applied to the intravenous administration of a victim drug without error if the victim drug can be assumed to have a very low hepatic extraction ratio (EH). For moderate to high EH drugs, either predictions have been made with the assumption that the drug is a low EH drug (Ito et al., 1998; Ernest et al., 2005; Fahmi et al., 2008; Shou et al., 2008) or a ratio of the full well stirred model has been used, necessitating an estimate of the true hepatic intrinsic clearance of the victim drug (Ibrahim et al., 2003). This second approach does account for the blood flow limitations of the well stirred model but requires more laborious calculations and generation of a unique relationship between change in intrinsic clearance and AUC ratio for each victim drug (Ibrahim et al., 2003). Many of the victim drugs used in drug-drug interaction (DDI) studies are moderate (EH >0.3) to high (EH ≥0.7) extraction ratio drugs: midazolam, 0.44 (Thummel et al., 1996); alfentanil, 0.28 (Kharasch et al., 2004); desipramine, 0.56 (Ciraulo et al., 1985, 1988); and metoprolol, 0.69 (Patrick, 2002). Therefore, we set out to develop a more generally applicable prediction model that does not assume a low EH, but retains the full well stirred model of hepatic clearance and is therefore applicable to the intravenous administration of a victim drug in the presence of a perpetrator drug.

Intravenous administration of victim drugs is used for a multitude of reasons including 1) determining the contribution of hepatic and/or intestinal enzyme inhibition or induction by a precipitant drug in a DDI study (Holtbecker et al., 1996; Kharasch et al., 2004; Galetin et al., 2010) and 2) determining the fraction of hepatic metabolism of a victim drug by a specific enzyme (f_{m, CYPi}) (Shou et al., 2008). In these situations, if the EH of the victim drug is not accounted for, the inherent error described above is propagated to the parameters gleaned from these investigations. Therefore, using our generally applicable model we were able to investigate the impact that this simplification has on the parameters determined. The magnitude of this error will vary based on the specific pharmacokinetic parameters of the victim drug (e.g., EH and f_{m, CYPi}) and the severity of the DDI (degree of inhibition or induction). Therefore, we determined boundaries outside which the simplification of ignoring the EH of the victim drug has a significant effect (≥30%) on the predicted AUC ratio, estimated f_{m, CYPi}, and the DDI contribution of intestinal enzyme alteration for some of the most common intravenously administered victim drugs. We found that for most of the commonly used probe drugs, ignoring the EH will incorporate ≥30% error under moderate enzyme inhibition (I/K_i or λ/k_deg = 1–10) or induction (∼3-fold). This mathematical error can be eliminated by using the slightly more complex yet easily manageable model proposed here.

In this report, we first present a comprehensive model that can be used to predict multiple mode DDIs, irrespective of the EH of the victim drug. Then, we present a sensitivity analysis of the model as well as practical guidelines on when this comprehensive model should be used.

Materials and Methods

Modified Model for Intravenously Administered Drugs.

The AUC ratio (AUC′_IV/AUC_IV) of a victim drug in the presence and absence of a perpetrator drug can be described by eq. 1, assuming that only hepatic clearance (Cl_hep) of the victim drug is affected but hepatic blood flow (Q), unbound fraction (f_u), and the renal clearance (Cl_renal) are not.

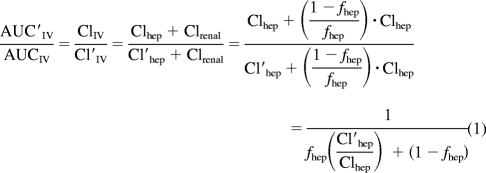Cl_hep and Cl′_hep are the hepatic clearance (determined by the well stirred model) in the absence and the presence of the perpetrator, respectively, and f_hep is the fraction of Cl_IV that is subject to the hepatic blood flow limitation. The ratio of Cl′_hep and Cl_hep can be simplified to eq. 2, where Q is liver blood flow and is assumed not to be affected by the DDI, f_u is the unbound fraction of the victim drug in blood and Cl′_int and Cl_int are the intrinsic clearance of the victim drug in the presence and absence of the perpetrator.

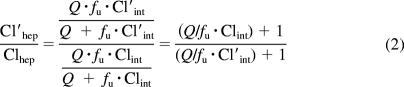An equation similar to the first half of eq. 2 has been described previously (Shou et al., 2008) but was simplified to either assume very low EH (Cl_hep = Cl_int) or high EH (Cl_hep = Q). A rearrangement of the well stirred model Cl_hep = Q · EH = [(Q · f_u*Cl_int)/(Q + f_u*Cl_int)] reveals that (Q/f_u*Cl_int) = [(1/EH) − 1], which can be substituted into eq. 2 to give eq. 3 in which f_Clint^Hep is the fraction of hepatic intrinsic clearance remaining as a result of the net effect of the perpetrator drug (Cl′_int = f_Clint^Hep · Cl_int).

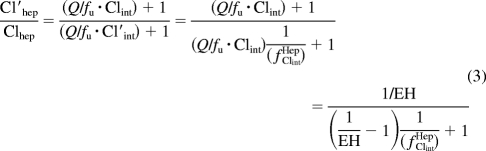f_Clint^Hep is the product of the fraction of intrinsic clearance remaining as a result of inactivation (f_Inactivation^Hep; eq. 4), induction (f_Induction^Hep; eq. 5), and inhibition (f_Inhibition^Hep; eq. 6), which are analogous to the A, B, and C terms, respectively, described previously (Fahmi et al., 2008).

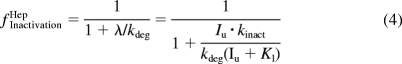where λ is the predicted inactivation rate of the enzyme, I_u is the unbound perpetrator drug concentration for which the plasma unbound concentration (maximum, average, or maximum portal vein) has been used as a surrogate (Ito et al., 2004; Obach et al., 2006), k_inact is the maximum inactivation rate constant, K_I is the concentration that produces half-maximum inactivation, k_deg is the normal degradation rate constant of the affected enzyme in the liver, d is the in vitro to in vivo scaling factor for induction, Ind_max is the maximum fold induction of mRNA of the affected enzyme, EC₅₀ is the concentration that results in half-maximal induction, and K_i is the inhibition constant. Equation 3 can then be substituted back into eq. 1 to arrive at eq. 7, which describes the AUC ratio of a victim drug administered intravenously in which the entire hepatic clearance is a result of one enzymatic process (f_{m, CYPi} = 1).

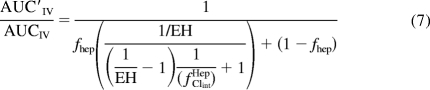To describe the hepatic clearance of a victim drug that is a result of multiple enzymatic processes (p), the inclusion of an f_{m, n} term, which is the fraction of the hepatic clearance of the victim drug that is a result of the nth enzyme is required and results in eq. 8.

When the EH in eq. 8 is set to a very small value (very low extraction ratio drug) the equation will collapse to an equation similar to that described by Fahmi et al. (2008) with the inclusion of the f_hep term and devoid of the term addressing the change in intestinal intrinsic clearance.

Sensitivity and Error Analysis of Key Prediction Parameters.

The main determinants of the AUC ratio as calculated in eq. 8 can be separated into five major variables: f_hep (the fraction of IV clearance that is hepatic elimination), f_{m, CYPi} (the fraction of hepatic clearance that is mediated by the affected enzyme), f_Clint^Hep (the combined effect of inactivation, induction, and inhibition or net change in intrinsic clearance), EH (hepatic extraction ratio of the victim drug), and other nonhepatic clearance mechanisms such as renal clearance denoted by (1 − f_hep). The contribution of some of these parameters such as f_{m, CYPi}, other clearance pathways, and enzyme degradation half-life (implicit to inactivation) to the AUC ratio have been evaluated and will not be addressed further (Venkatakrishnan and Obach, 2005; Galetin et al., 2006). A major focus of this article is to describe the impact of not accounting for victim drug hepatic extraction ratio on AUC predictions. Therefore, we conducted a sensitivity/error analysis to evaluate the contribution of f_hep, f_{m, CYPi}, EH, and net change in intrinsic clearance (f_Clint^Hep) to the error in predicted AUC ratio using a No EH model (where EH was set to a very low number 1 × 10⁻¹⁰) and the EH model in which the EH was accounted for. The percent error in the predicted AUC ratio as a result of using the No EH model was calculated by eq. 9.

Because this model accounts for inactivation, induction, and inhibition, it is important to note that these three terms are combined in a multiplicative fashion as justified previously (Fahmi et al., 2008). Therefore, if a precipitant elicits interactions through all three mechanisms, the overall effect on intrinsic clearance is the product of the inactivation (f_Inactivation^Hep), fold induction (f_Induction^Hep), and reversible inhibition (f_Inhibition^Hep) terms. For example, if a precipitant has f_Inactivation^Hep of 0.2 (1 + λ/k_deg = 5), f_Induction^Hep of 5 (5-fold induction), and f_Inhibition^Hep of 0.2 (1 + I_u/K_i = 5), the net result is that the intrinsic clearance will decrease to one-fifth (f_Clint^Hep = 0.2 · 5 · 0.2 = 0.2) of the basal intrinsic clearance. Historically the potencies of inactivation, induction, and inhibition have been quantified by λ/k_deg, fold increase in enzyme expression, and 1 + I_u/K_i, respectively. Because these terms are grouped, we conducted the sensitivity/error analysis with respect to the value of the product (f_Clint^Hep), which can be easily thought of as the fold change in intrinsic clearance or fraction of intrinsic clearance remaining as a result of the interaction. A value >1.0 implies a net induction, and a value <1.0 implies a net inhibition or inactivation.

Impact of EH on Estimating Intestinal Contribution to DDIs.

A more thorough understanding of intestinal metabolism and its contribution to DDIs has increased predictability of DDIs (Galetin, 2007; Galetin et al., 2007). One method that has been used to dissect the contribution of intestinal drug-metabolizing enzymes to DDIs, i.e., the intravenous and oral administration of a victim drug, was recently reviewed (Galetin et al., 2010). The degree of interaction observed with the intravenously administered victim drug is dissected from the interaction observed after oral administration of the object drug to yield the magnitude of interaction in the intestine. This can be done by solving a modified version of the model of Fahmi et al. (2008) (in which the f_Clint^GI term is the net effect on intestinal intrinsic clearance, similar to the f_Clint^Hep term for hepatic intrinsic clearance), namely, eq. 10 for f_Clint^GI as shown in eq. 11.

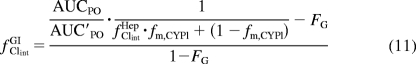The piece of information needed from the intravenously administered interaction is the fold change in hepatic intrinsic clearance (f_Clint^Hep). We determined the impact that incorrectly determining the fold change in hepatic intrinsic clearance using the No EH model has on the estimate of the intestinal interaction. To do this, we generated intravenous and oral AUC ratios using eqs. 8 and 10, respectively, for a victim drug with f_hep = 1.0, f_{m, CYPi} = 0.95, and F_G = 0.5 (values similar to those of midazolam, a widely used CYP3A victim drug) with EH ranging from 0.1 to 0.9 by setting the fold change in hepatic (f_Clint^Hep) and intestinal (f_Clint^GI) intrinsic clearance equal and varying the values from 25 to 0.0001 (25-fold induction to 99.99% inhibition). The intravenous AUC ratios were then used to estimate the fold change in hepatic intrinsic clearance using a rearrangement of the No EH model (eq. 12).

The No EH model determined fold change in hepatic intrinsic clearance values along with the generated oral AUC ratios were used in eq. 11 to estimate the fold change in intestinal intrinsic clearance (f_Clint^GI) and the F_G ratio (eq. 13).

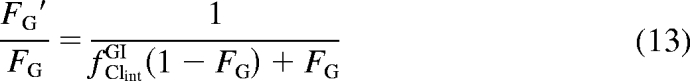These calculated values were compared with the parameter values, e.g., F_G values that were used to generate the AUC ratios. Percent error was calculated for the value determined using the No EH model relative to the true value. A similar analysis was done to show the impact of F_G on this error by varying F_G from 0.1 to 0.75 using a fixed EH of 0.25. This low EH of 0.25 (at the lower boundary of having a significant impact on the intravenous AUC ratio) was chosen to highlight the fact that a significant impact on F_G can be observed when there is minimal impact on intravenous AUC ratio. Mixed interactions (net induction in the liver and net inhibition in the intestine or vice versa) were evaluated using the simulation approach listed above to determine the boundaries at which net induction or inhibition in the intestine could be masked by net inhibition or induction in the liver, respectively.

Impact of EH on Estimating f_{m, CYPi}.

One method historically used to estimate f_{m, CYPi} (the fraction of the victim drug metabolized by a specific enzyme) is to administer the victim drug intravenously in the presence and absence of a very potent inhibitor (Shou et al., 2008). Based on the maximum observed AUC ratio, f_{m, CYPi} is calculated using eq. 14.

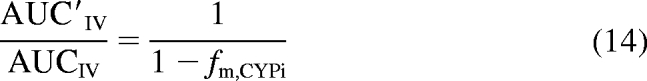Because this equation does not account for the blood flow-limited nature of hepatic clearance or nonhepatic elimination of the probe drug, the true f_{m, CYPi} is underestimated. To account for these shortcomings of eq. 14, eq. 8 was rearranged to eq. 15 by assuming that f_Clint^Hep was negligible (complete inhibition) and solving for f_{m, CYPi}.

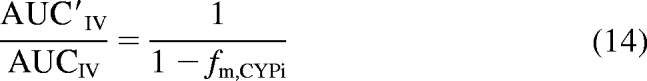To show the magnitude of underestimation of f_{m, CYPi} by eq. 14, intravenous AUC ratios were first simulated using eq. 8 for victim drugs with varying f_{m, CYPi} values, across a range of extraction ratios from 0.001 to 1.0, assuming complete inhibition (f_Clint^Hep ∼0), and f_hep was assumed to be 1.0 (negligible nonhepatic elimination). These simulated AUC ratios were then used to estimate the f_{m, CYPi} values using eq. 14 (the No EH model). The impact of the error in f_{m, CYPi} determined by the No EH model would be greatest when the victim drug was given orally in the presence of complete inhibition. Therefore, we determined the percent error in the predicted maximum AUC ratio (assuming f_Clint^Hep = 0) calculated using eq. 10 with the f_{m, CYPi} estimated by the No EH model (eq. 14) and the f_{m, CYPi} value used for the simulation. For simplicity no intestinal extraction was assumed for the simulation.

DDI Boundaries Where the Impact of EH Is Greatest.

Because of the multiple parameters that contribute to the impact of ignoring EH, it is difficult to immediately discern benchmarks at which ignoring the EH has a significant impact on accurately predicting DDIs. Therefore, we compiled the necessary parameters for some commonly used victim drugs across a range of EH (Table 1). For those drugs for which f_hep was not readily available, a value of 1.0 was assigned. Then, using the modified model, we determined the DDI boundaries, degree of inhibition or induction, that would result in ≥30% error in the predicted AUC ratio (for all victim drugs) or the contribution of intestinal enzymes to the DDI (CYP3A drugs only, following the same assumptions as in the section Impact of EH on Estimating Intestinal Contribution to DDIs).

TABLE 1.

DDI boundaries (magnitude of inhibition or induction) at which the error in ignoring EH for intravenous administration of commonly used victim drugs exceeds ±30% for predicted AUC ratio and intestinal contribution to a DDI and the error in estimated f_{m, CYPi} when EH is ignored for intravenously administered victim drugs

Victim Drug	EH	f m, CYPi	f hep	F G	AUC′IV/AUCIV Error ≥±30%		Clint, GI′/Clint, GI Error ≥±30%		Ignoring EH for Determination of fm, CYPi
					Inhibition I/Ki or λ/kdeg ≥	Fold Induction ≥	Inhibition I/Ki or λ/kdeg ≥	Fold Induction ≥	fm, CYPi Ignoring EH	%Error in Maximum Oral AUC Ratio (−fm, CYPi · EH · 100)
CYP3A
Midazolam	0.44 a	0.93 b	0.995 c	0.54 a	1.3	2.1	0.37	1.5	0.90	−41
Alfentanil	0.28 d	0.98 d	0.99	0.59 d	9.0	2.6	0.54	1.6	0.96	−27
Nifedipine	0.45 b	0.78 e	0.99	0.74 b	2.0	2.3	0.25	1.3	0.65	−35
CYP2C9
Tolbutamide	0.01 f	0.78 b	1	N.A.	Not possible	56	N.A.		0.78	−0.8
S-Warfarin	0.003 g	0.91 b	1	N.A.	Not possible	160	N.A.		0.91	−0.3
CYP2D6
Desipramine	0.48 h	0.88 i	1	N.A.	0.9	2.0	N.A.		0.79	−42
Imipramine	0.70 j	0.46 i	1	N.A.	2.6	2.3	N.A.		0.20	−32
Metoprolol	0.84 k	0.83 i	1	N.A.	0.5	1.6	N.A.		0.44	−70
Propranolol	0.62 l	0.37 i	1	N.A.	Not Possible	2.9	N.A.		0.18	−23

N.A., not applicable.

^a Data from Thummel et al. (1996).

^b Data from Obach et al. (2006).

^c Data from Midazolam HCL Injection package insert (Baxter Healthcare, Deerfield, IL).

^d Data from Kharasch et al. (2004).

^e Data from Ohno et al. (2007).

^f Data from Miners et al. (1982).

^g Data from Abernethy et al. (1991).

^h Data from Ciraulo et al. (1988).

ⁱ Data from Ito et al. (2005).

^j Data from Abernethy et al. (1984).

^k Data from Leemann et al. (1993).

^l Data from Feely et al. (1981).

Results

Sensitivity/Error Analysis.

A concise summary of the sensitivity/error analysis is provided here (for a comprehensive analysis, the reader is referred to the supplemental data). In brief, the impact of ignoring EH on the predicted AUC ratio of an intravenously administered victim drug is dependent on f_hep, f_{m, CYPi}, EH, and the degree of the interaction (inhibition or induction). The minor nonhepatic clearance mechanisms (f_hep > 0.9, which is the case for many victim drugs) (Table 1), have a measureable impact (≥30% error) on the predicted intravenous AUC ratio and should be taken into account when this ratio is predicted in the presence of potent inhibition interactions (f_Clint^Hep <0.1, >90% inhibition). Likewise, ignoring the hepatic blood flow dampening of the unaffected hepatic clearance pathways (1 − f_{m, CYPi} ≤ 0.1) for drugs with EH ≥0.35 for potent inhibition interactions (f_Clint^Hep <0.1, >90% inhibition) will contribute greater than 30% error to the predicted intravenous AUC ratio. For net induction interactions, the effect of EH is substantial (−25% error for EH = 0.25 and modest 2.5-fold induction) and should always be taken into consideration. For a specific inhibitor/inducer, as EH of the victim drug increases, the percent error in the AUC ratio increases irrespective of whether or not the victim drug is moderate or high EH.

Impact of EH on Estimating Intestinal Contribution to DDIs.

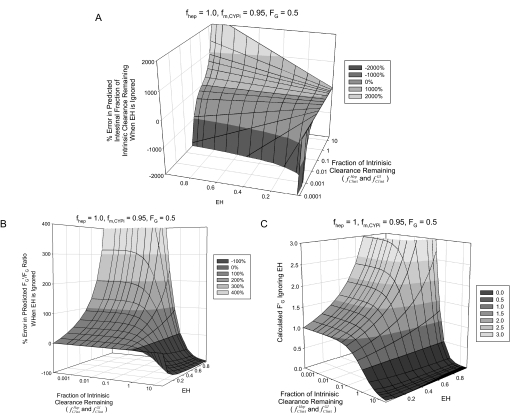
Figure 1, A through C, shows the impact of ignoring the hepatic extraction ratio of an intravenously administered victim drug on the estimation of the intestinal interaction when an intravenous and oral dose of the victim drug (F_G = 0.5) is used to dissect the intestinal and hepatic contribution to a DDI. The percent error in the estimated fraction of intestinal clearance remaining (f_Clint^GI) is shown to be greatly overpredicted (Fig. 1A), by as much as ∼140% for a net induction of 5-fold with a victim drug EH of 0.3. In contrast, when the DDI is a net inhibition interaction (f_Clint^Hep or f_Clint^GI <1), the predicted intestinal interaction is greatly underestimated (∼−280% for f_Clint^Hep = 0.1 with a victim drug EH of 0.3). This error in predicted fold change in fraction of intestinal clearance remaining is also shown as percent error in the predicted change in intestinal bioavailability, or F_G′/F_G ratio (Fig. 1B). Expressed as the F_G′/F_G ratio, the net induction interactions are underpredicted and the net inhibition interactions are overpredicted. The degree of under- or overprediction is dependent on EH and fold induction or inhibition, respectively. For net inhibition interactions, the predicted F_G′ is always higher than the true F_G′ and as the degree of inhibition and the EH of the victim drug increase, this difference is larger. For example, the predicted F_G′ will erroneously increase to a value greater than 1.0, which is not possible. The predicted F_G′ becomes overpredicted by ≥30% (F_G′ ≥1.3) when net inhibition is ≥90% for a victim drug with EH ≥0.35 (Fig. 1C). When the DDI is a net induction interaction, intestinal induction is overpredicted, resulting in predicted F_G′ values substantially less than the true value.

Fig. 1.

Impact of EH on estimating intestinal contribution to DDIs. The effect of ignoring the EH of an intravenously administered victim drug in estimation of the effect of a DDI on intestinal enzymes shows the following. A, the percent error in estimated fraction of intestinal intrinsic clearance remaining (f_Clint^GI) rapidly increases as fold induction (f_Clint^Hep and f_Clint^GI increase above 1) and EH increase. Net inhibition (f_Clint^Hep and f_Clint^GI <1) is greatly underpredicted as EH and degree of inhibition increase. B, the percent error in the predicted F_G′/F_G ratio (or fold change in intestinal bioavailability) shows that for net inhibition (f_Clint^Hep and f_Clint^GI <1), F_G′/F_G is overpredicted when EH is moderate to high (≥0.35) and underpredicted for net induction (f_Clint^Hep and f_Clint^GI >1) even when EH is low (≤0.3). C, the estimated F_G′ is shown to increase beyond the maximum theoretical value of 1.0 by greater than 30% (F_G′ ≥1.3) when the EH is ≥0.35 and net inhibition is ≥90% (f_Clint^Hep and f_Clint^GI ≤ 0.1). Note: the fraction of hepatic (f_Clint^Hep) and intestinal (f_Clint^GI) clearance remaining was set equal and varied between 25 and 0.0001; hepatic extraction ratio was varied between 0.1 and 0.9. The fraction of hepatic (f_Clint^Hep) and intestinal (f_Clint^GI) intrinsic clearance remaining axes are on a logarithmic scale.

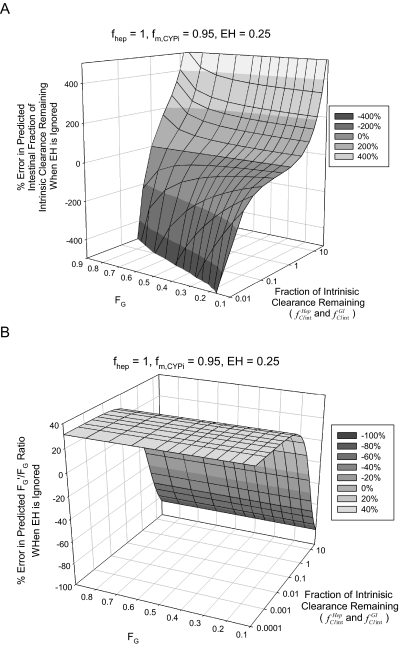
The percent error in predicted f_Clint^GI for victim drugs with varying F_G values assuming a fixed EH of 0.25 (typically thought of as low EH) is shown in Fig. 2A and is heavily dependent on F_G, but the percent error in the predicted F_G′/F_G ratio is not dependent on the value of F_G (Fig. 2B). Likewise, the degree of inhibition at which the predicted F_G′ value will exceed 30% of the theoretical maximum (1.0) is largely independent of F_G.

Fig. 2.

Impact of F_G on estimating intestinal contribution to DDIs. The effect of ignoring the EH of 0.25 across varying F_G values for an intravenously administered victim drug when the effect of a DDI on intestinal enzymes is estimated shows the following. A, the percent error in the estimated fraction of intestinal intrinsic clearance remaining (f_Clint^GI) increases to greater than 200% as fold induction increases above 2- to 3-fold irrespective of F_G and is greatly underpredicted by as much as −100% for 90% inhibition (f_Clint^Hep and f_Clint^GI = 0.1) for F_G >0.3. B, the percent error in the predicted F_G′/F_G ratio is independent of F_G. Note: the fraction of hepatic (f_Clint^Hep) and intestinal (f_Clint^GI) intrinsic clearance remaining was set equal and varied between 25 and 0.0001; intestinal bioavailability was varied between 0.1 and 0.9. The fraction of hepatic (f_Clint^Hep) and intestinal (f_Clint^GI) clearance remaining axes are on a logarithmic scale.

The results above show that when the EH of the victim drug is not accounted for, net induction in the liver can result in a perceived greater induction in the intestine and net inhibition in the liver can result in a perceived greater degree of inhibition in the intestine. Therefore, it is possible, if the EH of the victim drug is ignored, that induction in the liver could mask inhibition in the intestine and inhibition in the liver could mask induction in the intestine. With the hypothetical victim drug described above (f_hep = 1.0, f_{m, CYPi} = 0.95, and F_G = 0.5), we used the simulation approach described above to determine the EH and fraction of hepatic intrinsic clearance remaining (f_Clint^Hep), values that would be necessary to mask either a 2-fold induction or 100-fold inhibition in the intestine.

Ignoring the EH of a victim drug when it is 0.35 and f_Clint^Hep is 0.1 will completely mask (F_G′/F_G = 1.0 or no change in F_G) a 2-fold induction in the intestine (f_Clint^GI = 2). As the EH of the victim drug increases, the degree of hepatic inhibition necessary to mask intestinal induction will decrease. A dependence on F_G was also observed. As F_G increased above 0.5 (less intestinal extraction), a lower value of EH and less potent inhibition in the liver was necessary for this masking to occur. If F_G was smaller than 0.5 (more intestinal extraction), a higher EH and more potent inhibition in the liver was necessary to produce this masking.

To completely mask a 100-fold inhibition in the intestine (f_Clint^GI = 0.01) by ignoring the hepatic EH, the hypothetical victim drug described above must have an EH of 0.25 or greater and hepatic net induction of 5-fold or greater. As the EH of the victim drug increases, the fold induction in the liver necessary to mask the intestinal inhibition will decrease. In addition, as F_G was increased above 0.5, a lesser degree of hepatic induction was necessary to mask the 100-fold inhibition in the intestine. As F_G was decreased (greater intestinal extraction), a greater degree of hepatic induction was necessary to produce this masking.

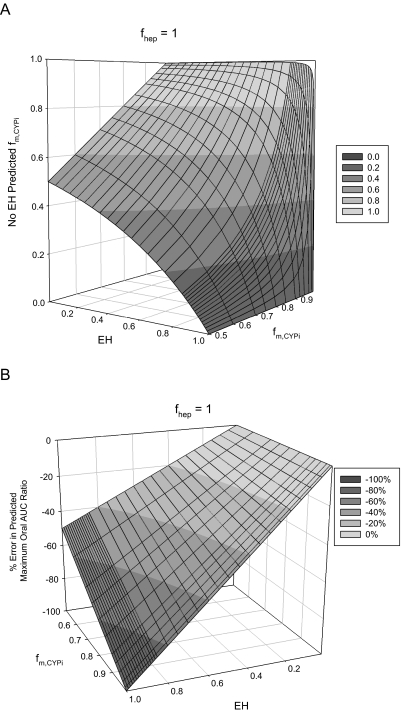
Impact of EH on Estimating f_{m, CYPi}.

Estimated fractions of hepatic clearance due to a specific enzymatic pathway (f_{m, CYPi}) calculated using eq. 14 (No EH model) are shown in Fig. 3A across an EH range of 0.01 to 0.9 for simulated victim drugs with true f_{m, CYPi} values of 0.5 to 0.95. As expected, as the EH of a victim drug increases, the estimated f_{m, CYPi} calculated by the No EH model decreases. To better illustrate the impact of the underprediction of f_{m, CYPi}, we calculated the percent error in the predicted maximum AUC ratio when the victim drug is given orally, assuming no intestinal extraction (Fig. 3B). The slope of this curve is larger for the victim drugs with higher f_{m, CYPi} values and shows a linear relationship dependent on EH. Therefore, the magnitude of this error can be directly calculated as percent error = −f_{m, CYPi} · EH · 100. The incorrect f_{m, CYPi} and percent error in the maximum predicted oral AUC ratio for commonly used victim drugs are listed in Table 1. For low EH drugs, this error is minimal, but for high EH drugs, the error is also dependent on the magnitude of f_{m, CYPi}. For example, the error in the maximum predicted oral AUC ratio for the high EH drugs metoprolol (0.84) and imipramine (0.70) is −70 and −32%, respectively. This result shows that the impact of ignoring EH when one is determining f_{m, CYPi} is dependent not only on the EH of the victim drug but also on the magnitude of f_{m, CYPi}.

Fig. 3.

Impact of EH on estimating f_{m, CYPi}. A, when the f_{m, CYPi} of a victim drug is determined by intravenous administration of the drug in the presence and absence of potent inhibition, ignoring the EH of the victim drug affects the estimated f_{m, CYPi}, and the error in this parameter is a function of both EH and f_{m, CYPi}. B, the impact of this error is most apparent in the percent error in the maximum oral AUC ratio. This error is linear with respect to EH with a slope equal to −f_{m, CYPi} · 100 and therefore can be directly calculated as percent error = −f_{m, CYPi} · EH · 100.

DDI Boundaries Where the Impact of EH Is Greatest.

Table 1 shows the empirically determined DDI boundaries at which there is a ≥30% error in the AUC ratio or contribution of intestinal interaction to a DDI as a result of ignoring EH of the victim drug when administered intravenously. For the widely used CYP3A victim drug midazolam, a net inhibition interaction with I/K_i of ≥1.3 or fold induction ≥2.1 will give rise to greater than 30% error in the predicted intravenous AUC ratio if the modified model described here is not used. The boundaries for ≥30% error in the contribution of intestinal DDIs for midazolam are lower than those of the AUC ratio, 0.37 and 1.5, for inhibition and induction, respectively. These boundaries are determined in a large part by f_{m, CYPi}, F_G, and EH with a much smaller contribution from f_hep. Varying f_hep from 1.0 to 0.95 resulted in only minor changes (<10% increase) in the DDI inhibition boundary for the victim drugs with high (>0.80) f_{m, CYPi} and ∼20% increase for the drugs with low f_{m, CYPi} (imipramine and metoprolol). The DDI boundaries for induction were not sensitive (<5% change) to changing f_hep from 1.0 to 0.95. In general, except for the two very low EH drugs (tolbutamide and warfarin) or the low f_{m, CYPi} drug propranolol, ignoring the EH of the victim drug will produce an error of ≥30% in the presence of moderate inhibition or modest induction.

Discussion

Mathematical models used to predict the AUC ratio of a victim drug as a result of a DDI have evolved to include multiple modes of interaction (enzyme inactivation, induction, and inhibition). These models have been derived for the oral administration of a victim drug, which is the most common route of drug administration. These models have been used, based on a simplifying assumption (low EH) for the intravenous administration of victim drugs even though the victim drug is in fact not a low EH drug. We developed a comprehensive, yet easily manageable model that does not rely on the assumption of the victim drug having a low EH. Using this model, we evaluated the error that is introduced when one is 1) predicting the AUC ratio, 2) estimating f_{m, CYPi}, and 3) estimating the contribution of intestinal enzymes to a DDI, by making the assumption that the victim drug is low EH when in fact it is not.

In our sensitivity analysis section (supplemental data), we described the impact that ignoring EH of the victim drug has on the predicted AUC ratio of that drug as a result of a DDI. We showed that the magnitude of error is dependent on the EH, f_{m, CYPi}, f_hep, and magnitude of the DDI. We also set boundaries of DDI magnitudes (degree of inhibition or induction) for which the impact of ignoring the victim drug EH is minimal for commonly used victim drugs (Table 1). These boundaries indicate that for most victim drugs (except those of very low EH, e.g., tolbutamide and warfarin, or low f_{m, CYPi}, e.g., propranolol) inhibition interactions with I/K_i between 0.5 and 9 and induction interactions of <3-fold will be susceptible to ≥30% error in the AUC ratio by ignoring EH of the victim drug.

With respect to the determination of the f_{m, CYPi} of a victim drug administered intravenously, a concept that is not readily apparent from our analyses is the fact that the contribution of the EH cannot be overcome in the presence of “complete metabolic inhibition,” which must be assumed to estimate f_{m, CYPi}. This implies that if the f_{m, CYPi} is to be determined by intravenous administration of the victim drug in the presence of a potent inhibitor, the EH of the victim drug must be considered. Consider the situation in which the EH of the victim drug is 0.44, f_hep = 1.0, and f_{m, CYPi} = 0.93 (a situation similar to that of midazolam). If we assume that hepatic blood flow is 1.5 l/min, the observed hepatic clearance (Cl_hep) using the well stirred model is 0.66 l/min, but the total hepatic intrinsic clearance is 1.18 l/min. Of this intrinsic clearance, 93% (1.097 l/min) is via the inhibited pathway (e.g., CYP3A) and 7% (0.083 l/min) is via the unaffected pathway. When CYP3A is completely inhibited, the remaining Cl_hep is 0.079 l/min (using the well stirred model with Cl_int = 0.083 l/min, the unaffected pathway). This would result in an observed AUC ratio of 8.4. The incorrect f_{m, CYPi} calculated using this AUC ratio would be 0.88 using a rearrangement of eq. 14. If the equation accounting for the EH of the victim drug were used (eq. 15), the resulting estimated f_{m, CYPi} would be the true value of 0.93. Even though the error in the estimated f_{m, CYPi} (0.88 versus 0.93) seems to be minor, it would equate to an observed maximum AUC ratio when the drug was orally administered in the presence of complete inhibition (assuming no intestinal involvement) of 8.4 versus 14.3 or ∼−41%. Our analysis showed that this underestimation can be directly calculated as −f_{m, CYPi} · EH · 100. Moreover, a comparison of the observed maximum intravenous AUC ratio (8.4) with the observed maximum oral AUC ratio (14.3) would imply contribution of intestinal extraction of ∼40% when none was assumed in this example. We have calculated this error for the victim drugs listed in Table 1. For the CYP2D6 drugs desipramine and metoprolol, an incorrect intestinal extraction of ∼40 to 70% may be implied if EH is ignored in an inhibition DDI study.

The previous example shows how intestinal extraction may be implied when in fact it is not present. If intestinal extraction is present, which is the case for midazolam and many of the other CYP3A drugs, the contribution of intestinal enzymes to the DDI can be greatly misestimated if the EH of the victim drug is not accounted for. For a net hepatic induction interaction, if the EH of the victim drug is not accounted for, even for low EH drugs, the fold induction in the liver is underestimated, and this error is propagated to the intestine, resulting in an overestimation of the intestinal induction (Fig. 1A). In a DDI study between nifedipine and rifampin (Holtbecker et al., 1996), a nonsignificant intravenous AUC ratio of 0.70 was observed and an oral AUC ratio of 0.08. The authors concluded that the interaction was not a result of hepatic enzymes but was a result of induction of intestinal CYP3A. Likewise, for net hepatic inhibition DDIs, if the EH of the victim drug is ignored, the degree of hepatic inhibition is underestimated, which results in an overestimate of the degree of intestinal inhibition. Depending on the EH, F_G, and degree of inhibition, this error can result in an apparent intestinal bioavailability of greater than 1 (Fig. 1C), which is not possible. Another, perhaps less likely, scenario is that of mixed-mode interactions (intestinal inhibition and hepatic induction) being masked as intestinal and hepatic induction by not accounting for the EH of the victim drug.

In summary, we have shown that not accounting for the EH of a victim drug administered intravenously can have a substantial impact on the interpretation and prediction of DDI studies. Correcting for this error by using our model will, of course, not eliminate errors from other sources (e.g., protein binding, choice of driving force concentration, active transport, in vitro to in vivo system differences, or inhibitory/inductive metabolites) in in vitro to in vivo extrapolation of DDI. We have described boundaries at which the mathematical error in predicted DDI is less than 30% for some of the commonly used victim drugs. It is unfortunate that these boundaries include only modest degrees of DDIs. Therefore, we propose that our comprehensive model be used to accurately predict the AUC ratio, intestinal contribution, or f_{m, CYPi} for all induction DDIs irrespective of the EH of the victim drug and for modest to potent inhibition DDIs unless the EH is truly low (<0.3).