Abstract
Humans have the arguably unique ability to understand the mental representations of others. For success in both competitive and cooperative interactions, however, this ability must be extended to include representations of others' belief about our intentions, their model about our belief about their intentions, and so on. We developed a “stag hunt” game in which human subjects interacted with a computerized agent using different degrees of sophistication (recursive inferences) and applied an ecologically valid computational model of dynamic belief inference. We show that rostral medial prefrontal (paracingulate) cortex, a brain region consistently identified in psychological tasks requiring mentalizing, has a specific role in encoding the uncertainty of inference about the other's strategy. In contrast, dorsolateral prefrontal cortex encodes the depth of recursion of the strategy being used, an index of executive sophistication. These findings reveal putative computational representations within prefrontal cortex regions, supporting the maintenance of cooperation in complex social decision making.
Introduction
The ubiquity of cooperation in society reflects the fact that rewards in the environment are often more successfully accrued with the help of others. For example, hunting in groups often yields much greater prey when divided equally among the group than that obtainable by hunting alone. Cooperation is optimal if we know that others are committed to it despite the occasional temptations for them to work alone, to our cost. Importantly, such knowledge of intentionality can be inferred through repeated interactions with others and provides a key process at the heart of “theory of mind” (ToM) (Premack and Woodruff, 1978). However, achieving such inference poses a unique computational problem for the brain because it requires the recursive representation of reciprocal beliefs about each other's intentions (Yoshida et al., 2008). How this is achieved in the brain remains unclear.
To investigate this, we designed a task based on the classic “stag hunt” from game theory in which human subjects interact with a computerized agent. The stag hunt game has a pro-cooperative payoff matrix (Table 1), in which each of two players choose whether to hunt highly valued stags together and share the proceeds or defect to hunt meager rabbits of small value. In this game, cooperation depends on recursive representations of another's intentions since, if I decide to hunt the stag, I must believe that you believe that I will cooperate with you. Thus, interactions of highly sophisticated players allow cooperation to emerge, whereby “sophistication” is defined by the number of levels of reciprocal belief inference they make.
Table 1.
Normal-form representation of a stag-hunt in terms of payoffs in which the following relations hold: A > B ≥ D > C and a > b ≥ d > c
| Hunter 2 |
||
|---|---|---|
| Stag | Rabbit | |
| Hunter 1 | ||
| Stag | A, a | C, b |
| Rabbit | B, c | D, d |
Uppercase letters represent the payoffs for the first hunter, and lowercase letters represent the payoffs for the second.
In the task we present below, human subjects interacted with a computerized agent that shifted its level of sophistication without notice. This design places demand on human subjects' ability to infer the level of sophistication of their opponent so as to optimize their own behavior and maximize rewards. We applied an ecologically valid computational model of dynamic belief inference (Yoshida et al., 2008) and show here that it accurately predicts subjects' behavior. This model comes with a precise computational specification that invokes two distinct components: level of sophistication and uncertainty (entropy) of belief inference. We estimate these two statistic components from subjects' actual behavior and provide neurophysiological [functional magnetic resonance imaging (fMRI) blood oxygen level-dependent (BOLD)] data that show how these are implemented in the brain. Specifically, we show how different regions of prefrontal cortex, within what is traditionally referred to as a theory of mind network, implement the predicted underlying component functions. Our findings provide neuronal evidence to validate and endorse our computational model and provide a new perspective on the role of prefrontal cortex in complex social decision making.
Materials and Methods
Subjects.
We scanned 12 healthy subjects (three females, 24.8 ± 3.0 years, mean age and SD). All were English speaking, had normal or corrected vision, and were screened for a history of psychiatric or neurological problems. All subjects gave informed consent and the study was approved by the Joint Ethics Committee of the National Hospital for Neurology and Neurosurgery (United College London Hospitals National Health Service Trust) and the Institute of Neurology, University College London (UCL) (London, UK).
Experimental task.
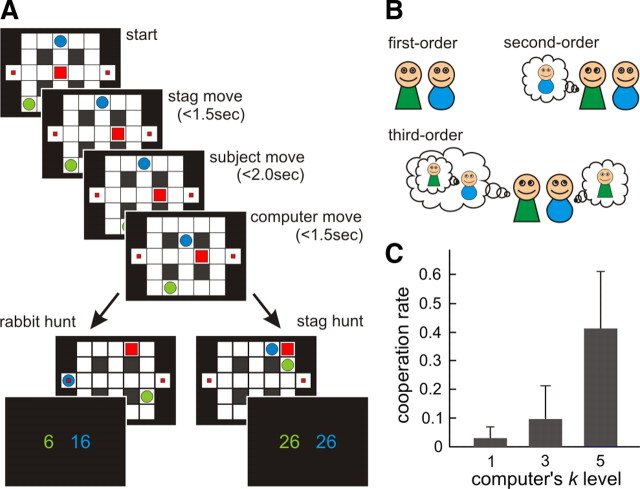
We designed a stag hunt game in which subjects navigated in a two-dimensional grid maze to catch rabbits or stags (Fig. 1A). In the game, there were two rabbits and one stag. The rabbits remained at the same grid location and consequently were easy to catch without requiring help from the other hunters. If one hunter moved to the same location as a rabbit, he/she caught the rabbit and received a small payoff. In contrast, the stag could move to escape the hunters and could only be caught if both hunters moved to the locations adjacent to the stag (in a cooperative “pincer” movement), after which they both received a bigger payoff. Note that as the stag can escape optimally, it was impossible for a hunter to catch the stag alone.
Figure 1.
Stag hunt game and theory of mind model. A, Two players (hunters), a subject (green circle) and a computer agent (blue circle), try to catch prey: a mobile stag (big square) or two stationary rabbits (small squares), in a maze. From an arbitrary initial state, they move to the adjacent states in sequential manner in each trial; the stag moves first, the subject moves, and then the computer agent moves. The players can capture either a small payoff (rabbit hunt; bottom left) or a big payoff (stag hunt, bottom right). Cooperation is necessary to hunt a stag successfully. At the end of each game, both players receive points equal to the sum of prey and points relating to the remaining time (see Materials and Methods). B, In our theory of mind model, the optimal strategies differ in the degree of recursion (i.e., sophistication): first-order strategies assume that other players behave randomly, second-order strategies are optimized under the assumption that other players use a first-order strategy, and third-order strategies pertain to an assumption that the other player assumes you are using a first-order strategy, and so on. Here, we assume bounds or constraints on the strategies available to each player and their prior expectations about these constraints. C, The subjects change their behavior based on the other player's sophisticated level (k) which was unknown. When the computer agents used fifth-order strategies, the rate of cooperative games (stag hunt) out of the total (mean ± variance = 0.405 ± 0.034) was significantly higher than when they used the lower third-order strategies (mean ± variance = 0.089 ± 0.012, p < 0.0001) and first-order strategies (mean ± variance = 0.026 ± 0.002, p < 0.00001).
In the experiment, the subjects played repeated games with a computer agent who changed strategy every 5–8 games without notice. The subjects were instructed that the other hunter was a computerized agent. However, to avoid bias from prior knowledge, we did not instruct the subjects that the agent's strategy changed with time (in fact, we did not tell subjects that the computer agent's behavior was strategic). The agent's strategies were defined by the optimal value functions with first-, third-, or fifth-order sophistication levels. In general, a computerized agent with the lower-order (competitive) strategy would try to catch a rabbit, provided both hunters were not close to the stag. On the other hand, an agent with a higher-order (cooperative) strategy would tend to chase the stag even if it was close to a rabbit. The order of computerized agent's strategies was randomized between subjects.
The start positions of all agents, hunters, and the stag were randomized on every game under the constraint that the initial distances between each hunter and the stag were more than four grids points. After that, at each trial both hunters and the stag moved one grid location sequentially; the stag moved first, the subject moved next, and the computer moved last. Thus, the subjects were able to change their decisions to hunt a stag or rabbit during each game in a manner dependent on their judgment of the other player's strategy. We specifically used this design so as to necessitate rapid on-line assessment of the computer's behavior as well as to render the task less abstract and artificial, thereby conferring a high degree of ecological realism. The subjects chose to move to one of four adjacent grid locations (up, down, left, or right) by pressing a corresponding button on a key response pad, after which they moved to the selected grid. Each time step lasted 2.5 s, and if the subjects did not press a key within this period they remained at the same location until the next trial. The reaction times for the stag and the computer were set between 1.25 to 1.75 s at random; thus, each trial took between 2.5 to 6 s.
At the beginning of each game subjects were given 15 points, which decreased by 1 point per trial, continuing below 0 beyond 15 trials. Therefore, to maximize the total number of points, it was necessary to catch the prey as quickly as possible. The game finished when either of the hunters (subject or agent) caught a prey or when a certain number of trials (15 ± 5) had expired. To prevent subjects changing their strategies depending on the inferred number of moves remaining, the maximum number of moves was randomized for each game. The total points acquired in each game was the remaining time points, plus the hunting payoff: 10 points for a rabbit and 20 points for a stag. For example, if the subject caught a rabbit on trial 6, he/she got the 10 points for catching the rabbit plus the remaining time points: 9 = 15 − 6 points, giving 19 points in total (10 + 9), whereas the other player received only their remaining time points; i.e., 9 points. If the hunters caught a stag at trial 8, both received the remaining 7 = 15 − 8 time points plus 20 points for catching the stag, giving 27 points in total. The remaining time points for both hunters were displayed on each trial, and the total number of points accrued was displayed at the end of each game. At the end of the experiment, the subjects were paid money based on accrued total points.
Before the scanning experiment, each subject received written instructions as well as training on a short version of the stag hunt game, which includes all three types of strategies of the computer agent in equal quantities. All subjects played at least 20 games until they indicated they had learned how to play the game and recognized that the computer agent's behavior was based on a dynamic strategy. In the scanning experiment, 11 of 12 subjects played two sessions, each of which comprised 40 games, so that they played 80 games in total while one subject played only one session due to a technical problem.
Belief inference model.
To address how subjects make inferences about the other player's strategy, we used a previously described computational model of theory of mind (Yoshida et al., 2008). Here, we briefly summarize the key concepts and application to our stag hunt game.
The ToM model deals with sequential games with multiple agents, where the payoffs and values are defined over a joint space. Under the joint state values, the values for one agent become a function of the other agent's value, and thus the optimal strategies are specified according to levels of sophistication, which refers to the number of recursive process, k, by which my model of your strategy includes a model of your model of my strategies, and so on (Fig. 1B). Importantly, if you infer that the order of the other's strategy is k, you should optimize your strategy with an order of k + 1. Cooperation in the stag hunt game depends on recursive representations since, when I decide to hunt the stag I must believe that you believe that I am going to cooperate with you. The intractable nature of the nested levels of inference that this recursion entails has led to the proposition that humans have a limit on the degree of recursion, an example of “bounded rationality” (Simon, 1955; Kahneman, 2003). In this way, “type” (Maynard Smith, 1982) of player K bounds both the prior assumptions about the sophistication of other players and the sophistication of the player per se. For example, a player of type K = 3 believes that the other player can have a level of recursive sophistication no more than k = 3, and he/she can have a strategy with recursive sophistication of no more than k = 4. We can infer the unknown bound k given their choice behaviors by accumulating evidence for different models specified by different bounds.
We applied the ToM model to the stag hunt game in which the state space is the Cartesian product of the admissible states of three agents: two hunters and a stag. However, for simplicity, we assumed that the hunters believed, correctly, that the stag was not sophisticated and then fixed the stag's strategy at first order. The stag's strategy does not explicitly appear in the model but was assumed to constitute the environmental dynamics. Under flat priors bounded by Ksub, subjects make an inference about the computerized agent's strategies p(kcom) as the evidence given the trajectory of states y = s1, s2, …, sT,
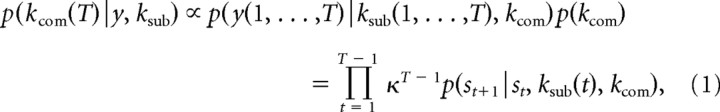 |
where k is a forgetting parameter that exponentially discounts previous evidence and allows the agent to respond more quickly to changes in the other's strategy. Using the posterior distribution, the subjects update the computer's strategy as a point mass at the mode k̂com and optimize their strategy ksub as follows:
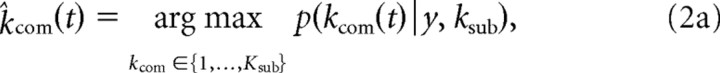 |
Thus, in the model, subjects update belief inference and optimize own sophistication only at computer agent's move event neither at subject's nor stag's move. For model-based imaging analysis based on the ToM model, we generated two parametric functions: one was the entropy of prior distribution of an opponent's sophistication level inferred by the subject, p(kcom) of Equation 1, and the other was the subject's sophistication level, ksub of Equation 2b.
We computed the posterior probabilities of a fixed-strategy model and the ToM model given the actual behavioral data. In the fixed-strategy model, both players use a fixed strategy and do not update the strategy; therefore, there is no need to infer the other's strategy. The players in the ToM model assume the other player might change his/her strategy and optimize their own after each move. We calculated the evidence using k1 = 1, …, 6 for the fixed-strategy model and K1 = 1, …, 6 for the ToM model; i.e., we used 12 models in total. This is because the difference between successive value functions becomes smaller with increasing order, and the value functions saturate at k1 ≥ 6 (supplemental Fig. S1, available at www.jneurosci.org as supplemental material). In the stag hunt game, the agent's behavior depends on the order of strategies kcom; the first-, third-, or fifth-order and the positions of other agents. The average cooperation rates simulated with two agents with matched sophistication level were 9.6, 20.8, and 83.9% for the fist-, third-, and fifth-order levels from all possible sets of initial states. Interestingly, the third- and fifth-order strategies show quite different behaviors (supplemental Fig. S2, available at www.jneurosci.org as supplemental material). For the model comparison, we used the true values of the strategies of computer agent; i.e., k1 = {1, 3, 5}. Supplemental Figure 3 (available at www.jneurosci.org as supplemental material) shows the results of Bayesian model selection (Stephan et al., 2009). Over model space of the ToM model, we inferred that the sophistication level of the subjects is K1 = 5. This is reasonable since the subjects did not have to use the strategies higher than k1 = 6, given that the computer agent's strategies never exceeded five.
Under the inferred (or best) model with K1 = 5, we optimized two model parameters. One is a subjective utility parameter α, which scales the utility of a rabbit relative to the utility of a stag: if the subjects overestimate a rabbit's utility, this parameter is larger and induces more competitive behaviors; if they underestimate a rabbit's utility, this parameter is smaller and leads to cooperation. The maximum likelihood estimation showed that the optimal value was in the range of 0.39 ≤ α ≤ 0.43 for each subject (mean ± SD = 0.41 ± 0.01) and α = 0.41 for all subjects. The other parameter is the forgetting parameter κ (Eq. 1), and it was in the range of 0.51 ≤ α ≤ 0.84 for each subject (mean ± SD = 0.68 ± 0.11) and estimated as 0.75 from all subjects' data. To test the efficacy of the forgetting parameter, we compared the log evidences of the ToM model with and without forgetting effect and verified that the ToM model with forgetting effect shows significantly better fit with the behavioral data (data not shown). To calculate the regression functions for the imaging analysis, we used the optimal utility parameter α = 0.4 for all subjects and optimized the forgetting parameter k for each subject.
The recursive or hierarchical approaches to multiplayer games have been adopted in behavioral economics (Stahl and Wilson, 1995; Costa-Gomes et al., 2001) in which individual decision strategies systematically exploit embedded levels of inference. The sophistication that we specifically address here pertains to the recursive representation of the other player's intentions, and this is distinct from the number of “thinking steps” in other models (Camerer et al., 2004), which corresponds to the depth of tree search.
In this article, we wanted to establish the neuronal correlates of our Bayes optimal model of cooperative play. However, it is important to note that our conclusions are conditioned upon the model that we use. It is possible that our subjects used different models, in particular belief learning models with a dynamic game (Fudenberg and Levine, 1998). We suggest that subsequent work might use Bayesian model comparison to adjudicate among Bayes optimal models and a family of heuristic approximators (Gigerenzer et al., 1999). Such an evaluation in terms of the evidence for alternative models from both behavioral and physiological (fMRI) data is clearly an important avenue to pursue.
fMRI acquisition.
A Siemens 3T Trio whole-body scanner with standard transmit–receive head coil was used to acquire functional data with a single-shot gradient echo isotropic high-resolution echo-planar imaging (EPI) sequence (matrix size: 128 × 128; field of view: 192 × 192 mm2; in-plane resolution: 1.5 × 1.5 mm2; 40 slices with interleaved acquisition; slice thickness: 1.5 mm with no gap between slices; echo time: 30 ms; asymmetric echo shifted forward by 26 phase-encoding lines; acquisition time per slice: 68 ms; reaction time: 2720 ms). The number of volumes acquired depended on the behavior of the subject. The mean number of volumes of each session was 318, giving a total experiment time of ∼14.4 min. A high-resolution T1-weighted structural scan was obtained for each subject (1 mm isotropic resolution three-dimensional modified driven equilibrium Fourier transformation) and coregistered to the subject's mean EPI. The mean of all individual structural images permitted the anatomical localization of the functional activations at the group level.
fMRI analysis.
Statistical parametric mapping (SPM) with SPM5 software (Wellcome Trust Centre for Neuroimaging, UCL) was used to preprocess all fMRI data, which included spatial realignment, normalization, and smoothing. To control for motion, all functional volumes were realigned to the mean volume. Images were spatially normalized to a standard space Montreal Neurological Institute template with a resample voxel size of 2 × 2 × 2 mm and smoothed using a Gaussian kernel with an isotropic full width at half maximum of 8 mm. In addition, high-pass temporal filtering with a cutoff of 128 s was applied to remove low-frequency drifts in signal, and global changes were removed by proportional scaling.
Following preprocessing, statistical analysis was conducted using a general linear model. We specified four events with impulse stimulus functions. In each trial, three events were modeled at the time of stag move, subject move, and computer move. At the end of each game, the time of presentation of the outcome (2.5 s after the last computer move) was also modeled as an event. For model-based analysis, we simulated the ToM model using the actual action sequences to produce per-subject, per-trial estimates of the subject's strategy and the other's strategy inferred by the subject. First, to see the brain activity related with belief inference, we generated two parametric functions: one was the entropy of prior distribution of the other's sophistication level inferred by the subject, and the other was the subject's sophistication level. These functions were then used as the parametric modulators at the computer move event when subjects observed the other's decision (action selection) and updated their inference of the other's strategies. For the reward-related activity, we used two parametric functions. The abstract reward level was modeled as a parametric function of total payoff amount at the outcome of each game. To index brain activity related to the social reward of cooperation, the parametric function of sophistication level was applied to the stag move event. All stimulus functions were then convolved with the canonical hemodynamic response function and entered as regressors into a standard general linear convolution model of each subject's fMRI data using SPM, allowing independent assessment of the activations that correlated with each model's predictions. Note that the two model-based regressions at the computer move event do not show any significant correlation, and switching the order of these regressors does not change the main results. The six scan-to-scan motion parameters produced during realignment were included as additional regressors in the SPM analysis to account for residual effects of motion. To enable inference at the group level, the parameter estimates for the two model-based parametric regressors from each subject were taken to a second-level: random effects group analysis using one-sample T tests. All results are reported in areas of interest at p < 0.001 (uncorrected) and k < 100 (Table 2). The predicted activations in the bilateral ventral striatum and the medial prefrontal (paracingulate) cortex (MPFC) were further tested using a spherical small volume correction (SVC) centered on coordinates derived from the meta-analysis of O'Doherty et al. (2004) for the striatum (x,y,z = 18, 14, −6 mm and −18, 14, −6 mm) with a radius of 8 mm and the review of Amodio and Frith (2006) for the medial prefrontal cortex (x, y, z = 0, 52, 16 mm) with a radius of 16 mm. To better localize activity, the activation maps were superimposed on a mean image of spatially normalized structure images from all subjects.
Table 2.
Maximally activated voxels in areas where significant evoked activity was related to payoff at the result event, and two parametric functions of the ToM model at the computer move
| R/L | BA | Talairach axis |
Z-value | |||
|---|---|---|---|---|---|---|
| x | y | z | ||||
| Payoff | ||||||
| Ventral striatum | R | — | 16 | 21 | −8 | 4.67 |
| Ventral striatum | L | — | −10 | 19 | 0 | 3.89 |
| Sophistication level (stag move event) | ||||||
| Ventral striatum | R | — | 8 | 8 | 0 | 3.55 |
| Ventral striatum | L | — | −10 | 8 | 0 | 3.84 |
| Entropy of other's strategy (computer move event) | ||||||
| Medial prefrontal cortex | L | 10 | −6 | 53 | 14 | 4.76 |
| Medial prefrontal cortex | R | 10 | 4 | 50 | 8 | 3.76 |
| Posterior cingulate | — | 31 | 2 | −50 | 32 | 4.00 |
| Sophistication level (computer move event) | ||||||
| Dorsolateral prefrontal cortex | L | 46 | −50 | 28 | 32 | 4.26 |
| Frontal eye field | L | 7 | −20 | 6 | 46 | 4.25 |
| Frontal eye field | R | 7 | 30 | 9 | 59 | 4.17 |
| Posterior parietal cortex | L | 6 | −16 | −55 | 65 | 4.22 |
| Dorsolateral prefrontal cortex | R | 9 | 40 | 38 | 36 | 3.55 |
R, Right; L, left; BA, Brodmann's area.
Results
Computational model and behavior
The agent's strategies were defined by the optimal strategies with first-, third-, or fifth-order levels of sophistication. The agent's behavior depends on the order of strategies and the positions of other agents. In general, a computerized agent with the lower-order (competitive) strategy would try to catch a rabbit, provided both hunters are not too close to the stag. On the other hand, an agent with a higher-order (cooperative) strategy would chase the stag even if they were close to a rabbit (see Materials and Methods). During the experiment, the computerized agent shifted its strategy occasionally without notice. Thus, to behave optimally (maximize their expected payoff), subjects should update their estimate of the degree of sophistication of the other player (computer agent) continuously and then play at one level higher. We found that the number of games in which the subjects attempted to catch a stag, in effect when they behaved more cooperatively, was significantly higher when the computerized agent was more sophisticated (Fig. 1C). This behavioral effect confirms that our subjects were affected by the level of sophistication of the other player.
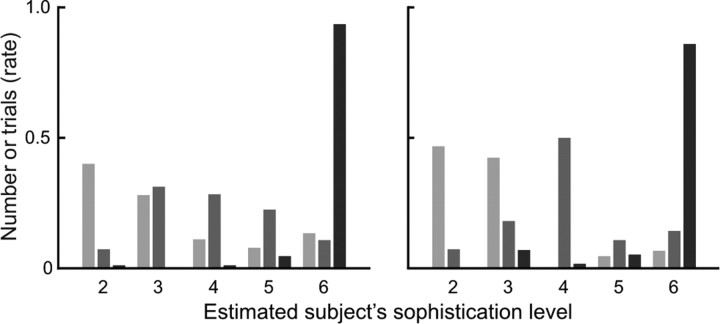
We then assessed the statistical fit of the computational model with actual behavioral data. We found that the belief inference (ToM) model explained subjects' behavior significantly better than a fixed strategy model in which both players use a fixed degree of sophistication without dynamic estimation of the other player's sophistication. Over model space of the ToM model, we inferred that the upper bound of sophistication (K) for the subjects was equal to 5, which means the subjects used strategies with up to a sixth sophistication level. This is reasonable, given that the computer agent's strategies never exceeded five. The ToM model with K = 5 was subsequently used to generate estimates of the subjects' inference about other player's strategies based on their action sequence (Fig. 2). Furthermore, the overall predictability showed that our model fit a subject's behavior well for all levels of computer agent's sophistication (Fig. 3).
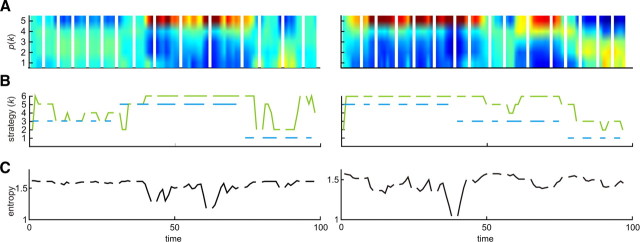
Figure 2.
Two examples of behavioral analysis based on the theory of mind model. A, Model selection for how the subject updated his/her posterior probabilities or belief inference over the computer agent's strategy at each trial. The posterior at the end of each game is used as a prior for the subsequent game. In the figure, each game is separated by a blank gap and has a variable number of trials according to performance. B, The time courses of sophistication level (k) of the computer agent's actual strategy (blue) and subject's strategy estimated by the model (green), which is used as a model-based regressor for brain imaging analysis. The subjects estimated the dynamical changes in the computer agent's strategy as a mode of posterior density and optimized their own strategies at the k + 1 level. C, The uncertainty of belief inference with time shown as the entropy of posterior density about the computer agent's strategy (A). Note that entropy increase lags behind the change in the computer's strategy because it takes time to estimate changes as evidence is accumulated.
Figure 3.
The rate of subject's sophistication level estimated by our model with three different computer agent's strategy; each bar shows the rate of number of trials with an agent of the fifth-, third-, and first-order sophistication (in dark, medium, and light gray color). The left and right panels show the result of all games and only last games in each condition, respectively.
Reward signal and ventral striatum
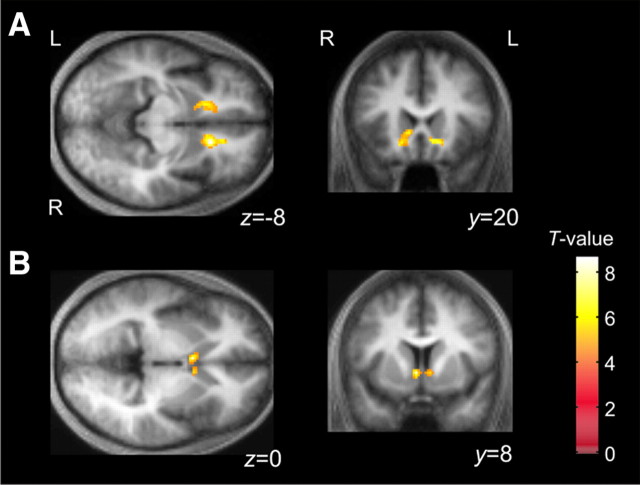
We then analyzed BOLD fMRI signals from subjects while they performed the task. At the time of the outcome of each game (when subjects obtain a reward in the form of prey) we observed significant activity in bilateral ventral striatum that correlated with the payoff amount in each game (Fig. 4A), consistent with this region's established role in encoding the magnitude of both primary and secondary (monetary) rewards in humans (O'Doherty et al., 2004; Knutson and Cooper, 2005). In the context of the current experiment, these effects for abstract rewards provide face validity to an assumption that our task was motivating and the ensuing outcomes were rewarding. During decision making involving social interaction, a similar area is implicated in reward-related outcomes not only for material goods, such as money (Sanfey et al., 2003; King-Casas et al., 2005), but also nonmaterial goods including the experience of mutual cooperation (Rilling et al., 2002) and the acquisition of a good reputation (Izuma et al., 2008). In our task, the total payoff points are converted directly into monetary reward. To address whether there might be specific striatal activity associated with cooperation over and above that associated with the expected monetary value, we modeled expected monetary value and the subject's sophistication level at the stag's move event of each trial in the same analysis. This analysis revealed a focus of activity in the ventral striatum (Fig. 4B), consistent with “added value” associated with cooperation per se (as indexed by sophistication level, which is strongly correlated with cooperativity).
Figure 4.
Ventral striatal activity correlated with nonsocial and social reward. A, Bilateral ventral striatum [right (R), x, y, z = 16, 22, −8 mm, Z = 4.67; left (L), −10, 20, 0 mm, Z = 3.89] showed significant activity correlated with payoff at the end of each game. Both of these areas survived correction for small volume within an 8 mm sphere centered on coordinates from areas implicated in previous studies of reward (R, p < 0.01; L, p < 0.05). B, At the stag's move event time point, activity in caudal ventral striatum (8, 8, 0 mm, Z = 3.55; −10, 8, 0 mm, Z = 3.84) showed a significant correlation with sophistication level, which is itself associated with the expected social reward of cooperation.
Belief inference and prefrontal cortex
The central feature of the computational model is that it predicts unobservable internal states of the subject required for belief inference. Critically, the fMRI data allowed us to investigate whether or not brain activity in putative ToM regions correlates with these states. When subjects observed the other player's action, according to the model they need to update the likelihood of the other player's strategy using Bayesian belief learning and then optimize their own strategy. Accordingly, we used two principal statistics for belief inference as parametric regressors. The first was the entropy of the belief about the other player's strategies (Fig. 2C), by which we mean the uncertainty or average surprise of belief inference. The second was the sophistication level of subjects' strategies (Fig. 2B, green line), which corresponds to their level of strategic thinking and, implicitly, the expected level of the other player's sophistication.
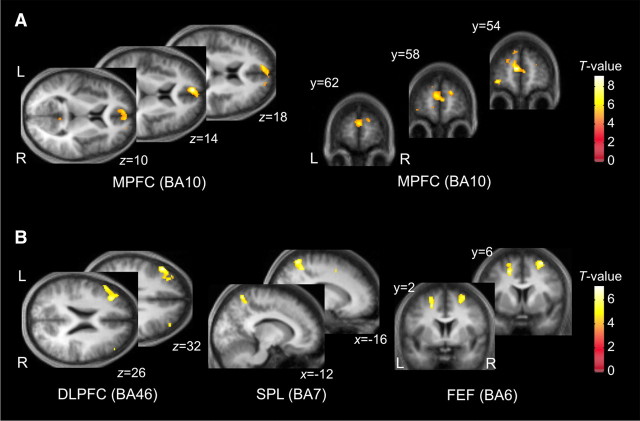
We found that the entropy of belief inference was correlated with activity in an anterior part of rostral medial prefrontal (paracingulate) cortex (MPFC), a region consistently identified in psychological tasks requiring mentalizing (McCabe et al., 2001; Gallagher et al., 2002) (Fig. 5A). That is, activity was greater when the subjects were more uncertain about the other player's level of sophistication.
Figure 5.
Statistical parametric maps showing where BOLD activity correlated with discrete components of the model parameters at the time of computer move. A, The uncertainty of belief inference (the entropy of computer agent's strategies in Fig. 2A) shows a significant correlation with the anterior part of the MPFC (−6, 54, 14 mm, Z = 4.76; p < 0.01 SVC). B, Based on the belief inference, the subjects optimize the level of their own strategies. The estimated sophistication level of subjects' strategy from the theory of mind model showed a significant correlation with BOLD responses in the left DLPFC (−50, 28, 32, Z = 4.26), the bilateral FEF on the superior frontal sulcus (−20, 4, 50, Z = 4.25; 30, 6, 64, Z = 4.17), and the left SPL (−16, −56, 66, Z = 4.22). L, Left; R, right; BA, Brodmann's area.
By contrast, we observed that the level of strategic thinking correlated with the BOLD signal in the left dorsolateral prefrontal cortex (DLPFC), bilateral frontal eye field (FEF) on the superior frontal sulcus, and the left superior parietal lobule (SPL) (Fig. 5B). Equivalent signals were present in the right DLPFC at the same threshold but did not pass our cluster extent criterion. All results are reported in areas of interest at p < 0.001 (uncorrected) and k < 100 (Table 2).
Discussion
In summary, brain activity in distinct prefrontal regions, including part of the classical theory of mind network, expresses a dynamic pattern of activity that correlates strongly with the statistical components of belief inference.
In the field of ToM in general, previous neuroimaging studies (Frith and Frith, 2003) have found that the anterior MPFC is important for representing the mental states of others (McCabe et al., 2001; Gallagher et al., 2002; King-Casas et al., 2008). However, these studies have left unanswered the question as to the precise computations invoked during the application of ToM (Wolpert et al., 2003; Lee, 2008) and, hence, which of the many subprocesses might be implemented in classical ToM regions. Indeed, it remains possible that the mere presence of a human conspecific engages ToM regions and, thus, that the corresponding activation might not be functionally related to the execution of the social games per se. Here, we looked specifically at belief inference, which is likely to be a central (but by no means the only) component of ToM. The fact that subjects knew they were playing a computer suggests that anterior MPFC activity relates (at least in part) to a computational component of belief inference, as described above, and is not purely related to belief about the humanness of the other players.
Recent evidence from the “inspection” game (Hampton et al., 2008) has suggested that ToM in games involves a prediction of how the other player changes his/her strategy as a result of one's own play. In the Hampton et al. (2008) study, neural responses in anterior MPFC related to predicting such changes are notable given that game theory has seldom considered “higher-order thinking” in learning during repeated games, although Bayesian updating of types has been proposed in reputation formation and teaching (Fudenberg and Levine, 1998; Camerer et al., 2002). Both Hampton's influence model and our ToM model involve the learning of the other's strategy, where the other individual learns the best response in repeated games. However, our ToM concerns something fundamentally different: while Hampton's model involves learning the influence of one's own action on the other player's strategy in “second-order” strategic thinking, here we propose that ToM refers to learning the other player's level of thinking itself. This formulation extends beyond accounts that assume both players maintain a constant level of thinking.
A recent imaging study using a “beauty contest” game compared the brain activity of subjects with low and high levels of reasoning, revealing greater MPFC activity in the high group (Coricelli and Nagel, 2009). The suggestion here was that higher-level subjects account for the other's strategy, in contrast to the lower level group. This finding supports previous studies implicating MPFC in ToM and is not inconsistent with the present findings that MPFC activity correlates with the entropy of belief inference. However, the previous data (Coricelli and Nagel, 2009) provide less insight into how belief inference is achieved, since in one-shot games like the beauty contest subjects do not have the opportunity to dynamically optimize an internal model of the other's intentions. By contrast, the cooperative game and its associated model used here suggest a mechanistic account of how beliefs are generated and represented in the brain.
From a psychological perspective, strategic thinking involves several typically “executive” processes, including the temporal ordering of mental representations, updating these representations, predicting the next action, maintaining expected reward, and selecting an optimal action. Although our study was not designed to determine how computation of the level of sophistication relates to the broader functions of different brain areas, the fact that we observed greater activity in DLPFC, FEF, and SPL is consistent with their known roles in executive processes. Notably, responses in these regions are known to correlate with complexity in classic working memory tasks (Braver et al., 1997; Owen et al., 2005). In social situations, DLPFC neurons encode signals related to a previous choice and its outcome conjunctively in a matching pennies task, as seen in monkeys (Barraclough et al., 2004) and Williams syndrome patients (Meyer-Lindenberg et al., 2005). In addition, DLPFC activation has been observed with high- versus low-level reasoning in a beauty contest (Coricelli and Nagel, 2009). With higher strategies, as in our task, subjects behave more cooperatively and, consequently, the DLPFC is likely to be involved in the complex strategic processes required for the establishment and maintenance of social goals governing mutual interaction. Recently, activity of posterior parietal cortex was found in a social game that can be solved by “deliberative” reasoning (Kuo et al., 2009). Furthermore, neurons in posterior parietal cortex are known to modulate their activity with expected reward or utility during foraging tasks (Sugrue et al., 2004) and competitive games (Dorris and Glimcher, 2004), and activity here may relate to social utility associated with cooperation in this task.
The fact that the brain engages in ToM does not preclude prosocial accounts of motivation in cooperative interactions. There is good reason to assume that different decision-making systems collectively contribute to behavioral output, with sophisticated goal-orientated decision processes existing alongside simpler mechanisms, for instance the associative learning rules used by reinforcement learning systems (Daw et al., 2005), or through observation of others (especially experts) (Behrens et al., 2008). Whereas strategic thinking almost certainly offers the most efficient way to determine actions early in the course of learning, given any population of potentially prosocial and antisocial opponents, these simpler (e.g., more automatic, prosocial) mechanisms assume greater importance in the control of behavior if outcomes are predicted reliably, thereby obviating the computational burden of strategic inference (Seymour et al., 2009). Indeed, we note that in this experiment the outcome for an abstract category of reward, the prey, correlated with activity in the striatum, a region that supports reinforcement and observation-based learning (King-Casas et al., 2005; Montague and King-Casas, 2007; Behrens et al., 2008). However, the fact that an individual's computational strategy may be hidden from observation or subjective insight illustrates the value of fMRI in determining precisely which strategy is being used.
Our account of ToM does not necessarily suggest that players compute their optimal strategy explicitly or indeed are aware of any implicit inference on the other player's strategy. Rather, the model is purely mechanistic in describing how brain states can encode theoretical quantities necessary to optimize behavior. In other words, we do not suppose that subjects necessarily engage in explicit cognitive operations but are sufficiently tuned to interactions with conspecifics to render choice behavior sophisticated. Furthermore, there are several limitations to the current study that ought to be addressed in future work. First, whereas an experimental design that incorporates a computer agent allows flexible control of the level of sophistication of the other player, it does not capture the full depth of strategic play in purely human games, since subjects should appreciate that the computer agent does not reciprocally adapt its behavior based on their actions. This is an important aspect of ToM not captured in this study. Second, it is possible that subjects' actions do not necessarily correspond precisely to their beliefs. Such mismatches have been shown in previous data (Bhatt and Camerer, 2005), and this might be caused by irrational learning or belief inference modified by the circumstances (or situations). For example, an observation that payoff balance between stag and rabbit has an effect on subjects' behavior (Battalio et al., 2001) suggests that the model parameters might be adjusted from trial to trial.
Our data provide a perspective on ToM that proposes a more multifaceted set of operations than hitherto acknowledged. In humans, ToM is implicitly achieved in the first year and explicitly acquired at around the age of 4 years, but in autistic spectrum disorders and related psychopathologies it is delayed or absent. This raises the possibility that one or other of the processes we propose might reflect core deficits in the corresponding behavioral phenotype. Although functional abnormality within midline anterior and posterior regions has been shown repeatedly in autism (Castelli et al., 2002; Saxe et al., 2004; Kennedy et al., 2006; Chiu et al., 2008), the precise nature of explanation for these abnormalities are unclear. Future studies might fruitfully explore whether this deficit can be understood as reflecting a computational dysfunction, yielding insight that could motivate novel therapeutic strategies.
Footnotes
This work was supported by Wellcome Trust Programme Grants to R.J.D. and K.J.F. We are grateful to Peter Dayan and Chris Frith for critical comments on this manuscript.
References
- Amodio DM, Frith CD. Meeting of minds: the medial frontal cortex and social cognition. Nat Rev Neurosci. 2006;7:268–277. doi: 10.1038/nrn1884. [DOI] [PubMed] [Google Scholar]
- Barraclough DJ, Conroy ML, Lee D. Prefrontal cortex and decision making in a mixed-strategy game. Nat Neurosci. 2004;7:404–410. doi: 10.1038/nn1209. [DOI] [PubMed] [Google Scholar]
- Battalio R, Samuelson L, Van Huyck J. Optimization incentives and coordination failure in laboratory stag hunt games. Econometrica. 2001;69:749–764. [Google Scholar]
- Behrens TEJ, Hunt LT, Woolrich MW, Rushworth MFS. Associative learning of social value. Nature. 2008;456:245–249. doi: 10.1038/nature07538. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bhatt M, Camerer C. Self-referential thinking and equilibrium as states of minds in games: FMRI evidence. Games Econ Behav. 2005;52:424–459. [Google Scholar]
- Braver TS, Cohen JD, Nystrom LE, Jonides J, Smith EE, Noll DC. A parametric study of prefrontal cortex involvement in human working memory. Neuroimage. 1997;5:49–62. doi: 10.1006/nimg.1996.0247. [DOI] [PubMed] [Google Scholar]
- Camerer CF, Ho TH, Chong JK. Sophisticated experience-weighted attraction learning and strategic teaching in repeated games. J Econ Theory. 2002;104:137–188. [Google Scholar]
- Camerer CF, Ho TH, Chong JK. A cognitive hierarchy model of games. Q J Econ. 2004;119:861–898. [Google Scholar]
- Castelli F, Frith C, Happe F, Frith U. Autism, Asperger syndrome and brain mechanisms for the attribution of mental states to animated shapes. Brain. 2002;125:1839–1849. doi: 10.1093/brain/awf189. [DOI] [PubMed] [Google Scholar]
- Chiu PH, Kayali MA, Kishida KT, Tomlin D, Klinger LG, Klinger MR, Montague PR. Self responses along cingulate cortex reveal quantitative neural phenotype for high-functioning autism. Neuron. 2008;57:463–473. doi: 10.1016/j.neuron.2007.12.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coricelli G, Nagel R. Neural correlates of depth of strategic reasoning in medial prefrontal cortex. Proc Natl Acad Sci U S A. 2009;106:9163–9168. doi: 10.1073/pnas.0807721106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Costa-Gomes M, Crawford VP, Broseta B. Cognition and behavior in normal-form games: an experimental study. Econometrica. 2001;69:1193–1235. [Google Scholar]
- Daw ND, Niv Y, Dayan P. Uncertainty-based competition between prefrontal and dorsolateral striatal systems for behavioral control. Nat Neurosci. 2005;8:1704–1711. doi: 10.1038/nn1560. [DOI] [PubMed] [Google Scholar]
- Dorris MC, Glimcher PW. Activity in posterior parietal cortex is correlated with the relative subjective desirability of action. Neuron. 2004;44:365–378. doi: 10.1016/j.neuron.2004.09.009. [DOI] [PubMed] [Google Scholar]
- Frith U, Frith CD. Development and neurophysiology of mentalizing. Philos Trans R Soc Lond B Biol Sci. 2003;358:459–473. doi: 10.1098/rstb.2002.1218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fudenberg D, Levine D. The theory of learning in games. Boston: MIT; 1998. [Google Scholar]
- Gallagher HL, Jack AI, Roepstorff A, Frith CD. Imaging the intentional stance in a competitive game. Neuroimage. 2002;16:814–821. doi: 10.1006/nimg.2002.1117. [DOI] [PubMed] [Google Scholar]
- Gigerenzer G, Todd PM ABC Research Group. Simple heuristics that make us smart. New York: Oxford UP; 1999. [Google Scholar]
- Hampton AN, Bossaerts P, O'Doherty JP. Neural correlates of mentalizing-related computations during strategic interactions in humans. Proc Natl Acad Sci U S A. 2008;105:6741–6746. doi: 10.1073/pnas.0711099105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Izuma K, Saito DN, Sadato N. Processing of social and monetary rewards in the human striatum. Neuron. 2008;58:284–294. doi: 10.1016/j.neuron.2008.03.020. [DOI] [PubMed] [Google Scholar]
- Kahneman D. Maps of bounded rationality: psychology for behavioral economics. Am Econ Rev. 2003;93:1449–1475. [Google Scholar]
- Kennedy DP, Redcay E, Courchesne E. Failing to deactivate: resting functional abnormalities in autism. Proc Natl Acad Sci U S A. 2006;103:8275–8280. doi: 10.1073/pnas.0600674103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- King-Casas B, Tomlin D, Anen C, Camerer CF, Quartz SR, Montague PR. Getting to know you: reputation and trust in a two-person economic exchange. Science. 2005;308:78–83. doi: 10.1126/science.1108062. [DOI] [PubMed] [Google Scholar]
- King-Casas B, Sharp C, Lomax-Bream L, Lohrenz T, Fonagy P, Montague PR. The rupture and repair of cooperation in borderline personality disorder. Science. 2008;321:806–810. doi: 10.1126/science.1156902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knutson B, Cooper JC. Functional magnetic resonance imaging of reward prediction. Curr Opin Neurol. 2005;18:411–417. doi: 10.1097/01.wco.0000173463.24758.f6. [DOI] [PubMed] [Google Scholar]
- Kuo WJ, Sjostrom T, Chen YP, Wang YH, Huang CY. Intuition and deliberation: two systems for strategizing in the brain. Science. 2009;324:519–522. doi: 10.1126/science.1165598. [DOI] [PubMed] [Google Scholar]
- Lee D. Game theory and neural basis of social decision making. Nat Neurosci. 2008;11:404–409. doi: 10.1038/nn2065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maynard Smith J. Evolution and the theory of games. Cambridge: Cambridge UP; 1982. [Google Scholar]
- McCabe K, Houser D, Ryan L, Smith V, Trouard T. A functional imaging study of cooperation in two-person reciprocal exchange. Proc Natl Acad Sci U S A. 2001;98:11832–11835. doi: 10.1073/pnas.211415698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meyer-Lindenberg A, Hariri AR, Munoz KE, Mervis CB, Mattay VS, Morris CA, Berman KF. Neural correlates of genetically abnormal social cognition in Williams syndrome. Nat Neurosci. 2005;8:991–993. doi: 10.1038/nn1494. [DOI] [PubMed] [Google Scholar]
- Montague PR, King-Casas B. Efficient statistics, common currencies and the problem of reward-harvesting. Trends Cogn Sci. 2007;11:514–519. doi: 10.1016/j.tics.2007.10.002. [DOI] [PubMed] [Google Scholar]
- O'Doherty J, Dayan P, Schultz J, Deichmann R, Friston K, Dolan RJ. Dissociable roles of ventral and dorsal striatum in instrumental conditioning. Science. 2004;304:452–454. doi: 10.1126/science.1094285. [DOI] [PubMed] [Google Scholar]
- Owen AM, McMillan KM, Laird AR, Bullmore E. N-back working memory paradigm: a meta-analysis of normative functional neuroimaging. Hum Brain Mapp. 2005;25:46–59. doi: 10.1002/hbm.20131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Premack DG, Woodruff G. Does the chimpanzee have a theory of mind? Behav Brain Sci. 1978;1:515–526. [Google Scholar]
- Rilling JK, Gutman DA, Zeh TR, Pagnoni G, Berns GS, Kilts CD. A neural basis for social cooperation. Neuron. 2002;35:395–405. doi: 10.1016/s0896-6273(02)00755-9. [DOI] [PubMed] [Google Scholar]
- Sanfey AG, Rilling JK, Aronson JA, Nystrom LE, Cohen JD. The neural basis of economic decision-making in the ultimatum game. Science. 2003;300:1755–1758. doi: 10.1126/science.1082976. [DOI] [PubMed] [Google Scholar]
- Saxe R, Carey S, Kanwisher N. Understanding other minds: linking developmental psychology and functional neuroimaging. Annu Rev Psychol. 2004;55:87–124. doi: 10.1146/annurev.psych.55.090902.142044. [DOI] [PubMed] [Google Scholar]
- Seymour B, Yoshida W, Dolan R. Altruistic learning: frontiers. Behav Neurosci. 2009;3:23. doi: 10.3389/neuro.08.023.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simon HA. A behavioral model of rational choice. Q J Econ. 1955;69:99–118. [Google Scholar]
- Stahl DO, Wilson PW. On players models of other players: theory and experimental-evidence. Games Econ Behav. 1995;10:218–254. [Google Scholar]
- Stephan KE, Penny WD, Daunizeau J, Morran RJ, Friston KJ. Bayesian model selection for group studies. Neuroimage. 2009;46:1004–1017. doi: 10.1016/j.neuroimage.2009.03.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sugrue LP, Corrado GS, Newsome WT. Matching behavior and the representation of value in the parietal cortex. Science. 2004;304:1782–1787. doi: 10.1126/science.1094765. [DOI] [PubMed] [Google Scholar]
- Wolpert DM, Doya K, Kawato M. A unifying computational framework for motor control and social interaction. Philos Trans R Society Lond B Biol Sci. 2003;358:593–602. doi: 10.1098/rstb.2002.1238. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yoshida W, Dolan RJ, Friston KJ. Game theory of mind. PLoS Comput Biol. 2008;4:e1000254. doi: 10.1371/journal.pcbi.1000254. [DOI] [PMC free article] [PubMed] [Google Scholar]