Evaluation of an improved algorithm for producing realistic 3D breast software phantoms: Application for mammography

Abstract

Purpose: This work presents an improved algorithm for the generation of 3D breast software phantoms and its evaluation for mammography.

Methods: The improved methodology has evolved from a previously presented 3D noncompressed breast modeling method used for the creation of breast models of different size, shape, and composition. The breast phantom is composed of breast surface, duct system and terminal ductal lobular units, Cooper’s ligaments, lymphatic and blood vessel systems, pectoral muscle, skin, 3D mammographic background texture, and breast abnormalities. The key improvement is the development of a new algorithm for 3D mammographic texture generation. Simulated images of the enhanced 3D breast model without lesions were produced by simulating mammographic image acquisition and were evaluated subjectively and quantitatively. For evaluation purposes, a database with regions of interest taken from simulated and real mammograms was created. Four experienced radiologists participated in a visual subjective evaluation trial, as they judged the quality of the simulated mammograms, using the new algorithm compared to mammograms, obtained with the old modeling approach. In addition, extensive quantitative evaluation included power spectral analysis and calculation of fractal dimension, skewness, and kurtosis of simulated and real mammograms from the database.

Results: The results from the subjective evaluation strongly suggest that the new methodology for mammographic breast texture creates improved breast models compared to the old approach. Calculated parameters on simulated images such as β exponent deducted from the power law spectral analysis and fractal dimension are similar to those calculated on real mammograms. The results for the kurtosis and skewness are also in good coincidence with those calculated from clinical images. Comparison with similar calculations published in the literature showed good agreement in the majority of cases.

Conclusions: The improved methodology generated breast models with increased realism compared to the older model as shown in evaluations of simulated images by experienced radiologists. It is anticipated that the realism will be further improved using an advanced image simulator so that simulated images may be used in feasibility studies in mammography.

INTRODUCTION

Breast cancer is the most common cancer in women. In Europe, one in ten women develops this type cancer in her lifetime, while in the United States, it is the second leading cause of cancer death. Currently, the best method for its early detection before it becomes clinically palpable is x-ray mammography. European studies have shown that breast cancer mortality is reduced by about 37% in women 50–69 yr of age who are subjected to screening mammography,¹ while in the United States, this number varies from 28% to 65%.² The latter is a result of a large study involving a consortium of investigators that developed seven statistical models of breast cancer incidence and mortality to investigate the contribution of screening mammography and adjuvant treatment to the reduction of breast cancer mortality in the period from 1975 to 2000.

The optimization of digital mammography is of critical importance as we make the transition from film to digital detectors and eventually to tomographic and 3D imaging of the breast. Emerging technologies include tissue perfusion imaging,³ digital breast tomosynthesis,⁴ and cone beam breast computer tomography.⁵ The performance of these new techniques should be assessed and optimized before clinical deployment. Clinical studies, however, can be expensive and time consuming. Three-dimensional phantoms are needed for the evaluation of image quality and the accurate depiction of fine anatomic detail. However, anatomically realistic physical phantoms are not widely available and the manufacturing of such phantoms is an extremely difficult task with the current technology. The use of computer modeling for the generation of computer or “virtual” phantoms offers an expedient and a potentially more effective alternative to physical phantoms.

Simulation and computer modeling offers a cost effective, practical, and flexible alternative approach to design experiments for the assessment and optimization of image quality of forthcoming x-ray breast imaging systems, prior to clinical deployment or for quality assurance purposes. Computer models mimic the anatomy and shape of the female breast and simulate the x-ray projection. Simple mathematical phantoms have been used very effectively for radiation dosimetry, optimization of acquisition geometry, x-ray spectrum, and detector optimization.^{5, 6, 7, 8, 9, 10, 11, 12} The breast is usually modeled in the form of a cylinder, half-ellipsoid, or simply parallelepiped with adjustable size and glandular to adipose tissue ratio. They are simulated as a homogeneous mixture of glandular and adipose tissue surrounded by an adipose layer. Tissue compositions are usually taken from Hammersteinet al.¹³ More complex phantoms can be generated by simulating 3D breast tissue distribution, obtained by applying the concept of 3D power law noise.^{14, 15}

Advanced breast models with 3D realistic breast tissue distribution and anatomical features^{16, 17, 18} have been developed in order to carry out feasibility studies with 2D and 3D x-ray breast imaging techniques, including optimization of image number and dose per image in digital breast tomosynthesis and breast dual energy,^{10, 15, 18, 19, 20} as well as to perform accurate breast dosimetry,²¹ evaluate nonrigid mammogram registration techniques,²² calculate the properties of the digital mammograms²³ and investigate the effect of digital breast tomosynthesis acquisition parameters on computer-extracted texture features.^{24, 25} These models offer complex breast tissue simulation and allow the generation of realistic synthetic mammograms which resemble the real ones. Recently, Ma et al.¹⁸ reported an advanced new breast model suitable for work with general purpose Monte Carlo codes for simulation of x-ray projection images.

Synthetic mammograms are calculated utilizing basically two approaches. The most popular approach is to simulate the beam transport through the mammographic system, as the transmitted intensity through the breast is calculated on the basis of exponential attenuation of incident beams.^{16, 17, 23, 26} This approach produces images quite quickly but is limited to the simulation of primary radiation effects only. In order to account for the photon noise under realistic conditions, quantum noise is added. Monte Carlo simulation programs^{18, 27, 28} that simulate the beam interaction including the scattered radiation have been developed.

Previously, we described a computer model of the breast that allows simulation of the internal structures under normal and compressed conditions.^{17, 29} This model is limited to low resolution due to computational and methodological limitations. Efforts were focused on the development of a new algorithm for a very realistic mammographic tissue texture generation. This paper reports on the improved methodology for 3D breast model generation and specifically presents a new algorithm for this task. The paper also focuses on the evaluation of the improved breast model for its application in mammographic studies. This has been accomplished by subjective and quantitative evaluation of synthetic mammograms obtained by simulating mammography imaging. In the subjective evaluation, experienced radiologists judged the quality of mammograms synthesized with the new and old methodology for the creation of breast models, while the objective evaluation involved comparison of texture features extracted from simulated and real mammograms as well as with published data. The results indicate that images of breast models, synthesized using the new methodology for mammographic breast texture creation, reach a high degree of similarity to real mammograms.

MATERIALS AND METHODS

Breast model

Briefly described, the breast phantom is a composite model of the female breast and includes the breast shape, the mammary duct system, the Cooper’s ligaments, the pectoral muscle, vessels, skin, mammographic texture, and breast abnormalities. The breast surface is modeled as a combination of two geometrical primitives: An elongated semiellipsoid and an elongated semihyperboloid. The duct system is simulated using a network of cylinders, probabilistically arranged in the breast as branches in a treelike arrangement, starting from the nipple and restricted by the external breast contour. The mammographic texture simulates the presence of adipose, fibrous, and connective tissues, as well as other nonglandular tissue types that are not explicitly modeled. Cooper’s ligaments are modeled as a set of thin ellipsoid shells, originating at randomly sampled positions in the breast model, while the pectoralis muscle is approximated as a cone shaped object. Breast abnormalities are modeled with round, ovoid, elongated, and irregular shapes. The lymphatic system is modeled as a set of cylinders, originating at sampled positions in a surface hyperboloid layer and in the medial edge of the semiellipsoid, while the lymph nodes are simulated as bean-shaped objects varying in size from several millimeters to several centimeters in diameter. Blood vessels are simulated in a similar way as the lymph vessels. The skin is represented as a surface layer of thickness 1–2 mm. All geometrical primitives are transformed to voxel values of the final breast matrix. The lymphs, the blood vessels, and the skin are new features introduced in the model. Finally, the mammographic texture that represents breast structures that are not explicitly modeled is synthesized.

The previous approach for mammographic texture simulation used generation of a set of 2D synthetic images from 2D power law noise.¹⁷ The 3D mammographic texture was obtained by mapping each image pixel gray-level value into this matrix at a height related to the pixel’s gray-level value, while the other two coordinates were considered the same. The voxel value was obtained by averaging the gray values of the synthetic pixel and the previous value of the matrix voxel.

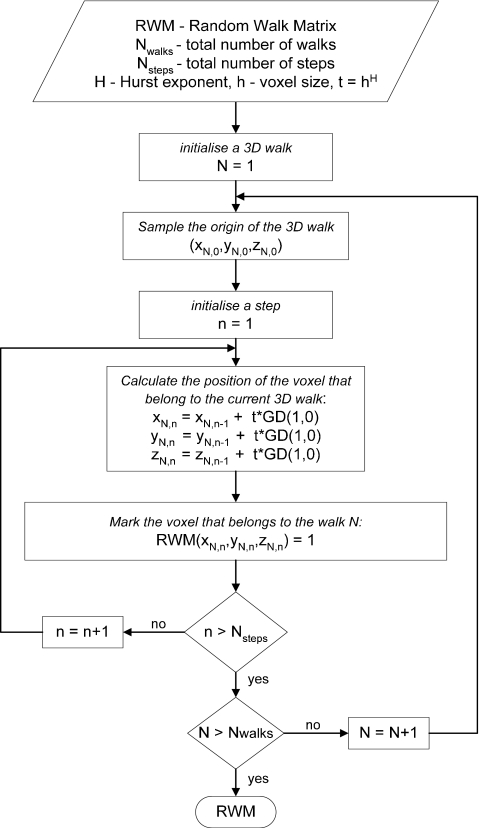
The steps of the new algorithm for generation of mammographic texture are shown in Fig. 1. Initially, the texture matrix is filled with random walks, calculated using the concept of the “fractional Brownian motion (fBm) model.” This was prompted by the fact the fBm has a Gaussian nature that allows long-range correlations and has strong scaling properties and features observed in mammograms.³⁰ A short description of the fBm process is given in the Appendix0. The algorithm for the initial filling of the breast matrix with three-dimensional random walks is outlined in Fig. 2. Three-dimensional random walks are simulated with coordinates (x_i,y_i,z_i) selected randomly around the nipple origin and anywhere in the breast matrix. Further on, each random walk moves to another voxel that has a position (x_i+1,y_i+1,z_i+1), calculated from the voxel positions, determined in the previous stage (x_i,y_i,z_i) as they first are displaced by the addition of a variable obtained from the multiplication of the increment t and a random variable GD(1,0) with a Gaussian distribution with standard deviation and mean value equal to one and zero, respectively,

$$\begin{array}{c}{x}_{i+1}=x_i+t\ast GD\left(1,0\right)\\ y_{i+1}=y_i+t\ast GD\left(1,0\right)\\ z_{i+1}=z_i+t\ast GD\left(1,0\right)\end{array},\begin{array}{c}t=h^H\\ i=0,1,2,\dots \dots \left(N_{\text{steps}}-1\right)\end{array},$$ (1)

where H is a parameter related to the fractal dimension of a fractal object and is called Hurst exponent, h is the step increment in mm, while N_steps is the number of steps that a random walk may take. The process described by Eq. 1 is repeated until the random walk reaches either the matrix boundary or the end of the number of steps N_steps. Similarly simulated are all random walks (N_walks) whose number is assigned by the user. The increment h is by default set to the size of the voxel in one dimension, while H can vary between 0 and 1 (Appendix0). The matrix obtained from the random walk operations, denoted as random walk matrix (RWM), may be further subjected to additional 3D imaging morphological operations as dilation and smoothing that aim to improve the realism of the 3D breast tissue distribution in the model. These operations are optional and selected by the user.

Figure 1.

The main steps in composing the mammographic texture. The images are slices extracted from a breast matrix with size of 75 mm in each direction and voxel dimension of 150 μm. The texture matrix was created using the following parameters: Number of random walks N_walks=1500, number of steps per walk N_steps=2000, increment h=0.1, and Hurst exponent H=0.95. Additionally, a 3×3×3 mask was used to perform the low pass filtering and dilation, while the standard deviation (σ) value for the Gaussian filtering was set to 1.5. For better understanding, the names of the matrices obtained after the steps are related with the imaging operation performed, namely, RWM: Random walk matrix; DM: Dilation matrix; LPM: Low pass filtering matrix; GM: Gaussian matrix; and FTM: Final texture matrix.

Figure 2.

Algorithm for random walks generation. N_walk and N_steps are the number of three-dimensional random walks and the corresponding random steps per walk.

Three-dimensional dilation is used to dilate the initial 3D texture in the neighborhood and to generate more data. For this purpose, a customized dilation is applied to the 3D walks to obtain the dilated matrix, denoted with DM in Eq. 2 and Fig. 1. The voxels that are already filled are preserved, while the neighbor voxels obtain values, sampled according to Eq. 2. The structuring element SE_DM is a cube with a dimension assigned by the user (by default 3×3×3) and defined in the following way:

$${\text{SE}}_{\text{DM}}\left(x,y,z\right)=\sum _{i=-w∕2}^{w∕2}\sum _{j=-w∕2}^{w∕2}\sum _{k=-w∕2}^{w∕2}\text{RWM}\left(x+i,y+j,z+k\right),$$$$\text{DM}\left(x,y,z\right)=\frac{p^2+\text{RWM}{\left(x,y,z\right)}^2}{\text{RWM}\left(x,y,z\right)+p}\{\begin{array}{cc}p=0,& {\text{SE}}_{\text{DM}}\left(x,y,z\right)>0.9\\ p\subset \left(0,1\right),& 0<{\text{SE}}_{\text{DM}}\left(x,y,z\right)\le 0.9\end{array}\phantom{\}},$$ 2

where (x,y,z) is the current voxel coordinate in the dilated matrix, w is the size of the structuring element, and p is a randomly generated value between 0 and 1.

Low pass filter is applied with a coefficient of 2 in the central voxel of the structuring element and a value of 1 in the neighboring voxels, in order to smooth the boundaries of the texture. The matrix obtained from this operation is denoted with LPM in Fig. 1 and the process is described by the following equations:

$$S{E}_{\text{LPM}}\left(x,y,z\right)=\frac{1}{w^3}\sum _{i=-w∕2}^{w∕2}\sum _{j=-w∕2}^{w∕2}\sum _{k=-w∕2}^{w∕2}g\cdot \text{DM}\left(x+i,y+j,z+k\right)\{\begin{array}{cc}g=2,& i=0,j=0,k=0\\ g=1,& \text{else}\end{array}\phantom{\}},$$$$\text{LPM}\left(x,y,z\right)=\frac{\text{DM}\left(x,y,z\right)}{{\text{SE}}_{\text{LPM}}\left(x,y,z\right)}.$$ 3

In the above equations, the DM should be replaced by the RWM matrix for the case where dilation is not performed.

More smoothing is achieved by applying a Gaussian filtering [Eq. 4]. Smoother and more blurred breast slices can be generated with higher standard deviation (σ). This operation is applied for each slice of the breast matrix and may be extended to a 3D case; however, this will not have a significant influence of the final result.

$$\text{GM}\left(x=\text{const},y,z\right)=\frac{\text{LPM}\left(x=\text{const},y,z\right)}{\sum _{j=-w∕2}^{w∕2}\sum _{k=-w∕2}^{w∕2}\text{exp}\left(-\frac{\left({\left(y+j\right)}^2+{\left(z+k\right)}^2\right)}{2\ast {\sigma }^2}\right)},$$ (4)

where the default size of the structuring element is w×w (by default 3×3). Similar to the previous operations, the numerator of Eq. 4 should be data extracted from the texture matrix obtained after dilation (DM) or random walks (RWM) in case low pass filtering or dilation is not performed.

The mammographic texture matrix (TM), obtained as a result of Eqs. 1, 2, 3, 4, contains voxels with values in the range 0–1. These values are converted to linear attenuation coefficients for the specified incident photon energy E to obtain the final texture matrix (FTM) using the following relationship:

$$\text{FTM}\left(x,y,z\right)=\left({\mu }_{\text{gland}}\left(E\right)-{\mu }_{\text{adipose}}\left(E\right)\right)\ast \frac{\left(\text{TM}\left(x,y,z\right)-{\text{TM}}_{\text{min}}\right)}{\left({\text{TM}}_{\text{max}}-{\text{TM}}_{\text{min}}\right)}+{\mu }_{\text{adipose}}\left(E\right),{\text{cm}}^{-1},$$ (5)

where μ_gland and μ_adipose are the linear attenuation coefficients of the glandular and adipose tissues, while TM_min and TM_max are the minimum and maximum values of the whole TM matrix. The voxel values in FTM represent linear attenuation coefficients that may take any value from the linear attenuation coefficient of the adipose tissue to the linear attenuation coefficient of the glandular tissue. Finally, this FTM is mapped to the volume, defined by the breast external surface.

The FTM together with the generated duct system, Cooper’s ligaments, breast abnormalities, lymphatic and blood vessels system, pectoralis muscle and skin compose the final breast matrix. Final tissue differentiation is accomplished using the following concept: The matrix voxel values of the final breast matrix that are linear attenuation coefficients are converted into Hounsfield units (HUs) using the relationship

$$\text{BreastMatrix}\left(x,y,z\right)=\left(\frac{\text{FTM}\left(x,y,z\right)}{{\mu }_{\text{water}}\left(E\right)}-1\right)\ast 1000,\text{HU},$$ (6)

where μ_water is the linear attenuation coefficient of the water for the incident energy E. This operation is applied for each voxel. The HU data are then divided into six materials groups with lower and higher HU limits specified in Table 1. These limits were derived from calculations performed for each tissue in the simulated breast in the range 15–30 keV using Eq. 6.

Table 1.

Attenuation coefficients at 19 keV incident energy. In the same table, the lower and upper limits of the HUs for the simulated tissues are specified.

Tissue	Attenuation coefficient (cm2 g−1)	ρ (g cm−3)	Attenuation coefficient (cm−1)	Lower HU	Upper HU
Adipose tissue	0.630	0.95	0.5985	−500	−251
Glandular tissue	0.772	1.02	0.7874	−250	−50
Cooper ligaments	0.772	1.02	0.7874	−250	−50
Breast skin	0.732	1.09	0.7979	−49	30
Lymph	0.935	1.03	0.9631	31	60
Pectoralis muscle	0.926	1.05	0.9723	61	70
Blood	0.934	1.06	0.9900	71	90

Simulation of projection images

Projection images were synthesized using the XRAYIMAGINGSIMULATOR.³¹ Source-to-detector and source-to-breast phantom entrance plane distances were set equal to 900 and 600 mm, respectively. These distances were chosen for comparison purposes with our previous study. Their choice was not critical since simulated imaging conditions were near ideal. The transport of monochromatic 19 keV beams was simulated through the breast phantoms using analytical relationships for x-ray matter interaction. An antiscatter grid was not included in the simulations. The atomic compositions of the simulated breast tissues are derived from data of the International Commission on Radiation Units and Measurements³² and the International Commission on Radiological Protection³³ for the lymphatic system. The attenuation coefficients of the modeled tissues were taken from Hubbell and Seltzer³⁴ and are summarized in Table 1. A stationary detector was simulated as a photon counting detector with a resolution of 10 pixels∕mm, while the synthetic images, with size of 1200×1200 pixels, corresponded to craniocaudal (CC) or mediolateral (MLO) views. For all simulations, the incident air kerma at the surface of the breast models was set to 7 mGy. The photon fluence was calculated according to the relationship

$$K_{c,\text{air}}={\left[\frac{{\mu }_{\text{en}}}{\rho }\right]}_{\text{air}}\cdot E\cdot \Phi ,$$ (7)

where K_c,air is the incident air kerma, E is the energy of the incident photons, Φ is the photon fluence, and [μ_en∕ρ]_air is the mass energy absorption coefficients for air, taken from Hubbell and Seltzer.³⁴

Poisson quantum noise was also added to the original ideal images, using a Gaussian random number generator, with a variance set equal to the mean number of the photons that strike each detector pixel.

Implementation

The software application called BREASTSIMULATOR runs under both Microsoft Windows and Linux operating systems. In order to generate higher resolution matrices, the 64-bit editions must be used. Moreover, in order to increase the speed of breast simulation, the code was parallelized on a Linux cluster using the message passing interface for interprocessor communication implemented through MPICH2.³⁵ Large and medium breast size phantoms are generated with the parallel code. For this purpose, a Dell dual-quad-core workstation with 32 GB RAM and seven slave processors was used.

EVALUATION

The new approach for breast model generation was evaluated subjectively and quantitatively. For this evaluation, a database with regions of interest (ROIs) extracted from synthetic and real mammograms was created.

Database

Clinical images

Two sources of clinical data were used to collect real images. Initially, 30 images, digitized at 200 μm pixel size, were chosen from the MIAS Mini Database³⁶ that contains images of compressed and uncompressed breasts. The selected 30 images are mammograms taken from women with ten fatty, ten glandular, and ten dense breasts. The breast tissue density classification has been decided by experienced radiologists for each image contained in this database and is included in the readme file. Thirty ROIs with size of 256×256 pixels were extracted from the central part of these mammograms and placed in the database. In addition, digital mammograms of women who had routine screening mammographic examination in Greece were used retrospectively. The images, acquired with GE Senograph 2000D full-field digital detector, were “processed” images obtained at 12-bit per pixel and a pixel pitch of 100 μm. One hundred mammograms taken from 25 patients were used to extract the ROIs for evaluation. Three to four ROIs per image were selected depending on the size of the breast. The size of the ROI was chosen 400×400 pixels based on literature review.^{37, 38} From these, 300 ROIs, 120 were free of breast abnormities and placed in the database for the purposes of this study. Forty of these ROIs were extracted from mammograms of breasts that were characterized by the radiologists as dense breasts while the rest encompass the fatty and fatty-glandular breast density. An example of selection of ROIs from a clinical mammogram is shown in Fig. 3.

Figure 3.

Example of defining ROIs on a mammogram.

Synthetic images

In order to create a database with synthetic images, several breast phantoms were designed to represent woman breasts with different glandularity. This was calculated by taking into account the percent of the glandular voxels in the central area of the breast phantom. The creation of fatty, glandular, or dense breasts was influenced by the various combination of the values of the following modeling parameters: The number of walks (N_walks), the number of steps per walk (N_steps), the Hurst exponent (H), the increment (h), the number of Cooper elements, and the ducts density. In order to find the range of values assigned to each of these parameters, an extensive simulation work with the new algorithm has been carried out. These simulations included the synthesis of replicating small, medium, and large simulated breast models with different parameters in order to define the set of values of each of these parameters corresponding to the creation of models with different dimension and glandularity. Default values for the creation of various breasts with different density and corresponding dimensions are summarized in Table 2. The voxel dimension of the synthesized breast models varied from 0.1 to 0.15 mm, as the former was assigned to small and medium breasts, while the second voxel size was used for large breast models. The breast dimensions correspond to that of the elongated semiellipsoid.

Table 2.

Default values for the creation of breast models of different glandularity and dimensions. F: Fatty breast; G: Glandular breast; D: Dense breast matrix size is in three dimensions.

Matrix size	Nwalk	Nsteps	h	H	Breast density	Breast size (mm)	Breast type
700	1000	(1–3)×103	0.1	0.8	D	40×40×40	Small
1000	300–500	(1–3)×104	0.1, 0.2	0.8, 0.9	F
1000	500–1000	(1–2)×104	0.1	0.9, 0.95	G
1000	5000	2×104	0.1	0.9	D
1200	500–1000	2×105	0.1	0.9	D	50×50×80	Medium
1500	1000	(1.5–2)×105	0.1	0.9	G	70×70×100	Large
1500	1000	(1–1.5)×105	0.1	0.9	F

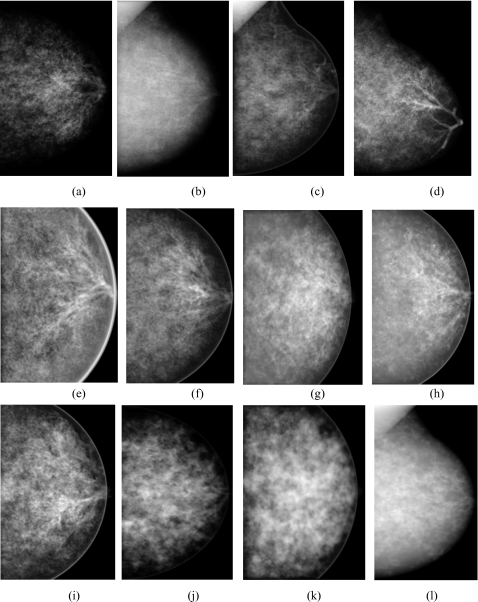
Thirty breast phantoms (ten large, ten medium, and ten small) with no pathology included were selected. Simulated projection images of these breast phantoms were obtained at CC and MLO view. Quantum noise was added according to Sec. 2B. Examples of simulated mammographic images of fatty, glandular and dense breasts are shown in Fig. 4. In this figure, (a)–(d) show mammograms of simulated fatty, (e)–(i) glandular, and (j)–(l) dense breast models. In images a, b, d, e, f, h, i, and l, parts of the duct tree can be observed, while in (c) and (l), simulated blood and lymph vessels are visible. One hundred twenty ROIs were extracted from these simulated images and placed in the database. The ROIs corresponded to a rectangular area of 400 pixels, located in different areas of the mammograms, similar to the clinical case.

Figure 4.

Examples of simulated mammograms at CC and MLO view obtained from [(a)–(d)] fatty breast models, [(e)–(i)] models of glandular breasts, and [(j) and (l)] dense breast models.

Subjective evaluation

In the qualitative approach, four radiologists (two from Greece and two from the United States) each with more than 10 yr experience in the field of clinical mammography examination participated. The purpose of this evaluation was to evaluate the realism of the synthetic mammograms obtained from the improved breast model in comparison to mammograms simulated for the evaluation of the previous approach. For this evaluation, 15 ROIs extracted from simulated mammograms obtained with the new methodology and 13 ROIs extracted from simulated mammograms obtained with the previous algorithm were mixed and placed in a PowerPoint presentation, with two ROIs per slide. A comparison of simulated images obtained with the new and previous methodology is shown in Fig. 5. The radiologists were asked to evaluate the realism of the simulated ROIs in terms of appearance with grades from 1 to 3. Grade 1 was used for images that are not realistic at all, grade 2 for images of medium realism, and grade 3 for images that look like real mammograms. The images were displayed in a dark room at the radiologists work. In one of the cases, a mammography viewing station was not available. Therefore, in order to conduct the subjective evaluation of the images under the similar conditions, a high quality flat panel PC screen was used. There was no restriction on the viewing time and distance to the screen.

Figure 5.

Examples of simulated mammograms with [(a)–(c)] the new and [(d)–(f)] the old algorithm for 3D mammographic texture.

Objective evaluation

The quantitative evaluation of the breast model included comparison of four texture features extracted from simulated and real ROIs: Histogram skewness and kurtosis, the exponential parameter β of the power law spectrum, and fractal dimension. Figure 6 shows examples of ROIs extracted from real (upper row) and simulated (lower row) mammograms. All simulated and real ROIs were involved in this study.

Figure 6.

Examples of [(a)–(f)] real and [(g)–(l)] simulated ROIs used in the evaluation.

Skewness and kurtosis

These features characterize the shape and the asymmetry of the histograms showing the distribution of gray values of the pixels in the ROIs. The skewness and kurtosis are the third and the fourth moment distribution about the mean gray value of the pixels in the ROIs. For a ROI containing N pixels, the kth moment m_k of the histogram is given by

$$m_k=\frac{\sum _{i=0}^{i_{\text{max}}}\left[h_i{\left(i-i_{\text{mean}}\right)}^k\right]}{N},k>1,$$ (8)

where $N={\sum }_{i=0}^{i_{\text{max}}}{h}_i$, h_i is the number of pixels at gray level i, and $i_{\text{mean}}={\sum }_{i=0}^{i_{\text{max}}}\left(i{h}_i∕N\right)$ is the mean gray value of the distribution. The normalized third and fourth moments are given by

$$S=\frac{m_3}{m_2^{3∕2}}K=\frac{m_4}{m_2^{4∕2}}.$$ (9)

Power law spectral analysis

The power law spectral analysis is based on the power spectrum of real and simulated ROIs. The power spectrum of the ROIs was calculated by integrating the power spectrum density over concentric rings in the 2D frequency plane using the method developed by Heine and Velthuizen.³⁹ The power spectrum (P(f)=B∕f^ß) of an image f(a,b) is computed from the discrete Fourier transform

$$P\left(f\right)={\left|F\left(k,l\right)\right|}^2,$$ (10)

$$F\left(k,l\right)=\frac{1}{MN}\sum _{a=0}^{M-1}\sum _{b=0}^{N-1}f\left(a,b\right)\text{exp}\left[-2\pi i\left(\frac{ka}{M}+\frac{lb}{N}\right)\right],$$$$k=0,1,\dots ,M-1l=0,1,\dots N-1,$$ 11

where k and l are the spatial frequencies in the two directions and M×N is the image size of f(a,b).

The concentric rings represent an octave sectioning of the frequency plane. The ring width is half the width of the adjacent ring that covers higher frequency information, as the first octave corresponds to the highest frequency ring. The highest frequency is the Nyquist one. The total power spectrum per concentric ring is further transformed to log₂ (total power spectrum) and plotted versus the octave number. The plot is almost linear and the data are fitted to a line obtained using linear regression analysis. The slop of the line m is related to exponential parameter β as following:

$$\text{m}=\beta -2.$$ (12)

Therefore, this approach of calculating β was preferred to the one that uses equally spaced rings and results in non linear plots. In this study, the number of the concentric rings was five. For example, in case of mammograms with pixel resolution of 0.1 mm, the width of the rings corresponded to (2.5–5), (1.25–2.5), (0.625–1.25), (0.312–0.625), and (0.156–0.312) cycles∕mm. The region around the zero frequency (0–0.156) was excluded in the analysis in order to avoid any influence due to the dc component of the power spectrum that usually varies from image to image and depending on the x-ray imaging system used for image acquisition. Before applying Fourier methods to the ROIs, data windowing with a Hanning window was performed.

Fractal dimension

The fractal dimension (FD) indicates how rough a surface is. There are several methods to measure the fractal dimension of an image such as variance method and box-counting technique, methods based on fast Fourier transform, thus producing a different estimate of the fractal dimension.^{40, 41} In this study, the fractal dimension was deducted from the β exponent from the power spectrum analysis using the following relationship:^{42, 43}

$$\text{FD}=\frac{8-\beta }{2}.$$ (13)

This method has proved to be accurate and effective across different imaging modalities.⁴⁴

For comparison purposes with other studies, the fractal dimension was evaluated as well with the conventional box-counting technique⁴⁵ described in detail in the Appendix0. Five pixel sizes (ε) were synthesized by averaging the pixels gray levels in squares of 1×1, 2×2, 4×4, 8×8, and 16×16 adjacent pixels. The exposed surface A(ε) was then calculated as described in the Appendix0 and the fractal dimension was computed from the plot of the log(A(ε)) versus log(ε).

RESULTS

Subjective evaluation

The results of the subjective evaluation are summarized in Table 3. More than half of the synthetic mammograms obtained with the previous methodology obtained grade 1 by radiologists. The evaluators observed that all images simulated with the old algorithm were blurred and therefore not realistic. There were few images synthesized with the improved algorithm that were rated with grade 1. These cases were commented by the radiologists as having either a high contrast [as, for example, the ROIs shown in Figs. 6i, 6j, 6k] or wrong anatomy [Fig. 4d]. In addition, the radiologists evaluated the whole synthetic mammograms obtained with the two approaches and shared their observation for the realism of the mammograms. Similar to the evaluation of the ROIs, all simulated projections obtained from breast models created with the previous approach were not realistic. Radiologists remarked that simulated projection images obtained with the new algorithm are featured with improved image quality and realistic mammographic texture and concluded that efforts should be directed toward improvements of the mammographic appearance at the edges of the breast model.

Table 3.

Results from the radiologists’ evaluation. A three grade scale is used in the evaluation. Grade 1: Images are not realistic at all, grade 2: Images of medium realism, and grade 3: Images look like real mammograms.

	ROIs	Grade 1	Grade 2	Grade 3
Reviewer 1	New	3	8	4
	Old	12	1	0
Reviewer 2	New	5	10	0
	Old	12	1	0
Reviewer 3	New	1	5	9
	Old	13	0	0
Reviewer 4	New	1	8	6
	Old	8	4	1

Objective evaluation

The exponential parameter β of the power law spectrum, the fractal dimension, skewness, and kurtosis were computed for each simulated and real ROI. An example of feature evaluation is depicted in Fig. 7, which shows a comparisonbetween calculated features for ROIs, extracted from simulated [Fig. 7a] and clinical [Figs. 7b, 7c] mammograms of glandular breasts. The linear trends for the β exponent and histogram distributions for the skewness were compared in Figs. 7a, 7b, 7c (the second and third column). Overall, similar linear trends of the log₂ (total power spectrum) versus the octave number, β exponents and histogram distributions are observed for the ROIs extracted from real and simulated images.

Figure 7.

(a) Examples of ROIs and their corresponding calculated β exponent, skewness (s), kurtosis (k), and fractal dimension (FD) from a simulated image; a clinical mammogram obtained with (b) GE Senograph 2000D and (c) taken form MIAS Mini Database mdb007.

The overall quantitative evaluation of simulated images against calculations performed on real images is summarized in Table 4. In the same table, data published in the literature are presented as well.

Table 4.

Results from the quantitative evaluation and comparison with results from literature.

	Fractal dimension		Skewness		Kurtosis		Power Spectrum
	Real	Simulated	Real	Simulated	Real	Simulated	Real	Simulated
Bliznakova et al.a	2.36±0.10 b	2.39±0.10 b	0.02±0.17	0.06±0.15
Li et al.c	(2.30, 3.00)d						2.47±0.20
							2.92±0.28
Li et al.e	(2.3, 2.93)b		(−2.0, 2.0)
Li et al.f	(2.50, 2.93)b
Bakic et al.g	2.32±0.10	2.36±0.10
Heine and Velthuizenh							2.76±0.12
Georgsson et al.i	(2.34, 2.70)b
Byng et al.10	(2.23, 2.54)b		(−0.30, 0.20)
Caldwell et al.11	(2.20, 2.50)b
Bochud et al.12			−0.10±0.80	0.10±0.40	2.50±1.00	2.60±0.40		(3.40, 4.0)
Castella et al.13							3.02±0.02	2.92±0.01
Heine et al.14							2.94±0.10
Turasi et al.15	2.71±0.08 d
Kontos et al.16	(2.45, 2.8)d
This study	2.51±0.03d, 4n17
	2.62±0.04d, 4n18	2.55±0.07d	−0.22±0.6417	0.03±0.33	3.33±1.3617	2.75±0.48	2.96±0.0517	2.90±0.08
	2.54±0.12b, 4n17	2.59±0.18b	0.23±0.4918		3.41±0.9018		2.78±0.0718
	2.67±0.11b, 4n18

^aReference ¹⁷.

^bFractal dimension calculated with box-counting technique.

^cReference ³⁷.

^dFractal dimension calculated with power spectral analysis.

^eReference ⁴⁹.

^fReference ⁵⁰.

^gReference ⁵³.

^hReference ³⁹.

ⁱReference ⁵¹.

¹⁰Reference ⁵².

¹¹Reference ⁴⁵.

¹²Reference ⁴⁸.

¹³Reference ⁴⁶.

¹⁴Reference ⁴⁷.

¹⁵Reference ⁴⁴.

¹⁶Reference ²⁵.

¹⁷Results for mammograms from MIAS MiniDatabase.

¹⁸Results for digital mammograms.

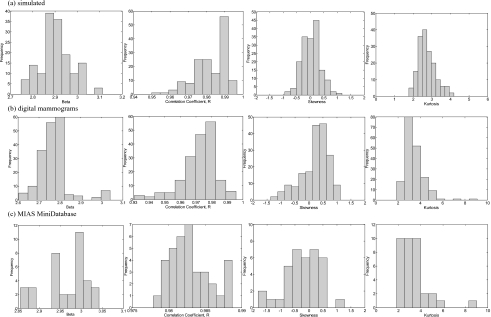
Further, the distributions of the β values calculated from the power spectrum analysis for ROIs extracted from simulated and real mammograms are presented in Figs. 8a, 8b, 8c (the first column). The mean value and standard deviation for the entire set of simulated images is ⟨β⟩=2.90±0.08 [Fig. 8a], while the mean value and standard deviation, calculated for ROIs extracted from real mammograms acquired with GE Senograph and taken from MIAS MiniDatabase is ⟨β⟩=2.78±0.07 [Fig. 8b] and ⟨β⟩=2.96±0.05 [Fig. 8c], respectively. Additionally, for each image, the correlation coefficient (R) for the least square fit between the log₂ (total power spectrum) and the octave number was calculated. Histogram distributions of these correlation coefficients for simulated and clinical images are shown in the same figure (the second column). In case of simulated images, the average correlation coefficient is ⟨R⟩=0.982±0.009, while for ROIs extracted from mammograms acquired with GE Senograph and taken from MIAS MiniDatabase, this coefficient corresponds to ⟨R⟩=0.975±0.011 and ⟨R⟩=0.983±0.001, respectively. Overall, a good agreement between β value for simulated and real data is observed, while the correlation coefficient for all linear fits is higher than 0.975.

Figure 8.

Distribution of ⟨β⟩ values, correlation coefficients ⟨R⟩ from the linear regression analysis, as well as distribution of skewness and kurtosis for ROIs extracted from (a) simulated images and real mammograms taken from (b) a private patient database and (c) MIAS MiniDatabase.

The results of the power law spectral analysis are also in good agreement compared to the published data by Castella et al.⁴⁶ for real and simulated images and studies with real images.^{37, 39, 47} These results differ from those reported by Bochud et al.⁴⁸ that are higher compared to the results of this and other published studies. This is attributed to the use of constant ring width approach and that the authors used the linear part of the fit to estimate the β value.

The power spectrum analysis was used to calculate the fractal dimensions of simulated and real ROIs. The mean value and the standard deviation of calculated fractal dimension of simulated images (⟨FD⟩=2.55±0.07) is in the range of the calculated fractal dimensions obtained for the two real sets of mammograms ⟨FD⟩=2.51±0.03 and ⟨FD⟩=2.62±0.04, respectively, for the MIAS Mini Database and digital mammograms. Fractal dimension was also calculated with the box-counting technique, showing a good agreement between calculated fractal dimension of simulated (⟨FD⟩=2.59±0.18) and clinical images (⟨FD⟩=2.54±0.12 and ⟨FD⟩=2.67±0.11). In addition, the calculated average fractal dimension for simulated images is in agreement with published calculations performed on real images using the power spectrum and the box-counting techniques.^{25, 37, 49, 50, 51} Other published results for the fractal dimension differ slightly from the results of this study.^{17, 44, 45, 52, 53}

The calculations for the histogram skewness (0.03±0.33) are also in the range of the results obtained for clinical images used in this study (0.23±0.49 and −0.22±0.64 for digital mammograms and mammograms taken from the MIAS Mini Database). The histograms of the calculated skewness values are shown in Figs. 8a, 8b, 8c (the third column). Skewness values calculated for clinical images have a wider range of fluctuations compared to simulated images, a fact that has been observed by Bochud et al.⁴⁸ Good agreement is observed with data published by the same author⁴⁸ for both simulated and real ROIs (0.10±0.40 and −0.10±0.80), as well as with the data provided by Li et al.⁴⁹ and Byng et al.⁵² for real images.

The histograms of the calculated kurtosis are shown in the last column in Figs. 8a, 8b, 8c. Similar to the skewness, the kurtosis has more variations in the clinical images compared to simulated images. Data for histogram kurtosis from similar calculations performed by Bochud et al.⁴⁸ agree well with our calculations.

Finally, a two-sample t-test was performed between the results for skewness, kurtosis, and fractal dimension using the new and previous methodology for creation of breast models to identify the difference between the two set of simulated images. Results show that the Pearson’s correlation coefficient (the p value) for the skewness and the fractal dimension was much less than 0.001, while for kurtosis, the p value corresponded to 0.4.

DISCUSSION

The new methodology for generation of 3D mammographic texture, and therefore the 3D breast phantom synthesis, is more flexible compared to the previous methodology and allows the generation of breast models with various glandularity. This algorithm also contributes significantly to the generation of synthetic mammograms that visually and quantitatively approach the real ones. The observer study by radiologists confirmed that the new algorithm for mammographic texture is superior compared to the previous approach. The subjective evaluation of the entire set of synthetic mammographic images suggested that efforts should be directed toward improvements of the mammographic appearance at the edges of the breast model for superior realism.

The quantitative analysis suggests that the new methodology generates improved breast models and the texture characteristics obtained from the simulated mammograms are close to those calculated on real mammograms. The results from the two-sample t-test indicated that the new algorithm differs significantly from the previous approach. Generally, there is a good coincidence between calculations performed in this study and published data as well.^{25, 37, 38, 39, 41, 46, 47, 48, 49, 50, 51, 52}

The comparison of extracted texture features from real and simulated mammograms shows that simulated results are between the calculated values for the two real mammogram sets. For example, the power spectrum analysis showed that the average β exponent for simulated images is higher than the average β exponent calculated for real images acquired with GE Senograph 2000D. This is attributed to the presence of noise in the real images coming from the scattered radiation and detector characteristics. From the other side, the average β exponent for simulated images is lower than the one calculated for real images from MIAS Mini Database. This is explained with the resolution of the images. Simulated images are generated with higher resolution and images with higher resolution exhibit slightly higher fractal dimension than those characterized by lower resolution due to the influence of small details.

Difference between various fractal dimensions published in the literature are eventually due to the use of different approach in the calculation of this parameter (for example, the use of variance techniques⁵³), the image acquisition system, the mammographic view at which images are acquired, or the limited number of images used in the study.^{17, 44, 45, 52}

Results for the skewness calculated from simulated images are between the calculated skewness from clinical data from the two different sources. The data from the MDB were acquired from ten fatty, ten glandular, and ten dense breasts. Regions of interest with more dense and glandular tissue yield negative skewness as calculated from Eqs. 8, 9, while ROIs with more fatty breast tissue are characterized with positive skewness values. Therefore, the skewness values obtained from images taken from MIAS Mini Database are negative. In case of digital mammograms, the ROIs contained predominantly fatty and fatty-glandular tissue; therefore, the mean value for the skewness is positive. From the other hand, the almost zero mean value of the skewness calculated for simulated images indicates equally distributed fatty and dense mammographic densities from the selected ROIs.

There are several applications where BREASTSIMULATOR can be successfully used, including digital breast tomosynthesis, breast cone beam computed tomography, and subtraction mammography to mention but a few. However, there are still several issues that require further development and adjustment in order to achieve better results and these mainly concern the x-ray image simulation chain. For the purposes of improving and testing the algorithm for creation of 3D breast models, the simulated mammograms were obtained with monochromatic incident beams, ideal detector, and simulation of primary radiation only. These are therefore the main limitations of the conducted study and were prompted by the large size of the breast matrices. Simulation of Cooper ligaments and other fine breast tissue structures require the use of large matrices with a voxel size in the order of 50 μm. This will guarantee their visualization in the mammograms and will contribute considerably to the synthesis of more realistic mammographic images. Due to the large size of these matrices, the use of Monte Carlo techniques to simulate in detail the x-ray interactions in the breast models is not efficient. Further on, modeling of detector characteristics and propagation of x rays in the detector would further complicate the current work, which at this stage is addressing the improvement and test of the proposed algorithm. For the purposes of this work, the analytical method for image simulation³¹ is fast and flexible and therefore convenient for accomplishing the tests and optimization operations.

Undoubtedly, the simulation of x-ray interactions in the whole imaging chain (x-ray source, breast model, and detector) will result to the inclusion of noise mainly in the form of x rays scattered in the breast model and detector noise. This may further improve the realism of the simulated images and influence slightly the qualitative and quantitative evaluations. In the latter case, it is expected that the inclusion of scattered radiation from the breast model and the introduction of the detector model will result in lower β values (and therefore higher values for the fractal dimension as in real images^{39, 41} and will better match the computed texture features with digital mammograms.

The improved algorithm for creation of breast models is currently used in a feasibility study that aims to compare the performance of three novel detectors for digital mammography. In this study, a Monte Carlo code⁵⁴ is exploited to simulate x-ray interactions in the breast models and in the detectors. In addition, clinical conditions are simulated taking into account acquisition geometry and typical mammography x-ray spectra.

These additional studies will further improve the computer models of the female breast and x-ray imaging chain and will establish the practical importance of this software model in carrying out feasibility studies in the field of breast x-ray imaging.

CONCLUSIONS

This paper described an improved methodology for generating realistic computer generated breast phantoms and its extensive evaluation for research purposes in mammography. The observer study with radiologists as observers and the feature measures suggest that the algorithm for creation of 3D breast models has been improved in terms of simulation of female breast models with improved realism. The use of these models with x-ray imaging simulation contributes to the simulation of mammograms with improved realism. The application of such anthropomorphic phantoms that closely resemble the breast anatomy and reflects the radiographic properties of the breast tissue may be suitable for the design and evaluation of new digital mammography systems and with further adaptations potentially for tomosynthesis and dedicated breast computed tomography systems.

APPENDIX: FRACTAL ANALYSIS OF IMAGES

Fractional Brownian motion

fBm, introduced by Mandelbrot in 1977,⁵⁵ is a generalization of the classical Brownian motion that is also called a random walk. Shortly described, the fBm model regards naturally occurring rough surfaces as the end results of random walks and utilizes a random iteration algorithm to produce fractal patterns.⁵⁶ In fBm, the change or increment from one moment to the next is random and normally distributed, so the present is not correlated with the past. A single parameter H∊(0,1), called Hurst exponent, characterizes fBm. A fBm is a stochastic process X(t) having increments X(t+h)−X(t) that are normally distributed with mean zero and standard deviation σ=h^H, i.e., the mean and the variance are

$$⟨X\left(t+h\right)-X\left(t\right)⟩=0,$$$$⟨{\left[X\left(t+h\right)-X\left(t\right)\right]}^2⟩\approx {\left|t+h-t\right|}^{2H}.$$ A1

t+h and t are two arbitrary points in the space.

The Hurst exponent is related to the fractal dimension of a fractal object and provides an indication of how rough a surface is and is given with the following relationship:

$$\text{FD}=2-H.$$ (A2)

A small Hurst exponent is related to a higher fractal dimension and a rougher surface. A larger Hurst exponent is related to a smaller fractional dimension and a smoother surface.

Various models of fBm simulation have been reported in the literature such as Poison faulting, Fourier spectrum, midpoint displacement, successive random additions, and summing band-limited noises. The approach we followed to generate fBm is related to an algorithm called successive random additions. This approach has four basic advantages: Simplicity, flexibility (for implementation and control), easy user understanding, and easy to implement.

Fractal Analysis

The fractal dimension of image surface can be calculated as

$$A\left(\epsilon \right)=\lambda {\epsilon }^{2-D},$$ (A3)

where A(ε) is the area of the surface measured with a square of side ε, λ is a scaling constant, and D is the surface’s fractal dimension. The area A(ε) is calculated using the technique suggested by Caldwell et al.⁴⁵ Each pixel in the two-dimensional image is considered as a skyscraper with the length and width equal to the pixel dimensions and the height equal to the pixel’s gray value, thus obtaining a collection of adjacent “skyscrapers.” The area of the surface is obtained by sum of the area of the roofs plus the sum of the areas of the exposed lateral sides of the skyscrapers

$$A\left(\epsilon \right)=\sum _{x,y}{\epsilon }^2+\sum _{x,y}\epsilon \left\{\left|I\left(x,y\right)-I\left(x+1,y\right)\right|+\left|I\left(x,y\right)-I\left(x,y+1\right)\right|\right\},$$ (A4)

where I(x, y) is the height of a “column,” found for a particular value of ε by averaging the values stored in adjacent image array elements to produce pixels with a side length of ε. The area A(ε) is recalculated for different sizes of ε by averaging adjacent pixels together in order to obtain new images with varying pixel size ε. The fractal dimension D is then related to the slope of a plot of log{A(ε)} versus log{ε}.