Skip to main content
NCBI home page
Acta Crystallographica Section D: Biological Crystallography logoLink to Acta Crystallographica Section D: Biological Crystallography
. 2010 Oct 20;66(Pt 11):1153–1163. doi: 10.1107/S0907444910026582

Joint X-ray and neutron refinement with phenix.refine

Pavel V Afonine a,*, Marat Mustyakimov b, Ralf W Grosse-Kunstleve a, Nigel W Moriarty a, Paul Langan b, Paul D Adams a,c
PMCID: PMC2967420  PMID: 21041930

The implementation of crystallographic structure-refinement procedures that include both X-ray and neutron data (separate or jointly) in the PHENIX system is described.

Keywords: structure refinement, neutrons, joint X-ray and neutron refinement, PHENIX

Abstract

Approximately 85% of the structures deposited in the Protein Data Bank have been solved using X-ray crystallography, making it the leading method for three-dimensional structure determination of macromolecules. One of the limitations of the method is that the typical data quality (resolution) does not allow the direct determination of H-atom positions. Most hydrogen positions can be inferred from the positions of other atoms and therefore can be readily included into the structure model as a priori knowledge. However, this may not be the case in biologically active sites of macromolecules, where the presence and position of hydrogen is crucial to the enzymatic mechanism. This makes the application of neutron crystallo­graphy in biology particularly important, as H atoms can be clearly located in experimental neutron scattering density maps. Without exception, when a neutron structure is determined the corresponding X-ray structure is also known, making it possible to derive the complete structure using both data sets. Here, the implementation of crystallographic structure-refinement procedures that include both X-ray and neutron data (separate or jointly) in the PHENIX system is described.

1. Introduction  

The experimental determination of H-atom positions provides important biochemical information and permits better modeling of electrostatic interactions. In particular, the location of hydrogen offers information on the geometry of hydrogen bonding involved in stabilizing molecules and allows the direct determination of the protonation states of catalytic groups. There are many cases in which water molecules play a key role in enzymatic reactions, molecular recognition and protein folding. The orientation and dynamics of H atoms in water molecules are important for characterizing these processes. Knowledge of hydrogen positions facilitates unambiguous ligand placement. The parameters of hydrogen bonds can be used in the calculation of hydrogen-bond energies, which in turn can be used in molecular-dynamics simulations. The fact that not all H atoms can undergo exchange with D atoms in solution, but only those in polarized bonds such as N—H and O—H, makes it a tool for studying protein flexibility and packing, since only solvent-accessible areas are exposed to exchange. Further details can be found in the following selected publications and numerous references therein: Kossiakoff & Spencer (1981 ▶), Wlodawer & Sjölin (1982 ▶), Kossiakoff (1985 ▶, 1986 ▶), McDowell & Kossiakoff (1995 ▶), Shu et al. (2000 ▶), Habash et al. (2000 ▶), Engler et al. (2003 ▶), Fenimore et al. (2004 ▶), Kurihara et al. (2004 ▶), Niimura et al. (2004 ▶), Bennett et al. (2006 ▶), Katz et al. (2006 ▶), Chatake et al. (2008 ▶), Blum et al. (2009 ▶), Fisher et al. (2010 ▶), Kovalevsky et al. (2010 ▶), Sukumar et al. (2010 ▶).

The positions of H atoms in macromolecules cannot be routinely determined from crystallographic X-ray data at typical resolutions (worse than ∼1.0 Å). Only subatomic resolution1 structures, of which there are currently only 358 out of a total of over 58 750 PDB entries (Bernstein et al., 1977 ▶; Berman et al., 2000 ▶), reliably reveal the position of some H atoms in residual maps (see, for example, Petrova & Podjarny, 2004 ▶; Ahmed et al., 2007 ▶). It should be emphasized that the visibility of H atoms in X-ray maps is highly dependent on the resolution, the overall model quality (R factor), local features such as flexibility and disorder, and the types of Fourier syntheses used. For example, only 54% of all possible H atoms are reliably observed in the structure of aldose reductase refined at 0.66 Å resolution (Howard et al., 2004 ▶). Therefore, the availability of high-resolution data alone is not a guarantee of locating all H atoms, including those of particular biological interest. Fortunately, in general, most H atoms (with a few exceptions) are well defined by the atoms they are bonded to and therefore can be placed at stereochemically predicted positions; hence, a complete model can still be obtained. However, the inability of X-ray data to directly reveal H atoms can become an obstacle since many chemical interactions involve hydrogen transfer and the protonation state cannot be determined from the geometry. Furthermore, H atoms with ambiguous geometry can be involved in important inter­actions (such as hydroxyl H atoms in Tyr, Ser or Thr). A novel ligand or an item with nonstandard stereochemistry may complicate the location of H atoms based on the geometry only.

For the reasons just described, neutron crystallography (NC) is an excellent complementary technique to X-ray crystallography. Since neutrons and X-rays interact differently with atoms, the experimental data obtained from the two experiments convey different but complementary information (Korszun, 1997 ▶; Niimura, 1999 ▶; Gutberlet et al., 2001 ▶; Hanson, 2004 ▶; Blakeley, Ruiz et al., 2008 ▶). The X-ray data contain information about the distribution of electrons, while neutrons are scattered by the nuclei and so provide information about nuclear positions (see, for example, Finney, 1995 ▶). Until recently, the experimental demands of NC experiments were fairly prohibitive, such as the requirement for a large crystal volume and the time scale of the experiment. However, with recent advances in technology these limits are being pushed towards smaller crystals and shorter data-collection times (Niimura et al., 2006 ▶; Blakeley, Langan et al., 2008 ▶). It should also be noted that there is no appreciable direct radiation damage during neutron data collection and hence no need for cryoprotection. Thus, data-collection experiments can be conducted at physiological temperatures.

The large incoherent scattering of neutrons by H atoms typically results in significant background scattering (Shu et al., 2000 ▶). Therefore, it is better to use fully or at least partially deuterated samples to improve the signal-to-noise ratio of the experiment. Also, deuteration facilitates the location of water molecules, since the scattering lengths of D and O are both positive and are very similar in value. Completely deuterated (perdeuterated) samples can be obtained, as described previously (Hazemann et al., 2005 ▶; Blum et al., 2010 ▶), while soaking in D2O buffer will result in partial deuteration. Since the scattering lengths of C, N, O, S and D are all positive, while that of H is negative (and almost half the value), this can result in partial or even full cancellation (Habash et al., 2000 ▶) of the hydrogen density by the density of adjacent heavy atoms or exchangeable D atoms (Shu et al., 2000 ▶; Ostermann et al., 2002 ▶). This sets a limit on the visibility and interpretation of H atoms.

Given the advances in experimental techniques and improved data-collection facilities, it is highly likely that the number of neutron structures will grow in the coming years, generating an increased demand for crystallographic software that can make the most of neutron diffraction data. Since most structures are solved by means of X-ray crystallography first and the number of neutron structures solved to date is still modest, all commonly used crystallographic packages are oriented towards X-ray-based structure solution and refinement. It has been common practice to modify existing programs to better account for neutron data by manually adopting the neutron scattering dictionary, adjusting the hydrogen parameters and other related procedures (Engler et al., 2003 ▶; Ostermann et al., 2002 ▶; Kurihara et al., 2004 ▶). This modification of existing software has often led to workable but non-optimal tools for neutron refinement. Although more recently a patch for CNS (Brünger et al., 1998 ▶), nCNS (Adams et al., 2009 ▶), has been developed that allows refinement against neutron or both X-ray and neutron data, specialized software is ultimately required.

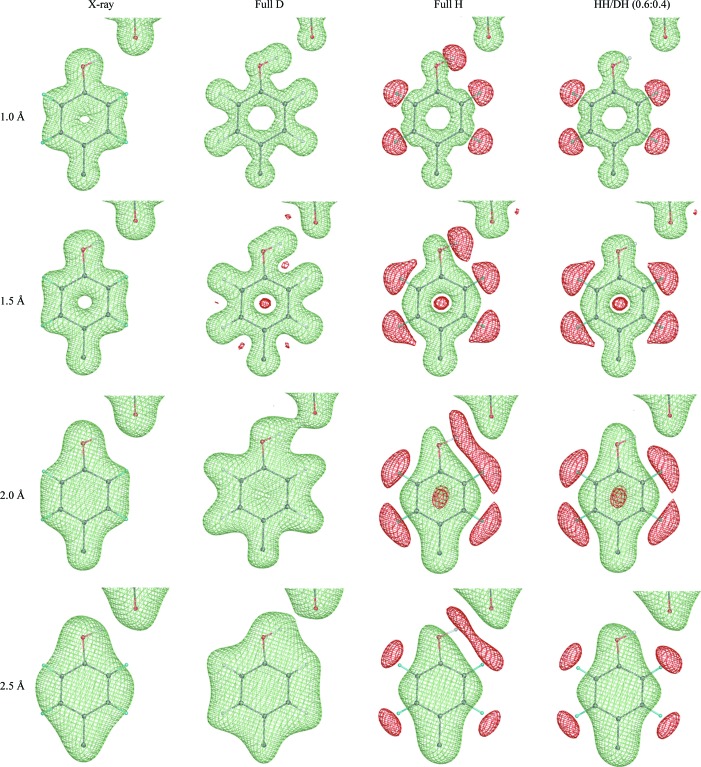
The nature of X-ray and neutron diffraction data requires different approaches to be implemented for the handling of H atoms in refinement. Fig. 1 ▶ shows the F calcexp(iαcalc) Fourier syntheses computed for a tyrosine residue at different high-resolution limits (1, 1.5, 2 and 2.5 Å) for four different cases: X-ray, neutron fully deuterated, neutron fully hydrogenated and neutron partially deuterated, in which the hydroxyl H atom of the tyrosine shares its site with a deuterium with an occupancy ratio of 0.6:0.4. This figure illustrates what can be seen for an ideal error-free model and data. For example, only at very high resolution do X-ray data reveal the positions of the H atoms and they are not visible at most ‘macromolecular’ resolutions (worse than 1.0 Å). In contrast, the neutron maps show D atoms as clearly as other atoms at resolutions from high to medium (Fig. 1 ▶, column 2). If, however, a partially deuterated sample is used then cancellation effects can cause problems, because the negative density of the H atom cancels the positive density of the atom it is bonded to, resulting in significantly reduced density (Fig. 1 ▶, columns 2–4) or even its absence (Fig. 1 ▶, column 4, atom HH/DH). Also, cancellation effects shift the apparent negative peak for the H atom along the bond vector further away from its correct position and diminish the density for the corresponding heavier atoms. The availability of higher resolution data makes this effect less intrusive. In practice, real-life syntheses appear nearly perfect only at subatomic resolutions and commonly look worse at typical resolutions (Fig. 2 ▶).

Figure 1.

Figure 1

Open in a new tab

(F calc, ϕcalc) Fourier syntheses computed at different resolutions (1, 1.5, 2 and 2.5 Å) and corresponding to four different cases: X-ray, neutron fully deuterated, neutron fully hydrogenated and neutron partially deuterated, in which the hydroxyl H (HH) of tyrosine shares its site with deuterium (DH) with an occupancy ratio of 0.6:0.4.

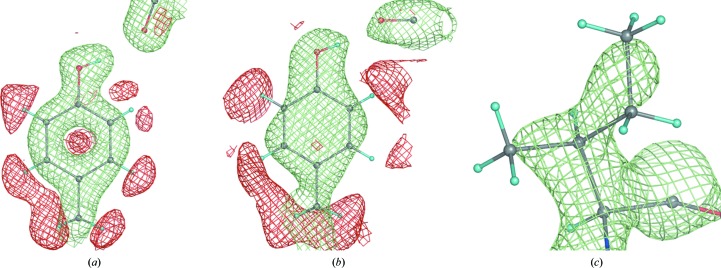
Figure 2.

Figure 2

Open in a new tab

Some typical 2F obs − DF model nuclear map appearances. (a) Tyr12 of 1iu5 (+1.2σ and −1.5σ, 1.6 Å resolution), (b) Tyr92 (+1.2σ and −1.4σ) and (c) Ile81 (+2.0σ) of 5rsa (2.0 Å resolution).

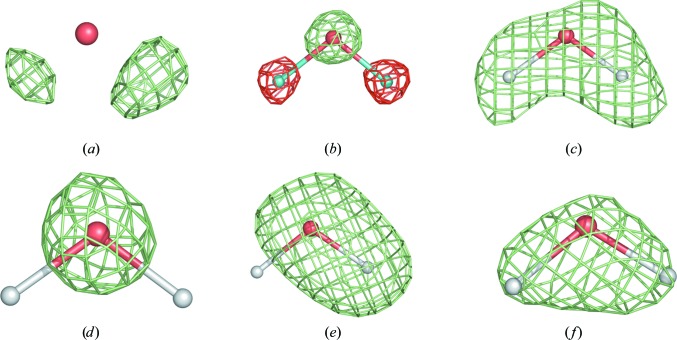
The H atoms of water molecules appear differently in X-ray and neutron maps and at different resolutions (Langan et al., 1999 ▶; Bon et al., 1999 ▶; Habash et al., 2000 ▶; Chatake et al., 2003 ▶, 2004 ▶, 2005 ▶; Niimura et al., 2004 ▶; Howard et al., 2004 ▶; Kang et al., 2004 ▶). Fig. 3 ▶ shows some of the typical occurrences. Only subatomic resolution X-ray maps show H-atom positions for some very well ordered waters (Figs. 3 ▶ a, 3 ▶ b and 3 ▶ c). They usually appear as small peaks around the water O atom. Depending on the degree of order, deuterated water molecules (D2O) can appear as various shapes in nuclear maps (maps computed using neutron data), showing spherical-shaped (the D atoms are smeared in space owing to random rotation around the O-atom position; Fig. 3 ▶ d), cylinder-shaped (partially fixed water having a rotational degree of freedom around a D—O bond axis; Fig. 3 ▶ e) or boomerang-shaped density (fully resolved; Fig. 3 ▶ f).

Figure 3.

Figure 3

Open in a new tab

A water molecule in (a) an mF obs − DF model X-ray map at 0.66 Å resolution and (b) a 2F obs − DF model nuclear map at 0.65 Å resolution; the remaining four nuclear maps are computed at 1.5 Å resolution.

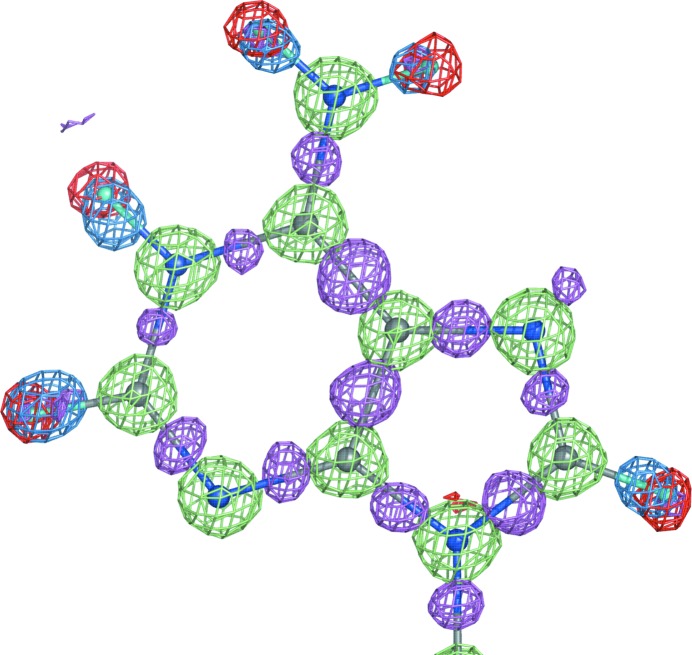
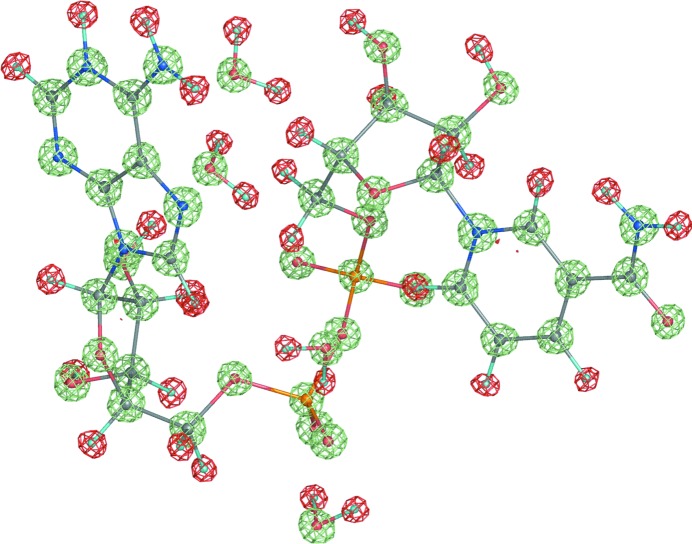
An X-ray structure of a macromolecule is almost always available before its neutron structure. An exception is protein structures that are complexed with different substrates or cofactors (Kovalevsky et al., 2008 ▶). If both data sets are collected from the same crystal (similar unit-cell parameters and identical space group) under the same conditions (temperature) then the structures derived from both data sets will be very similar. This makes it possible to use both data sets in refinement simultaneously [joint X-ray and neutron (XN) refinement]. This concept was pioneered in the field of small-molecule crystallography (Coppens et al., 1981 ▶) and was sub­sequently applied to macromolecules (Wlodawer & Hen­drickson, 1982 ▶; Wlodawer & Sjölin, 1982 ▶; Wlodawer et al., 1989 ▶); it has more recently been performed with the modified version of CNS, nCNS (Fisher et al., 2007 ▶, 2010 ▶; Coates et al., 2008 ▶; Blum et al., 2009 ▶; Kovalevsky et al., 2010 ▶; Sukumar et al., 2010 ▶). The obvious benefit of using two data sets is the increased number of experimental data, which compensates for the increased number of parameters as a result of adding H or D atoms. The increased information also compensates for the typically low completeness and resolution of neutron data. Since the neutron data contain information about H or D atoms on the same scale as that about the other atoms (in contrast to the H/D atoms in X-ray data) and the positions of all non-H atoms will be more accurately determined in the X-­ray model, a structure derived from both data sets is expected to be more complete and more accurate. As illustrated in Fig. 4 ▶, X-ray and neutron structures are still complementary even at sub­atomic resolution. There are two main areas of complementarity. Firstly, the neutron maps indicate the nuclear positions of H atoms, while the X-ray maps show the positions of valence-electron density for H atoms shifted along the bond vector (Sheldrick & Schneider, 1997 ▶; Afonine et al., 2004 ▶); secondly, the X-ray maps show the redistribution of electron density owing to covalent bonding.

Figure 4.

Figure 4

Open in a new tab

Three maps overlaid with a fragment of the NAD structure (UR0013): 2mF obs − DF model neutron map (shown at ±2.4σ; positive and negative contours are shown in lime and red, respectively; computed at 0.65 Å resolution) and two mF obs − DF model maps (X-ray; computed at 0.6 Å resolution; blue is contoured at 5σ and computed with H atoms omitted, magenta is contoured at 2.8σ and computed with all atoms included). Both structures, X-ray and neutron, were re-refined in phenix.refine to R factors (R work) of 2.09% and 7.97%, respectively. Red (negative) density corresponds to the hydrogen nucleus positions, blue density shows the shifted concentrations of hydrogen’s electron density revealed by X-rays, magenta shows the bonding electron density and lime is positive nuclear density.

This paper presents the tools available in the PHENIX system (Adams et al., 2010 ▶) for the refinement of macromolecular structures against X-ray and neutron data separately or simultaneously at resolutions from low to subatomic.

2. Methods  

X-ray and neutron data generate a number of different requirements for atomic model parameterization and refinement strategies. For example, at medium resolution one cannot refine H atoms individually using X-ray data, but it is possible using neutron data. If a partially deuterated sample is used for neutron diffraction then specific constraints on atomic positions, ADPs (atomic displacement parameters or B factors) and occupancies need to be used for exchangeable H/D sites. Furthermore, neutron structures typically suffer from cancellation effects (when not using full deuteration methods) and have a poor data-to-parameter ratio, rendering the refinement even more challenging. For such cases, parameter-saving refinement strategies can be used, such as grouped ADP refinement and torsion-angle parameterization for coordinates. If both X-ray and neutron data sets are collected from the same crystal under the same conditions, then they can be used simultaneously in refinement, increasing the effective number of observations.

Automatic water addition and refinement is integrated into the phenix.refine procedure. While in X-ray refinement at non-subatomic resolution the procedure consists of looking for a single water O atom, in neutron or subatomic X-ray refinement one needs to search for three templates, O, OD or DOD (or OH or HOH), and correctly place them. In PHENIX, a number of other tools have been implemented for the treatment of H atoms at any resolution and using any diffraction data source: X-ray, neutron or joint. Below, we discuss some implementation details specific to refinement using each type of data at different resolutions.

2.1. PHENIX tools for neutron and joint X-ray and neutron refinement  

Refinement against neutron data or ultrahigh-resolution X-­ray data requires the following functionalities to be available:

  • (i) adding H, D or exchangeable H/D sites to a model,

  • (ii) creating restraint files (CIF files) for novel ligands or nonstandard residues,

  • (iii) refining a structure against any combination of data sets,

  • (iv) exporting a PDB file with refined model and maps.

H or D atoms can be added to the model using the phenix.ready_set command-line tool that internally uses the REDUCE (Word et al., 1999 ▶) and eLBOW (Moriarty et al., 2009 ▶) programs. There are a number of options such as automatically adding exchangeable H/D sites at dual positions and adding H or D atoms to the macromolecule or water O atoms. If H or D atoms are added to a novel ligand then a file defining its stereochemical restraints (CIF file) is created. H atoms can also be added automatically to water molecules during refinement based on residual maps; this option requires either neutron or ultrahigh-resolution X-ray data.

phenix.refine is a crystallographic structure-refinement program (Afonine et al., 2005a ▶,b ▶) developed as part of the PHENIX system. An overview of phenix.refine can be found in Adams et al. (2010 ▶). Structure refinement with phenix.refine can be performed using X-ray data, neutron data or both data sets simultaneously. Highly customized refinement strategies are available for a broad range of experimental data resolutions: from ultrahigh resolution, where an interatomic scatterers (IAS) model can be used to model bonding features (Afonine et al., 2007 ▶), to highly optimized automatic rigid-body refinement (Afonine et al., 2009 ▶) and torsion-angle parameterized dynamics (Grosse-Kunstleve et al., 2009 ▶), which are important at low resolution. Most of the refinement strategies can be combined with each other and applied to any selected part of the structure. All refinement strategies available for refinement against X-ray data are also available for refinement using neutron data.

A round of structure refinement typically includes the execution of a refinement program and manual modification of the resulting structure using interactive computational graphics. Usually, two maps are used to assess or rebuild the structure: cross-validated σA-weighted 2mF obs − DF model and residual mF obs − DF model maps (Read, 1986 ▶; Urzhumtsev et al., 1996 ▶). In joint XN refinement four maps are required: two each for the X-ray and neutron data. phenix.refine creates all of these maps at the end of the refinement run. If additional maps are required (3F obs − 2F model or anomalous difference, for example), phenix.maps can be used. This tool can create any number of user-defined maps using X-­ray or neutron data. X-­PLOR-formatted maps can also be computed around any selected part of the structure.

A phenix.refine run always creates a PDB file with the header containing comprehensive statistics about the model, data and model-to-data fit. Two sets of refinement statistics (such as R factors, data amount and completeness etc.) relevant to each X-ray and neutron data set are reported after joint XN refinement (see, for example, PDB entry 2r24).

2.2. H atoms in X-ray refinement  

Even though H atoms are not visible in X-ray maps at typical macromolecular resolutions (worse than 1.0 Å), they still account for ∼50% of all atoms in a structure. Using stereochemical constraints or restraints as a priori knowledge, H atoms can be included in the model. If very high-resolution data (approximately 1.0 Å or better) and a high-quality refined model (R factors of ∼10% or better) are available, it is possible to see a significant fraction of the H atoms in difference maps and in favorable cases it is possible to refine all or some hydrogen parameters.

In the ‘riding model’ (Sheldrick & Schneider, 1997 ▶), H atoms are added to the structure at their theoretical positions with an ideal geometry (for example, X—H bond length, where X is an atom that the H is attached to). The riding model permits H atoms to be included in structure refinement at any resolution when they cannot be refined individually. The parameters of the X—H bond (bond length and angle, for example) are constrained and do not change during refinement; thus, the H atom rides on its bound atom, maintaining a rigid relative position. Additionally, the H atom inherits the occupancy of atom X and its isotropic ADP is multiplied by a number between 1.0 and 1.5 (Sheldrick & Schneider, 1997 ▶). This approach adds no additional refinement parameters and hence eliminates the risk of overfitting. However, the scattering contribution of the H atoms is included in the total model structure factors and in the nonbonded interactions. The benefits are improved R factors and thus improved maps and improved overall model geometry (such as clash scores, bad contacts and unfavorable rotamers; Davis et al., 2007 ▶) since the H atoms are involved in nonbonded interactions.

The availability of subatomic resolution X-ray data makes it possible to obtain a model of very high quality (low R factors) with significantly reduced noise in residual maps such that H atoms becomes visible in these maps. In this case, depending on the data-to-parameter ratio, model quality and resolution, the H-atom parameters can be refined either individually or with a ‘pseudo-riding model’; for example, (i) keeping the X—­H configuration fixed but refining the ADPs and occupancies of H atoms or (ii) refining the positions as well as the ADPs but keeping the deviations from ‘ideal’ (library) values within a certain range. Similarly to water H atoms, some protein H atoms have a rotational degree of freedom around the bond, such as O—H in Ser, Tyr or Thr or methyl (CH3) rotors in Ile, for example. In this case, the position of the H atom can also be optimized based on the residual map. phenix.refine allows H atoms to be included in X-ray refinement at any resolution using the strategies described above, including automatic difference-map-based addition of H atoms to water and their map-based optimization for ambiguous positions.

2.3. H atoms in neutron refinement  

The contribution of D atoms to neutron scattering is of the same order of magnitude as the contribution of heavier atoms such as C, N or O. The contribution of H atoms is half that of the heavier atoms and has a negative magnitude. This makes it possible to refine the parameters of H or D atoms individually, similarly to the other heavier atoms at macromolecular resolutions, but there are challenges. Refining H or D atoms individually significantly decreases the data-to-parameter ratio. This is compounded by the often poor completeness of neutron data compared with X-ray data (the average data completeness for all neutron structures currently in the PDB is 76%, while the corresponding value for X-ray structures is 94%) and the typical upper resolution limit of neutron data sets is lower (Table 1 ▶). Partial deuteration of the macromolecule also presents challenges. In this case, the resulting cancellation effects can significantly limit the interpretability of the density map around bonds involving H atoms. The riding model for H atoms combined with torsion-angle parameterization and grouped ADP refinement strategies implemented in phenix.refine can be used to mitigate the effects of data completeness and density cancellation. Also, it is of great help that the starting model for neutron refinement is almost always a previously determined X-ray structure in which the positions of non-H atoms are usually well determined.

Table 1. Selected models from the PDB refined using neutron data only.

The table compares the reported R-factor statistics with those obtained after re-refinement using phenix.refine.

Information from PDB file header Information computed in phenix.refine Average values in PDB at this resolution
PDB or NDB code Resolution () cutoff R (work/free) (%) R (work/free) (%) H/D ratio Data completeness (%) No. of reflections/atoms R (work/free) (%) Data completeness (%) No. of structures
1c57 2.415.79 0 27.0/30.1 20.5/25.7 90/10 87 8604/3677 21.1/26.0 94.2 3935
2dxm 2.18.0 1 19.7/26.0 18.1/23.6 88/12 65 21242/9317 20.1/24.6 94.3 5696
2efa 2.780.0 3 21.6/29.1 20.2/27.0 85/15 93 2198/788 21.9/27.1 94.1 2552
2gve 2.210.0 3 27.1/31.9 24.5/30.4 0/100 80 19619/6185 20.4/25.1 94.3 4701
3ins 1.5n/a 0 18.2/ 18.3/26.7 87/13 44 2797/1585 18.3/21.4 93.8 2737
1l2k 1.522.7 0 20.1/23.8 17.9/23.7 89/11 89 19060/2717 18.3/21.4 93.8 2737
1v9g 1.825.05 3 22.2/29.4 22.7/26.2 72/28 72 1817/495 19.1/22.8 94.8 5858
1vcx 1.527.6 2 18.6/21.7 16.5/21.2 87/13 80 7285/870 18.3/21.4 93.8 2737
1wqz 3.030.0 1 25.2/27.4 19.5/22.6 82/18 56 774/634 23.1/28.0 94.0 1165
1wq2 2.420.0 1 22.9/28.9 22.9/28.2 82/18 85 6458/1977 21.1/26.0 94.2 3935
1xqn 2.532.82 2 26.6/32.0 24.2/29.5 88/12 74 6338/3761 21.3/26.4 94.1 3660
2yz4 2.233.64 0 27.9/31.2 22.3/28.2 87/13 66 8507/3663 20.4/25.1 94.3 4701
1cq2 2.06.0 0 16.0/25.0 17.9/25.9 0/100 95 8360/2846 19.8/24.1 94.5 6484
2vs2 2.020.0 0 21.9/28.1 20.5/26.9 90/10 85 15766/5041 19.8/24.1 94.5 6484
2qws 2.534.0 0 26.2/27.3 21.3/28.4 90/11 88 3172/2294 21.3/26.4 94.1 3660
UR0013 0.6510.48 0 9.5/ 7.97/9.81 100/0 50 5987/83      
Open in a new tab

The presence of exchangeable H/D sites when a partially deuterated sample is used must be accounted for in neutron structures. phenix.refine automatically determines such sites and includes them for constrained occupancy refinement, ensuring that the sum of the occupancies for each H and D pair is equal to one. Currently, phenix.refine maintains the H and D atoms at coinciding positions and constrains their ADPs to be equal to each other. Alternate parameterizations are being investigated that account for the difference in position for electron and nuclear density and different order parameters arising from the use of cryocooling.

Most of the H atoms in a macromolecular structure can be placed at stereochemically predictable positions. However, there are a few exceptions. For example, a Tyr residue has two and Ser and Thr residues have three possible orientations for the O—H/D bonds. Unlike nonsubatomic resolution X-ray data, neutron data permit the actual positions to be uniquely identified. However, because of cancellation effects the density at exchangeable sites can be significantly weakened or even completely cancelled if the ratio of H/D occupancies is approximately 2:1. Therefore, in refinement the density at the H/D sites may not be significant enough to maintain their position and other stereochemically allowable conformations may result. In such cases phenix.refine automatically performs optimization of the H/D position by rotating around the corresponding torsion-bond axes in order to find the best fit to the 2mF obs − DF model density map.

2.4. Joint X-ray and neutron (XN) refinement  

Currently, in joint XN refinement phenix.refine refines a single crystallographic structure against two data sets simultaneously: X-ray and neutron. The corresponding total refinement target is

2.4.

where w nxc is determined automatically (Adams et al., 1997 ▶), T xray and T neutron can be any of the crystallographic targets available in phenix.refine computed with X-ray and neutron data, respectively [least-squares, maximum-likelihood, phased maximum-likelihood (mlhl) or twinned least-squares] and w xc_scale and w nc_scale are additional scales (set to 1 by default) that allow the user to adjust the automatically determined weights. By default w c is set to 1, but setting it to zero turns off the geometry restraints, allowing unrestrained refinement. The formula (1) is similar for both restrained coordinate and ADP refinement. Either or both reflection data sets can be treated for twinning in refinement using a twinned least-squares target. The parameters of the H and D atoms are refined in the same way as the other heavier atoms in the structure.

3. Results  

3.1. Refinement of structures against X-ray data alone  

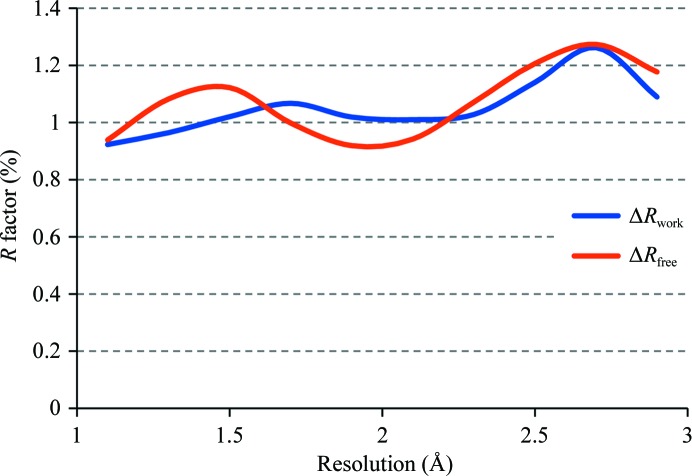
To determine the impact of using H atoms in refinement at lower resolution limits using the riding model, we selected 5752 structures from the PDB that cover the range of high-resolution limits from 1 to 3 Å, have structure factors and corresponding free R flags available and for which it is possible to reproduce the deposited crystallographic R factors to within 1%. We then re-refined these models in phenix.refine with and without the use of riding H atoms. Each refinement run consisted of ten refinement macrocycles (to allow for full convergence) of individual coordinates, constrained occupancies for alternative conformations and isotropic or anisotropic displacement parameters. To measure the impact of using H atoms in refinement, for each structure refined with and without H atoms we computed the differences in R factors, ΔR = R(no H) − R(H), for work and free reflections and averaged them in equally spaced resolution bins with a width of 0.2 Å. Fig. 5 ▶ shows the differences ΔR work and ΔR free as a function of resolution. As anticipated, the differences increase with resolution, i.e. the lower the resolution the larger the difference, as the H atoms are weak scatterers. This results in a proportionally larger contribution for lower resolution reflections. The results suggest that on average one can expect an approximately 1% improvement in both R factors, work and free, by the addition of H atoms to the model. Also, we observed a number of cases in which this gain was significantly above 1%, with a maximum of approximately 5%. Those are most likely to be cases where the H atoms not only contributed to the scattering but also significantly improved the model through changes in local geometry.

Figure 5.

Figure 5

Open in a new tab

Averaged ΔR work and ΔR free as a function of resolution computed for structures refined with and without H atoms added. See text for details.

3.2. Refinement of structures against neutron data alone  

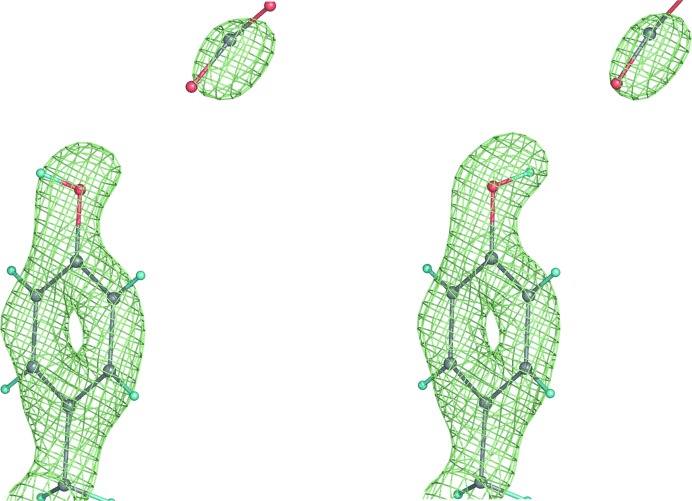
To assess the impact of the tools specifically implemented for neutron refinement in phenix.refine, we reanalyzed 16 structures previously refined using neutron data (15 structures from the PDB and one from the NDB; Berman et al., 1992 ▶). We automatically rebuilt the H/D atoms (single and exchangeable sites) and re-refined these models in phenix.refine. Table 1 ▶ shows the optimal refinement results that were achieved using the refinement options described above. The deuteration exchange rates are given for the best final refined structures. For some models the data-to-parameter ratio only allowed grouped parameter refinement, while individual parameters were refined for other models that possessed more experimental data. One structure was refined at an outstandingly high resolution of 0.65 Å (NDB code UR0013), where completely unrestrained refinement was possible and individual anisotropic atomic displacement parameters were refined for all atoms, including H atoms. In this case the R factor dropped by ∼1.5%. Fig. 6 ▶ shows a fragment of this structure in the exceptionally high-quality 2mF obs − DF model map. Some starting structures showed under-refinement, for example 2qws or 2yz4, which was indicated by a small gap between the R work and R free factors compared with the average value found for refined structures in the PDB at similar resolution. For some starting structures the reported R factors were somewhat higher than would be expected at their experimental data resolution (for example, 1c57, 2dxm, 1v9g and 1xqn). Re-refinement in phenix.refine brought the R factors for all these structures much closer to the expected values. In a number of cases phenix.refine was used to automatically perform a real-space search around rotatable bonds in order to determine the optimal D or H/D fit to the density. Fig. 7 ▶ illustrates the result of running phenix.refine with and without such corrections, where the originally incorrect orientation (Fig. 7 ▶ a) is automatically corrected during refinement (Fig. 7 ▶ b). Typically, only a small number of such corrections occur and thus they are unlikely to affect the overall R factor, but local changes in model/map quality are seen upon visual inspection.

Figure 6.

Figure 6

Open in a new tab

2mF obs − DF model nuclear map for the NAD structure (UR0013) contoured at ±2.4σ; lime is positive and red is negative.

Figure 7.

Figure 7

Open in a new tab

2mF obs − DF model nuclear map: orientation of an O—H/D bond before (wrong, left) and after (correct, right) automatic real-space correction performed during refinement in phenix.refine.

3.3. Refinement of structures against both X-ray and neutron data  

To assess the impact of joint XN refinement, we selected a number of structures from the PDB for which both data sets are available (Table 2 ▶). Unfortunately, free-R flags are not available for most of these data sets. For the data sets with free-R flags there are always mismatching flags between data sets (reflections that are marked as ‘free’ in one data set and as ‘work’ in another data set; Adams et al., 2009 ▶). The exception is PDB entry 2r24, for which joint XN refinement was performed originally and a consistent free-R set was used across both data sets (Blakeley, Ruiz et al., 2008 ▶). Since the R free factor is a primary metric for assessing the results of subsequent refinements, we created new free-R sets for all structures using phenix.refine and used the following protocol to minimize bias to these newly created ‘free’ reflections. To do so, we removed all water molecules, added a random Gaussian 1.5 Å shift to the co­ordinates, reset the atomic displacement parameters to a uniform value of 15 Å2 and re-built the H and/or D atoms for all starting models. We then performed ten macrocycles of refinement in phenix.refine using three protocols: refinement against X-ray data alone, refinement against neutron data alone and refinement in which both data sets were used simultaneously. In all cases ten macrocycles were sufficient to reach a level of convergence where the R factors no longer changed between macrocycles. Each macrocycle consisted of automatic water building, refinement of individual coordinates and isotropic or anisotropic atomic displacement parameters and constrained refinement of occupancies for atoms in alternative conformations or exchangeable H/D sites. Table 3 ▶ shows the original R factors extracted from PDB file headers and the R factors obtained in each of the three refinement protocols. The main results can be summarized as follows.

  • (i) Joint XN refinement significantly improved the neutron R work and R free (by 2–4 percentage points in several cases) compared with both the published values and those obtained using refinement against neutron data alone. The corresponding maps are of higher quality.

  • (ii) Refinement against neutron data alone can result in overfitting since the H-atom parameters are refined explicitly. Sometimes the R free − R work gap can be as large as 10 percentage points. Refinement against both data sets simultaneously significantly reduces this effect. A tightening of the geometric and displacement restraints can also be helpful (data not shown).

  • (iii) As expected, the improvement of X-ray R factors as a result of using H atoms is smaller in magnitude and is approximately 1–2%. The larger improvement in R factors seen for some of the structures is typically the result of an improved refinement strategy or model parameterization (for example, using anisotropic instead of isotropic ADPs).

Table 2. Statistics for structures for which X-ray and neutron data are available.

PDB code Refinement resolution () Data completeness (%) cutoff No. of reflections  
X N X N X N X N X N No. of atoms
1iu5 1iu6 10.01.5 10.01.6 95 85 3 3 8456 6308 839
1woe 1v9g 10.01.5 20.051.8 96 73 1 3 4054 1820 465
5pti 5pti 7.131.0 7.121.8 63 62     17615 3950 955
5rsa 5rsa 9.92.0 9.91.7 96 31 3 3 7708 4132 1980
2r24 2r24 1.7533.56 2.1940.11 99 73 0 0 31524 11884 5434
Open in a new tab

Table 3. Results of joint XN and individual refinement.

      phenix.refine R work/R free
PDB code Published R work/R free Joint X + N    
X N X N X N X-ray only Neutron only
1iu5 1iu6 18.7/20.3 19.4/25.4 12.3/17.4 15.2/22.6 17.1/26.5 13.3/21.7
1woe 1v9g 17.6/20.6 22.2/29.4 14.6/18.3 25.4/26.6 14.8/19.3 21.3/31.9
5pti 5pti 20.0/ 19.7/ 16.9/19.5 20.8/24.7 17.3/20.4 17.9/27.5
5rsa 5rsa 15.9/ 18.3/ 11.9/18.7 16.7/23.0 15.4/21.7 13.0/26.5
2r24 2r24 12.7/16.6 25.7/29.1 12.4/16.8 22.7/29.7 13.3/18.0 18.0/32.7
Open in a new tab

4. Discussion  

X-ray crystallography is the leading method for the determination of three-dimensional structures of macromolecules. If the goal of a structural study includes the direct experimental analysis of hydrogen positions, X-ray crystallography is limited by the weak signal of the H atoms. To date, only ultrahigh-resolution X-ray crystal structures have the potential to reveal H-atom positions. However, macromolecular crystals rarely yield ultrahigh-resolution diffraction data (less than 1% of all PDB structures are determined at resolutions of better than 1 Å). Moreover, the availability of such high resolution is not a guarantee for detecting all H atoms. This makes the study of H atoms by X-ray crystallography unreliable. In contrast, neutron crystallography is able to routinely reveal H-atom positions from macromolecular diffraction data.

PHENIX provides a comprehensive set of tools for refinement at resolutions from subatomic to low. Recent developments include refinement using neutron data and refinement using both X-ray and neutron data simultaneously. All standard tools available for refinement using X-ray data are also available for refinement using neutron data. Various strategies for the refinement of H atoms are implemented, enabling the use of H or D atoms at any resolution. Here, we have demonstrated that these tools for refinement against neutron data can significantly improve structures, especially when multiple types of experimental data are considered simultaneously.

Although significant progress has been made, there are still many challenges to address, such as accounting for the differences between X-ray and neutron structures, automated water placement in the presence of two data sets, automatic classification of different water shapes based on nuclear maps, integration of local real-space refinement using nuclear maps to minimize the use of manual interactive graphics, finding efficient ways of representing the results of joint X-ray and neutron refinement and joint refinement against data from non-isomorphous crystals. Finally, re-refinement of existing neutron structures demonstrates that modern algorithms can significantly improve their quality. Therefore, there is now an opportunity for these structures to be carefully re-refined and updated in the structural databases.

The PHENIX software is available from http://www.phenix-online.org. Implementing tools for neutron crystallography in the PHENIX framework is an ongoing collaboration between groups at Lawrence Berkeley National Laboratory and Los Alamos National Laboratory as part of the Macromolecular Neutron Consortium (MNC; http://mnc.lanl.gov/).

Acknowledgments

We gratefully acknowledge the financial support of NIH/NIGMS through grants 5P01GM063210 and 1R01GM071939. Our work was supported in part by the US Department of Energy under Contracts No. DE-AC03-76SF00098 and DE-AC02-05CH11231. All figures representing structures were prepared using PyMOL (http://www.pymol.org).

Footnotes

1

A number of publications define ultrahigh or subatomic resolution in the range 1.0–0.5 Å (Lecomte et al., 2008 ▶; Petrova et al., 2006 ▶; Howard et al., 2004 ▶; Guillot et al., 2008 ▶; Housset et al., 2000 ▶). An attempt to create a less arbitrary definition is described in Urzhumtsev et al. (2009 ▶).

References

  1. Adams, P. D. et al. (2010). Acta Cryst. D66, 213–221.
  2. Adams, P. D., Mustyakimov, M., Afonine, P. V. & Langan, P. (2009). Acta Cryst. D65, 567–573. [DOI] [PMC free article] [PubMed]
  3. Adams, P. D., Pannu, N. S., Read, R. J. & Brünger, A. T. (1997). Proc. Natl Acad. Sci. USA, 94, 5018–5023. [DOI] [PMC free article] [PubMed]
  4. Afonine, P. V., Grosse-Kunstleve, R. W. & Adams, P. D. (2005a). Acta Cryst. D61, 850–855. [DOI] [PMC free article] [PubMed]
  5. Afonine, P. V., Grosse-Kunstleve, R. W. & Adams, P. D. (2005b). CCP4 Newsl. 42, contribution 8.
  6. Afonine, P. V., Grosse-Kunstleve, R. W., Adams, P. D., Lunin, V. Y. & Urzhumtsev, A. (2007). Acta Cryst. D63, 1194–1197. [DOI] [PMC free article] [PubMed]
  7. Afonine, P. V., Grosse-Kunstleve, R. W., Urzhumtsev, A. & Adams, P. D. (2009). J. Appl. Cryst. 42, 607–615. [DOI] [PMC free article] [PubMed]
  8. Afonine, P. V., Lunin, V. Y., Muzet, N. & Urzhumtsev, A. (2004). Acta Cryst. D60, 260–274. [DOI] [PubMed]
  9. Ahmed, H. U., Blakeley, M. P., Cianci, M., Cruickshank, D. W. J., Hubbard, J. A. & Helliwell, J. R. (2007). Acta Cryst. D63, 906–922. [DOI] [PubMed]
  10. Bennett, B., Langan, P., Coates, L., Mustyakimov, M., Schoenborn, B., Howell, E. E. & Dealwis, C. (2006). Proc. Natl Acad. Sci. USA, 103, 18493–18498. [DOI] [PMC free article] [PubMed]
  11. Berman, H. M., Olson, W. K., Beveridge, D. L., Westbrook, J., Gelbin, A., Demeny, T., Hsieh, S.-H., Srinivasan, A. R. & Schneider, B. (1992). Biophys. J. 63, 751–759. [DOI] [PMC free article] [PubMed]
  12. Berman, H. M., Westbrook, J., Feng, Z., Gilliland, G., Bhat, T. N., Weissig, H., Shindyalov, I. N. & Bourne, P. E. (2000). Nucleic Acids Res. 28, 235–242. [DOI] [PMC free article] [PubMed]
  13. Bernstein, F. C., Koetzle, T. F., Williams, G. J., Meyer, E. F. Jr, Brice, M. D., Rodgers, J. R., Kennard, O., Shimanouchi, T. & Tasumi, M. (1977). J. Mol. Biol. 112, 535–542. [DOI] [PubMed]
  14. Blakeley, M. P., Langan, P., Niimura, N. & Podjarny, A. (2008). Curr. Opin. Struct. Biol. 18, 593–600. [DOI] [PMC free article] [PubMed]
  15. Blakeley, M. P., Ruiz, F., Cachau, R., Hazemann, I., Meilleur, F., Mitschler, A., Ginell, S., Afonine, P., Ventura, O. N., Cousido-Siah, A., Haertlein, M., Joachimiak, A., Myles, D. & Podjarny, A. (2008). Proc. Natl Acad. Sci. USA, 105, 1844–1848. [DOI] [PMC free article] [PubMed]
  16. Blum, M.-M., Mustyakimov, M., Rüterjans, H., Schoenborn, B., Langan, P. & Chen, J. C.-H. (2009). Proc. Natl Acad. Sci. USA, 106, 713–718. [DOI] [PMC free article] [PubMed]
  17. Blum, M.-M., Tomanicek, S. J., John, H., Hanson, B. L., Rüterjans, H., Schoenborn, B. P., Langan, P. & Chen, J. C.-H. (2010). Acta Cryst. F66, 379–385. [DOI] [PMC free article] [PubMed]
  18. Bon, C., Lehmann, M. S. & Wilkinson, C. (1999). Acta Cryst. D55, 978–987. [DOI] [PubMed]
  19. Brünger, A. T., Adams, P. D., Clore, G. M., DeLano, W. L., Gros, P., Grosse-Kunstleve, R. W., Jiang, J.-S., Kuszewski, J., Nilges, M., Pannu, N. S., Read, R. J., Rice, L. M., Simonson, T. & Warren, G. L. (1998). Acta Cryst. D54, 905–921. [DOI] [PubMed]
  20. Chatake, T., Higuchi, Y., Mizuno, N., Tanaka, I., Niimura, N. & Morimoto, Y. (2008). J. Synchrotron Rad. 15, 277–280. [DOI] [PMC free article] [PubMed]
  21. Chatake, T., Kurihara, K., Tanaka, I., Tsyba, I., Bau, R., Jenney, F. E., Adams, M. W. W. & Niimura, N. (2004). Acta Cryst. D60, 1364–1373. [DOI] [PubMed]
  22. Chatake, T., Ostermann, A., Kurihara, K., Parak, F. G. & Niimura, N. (2003). Proteins, 50, 516–523. [DOI] [PubMed]
  23. Chatake, T., Tanaka, I., Umino, H., Arai, S. & Niimura, N. (2005). Acta Cryst. D61, 1088–1098. [DOI] [PubMed]
  24. Coates, L., Tuan, H.-F., Tomanicek, S., Kovalevsky, A., Mustyakimov, M., Erskine, P. & Cooper, J. (2008). J. Am. Chem. Soc. 130, 7235–7237. [DOI] [PMC free article] [PubMed]
  25. Coppens, P., Boehme, R., Price, P. F. & Stevens, E. D. (1981). Acta Cryst. A37, 857–863.
  26. Davis, I. W., Leaver-Fay, A., Chen, V. B., Block, J. N., Kapral, G. J., Wang, X., Murray, L. W., Arendall, W. B. III, Snoeyink, J., Richardson, J. S. & Richardson, D. C. (2007). Nucleic Acids Res. 35, W375–W383. [DOI] [PMC free article] [PubMed]
  27. Engler, N., Ostermann, A., Niimura, N. & Parak, F. G. (2003). Proc. Natl Acad. Sci. USA, 100, 10243–10248. [DOI] [PMC free article] [PubMed]
  28. Fenimore, P. W., Frauenfelder, H., McMahon, B. H. & Young, R. D. (2004). Proc. Natl Acad. Sci. USA, 101, 14408–14413. [DOI] [PMC free article] [PubMed]
  29. Finney, J. L. (1995). Acta Cryst. B51, 447–467.
  30. Fisher, S. Z., Anderson, S., Henning, R., Moffat, K., Langan, P., Thiyagarajan, P. & Schultz, A. J. (2007). Acta Cryst. D63, 1178–1184. [DOI] [PMC free article] [PubMed]
  31. Fisher, S. Z., Kovalevsky, A., Mustyakimov, M., McKenna, R., Silverman, D. & Langan, P. (2010). Biochemistry, 49, 415–421. [DOI] [PMC free article] [PubMed]
  32. Grosse-Kunstleve, R. W., Moriarty, N. W. & Adams, P. D. (2009). Proceedings of ASME 2009 International Design Engineering Technical Conferences. Paper DETC2009-87737. New York: ASME Press.
  33. Guillot, B., Jelsch, C., Podjarny, A. & Lecomte, C. (2008). Acta Cryst. D64, 567–588. [DOI] [PubMed]
  34. Gutberlet, T., Heinemann, U. & Steiner, M. (2001). Acta Cryst. D57, 349–354. [DOI] [PubMed]
  35. Habash, J., Raftery, J., Nuttall, R., Price, H. J., Wilkinson, C., Kalb (Gilboa), A. J. & Helliwell, J. R. (2000). Acta Cryst. D56, 541–550. [DOI] [PubMed]
  36. Hanson, B. L. (2004). Proc. Natl Acad. Sci. USA, 101, 16393–16394. [DOI] [PMC free article] [PubMed]
  37. Hazemann, I., Dauvergne, M. T., Blakeley, M. P., Meilleur, F., Haertlein, M., Van Dorsselaer, A., Mitschler, A., Myles, D. A. A. & Podjarny, A. (2005). Acta Cryst. D61, 1413–1417. [DOI] [PubMed]
  38. Housset, D., Benabicha, F., Pichon-Pesme, V., Jelsch, C., Maierhofer, A., David, S., Fontecilla-Camps, J. C. & Lecomte, C. (2000). Acta Cryst. D56, 151–160. [DOI] [PubMed]
  39. Howard, E. I., Sanishvili, R., Cachau, R. E., Mitschler, A., Chevrier, B., Barth, P., Lamour, V., Van Zandt, M., Sibley, E., Bon, C., Moras, D., Schneider, T. R., Joachimiak, A. & Podjarny, A. (2004). Proteins, 55, 792–804. [DOI] [PubMed]
  40. Kang, B. S., Devedjiev, Y., Derewenda, U. & Derewenda, Z. S. (2004). J. Mol. Biol. 338, 483–493. [DOI] [PubMed]
  41. Katz, A. K., Xinmin, L., Carrell, H. L., Hanson, B. L., Langan, P., Coates, L., Schoenborn, B. P., Glusker, J. P. & Bunick, G. J. (2006). Proc. Natl Acad. Sci. USA, 103, 8342–8347. [DOI] [PMC free article] [PubMed]
  42. Korszun, Z. R. (1997). Methods Enzymol. 276, 218–232. [DOI] [PubMed]
  43. Kossiakoff, A. A. (1985). Annu. Rev. Biochem. 54, 1195–1227. [DOI] [PubMed]
  44. Kossiakoff, A. A. (1986). Methods Enzymol. 131, 433–447. [DOI] [PubMed]
  45. Kossiakoff, A. A. & Spencer, S. A. (1981). Biochemistry, 20, 6462–6474. [DOI] [PubMed]
  46. Kovalevsky, A., Chatake, T., Ishiwawa, T., Shibayama, N., Park, S.-Y., Mustyakimov, M., Fisher, S. Z., Langan, P. & Morimoto, Y. (2010). J. Mol. Biol. 398, 276–291. [DOI] [PubMed]
  47. Kovalevsky, A. Y., Katz, A. K., Carrell, H. L., Hanson, L., Mustyakimov, M., Fisher, S. Z., Coates, L., Schoenborn, B. P., Bunick, G. J., Glusker, J. P. & Langan, P. (2008). Biochemistry, 47, 7595–7597. [DOI] [PMC free article] [PubMed]
  48. Kurihara, K., Tanaka, I., Chatake, T., Adams, M. W. W., Jenney, F. E. Jr, Moiseeva, N., Bau, R. & Niimura, N. (2004). Proc. Natl Acad. Sci. USA, 101, 11215–11220. [DOI] [PMC free article] [PubMed]
  49. Langan, P., Lehmann, M., Wilkinson, C., Jogl, G. & Kratky, C. (1999). Acta Cryst. D55, 51–59. [DOI] [PubMed]
  50. Lecomte, C., Jelsch, C., Guillot, B., Fournier, B. & Lagoutte, A. (2008). J. Synchrotron Rad. 15, 202–203. [DOI] [PMC free article] [PubMed]
  51. McDowell, R. S. & Kossiakoff, A. A. (1995). J. Mol. Biol. 250, 553–570. [DOI] [PubMed]
  52. Moriarty, N. W., Grosse-Kunstleve, R. W. & Adams, P. D. (2009). Acta Cryst. D65, 1074–1080. [DOI] [PMC free article] [PubMed]
  53. Niimura, N. (1999). Curr. Opin. Struct. Biol. 9, 602–608. [DOI] [PubMed]
  54. Niimura, N., Arai, S., Kurihara, K., Chatake, T., Tanaka, I. & Bau, R. (2006). Cell. Mol. Life Sci. 63, 285–300. [DOI] [PMC free article] [PubMed]
  55. Niimura, N., Chatake, T., Kurihara, K. & Maeda, M. (2004). Cell Biochem. Biophys. 40, 351–370. [DOI] [PubMed]
  56. Ostermann, A., Tanaka, I., Engler, N., Niimura, N. & Parak, F. G. (2002). Biophys. Chem. 95, 183–193. [DOI] [PubMed]
  57. Petrova, T., Ginell, S., Mitschler, A., Hazemann, I., Schneider, T., Cousido, A., Lunin, V. Y., Joachimiak, A. & Podjarny, A. (2006). Acta Cryst. D62, 1535–1544. [DOI] [PubMed]
  58. Petrova, T. & Podjarny, A. (2004). Rep. Prog. Phys. 67, 1565–1605.
  59. Read, R. J. (1986). Acta Cryst. A42, 140–149.
  60. Sheldrick, G. M. & Schneider, T. R. (1997). Methods Enzymol. 277, 319–343. [PubMed]
  61. Shu, F., Ramakrishnan, V. & Schoenborn, B. P. (2000). Proc. Natl Acad. Sci. USA, 97, 3872–3877. [DOI] [PMC free article] [PubMed]
  62. Sukumar, N., Mathews, F. S., Langan, P. & Davidson, V. L. (2010). Proc. Natl Acad. Sci. USA, 107, 6817–6822. [DOI] [PMC free article] [PubMed]
  63. Urzhumtsev, A., Afonine, P. V. & Adams, P. D. (2009). Acta Cryst. D65, 1283–1291. [DOI] [PMC free article] [PubMed]
  64. Urzhumtsev, A. G., Skovoroda, T. P. & Lunin, V. Y. (1996). J. Appl. Cryst. 29, 741–744.
  65. Wlodawer, A. & Hendrickson, W. A. (1982). Acta Cryst. A38, 239–247.
  66. Wlodawer, A., Savage, H. & Dodson, G. (1989). Acta Cryst. B45, 99–107. [DOI] [PubMed]
  67. Wlodawer, A. & Sjölin, L. (1982). Proc. Natl Acad. Sci. USA, 79, 1418–1422. [DOI] [PMC free article] [PubMed]
  68. Word, J. M., Lovell, S. C., Richardson, J. S. & Richardson, D. C. (1999). J. Mol. Biol. 285, 1735–1747. [DOI] [PubMed]

Articles from Acta Crystallographica Section D: Biological Crystallography are provided here courtesy of International Union of Crystallography

RESOURCES