Enduring Medial Perforant Path Short-Term Synaptic Depression at High Pressure

Abstract

The high pressure neurological syndrome develops during deep-diving (>1.1 MPa) involving impairment of cognitive functions, alteration of synaptic transmission and increased excitability in cortico-hippocampal areas. The medial perforant path (MPP), connecting entorhinal cortex with the hippocampal formation, displays synaptic frequency-dependent-depression (FDD) under normal conditions. Synaptic FDD is essential for specific functions of various neuronal networks. We used rat cortico-hippocampal slices and computer simulations for studying the effects of pressure and its interaction with extracellular Ca²⁺ ([Ca²⁺]_o) on FDD at the MPP synapses. At atmospheric pressure, high [Ca²⁺]_o (4–6 mM) saturated single MPP field EPSP (fEPSP) and increased FDD in response to short trains at 50 Hz. High pressure (HP; 10.1 MPa) depressed single fEPSPs by 50%. Increasing [Ca²⁺]_o to 4 mM at HP saturated synaptic response at a subnormal level (only 20% recovery of single fEPSPs), but generated a FDD similar to atmospheric pressure. Mathematical model analysis of the fractions of synaptic resources used by each fEPSP during trains (normalized to their maximum) and the total fraction utilized within a train indicate that HP depresses synaptic activity also by reducing synaptic resources. This data suggest that MPP synapses may be modulated, in addition to depression of single events, by reduction of synaptic resources and then may have the ability to conserve their dynamic properties under different conditions.

Introduction

The high pressure neurological syndrome (HPNS), experienced by deep-divers and animals at pressures above 1.1 MPa (reviewed Bennett and Rostain, 2003; Talpalar, 2007), displays signs of cortico-hippocampal involvement, including impairment of episodic and spatial memory (Logue et al., 1986; Vaernes et al., 1989), and cognitive malfunction (Vaernes et al., 1985, 1988; Abraini et al., 1993; Abraini, 1997). Synaptic changes, including depression of Ca²⁺-entry into presynaptic terminals (reviewed Daniels and Grossman, 2003; Talpalar, 2007) and disruption of synaptic depression at short intervals (Talpalar and Grossman, 2003), distorts the low-pass filter properties of the dentate gyrus (DG) resulting in hyperexcitability (Talpalar and Grossman, 2004). The medial perforant path (MPP), originating at the entorhinal cortex and synapsing on granule cells of the DG, exhibits marked frequency-dependent-depression (FDD; Beck et al., 2000; Kilbride et al., 2001; Talpalar and Grossman, 2003). Neuronal networks use FDD (Liley and North, 1953; Elmqvist and Quastel, 1965; Zucker and Regehr, 2002) for low-pass filtering (Fortune and Rose, 2001; Fuhrmann et al., 2002; Stevens, 2003a), coding based on firing rate and spike-timing (Tsodyks and Markram, 1997), sorting information (Cook et al., 2003), avoiding habituation (Best and Wilson, 2004), dynamic gain-control of synaptic signaling (Abbott et al., 1997), for direction selectivity and contrast adaptation (Chance et al., 1998), and for sound localization (Stevens, 2003b; Cook et al., 2003). Excitatory synapses in the CNS display FDD because of limited synaptic resources (SR) including a relatively small readily releasable-pool (Schikorski and Stevens, 1997, 2001; Aravanis et al., 2003) and fast desensitization of non-NMDA receptors (Tsodyks and Markram, 1997). Then, FDD occurs when fast synaptic activity exceeds the recovery rate of SR (Bailey and Chen, 1988; Wang and Kaczmarek, 1998; Stevens and Wesseling, 1999). High extracellular calcium ([Ca²⁺]_o) increases both single EPSP responses and FDD (Dittman and Regehr, 1998) and the opposite happens at low [Ca²⁺]_o (Talpalar and Grossman, 2003). High pressure (HP) of 10.1 MPa decreases single fEPSP by about 50% (Fagni et al., 1987; Talpalar and Grossman, 2003; Etzion et al., 2009), but the effect on SR dynamics is still unclear. Quantal analysis of crustacean neuromuscular synapses revealed reduction of quantal content and number of available release sites and spared quantal size and release probability at HP (Golan et al., 1994, 1995). HP-induced reduction of synaptic inputs was relieved by increasing [Ca²⁺]_o, and mimicked by lowering [Ca²⁺]_o in both, brain and crustacean preparations. HP and low [Ca²⁺]_o increased facilitation/potentiation in crustacean neuromuscular (Grossman and Kendig, 1990; Golan and Grossman, 1992) and cerebellar parallel fiber (Etzion and Grossman, 2000) “unsaturated” synapses. But “saturated” synapses exhibited either pressure-independent paired-pulse-depression (PPD) at cerebellar climbing fibers (Etzion et al., 2009) or diminished MPP's PPD (Talpalar and Grossman, 2003). Curiously, while lowering [Ca²⁺]_o switched MPP's FDD into frequency-dependent-potentiation, HP preserved FDD (Talpalar and Grossman, 2003). This dichotomy led us to hypothesize that HP has special effects on the dynamics of SR. We used electrophysiology and quantitative mathematical modeling for studying the dynamics of the MPP synapse under different [Ca²⁺]_o and pressure conditions in an attempt to understand HPNS and adaptation to HP.

Materials and Methods

Brain slice preparation

Sprague-Dawley rats of both sexes (150–250 g) were anesthetized with pentobarbital (60 mg/kg) and then decapitated according to regulation of the Animal Care Committee of Ben-Gurion University. The brain was extracted in less than 1 min and immersed in cold Ringer's solution (4–6°C). As previously described (Talpalar and Grossman, 2003), brain slices (400 μm) containing cortico-hippocampal areas were cut in a horizontal vibratome (Campden Instruments) and conserved in an incubation container at 25°C for later utilization. Control Ringer's solution contained (in mM): NaCl 124, KCl 3, CaCl₂ 2, MgSO₄ 2, NaH₂PO₄ 1.25, NaHCO₃ 26, and d-Glucose 10. This solution was continuously bubbled with 95% O₂ and 5% CO₂ for a pH of 7.4.

Pressure and compression

fEPSPs experiments at HP were carried out in a pressure chamber (Canty Inc., USA). The compression/decompression procedures have been previously described (Talpalar and Grossman, 2003, 2004). Briefly, HP up to 10.1 MPa was attained by compressing inert helium gas at rates between 0.15 and 0.2 MPa/min. Electrophysiological samples were taken at control (0.1–0.4 MPa), 5.1 and 10.1 MPa. Ringer's solution was saturated at normal pressure with 95% O₂–5% CO₂ and was injected into the experimental bath by a fast high pressure pump (LDC analytical minipump, USA). Trials were collected under strict conditions of temperature (30°C) and at least after 15–20 min of stable recording. Complete recovery was attained during decompression from 10.1 to 5.1 MPa. Partial degree of recovery was observed in decompression from 5.1 to 0.4 MPa. Very slow decompression below 0.4 MPa was successful in ∼50% of the experiments.

Electrophysiological recordings

HP conditions do not allow the use of whole-cell recordings because of impossibility of manipulating pressures at the electrode level for opening of a seal for whole-cell configuration. Therefore, we used in the present study extracellular fEPSPs of the MPP, whose synaptic dynamics resembled those of synaptic currents (EPSCs) recorded during whole-cell configuration (Rush et al., 2002; Talpalar, 2002). Recordings of MPP fEPSPs at the inner dendritic region of the DG, their parameters, and interpretation have been previously described in detail (Talpalar and Grossman, 2003, 2004). In summary, fEPSP's amplitude indicating inward synaptic currents, and fEPSP's slope expressing the rate of activation of the glutamatergic non-NMDA receptors, were used for assessing synaptic activity. Though fEPSP's amplitude can be used for calculation of synaptic dynamics provided they do not elicit population spikes, contamination with voltage-dependent conductances, including the NMDA receptor fraction, may impair the estimation of synaptic strength. To avoid these interferences, we exclusively used fEPSPs’ slopes for the calculations. Trains of five stimuli at 50 Hz, delivered once per minute, were used to evaluate the frequency response. Parameters of each response in these trains (E_2–5) were usually normalized with respect to the first fEPSP (E₁). Paired-pulse-depression (PPD) and paired-pulse-facilitation (PPF) are used for referring respectively to the relative depression or enhancement of E₂ in relation with E₁. The “generic” expression paired-pulse-modulation (PPM; positive or negative) was used for both depression and facilitation. Frequency-dependent-potentiation (FDP), frequency-dependent-depression (FDD) and the generic term frequency-dependent-modulation (FDM) (positive or negative) are used for referring to such forms of dynamic synaptic modulation.

Statistical analysis of electrophysiological experiments

The results are expressed as mean ± SE. The n is the number of slices; each comes from a different animal successfully used in each experiment. Paired Student's t-test was used for parameters taken under control and experimental conditions in the same slice. Other statistical tests (independent t-test, ANOVA, etc.) were used for comparing parameters (slope, amplitude, time constant, etc.) under various conditions. Degree of significance was indicated by the values of p (the results were considered statistically different for p < 0.05).

Mathematical modeling

We considered a standard phenomenological model for the interpretation of our experimental results. This model was originally introduced by Tsodyks and Markram (1997) to account for use-dependent monosynaptic transmission in the cortex, and it was employed here to describe the dependence of field-responses on the frequency of repeated MPP extracellular stimulation as in Abbott et al. (1997). Because MPP synapses onto granule cells occur in their proximal dendritic area and because granule cells have no recurrent collaterals in healthy hippocampi, the validity of the model in the interpretation of population responses such as the fEPSPs has been assumed, invoking linearity and superposition of the elicited individual synaptic responses.

The model captures the frequency-dependent modulation of fEPSPs upon repetitive stimulation, by two variables: (i) the readily available synaptic resources r, and (ii) their fraction u, recruited at each stimulus for neurotransmission. It is then assumed that recruited resources r × u become instantaneously inactive, so that only the remaining amount r × (1 − u) is available for further neurotransmission. In the lack of synaptic activation, the unavailable resources slowly recover so that the value r increases back to its resting level R, exponentially with a time constant D. R represents therefore the upper limit to the amount of resources available for neurotransmission.

In order to capture possible short-term facilitation effects, u is not fixed but increases by U(1 − u) at each synaptic activation. Similarly to r, when no stimulation occurs u slowly decreases back to its resting level U, exponentially with a time constant F.

Then, the model predicts that each slope S₁, S₂, S₃,…S_N of fEPSPs, elicited by a train of N stimuli occurring at times t₁, t₂, t₃,…t_N, depends only on the time since last activation and on the running values of r and u, in the form S_i = A r_iu_i, where r_i+1 = R + [(1 − u_i) × r_i − R] × exp[−(t_i+1 − t_i)/D], u_i+1= U + [(1 − U) × u_i] × exp[−(t_i+1 − t_i)/F] (Tsodyks and Markram, 1997), and A representing an amplitude-scaling factor. Such a phenomenological approach is particularly appropriate when interpreting averaged or population responses, as opposed to quantal analysis (but see Loebel et al., 2009). On a first approximation, the following correspondences can be established (Markram et al., 1998; Fuhrmann et al., 2002): U relates to the probability of release, while A is equivalent to the product of the quantal size, the number of release sites (“quantal content” i.e., the mean number of released quanta), the maximal number of synapses recruited by extracellular MPP stimulation, and an extracellular attenuation factor.

In addition, because of linearity of the iterative equations reported above, a change in R cannot be distinguished from a change in A. For such a reason R was set to 1 in the equation, and A was interpreted as both pre- and postsynaptic effective parameter.

To some extent, the same model may also describe the desensitization of the postsynaptic receptors upon repeated activation (Destexhe et al., 1994).

Best-fit values and statistics of model parameters

Optimal fitting of the model parameters was carried out through minimization of the root mean square error X² among measured fEPSP slopes E₁, E₂, E₃,…E_N and the corresponding model responses S₁, S₂, S₃,…S_N. The quality of each fit was expressed as a percentage error, normalized to the maximal fEPSP in the train. In experiments with varying [Ca²⁺]_o, HP or both, simultaneous fit of two or three sets of responses were performed.

For each experiment, the Levenberg–Marquardt least-square algorithm (Press et al., 1992) was used to fit the model response to the data, adjusting A, U, D, and F to obtain the best-fit. The X²- goodness of fit (Press et al., 1992) was used as a standard test of the quality of the model in capturing the experimental observations, with a required level of significance above 99%.

Results

High [Ca²⁺]_o saturates MPP synaptic responses at normal and high pressure

We previously reported that single MPP fEPSPs were depressed by ∼25% and ∼55% at 5.1 and 10.1-MPa pressure (Talpalar and Grossman, 2003). These experimental pressures are relevant because of two reasons: (a) deep-diving cetaceans reach such ambient pressures during foraging (Talpalar and Grossman, 2005, 2006); (b) they better model HP effects in humans since rodents have higher threshold for pressure-induced seizures than primates (Brauer et al., 1979).

Synaptic release is dependent on cytosolic Ca²⁺ levels at the terminals. Consequently, a larger Ca²⁺ driving force (V_Ca) increases Ca-entry, strengthening synaptic response until reaching saturation. HP reduced MPP fEPSPs probably by depressing synaptic release (Talpalar and Grossman, 2003) but it is not clear how these changes affected the level of saturation in response to variable V_Ca. We dealt with this question by comparing synaptic saturation under different conditions of atmospheric pressure and HP.

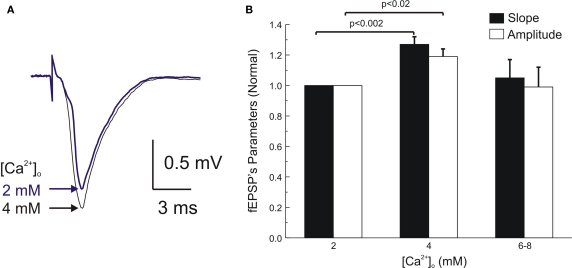
Raising [Ca²⁺]_o from 2 to 4 mM at control pressure (0.1 MPa) increased fEPSPs’ amplitudes and slopes by 19 ± 5% and 27 ± 5% respectively (n = 6; Figures 1A,B). Synaptic release apparently reached saturation at 4 mM [Ca²⁺]_o, since further increase of [Ca²⁺]_o to 6–8 mM (n = 4) did not maintained the elevated saturation level but rather brought it down to the control levels (Figure 1B).

Figure 1.

Enhancement of single MPP fEPSP's by elevated [Ca²⁺]_o under normobaric conditions. (A) fEPSPs recorded at the inner dendritic area of the dentate gyrus at [Ca²⁺]_o 2 and 4 mM. (B) Statistical analysis of single fEPSPs amplitudes and slopes under 2, 4, (n = 6) and 6–8 mM [Ca²⁺]_o (n = 4). Note that maximal slope and amplitude were reached at 4 mM [Ca²⁺]_o, apparently reaching saturation since further increase of [Ca²⁺]_o to 6–8 mM resulted in no change or even depression of the fEPSPs (not significantly different from fEPSPs at 2 mM). Scatter bars indicate mean ± SE.

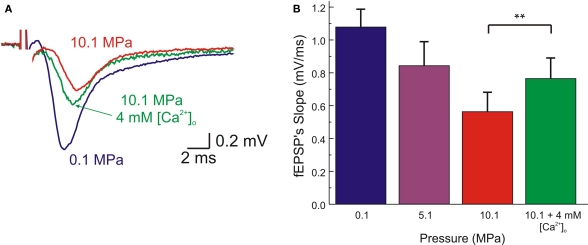
Compression to 10.1 MPa in the present experiments reduced MPP fEPSP's slope by 48 ± 11% (n = 8). Similarly, we assessed the ability of increased [Ca²⁺]_o to relieve this decline. Raising [Ca²⁺]_o from 2 to 4 mM increased fEPSPs slopes by 20% (Figures 2A,B). This enhancement of fEPSP's slope at 10.1 MPa was not statistically different (one-way ANOVA) from the enhancement produced by a similar raise in [Ca²⁺]_o at 0.1 MPa (27%, as above).

Figure 2.

High [Ca²⁺]_o partially antagonizes HP depression of single MPP fEPSP. (A) fEPSPs, recorded at the inner dendritic area of the dentate gyrus, showing the effects of pressure (0.1, 5.1, 10.1 MPa) at 2 mM [Ca²⁺]_o, and the partial restoration of fEPSPs at HP by 4 mM [Ca²⁺]_o. (B) Statistical analysis of the above experiments. fEPSPs are depressed in a pressure-dependent manner. At 10.1 MPa the fEPSP's slope is significantly increased at 4 mM [Ca²⁺]_o (p < 0.0001, n = 8). Further increasing [Ca²⁺]_o to 6 mM paradoxically resulted in reduction of fEPSP's slopes (p < 0.05, n = 2). Scatter bars indicate mean ± SE.

It is worth noticing that the enhancement of fEPSP's slope by raising [Ca²⁺]_o to 4 mM at 10.1 MPa was comparable to the effect of decompression from 10.1 to 5.1 MPa at 2 mM [Ca²⁺]_o, which increased single fEPSPs’ slope by approximately 22% with respect to 10.1 MPa (see below). However, this [Ca²⁺]_o increase was not sufficient to restore the responses to the control levels.

For quantitative comparison of differences in saturation level of MPP synapses under various conditions, all the responses were normalized with respect to a single “saturated” maximal fEPSP (E₁) under conditions of 4 mM [Ca²⁺]_o and 0.1 MPa pressure (for a more developed insight, see later Table 1). Thus, for example, the saturated response of E₁ at 10.1 MPa and 4 mM [Ca²⁺]_o decreased by approximately 56% (p < 0.01, n = 6) compared to 4 mM [Ca²⁺]_o at control pressure. Such a result may be the consequence of either a decrease in the fraction of synaptic resources (SR) used by E₁ (probably because of impaired Ca²⁺ entry into the terminals without a modification of SR), or a general decrease of SR dictating reduction of the E₁ fraction, or from both.

Table 1.

Estimation of E_T (SR) and P₁ for single fEPSPs under various conditions.

	2 mM [Ca2+]o		4 mM [Ca2+]o
Pressure	P1	ET	P1	ET
	0.1 MPa	0.35 ± 0.11	1.03 ± 0.37	0.44 ± 0.1§	1 ± 0.23 (ET’)
10.1 MPa	0.27 ± 0.04	0.64 ± 0.09**	0.39 ± 0.07§	0.53 ± 0.1*,**

P₁ at HP was calculated using the E_T for their respective conditions. Mean ± SE, n = 6. §p < 0.01 with respect of its respective control pressure; *p < 0.02, E_T is significantly smaller (17%) at constant HP and increased [Ca²⁺]_o, n = 6; **p < 0.01, HP significantly reduces E_T with respect to control pressure.

Empirical assessment of synaptic resources at different pressures and [Ca²⁺]_o

As a first approximation for the SR size under different conditions, we adopted a simplified empirical estimation. We activated the MPP with trains of five identical stimuli at frequency of 50 Hz, assuming that the inter-stimulus interval (20 ms) and the total duration of the train (100 ms) are short enough to avoid replenishment of used vesicles to their release sites. Thus the sum of the slopes of the five consecutive fEPSPs (E_T) should represent the SR at that time. Normalization of E_T with respect to E_T’, the E_T of saturated release at 0.1 MPa and 4 mM [Ca²⁺]_o, allowed comparing SR under different conditions. Since E_T represents the total resources of the synapse under each condition, we may also estimate how much of these resources are being used by the first fEPSP (E₁). For this matter we calculated P₁, the proportion of E_T used by E₁ (P₁ = E₁/E_T).

Table 1 reveals several characteristics of the SRs: (a) at normal pressure E_T remains constant despite [Ca²⁺]_o increase from 2 to 4 mM; (b) an analogous [Ca²⁺]_o change at HP paradoxically reduces E_T by 17 ± 12% (n = 6, p < 0.02); (c) E_T at HP is remarkably reduced in comparison with control pressure (n = 6, p < 0.01). These calculations also revealed changes in P₁: (a) elevated [Ca²⁺]_o at normal pressure increased P₁ by 27 ± 19% (n = 6, p < 0.01); (b) similar [Ca²⁺]_o change at HP enhanced P₁ by 46 ± 21% (n = 6, p < 0.005). Neither the P₁ for the same [Ca²⁺]_o at different pressures, nor the ΔP₁ generated by raising [Ca²⁺]_o were statistically significant between control and HP (n = 6, ANOVA).

We conclude that high [Ca²⁺]_o saturated synaptic responses by similar relative amount at control and HP. But, the saturation level of E₁ at HP (E₁/E_T’) was significantly lower than that at 0.1 MPa. This finding was correlated with reduction of P₁ and E_T at HP, suggesting that some of the normal SR became unavailable at HP.

High [Ca²⁺]_o increases paired-pulse depression under control and HP conditions

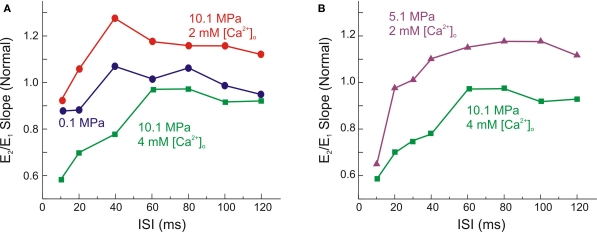
The above assessment of SR status showed reduction of the estimated SR at HP whereas change in [Ca²⁺]_o was not effective. Paired-pulse protocols normally allow the study of short-term synaptic plasticity, namely paired-pulse-facilitation (PPF) or paired-pulse-depression (PPD). By comparing the strength (slope) of the second fEPSP (E₂) with respect to E₁ we can also estimate the proportion of E_T used by subsequent E_i for the two responses. In a previous study (Talpalar and Grossman, 2003) we showed that under control conditions of [Ca²⁺]_o and pressure, the MPP input displayed variable plasticity depending on the duration of the inter-stimulus interval (ISI): ISIs of <30 ms produced pure PPD (E₂/E₁ < 1) while ISIs of 35–80 ms produced a small∼5% PPF (E₂/E₁ > 1). HP reduced PPD at short ISIs, and increased PPF of longer ISIs (Talpalar and Grossman, 2003), suggesting that synaptic release of E₁ was reduced shifting away from saturation. These observations were reproduced in the present set of experiments, in which 10.1 MPa pressure reduced PPD at the 10–20 ms ISIs and increased PPF at the 40–120 ms ISIs (Figure 3A). In addition, we compared the effect of raising [Ca²⁺]_o on similar paired-pulse modulation at control and HP.

Figure 3.

High [Ca²⁺]_o promotes paired-pulse-depression of MPP fEPSPs under HP. (A) Single experiment shows the antagonistic effect of high (4 mM) [Ca²⁺]_o on HP (10.1 MPa) paired-pulse modulation. At 10.1 MPa the initial phase of paired-pulse-depression (PPD) was attenuated, while the later paired-pulse-facilitation (PPF) was increased. Increased [Ca²⁺]_o at HP partially restored the slope of E₁, but increased PPD for short ISI and abolished the later phase of PPF for ISI 35–120 ms. (B) Comparison between PPM at 5.1 MPa (2 mM [Ca²⁺]_o) and 10.1 MPa (4 mM [Ca²⁺]_o). Note that E₁ under these two conditions is almost equal; however PPD is much greater under the latter condition.

Raising [Ca²⁺]_o from 2 mM to 4 mM at normal pressure increased PPD (20 ms ISI) from 0.76 ± 0.08 to 0.58 ± 0.08 (n = 6, p < 0.01). At 10.1 MPa, similar change of [Ca²⁺]_o increased E₁ by approximately 20% and relatively reduced E₂, consequently increasing PPD and reducing PPF (Figure 3A). For example, PPD at 20 ms ISI increased from 0.98 ± 0.11 at 2 mM [Ca²⁺]_o to 0.61 ± 0.07 at 4 mM [Ca²⁺]_o (by 36 ± 7%, n = 6, p < 0.01).

The increase of PPD by raising [Ca²⁺]_o at HP was not statistically different from that produced at 0.1 MPa (ANOVA, n = 6). Table 2 summarizes the combined effects of [Ca²⁺]_o and pressure on single, and paired-pulse fEPSPs.

Table 2.

Effects of pressure and [Ca²⁺]_o on single and paired fEPSPs at 20 ms ISI.

	2 mM [Ca2+]o				4 mM [Ca2+]o
Pressure	E1	E2	E2/E1		E1	E2	E2/E1
	0.1 MPa	0.79 ± 0.08	0.60 ± 0.06	0.76 ± 0.08		1.00 ± 0.04	0.58 ± 0.07	0.58 ± 0.08
10.1 MPa	0.41 ± 0.09	0.40 ± 0.09	0.98 ± 0.11		0.49 ± 0.09	0.30 ± 0.08	0.61 ± 0.07

Values display fEPSPs’ slopes normalized with respect to E₁ at 0.1 MPa and 4 mM [Ca²⁺]_o, n = 6 for 0.1 MPa, n = 8 for 10.1 MPa.

For easier comparison, all the values of E were normalized with respect to the largest E₁, obtained under 0.1 MPa and 4 mM [Ca²⁺]_o conditions. It should be noted that at 0.1 MPa, although the amount of PPD is greater at 4 mM than at 2 mM [Ca²⁺]_o, the size of E₂ was not statistically different for these two conditions. Under HP and regular [Ca²⁺]_o conditions, reduction of E₁ (>50%) was followed by an increase of E₂/E₁ suggesting that E₂ was utilizing a fraction of SR that was not available to E₁. In contrast, raising [Ca²⁺]_o at HP increased E₁ by 20% but produced an E₂ that was smaller by 24 ± 8% (p < 0.05, n = 6) than E₂ at 2 mM [Ca²⁺]_o. These observations suggest that the SR is more limited at HP than at 0.1 MPa. Thus, high [Ca²⁺]_o increases E₁ while keeping E₂ unchanged at control pressure, whereas it increases E₁ at the expenses of E₂ at HP. As noted above the synaptic responses can be modulated by pressure and [Ca²⁺]_o. We hypothesized that an identical E₁, obtained under different conditions may yield dissimilar paired-pulse modulation and thus may yield new insight into the availability of SR. To that goal, we compared paired-pulse plasticity under two conditions that produced similar E₁: increasing [Ca²⁺]_o to 4 mM at 10.1 MPa and decompressing to 5.1 MPa at 2 mM [Ca²⁺]_o. Despite the similar E₁, which increase by about 20% (compared to 10.1 MPa – 2 mM [Ca²⁺]_o condition) during changes in both variables, the relative size of E₂ differ greatly: PPF is present at ISIs > 30 ms at 5.1 MPa, while only pure PPD is evident at 4 mM [Ca²⁺]_o – 10.1 MPa (Figure 3B). These results suggest again that the SR is more limited at HP. Other possibility could be less effective summation of [Ca²⁺]_i due to reduced entry at the highest pressure.

Dynamics of synaptic resources during short train stimulation

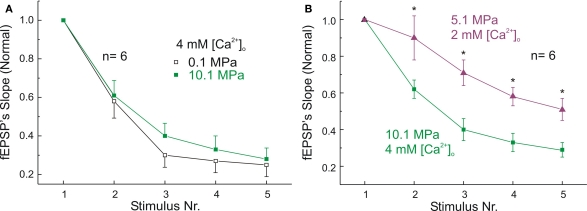
Synaptic activity at various frequencies leads to time-dependent changes in the availability of SR resulting either in FDD or frequency-dependent facilitation (FDF) (Tsodyks and Markram, 1997). Most of the mechanisms responsible for this modulation are presynaptic. Sustained action potentials firing, may initiate multivesicular release that facilitates the responses (Foster and Regehr, 2004) while the rates of vesicle docking, exocytosis, and replenishment determine the synaptic decay (Fernandez-Alfonso and Ryan, 2004). HP decreases the use of SR by single events (E₁), reduces the sum of five fEPSPs at 50 Hz (E_T), and modulates PPF/PPD.

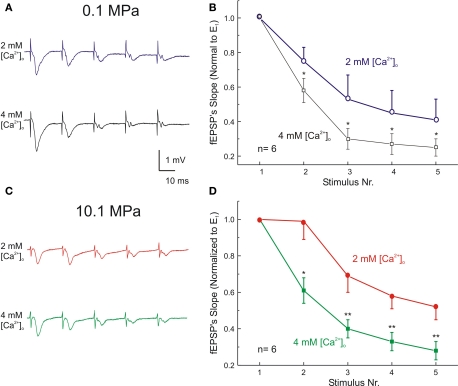
These observations suggest that HP reduces also the availability of SR. We suspected that these changes result from slowed SR dynamics (see the mathematical parameters expressing the kinetics of the synaptic response in the paragraph below). To assess SR dynamics, we analyzed the course of five stimuli trains at 50 Hz under various conditions (Figures 4A,C). Under control conditions of 0.1 MPa and 2 mM [Ca²⁺]_o stimulation at 50 Hz generated only PPD (between E₁–E₂) as part of the general exponential FDD, observed at E_2–5 (Figures 4A,B; see also Talpalar and Grossman, 2003). Increasing [Ca²⁺]_o from 2 mM to 4 mM at atmospheric pressure resulted in enhanced FDD, exhibiting shorter time constant of decay and reduction of the asymptotic level of the exponent compared with controls (Figure 4B, note that the responses in the train were normalized with respect to E₁ in each train). Compression to 10.1 MPa keeping 2 mM [Ca²⁺]_o reduced PPD, i.e., increased the component of PPF (as in Figure 3) and accelerated FDD during E_2–5 (Figures 4C,D). Raising [Ca²⁺]_o to 4 mM at HP increased E₁ by 20%, abolished any sign of PPF and namely returned the system to a “pure” PPD mode, with even faster exponential decay to a lower asymptotic level of FDD (Figure 4D).

Figure 4.

High [Ca²⁺]_o increases frequency-dependent-depression (FDD) at atmospheric pressure. Left: Dendritic recordings showing the effect of [Ca²⁺]_o on trains of 5 fEPSPs (50 Hz) at pressure of 0.1 MPa (A) and 10.1 MPa (C). Calibration bars are the same for both conditions. Right: Statistical analysis of FDD at 50 Hz. Each E_x was normalized with respect to its E₁ at its corresponding condition of [Ca²⁺]_o and pressure. Effect of [Ca²⁺]_o on FDD at pressure of 0.1 MPa (B) and at 10.1 MPa (D). *p < 0.05, **p < 0.01 depict statistical difference between stimuli at 2 mM and 4 mM [Ca²⁺]_o (independent t-test). All graphs display means ± SE (n = 6 for each condition).

The decay rates of the five stimuli train and the E₅/E₁ ratios obtained at 4 mM [Ca²⁺]_o under control and HP conditions were not significantly different from each other (Figure 5A).

Figure 5.

Effect of pressure on the dynamics of MPP's FDD. (A) Similar FDD is induced by 4 mM [Ca²⁺]_o at pressures of 0.1 MPa and 10.1 MPa. E_x were normalized with respect to their corresponding E₁ (n = 6 for each condition; differences at each stimulus were not statistically significant). (B) FDD is more significant at 10.1 MPa – 4 mM [Ca²⁺]_o than at 5.1 MPa – 2 mM [Ca²⁺]_o, (n = 6; *p < 0.05). Note that larger FDD occurs at 10.1 MPa despite of the similarity of E₁ under both conditions. All graphs show means ± SE.

These similar dynamics were observed despite the significant reduction of E_T and the difference in saturation levels of E₁ at increased [Ca²⁺]_o between the two pressure conditions.

Likewise the analysis of paired-pulse fEPSPs under two different conditions that generate similar E1, we compared also FDD (Figure 3B). An increase of E₁ by ≈ 20% with respect to E₁ at 10.1 MPa pressure and 2 mM [Ca²⁺]_o is brought about by either 4 mM [Ca²⁺]_o or decompression to 5.1 MPa. However, the FDD induced by 10.1 MPa and 4 mM [Ca²⁺]_o was significantly faster than the FDD observed at 5.1 MPa and 2 mM [Ca²⁺]_o (Figure 5B). This difference suggests that 10.1 MPa may indeed further reduce Ca²⁺-entry (Gilman et al., 1986; Grossman and Kendig, 1990) in comparison to 5.1 MPa, since the increased Ca²⁺-driving force at 10.1 MPa was not sufficient to induce additional synaptic release by E >1 when E₁ was already saturated at a subnormal level. Then, increasing [Ca²⁺]_o was followed by enhancement of E₁ and by a relative reduction of the following E₂–E₅ (see above) while keeping approximately constant the relationship E₅/E₁.

The above calculations compared how pressure and [Ca²⁺]_o modulated the relationship between E_2–5 with respect to E₁ under similar conditions. These calculations may serve for estimation of the utilization of E₅ fraction when compared to E_T (approximately SR) under different conditions, and then to compare it with E_T’, the maximal available SR.

Table 3 compares the relationship E₅/E₁ under various conditions indicating the degree of depression at the end of the train. E₁ and E₅ values were normalized with respect to the largest E₁ when SR is maximal at 0.1 MPa and 4 mM [Ca²⁺]_o. Using this normalization clearly demonstrates again (in addition to Figures 4B,D in which the normalization is to E₁ for each condition) that the amount of FDD (E₅/E₁) is quite similar for both pressure conditions but it is significantly larger for 4 mM [Ca²⁺]_o.

Table 3.

Effects of pressure and [Ca^2+;]_o on fEPSPs produced during five stimuli trains at 50 Hz.

	2 mM [Ca2+]o				4 mM [Ca2+]o
Pressure	E1	E5	E5/E1		E1	E5	E5/E1
0.1 MPa	0.79 ± 0.08	0.32 ± 0.09	0.41 ± 0.29		1.00 ± 0.04	0.25 ± 0.05	0.25 ± 0.13*
10.1 MPa	0.41 ± 0.09	0.21 ± 0.03	0.51 ± 0.16		0.56 ± 0.09	0.16 ± 0.03	0.28 ± 13**

Values display fEPSPs’ slopes normalized with respect to E₁ at 0.1 MPa and 4 mM [Ca²⁺]_o. n = 6 for 0.1 MPa, n = 8 for 10.1 MPa. Significance level for the E₅/E₁ between low and high [Ca²⁺]_o at the corresponding pressure is *p = 0.07 and **p < 0.001.

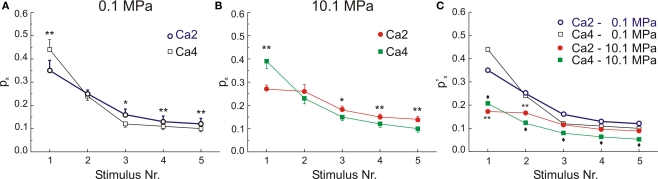
As described above (Table 1) HP reduced E₁ and E_T (the sum of E_1–5) but elevated [Ca²⁺]_o affected largely E₁ and much less E_T. This difference suggests that E_T is mainly pressure-sensitive whereas E_n is determined by both HP and [Ca²⁺]_o. In order to further elucidate these findings, we calculated the utility factor (P_n); the portion of SR used by each E_n. P_n is calculated as the ratio of E_n/E_T for each condition. Figure 6A depicts the values of P₁–P₅ at 2 and 4 mM [Ca²⁺]_o at 0.1 MPa. It should be noted that the increased P₁ at 4 mM [Ca²⁺]_o was at the expenses of later fEPSPs because the estimated E_T was similar for these two [Ca²⁺]_o. This excluded the possibility of changes in SR depletion and replenishment. At HP (Figure 6B), an identical increase in [Ca²⁺]_o produces a similar enhancement of P₁ and redistribution of the rest of P_X. By normalization of P_n with respect to E_T’ (0.1 MPa – 4 mM [Ca²⁺]_o) we may estimate how much of the maximally available SR is used by each E_n under the different conditions (Figure 6C).

Figure 6.

Effects of [Ca²⁺]_o on dynamics of MPP synaptic variables during 50 Hz stimulation at two different pressures. (A) High [Ca²⁺]_o significantly increases P₁, but it significantly reduces the P_3-5 with respect to their respective controls. (B) At 10.1 MPa high [Ca²⁺]_o also increases P₁ at expenses of P_2–5 denoting reduction of E_T. Graphs display means ± SE, n = 6 for each condition *p < 0.05 and **p < 0.01 (paired t-test). (C) Differential effects of [Ca²⁺]_o and pressure on the dynamics of MPP synaptic variables. All the fractions were normalized with respect to E_T at control pressure and 4 mM [Ca²⁺]_o, (E_T’). The effect of [Ca²⁺]_o and pressure on sequential Ps: P_1–2 display significant difference between 0.1 MPa and 10.1 MPa in control [Ca²⁺]_o (n = 6, **p < 0.01). At high [Ca²⁺]_o all Ps were significantly depressed by 10.1 MPa (n = 6, ♦p < 0.05 for all of them). SE bars have been omitted for the sake of clarity.

Comparison of HP effect at 2 mM [Ca²⁺]_o, showed that 10.1 MPa significantly reduced P₁ and P₂ alone (p < 0.01 for each, independent t-test, n = 6), while the size of the following P_3–5 were not significantly different from control pressure. In contrast, when comparing pressure effects at high [Ca²⁺]_o, all P_n values were significantly reduced at HP (p < 0.05 for all the events, n = 6 for each condition; Figures 5A and 6C).

In sum, at atmospheric pressure all the described dynamics occurred while E_T seemed to be constant. But at HP the E_T was severely diminished in a pressure-dependent manner.

Tsodyks-markram model: synaptic resources and their dynamic utilization under the experimental conditions

Empirical results suggest: (a) that SR and the utilization of these resources by individual synaptic inputs are reduced in a pressure-dependent manner; (b) that varying [Ca²⁺]_o at constant pressure changes the relative utilization of SR but not the absolute value of SR. We employed a standard mathematical model, originally proposed by Tsodyks and Markram (1997), to estimate the relative changes in dynamics of the processes. This model captures the frequency-dependent modulation of fEPSPs upon repetitive stimulation, by describing the temporal evolution of the amount of the readily available synaptic resources r, and of their fraction u, recruited at each stimulus for neurotransmission (see Materials and Methods).

The model is fully specified by (i) the time constant associated to the recovery from depression D, (ii) the time constant associated to the recovery from facilitation F, (iii) the phenomenological description of the probability of release U, and (iv) the maximal synaptic efficacy A, that captures both the postsynaptic receptor density and conductance as well as the presynaptic size of the readily releasable neurotransmitter pool.

Regardless of the experimental condition, the fit performance of the model was generally satisfactory in describing the experimental recordings. When its four free parameters were best-fitted to each of the 54 experiments (i.e., five fEPSP responses each), the relative root mean square error was below 4% in 45/54 cases, and below 1% in 26/54 cases. In addition, the statistical X²-test for assessing the goodness of the fit (Press et al., 1992) was passed in 38/54 cases, even though the conditions for this test were unfavorable in terms of the degrees-of-freedom of the X²-distribution (i.e., difference between the number of data points and optimized model parameters, 5–4, was small). Thus the model quantitatively captured the experimental data-set within the parameters range (mean ± SD) A ∼ 3.06 ± 3.05, U ∼ 0.37 ± 0.16, D ∼ 200.6 ± 130.2 ms, and F ∼ 50 ± 98.3 ms. When the experimental conditions (e.g., [Ca²⁺]_o, pressure, or both) changed, the fEPSP responses changed accordingly. In order to investigate which of the model parameters accounted for each experimental condition explored, we considered the best-fit performance as estimated by the X²-test, since this takes into explicit account the number of free parameters. We then focused on finding the minimal set of model parameters that most likely were affected by the experimental condition. In the case (e.g.) of the change in [Ca²⁺]_o, data from the two conditions were simultaneously fitted (i.e., 5 + 5 fEPSP responses). We then alternatively allowed one, two, three or all four parameters to change across the conditions, thus resulting in 5–8 free parameters. Ranking each fit performance on the basis of its X²-test score provided an explicit indication of the parameter(s) that most often appeared to result in a good fit, when changed.

From this systematic analysis, summarized in Table 4, we conclude that: (1) when [Ca²⁺]_o is increased, U is the parameter that is most sensitive to such a change, in agreement with the underlying biophysical interpretation of U as the presynaptic release probability; (2) when the pressure alone is varied, A is the parameter that is most sensitive to such a change, reminiscent of a change in the size of the readily-releasable pool and/or of postsynaptic excitability (see discussion).

Table 4.

Markram–Tsodyks model best-fit parameters for different conditions.

Cond	A	U	F(ms)	D (ms)	A'	U'	A''	U''	%Err	Conf.
[Ca2+]o 2 →4	3.0285	0.3422	19.8	128.4	2.5821	0.5057			2.7	0.0003
[Ca2+]o 2 →4	2.7921	0.3676	152.7	125.4	2.7921	0.4694			3.9	0.0002
HP: 0.1 →10.1 [Ca2+]o: 4	2.7824	0.4676	160.7	137.4	1.5361	0.4324			2.1	0.0005
HP: 0.1 →10.1 [Ca2+]o: 4	2.8584	0.4511	25000	138.4	1.5202	0.4511			2.5	0.0001
HP: 5.1 →10.1 [Ca2+]o: 2 →4	2.0318	0.3201	1400	105.8	1.4027	0.4731			3.3	0.0004
HP: 0.1 →10.1 [Ca2+]o: 2 →2 →4	3.0940	0.3087	30000	97.0	1.5708	0.3173	1.3482	0.4912	3.9	0.009

The table contains the best-fit parameters, accounting for the experimental data with the minimal number of parameters affected by the condition. Only U and A were found to be significantly affected by the changes in [Ca²⁺]_o and pressure, respectively while the other parameters remained fixed. The rightmost columns report for each case the fit error on the absolute response amplitudes and the best-fit confidence. For the experiments involving two conditions (i.e., before and after; the first five rows of the table), 2 × 5 fEPSPs were available to be fitted by the model. Therefore, five (e.g., A, U, F, D, A’) or six (e.g., A, U, F, D, A’, U’) free parameters were identified simultaneously. In bold we outlined the parameters that were allowed to change and, as expected, the lesser degrees or freedom, the higher fit confidence (underlined).

For the other experiments, 3 × 5 fEPSPs were available to be fitted by the model, therefore requiring identifying eight (e.g., A, U, F, D, A’, U’, A’’, U’’) parameters.

In details, we found that the change in [Ca²⁺]_o from 2 mM to 4 mM, decreased A by 10% while increasing U by 47%. Only the change in U was considered significant, on the basis of the parameters range indicated previously. Similar considerations apply when U alone was allowed to change, resulting in a slightly worse root mean square error of 3.9%, as expected, but an equally significant increase in U of ∼30%.

The change in HP from 0.1 to 10.1 MPa, while keeping [Ca²⁺]_o fixed at 4 mM (as in Figure 6A), caused A to decrease by 45% while U was unaffected (i.e., −7%). Similar conclusions could be drawn when only A was allowed to change.

When HP was changed from 5.1 to 10.1 MPa and simultaneously [Ca²⁺]_o from 2 to 4 mM (as in Figure 6B), A decreased significantly by 30% while U increased by 48%.

Finally, when HP was changed from 0.1 to 10.1 MPa, with [Ca²⁺]_o set first to 2 mM, and later to 4 mM, respectively (Figure 5B), A first decreased by 50% and later remained unaffected (−56% with respect to the initial 0.1 MPa condition), while U remained first unaffected (+3%) and then increased by 60%, confirming that [Ca²⁺]_o affects U while HP affects A.

Discussion

The results reported in this work were collected under strict steady-state conditions for both pressure and temperature (see Materials and Methods). As reported previously (Talpalar and Grossman, 2003) the reduction of MPP synapse parameters is directly proportional to the applied pressure, but the full effect of pressure is quantified after stabilization. Under these conditions, the MPP synaptic responses remain stationary for a long period of time (i.e., up to 2 h at maximal pressure, 10.1 MPa) with no obvious run-down (see also Etzion and Grossman, 2000). Then, we confidently assume that the response is stable and not affected in a time-dependent manner by the pressure. The relatively long (1 min) interval between subsequent stimulus trains apparently allows the replenishment of the RRP at all pressure conditions (we observed extremely small sample variance either at control or HP). We contemplated the possibility that the reduction of the single MPP fEPSP at HP may result also from a partial random “depletion” of its RRP, which was unable to recover its control size after synaptic release. But such kind of time-dependent depletion at HP may have produced a progressive and larger decline of single (not trains) fEPSP responses (sampled at 0.1 Hz), that we did not see in the experiments.

Single-fiber stimulation of the MPP at 50 Hz during whole-cell recordings of granule cells in perinatal rat slices showed failure of discrete 10–20 pA synaptic events (Talpalar, 2002). Such experiments suggest that FDD results from progressive exhaustion of discrete components at axon branches, terminals or release sites. However, the modest effect of HP on axon terminals (input volley) compared with the effect on synaptic inputs (Etzion and Grossman, 2000; Talpalar and Grossman, 2003) makes it unlikely a predominant effect of pressure on axonal branches. Moreover, quantal analysis in crustacean neuromuscular synapses exposed to HP resulted in reduction of p and n, and unchanged q, implying a pressure-dependent reduction of the release probability and a pressure-independent quantal size at the release sites.

The fact that synaptic responses elicited by the more challenging stimulation rate of 50-Hz decay more or less like controls, and the coincident effect of pressure on different types of synapses, led us to favor the hypothesis that HP reduces the number of release sites and unveils a “modular” organization of the RRP consisting in “pressure-sensitive” and “pressure-resistant” modules rather than a random “depletion” of the RRP. This last possibility could not be totally excluded since the mechanisms underlying short-term plasticity are inconclusive. The use of the phenomenological model for short-term synaptic plasticity to fit the experimental responses is a first attempt at exploring whether pressure might influence other features and mechanisms underlying frequency-dependent synaptic depression.

The input/output consequences of a potential reduction of the RRP have been investigated earlier for different pressures, by examining granule cell firing in response to MPP stimulation (Talpalar and Grossman, 2004). Despite of the reduction in synaptic inputs, the output was conserved for stimulation frequencies below 25 Hz, for which there is no difference between control and 10.1 MPa. For stimulation at higher frequencies (50 Hz), there was instead an increased excitability and loss of filter properties of the circuit. This may be likely attributed to a similar pressure-dependent effect on inhibitory synapses, leading to a proportional reduction in the inhibitory synaptic contributions from inhibitory interneurons.

HP and [Ca²⁺]_o

This study has compared the use of SR by MPP synapses under various conditions of pressure and [Ca²⁺]_o. Increasing [Ca²⁺]_o under both normal and HP conditions enhances MPP's single fEPSPs, E₁. Saturation of a single response was attained with 4 mM [Ca²⁺]_o, whereas higher [Ca²⁺]_o depressed E₁. This effect of [Ca²⁺]_o is probably due to increase in Ca²⁺-entry at the terminals and consequently an increase of the probability of synaptic release. Thus, these results suggest that release by E₁ is unsaturated at control [Ca²⁺]_o under both normal (Schneggenburger and Neher, 2000) and HP conditions (Golan and Grossman, 1992).

Under normobaric conditions the total synaptic release, E_T, during five stimuli at 50 Hz was used as a first estimation of the SR. E_T did not change in the range of 2–4 mM [Ca²⁺]_o, suggesting that [Ca²⁺]_o affects mainly the P₁, the proportion of E_T used by E₁. At 10.1-MPa pressure both, E₁ and E_T were significantly reduced in comparison with their normobaric controls. The effect of increasing [Ca²⁺]_o at HP was similar to that at normal pressure.

The reduced E₁ was associated with conserved FDD. If FDD is generated by depletion of synaptic vesicles (Abrahamsson et al., 2005), these results may disagree with the hypothesis that stimulation at high frequency increases Ca²⁺ influx which accelerate vesicle-recycling rate (Wang and Kaczmarek, 1998).

Raising [Ca²⁺]_o at HP enhanced synaptic release, but its maximal effect only partially restored synaptic transmission (Grossman and Kendig, 1990; Golan and Grossman, 1992; Golan et al., 1994, 1995, 1996). Thus, synaptic release was saturated but at a subnormal level, i.e., reduced RRP (which represents the presynaptic component of the SR), and exhibited exponential FDD during stimulation at 50 Hz. Similar to normal pressure, increasing [Ca²⁺]_o at HP enhanced E₁ concomitantly with faster rate of the FDD (Figure 4D). But FDD rates at high [Ca²⁺]_o were not significantly different at both pressures (Figure 5A). Interestingly, when identical E₁ to that at 10.1 MPa, 4 mM [Ca²⁺]_o was obtained by partial decompression to 5.1 MPa at 2 mM [Ca²⁺]_o, the FDD was reduced and its rate was slowed (Figure 5B). This indicates that similar to normal pressure, FDD is independent of E₁ initial size but depends on [Ca²⁺]_o.

Unexpectedly, higher [Ca²⁺]_o further reduced SR at HP (see Figure 6B). The reduction of PPD and/or increase PPF at HP suggests that E₁ receded from saturation, probably by reduced Ca²⁺-entry, leaving a larger fraction of unused RRP, which may partially enhance E₂. In addition, the data provide strong evidence for pressure reduction of the RRP, independent of Ca²⁺-entry.

Ca²⁺ domains and active zones

One of the major mechanisms postulated for the effects of HP on CNS synaptic function is reduced synaptic release that has been shown in chromaffin cells (Heinemann et al., 1987) and supported by an increased facilitation at reduced [Ca²⁺]_o mimicking HP effects (Talpalar and Grossman, 2003). Various lines of evidence suggest that HP impairs Ca²⁺-entry in protozoa (Otter and Salmon, 1979, 1985), brain synaptosomes (Gilman et al., 1986), and presynaptic terminals of crustacean synapses (Grossman and Kendig, 1990). Furthermore, detailed quantal analysis of crustacean neuromuscular synapses revealed that in all types of synapses HP depressed release (i.e., decreased quantal content, m) by reducing the number of active release sites (n) with variable small effect on the probability of release (p) depending on the type of the synapses (Golan et al., 1994, 1995, 1996). Similar quantal analysis for CNS and MPP synapses are not available. However, it is known that a combination of N- and P/Q-channels mediate synaptic release in the mice's MPP (Qian and Noebels, 2001). The facts that L-type Ca²⁺-currents were resistant to 40 MPa pressure (Heinemann et al., 1987) while Ca²⁺ spikes elicited by P/Q-channels were only minimally reduced at 10.1 MPa (Etzion and Grossman, 1999), suggest that N-type channels fraction is the likely target for HP depression. Though there is no information about HP effect on the kinetics of N-type currents, the fact that they seem to be mechano-sensitive (Calabrese et al., 2002), and potentially highly pressure-sensitive in guinea pig cerebellar synapses (Etzion and Grossman, 2000) and frog neuromuscular junction (Grossman et al., 1991) strongly suggest their involvement also in HP effects on MPP synapses. If this is the case, saturation of MPP synaptic response at a subnormal level and occurrence of exponentially decaying FDD, combined with reduction of the RRP suggest a close functional dependence between the N-type pressure-sensitive Ca²⁺-channels, and a specific portion of the RRP. In another words, a portion of the RRP seems to be dependent on a Ca-domain that is provided solely by N-type channels (for a review see Oheim et al., 2006). This is also consistent with the effect of raising [Ca²⁺]_o, which under both pressure conditions could increase P_n but not E_T whereas at HP increased Ca²⁺-entry through pressure-resistant channels could only partially enhance E₁ but not to restore release to control level. Moreover, these effects invoke the hypothesis that MPP synaptic strength may be based on a modular structure composed of different portions exclusively dependent on specific Ca²⁺-channels (N type-E_T, P/Q type-E_T, etc.), which at high [Ca²⁺]_o may behave as saturated pools.

CA1 hippocampal synapses (and possibly MPP synapses) active-zones contain approximately 10 (2–27) docked vesicles (the RRP) and nearly ∼200 free “storage” vesicles (Schikorski and Stevens, 1997) of potentially releasable vesicles (Fernandez-Alfonso and Ryan, 2004) while each terminal contains between 1 (Schikorski and Stevens, 1997) and 2–4 active-zones (Geinisman, 1993). These morphological features are suggestive of synaptic modularity; namely, observed LTP in CA1 may increase RRP (number of active zones) and LTD, may decrease RRP (Bolshakov et al., 1997; Toni et al., 1999; Geinisman et al., 2001). However, it is unknown if these suggested changes in RRP fit with our proposed Ca-channel-type dependent modules. It is worth noticing that Tsodyks and Markram (1997) concluded, based on a theoretical model and experimental data, that once the synaptic depression rate is set, release probability (i.e., by the model parameter U) becomes the important factor in determining and fine-tuning the neural code, by shaping and redistributing the synaptic efficacy across subsequent responses (Markram and Tsodyks, 1996). Here we suggest that the size of the RRP, especially if it is modular may also play a crucial role in determining the communication between neurons, acting as an absolute amplification or attenuation factor (i.e., by the model parameter A) of synaptic transmission but leaving the relative EPSPs amplitudes relationship unaffected.

General considerations

From a network point of view, a synapse composed of pressure-sensitive and pressure-resistant modules, depending on their Ca-channel domains, may have adaptational advantages. In environmental conditions such as pressure or temperature (thermodynamic equivalents) a modular synapse will allow the maintenance of constant frequency-dependent properties (FDD). Consistently, Moser and Andersen (1994) showed that changes in temperature (within a moderate range) did not significantly disturb the behavior of animals and function of cortico-hippocampal areas. A reduced but “scaled” dynamic RRP, may be functionally relevant for conserving behavior at low energy cost (Talpalar and Grossman, 2006).

Reduction of the RRP size at HP (or cooling) may be useful for maintaining a behaviorally important defined pattern of synaptic transmission even if Ca²⁺ influx is impaired and vesicles retrieval is slowed down because of metabolic reasons. This mechanism may be particularly efficient for maintaining a physiological function if combined with postsynaptic boosting (Talpalar and Grossman, 2004, 2006). In fact, a HP reduced MPP input was shown to produce a normal firing pattern if activation does not exceed 25 Hz, but shows the disadvantage of generating hyperexcitability with excessive stimulation at higher frequencies (Talpalar and Grossman, 2004, 2005).

In conclusion, these results support the hypothesis that portions of the MPP's RRP behave like separate synaptic modules that are dependent on Ca²⁺-entry through different channels. The utility of these module RRPs during stimulation at frequency can be redistributed (among the sequential E_x) in a Ca²⁺-dependent manner. These frequency-dependent phenomena may explain both, a relatively conserved performance at HP and also pathological features of HPNS that may depend on environmental stimuli inducing high-frequency activity. Such a mechanism may also explain behavioral adaptability and regular performance of diving mammals (whales, seals, etc.) at great depths, and may even shed light on the problem of their susceptibility to underwater noise and sonar activity (Talpalar and Grossman, 2005).

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.