Microelastic properties of lung cell-derived extracellular matrix

Abstract

Mechanical properties of the extracellular microenvironment regulate cell behaviors including migration, proliferation, and morphogenesis. Although elastic moduli of synthetic materials have been studied, little is known about the properties of naturally produced extracellular matrix. Here, we utilized atomic force microscopy to characterize the microelastic properties of decellularized cell-derived matrix from human pulmonary fibroblasts. This heterogeneous three-dimensional matrix had an average thickness of 5±0.4 μm and a Young’s modulus of 105±14 Pa. Ascorbate treatment of the lung fibroblasts prior to extraction produced a two-fold increase in collagen I content, but did not affect the stiffness of the matrices compared to matrices produced in standard medium. However, fibroblast-derived matrices that were crosslinked with glutaraldehyde demonstrated a 67% increase in stiffness. This work provides a microscale characterization of fibroblast-derived matrix mechanical properties. An accurate understanding of native three-dimensional extracellular microenvironments will be essential for controlling cell responses in tissue engineering applications.

1. INTRODUCTION

Cell behavior is directed by the complex physical and biochemical interactions between cells and their native three-dimensional extracellular matrix. The extracellular matrix (ECM) is composed of macromolecules secreted largely by fibroblasts. This network of proteins, proteoglycans, and sequestered growth factors provides a three dimensional microenvironment for cellular development, homeostasis, and regeneration [1, 2]. Biomaterials such as Matrigel, collagen gels, and fibrin gels have been used to support cell morphogenesis such as endothelial vessel formation [3–7]. However, such scaffolds lack the diversity of ECM components and the spatial heterogeneity that are found in in vivo ECM [8, 9]. We have recently developed an in vitro fibroblast-derived matrix system that supports the formation of endothelial microvessels [10]. Human lung fibroblasts secreted and organized a complex multi-component three-dimensional extracellular matrix, which was then decellularized. Human umbilical vein endothelial cells seeded on these matrices were able to remodel the matrix and form tubes with lumens. This model provides a unique platform to study the physical and biochemical properties of cell-produced matrices and the key signaling interactions between endothelial cells and this natural microenvironment.

In recent years the importance of substrate mechanics has been increasingly appreciated. The mechanical properties of scaffolds have been shown to significantly influence cell functions such as morphogenesis, proliferation, and differentiation [11–15]. Three dimensional gels of fibrin, collagen I, and Matrigel have all been used as scaffolds for neovessel formation. The mechanics of these substrates have been studied with a variety of compressive and tensile techniques and the findings vary widely, ranging from 175 Pa to 112,000 Pa [16–18]. Since this is a range that can clearly affect cell growth and differentiation [11], it is important to define the mechanical properties of natural cell-derived matrices to use as benchmarks for experimental design.

Many studies of substrate mechanics examine bulk properties via tensile stretching and rheology [19, 20], which often involve disrupting the native structure of the matrix and are not sensitive to spatial heterogeneities. Atomic force microscopy (AFM) has been used to quantitatively measure elasticity on a micrometer length scale in a variety of applications [21–23]. This technique has been adapted to study soft and thin materials whose mechanics and dimensions more closely resemble those that are found in natural biological environments [13, 24, 25]. Unique aspects of this approach include the ability to map local heterogeneities in the matrix environment that are relevant to the dimensions of cell adhesion, and in the ability to perform these measurements in a liquid environment, which is important for studying biological samples. Here we utilize AFM to characterize the microelastic properties of functional cell-derived matrix from human pulmonary fibroblasts. These fibroblast-derived matrices were mechanically compliant and heterogeneous. We showed that increasing the collagen I content of the fibroblast-derived matrices with ascorbate did not increase the matrix stiffness when compared to fibroblast-derived matrices prepared in standard medium. However, an increase in fibroblast-derived matrix stiffness was generated by crosslinking with glutaraldehyde.

2. MATERIALS AND METHODS

2.1 Cell Culture and Reagents

Human lung fibroblasts, WI-38, (ATCC, Manassas, VA) were cultured in Minimal Essential Medium Eagle (Sigma, St. Louis, MO) with 10% FBS (Atlanta Biologics, Lawrenceville, GA), antibiotic-antimycotic solution (Cellgro, Lawrence, KS), 1mM sodium pyruvate (Sigma), and non-essential amino acids (Sigma). When indicated, 500 μg/ml sodium L-ascorbate (Sigma) was added to the culture medium. The medium was changed every 2 days.

2.2 Production of Fibroblast-Derived Matrix

Fibroblast-derived matrices were prepared as previously described [10]. Briefly, samples for AFM analysis were produced by fibroblasts that were seeded onto fibronectin-coated 50mm petri dishes (Falcon, Franklin Lakes, NJ; surface area 19.6cm²) and cultured for 7–10 days prior to extraction with 0.05% Triton X-100 (Fisher Scientific, Pittsburgh, PA) and 50 mM NH₄OH (Sigma). They were then washed with 50 mM NH₄OH, incubated with 20 U/mL DNase I (Roche, Penzberg, Germany), gently washed with phosphate buffered saline (PBS) (Quality Biological Inc, Gaithersburg, MD) and stored overnight at 4°C.

2.3 Matrix Labeling for Imaging

Primary antibodies used in this study included the following: goat polyclonal anti-collagen I (1478, a gift from Hynda Kleinman, NIH); mouse anti-fibronectin monoclonal (BD/Transduction Laboratories, San Jose, CA); and rabbit polyclonal anti-collagen VI (Abcam, Cambridge, MA). The following affinity cross-adsorbed secondary antibodies were used: Cy3-conjugated donkey anti-rabbit IgG (Chemicon, Billerica, Massachusetts); Cy5-conjugated donkey anti-goat IgG; and FITC-conjugated donkey anti-mouse IgG (Jackson ImmunoResearch Laboratories, West Grove, PA). The amine-reactive probe Alexa Fluor 488 carboxylic acid, succinimidyl ester from Invitrogen (Carlsbad, California) was used in some experiments to label all of the matrix proteins.

2.4 Epifluorescence Microscopy

Fibroblast-derived matrices produced on 12 mm coverslips (No. 0, Fisher Scientific, Pittsburgh, PA) were processed as follows for the studies involving imaging of matrix components. Samples were fixed in 3% paraformaldehyde (Sigma) for 20 minutes and then incubated with 0.5% Triton X-100 in 3% paraformaldehyde for 2 minutes. All antibodies were diluted in 0.1% BSA and were incubated for 30 minutes. FluoroSave (CalBioChem, Darmstadt, Germany) was used a mountant. Images were captured with a 60x objective on an epifluorescence Nikon TE200 microscope (Melville, NY), a Coolsnap HQ CCD camera (Roper, Duluth, GA), and Openlab software (Perkin Elmer/Improvision, Lexington, MA). Z-stacks were collected with a 0.2 μm step size.

For studies of matrix thickness, interfiber spacing, and affects of AFM indentation on the matrix, samples were not fixed. Instead, they were directly incubated with 10 μg/ml Alexa Fluor 488 amine probe for 2 hours and then carefully washed with PBS. The amine labeled matrices imaged in the presence of PBS. The Nikon TE200 microscope was used for characterization of matrix thickness and interfiber spacing. An Asylum MFP-3D AFM mounted on an inverted epifluorescence microscope (Carl Zeiss Axiophot) was used to visualize amine labeled matrices before, during, and after contact with the cantilever.

2.5 Image Analysis

Huygens Essential software (Scientific Volume Imaging, Hilversum, The Netherlands) was used to deconvolve the z-stacks as previously described [10] with the following conditions: 100–150 iterations of the classic maximum likelihood estimation algorithm were used with a signal to noise ratio of 35.

Matrix thickness and interfiber spacing were determined from deconvolved images of Alexa Fluor 488-labeled matrices on custom glass-bottom p35 petri dishes fitted with a 25 mm round photo-etched glass coverslips (No. 1, Bellco, Vineland, NJ) and sealed with 20:1 Sylgard 184 Silicone Elastomer (Dow Corning, Midland, MI). Images were collected in the center of each coverslip, which was not coated by the PDMS sealant. Imaging was done in the presence of PBS. The average thickness was calculated from the first in-focus plane to the last by stepping through the z stack (4 samples measured at 3 different locations). The average interfiber spacing for 4 samples was calculated from manual measurements of 50 interfiber distances in each of 3 locations per sample [10].

The relative volume of each matrix protein compared to the total image volume was quantified in Volocity (Perkin Elmer/Improvision, Lexington, MA). The volume of each protein was measured using a percent intensity threshold to select the protein within a 6 μm thick section. The mean relative volume for each matrix protein (3 samples per condition) was reported as a percentage.

2.6 Microsphere Attachment and Cantilever Calibration

A 100 μm glass sphere (Duke Scientific, Waltham, MA) was attached to a tipless silicon microlever (MicroMasch, San Jose, CA) with a water resistant, two-part epoxy adhesive (Devcon, Danvers, MA) using a dissecting microscope and a micromanipulator. These microlevers were 350 μm in length and had a spring constant of ~0.03 N/m. After allowing the epoxy to dry for one day, cantilevers were coated overnight in 0.1% BSA. All cantilevers with spheres attached were calibrated using the calibration tool in the Asylum MFP 3D software (Santa Barbara, CA) to measure their thermal fluctuations prior to indentation experiments [26].

2.7 Electron Microscopy

AFM cantilevers were attached to aluminum stubs via carbon sticky tabs (Ted Pella Inc, Redding, CA). Stubs were viewed and digital images captured on a Leo 1530 Field Emission Scanning Electron Microscope (Carl Zeiss, Thornwood, NY) operating at 1 kV.

2.8 AFM Measurements

An Asylum MFP-3D AFM mounted on an inverted epifluorescence microscope (Carl Zeiss Axiophot) was used to collect indentation curves. Prior to interrogation of the fibroblast-derived matrices, the cantilever sensitivity was determined from the slope of the linear post contact portion of a force curve collected on a plastic dish in the presence of PBS, the same conditions as the matrix measurements. A scan rate of 0.002 Hz was used to minimize hysteresis between extension and retraction curves. All indentation curves were collected in relative trigger mode, such that all extension curves had the same maximum cantilever deflection of 120 nm. The investigators did not encounter any micro bubbles in any of the samples examined.

The mechanical properties of fibroblast-derived ECM produced in three different conditions were examined: matrices produced in standard culture conditions; matrices produced by fibroblasts grown in the presence of 500 μg/ml ascorbate; and standard condition matrices fixed after production with 0.1 % glutaraldehyde for 2 hours.

2.9 Force Volume

Heterogeneity of the matrix mechanical properties was evaluated with force volume maps. These maps contained 16 force curves collected over a 2500 μm² square area of each matrix. The scan rate and relative trigger mode used were as described above. For each matrix condition, 4 to 5 separate matrices were studied.

2.10 AFM Analysis

The MFP 3D software (Asylum Research, Santa Barbara, CA) based in IGOR Pro (version 6.05.0, WaveMetrics, Inc, Lake Oswego, OR) and custom code created in IGOR Pro were utilized for AFM data analysis. The Hertz equation for spherical indentation (equation 1) can be used to obtain the Young’s modulus of the fibroblast-derived matrix from an extension force-indentation curve [27].

$$F=\frac{4E\sqrt{R_s}}{3(1-{\gamma }^2)}{\delta }^{\frac{3}{2}}$$ equation 1

F is the force on the cantilever, E is the Young’s modulus, R_s is the radius of the sphere, γ is the Poisson ratio (assumed 0.5)[28, 29], and δ is the indentation. The identification of a contact point to determine the indentation is not trivial when dealing with soft materials and has been identified as a major source of error in such analysis [30]. Therefore, the approach described by Domke and Radmacher [25] was utilized. Briefly, this method applies the Hertz equation for two points ((z₁,d₁) and (z₂,d₂)) in the contact region of the baseline subtracted extension curve and then subtracts these two equations. The separation distance between the probe and the sample is represented as z and the d is the cantilever deflection. The resulting equation for spherical conditions is as follows.

$$E=\frac{k(3(1-{\gamma }^2))}{4\sqrt{R_s}{\left(\frac{z_1-z_2-d_1+d_2}{d_1^{\frac{2}{3}}-d_2^{\frac{2}{3}}}\right)}^{\frac{3}{2}}}$$ equation 2

Here k is the spring constant of the cantilever. The Young’s modulus was plotted against the cantilever deflection for each set of points along the curve. A line was fit between 20 nm and 100 nm of cantilever deflection and its y-intercept was taken to be equivalent to the Young’s modulus of the matrix. Points below 20 nm were excluded because of the increase in noise as the cantilever deflection approached 0. This analysis was conducted for all curves collected with a linear region between 20 nm and 100 nm of cantilever deflection (n=16). Curves with a nonlinear shape were subjected to an analysis that is based upon force integration to equal limits (FIEL), as described below.

To compare relative matrix stiffness between different conditions, an approach based on the robust FIEL analysis was applied [31]. For each force curve in a force volume, the area was measured under the baseline subtracted extension curves with a maximum force of 0.5 nN. This force threshold was selected to keep the indentation depths within 10% of the average matrix thickness for this analysis. The area under the curve is proportional to the work done by the AFM cantilever (w) and is bounded by the zero deflection line and the force threshold.

$$w=\underset{0}{\overset{{\delta }_1}{\int }}\frac{4}{3}\frac{E\sqrt{R_s}}{(1-{\gamma }^2)}{\delta }^{\frac{3}{2}}d\delta =\frac{8}{15}\frac{E\sqrt{R_s}}{(1-{\gamma }^2)}{{\delta }_1}^{\frac{5}{2}}$$ equation 3

Since the δ₁ is unknown, equation 1 can be rearranged to provide an expression for indentation and substituted into equation 3. The resulting expression for work is

$$w=\frac{C\ast {F_{max}}^{\frac{5}{3}}}{E^{\frac{2}{3}}\ast {R_s}^{\frac{1}{3}}}$$ equation 4

where F_max is the force threshold and C a constant equal to $\frac{1}{3}\ast {(1-{\gamma }^2)}^{\frac{2}{3}}$. Curves with negative work values were excluded, and this approach yielded 4 to 14 curves per force volume that were used to examine the work in each force volume. The work is inversely related to the stiffness of the matrix. The average work for each matrix condition was calculated (n = 4–5 matrices) and used to compare the relative stiffness of the different matrices.

The FIEL analysis approach was then extended to determine the micromechanics of the matrices prepared in the presence of ascorbate, and those fixed with glutaraldehyde. This was done using the following equations from A-Hassan et al., [31].

$$\frac{w_1}{w_2}={\left(\frac{k_1}{k_2}\right)}^{2/3}$$ equation 5

$$k_{1or2}=\frac{1-\gamma }{\pi E_{1or2}}$$ equation 6

In addition, histograms of the work values for each force volume were created. These histograms were used to examine the heterogeneity of the matrix. The minimum, maximum, and mean absolute differences in work values between adjacent locations within each force volume were also calculated.

2.11 Statistics

Statistical significance for differences in ascorbate volume fraction measurements and AFM work data were determined by the unpaired Student t-test in GraphPad Prism version 4.00 (GraphPad Software, San Diego California). All reported data represent the mean values and standard errors of the mean unless otherwise noted. Significance was considered to be present at p<0.05 for all data.

3. RESULTS

3.1 Matrix Characterization

The fibrous structure of the fibroblast-derived matrices examined here had an average thickness of 5±0.4 μm, and an interfiber spacing of 2±0.04 μm, and was composed of numerous proteins and proteoglycans including fibronectin, collagen I, collagen VI, collagen IV, tenascin C, decorin, and versican, as previously reported [10]. In this study, the mechanical properties of three different conditions of fibroblast-derived matrices were investigated: matrices produced in standard culture medium, matrices produced with the addition of 500 μg/ml ascorbate to the culture medium, and matrices produced in standard culture medium that were fixed with glutaraldehyde.

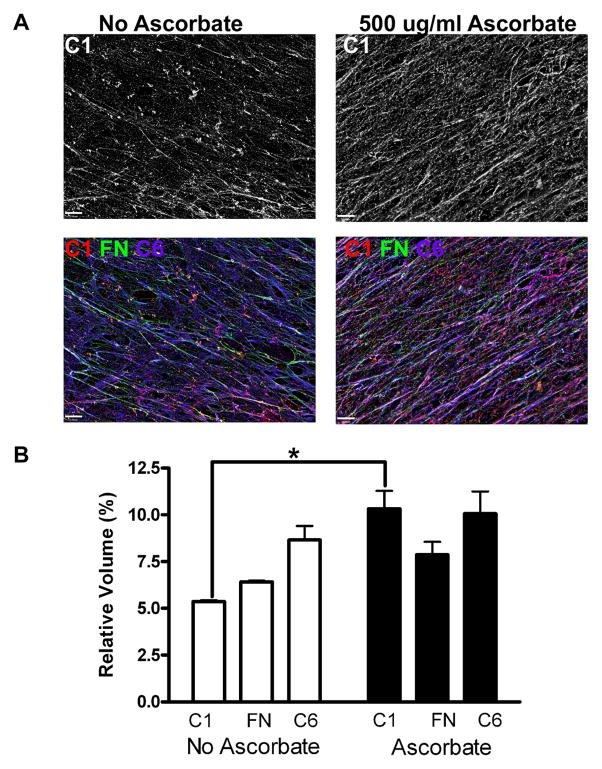
Ascorbate is a common additive to culture media that increases cellular collagen synthesis and crosslinking [10, 32, 33]. The addition of ascorbate increased the collagen I content in our fibroblast-derived matrices as anticipated (p<0.01) (Figure 1). These ascorbate-treated matrices had a higher relative volume of collagen I (10.3±1.0%) than the standard culture matrices (5.4±0.1%). The relative volumes of two other major components of the fibroblast-derived matrices, fibronectin and collagen VI, were not significantly affected by the ascorbate treatment. Fibronectin had a relative volume of 6.4±0.1% in standard media and 7.9±0.7% with ascorbate treatment. Matrices in standard culture had a relative volume of collagen VI of 8.7±0.7%, as compared with 10.1±1.2% in matrices produced in the presence of ascorbate.

Figure 1. Sodium Ascorbate Increases Volume Fraction of Collagen I in Fibroblast-Derived Matrices.

WI-38 cells were cultivated to produce extracellular matrix in either standard conditions or with the addition of 500 μg/ml sodium ascorbate to the nutrient medium. Deconvolved z-stacks of samples labeled for immunofluorescence analysis were collapsed into a single plane in panel A, and the scale bars each denote 10 μm. The top row shows the collagen I (grey) produced in both conditions and the bottom row contains composite images of fibronectin (green), collagen I (red), and collagen VI (magenta). Relative volumes of components of the fibroblast-derived matrices from these two conditions were analyzed (shown in B). Matrices produced by fibroblasts exposed to ascorbate had a higher relative volume of collagen I than the control condition without ascorbate (p<0.01). No statistical differences were noted between the two conditions for the relative volumes of fibronectin or collagen VI.

3.2 Determination of the Appropriate Microsphere Size

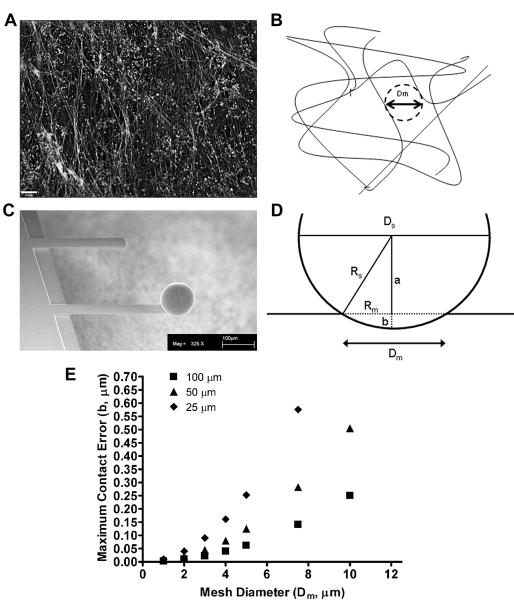
Alexa Fluor 488-labeling of the amine groups in the fibroblast-derived matrix helped to delineate its fibrous infrastructure (Figure 2A and 2B). In order to prevent the AFM cantilever from missing the surface of the matrix by landing in a pore of the ECM, a glass sphere was attached to the end of the cantilever (Figure 2C). Theoretical interfiber spacings and bead diameters were used to calculate the maximum contact error of the sphere if it was indenting at a location between two fibers (Figure 2D). A theoretical right triangle can be used to relate the radius of the sphere (R_s) and the radius of the mesh (interfiber spacing) (R_m) using equation 7

Figure 2. Sphere Size Selection.

Amine groups in fibroblast-derived matrix were labeled with Alexa Fluor 488. A single plane from a deconvolved z-stack is shown and the scale bar = 10 μm (A). The cartoon schematic in B depicts the fibrous structure of the fibroblast-derived matrix. The mesh (interfiber spacing) diameter (D_m) was measured as the diameter of the largest sphere that could fit between the fibrils. In order to prevent the AFM cantilever from landing between two matrix fibrils, a glass sphere was attached to each silicon cantilever. A scanning electron micrograph of a cantilever with a 100 μm sphere attached is shown in C. Scale bar = 100 μm. The relationship between the mesh radius (R_m), radius of the sphere (R_s), and maximum contact error of the sphere (b) is depicted in D (a = one side of the triangle). This relationship was used to calculate the maximum contact error for a given sphere diameter (D_s) (25 μm, 50 μm, and 100 μm) for different interfiber spacings (shown in E). With an average matrix interfiber spacing of approximately 2 μm, a 100 μm sphere will have a contact error of 10 nm, which is negligible given the indentation depths used in our AFM measurements.

$${R_m}^2+a^2={R_s}^2$$ equation 7

where a is one side of the triangle. The value of a and R_s can then be used to solve for the maximum contact error (b)

$$R_s=a+b$$ equation 8

With an interfiber spacing of 2 μm, a 100 μm sphere would have a maximum contact error of 10 nm, which is negligible given the indentation depths used here (Figure 2E). Therefore all measurements were conducted using cantilevers with 100 μm spheres attached.

3.3 AFM Measurements

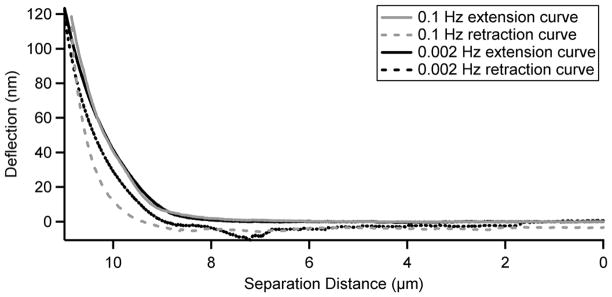
A hydrodynamic effect was noted when collecting cantilever calibration curves on plastic dishes. The 100 μm sphere on the AFM cantilever caused a hydrodynamic effect on the force measurements due to the liquid being squeezed out from between the sphere and the dish surface. This effect manifested as a rounding of the contact part of the curve at higher approach speeds (Supplemental Figure 1). At the slower scan rates, such as 0.002 Hz, the typical sharp contact was exhibited. The AFM cantilever was then indented on fibroblast-derived matrix at various speeds to determine the optimal conditions for the subsequent measurements. These curves were collected at the same location on the fibroblast-derived matrix. A curve collected at a slow scan rate of 0.002 Hz displayed decreased hysteresis - the separation between the extension and retraction curves (Figure 3). A slower scan rate was not practical due to the increased significance of thermal drift at such rates. The scan rate of 0.002 Hz was subsequently used for all of the experiments shown here in order to minimize hydrodynamic and hysteresis effects on our measurements of the fibroblast-derived matrix.

Figure 3. Minimizing Hysteresis.

The graph shows extension (solid lines) and retraction (dashed lines) curves collected at the same location on a fibroblast-derived matrix. The curves shown in grey were collected at a scan rate of 0.1 Hz and the black curves were at 0.002 Hz. Both curves were collected with a relative trigger at a cantilever deflection of 120 nm. The deflection of the cantilever is plotted on the y axis and the separation distance between the cantilever and the matrix is on the x axis. Hysteresis was minimized at 0.002 Hz, and thus it was used as the scan rate for all measurements. A slower speed was not practical due to increased significance of thermal drift.

3.4 Analysis

Each individual curve in a force volume was analyzed to describe the mechanical properties of the matrix (Figure 4A). These curves collected on the fibroblast-derived matrix displayed a rounded initial contact region that is characteristic of a soft substrate. Selecting a contact point would be arbitrary and would provide a source of error [30]. The Domke and Radmacher point-to-point analysis, which does not require contact point selection, was therefore employed [25]. The Young’s modulus of the standard matrix was calculated as the y-intercept of the line fit to the Young’s modulus-deflection curves with linear regions between 20–100 nm (Figure 4B). The resulting average Young’s modulus for fibroblast-derived matrix was 105±14 Pa (n = 16 determinations on five different matrices).

Figure 4. Young’s Modulus Calculation.

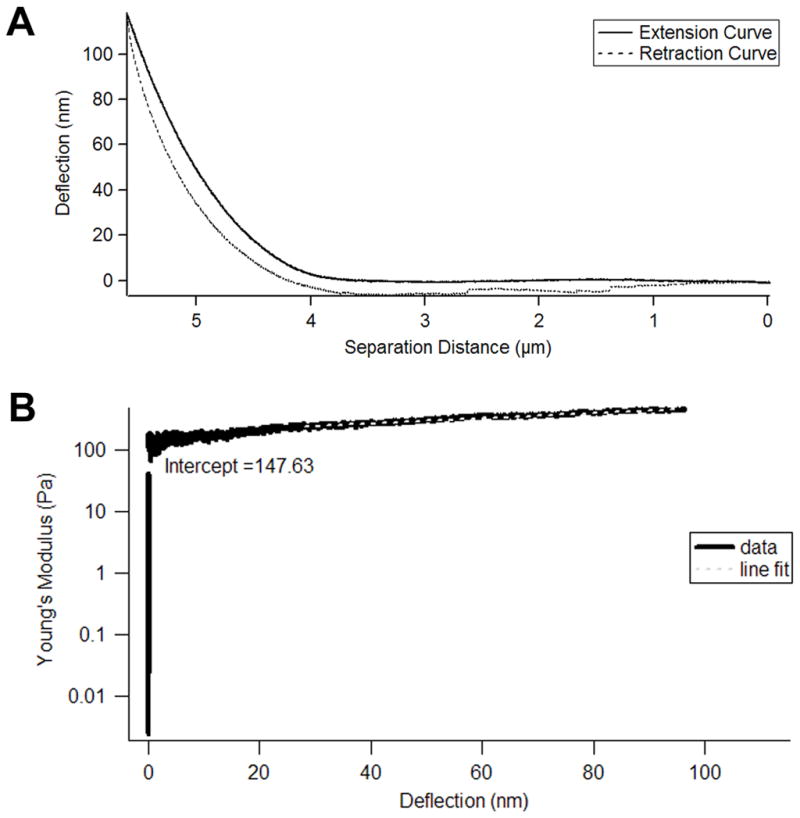
The graph in panel A demonstrates an example of a pair of extension (solid line) and retraction (dashed line) curves collected on fibroblast-derived matrix. The deflection of the cantilever is plotted on the y axis and the separation distance between the cantilever and the matrix is on the x axis. The Young’s modulus can be calculated from the extension curve using a pointwise approach previously described by Domke and Radmacher. The Young’s modulus for the region between every 350 data points on the extension curve is plotted in B. The Young’s modulus is shown on the y axis and the cantilever deflection is on the x axis. The y-intercept of a line that was fit between 20 and 100 nm deflection (grey dashed line) represented the Young’s modulus of the matrix. For the matrix analyzed in B, the Young’s modulus was 148 Pa.

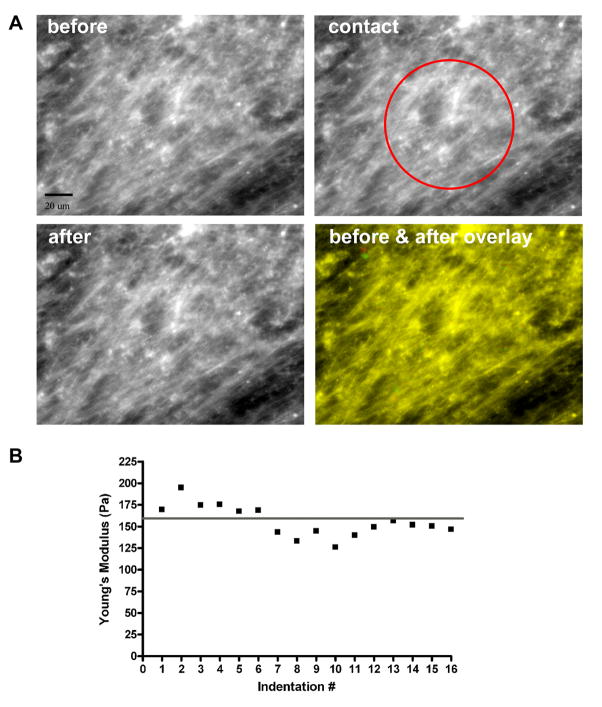
To assess damage to the matrix that might have been caused by the indentation of the sphere on the cantilever, two experiments were conducted. First, Alexa Fluor 488 labeling was used to visualize all protein constituents of the matrix prior to, during, and after contact with the 100 μm sphere attached to an AFM cantilever (Figure 5A). While above the matrix, the cantilever was centered in the field of view of the matrix using direct visualization, and the matrix was visualized with a FITC filter with the cantilever in this pre-contact position (top left panel). The cantilever was then moved into contact with the matrix and stopped at 120 nm deflection in order to acquire an image during contact (top right panel). Then, the cantilever was retracted from the matrix surface and a third, post contact, image of the matrix was captured. The overlay of the matrix before contact (green) and after contact (red) indicated that the matrix structure was not damaged by the indentation of the sphere (colocalization appears yellow) during a single discrete measurement.

Figure 5. The Effects of AFM Measurements on the Fibroblast-Derived Matrix.

A fibroblast-derived matrix was labeled with Alexa Fluor 488 and visualized with a 40x objective with the fluorescent microscope attached to the AFM (A). The matrix is shown before (top left), during (top right), and after (bottom left) indentation. Scale bar is 20 μm. The sphere attached to the AFM cantilever was centered in the field of view and its location is indicated in the top right image. The matrix structure appeared similar in all 3 images. The lack of matrix alteration by contact with the sphere is demonstrated in the overlay of the matrix images before (green) and after (red) contact (bottom right image). Yellow represents colocalization of the two images. Additionally, one location of fibroblast-derived matrix was repeatedly indented 16 times in order to assess mechanical changes in the matrix from repeated measurements. The Young’s modulus was calculated for all 16 curves and is displayed in B. The y axis is the Young’s modulus and the x axis is the number of indentations. The line represents the average of all 16 Young’s modulus measurements, 156±5 Pa. The consistency in Young’s modulus values suggested that the repeated measurements caused little alteration in matrix mechanical properties, and linear regression analysis corroborated this interpretation.

We then interrogated the effects of repeated cycles of indentation at the same location on the standard medium fibroblast-derived matrix. The AFM was left to repeat 16 cycles of indentation and each curve was analyzed for its Young’s modulus (Figure 5B). The average modulus for this location throughout the entire series of repetitive measurements was 156±5 Pa. Linear regression analysis of these data showed that repeated contacts with the glass sphere and the AFM cantilever caused no alteration of matrix mechanical properties through seven cycles of indentation (slope = −4.93±2.23; p=0.078). The damage to matrix incurred by indentation after 16 cycles was minimal (slope = −2.43±0.77; p=0.007).

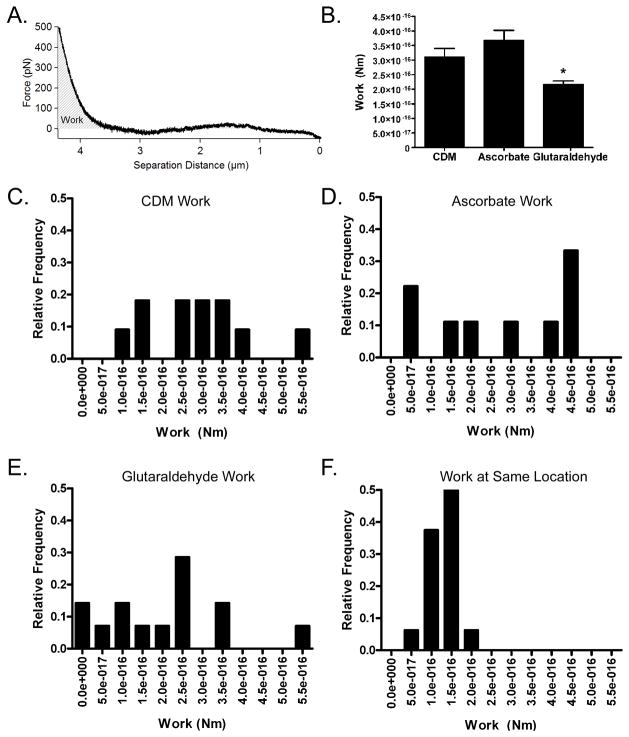
To compare the relative stiffness of the 3 types of matrices, analysis based on FIEL (force integration to equal limits) was conducted. The calculation of work done by the AFM cantilever - represented by the area under the extension curve - did not require identification of the contact point (Figure 6A). The average work for each matrix condition is shown in Figure 6B (n = 4–5 different matrices per condition). More work was done by the cantilever on the standard matrix (3.1×10⁻¹⁶ ± 6.6×10⁻¹⁷ Nm) than on the glutaraldehyde-fixed matrix (2.2×10⁻¹⁶ ± 2.3×10⁻¹⁷ Nm), which indicated that the glutaraldehyde matrix was stiffer than the standard matrix (p<0.05). This corresponds to an elastic modulus of 176 Pa Surprisingly, no significant difference was noted between the average work done by the cantilever on the ascorbate-treated matrix (3.7×10⁻¹⁶ ± 6.9×10⁻¹⁷ Nm) and the standard matrices. This corresponds to an elastic modulus of 80.6 Pa This latter result indicated that the increased collagen I content in the matrices produced by the ascorbate-treated fibroblasts had a very minimal effect on the matrix stiffness, which could not be detected by AFM.

Figure 6. Spatial Heterogeneity of Fibroblast-Derived Matrices Produced Under Different Conditions.

The effects of different preparation regimens on the relative mechanical properties of fibroblast-derived matrices were studied. FIEL based analysis was conducted on matrices produced under standard conditions, on matrices made by fibroblasts exposed to ascorbate, and on glutaraldehyde-fixed matrices. An example extension curve collected with the force plotted on the y axis and separation distance between the cantilever and the matrix on the x axis is shown in panel A. The work done by the AFM cantilever during indentation is proportional to the area under the extension curve and is represented by the grey diagonal lines. For this analysis, the area under the curve was analyzed to the same force threshold of 0.5 nN. The average work (y axis) per matrix preparation condition is displayed in B. Glutaraldehyde-treated matrices had significantly less work than matrices treated in standard conditions (CDM) (p<0.05), indicating that the glutaraldehyde fixation stiffened the fibroblast-derived matrix.

Histograms of work values (x axis) were compiled to examine matrix heterogeneity within the force volumes. Representative histograms for fibroblast-derived matrix in standard culture medium (CDM, C), ascorbate-treated fibroblast-derived matrix (D), glutaraldehyde-fixed fibroblast-derived matrix (E), and repeated curves collected in the same location (F) are shown. The relatively smaller variation in work values for the curves collected at the same location on fibroblast-derived matrix indicated that there was heterogeneity in the fibroblast-derived matrices for all conditions that was not explained by variability in the accuracy of the measurements.

Spatial heterogeneity in the 3 different types of matrices being studied was examined by comparing work values from force volumes that covered a 50 μm × 50 μm area, with repeated measurements at one point (Figure 6C–6F). The relatively larger variation in work from the curves within the force volumes for each of the matrix conditions as compared to the curves collected at one location on the matrix indicated that the matrices were heterogeneous over the length scale studied here. The mean difference in work between adjacent locations within the fibroblast-derived matrix force volumes, ascorbate-treated matrix force volumes, and glutaraldehyde-treated matrix force volumes were 1.8×10⁻¹⁶ Nm, 2.6×10⁻¹⁶ Nm, 2.1×10⁻¹⁶ Nm respectively. These values were larger than the mean difference in work from the control of 16 curves at the same location, 3.7×10⁻¹⁷ Nm (Supplemental Figure 2). The minimum and maximum work differences for these conditions were also utilized to qualitatively describe the matrix heterogeneity (Supplemental Figure 2). Taken together, these findings indicate that there is heterogeneity in these fibroblast-derived matrices on the length scale of ~ 14 μm.

4. DISCUSSION

The mechanical properties of scaffolds have been shown to significantly influence cell responses such as morphogenesis, proliferation, and differentiation [11, 13, 14, 34]. Understanding the mechanical properties of cell-derived matrices is therefore critical for designing tissue engineering scaffolds to mimic the in vivo environment. Commonly used polystyrene plastic tissue culture surfaces do not provide an ideal model for the mechanics of the in vivo environment. They have an Young’s modulus in the GPa range [35], whereas Young’s moduli that are five orders of magnitude smaller than this have demonstrated profound effects upon cell growth and differentiation [13]. Nanoindentation studies on polyacrylamide gels have been used to interrogate the mechanical sensitivity of human mesenchymal stem cell differentiation. These gels had Young’s moduli in the range of 1–17 kPa, depending upon the concentrations of acrylamide and bisacrylamide [13]. The Young’s modulus of the fibroblast-derived matrix described here, 105 Pa, is lower than that described for many synthetic bioscaffold materials, but fits well into the context of reports on nanoindentation studies for various natural extracellular matrix scaffolds. Paszek and coworkers described the Young’s modulus of many substrates used for cell culture. Reconstituted basement membrane has a reported Young’s modulus of 175 Pa and a 2 mg/ml collagen gel has a Young’s modulus of 328 Pa [17]. Mimicking the compliant nature of native tissue microenvironment is an important design feature for tissue engineering. For example, promising data regarding central nervous system regeneration have been noted in microenvironments with mechanics that model the native tissue [36].

The softer character of the fibroblast-derived matrix studied here may be an important factor in the instructive properties of these matrices with respect to microvascular network formation [10]. Other groups have demonstrated decreased endothelial cell tube formation in stiffer collagen and fibrin gels, but these environments also contained increased ligand densities [6, 37, 38]. Kuzuya demonstrated that increased crosslinking in collagen matrices by glycalation also had decreased tube formation compared to control gels [39]. In a system that controlled for ligand density, softer matrix mechanics were associated with increased tube formation [40]. Taken together, these studies suggest that a relatively compliant mechanical microenvironment may be optimal for neovessel formation.

The addition of ascorbate to cell culture medium has been shown to increase collagen synthesis and crosslinking in the extracellular matrix produced by cells [32, 33]. Here we showed that the addition of 500 μg/ml of ascorbate to the lung fibroblast culture medium increased the collagen I content in the fibroblast-derived matrices. However, ascorbate treatment did not produce a significant difference in the Young’s modulus of the fibroblast-derived matrices compared to matrices produced in standard culture conditions. This implies that the increased collagen I content has a small effect on the matrix mechanics. Throm used epidermal growth factor (EGF) in chemically defined culture medium to change the collagen content in human foreskin fibroblast-derived matrices [41]. A membrane inflation system was used to study the ultimate tensile strength (UTS) of these matrices. They noted the highest collagen density and UTS in samples treated with 0.5 ng/ml EGF, but did not see a significant correlation between the UTS and collagen I density [41]. In contrast with that study, where bulk mechanical properties were examined, our data were collected with an AFM to investigate the local mechanical properties of the human lung fibroblast-derived matrices. Additionally, the indentation experiments conducted here are based on compression of fibroblast-derived matrices. Collagen I is an abundant extracellular matrix protein and is believed to provide tensile strength to tissues, but the compressive properties of collagen I are still largely unknown [42]. We speculate that the ascorbate-treated fibroblast-derived matrices with increased collagen I might contain enhanced local tensile strength, which was not examined in this study. Our data implies that collagen I does not play a major role in resisting local compression, and this supports its putative role in providing tensile strength to the extracellular matrix.

Glutaraldehyde treatment has been shown to strengthen materials through extensive crosslinking between matrix proteins and has been used for that purpose with a variety of biomaterial scaffolds [43]. Glutaraldehyde fixation has been used in the preparation of bioprosthetic heart valves and to prepare decellularized esophageal tissue for studies on prosthetic patches for traumatic injury [44, 45]. In the current work, our measurements demonstrated that these crosslinked fibroblast-derived matrices had a 29% decrease in work on the AFM cantilever following 2 hours of 0.1% glutaraldehyde exposure. Hansen et al. used nanoindention to describe a large increase in Young’s modulus of glutaraldehyde-treated rat tail tendon that was probably related to the increased concentration of glutaraldehyde (15%) and incubation time (24hrs) used [46]. Our findings were corroborated more closely by the AFM experiments employing more comparable glutaraldehyde treatment conditions [47].

The present study offers an AFM approach to microscale characterization of matrix mechanics that advance our understanding of local properties of natural, reconstituted, and engineered matrices with data that are relevant for the study of cellular growth and development. Some important considerations for this application are capsulized here. First, an appropriately sized sphere is needed as a probe for indentation to minimize the chance of missing the surface of a porous sample. Second, when matrix samples are thin, the indentation distance of the cantilever must be limited to minimize any influence of the underlying stiff plastic in the analysis of Young’s modulus [25]. Next, the spring constant of the cantilever used in the measurements will determine the sensitivity of the measurements - typically cantilevers with spring constants in the range of 10–200pN/nm are used to measure biological samples [34]. Indentation speeds must be carefully chosen in order to minimize both hysteresis and cantilever drift. Finally, this technique provides local microscale mechanical properties, so comparisons of these data with bulk properties are difficult.

5. CONCLUSION

The local mechanical properties of natural extracellular matrices produced by human lung fibroblasts were characterized by AFM. As determined by indentation experiments and the point-to-point analysis, the Young’s modulus of the fibroblast-derived matrices was 105±14 Pa. The FIEL based analysis concluded that matrix stiffness was not affected by ascorbate treatment, but that glutaraldehyde fixation increased the stiffness of the fibroblast-derived matrices. All of the matrix conditions investigated were heterogeneous over the length scale studied here. Data on microenvironment mechanics of natural tissues have previously been difficult to obtain. The findings and methods presented here provide guidance for the assessment of this important component of bioscaffold design.