Actin Dynamics: From Nanoscale to Microscale

Abstract

The dynamic nature of actin in cells manifests itself in many ways: Polymerization near the cell edge is balanced by depolymerization in the interior, externally induced actin polymerization is followed by depolymerization, and spontaneous oscillations of the cell periphery are frequently seen. I discuss how mathematical modeling relates quantitative measures of actin dynamics to the rates of underlying molecular level processes. The rate of actin incorporation at the leading edge of a moving cell is roughly consistent with existing theories, and the factors determining the characteristic time of actin polymerization are fairly well understood. However, our understanding of actin disassembly is limited, in particular the interplay between severing and depolymerization and the role of specific combinations of proteins in implementing disassembly events. The origins of cell-edge oscillations, and their possible relation to actin waves, are a fruitful area of future research.

INTRODUCTION

The intracellular protein actin is crucial for the migration of eukaryotic cells, their mechanical integrity, and their shape (7). Actin polymerizes into semiflexible filaments, which in turn cross-link into a gel constituting the actin cytoskeleton. The growth of this gel leads to the formation of cellular protrusions having very distinct shapes. When a protrusion is spatially localized and coordinated with retraction occurring elsewhere, a cell can migrate. These processes rely on rapid polymerization and depolymerization of actin in response to external stimuli. Therefore, a quantitative treatment of cell motion and shape changes requires a detailed understanding of the mechanisms involved in the assembly and disassembly of actin. Experiments using carefully chosen mutants and sophisticated imaging techniques have revealed crucial features of the molecular pathways that control actin polymerization. Extracellular signals activate cell surface receptors, which in turn activate signaling cascades leading to actin polymerization or depolymerization. The signaling pathways are incompletely known, but some of the key proteins/complexes upstream of actin, and their functions, are established. These include specific proteins and complexes which nucleate new actin filaments, cap filament growth, and disassemble actin. The mode of action of these proteins has been studied via both in vitro studies of pure-protein mixtures and cell studies involving knockdowns or knockouts of these proteins, with substantial consistency between the in vitro and in vivo studies.

However, our understanding of the relationship between molecular level processes and the observable dynamics of actin polymerization in cells is limited. For example, we do not know how to relate the rate of intracellular actin assembly in response to a stimulus, to polymerization and branching rates; nor do we know how to relate the disassembly rates of actin networks to severing and depolymerization rates. The main focus of this review is the quest to quantitatively explain macroscopic actin dynamics in cells in terms of molecular level processes. Actin dynamics is a broad field, and recent reviews have treated it from different perspectives (15, 50, 59, 77). Here I focus on three limited classes of phenomena. I first introduce basic aspects of actin polymerization and define some key questions regarding actin dynamics in cells. I then describe and evaluate the role of theory in understanding three aspects of actin dynamics: assembly and disassembly of steady-state actin distributions, actin polymerization dynamics in response to external stimuli, and spontaneous spatiotemporal patterns formed by actin in cells.

BACKGROUND

Actin exists in unpolymerized and polymerized forms known as G-actin and F-actin, respectively. I do not treat the atomic level structure of actin, but rather focus on the structure of F-actin and the supramolecular structures that it forms. See Reference 58 for a more complete treatment. Figure 1a shows a recent molecular level structure of F-actin. The subunits are arranged in a double helix with a length increment of a = 2.7 nm per added subunit. This arrangement allows an incoming subunit to have connections to two subunits in the filament. This double connection means that binding of an incoming subunit to a filament can be strongly exothermic, even though a G-actin dimer is unstable. This renders spontaneous nucleation of actin filaments slow in comparison to polymerization of existing filaments. Spontaneous nucleation is further slowed by actin-binding proteins in the cellular environment. Actin filaments have two ends, barbed and pointed, that have distinct polymerization properties. Polymerization dynamics are much faster at barbed ends. Because polymerization is exothermic, it can supply the energy required to propel a cell through its environment, or pathogens through a cell.

Figure 1.

(a) Structure of F-actin filament based on electron microscopy (34). Total length of filament is about 40 nm. (b) Branched network structure in keratocyte lamellipodium (66). Width of field in top frame is about 3 μm. Closeups are taken from indicated boxes in top frame.

Actin in cells is dynamic and strongly out of equilibrium. Unlike an equilibrium polymer, whose polymerized state persists once formed, actin undergoes a cycle of polymerization and depolymerization fueled by a continuing input of chemical energy. This cycle allows the actin cytoskeleton to respond rapidly to changing external stimuli, and causes spontaneous dynamic behaviors. The nonequilibrium nature of actin is manifested in the different critical concentrations $A_c^B\approx 0.1\mu \mathrm{M}$ and $A_c^P$. The critical concentration for each end is the free-actin concentration at which polymerization precisely balances depolymerization, and the difference of the critical concentrations means that the two ends are thermodynamically inequivalent. The free energy driving the nonequilibrum behavior of actin is supplied by ATP. Actin binds a nucleotide, either ATP, ADP-P_i, or ADP, where ADP-P_i is hydrolyzed ATP whose phosphate has not yet been released. In intracellular G-actin, ADP is rapidly exchanged to ATP. In F-actin, ATP spontaneously hydrolyzes to ADP-P_i actin and subsequently becomes ADP. ADP-actin polymerizes less strongly than ATP-actin, and this causes the difference between $A_c^B$ and $A_c^P$.

Actin filaments in cells are assembled into extended structures such as branched networks and bundles. Branched networks often occur in lamellipodia, which are broad, thin protrusions extending at the front of a cell. As shown in Figure 1b, the branched networks have a polarized structure with barbed ends preferentially pointing toward the membrane. The filament length is typically a fraction of a micron. Assembly of branched networks is aided by the Arp2/3 complex, a seven-protein complex that binds to the sides of existing filaments and creates new daughter branches. Because the rate of new branch formation is proportional to the number of existing branches, filament nucleation by branching is an autocatalytic process. Additional mechanical stability is provided by cross-linking proteins. Polymerization occurs mainly near the membrane and depolymerization mainly away from the membrane. The assembly of branched actin networks is often signaled by upstream external agents such as growth factors. These activate receptors at the cell surface, which leads to activation of actin-binding proteins such as Arp2/3 complex. Disassembly of actin networks involves both severing of and depolymerization of actin filaments, with the balance between these two processes unclear. Disassembly is typically viewed as occurring in the absence of active intervention. However, since proteins which sever actin filaments, such as cofilin, can be activated from the membrane, such active intervention is a possibility. Bundles are composed of tightly cross-linked filaments and occur in protrusions such as filopodia. Several provocative recent papers (3, 35a, 43, 53, 83a) have treated the dynamics of filopodia.

I restrict this review to structures in cells, such as lamellipodia, that are based on branched networks. I follow the weight of experimental work in the field in treating cells on flat substrates rather than in three-dimensional media. I also focus on polymerization at cell membranes, rather than that induced by external pathogens such as Listeria. The following aspects of actin dynamics will be treated:

• ■Steady-state actin dynamics. This refers to a distribution of F-actin that appears stationary at a coarse-grained level but is maintained by an dynamic balance between polymerization and depolymerization. Actin assembly at the front of a lamellipodium and disassembly farther back combine to produce a steady-state F-actin profile. What factors determine the assembly and disassembly rates underlying this profile? How is polymerization modulated by the constraints of the membrane and by the influence of actin-binding proteins? Is there a single key process that determines the rate of actin network disassembly?
• ■Dynamics of actin polymerization in response to external stimuli. Several types of external stimulation can induce actin polymerization. How is the timescale of the polymerization response related to key rates such as those of branching and filament elongation? Is the timescale of response set by upstream signaling events or by actin polymerization itself? Is the polymerization response monotonic or peaked?
• ■Spontaneous dynamics of F-actin. Actin can form spontaneous spatiotemporal patterns such as traveling waves and moving patches. Formation of such patterns requires positive feedback, in which a molecular constituent fuels its own growth. Does this feedback reside in the F-actin itself or rather in upstream activators? What factors determine the speed, wavelength, and lifetime of actin waves and patches? How are actin waves related to the dynamics of the cell edge?

I emphasize the role of recent theoretical work in relating these phenomena, which are observed at a length scale of micrometers, to the rates of underlying nanoscale molecular level processes. Such relationships are understood for a few in vitro cases, but our study of actin in vivo is much more limited. Therefore, I focus on a few examples that show how theory can generate experimentally testable hypotheses, and define areas and questions that are particularly ripe for theoretical input.

STEADY-STATE DYNAMICS OF ACTIN

Two primary experimentally accessible measures of steady-state actin dynamics in cells are important for the shape of the F-actin distribution in cells: the polymerization velocity and the turnover time in actin networks.

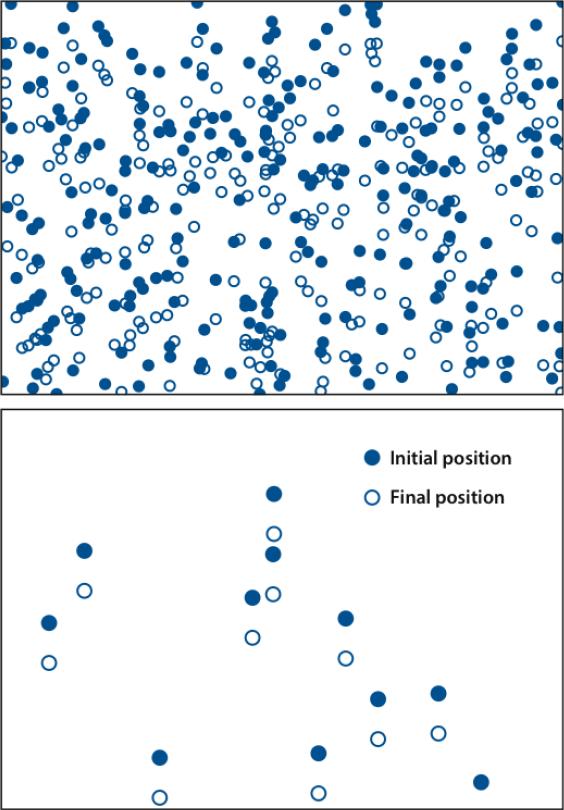
The polymerization velocity is the flow rate of actin relative to the cell membrane. It is the difference between the protrusion rate and the retrograde flow rate (backward flow of actin relative to the substrate). The polymerization velocity is most directly measured by speckle microscopy (21). In this method, illustrated in Figure 2, a small fraction of actin subunits are fluorescently labeled to create a nonuniform intensity distribution whose motion can be easily followed. The polymerization velocity in cells varies greatly, from 7 nm s^□1 for fibroblasts (76) to 170 nm s^□1 for keratocytes (70). Because the length increment per added subunit a is 2.7 nm, the corresponding monomer addition rates are in the range of 3 to 60 s^□1 if the filaments are nearly perpendicular to the membrane.

Figure 2.

Schematic of speckle microscopy. Membrane is at top. Solid blue circles denote areas with higher fluorescent labeling fraction. Open blue circles correspond to filled circles after they have moved away from the membrane. Bottom frame has lower labeling fraction, making the motion much easier to detect.

The polymerization velocity has often been related to the elongation rate v of a single average filament at the membrane. If the membrane acts as a diffusing hard wall, the filament is rigid, and polymerization is passive, compelling physical arguments lead to the following “Brownian-Ratchet” form for v (49):

$$v=k_{on}^{0}a(\left[A\right]-A_c^B)\cos \left(\theta \right)\exp [-Fa\cos \left(\theta \right)∕k_{B}T],$$ (1)

where $k_{on}^0$ is the barbed-end on-rate constant, [A] is the G-actin concentration, θ is the angle of the filament relative to the membrane normal, and F is the average force generated per filament. The order of magnitude of this estimate is roughly consistent with observed polymerization velocities (69) if one takes a value of θ between 0° and 60° and assumes that the opposing force is not too large.

However, the polymerization velocity is affected by several additional effects , which have been treated individually but not yet together in a single model:

• ■Variation of the number of filaments N at the membrane. Increasing N will reduce F, and also [A], because free monomers will be used up more rapidly. Our ability to predict N at this point is limited. A branching nucleation model (12) suggested that N is proportional to total force, whereas a model based on spontaneous nucleation (52) found that N is independent of force. A lamellipodium model combining several aspects of actin polymerization and force generation (51) found an optimal value of N for rapid protrusion. Too large a value of N causes [A] to drop at the membrane, whereas too small a value increases F, slowing protrusion.
• ■Attachment of some of the actin filaments to the membrane (7). If these filaments do not grow, they slow the growth of the free filaments (52). However, the attached filaments may grow, and several scenarios are possible. On the one hand, growth could be slowed owing to the proximity enforced by attachment (83). On the other hand, membrane proteins could accelerate polymerization by recruiting accessory proteins (71). Finally, membrane attachment could enhance force generation by coupling polymerization to filament-tip chemical reactions (22).
• ■Filament capping. Several types of proteins in cells can cap barbed ends and thus prevent growth. Is the polymerization velocity equal to that of the uncapped filaments, or rather is it weighted by the fraction of filament tips that are uncapped? The stochastic branched-network growth model (12) found that the polymerization velocity decreases when the uncapped fraction increases.
• ■Actin gel deformation. Studies of actin motion in lamellipodia have revealed substantial compression of the actin network (55, 60) when viewed from above. Furthermore, experiments measuring cellular protrusion forces showed that they can be limited by mechanical distortion of the lamellipodium (6). Actin gel deformation has been treated in an elastic model (46), and also in the recently developed moving-cluster model (39, 40). This model treats clusters that grow by branching nucleation of new filaments near a disk in a fluid. This model found a force dependence of the velocity distinct from that predicted by Equation 1: The velocity was constant at small forces, with a rapid drop occurring at larger forces.
• ■Actomyosin contraction. When the protein myosin is present in actin networks, the combination of these two proteins (“actomyosin”) can generate contractile forces which pull the actin network away from the cell membrane, supplementing the motion due to actin polymerization. Recent work (55) showed that myosin inhibition in keratocytes reduces the polymerization velocity by a factor of four [although this does not hold for all cell types (60)]. Thus, contractile forces can have a large impact on the polymerization velocity.

A comprehensive stochastic model of actin polymerization at a flexible membrane (62a) showed that the first four of these effects can combine to yield a force-velocity relation which, for some parameter choices, differs strongly from that of Equation (1): it is flat at small forces, and then curves downwards with increasing force. These simulations found that “work-sharing” is a robust feature of the model. This means that the distribution of filament-membrane distances self-organizes so that an entering monomer can attach at an optimal location.

The interaction between theory and experiment in analyzing the polymerization velocity in cells would be greatly aided by the development of new biomimetic systems more directly relevant to cells than existing ones. The most widely used biomimetic systems, protein-coated spherical beads, have a geometry very different from that of a lamellipodium. Development of an artificial system with the lamellipodial geometry is difficult because of the small dimension (0.2 m) in the vertical direction. However, such a system would allow a direct comparison between theory and experiment which is impossible in cells because of the large number of intracellular proteins that affect actin polymerization. For treating the full complexity of the cell, the most promising route to a comprehensible model at this point may well be a top-down approach, beginning with macroscopic models of the actin gel mechanics, with parameters informed by results of more detailed, filament-based models. Some promising steps have been taken in this direction (36, 46), and it is to be hoped that these models will become more closely interfaced with molecular level analysis.

The turnover time τ required for polymerized actin subunits to disappear from the actin network is measured most directly by speckle microscopy, but it can also be measured by other methods such as fluorescence recovery after photobleaching. Measured values of τ vary widely, from about 20 s in keratocytes (68) to nearly 500 s in some endothelial cells (47). One might expect that the lamellipodium width would be determined in a simple fashion as a product of τ and the polymerization velocity. However, this procedure can greatly underestimate the width (69), because assembly occurs simultaneously with turnover. The width is determined by the net loss rate of actin, which is the disassembly rate minus the assembly rate.

Turnover is driven by a combination of depolymerization, severing of filaments, detachment of branch points, and hydrolysis of ATP-actin to ADP-actin, which enhances depolymerization. A key protein is cofilin, which severs actin filaments and may enhance pointed-end depolymerization (11). The severing activity of cofilin is much stronger for ADP-actin than for ATP-actin.

It has been suggested that the disassembly rate is determined by the time required to depolymerize single actin filaments (51). If one ignores the effects of severing and the three-dimensional network structure, disassembly of a filament is a three-step process. Its barbed end becomes capped soon after nucleation, and its pointed end is capped at its base already upon nucleation. Because barbed-end uncapping is slow, pointed-end uncapping occurs first. Then, disassembly occurs sequentially with pointed-end uncapping preceding pointed-end depolymerization, so that

$$\tau ={\tau }_{\text{uncap}}+{\tau }_{\text{depol}},$$

where τ_uncap is the uncapping rate, τ_depol = L/k_off, k_off is the net pointed-end off-rate, and L is the filament length measured in subunits. If L = 100 and k_off = 0.8 s^□1 (57), the second contribution is about 100 s, in the middle of the range of measured values of τ. However, it has been suggested that cofilin can accelerate pointed-end depolymerization by as much as a factor of 30 (11), and then the second contribution is only 3 s. In this case, τ_uncap must be responsible mainly for the observed values of τ.

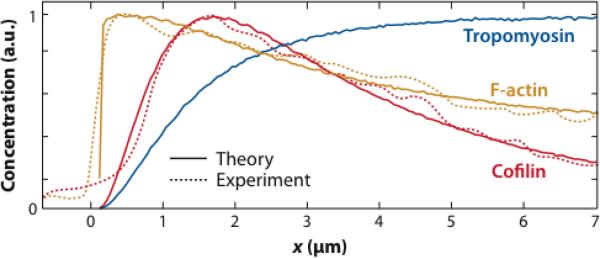
A more detailed model of disassembly in a keratocyte lamellipodium treated polymerization/depolymerization, as modified by hydrolysis of ATP in actin filaments, G-actin depletion near the leading edge, and accessory proteins which sever, anneal, and protect filaments (35). The model includes the effects of branching via pointed-end capping but does not have an explicit three-dimensional cross-linked network structure. Remains of severed filaments are taken to remain in place, so the only mechanism removing F-actin from the system is depolymerization. With appropriately chosen parameters, this model closely reproduces experimental lamellipodial F-actin profiles (see Figure 3). An estimate of τ ≈ 40 s, within a factor of two of the experimental result, is obtained from the ratio of the calculated depolymerization rate per unit volume to the F-actin concentration. This work made two surprising predictions regarding the effect of severing, First, severing increases the filament length away from the leading edge by exposing new barbed ends, which grow longer in the higher G-actin concentration away from the leading edge. Second, the effect of severing on the F-actin profile is limited.

Figure 3.

Theory (solid curves) versus experiment (dashed curves) for decay of F-actin (orange), cofilin (red), and tropomyosin (blue) densities away from leading edge of a keratocyte (35).

A highly idealized model complementary to these two approaches has emphasized the effects of the network topology on disassembly (14). It treated a cross-linked network of actin filaments, with idealized square or cubic symmetry, in which severing events occur randomly and depolymerization proceeds instantaneously from the severing point to the nearest cross-link. The lamellipodium width was nearly inversely proportional to the severing rate. Annealing was implemented by allowing filaments to reappear stochastically between cross-linking points. This gave a wider lamellipodium and, for a large value of the annealing rate, a transition to an infinitely wide lamellipodium.

Our incomplete understanding of the underlying molecular level processes is a major difficulty for theories of actin assembly. For example, cofilin is believed to enhance depolymerization by creating free pointed ends and decorating them (11) but also to enhance polymerization by exposing free barbed ends (75). Both experiments based on sudden release of cofilin in cells (31) and theoretical analysis (13) have shown that severing can cause actin assembly under some conditions. However, recent experiments on single actin filaments (37) suggest that the combination of the proteins cofilin, coronin, and Aip1 can have a strong depolymerizing effect. These experiments showed that filaments disassemble in large bursts of average size 0.7 μm (260 subunits), which last less than a second. The average time between bursts was about 14 s. If such a phenomenon occurs in cells, network filaments about 0.3 μm long will disassemble in a single burst. It has also been shown recently that coronin, like cofilin, can switch roles from inhibiting disassembly to promoting it (28).

In unraveling the interactions between many competing molecular level processes underlying actin disassembly, a useful and realistic task for theory would be prediction and measurement of the behavior of a single barbed or pointed end, as modulated by the varying protein concentrations in different parts of a cell. Even in the absence of actin-binding proteins, barbed-end dynamics are challenging. They display surprisingly large growth and shrinkage fluctuations (27, 36a,38), which theory is only beginning to explain (42, 65, 72). Understanding such properties of single filament ends would provide a solid underpinning for analyzing the more complex behaviors possible in the cellular environment.

DYNAMICS OF ACTIN POLYMERIZATION IN RESPONSE TO EXTERNAL STIMULI

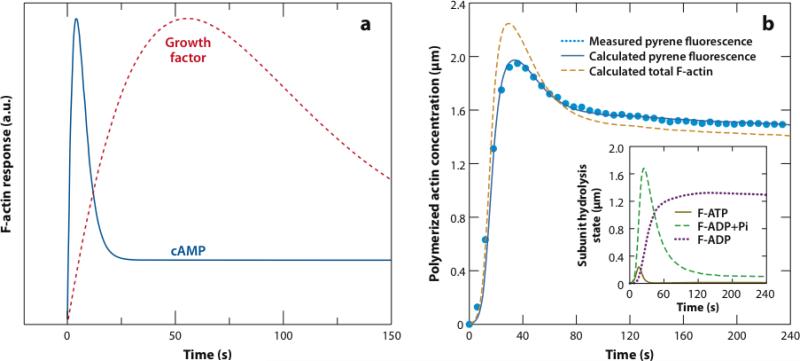
Actin polymerization in cells often occurs after stimulation by external agents such as growth factors (see Figure 4). These bind extracellular receptors and activate multistep signaling pathways that eventually make contact with actin. When actin polymerization is measured after stimulation, the polymerization time course combines features of the upstream signaling pathways and of the actin polymerization dynamics. The time courses shown in Figure 5a are schematic composites of measured polymerization time courses for Dictyostelium (18, 19) stimulated by cyclic adenosine monophosphate (cAMP), a small signaling molecule, and splenocytes and adenocarcinoma cells stimulated by growth factors (17, 41).

Figure 4.

Schematic of external stimulation of actin polymerization in a cell. Solid blue circles denote external stimulant, such as epidermal growth factor. After stimulant attaces to cell membrane, an actin network grows (right).

Figure 5.

(a) Schematic of actin polymerization in response to cAMP stimulation and growth factor stimulation. (b) Measured pyrene fluorescence (light blue dotted line) (67), calculated pyrene fluorescence (dark blue solid line), and calculated total F-actin (orange dashed line) versus time for rapidly polymerizing actin in vitro (10).

They illustrate basic features seen in stimulated actin polymerization: the polymerization time---the time to reach the maximum---and a drop after the maximum. For the cAMP-stimulated cells, polymerization occurs rapidly and the polymerization time is only a few seconds. Later, the F-actin content drops to a lower asymptotic value. In the growth-factor-stimulated cells the polymerization time is on the order of 1 min. A drop also occurs here. Theoretical analysis aims to relate these characteristic times to well-defined molecular-level processes, and to establish which features of curves like those in Figure 5a are due to elements of the upstream signaling network, such as built-in delays and feedback loops, and which are inherent features of the actin polymerization dynamics.

How Fast Does Actin Polymerize?

A simplified estimate of the actin polymerization time is obtained by assuming that stimulation suddenly creates a large density [B] of free barbed ends and by ignoring depolymerization. The subunit addition rate at a growing barbed end is ${\mathrm{k}}_{\mathrm{on}}={\mathrm{k}}_{\mathrm{on}}^0\left[\mathrm{A}\right]$, where ${\mathrm{k}}_{\mathrm{on}}^0\approx 10\mu {\mathrm{M}}^{◻1}{\mathrm{s}}^{◻1}$ (57). Thus, the total rate of consumption of G-actin, □d[A]/dt, is ${\mathrm{k}}_{\mathrm{on}}^0\left[\mathrm{A}\right]\left[\mathrm{B}\right]$. This relation gives the following time dependency:

$$\left[\mathrm{A}\right]={\left[\mathrm{A}\right]}_0\exp (-t∕{\tau }_{\mathrm{pol}}),$$

where the characteristic time of polymerization is

$${\tau }_{\mathrm{pol}}=1∕k_{\mathrm{on}}^0\left[\mathrm{B}\right].$$ (2)

The value of [B] is uncertain, but stimulation of mammary adenocarcinoma cells produced 13,000 new free barbed ends per cell (17). If one assumes that these are created within 2 μm of the cell edge, over a circumference of 150 μm, and in a lamellipodium of height 0.2 μm, one obtains [B] = 0.4 μM as a rough estimate. This gives |_pol = 0.25 s. Thus, the polymerization process is fast in comparison to the delays seen in Figure 5a.

However, new barbed ends are not created suddenly, but rather by branching and severing of existing filaments. Furthermore, free barbed ends eventually become capped. New branches are created only near the membrane, and therefore near filament barbed ends. Then, the creation rate of new free barbed ends is proportional to their concentration, so that d[B]/dt = k_br[B]□k_cap[B], where k_br is the branching rate per filament tip and k_cap is the capping rate (16). This gives a growing exponential with timescale

$${\tau }_{\mathrm{br}}=1∕({\mathrm{k}}_{\mathrm{br}}-{\mathrm{k}}_{\mathrm{cap}}).$$

Because k_br depends nonlinearly on [A] (16), it is hard to estimate k_br reliably from in vitro studies. However, the spacing between branches, measured in subunits, should equal k_on/k_br. Taking the value of k_on from the measured locomotion speed of 170 nm s^□1 for a keratocyte (68), one obtains k_on = 60 s^□1. A typical branch spacing is 15 subunits (66), so k_br = k_on/15 = 4 s^□1. In order for growth of a branched network to proceed, k_cap must be significantly less than k_br (12). This suggests that ≃_br 0.5 s, shorter than the characteristic polymerization times. Thus, branch creation does not appear to cause significant delays in comparison with the observed ones.

If new barbed ends are generated by severing of existing filaments, d[B]/dt is proportional to the amount of F-actin present. This leads to a pair of rate equations for [B] and [A], whose solution (13) gives a growing exponential with time constant

$${\tau }_{\mathrm{sev}}={(1∕{\mathrm{k}}_{\mathrm{sev}}{\mathrm{k}}_{\mathrm{on}})}^{1∕2}.$$

The value of k_sev in cells is uncertain, but the rate equations show that (if annealing processes can be ignored) k_sev = k_on/L², where L is the average filament length measured in subunits, which is typically of order 100 in cells. Thus, k_sev ≈ 60 s^□1/100² = 0.006 s^□1, and |_sev = 1.5 s, again short in comparison with the observed polymerization delays.

The above analysis has shown that actin in cells can polymerize rapidly. Thus, delays such as those seen in Figure 5a are imposed by the upstream signaling machinery, not the actin polymerization machinery. This is consistent with the observation that internal polymerization events can occur much faster than signaled events. For example, measurements of F-actin dynamics along the substrate-attached surface of Dictyostelium (23) showed polymerization occurring over times as short as 0.15 s.

Why Does Actin Polymerization Peak and Then Drop?

Classical equilibrium theories of polymerization produce monotonic polymerization curves, because the polymerized state has the lowest free energy and the system approaches this free-energy state monotonically. However, the time courses shown in Figure 5a show an overshoot---a peak in polymerization followed by a drop. This is not completely surprising, given the nonequilibrium nature of actin polymerization discussed above. Furthermore, some in vitro polymerization time courses display overshoots (33, 44, 54, 67, 82). Here I treat the mechanisms underlying the in vitro overshoots and discuss whether these mechanisms could explain the features of in vivo polymerization seen in Figure 5a. Figure 5b shows fluorescence of pyrene-labeled actin during in vitro polymerization accelerated by branching (67). The pyrene label (20) is often used as a measure of polymerized actin. The calculated fluorescence intensity is given by a stochastic-growth polymerization model including branching and ATP hydrolysis, and the dashed line shows the corresponding time course of F-actin (10). The curves differ because different nucleotide states have different pyrene fluorescence intensities, with the best-fit ADP intensity being about 60% greater than that for ATP or ADP-P_i. Both experimental and simulated fluorescence intensities show a pronounced overshoot. This feature has often been attributed to artifacts of the pyrene assay, but the simulations showed that the overshoot in the F-actin concentration is instead greater than that seen in the pyrene fluorescence.

The overshoot is a generic feature of rapid nonequilibrium actin polymerization (56a). It arises as follows. Initially (during the first 30 s), the G-actin is overwhelmingly ATP-bound (Figure 5b). Thus, the concentration of polymerized actin climbs to a value near that of the total actin concentration minus the ATP-actin barbed-end critical concentration $A_c^B\approx 0.1\mu \mathrm{M}$. Then, barbed ends convert ATP-G-actin monomers to ADP-G-actin monomers by subunit exchange (which is faster than direct phosphate release): An ATP-actin monomer attaches to a barbed end, is hydrolyzed to the ADP-P_i state, detaches from the barbed and, and releases the P_i into solution to become ADP-actin. Finally, the G-actin becomes more ADP-like and the critical concentration increases, leading to reduced polymerization at long times.

Can such a mechanism explain polymerization overshoots in cells? The key parameter in determining whether an overshoot occurs is the ratio of the polymerization time τ_pol (see Equation 2) to the nucleotide exchange time τ_ex required for a monomer in solution to replace ADP by ATP. In vitro, τ_ex ≈ 100 s (63), suggesting that if τ_pol □ 100 s overshoots will occur. This is consistent with the timescale of polymerization in known cases of overshoots. In cells, the exchange time is shorter because profilin accelerates exchange, and in vitro experiments (63) suggest that τ_ex ≈ 1 s. With τ_pol values on the order of 1 s in cells, hydrolysis-induced overshoots could occur. However, their duration would be limited by the time required for ADP-G-actin to equilibrate with ATP-G-actin. This time in turn should be comparable to or less than τ_ex, which is much smaller than the durations seen in Figure 5a. Thus, for the observed overshoots to be due to ATP hydrolysis, τ_ex must be much larger than is commonly believed. Other possible mechanisms for overshoot behavior include incoherent feedforward loops in the signaling network and barbed-end capping. An incoherent feedforward loop (1) creates a peaked response by the combination of a direct stimulatory path and a delayed inhibitory path. Barbed-end capping could lead to overshoots because early polymerization is dominated by barbed ends, but later on pointed ends, which have a higher critical concentration, dominate.

SPONTANEOUS DYNAMICS OF F-ACTIN IN CELLS

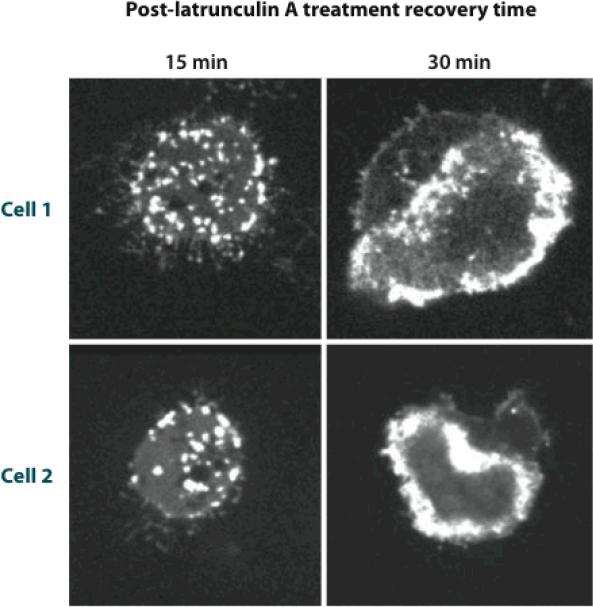
F-actin in cells often displays dynamic features such as waves and patches, despite the absence of time-varying stimuli. Pioneering studies of fluorescently labeled actin in Dictyostelium (73, 74) revealed rings of actin moving along the substrate-attached membrane of the cell. Such features are seen more clearly in total-internal-reflection microscopy (TIRF), in which the electromagnetic field exciting fluorescence acts only very near the substrate. TIRF studies of Dictyostelium (29) using well-tested fluorescent labels for F-actin treated actin dynamics during recovery from depletion of G-actin (see Figure 6). The first step in the recovery was the appearance of moving actin patches. With increasing free G-actin content, the patches coalesced into waves moving at speeds of 12–15 μm min^□1. Finally, the F-actin became concentrated at the cell periphery. Other observations of actin waves have been made in mouse embryonic fibroblasts (MEFs) (32) and neutrophils (78). Understanding actin waves in cells may help us understand other examples of spontaneous actin dynamics, such as (a) periodic patterns of actin turnover at the outer edges of epithelial cells (61), (b) time-varying distributions and moving patches of actin-binding proteins in fibroblasts (62), and (c) repeated cycles of actin assembly/disassembly on phagosomes in epithelial cells infected by pathogens such as Listeria (80).

Figure 6.

F-actin distribution in two Dictyostelium cells during recovery from latrunculin A treatment. (29).

The molecular scale mechanisms underlying such dynamic patterns are not well known, but it is likely that they consist of branched actin networks (9). Moving patches in yeast consist of such networks (81), but these patches move away from the membrane rather than alongside it. It is plausible (73) that actin waves and moving patches could be explained by a reaction-diffusion mechanism (48), based on two spatially varying quantities, an activator and an inhibitor. The activator diffuses and has positive feedback in the sense that it activates its own growth. It grows at the front of the wave, and the wave front is pushed forward by diffusion. Later, the inhibitor grows, which suppresses the activator. Basic properties of such waves and patches include (a) a wave speed roughly proportional to (D/τ_act)^1/2, where D is the diffusion coefficient of the activator and τ_act is a characteristic timescale of activator growth, and (b) growth or diffusion of the inhibitor that slows wave or patch motion.

Does Actin Generate Its Own Dynamics, or Rather Does It Respond to Signals from Upstream Pathways?

Nucleation of actin filaments is controlled by upstream signaling elements called nucleation-promoting factors (NPFs), which are active mainly at the cell membrane. Current mathematical models for actin waves view F-actin either as a negative feedback element in a signaling network containing positive feedback from NPFs (NPF-driven) or as having positive feedback itself (actin-driven). Two concrete realizations of the NPF-driven scenario (25, 78) have taken the NPF to be the protein Hem-1, which acts upstream of filament nucleation. They assume that positive feedback of NPFs results from its cooperative binding to the cell membrane, which is consistent with the observation of cooperativity in known NPFs. In addition, they assume delayed inhibition from F-actin. This delayed-inhibition assumption is supported by data that show that actin polymerization accelerates detachment of Hem-1 from the membrane (56). Weiner et al. (78) treated the actin polymerization dynamics using a simplified, local rate equation, whereas Doubrovinski & Kruse (26) treated them using a more complete model based on nucleating and treadmilling filaments. Both approaches gave rise to spontaneous waves, and Doubrovinski & Kruse also found regimes corresponding to patches.

A recent model of actin waves (79) has assumed an actin-driven scenario, taking an unspecified membrane constituent to be the inhibitor. Actin polymerization was treated with a quadratic positive feedback term, which could result from autocatalytic branching nucleation. The F-actin was assumed to undergo two types of motion: flow parallel to a local orientation, which develops spontaneously, and diffusive spreading resulting from the growth of new filaments. The F-actin terms were supplemented by terms describing a diffusing inhibitor, growing at a rate determined by the F-actin concentration. This model displayed a time-dependent transformation from static spots, to traveling spots, to traveling waves.

How could one experimentally distinguish between these competing models? If both the activator and inhibitor are known, one can see which leads the way by imaging them separately (78). In the absence of such information, manipulating the rate of actin polymerization could provide a useful test. In the actin-driven scenario, accelerating actin polymerization speeds up the waves because it reduces τ_act. In the NPF-driven scenario, if actin acts only as an inhibitor, accelerating actin polymerization slows the waves and reduces the wave period. However, if the motion of polymerizing actin ends is included (26), the net result is not clear. Recreation of wave and/or patch behavior in a biomimetic system would allow the cleanest interface between modeling and experiment. A minimal system would include a standard motility medium (46) used to grow branched actin networks in vitro, and a substrate containing an NPF complex that is detached by F-actin. If the NPF-driven scenario holds, this system should display waves or patches when appropriately tuned. If the actin-driven scenario holds, the inhibitor might be identified with absence of NPF. In this case, waves or patches would also occur, but with a different dependence on the experimental conditions.

Are Oscillations and Waves on the Cell Edge Driven by Actin Waves?

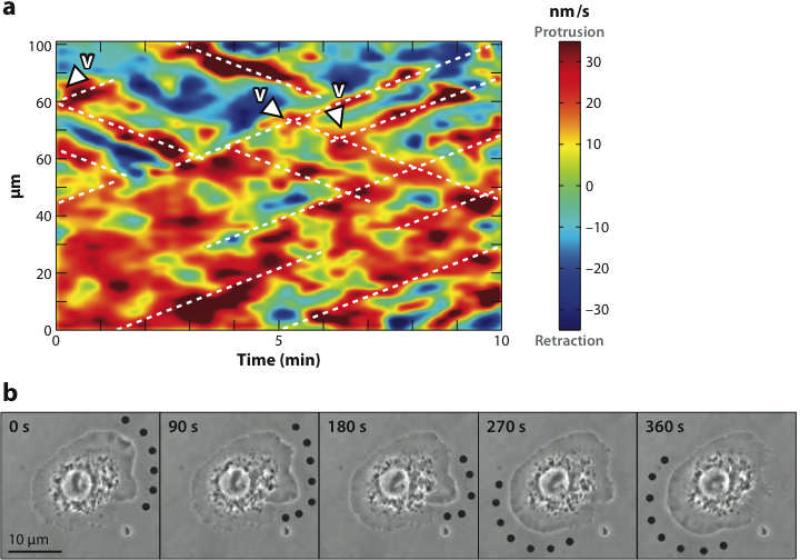
Spontaneous oscillations of the cell edge are seen in several cell types (5, 24, 45) and can be important for exploring the extracellular environment. Because actin polymerization can exert forces on the cell membrane, cell-edge oscillations could be driven by actin waves impinging the membrane. This connection is supported by data (8, 78) showing that impingement of a wave on the membrane correlates temporally with outward membrane motion. Four recent studies quantitatively analyze cell-edge waves and/or oscillations (2, 5, 24, 45). A geometric visualization of waves and oscillations in keratocytes, MEFs, newt lung epithelial (NLE) cells, and PtK1 epithelial cells (45) found two main types of behaviors: (a) global oscillations of large pieces of the cell periphery and (b) transverse waves, in which random bursts of protrusion trigger waves traveling away from the protrusion. Global oscillations were seen in NLE cells, whereas transverse waves were seen in PtK1 cells (see Figure 7a). Manipulation of protein activity changed the nature of the oscillations and waves. Enhancement of polymerization activators caused a transition from lateral waves to in-phase oscillations. Conversely, inhibition of branching nucleation in PtK1 cells maintained the transverse-wave state, but fewer and less persistent waves were formed. A TIRF study (24) treated transverse waves in MEFs, mouse T cells, and wing-disk cells from fruit flies. The MEFs displayed global oscillations at maximal outward speeds of about 400 nm s⁻¹ without much lateral motion, the fly cells displayed lateral waves moving at about 120 nm s⁻¹, and the mouse T cells displayed short-lived transverse waves moving at about 55 nm s⁻¹. These speeds are comparable to those of actin waves.

Figure 7.

(a) Patterns of protrusion in a PtK1epithelial cell. Color (red for protrusion and blue for retraction) indicates velocity of membrane motion. Vertical axis is the distance along the edge of the cell and horizontal axis is time. Diagonal lines demonstrate transverse motion of waves (45). (b) Transverse protrusion wave in fly wing-disk cell. Dots indicate region of protrusion. Scale bar is 10 μm (2).

A detailed study of the distribution of radial velocities at the cell edge has been performed for rat and NG108 neurons (5). It revealed a bimodal distribution of velocities. In the NG108 cells, the peaks were at □25 nm s⁻¹ (inward) and 35 nm s⁻¹; for the rat cells they were at □150 nm s⁻¹ and 180 nm s⁻¹. The actin polymerization contribution to the edge velocity in both types of cells also had two peaks, one of which was centered near zero. In addition, time-correlation analysis showed that fluctuations in the edge velocity were correlated to the actin polymerization contribution but not with the speed of retrograde flow, showing that actin polymerization is an important factor in these oscillations. Finally, transitions from steady protrusion to transverse membrane waves in fly wing-disk cells were induced by increasing their binding to a substrate (2). Suppression of an actin-polymerization inhibitor in these cells induced polarization of the cell periphery and F-actin. Then, stronger substrate binding replaced the static polarization by protrusion waves (see Figure 7b) circling the cells for a period of about 10 min, corresponding to a speed of about 7 μm min⁻¹.

The correlations found in these experiments demonstrate a connection between actin polymerization and cell-edge oscillations. Actin waves are a possible mechanism for this connection. They could propagate from the interior of a cell to the periphery and then push it out. If the waves hit at an angle, they could generate transverse cell-edge waves. But, other possible mechanisms connect actin polymerization and cell-edge oscillations. For example, a mechanical oscillator model is plausible because oscillations in the actin-propelled motion of the bacterium Listeria and biomimetic beads have mechanical origins (4, 21a). A mechanical model of cell-edge oscillations (30) treated freely polymerizing actin filaments that generateforce by impinging on the membrane, filaments attached to the membrane via flexible springs, and cross-links behind the polymerization front. Cell-edge oscillations in this model result from waves of attachment and detachment mediated by changes in the distance between the cross-linking front and the polymerization front. Shlomovitz & Gov (64) proposed that transverse membrane waves result from the interplay between protrusive force from actin filaments generated by NPFs coupled to membrane curvature, and contractile force from the actomyosin gel. In this mechanism, an initial protrusion caused by an accumulation of NPFs grows. Then, myosin builds up behind it and generates a contractile force. Eventually, this causes NPFs to move sideways from the initial protrusion, resulting in a spreading wave of protrusion.

How could one discriminate between these models for cell-edge oscillations? The dynamic F-actin distribution would likely look different in the three models. For oscillations driven by actin waves, precursors inside the cell should be seen, as they were by Weiner et al. (78). The F-actin distribution for oscillations generated by attachment/detachment or by contractile force has not been calculated, but it does not appear that precursors deep inside the cell are required for either model. Myosin inhibition, by blebbistatin, for example, can evaluate the applicability of contraction-based models. This experiment was performed on NLE cells (45), and no effect on the dynamic state of the membrane was seen, indicating a nonmyosin mechanism. However, such experiments have not been performed for transverse waves. Another quantitative experimental output that could be used to discriminate between the models is the velocity correlation function between different points on the periphery of the cell. This was calculated for the contractile-force model (64) and it agreed well with experimental data for fly wing-disk cells (24). Calculation of such correlation functions for the actin-wave model and the attachment/detachment model might allow experiments to distinguish between the models. Finally, the dependence of the oscillations on cell-substrate interaction could help distinguish between the models. The reported substrate-induced transitions (2) are consistent with cell-edge oscillations caused by actin waves. A lamellipodium could propagate forward by a mechanism in which forward motion of the cell edge allows the polymerizing actin or diffusing NPF to encounter fresh substrate in which to grow. If the forward motion were blocked, then the wave would have to turn sideways to find fresh substrate, consistent with the observed transition. It is not clear whether attachment/detachment oscillations or contractile-force-based waves would reproduce this behavior.

SUMMARY

Actin in cells manifests a cycle of assembly and disassembly. It polymerizes near the cell edge and depolymerizes farther way. In response to a stimulus, actin polymerizes and then depolymerizes, and an actin wave is a spatially segregated assembly/disassembly cycle. We understand the assembly phase of these cycles better than the disassembly phase. The polymerization rate is determined by a few key parameters such as the monomer on-rate constant, and the rates of branching, severing, and capping, interact in well-defined ways. Although several plausible hypotheses for disassembly mechanisms have been made, we do not know how processes such as depolymerization and severing are implemented, by combinations of several proteins, to disassemble networks.

Because the complexity of intracelullar processes limits the accuracy and predictive power of current models, progress in this field would be greatly aided by the development of a broader class of biomimetic systems. Development of such systems could build on existing systems based on protein-coated beads, by creating shapes similar to that of the membrane in a lamellipodium; already a solid understanding of actin polymerization on a flat protein-coated surface would be very informative. In such systems, membrane diffusion of relevant proteins such as NPFs could be included by placing them in a lipid bilayer on top of a hard surface. The significance of such studies would be greatly enhanced by development of a polymerization medium which more realistically models that in the cell. Current media treat rapid actin disassembly inadequately, and for this reason contain actin concentrations much lower than those in cells. The development of improved motility media, in combination with more sophisticated experimental geometries, will allow a more meaningful comparison between theory and experiment, and will ultimately provide a crucial guide to modeling actin dynamics in cells.

SUMMARY POINTS

1. Actin in cells is kept out of equilibrium by a continuing influx of free energy.

2. The nonequilibrium nature of actin is manifested in phenomena such as spatially localized polymerization, nonmonotonic polymerization, and spontaneous appearance of spatiotemporal patterns such as traveling waves.

3. The disassembly of actin is crucial for cell function and is implemented by depolymerization and severing influenced by specific combinations of proteins.

4. Traveling waves of polymerized actin involve positive feedback effects from either actin itself or upstream activators, in combination with a delayed inhibition mechanism.

5. Oscillations at cell edges are strongly influenced by actin polymerization and may in some cases be due to actin waves.

FUTURE ISSUES

1. Macroscopic mechanical models for actin polymerization and depolymerization, developed on the basis of input from molecular level simulations and theory, will be crucial for progress in linking theory and experiment

2. Theory and simulation should strive to obtain a quantitative understanding of the dynamics – particularly depolymerization – of a single actin filament as influenced by the varying concentrations of actin-binding proteins in a cell.

3. We need a broader class of biomimetic model systems, to shed light on lamellipodial dynamics and the origins of spontaneous actin waves.

4. Establishment of the mechanisms connecting actin polymerization to spontaneous oscillations and waves of the cell edge can shed light on the strategies that cells use to sample their environment.

TERMS/DEFINITIONS

ADP-P_i

adenosine diphosphate that has not released phosphate

Arp2/3 complex

a seven-protein complex that nucleates new filaments by branching

ATP hydrolysis

cleavage of phosphate from ATP

Cofilin

an intracellular protein that facilities severing and depolymerization of actin

F-actin

the polymerized (filamentous) form of actin

G-actin

the globular (unpolymerized) form of actin

Lamellipodium

a flat protrusion extended by a migrating cell

MEF

mouse embryonic fibroblast

Myosin

an intracellular protein that, together with actin, generates contractile force

NLE

newt lung epithelial cell

NPF

nucleation-promoting factor

Overshoot

a peak in actin polymerization followed by a drop

Turnover

disassembly of an actin network