A simplified formula for quantification of the probability of deterministic assignments in permuted block randomization

Abstract

Open label and single blinded randomized controlled clinical trials are vulnerable to selection bias when the next treatment assignment is predictable based on the randomization algorithm and the preceding assignment history. While treatment predictability is an issue for all constrained randomization algorithms, deterministic assignments are unique to permuted block randomization. Deterministic assignments may lead to treatment predictability with certainty and selection bias, which could inflate the type I error and hurts the validity of trial results. It is important to accurately evaluate the probability of deterministic assignments in permuted block randomization, so proper protection measures can be implemented. For trials with number of treatment arms T = 2 and a balance block size B = 2m, Matts and Lachin indicated that the probability of deterministic assignment is $\frac{1}{m+1}$. For more general situations, with T ≥ 2 and a block size $B=\sum _{j=1}^T{m}_j$, Dupin-Spriet provided a formula, which can be written as $\frac{1}{B}\sum _{j=1}^T\sum _{i=1}^{m_j}\prod _{k=1}^i\frac{m_j-k+1}{B-k+1}$. This formula involves extensive calculation in evaluation. In this paper, we simplified this formula to $\frac{1}{B}\sum _{j=1}^T\frac{m_j}{B-m_j+1}$ for general scenarios and $\frac{1}{B-m+1}$ for trials with a balanced allocation. Through mathematical induction we show the equivalence of the formulas. While the new formula is numerically equivalent to Dupin-Spriet’s formula, the simple format not only is easier for evaluation, but also is clearer in describing the impact of parameters T and m_i on the probability of deterministic assignments.

1. Introduction

In randomized clinical trials, selection bias occurs when an investigator uses advanced knowledge of the treatment assignment as the basis for deciding whom to enroll, potentially inflating the type I error rate of between group tests to 100%, regardless of the sample size. Selection biases hurt the validity of clinical trials, and have received extensive attentions in the literature. In sequential randomized trials, selection biases most likely occur when the next treatment assignment is predictable (Berger and Exner, 1999; Berger et al., 2003; Berger 2010). To quantify the risk of selection bias, Berger provided definitions for treatment predictability and deterministic assignment in randomized clinical trials (Berger 2003, Berger 2005). A treatment assignment is considered as predictable if its probability distribution under the condition of previous assignments differs from the unconditional distribution, which was specified by the treatment allocation ratio. A treatment assignment is considered as deterministic if it has a positive probability of only one outcome. Open label and single blinded trials are most vulnerable to selection biases due to deterministic assignments. A recent search on the ClinicaTrials.gov website on November 27, 2009 resulted 15,297 phase III interventional trials, including 6,893 double blinded, 832 single blinded, 3,410 open label, 3239 no randomized/not applied and 905 without information. This result indicates that at least 35% (4,242 out of 12,040) of randomized phase III interventional trials are not fully blinded. No further information about the details of treatment masking for the 6,893 double blinded trials is available from that website. However, a perfect treatment masking can not be successfully achieved in each of these double blinded trials. Therefore, the proportion of trials threatened by selection biases caused by deterministic and predictable assignments will be greater than 35%.

Permuted block randomization is the most popular randomization method in clinical trials, mainly because of its effective control on imbalance and its simplicity in implementation (McEntegart, 2003; Berger, 2006; Salama, 2008). It is also the most vulnerable randomization method to selection biases, when used in open label or single blinded trials, because of the high predictability of treatment assignments. Matts and Lachin (1988) indicated that when permuted block randomization is applied to a two-arm trial with a balanced allocation and a known block size of B = 2m, the number of predictions with certainty can range from 1 to m within a block and the expected number of known assignments within a block is $\frac{2m}{m+1}$. In other words, the probability of deterministic assignments is:

$$p=\frac{1}{m+1}$$ (1)

Following Matts and Lachin’s approach, Dupin-Spriet presented a general formula for predictability with certainty in permuted block randomization (Dupin-Spriet et al., 2004):

$$p=\frac{1}{B}\sum _{j=1}^T\left[\frac{m_j}{B}+\frac{m_j(m_j-1)}{B(B-1)}+\cdots +\frac{m_j(m_j-1)(m_j-2)\cdots 1}{B(B-1)(B-2)\cdots (B-m_j+1)}\right]$$ (2)

Here T is the number of treatments, m_j (j = 1,2,⋯,T) is the number of assignments for treatment j within each block, $B=\sum _{j=1}^T{m}_j$ is the block size. This formula applies to trials with two or more treatment arms and balanced or unbalanced allocations.

In this paper, we focus on the quantification of the probability of deterministic assignment in permuted block randomization. Following the similar approach described by Dupin-Spriet, we present a simple formula, which is numerically equivalent to formula (2). The impacts of block size, the number of treatment arms, and the treatment allocation ratio on the probability of deterministic assignment are analyzed.

2. Dupin-Spriet’s Formula

Dupin-Spriet provided formula (2) for the quantification of the probability of deterministic assignment in permuted block randomization (Dupin-Spriet et al. 2004). In the process of permuted block randomization, all possible treatment assignment sequences in a block have the same probability of occurring. By definition, deterministic assignments always occur at the end of each block. Based on the property of hypergeometric distribution, the chance a certain number of consecutive assignments for a specific treatment arm occur at the end of the block equals to the chance that these assignments occur at the beginning of the block. Therefore, in a block of size B with m_j assignments for treatment j, the probability of having 1 or 2 assignments for treatment j at the beginning (or end) of the block is $\frac{m_j}{B}$ or $\frac{m_j}{B}\times \frac{m_j-1}{B-1}$ respectively. More general, the chance of having i assignments for treatment j at the beginning (or end) of the block is:

$$p_{\mathit{ij}}^{\ast }=\frac{m_j}{B}\times \frac{m_j-1}{B-1}\times \cdots \times \frac{m_j-(i-1)}{B-(i-1)}$$ (3)

The difference between $p_{\mathit{ij}}^{\ast }$ and $p_{i+1,j}^{\ast }$ represents the probability of having i assignments for treatment j at the beginning (or end) of the sequence followed by (or following to) an assignment for a different treatment. By the definition of deterministic assignment, this is the probability of having i deterministic assignments for treatment j.

$$p_{ij}=p_{ij}^{\ast }-p_{i+1,j}^{\ast }(i=1,2,\dots ,m_j;j=1,2,\dots ,T;p_{m_{j+1,j}}^{\ast }=0)$$ (4)

Within a block of size B, the expected number of deterministic assignments for treatment arm j will be $\sum _{i=1}^{m_j}i\times p_{\mathit{ij}}$. The probability an assignment randomly picked from a block is a deterministic assignment for any treatment arm will be:

$$\begin{array}{l}p=\sum _{j=1}^T\frac{1}{B}\sum _{i=1}^{m_j}i\times p_{\mathit{ij}}=\frac{1}{B}\sum _{j=1}^T(p_{1j}^{\ast }-p_{2j}^{\ast })+2(p_{2j}^{\ast }-p_{3j}^{\ast })+\cdots +m_j(p_{m_j,j}^{\ast }-0)\\ =\frac{1}{B}\sum _{j=1}^T{p}_{1j}^{\ast }+p_{2j}^{\ast }+\cdots +m_j{p}_{m_j,j}^{\ast }\end{array}$$ (5)

Formula (2) can be obtained by inserting (3) into (5). Dupin-Spriet stopped by formula (2) and gave numerical results for several balanced and unbalanced scenarios.

3. Simplification of Dupin-Spriet’s formula

Evaluation of formula (2) involves heavy calculation. To simplify the formula, we define a working variable q_kj:

$$q_{\mathit{kj}}=\sum _{i=k}^{m_j}{p}_{\mathit{ij}}^{\ast },(k=1,2,\dots ,m_j)$$ (6)

Comparing with (5), we have:

$$q_{1j}=\sum _{i=1}^{m_j}{p}_{\mathit{ij}}^{\ast }=B{p}_j,q_{m_j,j}=p_{m_{j,}j}^{\ast }$$ (7)

From the definition of q_kj (6), we have

$$q_{\mathit{kj}}=p_{\mathit{kj}}^{\ast }+q_{k+1,j}(k=1,2,\dots ,m_j-1)$$ (8)

Our goal is to find out q_1j. We start from q_mj,j. Based on (3):

$$q_{m_j,j}=p_{m_j,j}^{\ast }=\frac{m_j(m_j-1)\cdots 2\times 1}{B(B-1)\cdots (B-m_j+2)(B-m_j+1)}=\frac{1}{B-m_j+1}{p}_{m_{j-1},j}^{\ast }$$ (9)

$$\begin{array}{l}{q}_{m_j-1,j}^{\ast }=p_{m_j-1,j}^{\ast }+q_{m_{j,}j}=p_{m_j-1,j}^{\ast }\left(1+\frac{1}{B-m_j+1}\right)\\ =\frac{m_j(m_j-1)\cdots 3\times 2}{B(B-1)\cdots (B-m_j+3)(B-m_j+2)}\left(\frac{B-m_j+2}{B-m_j+1}\right)\\ =\frac{m_j(m_j-1)\cdots 3}{B(B-1)\cdots (B-m_j+3)}\left(\frac{2}{B-m_j+1}\right)=\frac{2}{B-m_j+1}{p}_{m_j-2,j}^{\ast }\end{array}$$ (10)

Based on (9) and (10), we assume:

$$q_{\mathit{kj}}=\frac{m_j-k+1}{B-m_j+1}{p}_{k-1,j}^{\ast }$$ (11)

Formula (11) works for k = m_j, as shown in (9), and k = m_j − 1, as shown in (10). Assume it works for k, check the scenario of (k − 1) :

$$\begin{array}{l}{q}_{k-1,j}=p_{k-1,j}^{\ast }+q_{\mathit{kj}}=p_{k-1,j}^{\ast }\left(1+\frac{m_j-k+1}{B-m_j+1}\right)\\ \frac{m_j(m_j-1)\cdots (m_j-k+3)(m_j-k+2)}{B(B-1)\cdots (B-k+3)(B-k+2)}\left(\frac{B-k+2}{B-m_j+1}\right)\\ =\frac{m_j(m_j-1)\cdots (m_j-k+3)}{B(B-1)\cdots (B-k+3)}\left(\frac{m_j-k+2}{B-m_j+1}\right)=\frac{m_j-(k-1)+1}{B-m_j+1}{p}_{k-2,j}^{\ast }\end{array}$$ (12)

Based on mathematical induction theorem, result (12) confirms that formula (11) for all values of k(k = 2,3,…,m_j):

$$q_{2j}=\sum _{i=2}^{m_j}{p}_{\mathit{ij}}^{\ast }=\frac{m_j-1}{B-m_j+1}{p}_{1j}^{\ast }$$ (13)

$$\sum _{i=1}^{m_j}{p}_{ij}^{\ast }=p_{1j}^{\ast }+q_{2j}=\left(1+\frac{m_j-1}{B-m_j+1}\right)p_{1j}^{\ast }=\frac{B}{B-m_j+1}\times \frac{m_j}{B}=\frac{m_j}{B-m_j+1}$$ (14)

According to (4) and (5), formula (14) represents the expected number of deterministic assignments for treatment j in one block. The probability an assignment randomly selected from a block being deterministic is:

$$p=\frac{1}{B}\sum _{j=1}^T\frac{m_j}{B-m_j+1}$$ (15)

While numerically equivalent to (2), formula (15) is much simpler for evaluation. For balanced trials where m_j = m(j = 1,2,…,T) and B = mT, we have:

$$p=\frac{1}{B-m+1}=\frac{1}{m(T-1)+1}$$ (16)

For balanced trials with 2 treatment arms, B = 2m. Formula (16) is reduced to (1).

4. Calculation and Examples

For an unbalanced trial with 3 treatment arms, if the treatment allocation ratio is 1:2:3 and the block size B = 6, based on (15) we have:

$$p=\frac{1}{6}\left(\frac{1}{6-1+1}+\frac{2}{6-2+1}+\frac{3}{6-3+1}\right)=\frac{79}{360}=21.9444\%$$

For a balanced trial with 3 treatment arms and each arm has 3 assignments in a block, based on (16), we have:

$$p=\frac{1}{3(3-1)+1}=\frac{1}{7}=14.2857\%$$

All results listed in Table 1 and Table 2 of Dupin-Spriet et al. (2004) are verified by formula (15) without discrepancy.

5. Discussion

Formulas (15) and (16) not only provided an easy tool for the calculation of the probability of deterministic assignments in permuted block randomization, but also paint an informative picture for the impacts of parameters T, B and m_j on the probability of deterministic assignments p.

1. For balanced allocation permuted block randomization, the probability of deterministic assignment increases as the number of treatment arm increases, and decreases as the block size increases. Figure 1 plots the result of (16) for trials with the number of treatment arms T varying from 2 to 6, and number of assignments per treatment arm in a block m varying from 1 to 10. In order to control the probability of deterministic assignment under 10 percent, the required block size will be 20, 15 and 12 for a trial with 2, 3 or 4 treatment arms respectively.

2. For the same number of treatment arms T and block size B, unbalanced allocation design will have a higher probability of deterministic assignment. For example, for a trial with 2 treatment arms and a block size of 6, with balanced allocation randomization, the probability of deterministic assignment is 25%. If a 1:2 allocation ratio is used, the probability of deterministic assignment will be 28.9%. Figure 2 shows the relationship between the treatment allocation ratio and the probability of deterministic assignment for trials with different 2 treatment arms.

3. For trials with unequal block sizes, as recommended by ICH guidelines (ICH E9-document, 1998), the probability of deterministic assignment can be calculated by the weighted average of the probability of deterministic assignment for each block size. For example, a trial comparing 3 treatment arm with an unbalanced allocation ratio of 1:2:3. Block sizes of 6 and 12 are used with equal chance. In this case, one-third of the assignments come from blocks with a size of 6, and the remaining two-third assignment come from blocks with a size of 12. Based on formula (15), the probability of deterministic assignment is 21.9% for the smaller block (size 6), and 12.4% for the larger block (size 12). The overall probability will be 15.6%.

Figure 1.

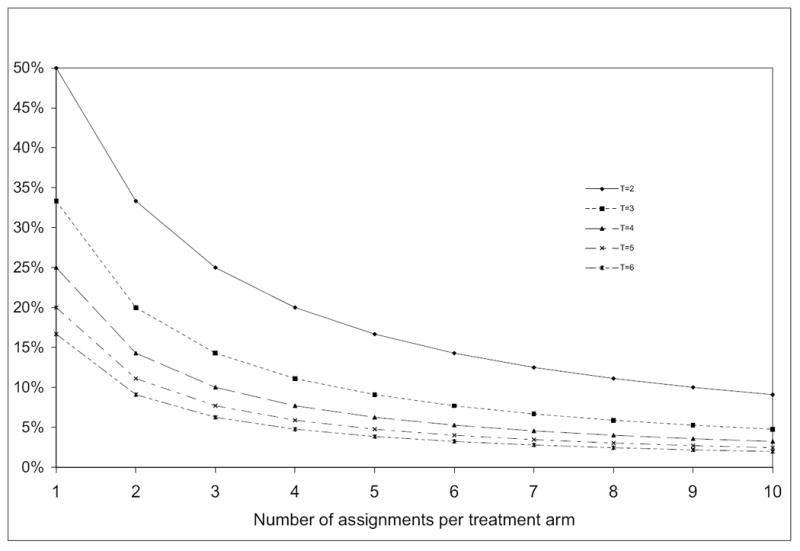
Proportion of determinative assignment in permuted block randomizaiton for balanced trials

Figure 2.

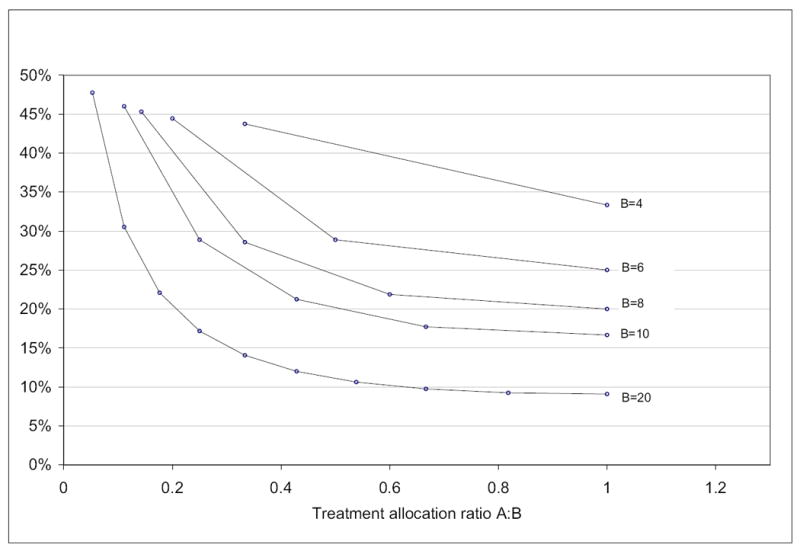
Treatment allocation ratio v.s. probability of deterministic assignment for two-arm trials