A CTRW-based model of time-resolved fluorescence lifetime imaging in a turbid medium

Abstract

We develop an analytic model of time-resolved fluorescent imaging of photons migrating through a semi-infinite turbid medium bounded by an infinite plane in the presence of a single stationary point fluorophore embedded in the medium. In contrast to earlier models of fluorescent imaging in which photon motion is assumed to be some form of continuous diffusion process, the present analysis is based on a continuous-time random walk (CTRW) on a simple cubic lattice, the object being to estimate the position and lifetime of the fluorophore. Such information can provide information related to local variations in pH and temperature with potential medical significance. Aspects of the theory were tested using time-resolved measurements of the fluorescence from small inclusions inside tissue-like phantoms. The experimental results were found to be in good agreement with theoretical predictions provided that the fluorophore was not located too close to the planar boundary, a common problem in many diffusive systems.

1. Introduction

Fluorescence techniques are increasingly being used to describe biological processes at molecular and cellular levels. Newly developed fluorophore-conjugated probes can greatly improve the specificity of optical imaging, potentially making it a tool of choice for many biomedical applications, in particular for those applied to cancer diagnostics and related animal models [1, 2]. Different data collection modalities have been suggested in the literature to realize fluorescent imaging starting from the least expensive continuous-wave (CW) schemes to frequency- and time-domain techniques capable of providing significant amounts of biomedically useful information.

A good recent review of fluorescence imaging is given in an article by Ntziachristos together with an extensive list of references, [3]. Until now, biomedical applications of fluorescence techniques have mainly been restricted to imaging thin samples or surface imaging because of the deleterious effects of random scattering of photons in tissues. Such scattering can significantly increase the observed fluorescence lifetime relative to the intrinsic lifetime of a single fluorophore. This problem can be partially compensated for by a judicious application of theoretical analysis based on some variant of transport theory. Several approaches to it have been discussed in recent papers by Kumar et al, [4, 5]. An analytical approach to fluorescence problems based on random walk theory by Hattery et al [6] has been used to analyze the case in which the fluorescence lifetimes are quite short. In the present paper we analyze the converse case which is more consistent with experimental data gathered in our laboratory, as described below. The model is simplified in that the trajectory of only a single photon, rather than those of an ensemble of photons, is followed.

There are many approaches to modeling the motion of photons in a turbid medium. Certainly the most accurate of these requires the application of a rigorous formulation of transport theory. In practice this requires a considerable investment in numerical analysis as well as a knowledge of physical parameters not easily estimated experimentally. This is not really practical because transport theory can furnish results valid only for specific sets of parameters. Due to inherent difficulties in the practical application of transport theory as a compromise it is generally replaced by some simpler variant of diffusion theory. An early version that goes one step beyond the diffusion approximation is that of the lattice random walk in discrete time, [7]. This was later generalized to a model based on the continuous-time random walk (CTRW)[8].

A discussion of some advantages of the random walk approach is to be found in a review in [9]. A formulation based on lattice random walk methodology is applied here to problems raised by fluorescent imaging and several details of the theory are described in the next section. Alternative approaches have been proposed recently for measuring fluorophore lifetimes, [10, 11]. In [10] the authors used an empirical linear relationship between the fluorophore depth and time of the maximum fluorescence intensity together with the relationship between the observed time decay slope and the actual fluorescence to estimate the fluorophore depth and lifetime, However, the range of applicability of these basic relationships has not been fully investigated.

This defect will be eliminated in our present formulation. In [11] application of scaling relations for a given target depth is proposed to extract the intrinsic lifetime from the observed time decay slope of a deeply embedded fluorophore (the corresponding depth is to be estimated in advance, using for example, the method of [12], based on the analysis of 2D continuous-wave fluorescence intensity distributions. In the present paper we analyze a more general case, deriving an analytical expression for the flux of the time-resolved fluorescence photons from a target embedded in a semi-infinite turbid media and bounded by an absorbing plane. By fitting the experimentally obtained curve of the time-resolved flux to this model we are able, in principle, to reconstruct the position and the lifetime of a fluorophore, which, in our experiment, was modeled by a fluorescent pellet.

2. Theory

2.1. Specifics of the model

Two optical constants will be used to characterize physical properties of the medium: the transport-corrected scattering coefficient, ${\mu }_s^{\prime }$, and the absorption coefficient, μ_a. In the simplest version of the random walk model, the turbid medium is modeled as a semi-infinite simple cubic lattice in which the spacing between adjacent sites is taken to be a single transport-corrected scattering length, $k_0=\sqrt{2}∕{\mu }_s^{\prime }$ as derived in [13, 14]. The coordinates of a single site will be denoted by r = (x,y,z), each component of which is taken to be an integer. The ranges of these component are −∞ < x, y < ∞ and 0 ≤ z < ∞ so that z = 0 defines the plane separating the medium from the exterior, and the initial position of the photon is taken to be r₀ = (0, 0,1).

Let p_n(r|r′) be the probability that a random walker, i.e. a photon, originally at r′, is at r at step n. One defines a CTRW in Laplace transform space by multiplying the propagator in discrete time by the n'th power of the Laplace transform of the appropriate pausing time density, [15, 16]. The plane z = 0 is assumed to be an absorbing boundary so that p_n(r|r′), or the equivalent transform, is required to vanish on that plane. We will later be interested in the probability that the photon, or random walker, reaches the exit site R_exit = (X,Y,0) at a dimensionless time τ* which may be written in factored form as ${\mu }_s^{\prime }{\mathit{ct}}^{\ast }$, c being the assumed constant speed of light in the medium. Another important descriptor of the trajectory in random walk terminology will be denoted by $f_n^{\left(j\right)}(\mathbf{r}\mid {\mathbf{r}}^{\prime })$, which is the probability that the photon arrives at r for the j'th time at step n having initially been at r′. In this notation $f_n^{\left(1\right)}(\mathbf{r}\mid {\mathbf{r}}^{\prime })$ is the probability to move from r′ to r for the first time in n steps.

In the simplest version of the model treated here, i.e., the single fluorophore model the fluorophore site is s = (s₁, s₂, s₃). The photon begins moving through the medium at τ = 0, the course of its motion being described in terms of a CTRW, to be described in more detail shortly. During its trajectory the photon may or may not be excited before eventually being absorbed on the plane z = 0. By an excitation event we will mean a change of state at a time τ′ < τ at which the photon comes into contact with the fluorophore and, with efficiency ε, produces a change in wavelength. It will be assumed that the occurrence of a single excitation precludes any further excitation events. Whether such an excitation has occurred can be determined from reflectance measurements made on the planar interface since the wavelength is changed by the excitation. A second effect of an excitation event is to introduce an extra time delay into the overall photon migration.

The random walk in our model will be simplified in that steps will be allowed to nearest neighbors only. The surface of the plane is taken to be absorbing, which means that when a photon, or its surrogate random walk, reaches the plane itregisters as a source of intensity and is immediately removed from the system, the time and exit site noted at the event. These provide information related to the state of the underlying tissue.

To describe the process more precisely we define two pausing-time densities, ψ₁(τ) and ψ_T(τ). The definition of a pausing-time density for a CTRW is a probability density for the amount of time taken between two successive steps of the random walk. The time taken to step between two adjacent sites, neither of which contains a fluorophore is described by an exponential pausing-time density, ψ₁(τ)= e^−τ. When the photon comes into contact with the fluorophore it is either transformed into an excited state by the fluorophore, in which case the pausing-time density is either taken to be ψ_T(τ) = (1/T)e^−τ/T, the excitation efficiency being equal to ε, or it is not, in which case the pausing-time density remains equal to ψ₁(τ). No more than a single excitation is allowed to occur during a single trajectory. After an excitation event the pausing-time density returns to the original ψ₁(τ) under the assumption that the scattering coefficient remains unchanged. The measureable data from a single photon consists of the time and position of its arrival at the interface.

The pausing time densities are therefore

$${\psi }_1\left(\tau \right)=e^{-\tau },{\psi }_T\left(\tau \right)=\frac{1}{T}{e}^{-\tau ∕T}$$ (1)

The first of these governs the times between successive steps in which a) either the photon moves to one of six adjacent sites, none of which contains the fluorophore, or b) the photon has interacted with the fluorophore on an earlier step and therefore cannot interact with it again. In either situation the probability density for the time between successive steps of the random walk is equal to ψ₁(τ) with a mean time equal to 1. Only at the time of an excitation event does the pausing time density switch to being ψ_T(τ) for a single step. Since the occurrence of an excitation slows the process of photon migration the physically interesting range of T is T > 1. We parenthetically remark that it is also possible to deal with more general choices of pausing-time densities than the ones in Eq.(1) but our analysis will be restricted to the simplest case specified above.

2.2. Surface flux

2.2.1. Discrete time

There have been a number of earlier theoretical analyses of fluorescence-based lifetime imaging techniques at all levels of mathematical sophistication, e.g., investigations by Patterson and Pogue, [17], and Hebden and Arridge, [18]. We follow the analysis given in [19] which has most of the results needed for the preliminary derivation in discrete time except that the delay time at the fluorophore in the earlier works restricted the delay caused by an excitation event to be an integer number of time steps rather than being arbitrary as would be required for general estimation purposes. This defect is overcome by the use of the CTRW analysis based on the two pausing-time densities exemplified by Eq.(1). We refer the reader to [19] for details of the analysis in the discrete time domain which is the natural starting point for the analysis.

By way of notation the generating function corresponding to a discrete sequence {h_n}, n = 0,1,2,… will be denoted by $\stackrel{-}{h}\left(\xi \right)={\Sigma }_{n=0}^{\infty }{h}_n{\xi }^n$. The result found in [19] for the generating function corresponding to the trajectory taking a photon from r₀ to s at least once in which an activation event occurs and then to R_exit was found to be

$$\begin{array}{cc}\hfill \stackrel{-}{g}(\xi ;{\mathbf{R}}_{\text{exit}}\left|\mathbf{s}\right|{\mathbf{r}}_0)& =\underset{n=0}{\overset{\infty }{\Sigma }}{g}_n\left({\mathbf{R}}_{\text{exit}}\left|\mathbf{s}\right|{\mathbf{r}}_0\right){\xi }^n\hfill \\ \hfill & =\frac{\xi \epsilon \stackrel{-}{p}(\xi ;{\mathbf{R}}_{\text{exit}}\mid \mathbf{s})\stackrel{-}{p}(\xi ;\mathbf{s}\mid {\mathbf{r}}_0)}{6(1+\epsilon [\stackrel{-}{p}(\xi ;\mathbf{s}\mid \mathbf{s})-1])}\hfill \end{array}$$ (2)

In particular, when ε[p̄(ξ;s|s) − 1] ≪ 1, this simplifies to

$$\stackrel{-}{g}(\xi ;{\mathbf{R}}_{\text{exit}}\left|\mathbf{s}\right|{\mathbf{r}}_0)\approx \frac{\epsilon }{6}\xi \stackrel{-}{p}(\xi ;{\mathbf{R}}_{\text{exit}}\mid \mathbf{s})\stackrel{-}{p}(\xi ;\mathbf{s}\mid {\mathbf{r}}_0)$$ (3)

The indicated inequality is rarely violated for parameters typical in biological tissues. We therefore use the simplified representation in Eq.(3) rather than the full Eq.(2) in later calculations.

2.3. Transition to time dependence

Our ultimate goal is to find the time-dependent behavior of the flux of photons which have passed through s with at least one activation event and is thereafter absorbed at R_exit at time τ*. The analysis is based on the time-dependent inverse of the generating function in Eq.(3), a function to be denoted by g (τ*; R_exit|s|r₀). Observe that in this picture the trajectory taking the photon from r ₀ to R_exit can be decomposed into four parts; the path from r₀ to s at which the excitation occurs, the sojourn at s, a journey made from s to (X, Y, 1) and the final step taking the photon from (X, Y, 1) to R_exit = (X, Y, 0). Since an activation event is assumed to occur, the derivation necessarily depends on both of the pausing-time densities appearing in Eq.(1).

In the present analysis the generating functions of the last subsection play an important intermediate role in translating discrete results to ones in continuous time. A standard technique for doing this in CTRW methodology is to replace the generating function parameter by the Laplace transform of the pausing time density. This is modified slightly in the present analysis because there are now two pausing-time densities in Eq.(1). By way of notation we denote the Laplace transform of an arbitrary function of τ, g (τ), by $\widehat{g}\left(\eta \right)={\int }_0^{\infty }{e}^{-\eta \tau }g\left(\tau \right)d\tau$, so that ψ̂₁(η) = 1/(1 + η) and ψ̂_T (η) = 1/(1 + ηT).

Out of the n steps taken in the discrete picture an excitaton occurs in a single step but not in the remaining n – 1 ones. Therefore the Laplace transform of the probability density for the total time spent during a single trajectory consisting of n steps using the pausing time density ψ₁(τ) and a single one using ψ_T(τ) is

$${\widehat{\vartheta }}_n(\eta ,T)=\frac{1}{{(1+\eta )}^{n-1}(1+\eta T)}=\frac{1}{T{(1+\eta )}^{n-1}\left(\eta +\frac{1}{T}\right)}$$ (4)

The formal expression for the Laplace transform of the propagator which takes the photon from r₀ to R_exit, including a visitto thefluorophore producing an excitation, is

$$\widehat{g}(\eta ;{\mathbf{R}}_{\text{exit}}\left|\mathbf{s}\right|{\mathbf{r}}_0)=\frac{\epsilon }{6(1+\eta T)}\underset{n=1}{\overset{\infty }{\Sigma }}\frac{g_n\left({\mathbf{R}}_{\text{exit}}\left|\mathbf{s}\right|{\mathbf{r}}_0\right)e^{-n{\mu }_a}}{{(1+\eta )}^n}$$ (5)

where the g_n (R_exit|s|r₀) are the coefficients generated by expanding Eq.(3) in powers of ξ. Equation (5) can therefore be regarded as a generating function defined in terms of the parameter e^−μ_a/(1 + η). The efficiency coefficient, ε, plays a secondary role in the calculations since only the space- and time- dependence of the detected intensity provides potentially useful data while ε itself is not readily measureable. It is physically obvious that one or the other of the two parameters, μ_a or T, will predominate in determining the asymptotic behavior of the time-dependent g (τ; R_exit|s|r₀). Dominance of the absorption or fluorescence lifetime in the asymptotic behavior of g (τ; R_exit|s|r₀) is determined by the product μ_aT, i.e., if μ_aT ≤ 1 then the asymptotic slope of the time dependence of the fluorescence intensity is determined by absorption (decays as exp(−μ_aτ)), while in the opposite case the duration of emission (fluorescence lifetime) overwhelms the effect of internal absorption and the asymptotic slope decays as exp(−τ/T) as a function of time.

Two generating functions will be needed in the determination of g (τ; R_exit|s|r₀). These will be expressed in terms of Laplace transforms of a function H(τ; u|v) which will appear quite frequently in the following analysis:

$$H(\tau ;\mathbf{u}\mid \mathbf{v})=e^{-\tau (1+{\mu }_a)}{I}_{u_1-v_1}\left(\frac{\tau }{3}\right)I_{u_2-v_2}\left(\frac{\tau }{3}\right)I_{u_3-v_3}\left(\frac{\tau }{3}\right)\frac{1}{\tau }$$ (6)

which can be written in factored form as H(τ; u|v) = Q(τ; u|v)e^−μ_aτ. The vectors u and v are (u₁, u₂, u₃) and (ν₁, ν₂, ν₃) respectively and the I_m(τ/3) are modified Bessel functions of the first kind, [20]. A derivation of this formula is provided in the section A of the Supplementary Material accompanying this paper. A significant property of Q(τ; u|v) is its approximate behavior as τ → ∞ where it is found that for fixed |u − v|² it behaves as

$$Q(\tau ;\mathbf{u}\mid \mathbf{v})={\left(\frac{3}{2\pi }\right)}^{3∕2}\frac{1}{{\tau }^{5∕2}}\exp \left[-\frac{3{|\mathbf{u}-\mathbf{v}|}^2}{2\tau }\right]$$ (7)

Two generating functions will be needed to derive an approximation to the function ĝ (η; R_exit|s|r₀) follows from Eq.(3) (see section A in the Supplementary Material). These are

$$\begin{array}{cc}\hfill & \stackrel{-}{p}\left(\frac{e^{-{\mu }_a}}{1+\eta };\mathbf{s}\mid {\mathbf{r}}_0\right)=6(1+\eta ){\int }_0^{\infty }{e}^{-(\eta +{\mu }_a){\tau }^{\prime }}Q({\tau }^{\prime };\mathbf{s}\mid {\mathbf{r}}_0)d{\tau }^{\prime }\hfill \\ \hfill & \stackrel{-}{p}\left(\frac{e^{-{\mu }_a}}{1+\eta };{\mathbf{R}}_{\text{exit}}\mid \mathbf{s}\right)=6(1+\eta ){\int }_0^{\infty }{e}^{-(\eta +{\mu }_a){\tau }^{\prime }}Q({\tau }^{\prime };{\mathbf{R}}_{\text{exit}}\mid \mathbf{s})d{\tau }^{\prime }\hfill \end{array}$$ (8)

To simplify the calculations we will assume that the time is sufficiently long that the coefficient (1 + η) can be replaced by unity. It is then possible to express the transform as an infinite series:

$$\widehat{g}(\eta ;{\mathbf{R}}_{\text{exit}}\left|\mathbf{s}\right|{\mathbf{r}}_0)\approx \frac{1}{T\left(\eta +\frac{1}{T}\right)}\stackrel{-}{g}\left(\frac{e^{-{\mu }_a}}{1+\eta };{\mathbf{R}}_{\text{exit}}\left|\mathbf{s}\right|{\mathbf{r}}_0\right)$$ (9)

There are two approaches to representing the function g (τ ;R_exit|s|r₀); the first in which one finds the Laplace representations in Eq.(3) with thecomponents specified in Eq.(8) and the second requires one to find the equivalent convolution form in the time domain that follows from the transforms. In this work we employ the second approach and return to Eq.(3) to find an explicit representation of g(τ; R_exit|s|r) in terms of a double integral because that equation, as written, is a product of transforms. Therefore the Laplace inverse is equivalent to a convolution in thetime domain. The product in Eq.(3) is equivalent, at long times, in the time domain to

$$g(\tau ;{\mathbf{R}}_{\text{exit}}\left|\mathbf{s}\right|{\mathbf{r}}_0)\approx \frac{6}{T}{\int }_0^{\tau }{e}^{-{\mu }_a{\tau }^{\prime }}Q({\tau }^{\prime };{\mathbf{R}}_{\text{exit}}\mid \mathbf{s})d{\tau }^{\prime }\times {\int }_0^{\tau -{\tau }^{\prime }}{e}^{-{\mu }_a{\tau }^{″}}Q({\tau }^{″};\mathbf{s}\mid {\mathbf{r}}_0)e^{-(\tau -{\tau }^{\prime }-{\tau }^{″})∕T}d{\tau }^{″}$$ (10)

A numerical evaluation of the double convolution in this last equation is computationally demanding due to the long tails of the terms in the integrand so that using that representation directly for fitting experimental data presents extreme difficulties. However, the expression can be reduced to a single convolution with a somewhat more complicated integrand. We first note that Eq. 10 can be written as (see Appendix A)

$$g(\tau ;{\mathbf{R}}_{\text{exit}}\left|\mathbf{s}\right|{\mathbf{r}}_0)=\frac{6}{T}{\int }_0^{\tau }{e}^{-(\tau -{\tau }^{\prime })∕T-{\mu }_a{\tau }^{\prime }}I\left({\tau }^{\prime }\right)d{\tau }^{\prime },$$ (11)

where I(τ′) incorporates the integration over τ″, i.e.,

$$I\left({\tau }^{\prime }\right)={\int }_0^{{\tau }^{\prime }}Q({\tau }^{″};{\mathbf{R}}_{\text{exit}}\mid \mathbf{s})Q({\tau }^{\prime }-{\tau }^{″};\mathbf{s}\mid {\mathbf{r}}_0)d{\tau }^{″}$$ (12)

An analytic expression can be derived for I(τ) in terms of the variables

$${\beta }_1=\frac{3{|{\mathbf{R}}_{\text{exit}}-\mathbf{s}|}^2}{2},{\beta }_2=\frac{3{|\mathbf{s}-{\mathbf{r}}_0|}^2}{2},\beta ={\left(\sqrt{{\beta }_1}+\sqrt{{\beta }_2}\right)}^2$$ (13)

(see Appendix A) given by

$$I\left(\tau \right)=\frac{27{\beta }^{3∕2}{e}^{-\beta ∕\tau }}{8{\pi }^{5∕2}{\beta }_1{\beta }_2}\left(\frac{1}{{\tau }^{7∕2}}+\frac{\gamma }{{\tau }^{5∕2}}\right),$$ (14)

so that Eq.(11) represents g(τ; R_exit|s|r₀) as a single convolution integral. The indicated representation reduces the required amount of computation over that needed when starting from the double convolution form. It enables parameter estimates to be obtained on the order of several seconds (more than a 100-fold speed-up over the double convolution form for typical parameters). An expression for g(τ; R_exit|s|r₀) in closed form can be derived when μ_a = 0.

Finally, the theoretical predictions in Eqs.(11) and (14) do not include the effects of instrumental noise on the experiment. By this we mean the error in the arrival time of a photon at the absorbing boundary relative to its theoretically predicted value. This effect will be quantified in terms of a function, φ(τ), defined as the probability density of the error in the arrival time of a photons due to system noise. Using Eq.(11) as a basis of a forward model we incorporate the finite width of instrumental response function (IRF), φ(τ) into the forward model by an additional convolution. In other words, the expected experimental curve G(τ) is defined to be the convolution of g(τ; R_exit|s|r₀) and φ(τ),

$$G(\tau ;{\mathbf{R}}_{\text{exit}}\left|\mathbf{s}\right|{\mathbf{r}}_0)=g(\tau ;{\mathbf{R}}_{\text{exit}}\left|\mathbf{s}\right|{\mathbf{r}}_0)\ast \phi \left(\tau \right),$$ (15)

where * denotes a convolution. The reconstruction algorithm as implemented was based on curve fitting to the model described in Eq.(15), which we use to analyze experimental data and directly compare theoretical estimates with experimental data over a wide time range.

3. Results

Before presenting the results of model simulations and the results from a gel-phantom experiment, it is useful to mention some estimates of the experimental parameters derived earlier from measurements made in our laboratory. As already mentioned the translation of the real time, t, to dimensionless time, τ, is achieved by means of the formula $\tau ={\mu }_s^{\prime }\mathit{ct}$. In particular, fluorescence lifetime in physical units, T̃, is related to the corresponding dimensionless parameter T by

$$\tilde{T}=\frac{T}{{\mu }_s^{\prime }c}$$ (16)

It is well known that in many biological tissues ${\mu }_s^{\prime }$ is on the order of 1 mm⁻¹, and that the absorption coefficient, μ_a is likely to be in the range from 0.002 to 0.05 mm⁻¹. Nominal fluorescence lifetime T for many commercial near-infrared fluorescent dyes (e.g., AlexaFluor750 from Invitrogen™ or IRD from LiCor™), is in the range 600ps ≤T̃≤ 1000 ps.

Physical coordinates r̃ in the infinite turbid medium are usually related to the dimensionless coordinates r on the random walk lattice model through the transport-corrected scattering length [13, 14], $k_0=\sqrt{2}∕{\mu }_s^{\prime }$, as a conversion factor. More generally, the relationship between r̃ and r can be written as where

$$\tilde{\mathbf{r}}=k_0\mathbf{r}+{\mathbf{d}}^{\left(e\right)},$$ (17)

d_e is an offset factor which can be non-zero depending on the type of the boundary conditions used. It should be noted that the solutions of the photon migration equations for the semi-infinite medium, e.g. Eqs. 10 and 11, are obtained using the method of images [9], in which the imaginary sources are added which then together with the real sources satisfy the necessary boundary conditions. Two of the most popular types of the boundary conditions are so-called “zero boundary”, requiring zero flux at the z = 0 plane, and “extrapolated boundary” which requires that the zero flux exists at some plane different from z = 0 plane which is shifted outward from the scattering medium by some distance d_z (hence d^(e) = (0,0,d_z), in equation 17). For a totally absorbing boundary without refraction index mismatch it is shown [21-23] that the most accurate description of photon diffusion in a semi-infinite medium is obtained, if one assumes $d_z\approx 0.71∕{\mu }_s^{\prime }$. In many tissues (and phantoms, used to simulate them) the refraction index is approximately n ≈ 1.4 (corresponding speed of light c ≈ 0.21 mm/ps). Corresponding refraction index mismatch between the turbid medium and the air results in increased value of $d_z\approx 1.86∕{\mu }_s^{\prime }$ (see Table 2 of the paper [22], presenting values of for the wide range of index mismatches). In the random walk framework such “extended boundary” approach is equivalent to an assumption of larger depth of the fluorophore, if “zero boundary”-based equations (that we used in the text and the Appendix A) are applied. Thus, the physical depth of the fluorophore should be replaced by

$${\tilde{s}}_z^{\left(e\right)}={\tilde{s}}_z+d_z={\tilde{s}}_z+\frac{1.86}{{\mu }_s^{\prime }}.$$ (18)

Since our model equations (Eqs. 10,11) are written in dimensionless units, we also write the expression for the equivalent fluorophore depth (Eq. 18) in the dimensionless random walk lattice units using the conversion rule in Eq. 17,

$$s_z^{\left(e\right)}=s_z+d_z{\mu }_s^{\prime }∕\sqrt{2}\approx s_z+1.32$$ (19)

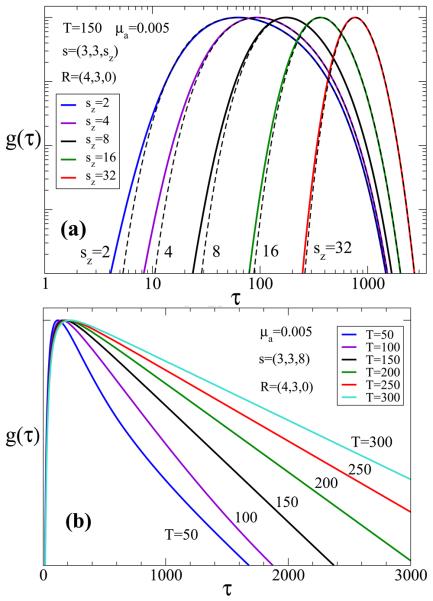
In many biomedical applications the fluorophore depth cannot be directly measured, requiring the development of specific analytical tools to estimate this parameter from 2-D imaging data (see, e.g., [10, 12]). An alternative approach is to apply curve fitting of experimental time-resolved data to the theoretical model of fluorescence intensity distribution. To avoid overestimating of the depth, proper boundary conditions and refractive index mismatch should be taken into account, using Eq. 19. For medium refraction index of n ≈ 1.4 true dimensionless fluorophore depth can be obtained from the fitted value, using the relation $s_z=s_z^{\left(e\right)}-1.32$, or in physical units ${\tilde{s}}_z=k_0(s_z^{\left(e\right)}-1.32)$. The second major parameter, T, can be easily measured for isolated fluorophores. However, to extract potential variations in the fluorescence lifetime due to fluorophore environment (pH, temperature etc), which is considered a promising tool for medical diagnostics [24], it is important to take into account photon migration effects [4, 5]. The influence of the major optical/geometrical parameters on the shape of the proposed forward model is illustrated in Fig. 1, where several curves g(τ; R_exit|s|r₀), corresponding to different values of the fluorophore depth (Fig. 1a) and lifetime (Fig. 1b) are shown. It is evident that the main effect of changing the depth of the fluorophore, s_z, is to shift the peak of g(τ; R_exit|s|r₀). As s_z increases the time τ_max at which the peak occurs also increases. The main effect of the parameter T in the range of interest, is to change the slope of the tails in the resulting curves, i.e., the rate of the exponential decay. It is therefore possible that the two parameters might be obtained indirectly, without fitting the full model to the data. Note that the convolution with φ(τ) will change the position of the peak for small s_z, without affecting the slope of T. To analyze our data we assumed that φ(τ) is a Gaussian whose width is specified using the standard deviation parameter, σ_IRF. This parameter can be measured or estimated as one of the model parameters in our model-based reconstruction.

Figure 1.

Model predictions for different values of (a) s_z = 2, 4, 8, 16, 32, and (b) T = 50, 100, 150, 200, 250 and 300 in dimensionless units.

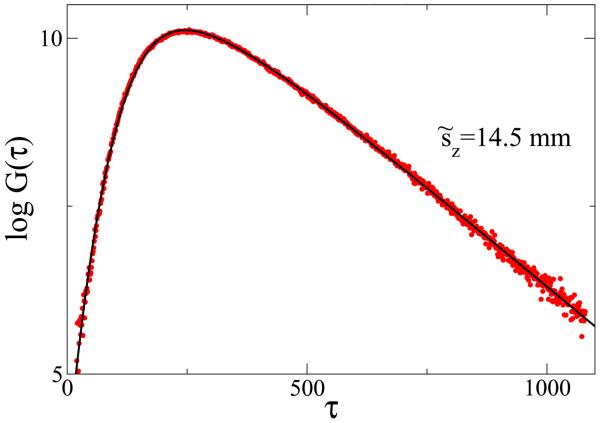
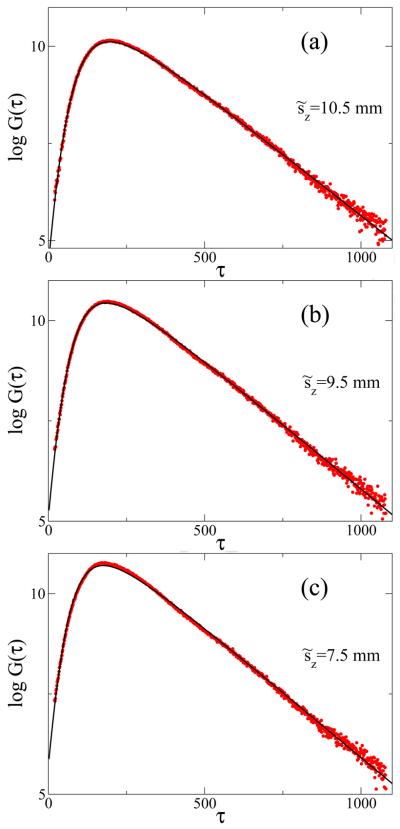
To verify our model we used time-resolved measurements from small fluorescent inclusions (fluorophores) inside the tissue-like phantoms. Agarose-based gels for these phantoms were prepared by dissolving 0.8 g agarose (Ultra pure Agarose, GIBCO@Invitrogen, CA, USA) in 36.6 ml phosphate- buffer saline (PBS) (Biosource,Rockville, MD, USA) while boiling and stirring the solution for 5 minutes. To model scattering properties of the biological tissues, 3.4 ml of Intralipid (Intralipid 20%,Baxter Healthcare Corporation, IL, USA) was gradually added to the solution while cooling and shaking the sample appropriately. The agarose solution is spread uniformly in petri dishes to prepare phantoms with different thicknesses [25]. Small fluorophores were embedded at varying depths into these tissue-like phantoms. The measurement of the fluorophore lifetime was performed using measurements from the same fluorophores placed at the surface of the gel. The experimental set-up was described in [25], where the excitation/emission wavelengths used were 750 and 780 nm, respectively. The optical properties of the background were ${\mu }_s^{\prime }=0.9{\mathrm{mm}}^{-1}$ ([11]) and μ_a = 0.0035 mm⁻¹ (as determined from an asymptotic slope of time-resolved intensity of backscattered excitation light, [26]). The measured instrumental response function, φ(τ), to a first approximation can be considered Gaussian with σ_IRF = 145 ps, although it is possible also to analyze a model in which Eq. 15 is convolved directly with a more accurate empirical function φ(τ). We measured G(τ) on a gel phantom with a fluorophore embedded at different values of s_z. The expected values of other parameters were T = 135 ± 14 ns (corresponding to T = 0.7 ns), and μ_a = 0.004 ± 0.0004 mm⁻¹. The random walk model in Eq.(11) itself does not give a good fit to the data (circles) for short times of flight, but combined with the proper instrumental response function it gives an excellent fit (Fig. 2). The estimates of the parameters obtained T̂ = 129, ŝ_z = 10.2 are in very good agreement with the expected values (135 and 10.3 in dimensionless units). Figure 3 shows the result of fitting G(τ; R_exit|s|r₀) to the experimental data. The random walk model yields very good agreement with the experimental data, but deviations from the model predictions start to appear rapidly as s_z decreases (s_z = 7.5 mm, Fig. 3c).

Figure 2.

The random walk model G(τ) (solid black line) agrees very well with experimentally observed data (circles). The model parameters obtained from the fit agree well with the expected values, T_fit = 129 vs expected T = 135, s̃_z = 14 mm vs 14.5 mm, and σ_IRF = 151 ps vs 145 ps. Parameter μ_a was fixed at μ_a=0.0035.

Figure 3.

The CTRW model fitted to the observed value of G(τ), with a fluorophore lifetime of T̃=0.7 ns, μ_a = 0.004 mm ⁻¹ and for s̃_z=7.5, 9.5, and 10.5 mm We used the experimentally observed φ(τ) with σ_IRF = 145 ps.

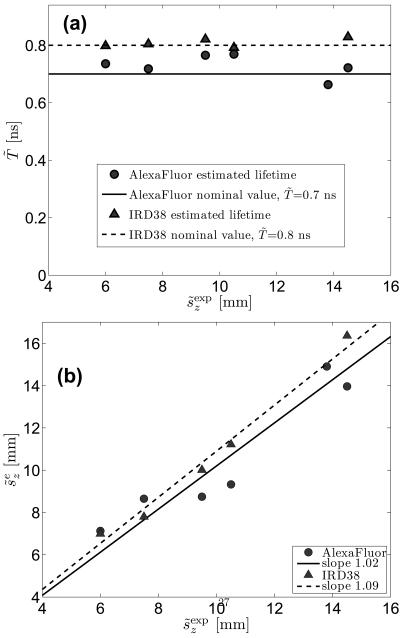
Results of curve fitting of the theoretical model to experimental data, obtained for different fluorophore depths are shown in Figs. 4a, b, where estimated values of the inclusion depth and fluorescence lifetime are plotted versus measured depth and intrinsic lifetime, respectively. Discrepancies between the reconstructed lifetimes and the nominal value of 0.7 ns, reported by the dye manufacturer (Invitrogen), are within 10%. The accuracy of estimates of depths proved to be better than 12% for s̃_z ≥ 9.5 mm. At shallower depths the reconstruction errors increase and at depths s̃_z = 6 and 7.5 mm they reach 29% and 21%, respectively. Two factors contribute to these larger deviations. One is that we have used a Gaussian IRF, which is only an approximation to the true IRF, and for narrower intensity distributions, G(τ), corresponding to smaller fluorophore depth, these deviations can play a major role in the accuracy of reconstruction. As already mentioned, this limitation can be alleviated by using a more accurate empirical function φ(τ). The second factor is the limitation of the random walk model (similar to that for a diffusion approximation) which fails for superficially embedded fluorophores, i.e., at depths less than several scattering lengths, corresponding in our case to a few millimeters (s̃_z < 5 mm).

Figure 4.

Comparison of the reconstructed (estimated) values vs. experimental setup. Estimates for the (a) fluorophore lifetime, T, and (b) the depth of the fluorophore, s_z vs the experimental value of s_z. In (b) the estimated depth in mm is obtained from the dimensionless value of s_z using Eq. 19.

We have performed similar experiments with a different type of fluorescent pellet (IRD38, Li-Cor™), embedded at several depths into the agarose-based phantom, described above. This dye operates in the near infrared spectral range with excitation and emission wavelengths being 778 nm and 806 nm, respectively. The results of reconstruction for IRD38 proved to be similar to the case of AlexaFluor750: the accuracy of the fluorophore depth estimate is better than 13% for s̃_z ≥ 7.5 mm, while the estimated fluorescence lifetime is within 4% from the average value of 0.8 ns. For comparison, a value of T̃ ≈ 0.79 ns has been reported in the literature [27]. Results of our reconstruction for IRD38 fluorophore are presented in Figs. 4a and 4b along with the data for AlexaFluor750.

4. Discussion

We have shown that using the CTRW model on a three-dimensional simple cubic lattice describes experimentally observed curves quite well when the depth of the fluorophore is greater than 9 mm in our laboratory. We also demonstrated experimentally that the two most important parameters, the depth of the fluorophore, s_z and the fluorophore lifetime, T, can be estimated with reasonable accuracy, i.e., on the order of 10%, while similar accuracy can be achieved for s_z, provided that s_z is sufficiently deep, i.e. at deeper depths of the fluoresence pellet, but is sensitive to the value of s_z. This reconstruction technique is yet to be tested on a biological tissue sample but it seems reasonable to expect that this would not change the outcome.

Limitations on the optical parameters of the media for the suggested model are similar to that of the diffusion approximation, i.e., scattering in the medium is much higher than absorption, ${\mu }_s^{\prime }\gg {\mu }_a$ and pathlengths of the photons, whose time-of-flight intensity distribution is observed, are much greater than a scattering length $1∕{\mu }_s^{\prime }$. These conditions are usually fulfilled for near infrared optical imaging of biological tissues, for example, optical mammography [28].

The implementation of the model that we use is not fully analytical but relies on numerical evaluation of the integral in Eq.(11). With the reduction of the relevant integrals from a double-convolution form to a single-convolution form, using Eq.(14) the computational demand can be significantly reduced and a single estimate on a given time-resolved curve can be obtained in a matter of several seconds using the Python programming language and the associated scientific libraries for Python (NumPy, SciPy).

Our analysis has been considerably simplified by restricting the form of the random walk to be nearest-neighbor and isotropic, the form of the pausing-time densities to be negative exponentials, by considering the effect of a single fluorophore only, and by assuming that the turbid medium is semi-infinite. These restrictions, however, are not strictly necessary for obtaining the major results presented in this paper. The major conclusions of our analysis for time-gated measurements remain valid provided that distances are macroscopic on the scale of transport-corrected scattering coefficients, that the pausing-time densities have finite first moments, and that the transition probabilities are isotropic. For example, the assumption of optically isotropic optical parameters can be dispensed with and the problem analyzed using techniques similar to those in a study by Dudko et al, [29]. An extension of the analysis to allow for more than a single fluorophore can be developed following formalism originally given in [30] and applied to an optical problem in [31]. The present theory can also be generalized to deal with both transillumination measurements and anisotropic optical parameters using mathematical techniques developed recently in [32].

A. Reducing the double convolution to a single convolution

We first rewrite the double convolution in Eq.10 as

$$\begin{array}{cc}\hfill g^{\mathrm{A}}& (\tau ;{\mathbf{R}}_{\text{exit}}\left|\mathbf{s}\right|{\mathbf{r}}_0)=\frac{6}{T}{\int }_0^T{e}^{-{\mu }_a{\tau }^{\prime }}Q({\tau }^{\prime };{\mathbf{R}}_{\text{exit}}\mid \mathbf{s})d{\tau }^{\prime }\times \hfill \\ \hfill & \times {\int }_0^{\tau -{\tau }^{\prime }}{e}^{-{\mu }_a{\tau }^{″}}Q({\tau }^{″};\mathbf{s}\mid {\mathbf{r}}_0)e^{-(\tau -{\tau }^{\prime }-{\tau }^{″})∕T}d{\tau }^{″}={\int }_0^{\tau }d{\tau }^{\prime }\times \hfill \\ \hfill & \times {\int }_0^{\tau -{\tau }^{\prime }}d{\tau }^{″}{e}^{-{\mu }_a({\tau }^{\prime }+{\tau }^{″})}Q({\tau }^{\prime };{\mathbf{R}}_{\text{exit}}\mid \mathbf{s})Q({\tau }^{″};\mathbf{s}\mid {\mathbf{r}}_0)e^{-\frac{\tau -{\tau }^{\prime }-{\tau }^{″}}{T}},\hfill \end{array}$$ (20)

and after substituting τ′ = u – τ″, 0 ≤ u ≤ T we find

$$\begin{array}{cc}\hfill g& (\tau ;{\mathbf{R}}_{\text{exit}}\left|\mathbf{s}\right|{\mathbf{r}}_0)=\frac{6}{T}{\int }_0^T\mathit{du}{\int }_0^{\tau -u}d{\tau }^{″}\times \hfill \\ \hfill & \times e^{-{\mu }_{a}u}Q(u-{\tau }^{″};{\mathbf{R}}_{\text{exit}}\mid \mathbf{s})Q({\tau }^{″};\mathbf{s}\mid {\mathbf{r}}_0)e^{-\frac{\tau -u}{T}}\hfill \\ \hfill & =\frac{6}{T}{\int }_0^{\tau }{\mathit{due}}^{-{\mu }_{a}u}{e}^{\frac{\tau -u}{T}}{\int }_0^{u}d{\tau }^{″}Q(u-{\tau }^{″};{\mathbf{R}}_{\text{exit}}\mid \mathbf{s})Q({\tau }^{″};\mathbf{s}\mid {\mathbf{r}}_0)\hfill \end{array}$$ (21)

This double-convolution integral can be written as

$$g(\tau ;{\mathbf{R}}_{\text{exit}}\left|\mathbf{s}\right|{\mathbf{r}}_0)=\frac{6}{T}{\int }_0^{\tau }{e}^{-(\tau -{\tau }^{\prime })∕T-{\mu }_a{\tau }^{\prime }}I\left({\tau }^{\prime }\right)d{\tau }^{\prime },$$ (22)

where the function I(τ′) includes the integration over τ″. An analytic expression for I(τ′) will now be derived, thus reducing the double- to a single convolution. We first define functions U_i(τ,β),

$$U_l(\tau ,\beta )=e^{-(\beta ∕\tau )}∕{\tau }^{l∕2},$$ (23)

and their Laplace transform can be written as

$${\widehat{U}}_l(\eta ,\beta )={\int }_0^{\infty }{e}^{-\eta \tau -(\beta ∕\tau )}\frac{d\tau }{{\tau }^{l∕2}}$$ (24)

$$=2{\left(\frac{\beta }{\eta }\right)}^{\frac{2-l}{4}}{K}_{\frac{l-2}{2}}\left(2\sqrt{\eta \beta }\right),$$ (25)

where K_n(z) is the modified Bessel function of the second kind.

Of particular interest here are the cases l = 5 and l = 7, and their Laplace transforms can be written

$${\widehat{U}}_5(\eta ,\beta )=\frac{\sqrt{\pi }{e}^{-2\sqrt{\eta \beta }}\left(2\sqrt{\eta \beta }+1\right)}{2{\beta }^{3∕2}}$$ (26)

$${\widehat{U}}_7(\eta ,\beta )=\frac{\sqrt{\pi }{e}^{-2\sqrt{\eta \beta }}\left(4\eta \beta +6\sqrt{\eta \beta }+3\right)}{4{\beta }^{5∕2}}$$ (27)

The expression for Q(τ; R_f|R_i) can now be written in terms of U_l (see Eqs. 7 and 23) as

$$Q(\tau ;{\mathbf{R}}_f\mid {\mathbf{R}}_i)={\left(\frac{3}{2\pi }\right)}^{\frac{3}{2}}{U}_5(\tau ,3{|{\mathbf{R}}_f-{\mathbf{R}}_i|}^2∕2).$$ (28)

Using the abbreviations β₁ = 3|R_exit – s|²/2 and β₂ = 3|s – r₀|²/2 the convolution in the expression for I(τ) is then expressed simply as a product of the two Laplace transforms, U₅(η, β₁) and U₅(η, β₂) (times a constant) which yields

$$\widehat{I}\left(\eta \right)=\frac{27e^{-2\sqrt{\eta \beta }}}{32{\pi }^2{\left({\beta }_1{\beta }_2\right)}^{3∕2}}\left(1+2\sqrt{\eta \beta }+4\eta \sqrt{{\beta }_1{\beta }_2}\right),$$ (29)

where $\beta ={(\sqrt{{\beta }_1}+\sqrt{{\beta }_2})}^2$ The expression in Eq. 29 can now be written as

$$\widehat{I}\left(\eta \right)=\frac{27{\beta }^{\frac{3}{2}}}{8{\pi }^{5∕2}{\beta }_1{\beta }_2}(U_7(\eta ,\beta )+\gamma U_5(\eta ,\beta )),$$ (30)

where

$$\gamma =\frac{\beta -3\sqrt{{\beta }_1{\beta }_2}}{2\beta \sqrt{{\beta }_1{\beta }_2}}$$ (31)

Inverting the expression in Eq. 30 to time domain we have

$$I\left(\tau \right)=\frac{27{\beta }^{\frac{3}{2}}{e}^{-\frac{\beta }{\tau }}}{8{\pi }^{5∕2}{\beta }_1{\beta }_2}\left(\frac{1}{{\tau }^{7∕2}}+\frac{\gamma }{{\tau }^{5∕2}}\right),$$ (32)

which is the analytic expression for I(τ) that we sought.