Harmonic Surface Mapping With Laplace-Beltrami Eigenmaps

Abstract

In this paper we propose a novel approach for the mapping of 3D surfaces. With the Reeb graph of Laplace-Beltrami eigenmaps, our method automatically detects stable landmark features intrinsic to the surface geometry and use them as boundary conditions to compute harmonic maps to the unit sphere. The resulting maps are diffeomorphic, robust to natural pose variations, and establish correspondences for geometric features shared across population. In the experiments, we demonstrate our method on three subcortical structures: the hippocampus, putamen, and caudate nucleus. A group study is also performed to generate a statistically significant map of local volume losses in the hippocampus of patients with secondary progressive multiple sclerosis.

1 Introduction

In many imaging studies, surface mapping plays an important role as it can provide localized information complementary to volume measurements [1]. The task of mapping general 3D surface models, however, remains challenging because it is usually difficult to define homologous points across population. In this paper, we propose a novel method of computing maps for a class of subcortical structures by using Laplace-Beltrami eigenmaps to capture their salient geometry and harmonic maps to establish diffeomorphic correspondences.

Various approaches have been proposed in previous work for the automated construction of surface maps. The first approach computes surface maps based on a canonical parameterization such as the spherical parameterization [2–5]. Using techniques from image registration, a map between two surfaces can be established by warping the image space surrounding the anatomical structure of interest [6–8]. The medial model, or skeleton, is a popular tool to represent shapes and it can also be used to construct geometrically intuitive maps between surfaces [9]. Because the skeleton is sensitive to noise, a simplified topology was usually assumed for robustness and consistency [10, 11].

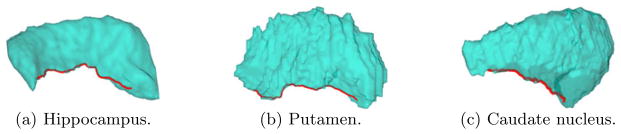
In this work we propose a novel approach for the automated mapping of three subcortical structures: the hippocampus, putamen and caudate nucleus. As shown in Fig. 1, these shapes share a similar profile globally. For each shape, we can consider its thinner part on the left as the “tail”, and the thicker part on the right as the “head”. This kind of division can also be useful in anatomical and functional studies. Not only globally, these shapes also have locally similar ridge features as highlighted by the red curve in each picture. By using Laplace-Beltrami eigenmaps, we describe in section 2 an automated approach to capture these salient features. After that, the landmarks are used to guide harmonic maps to the sphere in section 3 and generate feature-aligned, one-to-one correspondences across shapes. Experimental results will be presented to demonstrate our algorithm in section 4. Finally, conclusions are made in section 5.

Fig. 1.

Examples of subcortical structures.

2 Laplace-Beltrami Eigenmaps of Surfaces

Given a surface , we compute a function f: → ℝ that maps smoothly into ℝ by solving

$$f=arg\underset{\left|\right|f\left|\right|=1}{min}{\int }_{\mathcal{M}}{\left|\right|{\nabla }_{\mathcal{M}}f\left|\right|}^{2}d\mathcal{M},$$ (1)

where is the intrinsic gradient operator on . Using Stokes’ theorem, we have

$${\int }_{\mathcal{M}}{\left|\right|{\nabla }_{\mathcal{M}}f\left|\right|}^{2}d\mathcal{M}={\int }_{\mathcal{M}}(-{\mathrm{\Delta }}_{\mathcal{M}}f)fd\mathcal{M}$$ (2)

where is the Laplace-Beltrami operator on . For a manifold with boundary, the above equation still holds if we choose the Neumann boundary condition. Based on (2), we find the optimal map f by considering the spectrum of the operator , which is discrete for a compact manifold. Let us denote the eigenvalues of 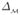as λ₀ ≤ λ₁ ≤ λ₂ ≤ ··· and the corresponding eigenfunctions as f₀, f₁, f₂, ···. In previous work on shape analysis, the set of eigenvalues was used for classification [12] and the eigenfunctions were used for denoising [13]. Here we use the spectrum to characterize the salient geometry of . For λ₀ = 0, the eigenfunction f₀ is constant. So the smoothest and non-trivial map from to ℝ is f₁ because it achieves the minimal energy λ₁ = 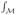|| 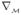f₁||² d.

For compact manifolds, a generic property of the Laplace-Beltrami operator is that its eigenfunctions are Morse functions [14]. This motivates us to use the Reeb graph [15] of f₁ to capture the global property of the surface intrinsically. For the eigenmap f₁: → ℝ, its Reeb graph is defined as the quotient space of × ℝ with the equivalent relation (x₁, f₁(x₁)) ≃ (x₂, f₁(x₂)) for x₁, x₂ ∈ . The structure of the Reeb graph is closely related to the global characteristics, such as topology, of the manifold . For example, the number of loops in the Reeb graph of a Morse function on equals its number of genus. Besides that, we can see below it reveals richer structural similarities between different shapes, such as the hippocampus and the sphere. To build the Reeb graph numerically, we assume the surface is represented as a triangular mesh and compute its Laplace-Beltrami spectrum with the finite element method [12, 13]. As a result, the eigenmap f₁ is defined on each vertex of . Let f₁ ∈ [f_min, f_max]. We trace the level sets of f₁ on at K values (α₁, α₂, ···, α_K) such that f_min = α₀ < α₁ < α₂ < ··· < α_K < f_max = α_K+1 and

$$\frac{({\alpha }_{k+1}-{\alpha }_k){\int }_{M_k}d{\mathcal{M}}_k}{{\int }_{M_k}\left|\right|\nabla f_1\left|\right|d{\mathcal{M}}_k}=\mathit{constant},k=0,1,\cdots ,K$$ (3)

where 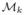= {x ∈ |α_k < f₁(x) ≤ α_k+1}. This generates a set of level contours distributing evenly spaced on the surface. Note that each level set can be composed of multiple contours for arbitrary surfaces. With each contour as a node in the Reeb graph, two neighboring level contours are connected with an edge if they can deform into each other without crossing other contours.

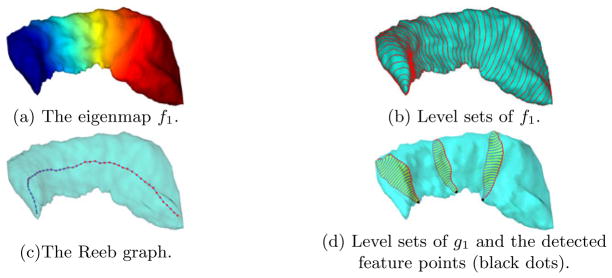
With the hippocampus in Fig. 1(a) as an example, we visualize in Fig. 2(a), (b), (c) the eigenmap f₁, its level contours, and the Reeb graph, respectively. If we assume the hippocampus is aligned in Talairach orientation and fix the sign of f₁ to be negative at the most posterior vertex of , we have the Reeb graph as an explicit representation of the simple, tail-to-head structure of the hippocampus. As we traverse the graph from the node representing the level set f₁ = α₁ to the other end, we move from the tail of the hippocampus to its head. Interestingly, if we compute the Laplace-Beltrami eigenmap of the sphere, its Reeb graph also has a chain structure as in Fig. 2(c). Using the Reeb graph of the Laplace-Beltrami eigenmap, we thus have a richer and intrinsic characterization of structural similarities between shapes beyond topology. In this case, it provides a deeper justification of using spherical parameterizations for the mapping of hippocampal surfaces besides the fact they both have genus-zero topology. On the other hand, it might improve our understanding of the difficulties in building spherical parameterizations for more irregular shapes and eventually lead to the selection of more suitable parameterization domains.

Fig. 2.

The Laplace-Beltrami eigenmaps of a hippocampal surface.

With the Reeb graph providing information about the global structure of a surface, we compute a second Laplace-Beltrami eigenmap to detect the point on level contours that marks the salient local feature highlighted in Fig. 1. For this purpose, we represent a contour as a set of L points x_l(1 ≤ l ≤ L) and build a smooth mesh in ℝ³ with the contour as the boundary. As a first step, we construct a Delaunay triangulation from these points using the software triangle [16]. The final smooth mesh 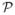is then obtained by applying Laplacian smoothing to vertices belonging to the interior of this mesh while fixing the boundary points x_l. Using the Neumann boundary condition, we map this surface patch to ℝ by computing the first eigenfunction of the Laplace-Beltrami operator on 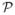, which we denote as g₁. As in the first eigenmap, we remove the ambiguity in the sign of g₁ by fixing it to be negative at the most lateral vertex in .

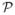As an illustration, we visualize the second eigenmap in Fig. 2(d) by plotting the level sets of the eigenmap g₁ on three interpolated surface patches. From the results we can see the second eigenmap g₁ projects each patch along the medial-to-lateral direction for brains in Talairach orientation, and we can locate the feature point on the ridge by picking the point on the level contour attaining the maximal values in g₁. To detect the whole ridge line, we compute the above eigenmap g₁ for the level sets of f₁ at the value α_k for K₁ ≤ k ≤ K₂ and connect their feature points sequentially to form the landmark curve 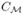shown as the red contour in Fig. 1(a). For the subcortical surfaces under study here, the ridge feature becomes less salient as we approach the tail or head part, thus we choose K₁ > 1 and K₂ < K to pick out the most distinguished part of the ridge line and use it to guide the mapping process. For all surfaces tested so far in our work, we sample K = 100 level contours from the first eigenmap and find that choosing K₁ = 20, K₂ = 85 gives robust results in the second embedding. More generally, these parameters may as well be determined with a learning-based approach.

3 Spherical Mapping With Landmark Constraints

Following the landmark detection process with Laplace-Beltrami eigenmaps, we compute a harmonic map from each surface to the sphere. By combining these harmonic maps, we can obtain diffeomorphic maps between different surfaces[17].

To ensure the one-to-one correspondences on the landmark curve 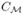of different surfaces are maintained in their spherical parameterizations, we sample a curve 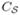= {(θ, φ)|0.25π ≤ θ ≤ 0.75π, φ = 0} on the unit sphere 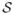with K₂ − K₁ + 1 evenly spaced points and define a boundary condition by fixing the map from each landmark point on 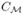to the corresponding point on 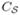with the same index. 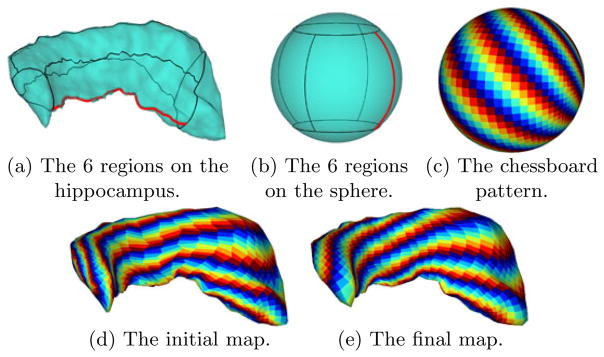Besides the boundary condition, the Laplace-Beltrami eigenmaps also provide a convenient way of estimating a good initial map from to 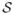. Using the detected feature point as the origin, we divide each level contour of f₁ with its index K₁ ≤ k ≤ K₂ into 4 segments of equal length and connect the corresponding end points of these segments to divide the hippocampus into 6 regions as shown in Fig. 3(a). Similarly we divide the sphere into 6 regions as shown in Fig. 3(b). For a point in a specific region on , we find its initial map as the point in the corresponding region on 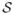that correlates best with it in terms of their distances to the 4 boundary segments of the regions. The quality of the map is visualized in Fig. 3(d), which is obtained by using the initial map to project a colored chessboard on the sphere shown in Fig. 3(c) to the hippocampus.

Fig. 3.

The computation of the harmonic map from a hippocampus to the unit sphere.

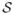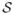Starting from the initial map, the numerical algorithm we developed previously [18] is then used to compute the harmonic map from to while respecting the boundary condition. By representing the surface and the sphere implicitly as a signed distance function ϕ and ψ, respectively, we compute the harmonic map u: → 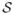by solving the following PDE iteratively:

$$\frac{\partial \mathbf{u}}{\partial t}=(I-\nabla \psi (\mathbf{u}(x,t))\nabla \psi {(\mathbf{u}(x,t))}^T)\nabla ·{(J_{\mathbf{u}}^{\varphi })}^T$$ (4)

where $J_{\mathbf{u}}^{\varphi }=J_{\mathbf{u}}(I-\nabla \varphi \nabla {\varphi }^T)$ is the intrinsic Jacobian of the map u with J_u denoting the regular Jacobian in ℝ³. When discretizing the gradient operators in (4), adaptive numerical schemes were developed in [18], where more numerical details can be found, to take into account the boundary condition on the landmark curve. For the hippocampus in Fig. 3, the result of the harmonic map is visualized in Fig. 3(e). The quality of the map is illustrated in its ability of preserving the regularity of the chessboard pattern.

4 Experimental Results

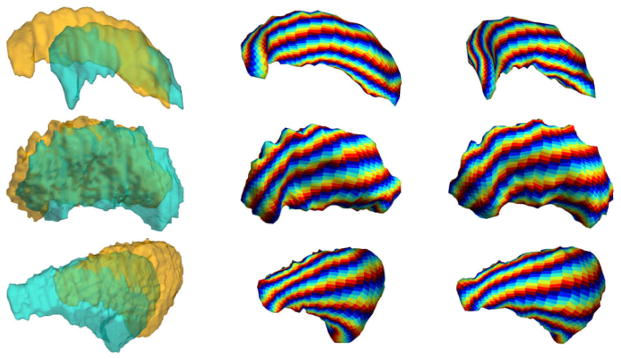
In this section we present experimental results to demonstrate the application of our algorithm in brain mapping. In our method, the only assumption on the input data is that they are from brains in Talairach orientation. Both the landmark detection step using Laplace-Beltrami eigenmaps and the harmonic mapping process are intrinsic to the surface geometry, so natural pose variations among shapes can be handled automatically. In the first experiment, we demonstrate this property of our algorithm and its ability in aligning common geometric features on three subcortical structures: the hippocampus, putamen, and caudate nucleus. Two examples from each structure are used as input data and shown in the first column of Fig. 4. The whole mapping process is completely automated, and it takes around 10 minutes on a PC for each surface. For each structure, the harmonic maps of the two surfaces are visualized in the second and third column of Fig. 4 by using the maps to project the chessboard pattern in Fig. 3(c) onto the surfaces. For all examples, we can see geometrically salient features are correctly aligned with our mapping algorithm even though they have different poses.

Fig. 4.

Mapping results of subcortical structures with different poses. Row one: hippocampi; row two: putamens; row three: caudate nuclei.

In the second experiment, we apply our method to study changes in hippocampal morphometry for patients with secondary progressive multiple sclerosis (SPMS). The input data are the left hippocampi from a group of 16 normal controls and 11 patients with SPMS shown in their natural poses in Fig. 5. Once the mapping to the sphere is completed, we project a regular triangular mesh of the sphere to each surface, establishing one-to-one correspondences that are critical for group analyses. 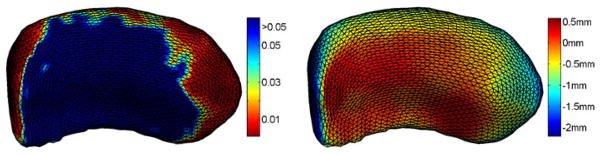After factoring out rotation and translation, we compute an atlas , shown in Fig. 6, by averaging shapes from the control group. By aligning each surface rigidly with the atlas, we compute the displacement from each vertex on the surface to the corresponding vertex on . To test group differences, a Wilcoxon rank-sum test is applied to the displacement values of the control and patient group at each vertex. The map of P values on all vertices are visualized in Fig. 6(a), together with the average displacement of the patient group in Fig. 6(b). From the results we can see large areas of volume losses in the hippocampi of patients with SPMS are successfully localized. To correct for multiple comparisons, we apply a permutation test [1] for 1 million times and an overall P value of 0.000076 is obtained, which clearly shows the significance of our mapping results.

Fig. 5.

The hippocampal surfaces of (a) the control group; (b) the patient group.

Fig. 6.

The mapping results. (a) The map of P values. (b) The map of the average displacement of the patient group.

5 Conclusions

In this paper we have developed a novel surface mapping algorithm applicable to a class of subcortical structures. The maps from our method are diffeomorphic, and also correctly align geometric features, both locally and globally, that are automatically detected with Laplace-Beltrami eigenmaps. An application of our method in group analyses has also been presented to demonstrate its robustness and ability of detecting anatomical changes due to pathology.