Cortical Shape Analysis in the Laplace-Beltrami Feature Space

Abstract

For the automated analysis of cortical morphometry, it is critical to develop robust descriptions of the position of anatomical structures on the convoluted cortex. Using the eigenfunction of the Laplace-Beltrami operator, we propose in this paper a novel feature space to characterize the cortical geometry. Derived from intrinsic geometry, this feature space is invariant to scale and pose variations, anatomically meaningful, and robust across population. A learning-based sulci detection algorithm is developed in this feature space to demonstrate its application in cortical shape analysis. Automated sulci detection results with 10 training and 15 testing surfaces are presented .

1 Introduction

The analysis and registration of cortex morphometry is an important area in human brain mapping and has produced valuable findings for the modeling of both normal and pathological brains[1]. With the increasing availability of brain scans from large scale studies[2], manual labeling becomes infeasible and it is thus critical to automate the cortical shape analysis process and robustly resolve its complicated and highly variable convolution pattern. In this paper, we propose a novel feature space derived from the eigenfunction of the Laplace-Beltrami operator to study the cortical surface. This feature space provides an intrinsic and anatomically interesting characterization of locations on the cortical surface and leads to compact modeling of anatomical landmarks invariant to scale and natural pose differences.

One main goal of cortical shape analysis is the automatic labeling of the major sulci that can serve as the landmarks for cortical normalization[1, 3]. Various learning-based approaches have been developed to incorporate priors from manual labeling[4–8]. The features used in previous work, however, rely on coordinates in canonical spaces such as the Euclidean space of a brain atlas or the unit sphere to model the position of anatomical landmarks on the cortex, which is not intrinsic and can be sensitive to the image registration results. This is especially problematic for pathological brains as they can exhibit large deviations from standard atlases. To overcome this limitation, we propose to characterize the relative locations of cortical landmarks with an intrinsic feature space that has the nice property of being invariant to pose and scale variations. This feature space is computed using the eigenfunction of the Laplace-Beltrami operator[9–12] of the cortex and a series of surface patches to describe intrinsically the anterior/posterior, superior/inferior, and medial/lateral profile of the cortex. A sulci detection algorithm in the feature space is also developed to demonstrate the application of this feature space in cortical shape analysis.

The rest of the paper is organized as follows. In section 2, we propose the Laplace-Beltrami feature space and develop the algorithm for its numerical computation. In section 3, we develop a learning-based sulci detection algorithm in the feature space to demonstrate its value in analyzing cortical anatomy. Preliminary experimental results are presented in section 4. Finally conclusions are made in section 5.

2 Laplace-Beltrami Feature Space of Cortical Surfaces

For general data analysis, a subset of the Laplacian eigenfunctions were used to form a feature space [13]. To study medical shapes, however, this is not sufficient because it does not take into account the anatomical knowledge of the underlying structure. For elongated structures such as hippocampus, the second eigenfunction of the Laplace-Beltrami operator was used to detect stable anatomical landmarks [14]. In this section, we generalize this approach to cortical surfaces and define a Laplace-Beltrami(LB) feature space $\mathcal{F}=({\mathcal{F}}_1,{\mathcal{F}}_2,{\mathcal{F}}_3)$, where ${\mathcal{F}}_i:\mathcal{M}\to \mathbb{R}(i=1,2,3)$ and $\mathcal{M}$ is a cortical surface, to capture the anatomical characteristics of cortex morphometry. We assume all brains are in the neurological orientation to remove ambiguity in the sign of eigenfunctions.

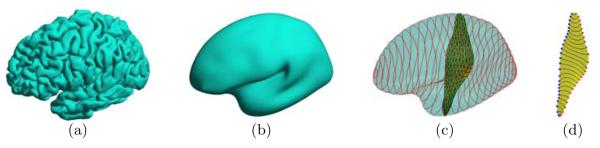
Compared with simple shapes such as hippocampus, the cortical surface is a much more complicated structure. In particular, the highly variable convolution pattern makes the extraction of stable features a challenging problem. To tackle this difficulty, we follow the multi-scale strategy. Given a cortical surface $\mathcal{M}$, we construct its feature space using a surface $\tilde{\mathcal{M}}$ that represents $\mathcal{M}$ at a coarser scale. For numerical computation, we represent both $\mathcal{M}=(\mathcal{V},\tau )$ and $\tilde{\mathcal{M}}=(\tilde{\mathcal{V}},\tau )$ as triangular meshes, where $\mathcal{V}$ and $\tilde{\mathcal{V}}$ are the set of vertices and Τ is the set of triangles. In this work, the surface $\tilde{\mathcal{M}}$ is obtained by applying the Laplacian smoothing to the original surface $\mathcal{M}$, thus the vertices in $\tilde{\mathcal{V}}$ have one-to-one correspondences to vertices in $\mathcal{V}$. As shown in Fig. 1(a) and (b), the smoothing process filters out the fine details in the convolution pattern and keeps geometric structures at the coarser scale shared across population, thus making the smoothed surface suitable to derive intrinsic location characterizations that are stable across population. Using the correspondences between $\tilde{\mathcal{V}}$ and $\mathcal{V}$, we can then compare detailed cortical features defined on the vertices of $\mathcal{M}$ in the common feature space $\mathcal{F}$ and perform analysis tasks such as sulci and gyri labeling.

Fig. 1.

(a) $\mathcal{M}$. (b) $\tilde{\mathcal{M}}$. (c) Level contours of f₁ and the surface patches used to define ${\mathcal{F}}_2$ and ${\mathcal{F}}_3$. (d) Medial(blue) and lateral(red) points of D_j.

For the surface $\tilde{\mathcal{M}}$, the eigenfunctions of its Laplace-Beltrami operator ${\Delta }_{\tilde{\mathcal{M}}}$ are defined as:

$${\Delta }_{\tilde{\mathcal{M}}}f=-\lambda f$$ (1)

The eigenvalues of ${\Delta }_{\tilde{\mathcal{M}}}$ can be ordered according to their magnitude as 0 = λ₀ ≥ λ₁ ≥ λ₂ ≥⋯. The corresponding eigenfunction of λ_i is denoted as $f_i:\tilde{\mathcal{M}}\to \mathbb{R}$. By using the weak form of (1) and the finite element method, we can compute the eigenfunctions by solving a generalized matrix eigenvalue problem:

$$Qf=\lambda Uf$$ (2)

where Q and U are matrices derived with the finite element method.

The first feature function ${\mathcal{F}}_1$ is defined using the Reeb graph [15] of the second eigenfunction f₁, which minimizes the smoothness measure ${\int }_{\tilde{\mathcal{M}}}\Vert \nabla f\Vert d\tilde{\mathcal{M}}$ and can be viewed as the smoothest non-constant projection from $\tilde{\mathcal{M}}$ to the real line $\mathbb{R}$. As shown in Fig. 1(c), the nodes of the Reeb graph are the level contours of the eigenfunction. Because the eigenfunction is generally a Moss function [16], the Reeb graph of f₁ has a tree structure. Small branches in the Reeb graph are pruned according to the length of the associated level contour such that the final graph has a chain structure. The level contours of the Reeb graph are denoted as C_i(i = 0, ⋯ ,N) with their order determined by the corresponding value of the eigenfunction f₁. Numerically we represent each contour as a polyline of K points C_i = [C_i,1, C_i,2,, ⋯ ,C_i,K]. The linear interpolation relation between these points and the vertices of $\tilde{\mathcal{M}}$ can be expressed as the following equation:

$$C=A\tilde{\mathcal{V}}$$ (3)

where C = [C₀, C₁, ⋯ ,C_N]^T and A is the matrix representing the linear interpolation operation. To quantitatively describe the anterior/posterior distribution of the cortical surface, we define ${\mathcal{F}}_1$ on the level contours as ${\mathcal{F}}_1\left(C_{i,k}\right)=-1+2\ast i∕N$. To extend ${\mathcal{F}}_1$ from the level contours to the vertices of the entire mesh, we solve the following regularized linear inverse problem:

$${\Vert {\mathcal{F}}_1\left(C\right)-A{\mathcal{F}}_1\left(\tilde{\mathcal{V}}\right)\Vert }^2+\beta {\mathcal{F}}_1{\left(\tilde{\mathcal{V}}\right)}^{T}Q{\mathcal{F}}_1\left(\tilde{\mathcal{V}}\right)$$ (4)

where ${\mathcal{F}}_1\left(C\right)$ and ${\mathcal{F}}_1\left(\tilde{\mathcal{V}}\right)$ are vectors of the values of ${\mathcal{F}}_1$ on the level contours and the vertices of the mesh $\tilde{\mathcal{M}}$, respectively, and the matrix Q is the same as in (2). The regularization term ${\mathcal{F}}_1{\left(\tilde{\mathcal{V}}\right)}^{T}Q{\mathcal{F}}_1\left(\tilde{\mathcal{V}}\right)$ encourages smoothness of the feature function. By solving this least square problem, we obtain ${\mathcal{F}}_1\left(\tilde{\mathcal{V}}\right)$ as

$${\mathcal{F}}_1\left(\tilde{\mathcal{V}}\right)={(A^{T}A+\beta Q)}^{-1}{A}^T{\mathcal{F}}_1\left(C\right).$$ (5)

To define the second feature function ${\mathcal{F}}_2$, we first compute a surface patch approximating the minimal surface of each level contour C_i as proposed in [14]. As shown in Fig. 1(c), this surface patch smoothly interpolates the interior of the contour. We use the eigenfunction of each surface patch to define ${\mathcal{F}}_2$ and characterize the superior/inferior profile of cortical surfaces. Let $g_1^i$ denote the second eigenfunction of the Laplace-Beltrami operator of the i-th surface patch. We then compute the Reeb graph of $g_1^i$ by sampling it at N + 1 level contours D_j(j = 0, ⋯ ,N) and assign a value $1-\frac{2L_i(N-j)}{N{L}_{\mathit{max}}}$ to D_j to describe its superior-to-inferior position on the surface, where L_i is the length of C_i and L_max is the maximal length of all level contours. The value of ${\mathcal{F}}_2$ on the points C_i,k is defined using linear interpolation from the values of neighboring level contours of $g_1^i$. Following the same approach of computing ${\mathcal{F}}_1$, we can extend the second feature function to the vertices of the entire mesh:

$${\mathcal{F}}_2\left(\tilde{\mathcal{V}}\right)={(A^{T}A+\beta Q)}^{-1}{A}^T{\mathcal{F}}_2\left(C\right)$$ (6)

where ${\mathcal{F}}_2\left(C\right)$ and ${\mathcal{F}}_2\left(\tilde{\mathcal{V}}\right)$ are the vectors of values of ${\mathcal{F}}_2$ on the level contours and the vertices, respectively.

We use the same eigenfunction $g_1^i$ of the surface patches to define the third feature function ${\mathcal{F}}_3$ to characterize the medial/lateral distribution of the cortical surface. Using the assumption that the cortical surface is in the neurological orientation, we denote the two end points of the level contour D_j as the medial and lateral point of D_j by comparing the magnitude of their x-coordinates, which are plotted as the blue and red dots in Fig. 1(d). For the medial point of D_j, we assign a value $\frac{(\mid 2j-N\mid -N)L_i}{N{L}_{\mathit{max}}}$. For the lateral point of D_j, we assign a value $\frac{(N-\mid 2j-N\mid )L_i}{N{L}_{\mathit{max}}}$. The same interpolation procedure of computing ${\mathcal{F}}_2$ is then applied to extend these values to the entire mesh and obtain the feature function ${\mathcal{F}}_3$.

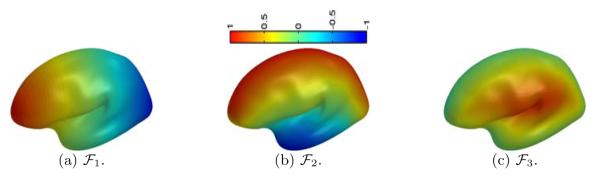
As an illustration, we plot in Fig. 2(a), (b) and (c) the three feature functions of the surface in Fig. 1(b) with the parameter β =1, N = 100, K = 100. Using the sign of ${\mathcal{F}}_3$, we can easily separate the medial and lateral side of the surface. For each point on the medial or lateral side, the two functions (${\mathcal{F}}_1,{\mathcal{F}}_2$) provide an intrinsic description of its relative location on the cortex. With the only assumption that the brain is in neurological orientation, these descriptions are invariant to scale differences and natural pose variations.

Fig. 2.

Feature functions plotted on $\tilde{\mathcal{M}}$.

3 Sulci Detection in the Feature Space

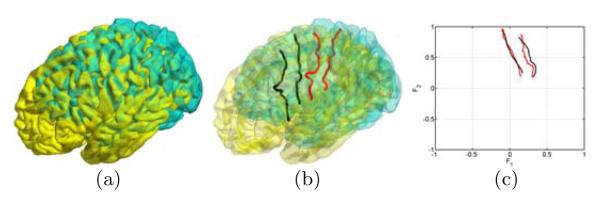
In this section, we demonstrate the application of the LB feature space in cortical shape analysis by applying it to the automated detection of major sulci. To illustrate the advantage of the LB feature space in describing the location on cortical surfaces, we show in Fig. 3(a) two cortical surfaces in the Euclidean space and their central and pre-central sulcus in Fig. 3(b). After we compute the LB feature functions, we project the sulci of both surfaces into the common space (${\mathcal{F}}_1,{\mathcal{F}}_2$). From the result in Fig. 3(c), we can see the sulci are much better aligned in the feature space than in the original space. This shows the invariance of LB features and suggests their ability of building more compact sulcal models.

Fig. 3.

Sulci in the Euclidean and LB feature space.

For automated sulci detection, we follow the learning-based approach in [8] by first generating a sample space of candidate curves in the feature space and then finding the most likely curve as the projection of the detected sulci in $\mathcal{F}$. Due to space limitation, we describe our method briefly in the following. To learn the prior model of a sulcus in the feature space, we assume a training set of cortical surfaces with manually labeled sulcal curves and compute the feature functions for each surface to project the sulcus into the feature space. Using these projected training curves, we estimate a density function $p(\overrightarrow{x},\overrightarrow{v})$ with the Parzen window method, where $\overrightarrow{x}$ represents a point of a curve in the feature space and $\overrightarrow{v}$ is the tangent vector of the curve at the point $\overrightarrow{x}$. For a curve in the feature space, we can then compute its likelihood of being part of the major sulcus as the integral of the density function on this curve divided by its length. Besides this local model, we also apply the principal component analysis (PCA) [17] to the set of projected training curves to capture their global characteristics.

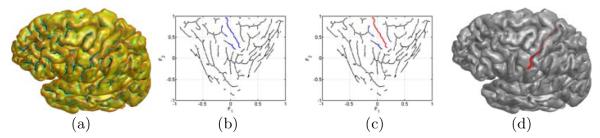
There are four main steps in our sulci detection algorithm. Using the central sulcus as an example, we illustrate the result generated from each step in Fig. 4. Given a cortical surface $\mathcal{M}$, we first construct the skeletal representation of the folding pattern by computing the Hamilton-Jacobi skeleton of the sulcal regions [18] as shown in Fig. 4(a). After that, we compute the feature space (${\mathcal{F}}_1,{\mathcal{F}}_2,{\mathcal{F}}_3$). For major sulci on the lateral surface, we then project all skeletal branches with ${\mathcal{F}}_3>0$ onto the feature space (${\mathcal{F}}_1,{\mathcal{F}}_2$). Similarly, skeletal branches with ${\mathcal{F}}_3<0$ will be processed for major sulci on the medial surface. We divide each skeletal branch into curve segments of fixed length and compute their probability of being on the major sulcus of interest using the density function $p(\overrightarrow{x},\overrightarrow{v})$. Curve segments with the probability greater than a threshold, which we set as 0.01 in all our experiments, are then chosen as candidate segments on the major sulcus, which we plot in blue in Fig. 4(b). In the third step, we follow the sample space generation algorithm in [8] to construct a graph model from these curve segments and generate a set of candidate curves via random walking on the graph model. For each candidate curve, we compute its likelihood of being the major sulcus as the product of the probability obtained from the density function and the PCA model to account for both local and global information. The most likely path, as shown in red in Fig. 4(c), is chosen as the projection of the detected sulcal curve in the feature space. Finally we connect the skeletal segments of the most likely path with curvature-weighted geodesics on the original surface $\mathcal{M}$ as the automatically generated major sulcus shown in Fig. 4(d).

Fig. 4.

(a) Hamilton-Jacobi skeletons of sulcal regions. (b) Skeletons in the LB feature space. (c) The most likely path (red) in the LB feature space. (d) The detected central sulcus on the original cortical surface.

4 Experimental Results

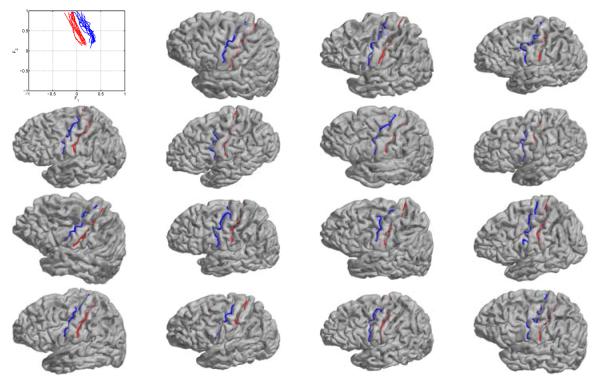
In this section, we present preliminary experimental results on the detection of two major sulci: the central and precentral sulcus using the LB feature space. The data set is composed of 25 right hemispherical cortical surfaces of spherical topology[19]. We manually labeled the two sulci on 10 of the 25 surfaces and use them as the training data. The projection of these training curves in the feature space is shown in the upper left of Fig. 5. From these training curves, we learn the density function and PCA model. Using these prior models, we tested our sulci detection algorithm on the other 15 cortical surfaces. The automatically detected sulcal curves on these surfaces are plotted in Fig. 5.

Fig. 5.

Training data (upper left) and sulci detection results on the 15 testing surfaces (red: central sulcus; blue: pre-central sulcus).

From the results we can see that our method is able to successfully detect the two major sulci on all testing surfaces. Even though the brains vary quite significantly in terms of shape and orientation, our method is robust to such pose and geometric variations because it is designed in the space of intrinsic eigenfeatures. In our future work, we will incorporate Markovian priors of neighboring sulci in the feature space for the detection of multiple sulci and validate on larger data sets of different populations.

5 Conclusion

In this paper, we proposed a novel approach of constructing feature spaces for cortical shape analysis using the eigenfunction of the Laplace-Beltrami operator. The LB feature space provides an intrinsic and anatomically meaningful way of characterize locations on the cortical surfaces. We demonstrated its application in automated sulci detection and preliminary experimental results have been presented.