Accurate proton affinity and gas-phase basicity values for molecules important in biocatalysis

Abstract

Benchmark quantum calculations of proton affinities and gas phase basicities of molecules relevant to biochemical processes, particulsarly acid/base catalysis, are presented and compared for a variety of multi-level and density-functional quantum models. Included are nucleic acid bases in both keto and enol tautomeric forms, ribose in B-form and A-form sugar pucker conformations, amino acid side chains and backbone molecules, and various phosphates and phosphoranes including thio substitutions. This work presents a high-level thermodynamic characterization of biologically relevant protonation states, and provides a benchmark database for development of next-generation semiempirical and approximate density-functional quantum models, and parameterization of methods to predict pKa values and relative solvation energies.

I. INTRODUCTION

The charge state of proteins and nucleic acids play an important role in both structure and reactivity. A key mechanism of controlling charge state and influencing acid-base catalysis is through protonation/deprotonation events of ionizable residues¹. There has been considerable effort devoted to the prediction of proton affinities and pK_a values with quantum chemistry and implicit/explicit solvation models^2–29. Much of the quantitative work has focused on the prediction of pK_a shifts of ionizable residues with respect to a closely related reference state (for which reliable absolute pK_a values have been determined) rather than on the prediction of the absolute pK_a values themselves.

When carefully tested, this type of indirect approach often leads to cancellation of systematic errors that ultimately results in more quantitative accuracy. Examples of commonly used reference state for calculation of pK_a shifts include a closely related molecule or residue, or else the same molecule or residue in a different environment. The absolute pK_a values can be recovered from the calculated pK_a shift and the experimentally known absolute pK_a value of the reference state. Nonetheless, this area remains a challenge due to the small differences in free energy that give rise to pK_a shifts (a pK_a unit corresponds to 1.364 kcal/mol of energy at 298.15 K).

Reliable prediction of pK_a shifts using known experimental data may not always be possible, since the determination of the experimental pK_a value of an appropriate reference state might not be available, e.g., metaphosphates and phosphoranes that form reactive intermediates in phosphoryl transfer reactions. For these important intermediates, experiment can only provide a rough estimate of the pK_a values. Consequently, methods that improve the prediction of absolute pK_a values are also of importance, and ultimately, may lead to the determination of pK_a shifts with increased reliability.

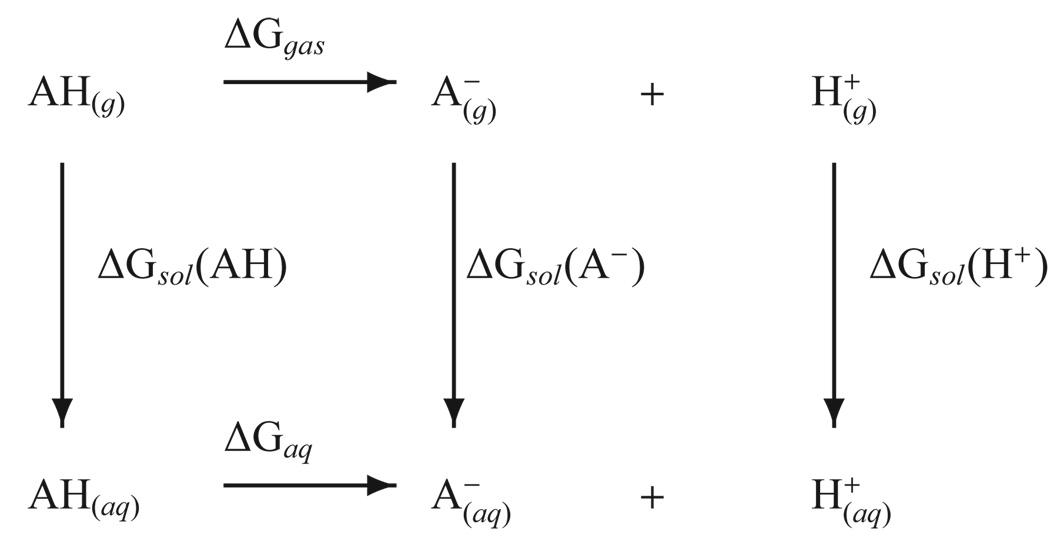
The accurate prediction of absolute pK_a values is often made using a thermodynamic cycle such as the one shown in Figure 1, although many variations have also been tested.^17,20,30 A key quantity in the cycle is the gas-phase basicity (GPB) that involves deprotonation of the species of interest in the gas-phase (ΔG_gas in Figure 1). Related to the gas-phase basicity is the proton affinity (PA), which is the enthalpic component of the same process³¹. Given the active site of most enzymes or the center of large biomolecules is an environment that is neither that of bulk solution nor gasphase, benchmarking these two end point environments is key to making pK_a predictions.

FIG. 1.

A commonly employed thermodynamic cycle for calculating pK_a values.

The purpose of the present work is to deliver a consistent, benchmark database of quantum calculations for proton affinities and gas-phase basicities of residues involved in biocatalysis. Compounds were considered that represent titratable amino acid backbone and side-chain residues, nucleic acid bases, sugar and phosphate moieties as well as biological and chemically modified phosphates and phosphoranes important in phosphoryl transfer reactions and RNA catalysis. The accuracy of a series of high-level quantum model chemistries was assessed against known experimental proton affinity and gas-phase basicity values. This comparison was then used to derive a set of empirical bond enthalpy and free energy corrections and a linear regression correction that improves the accuracy and, for closely related molecules, the predictive capability of the methods. The results presented herein provide valuable data for the development of next-generation approximate quantum models that can be used in combined QM/MM simulations of biocatalysis,^32–34 for the determination of relative solvation free energies of conjugate acid/base pairs from pK_a data in solution,^35–38 and for the development of improved models for the theoretical determination of pK_a shifts in biomolecules.^29,39–44

II. METHODS

A. Electronic structure calculations

All electronic structure and thermochemical analyses were performed using the Gaussian03 suite of programs.⁴⁵ Three “multi-level” methods were studied: CBS-QB3^46,47, G3B3⁴⁸, and G3MP2B3⁴⁸. CBS-QB3 (abbreviated CBS in this article) is a multi-level model chemistry that combines the results of several electronic structure calculations and empirical terms to predict molecular energies to around 1 kcal/mol accuracy.⁴⁹ The required electronic structure calculations are outlined below, see Ref. 46 for details:

CBS

• B3LYP/6–311G(2d,d,p) geometry optimization and frequencies

• MP2/6–311+G(3df,2df,2p) energy and CBS extrapolation

• MP4(SDQ)/6–31+G(d(f),p) energy

• CCSD(T)/6–31+G^† energy

The G3B3 and the related G3MP2B3 (abbreviated G3MP2 in this article and not to be confused with the usual meaning referring to the method that uses Hartree-Fock geometry and frequency calculations) methods are both modifications of the Gaussian-3 multi-level theory for the calculation of molecular energies.⁵⁰. Like CBS-QB3, G3B3 and G3MP2 use density functional theory with the B3LYP functional for geometries and frequencies and combine the results of several electronic structure calculations and empirical terms to predict molecular energies to around 1 kcal/mol accuracy. The required electronic structure calculations for the G3B3 method are outlined below, see Ref. 48 for details:

G3B3

• B3LYP/6–31G(d) geometry optimization and frequencies

• MP2/G3Large energy

• MP4/6–31G(d) energy

• MP4/6–31+G(d) energy

• MP4/6–31G(2df,p) energy

• QCISD(T)/6–31G(d) energy

The G3MP2 method eliminates all of the MP4 calculations above, trading some accuracy for speed.

All of the multi-level methods studied here formally scale as O(N⁷) due to the CCSD(T) step in CBS, the QCISD(T) step of the G3 methods, and the MP4 steps in G3B3 (for the molecules in the present study, the large basis set MP4 step was usually the computational bottleneck with the G3B3 method). For the systems studied in this paper the scaling of the multi-level methods was not prohibitive, but for larger systems of biological interest the O(N⁷) will eventually dominate and make the calculation unfeasible. Therefore several model chemistries based solely on hybrid density functionals were investigated that have more favorable scaling properties, specifically PBE0/6–311++G(3df,2p) (designated PBE0), B1B95/6–311++G(3df,2p) (designated B1B95), and B3LYP/6–311++G(3df,2p) (designated B3LYP). Additionally, the B3LYP/6–311++G(3df,2p)//B3LYP/6–31++G(d,p) model chemistry (designated QCRNA) that has been extensively applied to model biological phosphorous compounds^7,51–57 was also included.

B3LYP is a three parameter hybrid functional⁵⁸ using the B88 exchange functional of Becke⁵⁹ and the Lee, Yang, and Parr correlation functional⁶⁰. PBE0 is a zero parameter hybrid functional⁶¹ using the Perdew, Burke, Ernzerhof exchange and correlation functional⁶². B1B95 is a one parameter hybrid functional⁶³ using the B88 exchange functional of Becke⁵⁹ and B95 correlation functional⁶³.

In an effort to give the hybrid density functional methods the best possible accuracy for benchmark purposes and avoid problems in the frequency calculations⁶⁴ all calculations (except the QCRNA and multilevel theories) were run with the so-called “ultrafine” numerical integration grid (a pruned grid based on 99 radial shells and 590 angular points per shell) and tight convergence criteria for the geometry optimizations. The use of large basis sets, ultrafine numerical integration meshes, and tight convergence criteria serve to make these calculations benchmark quality. The QCRNA model is significantly less expensive than the related B3LYP model since it avoids the geometry optimization and frequency calculation steps with the large 6–311++G(3df,2p) basis, and uses the default integration grid (a pruned grid based on 75 radial shells and 302 angular points per shell) and geometry convergence criteria. As demonstrated below, QCRNA gives results in very close agreement to that of B3LYP.

B. Calculation of proton affinities and gas-phase basicities

The proton affinity (PA) and gas-phase basicity (GPB) of a species A⁻ are related to the gas-phase reaction:

$${\mathrm{A}}_{(g)}^{-}+{\mathrm{H}}_{(g)}^{+}\to {\text{AH}}_{(g)}$$ (1)

The proton affinity of A⁻ is defined as the negative of the enthalpy change (ΔH) of the process in Eq. 1, and the gas-phase basicity of A⁻ is defined as the negative of the corresponding Gibbs free energy change (ΔG).³¹ Here, the A⁻ is the conjugate base associated with the neutral acid AH.

The required thermodynamic properties were obtained from the electronic structure calculations using standard statistical mechanical expressions for separable vibrational, rotational, and translational contributions within the harmonic oscillator, rigid rotor, ideal gas/particle-in-a-box models in the canonical ensemble⁶⁵. The standard state in the gas-phase was for a mole of particles at 298.15 K and 1 atm pressure.

In the case that a molecule has more than one conformational state accessible at a given temperature, these conformations should be appropriately sampled with Boltzmann-weighted averaging to obtain the most accurate PA and GPB. In this work the free energies were used to determine the Boltzmann average and only conformations that changed the PA or GPB by more than 0.1 kcal/mol were considered. This occurred for propanol and propanethiol where the trans conformation is higher in energy than the gauche conformation but by less than 0.5 kcal/mol in free energy.

The enthalpy of the proton was calculated from the ideal gas expression

$$H({\mathrm{H}}^{+})=U+pV=\frac{5}{2}RT$$ (2)

where U is the internal energy, p and V are the pressure and volume, respectively, R is the universal gas constant, and T is the absolute temperature. The entropy of the proton was calculated from the Sackur-Tetrode equation⁶⁶,

$$S({\mathrm{H}}^{+})=R\text{ln}\left(\frac{e^{\frac{5}{2}}{k}_{B}T}{p{\mathrm{\Lambda }}^3}\right)$$ (3)

where k_B is the Boltzmann constant and Λ is the thermal De Broglie wavelength [Λ = (h²/2πmk_BT)^1/2, where h is Planck’s constant and m is the mass of the proton]. Under the standard state conditions, the values of the enthalpy and entropy of the gas-phase proton are H(H⁺) = 1.48 kcal/mol and S(H⁺) = 26.02 cal/(mol · K), respectively, and lead to a gas-phase Gibbs free energy value of G(H⁺) = H(H⁺) − TS(H⁺) = −6.28 kcal/mol.

It is sometimes the case that a molecule and/or its conjugate base has more than one indistinguishable microscopic protonation state. All of the GPB values in this paper are microscopic gas-phase basicities, since that is what naturally comes out of electronic structure calculations of a single protonation state. The conversion between microscopic and macroscopic GPB values was performed as follows.

The equilibrium constant, K^M, (where the M indicates macroscopic) for the reverse process to that of Eq. 1, assuming unit activity coefficients, is given by:

$$K^M=\frac{{[A^{-}]}_M[H^{+}]}{{[AH]}_M}$$ (4)

If A⁻ has m indistinguishable microscopic protonation states and AH has n indistinguishable microscopic protonation states, then:

$$K^M=\frac{m{[A^{-}]}_{\mu }[H^{+}]}{n{[AH]}_{\mu }}=K^{\mu }\left(\frac{m}{n}\right)$$ (5)

where µ indicates microscopic quantities and K^µ = [A⁻]_µ[H⁺]/[AH ]_µ. The free energy change (ΔG) for a process is related to the equilibrium constant by:

$$\mathrm{\Delta }G=-RT\text{ln}K$$ (6)

where R is the ideal gas constant and T is the temperature of interest. Substitution of Eq. 6 into Eq. 5 yields the following equation for interconversion of microscopic and macroscopic free energy changes:

$$\mathrm{\Delta }{G}^{\mu }=\mathrm{\Delta }{G}^M+RT\text{ln}\left(\frac{m}{n}\right)$$ (7)

For example, H₃PO₄ has 4 indistinguishable microscopic protonation states (distribution of 3 protons among 4 sites gives ₄C₃ = 4, where _nC_k = n!/(n − k)!k! is a binomial coefficient) and its conjugate base, ${\mathrm{H}}_2{\text{PO}}_4^{-}$, has 6 indistinguishable microscopic protonation states (₄C₂ = 6). The experimental (macroscopic) GPB of H₃PO₄ is 323.0 kcal/mol⁶⁷. Application of Eq. 7 yields a microscopic GPB of 323.2 kcal/mol at 298.15 K.

III. RESULTS AND DISCUSSION

In this section, we present calculated proton affinity and gas-phase basicity results for a wide range of biologically relevant molecules. The first section presents results for a series of O-H, N-H and S-H molecules that have experimental PA and GPB values for comparison, from which a set of empirical corrections to the calculated values are derived. The second section presents results for molecules that represent amino acid backbone and side chain residues. The third section presents results for nucleic acid nucleobases, including tautomerization energies. The fourth section presents results for nucleic acid ribose sugar models, including different sugar pucker conformations. The fifth section presents results for native and thio-substituted phosphates and phosphoranes of interest in the study of phosphoryl transfer reactions. Throughout this section, we have endeavored, where possible, to consider model compounds th have limited flexibility in order to avoid complications due to multiple minima that can significantly influence PA and GPB values. For example, side chain conformation in methionine can tune the PA and GPB by ~10 kcal/mol from the value for glycinium.⁶⁸ The complete geometrical and thermodynamic data is available in the supporting information and via the QCRNA database.^57,69

A. Experimental Comparison

Table 1 summarizes the PA and GPB errors (calculated - experimental value) for O-H, S-H, and N-H bond containing molecules. All experimental values are taken from the NIST online database⁶⁷ unless where otherwise noted. Included are the maximum error (MAXE), root mean squared error (RMSE), mean unsigned error (MUE), and mean signed error (MUE). As expected the multi-level methods preform better than the density functional methods for both PA and GPB, with PBE0 and B1B95 generally overestimating and B3LYP and QCRNA underestimating the values. As QCRNA consists only of B3LYP calculations, it very closely resembles the B3LYP results except for propanoic acid GPB where they differ by 1.8 kcal/mol. The largest outliers for all the multilevel models are dimethylphosphate and phosphoric acid. For PBE0 and B1B95, water and 4-methyl-imidazolium have the largest deviation, while B3LYP and QCRNA have maximum error on p-nitrophenol. For all models the PA and GPB generally have the same trends and error metrics. Also provided in supplementary information for comparison are the dipole moments of the neutral molecules in Table 3 with available experimental data.

TABLE 1.

Proton affinity (left column) and gas-phase basicity (right column) error analysis. All quantities are in kcal/mol. Experimental values are from ref. 67 with error estimates given in parentheses. Error is given as quantum model chemistry minus experimental value (error = calculated - experiment). Error metrics of maximum error (MAXE), root-mean-squared error (RMSE), mean unsigned error (MUE), and mean signed error (MSE) are given below.

Moleculea	CBS		G3B3		G3MP2		PBE0		B1B95		B3LYP		QCRNA		Experiment
water	1.7	1.7	1.2	1.2	1.3	1.3	3.2	3.2	3.3	3.3	0.1	0.1	0.1	0.1	390.3 (0.2)	383.7 (0.2)
hydronium	−1.0	−1.1	−0.3	−0.4	−0.4	−0.5	0.6	0.5	0.5	0.3	−1.1	−1.2	−1.1	−1.2	165.0 (1.0)	157.7 (0.1)
methanol	1.1	1.3	2.2	2.4	2.2	2.3	−0.5	−0.3	−0.1	0.1	−2.3	−2.0	−2.3	−2.1	381.5 (1.0)	374.8 (0.7)
ethanol	0.7	0.4	1.5	1.3	1.7	1.4	−0.3	−0.5	0.3	−0.0	−2.2	−2.5	−2.2	−2.4	378.2 (0.8)	371.3 (1.0)
propanol	1.1	0.7	2.0	1.6	2.2	1.8	0.4	−0.1	0.9	0.4	−1.2	−1.8	−1.2	−1.7	376.0 (1.1)	369.4 (1.1)
2−propanol	0.8	0.3	1.4	1.0	1.7	1.3	0.7	0.3	1.2	0.8	−1.4	−1.8	−1.3	−1.7	375.7 (0.8)	368.8 (1.0)
DMPHb	−2.4	−1.7	−1.8	−1.2	−1.3	−0.7	−0.6	0.2	−0.7	0.3	−1.6	−0.8	−1.5	−0.9	331.6 (4.1)	324.6 (4.0)
phosphoric acid	−2.6	−2.5	−2.2	−2.2	−1.8	−1.8	−0.5	−0.3	−0.6	−0.4	−2.4	−2.2	−2.3	−2.2	330.5 (5.0)	323.2 (4.9)
formic acid	−0.4	−1.3	0.4	−0.6	0.9	−0.1	−0.2	−1.1	0.1	−0.8	−2.0	−2.9	−2.0	−2.9	344.0 (1.6)	337.9 (1.2)
acetic acid	0.2	−2.0	1.0	−1.2	1.4	−0.8	0.4	−0.1	0.7	0.1	−1.4	−1.9	−0.8	−3.1	347.2 (1.1)	341.4 (1.2)
propanoic acid	−1.2	−0.3	−0.4	0.6	−0.0	1.0	0.4	−1.2	0.5	−0.5	−1.3	−2.8	−1.9	−1.0	347.4 (1.8)	340.4 (1.4)
glycine	1.5	−0.4	2.3	0.5	2.7	0.8	2.7	0.7	2.9	0.9	1.2	−0.9	1.2	−0.8	340.3 (1.1)	335.1 (1.4)
proline	−0.2	−0.9	0.7	−0.0	0.9	0.2	1.8	1.0	1.8	1.0	0.1	−0.8	0.1	−0.8	340.3 (3.1)	333.4 (3.0)
phenol	−0.8	−0.6	−0.6	−0.5	−0.6	−0.5	−1.4	−1.3	−0.7	−0.7	−2.4	−2.3	−2.5	−2.4	350.1 (1.1)	342.9 (1.4)
o-chlorophenol	0.7	−0.7	1.0	−0.4	1.0	−0.4	0.4	−1.1	1.0	−0.5	−1.0	−2.4	−1.0	−2.4	343.4 (2.3)	337.1 (2.0)
m-chlorophenol	−0.5	−1.2	−0.2	−0.9	−0.2	−0.9	−1.2	−1.8	−0.6	−1.2	−2.4	−3.0	−2.3	−2.9	342.1 (3.1)	335.2 (1.4)
p-chlorophenol	−0.5	−0.9	−0.2	−0.5	−0.2	−0.5	−1.0	−1.3	−0.5	−0.7	−2.2	−2.4	−2.3	−2.6	343.4 (1.6)	336.5 (1.4)
p-methylphenol	−0.3	−0.6	0.0	−0.4	0.0	−0.4	−0.7	−1.0	−0.1	−0.6	−1.8	−2.0	−1.8	−2.2	350.7 (1.3)	343.8 (1.2)
p-nitrophenol	−0.2	−0.1	0.2	0.2	0.7	0.7	−2.3	−2.3	−1.7	−1.8	−4.1	−4.1	−4.1	−4.2	327.8 (2.1)	320.9 (2.0)
hydrogen sulfide	−0.5	−0.5	−0.1	0.0	0.2	0.2	0.5	0.5	0.8	0.8	−0.3	−0.3	−0.4	−0.4	351.3 (0.8)	344.9 (2.0)
methanethiol	−0.5	−0.2	0.1	0.2	0.4	0.7	0.9	1.2	1.4	1.7	0.0	0.4	−0.0	0.3	357.3 (1.2)	350.6 (2.0)
ethanethiol	−1.2	−1.5	−0.5	−0.0	−0.2	−0.6	0.3	−0.1	1.0	0.7	−0.4	−0.9	−0.4	−0.8	355.4 (1.5)	348.9 (2.0)
propanethiol	−1.0	−1.0	−0.4	0.4	−0.1	−0.2	0.6	0.5	1.2	1.0	0.2	−0.2	0.2	−0.2	354.2 (2.2)	347.9 (2.0)
2-propanethiol	−0.5	−1.2	0.1	−0.9	0.4	−0.3	1.4	0.6	2.0	1.2	0.6	−0.1	0.6	−0.1	353.4 (2.2)	347.1 (2.0)
ammonium	0.2	0.3	0.5	−0.5	0.3	0.3	0.6	0.7	0.2	0.3	−1.1	−1.0	−1.1	−1.0	204.0 (0.5)	195.7 (0.5)
methylammonium	0.1	0.2	0.6	−0.6	0.4	0.6	0.5	0.5	0.2	0.3	−0.6	−0.6	−0.6	−0.6	214.9 (0.5)	206.6 (0.5)
ethylammonium	0.1	0.6	0.6	0.6	0.5	1.0	0.9	1.4	0.5	1.0	−0.1	0.3	−0.1	0.3	218.0 (0.5)	210.0 (5.0)
propanammonium	−0.1	0.5	0.4	0.7	0.2	0.9	0.9	1.5	0.7	1.3	−0.0	0.5	−0.1	0.6	219.4 (0.5)	211.3 (0.5)
2-propanammonium	−0.6	0.2	−0.1	1.1	−0.2	0.6	1.0	1.8	0.7	1.5	−0.1	0.8	−0.1	0.7	220.8 (0.5)	212.5 (0.5)
1H-3H–imidazolium	−0.0	−0.5	0.7	1.0	0.4	−0.1	1.9	1.4	1.8	1.2	1.3	0.8	1.3	0.8	225.3 (0.5)	217.7 (0.5)
4-methyl-imidazolium	1.3	1.1	1.9	0.7	1.7	1.5	3.6	3.5	3.5	3.4	3.0	2.9	3.0	2.9	227.7 (2.0)	220.1 (2.0)
pyridinium	−0.4	−0.8	0.3	0.1	0.0	−0.3	2.0	1.7	1.8	1.5	1.8	1.5	1.9	1.5	222.0 (5.0)	214.7 (0.5)
pyrrolidinium	0.1	0.4	0.8	1.7	0.7	1.2	1.0	1.3	0.8	1.1	0.6	0.9	0.6	1.0	226.6 (0.5)	218.8 (0.5)
glycinium	−0.0	0.4	0.4	−0.0	0.3	0.7	1.7	1.7	1.3	1.5	0.1	0.3	0.1	0.5	211.9 (0.5)	203.7 (0.5)
MAXE	−2.6	−2.5	2.3	2.4	2.7	2.3	3.6	3.5	3.5	3.4	−4.1	−4.1	−4.1	−4.2
RMSE	1.0	1.0	1.1	1.0	1.1	0.9	1.4	1.3	1.4	1.2	1.6	1.8	1.6	1.8
MUE	0.7	0.8	0.8	0.8	0.8	0.8	1.1	1.1	1.1	1.0	1.2	1.5	1.2	1.5
MSE	−0.2	−0.4	0.4	0.2	0.5	0.3	0.6	0.3	0.8	0.5	−0.7	−0.9	−0.7	−0.9

^a”Molecule” refers to AH in Eq. 1.

^bhydrogen dimethyl phosphate.

TABLE 3.

Proton affinity error analysis for each model broken down by bond type and fitting method. Raw indicates no correction has been made. BEC and LRM are bond energy correction and linear regression model, respectively (see text for details). Error metrics given are mean unsigned error (MUE) and mean signed error (MSE) with their standard deviations in parentheses, and sum of the squares of the deviations(S).

Model		CBS	G3B3	G3MP2	PBE0	B1B95	B3LYP	QCRNA
Raw O-H	MUE	0.9 (0.7)	1.1 (0.8)	1.2 (0.8)	1.0 (0.9)	1.0 (0.9)	1.7 (0.9)	1.7 (1.0)
	MSE	−0.1 (1.2)	0.5 (1.3)	0.7 (1.2)	0.1 (1.4)	0.4 (1.3)	−1.6 (1.2)	−1.6 (1.2)
	S	24.381	31.889	34.482	33.285	31.089	67.804	68.687
BEC O-H	MUE	0.9 (0.7)	1.0 (0.7)	1.0 (0.7)	1.1 (0.9)	1.0 (0.8)	0.8 (0.8)	0.8 (0.8)
	MSE	−0.0 (1.2)	−0.0 (1.3)	−0.0 (1.2)	0.0 (1.4)	0.0 (1.3)	0.0 (1.2)	0.0 (1.2)
	S	24.274	27.729	25.808	33.196	27.920	23.501	23.501
LRM O-H	MUE	0.6 (0.6)	0.7 (0.6)	0.8 (0.5)	0.9 (0.8)	0.8 (0.7)	0.8 (0.8)	0.9 (0.8)
	MSE	−0.0 (0.8)	0.0 (0.9)	−0.0 (1.0)	−0.0 (1.3)	0.0 (1.1)	0.0 (1.1)	0.0 (1.2)
	S	11.656	14.891	15.529	26.839	20.982	21.951	23.206
Raw S-H	MUE	0.7 (0.3)	0.2 (0.2)	0.3 (0.1)	0.7 (0.4)	1.3 (0.5)	0.3 (0.2)	0.3 (0.2)
	MSE	−0.7 (0.3)	−0.2 (0.3)	0.1 (0.3)	0.7 (0.4)	1.3 (0.5)	0.0 (0.4)	−0.0 (0.4)
	S	3.074	0.447	0.435	3.357	8.983	0.736	0.746
BEC S-H	MUE	0.3 (0.1)	0.2 (0.1)	0.2 (0.1)	0.3 (0.2)	0.3 (0.3)	0.3 (0.2)	0.3 (0.2)
	MSE	−0.0 (0.3)	−0.0 (0.3)	−0.0 (0.3)	0.0 (0.4)	0.0 (0.5)	−0.0 (0.4)	0.0 (0.4)
	S	0.388	0.317	0.332	0.626	0.812	0.734	0.745
LRM S-H	MUE	0.3 (0.1)	0.2 (0.1)	0.2 (0.1)	0.3 (0.3)	0.3 (0.3)	0.3 (0.2)	0.3 (0.2)
	MSE	0.0 (0.3)	0.0 (0.3)	−0.0 (0.3)	0.0 (0.4)	−0.0 (0.4)	−0.0 (0.4)	−0.0 (0.4)
	S	0.386	0.316	0.331	0.608	0.685	0.709	0.722
Raw N-H	MUE	0.3 (0.4)	0.6 (0.5)	0.5 (0.5)	1.4 (0.9)	1.2 (1.0)	0.9 (1.0)	0.9 (1.0)
	MSE	0.1 (0.5)	0.6 (0.5)	0.4 (0.5)	1.4 (0.9)	1.2 (1.0)	0.5 (1.2)	0.5 (1.2)
	S	2.280	6.047	4.266	27.750	22.455	16.292	16.149
BEC N-H	MUE	0.3 (0.4)	0.3 (0.4)	0.3 (0.4)	0.7 (0.6)	0.7 (0.6)	1.0 (0.7)	1.0 (0.7)
	MSE	0.0 (0.5)	0.0 (0.5)	0.0 (0.5)	−0.0 (0.9)	0.0 (1.0)	−0.0 (1.2)	0.0 (1.2)
	S	2.249	2.491	2.439	7.869	8.989	13.840	13.888
LRM N-H	MUE	0.3 (0.3)	0.3 (0.3)	0.3 (0.3)	0.6 (0.4)	0.6 (0.4)	0.6 (0.3)	0.6 (0.3)
	MSE	0.0 (0.5)	−0.0 (0.5)	0.0 (0.5)	−0.0 (0.7)	−0.0 (0.7)	−0.0 (0.7)	−0.0 (0.7)
	S	2.095	2.000	1.876	4.655	4.687	4.191	4.374

To investigate the relative energy lowering between the acid and conjugate base with increasing basis set and the effect on the PA and GPB, the values in Table 1 were obtained using five increasingly larger Dunning basis sets (cc-pVTZ, cc-pVQZ, cc-pV5Z, aug-cc-pVTZ, aug-cc-pVQZ)⁷⁰ with the B3LYP functional and compared to the experimental values. Table 2 provides the error metrics for these calculations, while the full table of individual values is provided in supporting information. Note that the basis set used for Table 1, is most closely related to aug-cc-pVTZ Dunning basis set, which is expected. From the error metrics two general observations can be made. First, basis sets lacking diffuse functions overestimate both PA and GPB, while those with diffuse functions underestimate them slightly. This is most likely associated with the importance of diffuse functions for the anions. Second, the cc-pV5Z, aug-cc-pVTZ, and aug-cc-pVQZ have similar errors, showing that we are approaching the complete basis set limit, with the augmented triple zeta basis set offering significant computational advantage.

TABLE 2.

Proton affinity (left column) and gas-phase basicity (right column) error analysis for B3LYP functional with various dunning basis sets. All quantities are in kcal/mol. Error metrics are maximum error (MAXE), root-mean-squared error (RMSE), mean unsigned error (MUE), and mean signed error (MSE).

	cc-pVTZ		cc-pVQZ		cc-pV5Z		aug-cc-pVTZ		aug-cc-pVQZ
MAXE	22.7	22.7	13.6	13.7	5.1	5.1	−3.7	−3.7	−3.5	−3.5
RMSE	5.6	5.4	3.1	2.9	1.7	1.8	1.5	1.7	1.4	1.6
MUE	4.2	4.0	2.0	1.9	1.2	1.3	1.3	1.5	1.1	1.3
MSE	4.2	4.0	1.9	1.6	0.6	0.3	−0.6	−0.9	−0.4	−0.6

In previous work for the PA and GPB of O-H containing compounds,^8,71, it was found that for the DFT methods the |MSE| ≈ MUE, indicating a systematic error⁷¹. This observation motivated a simple additive correction for the bond enthalpy and entropy that brought the error metrics of the density function models closer to those of the multi-level models for both the PA and GPB, This PA correction (ΔH^C) is applied as

$$\mathrm{\Delta }{H}_X^{‘}=\mathrm{\Delta }{H}_X+\mathrm{\Delta }{H}_X^C$$ (8)

where X is either O-H, S-H, or N-H bonds. This correction is similarly added for the GPB. $\mathrm{\Delta }{\mathrm{H}}_X^C$ and $\mathrm{\Delta }{\mathrm{G}}_X^C$ are assigned to enforce the MSE to be zero. This bond energy correction (BEC) model is now compared to a more flexible model based on a linear regression using

$${\text{PA}}_{\text{pred}}={\mathrm{b}}_{\mathrm{X}}\cdot {\text{PA}}_{\text{model}}+{\mathrm{a}}_{\mathrm{X}}$$ (9)

where PA_model is the proton affinity predicted by a computational model, a_X and b_X are parameters optimized to best fit the experimental data, X is either O-H, S-H, or N-H bond, and PA_pred is the linear regression model (LRM) prediction. The equation for the GPB is analogous to equation 9. Parameters for both the BEC and LRM models are provided in supporting information.

Table 3 presents PA error metrics for the uncorrected (Raw), BEC, and LRM models. Shown are the MUE and MSE with standard deviation following in parenthesis and the total residual, S (i.e., the sum of the deviation squares). Also calculated was the linear correlation coefficients, but for all models this value was near unity. Similar trends are found for the GPB and the table is provided in supporting information.

For the uncorrected (Raw) values, the CBS model outperforms all other models for O-H and N-H compounds as shown by a lower residual. Further, CBS shows a tighter distribution around the experimental values, shown in the standard deviation of the MUE and MSE. The BEC model significantly lowers the residual and MUE for the DFT methods as well as the CBS model for the S-H compounds, as discussed above this is an indication of a systematic error in the methods.

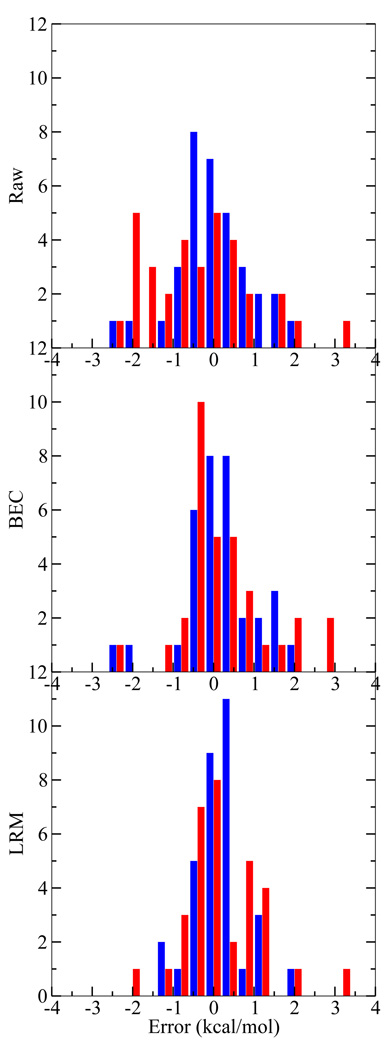
Figure 2 displays a histographic comparison of the CBS (the most accurate on average) and QCRNA (the most computationally inexpensive) method for the uncorrected, BEC, and LRM. From this comparison it is apparent how the uncorrected QCRNA is systematically underestimating the PA values. After the BEC or LRM correction, the QCRNA has a more evenly distributed error distribution, but is still is not as tightly distributed as the CBS model.

FIG. 2.

Proton affinity error histogram for the CBS (blue, left bar) and QCRNA (red, right bar) against experiment (top), with bond energy correction (middle), and linear regression model (bottom). See text for bond energy correction (BEC) and linear regression model (LRM) information. Histogram bins are width 0.5 kcal/mol.

Summarizing the model comparison, all models, with corrections, give comparable error metrics and have errors within 1–3 kcal/mol. The CBS model generally is the most reliable model except for the S-H compounds, which is easily compensated by the BEC or LRM correction. The main purpose of presenting the BEC and LRM correction models is to analyze the nature of systematic errors in the various model chemistries. For molecules that are similar to those for which the corrections have been derived, it is expected that application of the corrections may lead to improved quantitative accuracy (coefficients in eqn 8 and eqn 9 for the models are available in the supporting information). Although the model corrections lead to considerable improvement for the set of data from which they were derived, we do not advocate their use as general corrections. In the following sections, we provide the uncorrected (i.e., “Raw”) PA and GPB values in tables and discussion.

B. Amino Acids

Amino acids contain two protonation sites along the backbone (an amine and a carboxylic acid) and possibly one or two more on the side chain. In the gas-phase, the amino acid backbone does not exist in isolation as a zwitterion as it does in solution^72,73. It is known that the backbone titratable sites, isolated in gas-phase, are highly sensitive to the side chain conformation^5,74. Here we report model compounds for the amino acid backbone and side chains separately to reduce the conformational complexity⁷⁵ and focus more directly on the intrinsic affinity of each site for protonation. These model compounds are based on the amino acid side chain capped by a methyl group. Table 4 reports the PA and GPB for the amino acid model compounds as well as both titratable sites of glycine and proline to provide reference values for the backbone sites.

TABLE 4.

Proton Affinities and Gas-Phase Basicities for amino acids model compounds with experimental value^a (experimental error in parenthesis) and pK_a values^b in solution as a reference. All quantities are in kcal/mol except pK_a.

Model (Amino Acid)	CBS-QB3	G3B3	G3MP2B3	PBE0	B1B95	B3LYP	QCRNA	Experiment	pKa
Proton Affinity
prolinium (Pro)	224.3	224.8	225.0	225.4	225.3	225.0	225.0	224.0 (2.0)	1.9
glycinium (Gly)	211.9	212.3	212.2	213.6	213.2	212.0	212.0	211.9 (0.5)	2.4
acetic acid (Asp)	347.4	348.2	348.6	347.6	347.9	345.8	346.4	347.2 (1.1)	3.9
propanic acid (Glu)	346.2	347.0	347.4	347.8	347.9	346.1	345.5	347.4 (1.8)	4.1
4-methyl-imidazolium (His π)	229.0	229.6	229.4	231.3	231.2	230.7	230.7	227.7 (2.0)	6.0
4-methyl-imidazolium (His τ)	229.6	230.3	230.1	231.8	231.7	231.3	231.3	− (−)	6.0
methanethiol (Cys)	356.8	357.4	357.7	358.2	358.7	357.3	357.3	357.3 (1.2)	8.4
glycine (Gly)	341.8	342.6	343.0	343.0	343.2	341.5	341.5	340.3 (1.1)	9.8
p-methylphenol (Tyr)	350.4	350.7	350.7	350.0	350.6	348.9	348.9	350.7 (1.3)	10.5
propanammonium (Lys)	219.3	219.8	219.6	220.3	220.1	219.4	219.3	219.4 (0.5)	10.5
proline (Pro)	340.1	341.0	341.2	342.1	342.1	340.4	340.4	340.3 (3.1)	10.6
n-methylguanidine (Arg)	239.5	239.6	239.0	243.1	242.9	241.9	241.8	− (−)	12.5
Gas Phase Basicity
prolinium (Pro)	216.8	217.3	217.4	217.8	217.6	217.4	217.4	216.0 (2.0)	1.9
glycinium (Gly)	204.1	204.5	204.4	205.4	205.2	204.0	204.2	203.7 (0.5)	2.4
acetic acid (Asp)	339.4	340.2	340.6	341.3	341.5	339.5	338.3	341.4 (1.2)	3.9
propanic acid (Glu)	340.1	341.0	341.4	339.2	339.9	337.6	339.4	340.4 (1.4)	4.1
4-methyl-imidazolium (His π)	221.2	221.8	221.6	223.6	223.5	223.0	223.0	220.1 (2.0)	6.0
4-methyl-imidazolium (His τ)	221.9	222.6	222.4	224.2	224.0	223.7	223.6	− (−)	6.0
methanethiol (Cys)	350.4	351.0	351.3	351.8	352.3	351.0	350.9	350.6 (2.0)	8.4
glycine (Gly)	334.7	335.6	335.9	335.8	336.0	334.2	334.3	335.1 (1.4)	9.8
p-methylphenol (Tyr)	343.2	343.4	343.4	342.8	343.2	341.8	341.6	343.8 (1.2)	10.5
propanammonium (Lys)	211.8	212.3	212.2	212.8	212.6	211.8	211.9	211.3 (0.5)	10.5
proline (Pro)	332.5	333.4	333.6	334.4	334.4	332.6	332.6	333.4 (3.0)	10.6
n-methylguanidine (Arg)	232.7	232.9	232.3	236.8	237.3	235.5	235.0	- (−)	12.5

^aAll experimental values are from NIST (Ref. ⁶⁷), except for prolinium which can be found in reference ⁷⁶.

^bpK_a values are taken from reference ⁷⁷.

Overall, the quantum models are internally consistent and reliably predict the experimental values for the model compounds. The largest errors are for histidine, though most models are still within the experimental error. For the arginine side chain model (n-methyl-guanidine) no experimental value was found. Hunter and Lias report a PA of 235.7 kcal/mol and GPB of 226.9 kcal/mol for guanidine⁷⁸, which is close to our calculated value (e.g., the calculated PA values ranged from 232.3 to 236.8 kcal/mol). Norberg et al. report a computational prediction for n-methyl-guanidine PA as 242 – 248 kcal/mol (MP2/6–31G*), but notes that this structure is basis set dependent and that correlated methods provide lower values. Our quantum models diverge for this compound, with the DFT models predicting a significantly larger (~3 kcal/mol) PA and GPB compared to the multi-level models, consistent with Norberg et al. suggestion.

Histidine values are provided both for the π (near backbone) and τ (far from backbone) nitrogen positions⁷⁹. All the models show a preference for deprotonation at the π position, but only by ~0.5 kcal/mol, which indicates the system environment and solvation will dominate the site preference.

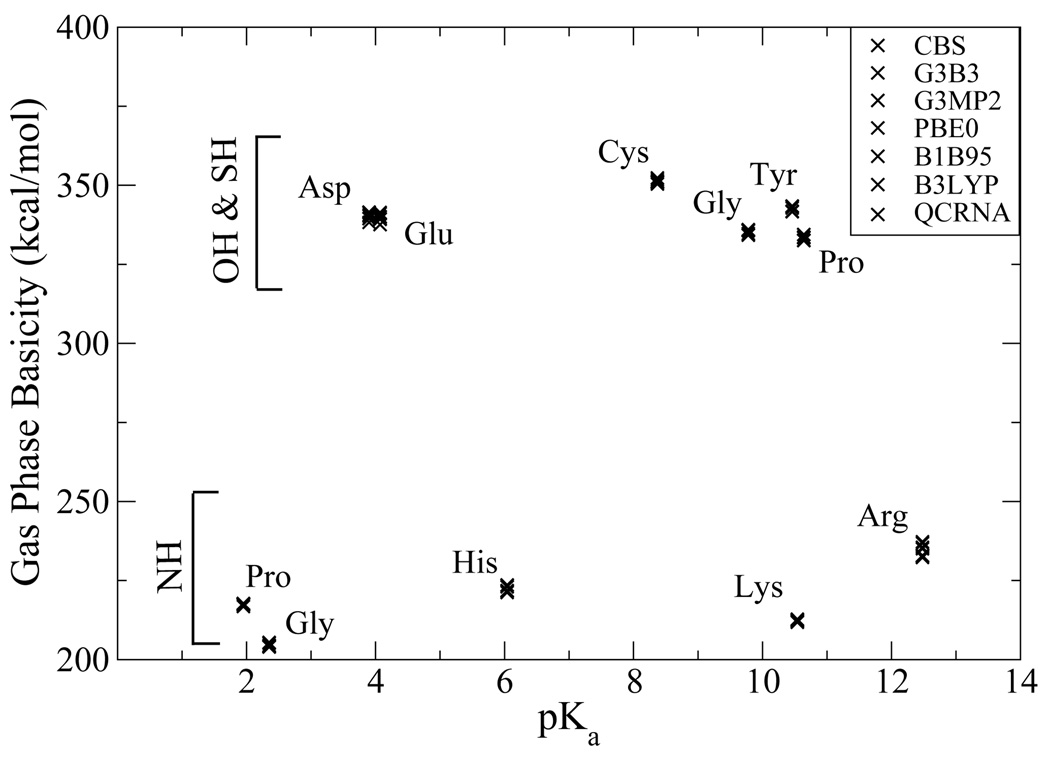
Figure 3 shows the GPB values plotted as a function the experimental pK_a value in solution. It is apparent that the GPB values do not correlate directly with the pK_a values. It is, nonetheless, noteworthy that while certain residues have very disparate pK_a values they can have similar GPB and alternatively similar pK_a values can have significantly different GPB. For example, tyrosine and glutamic acid only differ 3.4 kcal/mol (equivalent to 2.5 pK_a units) in the gas phase, but are 6.4 pK_a units apart in solution, indicating most of the difference is the preferential solvation of the propanate ion relative to the p-methylphenolate ion. Alternatively, glycinium’s GPB is 12.3 kcal/mol (9 pK_a units) greater than prolinium, but the solution pK_a values differ by only 0.5 pK_a units. Moreover, in several instances, the basicity trend is reversed in the gas phase relative to in solution. Examples include histidine and lysine, the latter which is more basic in solution by 4.5 units, but less basic in the gas phase. In this case, although the His side chain has a greater GPB value than that of Lys, the smaller primary ammonium of the protonated Lys side chain is much smaller and better solvated than the imidazolium of the protonated His side chain. Analogously, Asp is more acidic than Cys in solution by 4.5 pK_a units, but less acidic in the gas phase. The soft sulfur of Cys is able to more effectively accommodate the negative charge on the deprotonated side chain than the hard oxyacid group of Asp, but in solution this larger size of the thiolate anion of Cys makes is less well solvated than the carboxylate anion of Asp. There is great interest in the study of the protonation state of amino acids in proteins, the local dielectric of which may be considerably less than that of aqueous solution. Consequently, a quantitative understanding of the balance between intrinsic electronic effects and the effect of generalized solvation is critical.

FIG. 3.

Calculated gas phase basicities of amino acid model compounds versus pK_a values.

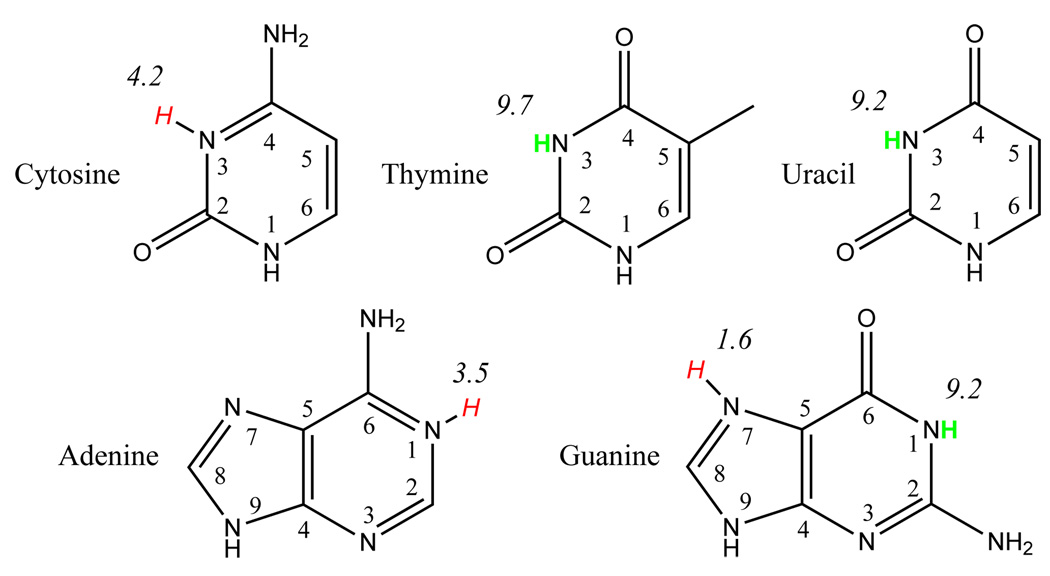
C. Nucleic Acid Bases

The DNA and RNA bases each contain multiple protonation sites, but the most biologically relevant (titratable) sites are shown in Figure 4^80,81 along with their pK_a values.^82–84 Table 5 gives the PA and GPB values for protonation (+) and deprotonation (−) at selected sites in their standard tautomeric forms, along with available experimental values.^78,85

FIG. 4.

DNA/RNA basepair protonation points with pK_a values. Hydrogens in green are points of deprotonation. Hydrogens in red are points of protonation.

TABLE 5.

Proton Affinity (top) and Gas-Phase Basicity (bottom) values for DNA and RNA bases. The uncertainty of the experimental values is ~ 2.0 kcal/mol⁷⁸. All quantities are in kcal/mol.

Basea	CBS	G3B3	G3MP2	PBE0	B1B95	B3LYP	QCRNA	Expt
Proton Affinity
A:N1(+)	223.6	224.9	224.7	227.1	227.1	226.7	226.8	225.3
C:N3(+)	226.9	227.6	227.4	229.5	229.3	228.9	228.8	227.0
G:N7(+)	227.6	228.2	227.9	231.0	230.8	230.5	230.5	229.3
G:N1(−)	337.7	338.2	338.0	340.9	341.0	339.9	339.9	-
T:O4(+)	206.1	207.1	207.3	209.2	209.3	208.1	208.2	210.5
T:N3(−)	346.3	347.0	346.9	348.2	348.1	347.1	346.9	-
U:O4(+)	204.4	205.4	205.5	207.3	207.4	206.4	206.4	208.6
U:N3(−)	346.3	347.0	346.9	348.2	348.1	347.1	346.9	-
Gas Phase Basicity
A:N1(+)	216.3	217.1	217.0	218.3	218.4	218.2	218.3	218.1
C:N3(+)	218.9	219.8	219.7	220.9	220.2	220.4	219.9	219.0
G:N7(+)	220.2	220.9	220.6	223.6	223.3	223.0	223.0	221.7
G:N1(−)	330.2	330.6	330.4	333.3	333.5	332.4	332.3	-
T:O4(+)	198.4	199.3	199.5	201.4	201.5	200.4	200.5	203.2
T:N3(−)	338.5	339.1	339.1	340.4	340.4	339.3	339.0	-
U:O4(+)	196.7	197.6	197.8	199.6	199.6	198.6	198.7	201.2
U:N3(−)	338.1	338.6	338.5	339.9	340.0	338.7	338.4	-

^aBase identifies the nucleic acid base (A, C, G, T, or U) and the position the proton is being removed (−) or added (+).

The deviation between the calculated and experimental values for the nucleic acids are generally larger for the nucleobases than for the amino acid side chains considered above, although there remains a high degree of correlation. In particular, thymine and uracil have some of the largest deviations for the multi-level models, even after proton orientation and conformational averaging were considered. Additionally, CBS seems to underestimate the experimental values. Alternatively if we compare our computation to experimental values derived from fast-atom-bombardment mass spectrometry provided by Greco et al.⁸⁶ we see different levels of deviation depending on the models used to interpret the data and derive PA values. Wolken and Tureček suggest a PA of 205.1 kcal/mol for uracil⁸⁷ that lies within the range of the calculations using multi-level models (204.4 to 205.5 kcal/mol), but somewhat outside the range of the DFT methods (206.4 to 207.4 kcal/mol). The large variation in experimentally determined PA and GPB values underscore the need for a systematic high-level quantum chemical characterization.

Overall, the PA and GPB follow the trend: GUA > CYT > ADE > THY > URA which is consistent with previous studies^88,89.

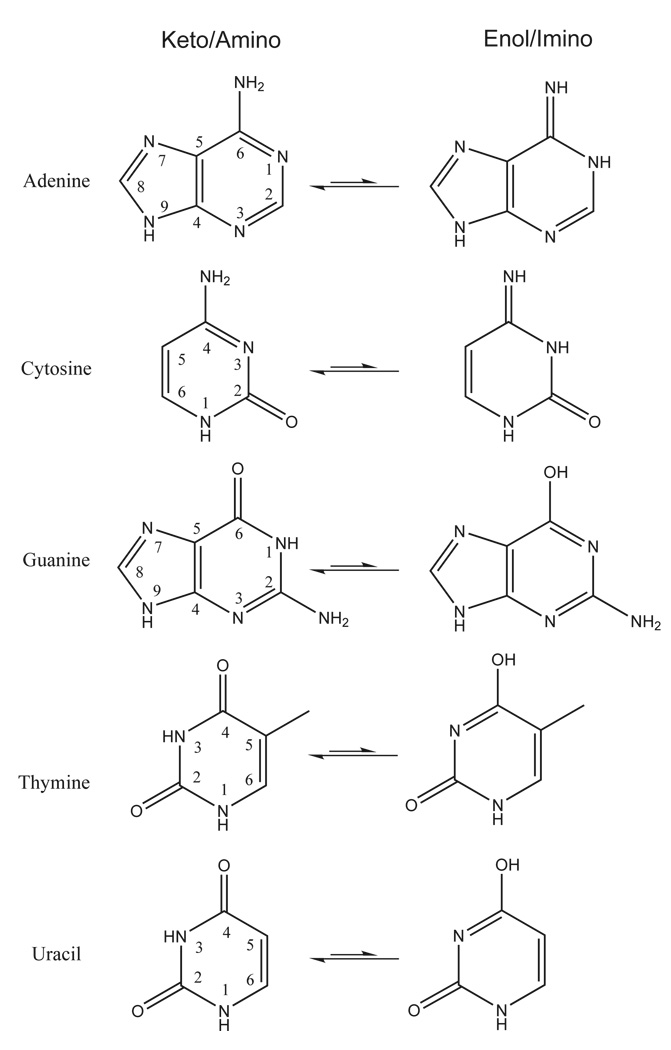
Another important aspect in the consideration of protonation states of nucleobases is their tautomeric equilibria. The nucleobases can exist in different tautomeric forms (Figure 5) which are sometimes accessible in biological systems⁸². The enthalpy and free energy values for the tautomerization reactions shown in Figure 5 are listed in Table 6. In the gas phase, the enol/imino forms for cytosine and guanine are the most accessible relative to the standard keto/amino forms. The calculated free energy difference between keto and enol forms for guanine ranges from −0.4 to 1.1 kcal/mol, and the free energy difference between amino and imino forms of cytosine ranges from 0.8 to 2.1 kcal/mol. The protonation state for these nucleobases may have implications in RNA enzymes, as guanine and cytosine have been implicated as acting as general base and acid catalysts, respectively.⁹⁰ The remainder of the tautomerization free energy values are more than 10 kcal/mol in the gas phase. A complete list of the PA and GPB of all protonation sites for DNA/RNA bases in both their keto and enol form as well as the tautomerization energies are provided in supporting information.

FIG. 5.

DNA/RNA basepair tautomers.

TABLE 6.

Enthalpy (top) and Free Energy (bottom) of tautomerization for DNA and RNA basepairs in the gas phase. All quantities are in kcal/mol.

	CBS	G3B3	G3MP2	PBE0	B1B95	B3LYP	QCRNA
Enthalpy
Adenine	12.5	11.7	11.4	12.3	12.2	11.9	11.9
Cytosine	1.2	1.0	0.8	2.4	2.4	2.1	2.1
Guanine	−0.4	−0.2	−0.3	0.7	0.5	1.1	1.1
Thymine	12.0	11.8	11.6	12.3	11.9	12.5	12.5
Uracil	11.1	10.9	10.7	11.3	10.9	11.6	11.5
Free Energy
Adenine	12.3	12.0	11.7	13.6	13.4	13.0	12.8
Cytosine	1.5	1.2	1.0	3.4	3.8	3.0	3.4
Guanine	−0.3	0.0	−0.1	0.8	0.6	1.2	1.2
Thymine	12.2	12.0	11.8	12.5	12.0	12.7	12.6
Uracil	11.2	11.1	10.8	11.4	11.1	11.7	11.6

D. RNA Ribose Models

One of the defining difference between DNA and RNA is the RNA 2’ hydroxyl group. This group is a very weak acid, but plays an important role in DNA and RNA cleavage and ligation,⁹¹ and has been implicated as a general acid catalyst in the hammerhead ribozyme⁹² possibly activated by a divalent metal ion.⁹³ Based on experimental and computational estimates, the O2’ pK_a ranges between approximately 12.5 and 14.9^19,94–96. This range is likely due to the local chemical environment (including a mild dependence on the attached nucleobase⁹⁵), sugar pucker, and solution ionic strength.

To provide the most biologically relevant sugar pucker conformations, we have calculated the PA and GPB using C2’-endo (P=163.797, τ_m=34.495) and C3’-endo (P=13.506, τ_m=37.747) sugar puckers,⁹⁷ where P is the pseudorotation phase angle and τ_m is the degree of puckering. These conformations are based on based on X-ray diffraction data^98,99 and are consistent with canonical B and A form DNA and RNA^82,100. Additionally, the dihedral synonymous to the the ε dihedral (C4’-C3’-O2’-P) for the nucleic acid phosphodiester backbone was in the biological trans conformation.

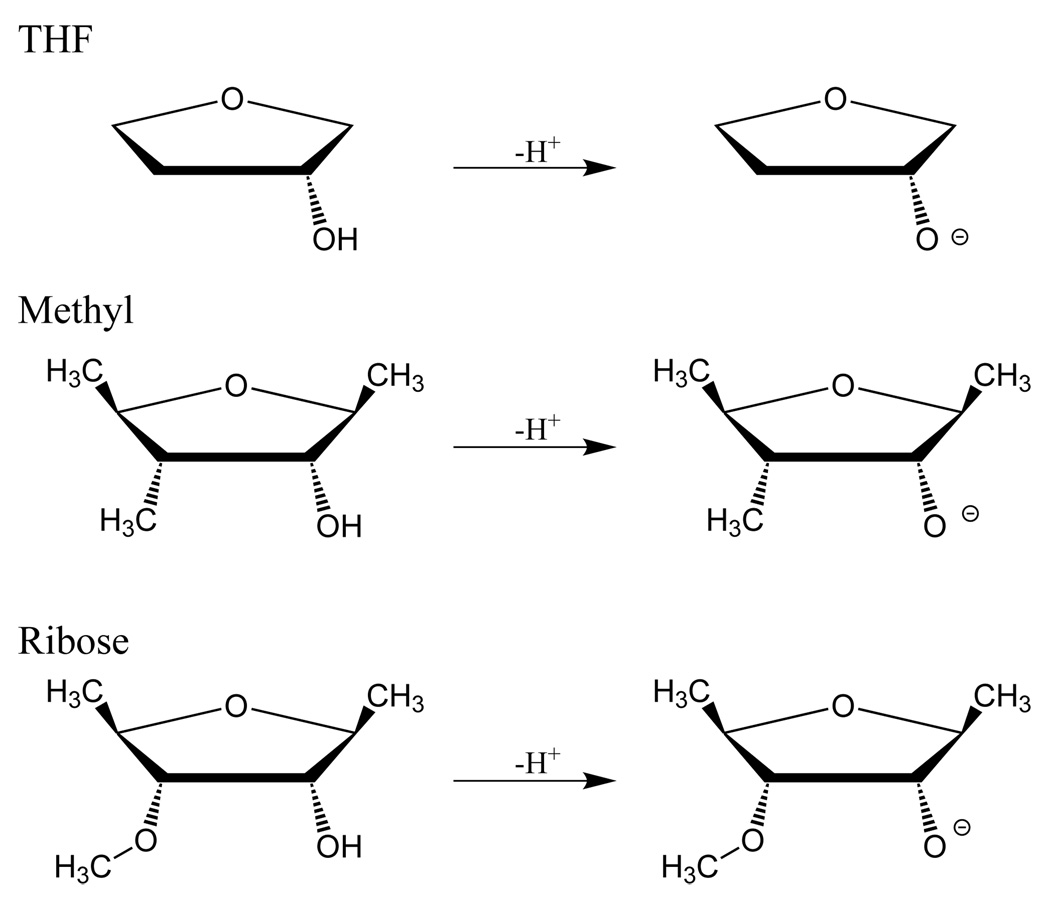
Similar to the amino acids, use of the full ribose structure created conformational obstacles that obfuscate the intrinsic acidity of the 2’ oxygen. In particular a hydroxyl group at the 3’ position created a significant intramolecular hydrogen bond that strongly shifted the O2’ values. We consider here three model compounds for the RNA ribose (Figure 6): 2-hydroxy-tetrahydrofuran (THF), 2-hydroxy-1,3,4-trimethyl-tetrahydrofurn (Methyl), and 2-hydroxy-1,4-dimethyl-3-methoxy-tetrahydrofuran (Ribose). These successively more complicated models provide insight into how the ribose structure tunes the intrinsic PA and GPB of the 2’-hydroxyl group, with the “Ribose” model being the most similar to the sugar ring of RNA.

FIG. 6.

Neutral and deprotonated model compounds for d-ribofuranose sugar: THF (2-hydroxy-tetrahydrofuran), Methyl (2-hydroxy-1,3,4-trimethyl-tetrahydrofuran), and Ribose (2-hydroxy-1,4-dimethyl-3-methoxy-tetrahydrofuran).

Table 7 provides the PA and GPB for THF, Methyl, and Ribose models illustrated in Figure 6. Unlike the nucleic acid bases, the multi-level and DFT calculations have a more narrow distribution of values (typically around 2 kcal/mol) for a given model system. C3’-endo has a greater PA and GPB for all models compared to the C2’-endo sugar pucker conformation, and this gap increases with model complexity. The CBS GPB is 3.3 kcal/mol larger and more acidic for the ribose model in the C3’-endo conformation than in the C2’endo conformation. The addition of the 3’ methyl then the 3’ methoxy group successively raises the PA and GPB of the 2’ hydroxyl group making it less likely to release its proton. This is mainly due to the stabilization of the protonated structure via intramolecular hydrogen bonding, as shown by the difference with the THF model and the larger effect for C2’-endo conformation.

TABLE 7.

Proton Affinity (top) and Gas-Phase Basicity (bottom) values for RNA like sugar molecules: 2-hydroxy-tetrahydrofuran (THF), 2-hydroxy-1,3,4-trimethyl-tetrahydrofuran (Methyl), and 2-hydroxy-l,4-dimethyl-3-methoxy-tetrahydrofuran (Ribose). Figures in supporting information. All molcules are given in conformations consistant with B-form and A-form DNA/RNA. All quantities are in kcal/mol.

Pucker	Model	CBS	G3B3	G3MP2	PBE0	B1B95	B3LYP	QCRNA
Proton Affinity
C2’a	THF	369.2	369.1	370.1	370.2	370.6	368.2	368.3
	Methyl	366.4	367.0	367.4	367.3	367.4	365.6	365.7
	Ribose	360.4	361.2	361.6	362.9	363.2	360.8	361.5
C3’b	THF	370.2	370.9	371.2	370.8	371.3	368.7	368.8
	Methyl	367.7	368.3	368.7	368.2	368.6	366.4	366.5
	Ribose	364.9	365.7	366.1	365.6	365.8	363.9	363.9
Gas Phase Basicity
C2’a	THF	361.2	360.9	362.0	362.1	362.4	360.1	360.1
	Methyl	358.0	358.6	359.0	358.7	358.8	357.1	357.2
	Ribose	354.5	355.4	355.8	354.9	355.1	355.1	353.5
C3’b	TFIF	362.9	363.5	363.9	363.6	364.1	361.4	361.5
	Methyl	360.3	360.9	361.3	360.8	361.2	359.0	359.2
	Ribose	357.8	358.6	359.0	358.5	358.7	356.8	356.8

^aP=163.797, τ_m4=34.495.

^bP=13.506, τ_m=37.747.

E. Phosphates

Metaphosphates, phosphates and phosphoranes represent important states in phosphoryl transfer reactions.^91,101–105 Metaphosphates, for example, are presumed intermediates in dissociative phosphoryl transfer mechanisms for phosphate monoesters in solution.^{101,106–110} Acyclic and cyclic phosphates and cyclic phosphoranes are models for different states along the reaction path of RNA transesterification, hydrolysis, and ligation^91,103,105. Thio substitutions at native phosphoryl oxygen positions are useful experimental probes that give insight into catalytic mechanism in ribozymes.^111,112 The interpretation of thio effect experiments can be aided by computational techniques,^55,113 and hence their high-level quantum characterization is of considerable interest.

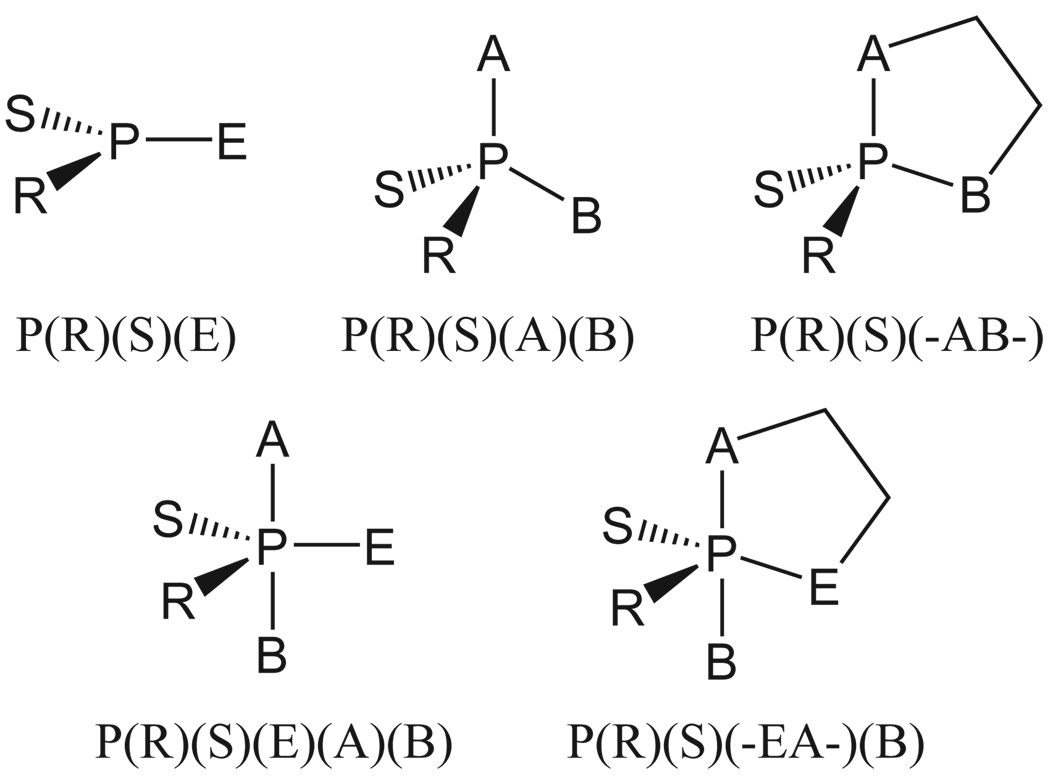
To fully investigate the protonation states of the phosphate moiety, we provide benchmark values for metaphosphates, acyclic and cyclic phosphates and phosphoranes, each with thio-substitutions (see supporting information for full tables). Figure 7 provides the nomenclature for the different compounds and Table 8 reports the PA values using the CBS and QCRNA methods. PA and GPB shows similar trends and values for all the quantum models can be found in the supporting information. The quantitative discussion and analysis here will be largely restricted to the CBS PA data, although the qualitative insights thus provided are more generally applicable.

FIG. 7.

Nomenclature convention for ligand designations in metaphosphate, acyclic and cyclic phosphate and phosphorane compounds of biological interest. This nomenclature is consistent with the naming convention used for similar compounds in previous work⁷,⁵³,⁷¹.

TABLE 8.

Predicted proton affinities for metaphosphate, phosphate, and cyclic phosphate (left columns) and acyclic and cyclic phosphorance compounds (right column) of biological interest. All values are in kcal/mol. See Figure 7 for naming scheme.

Moleculea	CBS	QCRNA	Moleculea	CBS	QCRNA
P(O)(O)(OH)	310.5	311.1	P(OH*)(OH)(OH)(OH)(OH)	340.8	339.3
P(O)(O)(SH)	304.5	306.2	P(OH)(OH)(OH)(OH)(OH*)	350.8	350.5
P(S)(O)(OH)	307.5	308.5	P(OH*)(OH)(−O-CH2CH2-O-)(OH)	343.1	342.6
P(S)(S)(OH)	307.2	308.6	P(OH)(OH*)(−O-CH2CH2-O-)(OH)	343.4	342.9
P(S)(O)(SH)	303.3	305.2	P(OH*)(OH)(−O-CH2CH2-O-)(OCH3)	343.8	343.0
P(O)(OH)(OH)(OH)	327.9	328.2	P(OH)(OH*)(−O-CH2CH2-O-)(OCH3)	343.4	342.9
P(O)(O)(OH)(OH) −	458.7	457.8	P(OH*)(OH)(−O-CH2CH2-S-)(OH)	335.2	335.0
P(O)(O)(O)(OH) 2−	580.9	579.5	P(OH)(OH*)(−O-CH2CH2-S-)(OH)	335.4	335.4
P(S)(OH)(OH)(OH)	322.5	322.9	P(OH*)(OH)(−O-CH2CH2-S-)(OCH3)	331.8	334.5
P(O)(OH)(OH)(SH*)	318.2	319.9	P(OH)(OH*)(−O-CH2CH2-S-)(OCH3)	332.1	334.4
P(O)(OH)(OH*)(SH)	320.9	320.9	P(OH*)(OH)(−S-CH2CH2-O-)(OH)	336.1	336.2
P(O)(OCH3)(OH)(OH)	330.0	330.3	P(OH)(OH*)(−S-CH2CH2-O-)(OH)	336.0	336.2
P(O)(OCH3)(O)(OH) −	453.9	452.9	P(OH*)(OH)(−S-CH2CH2-O-)(OCH3)	339.0	338.6
P(S)(OCH3)(OH)(OH)	323.5	324.1	P(OH)(OH*)(−S-CH2CH2-O-)(OCH3)	339.6	338.8
P(S)(OCH3)(O)(OH) −	437.9	437.5	P(OH*)(OH)(−O-CH2CH2-O-)(SCH3)	333.1	333.0
P(O)(OCH3)(OH)(SH*)	319.1	321.4	P(OH)(OH*)(−O-CH2CH2-O-)(SCH3)	333.1	333.0
P(O)(OCH3)(OH*)(SH)	321.6	322.1	P(SH*)(OH)(−O-CH2CH2-O-)(OH)	333.6	335.0
P(O)(SCH3)(OH)(OH)	322.2	322.8	P(SH)(OH*)(−O-CH2CH2-O-)(OH)	338.4	337.7
P(O)(SCH3)(O)(OH)	443.7	441.0	P(SH*)(OH)(−O-CH2CH2-O-)(OCH3)	335.3	336.8
P(O)(OCH3)(OCH3)(OH)	329.2	330.1	P(SH)(OH*)(−O-CH2CH2-O-)(OCH3)	339.1	338.2
P(S)(OCH3)(OCH3)(OH)	325.1	325.9	P(OH*)(SH)(−O-CH2CH2-O-)(OH)	337.3	336.7
P(O)(SCH3)(OCH3)(OH)	324.2	326.2	P(OH)(SH*)(−O-CH2CH2-O-)(OH)	332.6	334.1
P(O)(OCH3)(OCH3)(SH)	320.8	323.2	P(OH*)(SH)(−O-CH2CH2-O-)(OCH3)	341.1	340.1
P(O)(OH)(−O-CH2CH2-O-)	329.4	329.5	P(OH)(SH*)(−O-CH2CH2-O-)(OCH3)	335.9	336.8
P(O)(SH)(−O-CH2CH2-O-)	320.1	321.9
P(S)(OH)(−O-CH2CH2-O-)	324.0	324.5
P(O)(OH)(−S-CH2CH2-O-)	324.1	324.7

^a”Molecule” refers to AH in Eq. 1

We report a PA for metaphosphate of 310.5 kcal/mol using the CBS method, in excellent agreement with the experimental value of 310.8±2.0 kcal/mol⁶⁷. For the phosphates recall from Table 1 that the error in PA calculation for phosphoric acid and dimethyl phosphate are −2.6 and −2.4 kcal/mol, respectively, which is well within the 5.0 and 4.1 kcal/mol error bars from the experimental data. These results specifically, along with the general successes noted above, indicate that the predictions presented in Table 8 and the supporting information are of similar quality to those that might be obtained by further experiments. Additionally, these calculations provide values for systems that may be very difficult to probe directly via experiment.

Single sulfur substitution (not at the protonation site) lowers the PA of metaphosphates by 3.0 kcal/mol, whereas substitution at the protonation site lowers the PA by 6.0 kcal/mol. The corresponding double sulfur substitutions lower the PA values further by 3.3 and 7.2 kcal/mol, respectively.

The PA value for the cyclic phosphates are quite similar to those of the acyclic analogs, for example the PA values for dimethyl phosphate and ethylene phosphate differ by only 0.2 kcal/mol. Sulfur substitution at the site of protonation has the largest effect on the PA, lowering it from the corresponding unsubstituted phosphate by 8.4 to 10.9 kcal/mol. Sulfur substitution at an unprotonated non-bridge position has the smallest effect, lowering the PA relative to the unsubstituted phosphate by 4.1 to 6.5 kcal/mol. It should be noted that this large effect on the PA value is likely to have considerably less effect on the corresponding pK_a values in solution due to the reduced solvation of the larger sulfur atom.

The protonation state of phosphoranes is of considerable interest, as it affects the lifetime of intermediates in phosphoryl transfer reactions, and could lead to formation of alternate reaction products such as in RNA migration.¹⁰⁴ Dianionic phosphoranes are generally believed to exist as high-energy intermediates or else true transition states. Further, it is known from Westheimer’s rules that anionic ligands prefer to occupy equatorial positions,¹¹⁴ and serve as pivotal positions in pseudorotations.^51,53 Indeed, in the present work, we find that the difference in PA for deprotonation at the equatorial and apical positions differ by 10 kcal/mol for pentahydroxyphosphorane with the CBS model (Table 8). We have endeavored to provide a fairly comprehensive set of native and thio substituted phosphoranes in neutral and monoanionic forms in the supporting information. Here, we restrict discussion to the PA values in only the equatorial positions for a series of native and thio substituted cyclic phosphoranes that represent models for reactive intermediates in RNA transesterification and hydrolysis reactions (Table 8). It should be noted that the pro-R and pro-S non-bridging oxygens are not equivalent in many biological systems.^115,116 In the present model systems, the pro-R and pro-S non-bridging positions are not necessarily equivalent for a given conformational minima of the puckered five-membered ring. In Table 8, we list PA values for both the pro-R and pro-S positions for a given conformational minima, the values for which differ by typically only 0.5 kcal/mol or less.

The cyclic oxyphosphoranes have PA values between 343.1 to 343.8 kcal/mol, and are 2–3 kcal/mol larger than for the acyclic pentahydroxyphosphorane reference of 340.8 kcal/mol. Sulfur substitution at the non-bridge position decreases the PA values by around 4.5 kcal/mol relative to the native cyclic phosphorane, and sulfur substitution at the non-bridge deprotonation site decreases the PA value by around 8–9.5 kcal/mol. Substitution at the equatorial and apical positions within the ring decreases the PA value by about 3.8–7.2 and 8.0–11.7 kcal/mol, respectively. Substitution at the acyclic apical position decreases the PA by around 12 kcal/mol.

IV. CONCLUSION

Benchmark calculations of the proton affinity and gas-phase basicity for oxygen, sulfur, and nitrogen containing compounds are compared for a variety of multi-level and density functional quantum methods against experimental values. These methods are corrected using a bond energy correction and linear regression model to evaluate the quantum methods’ performance. Here we report that while all the tested quantum chemistries provide reliable predictions, the CBS-QB3 method in general is the most reliable.

These models are then used to predict the proton affinity and gas-phase basicity for approximately 150 different molecules of biological interest comprising more than 2000 quantum calculations. These systems include amino acid backbone and side chains, nucleic acids in two tautomeric forms, ribose like structures for RNA sugar’s O2’, and various metaphosphates, cyclic and acyclic phosphates, and phosphoranes all with and without thio substitution.

This work provides a consistent database of PA and GPB to be used in pK_a prediction, biochemical evaluation of protonation/deprotonation events, parametrization of improved semiempirical quantum models used in QM/MM biocatalysis simulation, and comparison to experimental PA and GPB determination.