Abstract
Background
Epidemiological data show that radiation exposure during childhood is associated with larger cancer risks compared with exposure at older ages. For exposures in adulthood, however, the relative risks of radiation-induced cancer in Japanese atomic bomb survivors generally do not decrease monotonically with increasing age of adult exposure. These observations are inconsistent with most standard models of radiation-induced cancer, which predict that relative risks decrease monotonically with increasing age at exposure, at all ages.
Methods
We analyzed observed cancer risk patterns as a function of age at exposure in Japanese atomic bomb survivors by using a biologically based quantitative model of radiation carcinogenesis that incorporates both radiation induction of premalignant cells (initiation) and radiation-induced promotion of premalignant damage. This approach emphasizes the kinetics of radiation-induced initiation and promotion, and tracks the yields of premalignant cells before, during, shortly after, and long after radiation exposure.
Results
Radiation risks after exposure in younger individuals are dominated by initiation processes, whereas radiation risks after exposure at later ages are more influenced by promotion of preexisting premalignant cells. Thus, the cancer site–dependent balance between initiation and promotion determines the dependence of cancer risk on age at radiation exposure. For example, in terms of radiation induction of premalignant cells, a quantitative measure of the relative contribution of initiation vs promotion is 10-fold larger for breast cancer than for lung cancer. Reflecting this difference, radiation-induced breast cancer risks decrease with age at exposure at all ages, whereas radiation-induced lung cancer risks do not.
Conclusion
For radiation exposure in middle age, most radiation-induced cancer risks do not, as often assumed, decrease with increasing age at exposure. This observation suggests that promotional processes in radiation carcinogenesis become increasingly important as the age at exposure increases. Radiation-induced cancer risks after exposure in middle age may be up to twice as high as previously estimated, which could have implications for occupational exposure and radiological imaging.
CONTEXT AND CAVEATS
Prior knowledge
Standard models and epidemiological data have suggested the patterns of radiological cancer risk observed for exposures in childhood and young adulthood, in which the excess cancer risks decrease with increasing age at exposure, continue for exposure in middle age. However, the weight of epidemiological evidence suggests that for adult exposures, radiation-induced cancer risks do not generally decrease with increasing age at exposure.
Study design
A biologically based quantitative model of radiation carcinogenesis that incorporates both radiation induction of premalignant cells (ie, initiation) and radiation-induced promotion of premalignant damage was used to investigate the biological plausibility of observed cancer risk patterns as a function of age at exposure in Japanese atomic bomb survivors.
Contribution
A model of radiation-induced cancer that uses realistic parameters and includes both initiation, which dominates at younger ages, and promotion, which dominates at older exposure ages, reproduced the observed cancer risk patterns as a function of age at exposure for the six analyzed cancers, as well as that of all cancers combined.
Implications
Radiation-induced cancer risks after exposure in middle age may be up to twice as high as previously estimated.
Limitations
There were large statistical uncertainties associated with the underlying data from the atomic bomb survivors. Other interpretations of the risk patterns modeled here (besides reflecting the influence of tumor initiation and promotion on radiation carcinogenesis) are possible.
From the Editors
Epidemiological data from Japanese atomic bomb survivors and from children exposed to radiation for medical reasons suggest that excess relative risks (ERRs) for radiation-induced cancers at a given attained age are substantially higher for individuals who are exposed during childhood than for those exposed at older ages (1–12). This finding is reflected in recent estimates of radiation-induced cancer risks as a function of age at exposure produced by the International Commission on Radiological Protection (13) and the National Academy of Sciences Committee on the Biological Effects of Ionizing Radiation [BEIR Committee; (14)]. In these evaluations (13,14), the epidemiological data were described by empiric relationships that predicted that the eventual risks of developing radiation-induced cancer would continue to decrease with increasing age at exposure, for any exposure age.
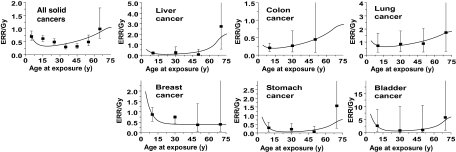
Whereas the cancer risks due to radiation exposures in childhood have been extensively documented in the literature (7–12), the relationship between radiation-induced cancer risk and age at exposure in adulthood is less clear. Relevant epidemiological data—typically from adults treated with radiotherapy (15–22)—generally do not have sufficient statistical power to assess the dependence of radiation-induced cancer risk on age at exposure in exposed adult populations. More recent analyses of Japanese atomic bomb survivors (1,5,6,14) have shed some light on this issue: As illustrated in Figure 1, these analyses (1,5,6) suggest that the radiation-related ERR for cancer induction decreases with increasing age at exposure only until exposure ages of 30–40 years; at older ages at exposure, the ERR does not decrease further and, for many individual cancer sites (as well as for all solid cancers combined), the ERR may actually increase.
Figure 1.
Excess relative risks (ERRs) per Gy for cancer incidence in Japanese atomic bomb survivors as a function of age at radiation exposure. ERRs were estimated at an attained age of 80 years and sex averaged, except for female breast cancer. Solid cancers refers to all primary malignant tumors excluding hematopoietic cancers. The data points are derived from Walsh (5) and Little (6) and the error bars represent 90% confidence intervals. The curves represent fits to the ERR data using the quantitative mechanistic model (23) described in the text and the parameters detailed in Table 1.
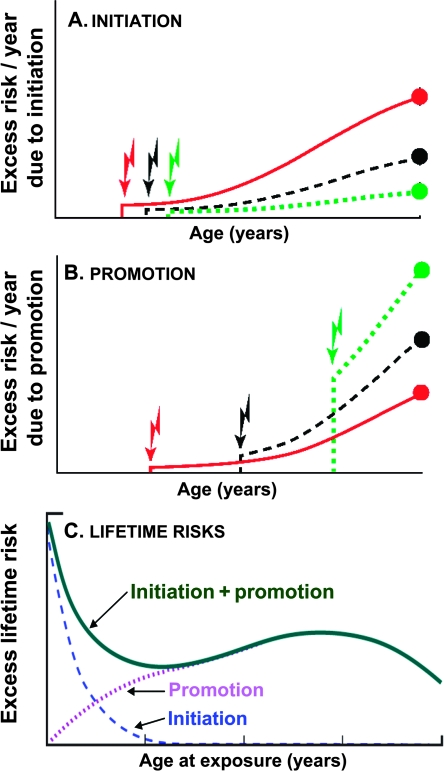
Patterns of radiation risk that do not decrease monotonically as a function of increasing age at exposure represent a challenge to our conceptual understanding of the mechanisms of cancer induction. From a mechanistic perspective, the commonly used biologically based models of carcinogenesis such as the Armitage–Doll model (24), the standard two-stage clonal expansion model (4), and multistage extensions of these models (25–27), all predict that ERRs should decrease continuously with increasing age of radiation exposure. This is because they essentially model the effects of radiation-induced initiation—the induction of irreversibly altered premalignant cells—that are frequently equated with a mutational event in a critical gene. As schematized in Figure 2, A, such initiation processes result in a predicted monotonic decrease in risk with increasing age at radiation exposure, because premalignant cells formed at earlier ages have longer times available to exploit their growth advantage during tumorigenesis, and also potentially through the more rapid cellular proliferation rates in children compared with adults (28).
Figure 2.
Schematic illustrating the dominant factors determining the variation in radiation-induced cancer risk with age at exposure. Jagged arrows indicate different times of radiation exposure, and the solid circles represent risks at a given attained age (eg, 80 years). A) Excess risk per year due to radiation initiation; for an exposure at a younger age, initiated cells have longer to exploit their growth advantage over normal cells. B) Excess risk per year due to radiation promotion; people irradiated at older ages, when there are more premalignant cells for promotion to act upon, are expected to have larger promotion-driven risks. C) Excess lifetime risks due to radiation-induced initiation and promotion. Initiation and promotion result in very different variations in cancer risk as a function of age at exposure; the downturn in excess lifetime risk shown in (C) for very old ages at exposure is due mainly to competing risks.
More recent biologically based models of radiation carcinogenesis (3,23,29,30) not only allow ionizing radiation to act as an initiator of premalignant clones but also consider ionizing radiation as a promoter of preexisting premalignant damage. Promotion is the process by which an initiated cell (radiation-induced initiation or otherwise) clonally expands, proportionately increasing the preexisting average number of premalignant stem cells per clone. As discussed above, initiation processes would be expected to result in decreasing excess lifetime cancer risks with increasing ages at exposure. By contrast, as illustrated in Figure 2, B, promotional processes can result in increasing excess lifetime cancer risks with increasing ages at exposure because the number of preexisting premalignant clones on which promotional processes can act increases with age (31). Overall, because initiation effects are expected to dominate radiation-induced premalignant clone production at younger ages at exposure, whereas promotional effects will dominate for older ages at exposure, a combination of these two effects would produce cancer risk patterns as a function of age at radiation exposure that are schematized in Figure 2, C.
In this study, we analyzed radiation-induced cancer risks as a function of age at radiation exposure of Japanese atomic bomb survivors (1,5,6). Because these data are prima facie inconsistent with a standard initiation-based model predicting monotonically decreasing radiation risks with increasing age at exposure (Figure 1), our primary goal was to assess whether these data are consistent with a model of radiation-induced cancer that includes both initiation and promotion (23,30) components (Figure 2). Then, we used such a combined model to estimate age-dependent lifetime radiation-induced cancer risks after adult radiation exposure and compared these risk estimates with those generated from standard empirical models in which radiation risks are constrained to decrease with increasing age at exposure.
Methods
Biological Model
A primary goal of this analysis was to assess whether an observed pattern of radiation-induced cancer risks that do not decrease monotonically with increasing age at exposure (see Figure 1) is biologically plausible. On basis of the considerations described above (Figure 2), we hypothesized that a sharp decrease in cancer risk with increasing age at childhood exposure, and a flatter dependence on age at exposure for adult exposures, could potentially be consistent with a model of radiation-induced cancer that includes both initiation and promotion components (23,30).
Multistage initiation and promotion models of carcinogenesis originated many decades ago in the field of chemical carcinogenesis (32–34). To apply these concepts to the Japanese atomic bomb survivor data, we have used a quantitative biologically motivated model of radiation carcinogenesis that has been described (30) and applied (23) previously. This approach emphasizes the different kinetics of radiation-induced initiation and promotion and tracks the yields of premalignant cells before, during, shortly after, and long after radiation exposure.
Brief details of the mathematical formalism are summarized in Appendix, and further details are available elsewhere (30). Briefly, the model integrates analyses of processes that operate during irradiation with those that operate on longer time scales before and after exposure. The model assumes that normal organ-specific stem cells, which reside in compartments generically called niches (35), can undergo initiation to a premalignant state, either spontaneously or by radiation, and can then undergo transformation into fully malignant cells that can eventually form tumors. Of importance here is that radiation is also assumed to have the potential to increase the mean number of premalignant cells per niche (ie, promotion). The model used here (30) tracks the average number of initiated niches filled with premalignant cells and the average number of premalignant cells per initiated niche. In earlier work (23), we have shown that this model can reproduce the main dose-dependent features of radiation-induced second cancers after radiotherapy.
Because our goal here was to analyze cancer risks after relatively low-dose radiation exposures, we did not consider the effects of cell killing, and this simplification resulted in a model with fewer parameters than typically required for high-dose (radiotherapy) applications. This simplified model has three parameters that characterize the age dependence of the background (ie, radiation-independent) cancer risk, and three parameters that together describe the short- and long-term radiation-induced modulations of these cancer risks.
The three background cancer risk parameters, which can be determined by the known age dependence of cancer incidence in the population of interest, describe spontaneous stem cell initiation and subsequent malignant transformation (parameter a), premalignant niche replication (parameter b), and effects of age on premalignant niches (parameter c), such as reduced proliferation rates, reduced background malignant transformation rates, and/or elevated death rates.
The three radiation-related parameters characterize the dose dependence of the initiation (parameter X) and promotion (parameter Y) processes and the homeostatic regulation of the number of premalignant stem cells per niche (parameter δ). Thus, the ratio X/Y, although not an independent parameter, characterizes the relative yield of radiation-induced premalignant cells produced through initiation vs promotion processes.
As in most such analyses, the lag period (L) from the appearance of the first fully malignant cell until the appearance of a cancer is fixed at a given time; here, the lag period was 10 years. Sensitivity analyses indicated that varying this value altered the best-fit parameter estimates somewhat, but did not markedly alter the quality of the model fit (23).
Analyzed Dataset
We analyzed ERRs of cancer incidence as a function of age at exposure within the Life Span Study cohort of the Japanese atomic bomb survivors (1,5,6). The data were estimated for an attained age of 80 years. The atomic bomb survivors have been studied extensively for many decades, both in terms of cancer incidence (1) and cancer mortality (2); the data that have been acquired serve as the principal source of quantitative information about radiation-induced carcinogenesis at low and intermediate radiation doses, in that these data are based on long-term follow-up of a large healthy population, including all ages and both sexes, that was exposed to a wide range of radiation doses. The ERR data analyzed here were for all solid cancers combined (all first primary malignant tumors excluding hematopoietic cancers) and, individually, for cancers of the liver, colon, lung, breast, stomach, and bladder. The six individual cancer sites were chosen as being the most common radiogenic solid cancer sites.
Model Fitting and Parameter Estimation
The model parameters that determine background cancer incidence (parameters a, b, and c) were estimated for each tumor type by fitting the model (equation 1, see Appendix) to cancer incidence data for Japanese atomic bomb survivors who received very low radiation doses (<5 mSv); these data, stratified by cancer type and age at exposure, were taken from Preston et al. (1). Fitting the data further stratified by attained age and sex (D. L. Preston, Hirosoft International Corporation, personal communication) made almost no difference in the parameter estimates. Fitting the model to the cancer incidence data was performed by using a random-restart simulated annealing algorithm (36). On the basis of earlier results (23), and to minimize the number of free parameters, the premalignant niche replication rate (b) was fixed at 0.2 y−1 for all analyzed cancers; this restriction did not substantially change the quality of the model fits.
The radiation-specific model parameters (δ, X, and Y) were estimated by fitting the model (equation 2, see Appendix) to the published ERR results (5,6) for the incidence of each selected tumor type in Japanese atomic bomb survivors at different ages of exposure (Tx). These ERRs were sex averaged (except that for female breast cancer), and normalized for an attained age of 80 years. We focused on the data for all malignant solid cancers combined, as well as for six individual tumor types that are known to be among the most radiogenic (ie, stomach, bladder, liver, breast, lung, and colon). On the basis of earlier results (23) and to further simplify the model, we fixed the parameter δ, which describes the homeostatic regulation of the number of premalignant stem cells per niche, to plausible values (0.00–0.05 y−1); this restriction did not change the quality of the model fits substantially.
Ninety-five percent confidence intervals (CIs) were generated for each of the four freely adjustable parameters (a, c, X, and Y) by fitting the model to multiple synthetic datasets produced by Monte Carlo simulation (37).
Radiation Risk Estimation in a Western Population as a Function of Age at Exposure
Finally, we used the model-fitted estimated age-dependent ERR results in atomic bomb survivors, along with sporadic (non–radiation related) cancer incidence data for the US population, to estimate absolute lifetime radiation-induced cancer risks per unit radiation dose in the US population, as a function of age at exposure. Our motivation was to compare these results with the corresponding risk estimates in which an increasing ERR with increasing age at exposure was not permitted as, for example, in the recent BEIR-VII report (14) of health risks after exposure to low doses of ionizing radiation.
Apart from this assumption made in the BEIR-VII report about radiation risks as a function of age at exposure, the datasets and methodologies used in the current analysis were largely the same as those used in the BEIR-VII risk estimates: Radiation risks were estimated in the US population based on modifying those in the atomic bomb survivors, typically by using a weighted average of 70% ERR and 30% excess absolute risk. For this calculation, the age-dependent survival function S(T) for the Japanese atomic bomb survivors was taken from Preston et al. (1), and the corresponding function for the US population was taken from standard US life tables (38). The background model parameters for the US population were estimated as previously described (23) by fitting equation 1 (see Appendix) to contemporary US cancer incidence data from the Surveillance, Epidemiology, and End Results database (39). Ninety-five percent confidence intervals for the resulting absolute radiation risk estimates were estimated using standard Monte Carlo techniques (37), which involve multiple sampling from the distribution of the model parameters.
Results
Model Fit to Age-Dependent Cancer Risks in Atomic Bomb Survivors
We first fit the ERR data (5,6) (Figure 1) for atomic bomb survivors, as a function of age at exposure, to the mechanistic model (23,30) summarized here. The results, also shown in Figure 1, indicated that the model can indeed provide a good description of the observed dependencies of radiation-induced cancer risk on age at exposure. This was the case both for all malignant solid cancers combined and for the six individual radiogenic cancers analyzed here.
The estimated parameter values and 95% confidence intervals are given in Table 1. The model includes only two radiation-related free parameters for each site, one characterizing the dose dependence of the radiation-induced initiation process (X), and the other representing the dose dependence of radiation-related promotional processes (Y). The absolute values of these two radiation-related parameters are of the same order as those estimated in an analysis of radiotherapy-induced second cancers (23). The ratio of these two parameters, X/Y, is a measure of the yield of premalignant cells produced by the two processes, initiation and promotion, and thus, the value of X/Y for different sites provides an insight into the relative importance of initiation vs promotion for different tumor sites. For example, for radiation-induced breast cancer, X/Y is approximately 35 years, indicating that initiation dominates promotion in terms of the radiation-associated production of premalignant clones, whereas for lung cancer, X/Y is approximately 3.5 years, indicating a more even balance between the two processes. These site-specific differences are reflected in the shape of the age–response curves shown in Figure 1: Thus, for example, radiation-induced breast cancer risks do monotonically decrease with age at exposure, indicating the dominance of initiation; by contrast, radiation-induced lung cancer risks do not monotonically decrease with increasing age at exposure, and, in fact, increase in middle age, reflecting the increased importance of promotion.
Table 1.
Fitted model parameter values in Japanese atomic bomb survivors*
| Cancer site | Background parameter |
Radiation parameter |
|||||
| a × 10−8, y−2 | b,† y−1 | c × 10−3, y−2 | X, y Gy−1 | Y, Gy−1 | X/Y‡, y | δ,† y−1 | |
| All solid cancers§ | 62.4 (4.98 to 116) | 0.2 | 1.11 (1.08 to 1.40) | 5.97 (3.07 to 8.78) | 1.04 (0.60 to 1.22) | 5.74 | 0.015 |
| Liver | 4.03 (2.56 to 5.91) | 0.2 | 0.99 (0.96 to 1.03) | 6.11 (2.92 to 7.82) | 2.13 (1.10 to 6.13) | 2.87 | 0.050 |
| Colon | 1.01 (0.79 to 1.63) | 0.2 | 0.73 (0.62 to 0.78) | 2.08 (0.14 to 2.86) | 0.874 (0.43 to 1.20) | 2.38 | 0.020 |
| Lung | 7.02 (4.21 to 11.5) | 0.2 | 1.04 (0.96 to 1.13) | 6.20 (0.21 to 8.47) | 1.73 (1.20 to 2.72) | 3.58 | 0.010 |
| Breast | 9.98 (6.12 to 17.1) | 0.2 | 1.29 (1.18 to 1.37) | 13.9 (4.27 to 16.4) | 0.396 (0.12 to 0.85) | 35.1 | 0.000 |
| Stomach | 24.8 (16.3 to 32.8) | 0.2 | 1.19 (1.11 to 1.24) | 10.4 (5.30 to 14.2) | 0.682 (0.13 to 1.86) | 15.2 | 0.050 |
| Bladder | 0.71 (0.53 to 1.46) | 0.2 | 0.95 (0.87 to 1.01) | 61.6 (49.1 to 108) | 5.22 (1.90 to 6.72) | 11.8 | 0.020 |
Values in parentheses are 95% confidence intervals. a = spontaneous stem cell initiation and subsequent malignant transformation; b = premalignant niche replication; c = stem cell aging; X = radiation initiation; Y = radiation promotion; δ = homeostatic regulation of the premalignant stem cell number per niche.
Parameters were restricted to certain values to simplify the model and enhance biological plausibility.
The ratio X/Y is shown for easier comparison of the balance between initiation and promotion balance at different cancer sites; this ratio is not an independent model parameter.
All first primary malignant tumors excluding hematopoietic cancers.
Radiation Risk Estimates in a Western Population as a Function of Age at Exposure
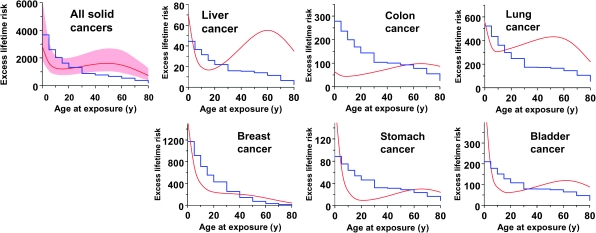
Using the methodology described above, we next used the model-fitted estimated age-dependent ERR results, along with sporadic cancer incidence data in the US population, to estimate absolute lifetime radiation-induced cancer risks per unit radiation dose in the US population, as a function of age at exposure. These estimates are shown in Figure 3 and Table 2. As in the BEIR-VII report (14), and to facilitate comparisons, all values were divided by a dose and dose-rate effectiveness factor of 1.5. Typical 95% confidence intervals for these estimates, based on Monte Carlo simulations, are also illustrated in Figure 3 for all solid cancers combined. The stepwise lines in Figure 3 represent the corresponding absolute lifetime radiation-induced cancer risk estimates taken from the 2007 National Academy of Sciences BEIR-VII report (14), which are largely derived from the same underlying atomic bomb survivor data as used here except that the BEIR-VII data analysis was constrained such that the ERRs could not increase with increasing age at exposure.
Figure 3.
Estimates of absolute lifetime radiation-induced cancer risks (per 0.1 Gy per 100 000 persons), as a function of age at exposure. The smooth curves, results of this analysis, are predicted absolute radiation-induced lifetime cancer risks in a US population as a function of age of exposure; the shaded band represents the 95% confidence intervals, estimated with Monte Carlo simulations described in the text. The stepwise lines represent estimates of the same absolute lifetime radiation-induced cancer risks taken from table 12D-1 of the Biological Effects of Ionizing Radiation-VII report (14); these latter estimates were based on analysis of essentially the same datasets as the current analysis, but with the constraint that the excess relative risk was not permitted to increase with increasing age at exposure.
Table 2.
Estimates of excess lifetime radiation-induced cancer risks in a US population*
| Cancer site | Age at radiation exposure, y |
||||||||||
| 0 | 5 | 10 | 15 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | |
| All sites | 2830 | 1650 | 1280 | 1200 | 1230 | 1390 | 1550 | 1610 | 1490 | 1160 | 737 |
| Liver | 70 | 32 | 20 | 17 | 18 | 27 | 39 | 60 | 55 | 49 | 35 |
| Colon | 64 | 47 | 44 | 47 | 51 | 62 | 75 | 87 | 96 | 97 | 87 |
| Lung | 565 | 336 | 311 | 320 | 335 | 372 | 408 | 431 | 416 | 340 | 220 |
| Breast | 1560 | 712 | 399 | 284 | 240 | 215 | 201 | 175 | 133 | 83 | 41 |
| Stomach | 191 | 67 | 26 | 13 | 10 | 12 | 17 | 24 | 29 | 29 | 24 |
| Bladder | 564 | 186 | 88 | 64 | 62 | 73 | 91 | 108 | 119 | 113 | 88 |
Risks are sex averaged (except for female breast cancer) and normalized for a dose of 0.1 Gy per 100 000 persons. As in the Biological Effects of Ionizing Radiation (BEIR)-VII report (14), and to facilitate comparisons, all values have been divided by a dose and dose rate effectiveness factor of 1.5. Graphical comparisons with the BEIR-VII predictions (which are based on analysis of essentially the same datasets, but with the constraint that the excess relative risks cannot decrease with increasing age at exposure) are given in Figure 3, and the corresponding BEIR-VII numerical data are in table 12D-1 of the BEIR-VII report (14).
It should be noted that the absolute radiation-associated excess cancer risk estimates shown by the curves in Figure 3 as a function of age at exposure have essentially the same shape as the relative risk curves for atomic bomb survivors shown in Figure 1. Thus, for example, the excess lifetime cancer risks for all solid cancers combined and for five of the six most radiogenic cancers (the exception being breast cancer) decreases with increasing age at radiation exposure through childhood and through to exposure at approximately age 20 years but then slowly increases for older ages at exposure up to approximately age 60 years. By contrast, the estimated excess lifetime risk of radiation-induced breast cancer decreases monotonically with increasing age at radiation exposure, as discussed above. As expected, the excess lifetime cancer risks for exposures at still older ages (>60 years) decreases (40), mainly because of competing risks.
Discussion
For individuals exposed to radiation in middle age, standard models and evaluations of radiological cancer risk (13,14) have suggested the patterns of risk observed for exposures in childhood and young adulthood, in which the excess cancer risks decrease with increasing age at exposure, are maintained for exposure in middle age. However, as discussed below, the weight of epidemiological evidence now suggests that, for adult exposures, radiation-induced cancer risks do not generally decrease with increasing age at exposure. Here we have investigated whether this pattern of radiation-induced cancer risks that do not decrease monotonically with increasing age at exposure, as observed in the atomic bomb survivors (see Figure 1), is biologically plausible. We have shown that a model of radiation-induced cancer that uses realistic parameters and includes both initiation and promotion components (23,30) can reproduce the observed dependencies of radiation-induced cancer risks as a function of age at exposure, both for individual cancers as well as for all cancers combined. This is because initiation, which dominates at younger ages, results in risks that decrease with increasing age at exposure, whereas promotion, which dominates at older exposure ages, does not (Figure 2). Thus, different balances between initiation and promotion (the ratio of parameters X and Y in Table 1) will produce different dependencies of radiation risk as a function of age at exposure.
We conclude that the observed patterns of radiation-induced cancer risks as a function of age of exposure are not consistent with standard models of radiation carcinogenesis in which radiation solely initiates premalignant cells but are consistent with models of radiation carcinogenesis that include both radiation-induced initiation and promotion. This conclusion is conceptually important because many commonly used biologically based models of radiation-induced carcinogenesis, such as various derivatives of the original Armitage–Doll model (24,27), describe only the initiating component of radiation carcinogenesis, and do not describe potential radiation-induced promotional effects. More recently, however, several investigators have also published mechanistically based models of radiation-induced carcinogenesis that consider, in effect, both radiation-induced initiation and promotion (3,29).
Our second goal was to use an initiation- and promotion-based model, with radiation parameters estimated from fitting the atomic bomb survivor ERR data, to generate absolute lifetime radiation-induced cancer risks per unit dose in the US population, as a function of age at exposure. The results, summarized in Figure 3, suggest that the radiation-related cancer risk for an exposure at, for example, age 50 years, could be twice as high as estimated using standard models in which radiation-induced cancer risks are constrained such that the ERRs cannot increase with increasing age at exposure.
Practically speaking, there could be considerable societal consequences if the excess lifetime cancer risks for radiation exposure in middle age are somewhat higher than previously estimated, for example, in the recent BEIR-VII (14) or International Commission on Radiological Protection (13) reports. The majority of the radiation exposures in the population, both medical and occupational radiation exposures, occur in individuals who are older than 30 years (41). The relevant regulatory occupational exposure limits for ionizing radiation are derived almost entirely from analyses of atomic bomb survivors who were exposed in adulthood (13,42–44). Thus, an increase in the best estimate of the excess lifetime cancer risk after radiation exposure in middle age might be reflected in a corresponding change in occupational radiation exposure limits. The practical implications of such a change would probably not be wide ranging because it is unusual for radiation workers to be exposed to doses close to the regulatory limits; however, there could be implications for those activities in which individuals are occasionally exposed to doses near these limits, such as for staff in interventional radiology facilities (45) or for some emergency responder scenarios (46).
A far more common source of radiation exposure in middle age is from diagnostic radiology (41). The medically related component of the US population exposure to ionizing radiation has increased sixfold in the past three decades (47), mostly because of the rapid increase in computerized tomography (CT) imaging (48). The most common ages at which individuals undergo CT examinations are approximately 35 to 50 years (49). When a CT scan is medically warranted, its benefits far outweigh any radiation risks, so that even increasing the estimated risks by a factor of 2 would not materially affect the risk–benefit balance (48). However, the risk–benefit balance is potentially relevant for CT-based screening of asymptomatic “healthy” adults. Specifically, routine CT screening of the colon (50,51), lung (52–55), and heart (56–58) are increasingly being advocated. Lung and cardiac CT screening are of particular relevance here because in both cases, the most important organ in terms of radiation risk is the lung, and we have shown here that there is good evidence (Figures 1 and 3) that the excess lifetime risks of lung cancer do not decrease in middle age and indeed may peak at around age 50 years, the most likely age for individuals to undergo CT screening.
This study has several limitations, the primary one being the statistical uncertainties associated with the underlying data (5,6) from the atomic bomb survivors (see error bars in Figure 1). As can be seen in Figure 1, because the data are stratified by age at exposure, the individual confidence intervals are quite wide, particularly when further stratification by cancer site is made. Little (6) has shown that the data for all solid cancer cancers combined, as shown in Figure 1, are inconsistent with an ERR that decreases monotonically with increasing age at exposure. Although data for cancer mortality are not analyzed here, similar empiric conclusions have been reached for the variation in radiation-induced cancer mortality with age at radiation exposure (6). The corresponding atomic bomb survivor data for individual cancer sites (Figure 1) did not reach statistical significance, which is not surprising given the decreased statistical power (6) but, as shown in Figure 1, the same trends, for adult exposure (radiation risks not monotonically decreasing with increasing age at adult exposure), were consistently seen for liver, colon, lung, stomach, and bladder, but not for breast cancer. A recently detailed analysis of combined radiation and smoking effects among atomic bomb survivors (59) strongly suggests that the observed increase in ERR with age at exposure for lung cancer is present irrespective of smoking status. This same pattern of increasing ERR with increasing age at adult exposure was seen in a large study of cancer risks in more than 400 000 radiation workers in the nuclear industry (30), where a lower ERR for all solid cancers was observed in workers exposed at ages 20–35 years compared with workers exposed at older ages (P = .09). This pattern of increasing ERR with increasing age at adult exposure was not, however, seen in a smaller study of cancer mortality in 20 000 radiation workers at the Russian Mayak nuclear complex (60), although a study of approximately 30 000 individuals exposed to protracted radioactive contamination from the Mayak complex (61) showed increased (P = .08) cancer mortality per unit dose with increasing age at first exposure. Overall, the weight of the epidemiological evidence suggests that for adult exposures, radiation risks do not generally decrease with increasing age at exposure, and the mechanistic underpinning described here provides this conclusion with some biological plausibility.
Another limitation is that although we have hypothesized that the risk patterns modeled here reflect the influence of promotion as well as initiation, other interpretations are possible. For example, the data may be consistent with an abrupt age-dependent increase in smoking and/or drinking patterns among survivors after the atomic bomb explosions; however, data for Japan as a whole do not show age-specific changes in smoking patterns in the immediate post–World War II period (62). There are also possible alternative biological interpretations of the data. For example, organ-specific stem cells might have greater sensitivity to radiogenic initiation and/or promotion in older individuals than in younger individuals. Alternatively, an increased cancer risk in middle age may be due to stimulation of tumor progression by radiation, for example, by activation of microscopic dormant tumors, which may accumulate in older individuals (as opposed to promotion of premalignant cells, as discussed here) (63). We do not, however, have any direct evidence for these alternative explanations, and alternative biological explanations consistent with the data shown in Figure 1 would not substantively affect the absolute age-dependent risks shown in Figure 3, nor would they change the societal implications of the increased radiation risks for adult exposure.
Funding
National Institutes of Health National Institute of Allergy and Infectious Diseases (U19-AI67773 to D.J.B.); NASA (NSCOR04-0014-0017/NNJ04HJ12G/NNJ06HA28G. to R.K.S.).
Appendix: Summary of the Mathematical Formalism
Based on the biological model summarized above, expressions for the background cancer risk have been derived (30) as a function of attained age (T), and also for the radiation-related cancer risk as a function of age at exposure (Tx) and time after exposure (Ty, such that T = Tx + Ty).
The age-dependent expected mean number of fully malignant cells per individual per unit time under background (ie, no additional radiation) conditions (Abac) is (30):
| [1] |
with the biological interpretation of the parameters a, b, and c as summarized above. Abac(T) is an estimate of the cancer incidence hazard function at time t + L, where L is the lag time.
The corresponding approximate risk expression for the radiation-related cancer risk (Arad) after a brief single low radiation dose (D) has the following form:
| [2] |
Thus, the ERR at a particular age at exposure Tx and time since exposure Ty is:
On the basis of these equations, estimates of the lifetime background cancer risk (B) and the cancer risk for irradiated individuals (R) are as follows:
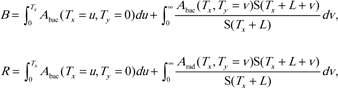 |
where S(T) is the probability for an individual in the given population to survive until age T. In the equations for both B and R, the first integral refers to the time before exposure, and the second integral refers to the time since exposure. Thus, the excess lifetime risks for radiation-induced cancer can be calculated as R minus B. It should be noted that these cancer risk estimates are not corrected for multiple cancers per person, for an accelerated onset of cancer in radiation-exposed compared with unexposed individuals, or for early death due to radiation-induced cancer. None of these effects are expected to be substantial at the low radiation doses considered here.
Footnotes
We are most grateful for helpful statistical and modeling advice from Drs Dale Preston and Mark Little. The study sponsors did not have any role in the design of the study, analysis or interpretation of the data, the writing of the article, or the decision to submit the article for publication.
References
- 1.Preston DL, Ron E, Tokuoka S, et al. Solid cancer incidence in atomic bomb survivors: 1958–1998. Radiat Res. 2007;168(1):1–64. doi: 10.1667/RR0763.1. [DOI] [PubMed] [Google Scholar]
- 2.Preston DL, Shimizu Y, Pierce DA, Suyama A, Mabuchi K. Studies of mortality of atomic bomb survivors. Report 13: Solid cancer and noncancer disease mortality: 1950–1997. Radiat Res. 2003;160(4):381–407. doi: 10.1667/rr3049. [DOI] [PubMed] [Google Scholar]
- 3.Heidenreich WF, Cullings HM, Funamoto S, Paretzke HG. Promoting action of radiation in the atomic bomb survivor carcinogenesis data? Radiat Res. 2007;168(6):750–756. doi: 10.1667/RR0919.1. [DOI] [PubMed] [Google Scholar]
- 4.Heidenreich WF, Luebeck EG, Hazelton WD, Paretzke HG, Moolgavkar SH. Multistage models and the incidence of cancer in the cohort of atomic bomb survivors. Radiat Res. 2002;158(5):607–614. doi: 10.1667/0033-7587(2002)158[0607:mmatio]2.0.co;2. [DOI] [PubMed] [Google Scholar]
- 5.Walsh L. Heterogeneity of variation of relative risk by age at exposure in the Japanese atomic bomb survivors. Radiat Environ Biophys. 2009;48(3):345–347. doi: 10.1007/s00411-009-0229-9. [DOI] [PubMed] [Google Scholar]
- 6.Little MP. Heterogeneity of variation of relative risk by age at exposure in the Japanese atomic bomb survivors. Radiat Environ Biophys. 2009;48(3):253–262. doi: 10.1007/s00411-009-0228-x. [DOI] [PubMed] [Google Scholar]
- 7.Cardis E, Kesminiene A, Ivanov V, et al. Risk of thyroid cancer after exposure to 131I in childhood. J Natl Cancer Inst. 2005;97(10):724–732. doi: 10.1093/jnci/dji129. [DOI] [PubMed] [Google Scholar]
- 8.Kleinerman RA. Cancer risks following diagnostic and therapeutic radiation exposure in children. Pediatr Radiol. 2006;36(suppl 2):121–125. doi: 10.1007/s00247-006-0191-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Little MP. Leukaemia following childhood radiation exposure in the Japanese atomic bomb survivors and in medically exposed groups. Radiat Prot Dosimetry. 2008;132(2):156–165. doi: 10.1093/rpd/ncn264. [DOI] [PubMed] [Google Scholar]
- 10.Preston DL, Cullings H, Suyama A, et al. Solid cancer incidence in atomic bomb survivors exposed in utero or as young children. J Natl Cancer Inst. 2008;100(6):428–436. doi: 10.1093/jnci/djn045. [DOI] [PubMed] [Google Scholar]
- 11.Ron E, Modan B. Benign and malignant thyroid neoplasms after childhood irradiation for tinea capitis. J Natl Cancer Inst. 1980;65(1):7–11. [PubMed] [Google Scholar]
- 12.Little MP, De Vathaire F, Charles MW, Hawkins MM, Muirhead CR. Variations with time and age in the risks of solid cancer incidence after radiation exposure in childhood. Stat Med. 1998;17(12):1341–1355. doi: 10.1002/(sici)1097-0258(19980630)17:12<1341::aid-sim852>3.0.co;2-6. [DOI] [PubMed] [Google Scholar]
- 13.ICRP. International Commission on Radiological Protection (ICRP) Publication 103: Recommendations of the ICRP. Washington, DC: Elsevier; 2007. [DOI] [PubMed] [Google Scholar]
- 14.BEIR. BEIR VII Report. Health risks from exposure to low levels of ionizing radiation. BEIR VII Report, Phase 2. Washington, DC: The National Academic Press; 2005. [PubMed] [Google Scholar]
- 15.Boice JD, Jr, Blettner M, Kleinerman RA, et al. Radiation dose and leukemia risk in patients treated for cancer of the cervix. J Natl Cancer Inst. 1987;79(6):1295–1311. [PubMed] [Google Scholar]
- 16.Boice JD, Jr, Engholm G, Kleinerman RA, et al. Radiation dose and second cancer risk in patients treated for cancer of the cervix. Radiat Res. 1988;116(1):3–55. [PubMed] [Google Scholar]
- 17.Boice JD, Jr, Lubin JH. Occupational and environmental radiation and cancer. Cancer Causes Control. 1997;8(3):309–322. doi: 10.1023/a:1018496919324. [DOI] [PubMed] [Google Scholar]
- 18.Chaturvedi AK, Engels EA, Gilbert ES, et al. Second cancers among 104,760 survivors of cervical cancer: evaluation of long-term risk. J Natl Cancer Inst. 2007;99(21):1634–1643. doi: 10.1093/jnci/djm201. [DOI] [PubMed] [Google Scholar]
- 19.Travis LB, Andersson M, Gospodarowicz M, et al. Treatment-associated leukemia following testicular cancer. J Natl Cancer Inst. 2000;92(14):1165–1171. doi: 10.1093/jnci/92.14.1165. [DOI] [PubMed] [Google Scholar]
- 20.Travis LB, Curtis RE, Boice JD, Jr, Platz CE, Hankey BF, Fraumeni JF., Jr Second malignant neoplasms among long-term survivors of ovarian cancer. Cancer Res. 1996;56(7):1564–1570. [PubMed] [Google Scholar]
- 21.Travis LB, Fossa SD, Schonfeld SJ, et al. Second cancers among 40,576 testicular cancer patients: focus on long-term survivors. J Natl Cancer Inst. 2005;97(18):1354–1365. doi: 10.1093/jnci/dji278. [DOI] [PubMed] [Google Scholar]
- 22.Travis LB, Hill DA, Dores GM, et al. Breast cancer following radiotherapy and chemotherapy among young women with Hodgkin disease. JAMA. 2003;290(4):465–475. doi: 10.1001/jama.290.4.465. [DOI] [PubMed] [Google Scholar]
- 23.Shuryak I, Hahnfeldt P, Hlatky L, Sachs RK, Brenner DJ. A new view of radiation-induced cancer: integrating short- and long-term processes. Part II: second cancer risk estimation. Radiat Environ Biophys. 2009;48(3):275–286. doi: 10.1007/s00411-009-0231-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Armitage P, Doll R. The age distribution of cancer and a multi-stage theory of carcinogenesis. Br J Cancer. 1954;8(1):1–12. doi: 10.1038/bjc.1954.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Little MP, Li G. Stochastic modelling of colon cancer: is there a role for genomic instability? Carcinogenesis. 2007;28(2):479–487. doi: 10.1093/carcin/bgl173. [DOI] [PubMed] [Google Scholar]
- 26.Little MP, Wright EG. A stochastic carcinogenesis model incorporating genomic instability fitted to colon cancer data. Math Biosci. 2003;183(2):111–134. doi: 10.1016/s0025-5564(03)00040-3. [DOI] [PubMed] [Google Scholar]
- 27.Pierce DA, Vaeth M. Age-time patterns of cancer to be anticipated from exposure to general mutagens. Biostatistics. 2003;4(2):231–248. doi: 10.1093/biostatistics/4.2.231. [DOI] [PubMed] [Google Scholar]
- 28.Chang M, Parker EA, Muller TJ, et al. Changes in cell-cycle kinetics responsible for limiting somatic growth in mice. Pediatr Res. 2008;64(3):240–245. doi: 10.1203/PDR.0b013e318180e47a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Curtis SB, Luebeck EG, Hazelton WD, Moolgavkar SH. The role of promotion in carcinogenesis from protracted high-LET exposure. Phys Med. 2001;17(suppl 1):157–160. [PubMed] [Google Scholar]
- 30.Shuryak I, Hahnfeldt P, Hlatky L, Sachs RK, Brenner DJ. A new view of radiation-induced cancer: integrating short- and long-term processes. Part I: approach. Radiat Environ Biophys. 2009;48(3):263–274. doi: 10.1007/s00411-009-0230-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Anisimov VN. Biology of aging and cancer. Cancer Control. 2007;14(1):23–31. doi: 10.1177/107327480701400104. [DOI] [PubMed] [Google Scholar]
- 32.Rous P, Kidd JG. Conditional neoplasms and subthreshold neoplastic states: a study of the tar tumors of rabbits. J Exp Med. 1941;73(3):365–390. doi: 10.1084/jem.73.3.365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Berenblum I, Shubik P. A new, quantitative, approach to the study of the stages of chemical carcinogenesis in the mouse skin. Br J Cancer. 1947;1(4):383–391. doi: 10.1038/bjc.1947.36. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Barrett JC. Mechanisms of multistep carcinogenesis and carcinogen risk assessment. Environ Health Perspect. 1993;100:9–20. doi: 10.1289/ehp.931009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Li L, Neaves WB. Normal stem cells and cancer stem cells: the niche matters. Cancer Res. 2006;66(9):4553–4557. doi: 10.1158/0008-5472.CAN-05-3986. [DOI] [PubMed] [Google Scholar]
- 36.Kirkpatrick S, Gelatt CD, Vecchi MP. Optimization by simulated annealing. Science. 1983;220(4598):671–680. doi: 10.1126/science.220.4598.671. [DOI] [PubMed] [Google Scholar]
- 37.Press WH, Flannery BF, Teukolsky SA, Vetterling WT. Numerical Recipes: The Art of Scientific Computing. Cambridge: Cambridge University Press; 1986. [Google Scholar]
- 38.Arias E. United States life tables, 2004. Natl Vital Stat Rep. 2007;56(9):1–39. [PubMed] [Google Scholar]
- 39.Horner MJ, Ries LAG, Krapcho M, et al. SEER Cancer Statistics Review, 1975–2006. Bethesda, MD: National Cancer Institute; 2009. seer.cancer.gov/csr/1975_2006. [Google Scholar]
- 40.Hincal E. Mathematical models for human cancer incidence rates: application to results from Europe, including North Cyprus. Asian Pac J Cancer Prev. 2009;10(2):325–335. [PubMed] [Google Scholar]
- 41.NCRP. Ionizing Radiation Exposure of the Population of the United States. NCRP Report 160. Washington, DC: The National Academic Press; 2009. [Google Scholar]
- 42.ICRP. International Commission on Radiological Protection (ICRP) Publication 75: Recommendations of the ICRP. General Principles for the Radiation Protection of Workers. Washington, DC: Elsevier; 1997. [Google Scholar]
- 43.UNSCEAR. United Nations Scientific Committee on the Effects of Atomic Radiation: Effects of ionizing radiation. New York, NY: United Nations Publication; 2006. [Google Scholar]
- 44.NCRP. Risk Estimates for Radiation Protection. NCRP Report 115. Washington, DC: The National Academic Press; 1993. [Google Scholar]
- 45.Hausler U, Czarwinski R, Brix G. Radiation exposure of medical staff from interventional x-ray procedures: a multicentre study. Eur Radiol. 2009;19(8):2000–2008. doi: 10.1007/s00330-009-1388-4. [DOI] [PubMed] [Google Scholar]
- 46.Kitchen RH, Hendee EG, Orton CG. Point/counterpoint. Exposure limits for emergency responders should be the same as the prevailing limits for occupational radiation workers. Med Phys. 2008;35(1):1–3. doi: 10.1118/1.2815355. [DOI] [PubMed] [Google Scholar]
- 47.Mettler FA, Jr, Bhargavan M, Faulkner K, et al. Radiologic and nuclear medicine studies in the United States and worldwide: frequency, radiation dose, and comparison with other radiation sources—1950–2007. Radiology. 2009;253(2):520–531. doi: 10.1148/radiol.2532082010. [DOI] [PubMed] [Google Scholar]
- 48.Brenner DJ, Hall EJ. Computed tomography—an increasing source of radiation exposure. N Engl J Med. 2007;357(22):2277–2284. doi: 10.1056/NEJMra072149. [DOI] [PubMed] [Google Scholar]
- 49.Mettler FA, Jr, Wiest PW, Locken JA, Kelsey CA. CT scanning: patterns of use and dose. J Radiol Prot. 2000;20(4):353–359. doi: 10.1088/0952-4746/20/4/301. [DOI] [PubMed] [Google Scholar]
- 50.Brenner DJ, Georgsson MA. Mass screening with CT colonography: should the radiation exposure be of concern? Gastroenterology. 2005;129(1):328–337. doi: 10.1053/j.gastro.2005.05.021. [DOI] [PubMed] [Google Scholar]
- 51.Pickhardt PJ, Kim DH. Colorectal cancer screening with CT colonography: key concepts regarding polyp prevalence, size, histology, morphology, and natural history. AJR Am J Roentgenol. 2009;193(1):40–46. doi: 10.2214/AJR.08.1709. [DOI] [PubMed] [Google Scholar]
- 52.Bach PB, Jett JR, Pastorino U, Tockman MS, Swensen SJ, Begg CB. Computed tomography screening and lung cancer outcomes. JAMA. 2007;297(9):953–961. doi: 10.1001/jama.297.9.953. [DOI] [PubMed] [Google Scholar]
- 53.Brenner DJ. Radiation risks potentially associated with low-dose CT screening of adult smokers for lung cancer. Radiology. 2004;231(2):440–445. doi: 10.1148/radiol.2312030880. [DOI] [PubMed] [Google Scholar]
- 54.Gierada DS, Garg K, Nath H, Strollo DC, Fagerstrom RM, Ford MB. CT quality assurance in the lung screening study component of the National Lung Screening Trial: implications for multicenter imaging trials. AJR Am J Roentgenol. 2009;193(2):419–424. doi: 10.2214/AJR.08.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Henschke CI, Yankelevitz DF. CT screening for lung cancer: update 2007. Oncologist. 2008;13(1):65–78. doi: 10.1634/theoncologist.2007-0153. [DOI] [PubMed] [Google Scholar]
- 56.Hall EJ, Brenner DJ. Cancer risks from diagnostic radiology. Br J Radiol. 2008;81(965):362–378. doi: 10.1259/bjr/01948454. [DOI] [PubMed] [Google Scholar]
- 57.Kim KP, Einstein AJ. Berrington de Gonzalez A. Coronary artery calcification screening: estimated radiation dose and cancer risk. Arch Intern Med. 2009;169(13):1188–1194. doi: 10.1001/archinternmed.2009.162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Waugh N, Black C, Walker S, McIntyre L, Cummins E, Hillis G. The effectiveness and cost-effectiveness of computed tomography screening for coronary artery disease: systematic review. Health Technol Assess. 2006 doi: 10.3310/hta10390. 10(39):iii–iv, ix–x, 1–41. [DOI] [PubMed] [Google Scholar]
- 59.Furukawa K, Preston DL, Loenn S, et al. Radiation and smoking effects on lung cancer incidence among atomic bomb survivors. Radiat Res. 2010;174(1):72–82. doi: 10.1667/RR2083.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Shilnikova NS, Preston DL, Ron E, et al. Cancer mortality risk among workers at the Mayak nuclear complex. Radiat Res. 2003;159(6):787–798. doi: 10.1667/0033-7587(2003)159[0787:cmrawa]2.0.co;2. [DOI] [PubMed] [Google Scholar]
- 61.Krestinina LY, Preston DL, Ostroumova EV, et al. Protracted radiation exposure and cancer mortality in the Techa River Cohort. Radiat Res. 2005;164(5):602–611. doi: 10.1667/rr3452.1. [DOI] [PubMed] [Google Scholar]
- 62.Marugame T, Kamo K, Sobue T, et al. Trends in smoking by birth cohorts born between 1900 and 1977 in Japan. Prev Med. 2006;42(2):120–127. doi: 10.1016/j.ypmed.2005.09.009. [DOI] [PubMed] [Google Scholar]
- 63.Fakir H, Tan WY, Hlatky L, Hahnfeldt P, Sachs RK. Stochastic population dynamic effects for lung cancer progression. Radiat Res. 2009;172(3):383–393. doi: 10.1667/RR1621.1. [DOI] [PubMed] [Google Scholar]